| Issue |
A&A
Volume 570, October 2014
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 3 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201424357 | |
| Published online | 06 October 2014 | |
Research Note
The applicability of the wind compression model
Astronomical Institute, Slovak Academy of Sciences 059 60 Tatranská Lomnica Slovakia
e-mail:
zcarikova@ta3.sk
Received: 9 June 2014
Accepted: 22 August 2014
Compression of the stellar winds from rapidly rotating hot stars is described by the wind compression model. However, it was also shown that rapid rotation leads to rotational distortion of the stellar surface, resulting in the appearance of non-radial forces acting against the wind compression. In this note we justify the wind compression model for moderately rotating white dwarfs and slowly rotating giants. The former could be conducive to understanding density/ionization structure of the mass outflow from symbiotic stars and novae, while the latter can represent an effective mass-transfer mode in the wide interacting binaries.
Key words: stars: activity / stars: winds, outflows
© ESO, 2014
1. Introduction
Rotation of the hot stars with radiation-driven winds leads to compression of the outflowing material towards the equatorial regions. The mechanism is described by the wind compression model developed by Bjorkman & Cassinelli (1993). Because of conservation of the angular momentum vector, each particle launched at the surface of the star has to move in its own orbital plane, which is perpendicular to this vector. The streamlines of the gas from both hemispheres of a rotating wind are bent towards the equatorial plane. As a result the wind is compressed towards equatorial regions of the star. Two forms of the equatorial density enhancements can be recognized: (i) if the flow from the hemispheres has a supersonic component of the velocity perpendicular to the equatorial plane, a shock zone or disk will develop and we get the wind-compressed disk (WCD) model elaborated by Bjorkman & Cassinelli (1993); and (ii) if the streamlines do not cross the equatorial plane of the star we get the wind-compressed zone (WCZ) model described by Ignace et al. (1996).
However, following studies on the mass loss from the oblate stellar surface, caused by a rapid rotation of the star, showed the presence of inverse effects inhibiting the equatorial wind compression. Cranmer & Owocki (1995) investigated the effect of oblateness and gravity darkening on the radiation driving in winds from rapidly rotating Be stars. They revealed the presence of non-radial radiative driving, directed away from the equatorial plane and acting against the sense of rotation. These effects thus weaken the equatorward wind compression compared to wind models calculated for spherical stars. Inhibition of the WCD formation was also confirmed by radiation-hydrodynamical simulations of Owocki et al. (1996), who showed that these non-radial forces can lead to an effective suppression of the equatorward flow needed to form a WCD.
An interesting effect of the rotational distortion of the star is gravity darkening. According to the von Zeipel theorem, the surface radiative flux is proportional to the local effective gravity, F ∝ geff, which is reduced at the equator. Since the poles of the star have a higher geff, they also have a higher temperature Teff (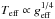 ) and thus higher brightness F. On the other hand, the equatorial regions of the star have a lower geff and thus also a lower brightness F (called gravity darkening). As a result, the gravity darkening reduces the mass loss rate from equatorial regions and strengthens it toward the relatively bright poles of rapidly rotating Be stars (Owocki et al. 1996, 1998).
) and thus higher brightness F. On the other hand, the equatorial regions of the star have a lower geff and thus also a lower brightness F (called gravity darkening). As a result, the gravity darkening reduces the mass loss rate from equatorial regions and strengthens it toward the relatively bright poles of rapidly rotating Be stars (Owocki et al. 1996, 1998).
In this contribution we justify applicability of the wind compression model to other rotating stellar objects, whose observational phenomena could be understood within this model. In particular, to (i) white dwarfs (WDs) in symbiotic binaries and cataclysmic variables, whose presumable moderate rotation could influence the shaping of their mass outflow during outbursts; and (ii) slowly rotating red giants (RGs) in wide interacting binaries, where the wind compression towards the equatorial plane can significantly enhance the accretion from the wind of the giant by its compact companion. In Sect. 2 we introduce distortion of the stellar surface due to rotation; Sect. 3 gives examples of such flattening for a rapidly rotating Be star, moderately rotating WD, and slowly rotating RG. A brief discussion and conclusion are found in Sects. 4 and 5, respectively.
2. Rotational distortion of the stellar surface
Rotation of a star leads to a distortion of its surface. The shape of the star, i.e. the latitude dependence of the stellar radius R(θ), where θ is the stellar co-latitude with θ = 0 at the pole of the star, is determined by the equipotential surfaces. For the rigid rotation, the ratio R(θ) to its value at the equator, Req, can be expressed as (see Kraus 2006) 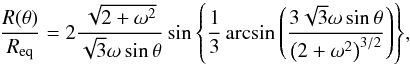 (1)where the limit for θ = 0 yields the ratio
(1)where the limit for θ = 0 yields the ratio 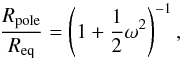 (2)where the polar radius Rpole = R(θ = 0), ω = vrot/vcrit, and vrot is the equatorial rotation velocity of the star. The critical velocity vcrit can be written as
(2)where the polar radius Rpole = R(θ = 0), ω = vrot/vcrit, and vrot is the equatorial rotation velocity of the star. The critical velocity vcrit can be written as 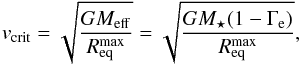 (3)where G is the gravitational constant,
(3)where G is the gravitational constant, 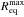 is the maximum equatorial radius when the star is rotating at the critical velocity (i.e. for ω = 1), and Meff is the effective stellar mass, i.e. the stellar mass reduced by the effects of radiation pressure due to electron scattering. It is defined as Meff = M⋆(1 − Γe), where M⋆ is the mass of the star and Γe is the Eddington factor. For a non-rotating star, Γe is the ratio of the stellar luminosity L⋆ to the Eddington luminosity LEdd, i.e. Γe = L⋆/LEdd. The Eddington luminosity is given by
is the maximum equatorial radius when the star is rotating at the critical velocity (i.e. for ω = 1), and Meff is the effective stellar mass, i.e. the stellar mass reduced by the effects of radiation pressure due to electron scattering. It is defined as Meff = M⋆(1 − Γe), where M⋆ is the mass of the star and Γe is the Eddington factor. For a non-rotating star, Γe is the ratio of the stellar luminosity L⋆ to the Eddington luminosity LEdd, i.e. Γe = L⋆/LEdd. The Eddington luminosity is given by 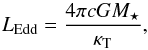 (4)where c is the speed of the light, and κT is the electron scattering opacity per unit mass, which depends on the chemical composition of the wind and the degree of ionization. For example, κT ~ 0.30 cm2 g-1 for the winds of hot stars (Lamers & Cassinelli 1999).
(4)where c is the speed of the light, and κT is the electron scattering opacity per unit mass, which depends on the chemical composition of the wind and the degree of ionization. For example, κT ~ 0.30 cm2 g-1 for the winds of hot stars (Lamers & Cassinelli 1999).
According to Maeder & Meynet (2000) relation (3) with a general Γ (i.e. including total opacity, not only electron opacity) is true if we assume that the brightness of the rotating star is uniform over its surface, which is in contradiction to the von Zeipel theorem. In rotating stars the effective gravity and the flux vary over the stellar surface (Sect. 1). Therefore, we have to consider the local Eddington factors Γ (Maeder 1999). Maeder & Meynet (2000) showed that the correct Eddington factors in a rotating star depend on the rotation. As a consequence, the maximum possible stellar luminosity is reduced by rotation. The critical velocity has a different expression depending on the luminosity of the star. If the Eddington factor Γ < 0.639, the critical velocity is independent of the Eddington factor and is given by the classical expression (e.g. Puls et al. 2008)
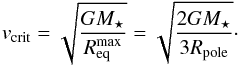 (5)Physically, this means that when the luminosity of the star is sufficiently below the Eddington limit, the reduction of the effective mass by the rotation is not so important and the classical Eq. (5) can be used. For Γ > 0.639, the critical velocity is significantly reduced by the proximity to the Eddington limit. When the Eddington factor Γ tends towards 1, the critical velocity tends to 0 (for more details see Maeder & Meynet 2000).
(5)Physically, this means that when the luminosity of the star is sufficiently below the Eddington limit, the reduction of the effective mass by the rotation is not so important and the classical Eq. (5) can be used. For Γ > 0.639, the critical velocity is significantly reduced by the proximity to the Eddington limit. When the Eddington factor Γ tends towards 1, the critical velocity tends to 0 (for more details see Maeder & Meynet 2000).
3. Examples of different types of rotating stars
In this section we compare the oblateness of a rapidly rotating Be star, rotating WD, and RG in symbiotic binaries. Table 1 introduces the ratio of the polar radius to the equatorial radius Rpole/Req calculated according to Eq. (2) for typical parameters of selected types of stars.
3.1. Rapidly rotating Be star
To study inhibition of the WCD formation by non-radial line forces in rotating hot star winds, Owocki et al. (1996) chose model S350 by Owocki et al. (1994) as a representative Be star model: vrot = 350 km s-1, M⋆ = 7.5 M⊙, Rpole = 4 R⊙ (at the critical velocity 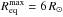 ), and L⋆ = 2 310 L⊙. Equation (3) gives vcrit = 487 km s-1 (the Eddington factor Γe = 0.007), while the classical expression Eq. (5) yields vcrit = 488 km s-1. Thus, according to Eq. (2) the ratio of the polar to the equatorial radius Rpole/Req ~ 0.794. As was shown by Owocki et al. (1994), the wind particles emitted by such a flattened stellar surface cannot form the WCD or WCZ.
), and L⋆ = 2 310 L⊙. Equation (3) gives vcrit = 487 km s-1 (the Eddington factor Γe = 0.007), while the classical expression Eq. (5) yields vcrit = 488 km s-1. Thus, according to Eq. (2) the ratio of the polar to the equatorial radius Rpole/Req ~ 0.794. As was shown by Owocki et al. (1994), the wind particles emitted by such a flattened stellar surface cannot form the WCD or WCZ.
3.2. Moderately rotating WD
Here we consider a typical WD in symbiotic binary with vrot = 300 km s-1 (Cariková & Skopal 2012), M⋆ = 1 M⊙ , Rpole = 0.01 R⊙, L⋆ = 1000 L⊙. Then vcrit = 3520 km s-1 (Γe = 0.023) or vcrit = 3560 km s-1 according to Eq. (3) or Eq. (5), respectively. This corresponds to the ratio Rpole/Req ~ 0.996. During active phases the luminosity of the WDs can increase to ~104L⊙. However, the Eddington factor Γe would be still lower than 0.639, so the classical expression for the critical velocity given by Eq. (5) can be used. Thus, in the case of rotating WDs the effects of the stellar surface distortion to inhibition of the wind compression to the equatorial plane will probably be negligible. An application of the WCZ model to moderately rotating WDs in symbiotic binaries was recently suggested by Cariková & Skopal (2012).
3.3. Slowly rotating RG
According to Zamanov et al. (2008), the median vrotsini for M0-M6 giants in symbiotic binaries is ~8 km s-1. Thus we adopt vrot = 8 km s-1, M⋆ = 1 M⊙ , Rpole = 100 R⊙ (e.g. van Belle et al. 1999), L⋆ = 1600 L⊙ (e.g. Skopal 2005). Then Eqs. (3) and (5) yield vcrit = 35 km s-1 (Γe = 0.037) and 36 km s-1, respectively. According to Eq. (2) the flattening ratio Rpole/Req ~ 0.975. This result suggests that the equatorward compression of wind particles emitted by the surface of a slowly rotating RG can be expected (see Sect. 4).
Ratio Rpole/Req for a Be star, WD, and RG and possible applicability of the WCZ model (Sect. 3).
4. Discussion
The above mentioned examples suggest that we can eliminate the problem with the distortion of the stellar surface of rapidly rotating hot stars for compact objects (e.g. WDs), which cannot be easily deformed at moderate rotational velocities, and/or objects rotating slowly (e.g. RGs).
Recently, we applied the wind compression model to the WDs in symbiotic binaries (Cariková & Skopal 2012). We calculated the WCZ formation of their enhanced winds during active phases and the corresponding ionization structure. Both the geometrical and ionization properties of our models were consistent with those derived from observations. In this way we justified the applicability of the wind compression model to WDs in symbiotic binaries.
In the light of the above mentioned case, the observed non-spherical structure of the ejected material during the nova event (see e.g. the recent summarization by Shore 2013) could also have an origin in the rotation of a WD, from whose surface the accumulated material is ejected. This possibility was investigated for the first time by Ignace et al. (1996). They found that the wind compression model may have relevance for slow novae, which tend to maintain winds with low terminal speeds of a few hundred km s-1 throughout their outbursts. Recently, the observed evolution of the biconical ionization structure of fast novae V339 Del (v∞ ~ 2700 km s-1) and RS Oph (v∞ ~ 4000 km s-1) was also possible to interpret qualitatively in terms of the WCZ model (see Skopal et al. 2014; Skopal 2014). However, a theoretical application of the WCZ model to the fast nova mass outflow is needed to test this interpretation.
As the flattening ratio for RGs in symbiotic binaries is comparable with that of their WDs (Table 1), one can assume that the inhibition of the WCZ (or WCD) formation will also be negligible for the slowly rotating RGs. Here, the major astrophysical consequence is a possible increase in the wind mass transfer efficiency in wide interacting binaries containing an evolved star, which could be an alternative to gravitationally focused wind accretion (see de Val-Borro et al. 2009; Mohamed & Podsiadlowski 2012). A particular application of the WCZ model to evolved giants was introduced by Ignace et al. (1996), who calculated a density contrast between the equator and pole as a function of the rotation rate ω = vrot/vcrit and the parameter β, which characterizes the wind acceleration. For comparison, a slow wind of RGs with β = 2.5 (Schröder 1985) and ω = 0.23 (Sect. 3.3) imply the density contrast of ~9 (see Fig. 3 for asymptotic giant branch stars in Ignace et al. 1996), which suggests a significant effect of the wind compression. A detailed application of the WCZ model to stellar winds of normal giants in S-type symbiotic stars is presented in our following paper (Skopal & Cariková 2014).
5. Conclusion
Previous work of Cranmer & Owocki (1995) and Owocki et al. (1996) demonstrated that a strong stellar surface distortion of the rapidly rotating Be stars causes the appearance of non-radial line forces and the effect of gravity darkening that effectively suppress the equatorward flow needed to form a WCD.
In this note we investigated the possibility of applying the wind compression model to moderately rotating WDs in interacting binaries, e.g. symbiotic stars, and to slowly rotating RGs in wide interacting binaries. We determined the rotational flattening ratio Rpole/Req ~ 0.794, 0.996, and 0.975 for parameters of a typical Be star, WD, and RG in a symbiotic binary, respectively. Applicability of the WCZ formation to WDs in symbiotic stars was already demonstrated by Cariková & Skopal (2012). Consequently, the very small distortion of slowly rotating RGs in symbiotic stars, which is comparable to that of their WDs, suggests that the wind compression model can also be applied to the slowly rotating RGs in wide interacting binaries.
The first case can be used in modelling the structure of the enhanced mass outflow (wind) from WDs during outbursts of symbiotic stars and/or novae, while the second case can be used to model a very efficient wind mass transfer from a giant to its WD companion as indicated in wide interacting binaries.
Acknowledgments
The authors thank the anonymous referee for constructive comments. Daniela Korc˘áková is thanked for discussions. This project was supported by the Slovak Academy of Sciences under grant VEGA No. 2/0002/13.
References
- Bjorkman, J. E., & Cassinelli, J. P. 1993, ApJ, 409, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Cariková, Z., & Skopal, A. 2012, A&A, 548, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cranmer, S. R., & Owocki, S. P. 1995, ApJ, 440, 308 [NASA ADS] [CrossRef] [Google Scholar]
- de Val-Borro, M., Karovska, M., & Sasselov, D. 2009, ApJ, 700, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Ignace, R., Cassinelli, J. P., & Bjorkman, J. E. 1996, ApJ, 459, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, M. 2006, A&A, 456, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamers, H. J. G. L. M., & Cassinelli, J. P. 1999, Introduction to stellar winds (Cambridge University Press) [Google Scholar]
- Maeder, A. 1999, A&A, 347, 185 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 2000, A&A, 361, 159 [NASA ADS] [Google Scholar]
- Mohamed, S., & Podsiadlowski, Ph. 2012, Balt. Astron., 21, 88 [Google Scholar]
- Owocki, S. P., Cranmer, S. R., & Blondin, J. M. 1994, ApJ, 424, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., Cranmer, S. R., & Gayley, K. G. 1996, ApJ, 472, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., Gayley, K. G., & Cranmer, S. R. 1998 ASP Conf. Ser., 131, 237 [Google Scholar]
- Puls, J., Vink, J. S., & Najarro, F. 2008, A&ARv, 16, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shen, K. J., & Bildsten, L. 2007, ApJ, 660, 1444 [NASA ADS] [CrossRef] [Google Scholar]
- Schröder, K.-P. 1985, A&A, 147, 103 [NASA ADS] [Google Scholar]
- Shore, S. N. 2013, A&A, 559, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skopal, A. 2005, A&A, 440, 995 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skopal, A. 2014, New Astron., 34, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Skopal, A., & Cariková, Z. 2014, A&A, submitted [Google Scholar]
- Skopal, A., Drechsel, H., Tarasova, T. N., et al. 2014, A&A, in press, DOI: 10.1051/0004-6361/201424284 [Google Scholar]
- Tutukov, A. V., & Yungelson, L. R. 1976, Astrophysics, 12, 342 [NASA ADS] [CrossRef] [Google Scholar]
- van Belle, G. T., Lane, B. F., Thompson, R. R., et al. 1999, AJ, 117, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Zamanov, R. K., Bode, M. F., Melo, C. H. F., et al. 2008, MNRAS, 390, 377 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Ratio Rpole/Req for a Be star, WD, and RG and possible applicability of the WCZ model (Sect. 3).
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


