EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 568 (August 2014) A&A, 568 (2014) A104 Full HTML
Free Access
Issue
A&A
Volume 568, August 2014
Article Number A104
Number of page(s) 9
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201423960
Published online 29 August 2014

© ESO, 2014

1. Introduction

The rotation curves observed in galaxies are generally explained by a dominating contribution of dark matter (see e.g. the review by Sofue & Rubin 2001), but the nature of dark matter is still not known. Several ideas have been proposed in the literature that the Lorentz force could support the rotation of the gas and hence reduce the need for dark matter (Battaner & Florido 2000; Ruiz-Granados et al. 2010, 2012; Jałocha et al. 2012; Sánchez-Salcedo & Santillán 2013). This however requires Alfvén speeds of the order of 100 km s-1, and moreover a large radial extent of the magnetic field. Observed motions of stars or stellar clusters also favour gravitation for the support of gas rotation (Persic & Salucci 1993).

The increased amount and quality of radio continuum data enables a re-investigation of the role of magnetic fields for the rotation of gas in galaxies. From the radial scale lengths of synchrotron emission and the gas density scale length, the Alfvén speed and its radial profile can be computed. The contribution of magnetic forces to the gas rotation can be estimated for various profiles of the radial distribution of the magnetic field.

Magnetic fields in galaxies are mostly turbulent and are closely related to star-forming activity (Tabatabaei et al. 2013). The weaker regular fields show a coherent structure over kpc scales, which may be due to a mean-field αΩ dynamo (Beck et al. 1996; Gressel et al. 2008b,a). There is observational evidence that regular fields have larger radial scale lengths than turbulent fields because their amplification is not restricted to energy input from star formation. The action of the magneto-rotational instability (MRI) may be responsible for the field amplification in the outer parts (Sellwood & Balbus 1999). The field may appear more ordered because of a highly anti-parallel field connected to the channel modes (Elstner et al. 2009). As a consequence, the azimuthal and radial components of the regular field may contribute to magnetic forces in the outer parts of a galaxy.

The general concept is presented in Sect. 2. From radial profiles of the total and polarised synchrotron intensity we derive the magnetic field strength of the turbulent and regular magnetic components (Sect. 3). Together with gas density profiles we estimate the influence of the Lorentz force on the gas rotation (Sect. 4). Moreover, we use recent results from a hybrid dynamo simulation for a Milky Way-type galaxy (Gressel et al. 2013) to test our findings (Sect. 5). In this simulation, the classical αΩ description of the mean-field dynamo is complemented with a dynamically evolving disc model. This treatment allows for the development of magnetic instabilities, which occur on scales large enough not to be affected immediately by turbulent diffusion. One outcome of the simulation is a radial reversal in the magnetic field strength, which we show to be associated with a local modulation of the galactic rotation curve.

2. The Lorentz force in galactic discs

The radial component of the stationary momentum equation in cylindrical geometry is 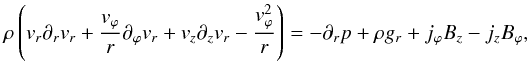ρ(vr∂rvr+vϕr∂ϕvr+vz∂zvr−vϕ2r)=−∂rp+ρgr+jϕBz−jzBϕ,\begin{equation} \rho \left( \vv_r \partial_{r} \vv_r + \frac{\vv_\varphi}{r} \partial_\varphi \vv_r + \vv_z \partial_z \vv_r - \frac{\vv_\varphi^2}{r} \right) = - \partial_r p + \rho g_r + j_\varphi B_z - j_z B_\varphi, \! \! \label{eq0} \end{equation}(1)where the last two terms represent the Lorentz force, j × B and ρgr the gravitational force. Neglecting the radial velocity in the above equation yields 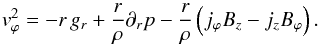vϕ2=−r gr+rρ∂rp−rρ(jϕBz−jzBϕ).\begin{equation} \vv_\varphi^2 = - r\,g_r + \frac{r}{\rho} \partial_r p - \frac{r}{\rho}\left(j_\varphi B_z - j_z B_\varphi\right). \label{eq0a} \end{equation}(2)In order to discuss the influence of the magnetic field on the circular rotation we define the magnetic rotation velocity as vmag2=1μρ[(∂rrBϕ−∂ϕBr)Bϕ−r(∂zBr−∂rBz)Bz],\begin{equation} \vv_{\rm mag}^{ 2 }=\frac { 1 }{ \mu \rho } \left[\left( \partial_{r} rB_{ \varphi } - \partial _{ \varphi }B_{ r } \right) B_{ \varphi } - r \left( \partial _{ z }B_{ r }- \partial _{ r }B_{ z } \right) B_{ z } \right], \label{eq1} \end{equation}(3)and the gravitational part, also including the small contribution of gas pressure vgrav2=−rgr+rρ∂rp.\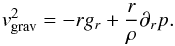begin{equation} \vv_{\rm grav}^2= - r g_r + \frac{r}{\rho} \partial_r p. \label{eq1a} \end{equation}(4)The gravitationally balanced rotation velocity is usually split into contributions from stellar and gaseous disc, bulge and dark matter, but we will not discuss the details of the individual gravitational effects here. The total circular velocity of the gas is given by 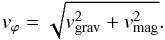vϕ=vgrav2+vmag2.\begin{equation} \vv_{ \varphi }=\sqrt{\vv_{\rm grav}^2+\vv_{\rm mag}^2}. \label{eq3} \end{equation}(5)We first consider a large-scale axisymmetric field with a negligible vertical field component, as typical for the regular magnetic field in the midplane of nearby galaxies (Beck & Wielebinski 2013). Then only the first term of the right-hand side of Eq. (3) has to be considered. For a power-law distribution of the magnetic field strength Bϕ = B0rn, we get 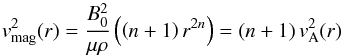vmag2(r)=B02μρ((n+1)r2n)=(n+1) vA2(r)\begin{equation} \vv_{\rm mag}^{ 2 }(r) = \frac { B_{ 0 }^{ 2 } }{ \mu \rho } \left( \left( n+1 \right) r^{ 2n } \right) = (n+1)\,\vv_{\rm A}^2(r) \label{eq2} \end{equation}(6)with the Alfvén speed vA ≡ Bϕ (μρ)− 1/2.

For a radial profile of the azimuthal field decaying slower than r-1, the Lorentz force acts inwards and needs to be balanced by the centrifugal force of the gas rotation, hence reducing the need for gravitational pull from dark matter. For a decay profile of the magnetic field steeper than r-1 the right hand side of Eq. (6) becomes negative, leading to a slower rotation than predicted by the balance of the centrifugal force with the gravitational force only, with the consequence that even more dark matter is needed than in the non-magnetic case.

The singularity of the r-1 profile at the origin can be avoided by an ansatz 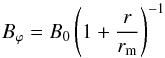Bϕ=B0(1+rrm)-1\begin{equation} B_{ \varphi }=B_{0} \left( 1+\frac{r}{r_{\rm m}} \right)^{-1} \label{eq3aa} \end{equation}(7)as used by Ruiz-Granados et al. (2012), leading to a magnetic velocity 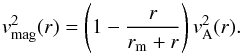vmag2(r)=(1−rrm+r)vA2(r).\begin{equation} \vv_{\rm mag}^{ 2 }(r) = \left(1- \frac{r}{r_{\rm m}+r} \right) v_{\rm A}^2(r). \label{eq3ab} \end{equation}(8)This more or less artificial approach always yields an inward directed force, because it is always flatter than a 1/r profile, which is unlikely because it corresponds to a vertical current with a single sign through the whole galactic disc. Dynamo-excited magnetic fields never show such configurations (Gressel et al. 2013).

The Alfvén velocity is an upper limit for the change of the rotation by the magnetic force for the above defined profiles. Typical values of 30 km s-1in the thin disc may affect the circular velocity of 200 km s-1only by 1%. The situation may be different in the very outer disc or in the halo where the Alfvén speed may be 150 km s-1or higher because of the density decrease in gas density. However, if the generally observed relation B ∝ ρ0.5 (Crutcher et al. 2010; Niklas & Beck 1997) also holds for the large-scale field in the outer disc, a constant Alfvén speed follows (see Sect. 3).

In accordance with exponential profiles of synchrotron emission, we assume an exponential profile for the regular magnetic field with scale length rm (see Sect. 3). Here we find 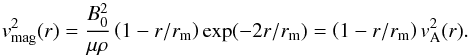vmag2(r)=B02μρ(1−r/rm)exp(−2r/rm)=(1−r/rm)vA2(r).\begin{equation} \vv_{\rm mag}^{ 2 }(r) = \frac { B_{ 0 }^{ 2 } }{ \mu \rho } \left(1-r/r_{\rm m} \right) \exp(-2r/r_{\rm m}) = \left(1-r/r_{\rm m} \right) v_{\rm A}^2(r). \label{eq3a} \end{equation}(9)Now the magnetic force is directed inwards (positive 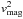vmag2\hbox{$\vv_{\rm mag}^2$}) only in the inner part r<rm. In the outer parts it acts outwards against the gravitational force. We note that the absolute value of the magnetic force increases already for a constant Alfvén speed. In this case the vertical current associated with the azimuthal magnetic field changes its sign at the scale length. 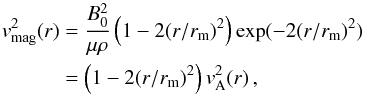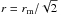The situation is quite similar for a Gaussian profile, vmag2(r)=B02μρ(1−2(r/rm)2)exp(−2(r/rm)2)=\begin{eqnarray} \vv_{\rm mag}^{ 2 }(r) &=& \frac { B_{ 0 }^{ 2 } }{ \mu \rho } \left(1-2 (r/r_{\rm m})^2 \right) \exp(-2(r/r_{\rm m})^2) \nonumber \\ &=& \left(1-2 (r/r_{\rm m})^2 \right)\vv_{\rm A}^2(r) \, , \label{eq3b} \end{eqnarray}(10)where the sign of the magnetic force changes at r=rm/2\hbox{$r=r_{\rm m}/\sqrt{2}$}.

We now consider magnetic fields also including radial and vertical fields. Rewriting Eq. (3) using div(B) = 0, we obtain 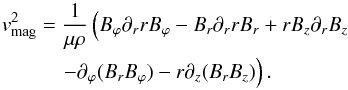vmag2=1μρ(Bϕ∂rrBϕ−Br∂rrBr+rBz∂rBz\begin{eqnarray} \vv_{\rm mag}^{ 2 }&=&\frac { 1 }{ \mu \rho } \left( B_{\varphi}\partial _{r} rB_{\varphi} - B_{ r }\partial _{r}rB_{r} + rB_{z}\partial_{r}B_{z} \right.\nonumber \\ && \quad \left. - \partial_{\varphi} (B_{r}B_{\varphi}) - r\partial_{z}(B_{r}B_{z})\right). \label{eq40} \end{eqnarray}(11)Because we are interested in a mean radial dependence, we apply the average 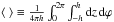⟨ ⟩≡14πh∫02π∫−hhdz dϕ\hbox{$\avg{\,} \equiv \frac{1}{4\pi h} \int_{0}^{2\pi}{ \int_{-h}^{h}{ {\rm d}z\, {\rm d}\varphi } }$} to Eq. (11) to yield ⟨ρvmag2⟩=1μ[ (⟨Bϕ2⟩+r2∂r⟨Bϕ2⟩)−(⟨Br2⟩+r2∂r⟨Br2⟩) −r4πh∫02π(Br(h)Bz(h)−Br(−h)Bz(−h))dϕ\begin{eqnarray} \avg{\rho \vv_{\rm mag}^{ 2 }} &=&\frac { 1 }{ \mu } \left[\, \left( \avg{B_{\varphi}^2} + \frac{r}{2}\partial _{ r } \avg{B_{\varphi}^2} \right) - \left( \avg{B_{r}^2} + \frac{r}{2}\partial_{r} \avg{B_{r}^2} \right) \right. \nonumber \\ && \quad - \frac{r}{4\pi h} \int_{0}^{2\pi}{ \left(B_r(h) B_z(h) - B_r(-h) B_z(-h)\right) {\rm d}\varphi} \nonumber \\ && \quad \left. + \frac{r}{2}\partial_{r}\avg{B_{z}^2} \,\right]. \label{eq4a} \end{eqnarray}(12)The term in the second line vanishes for periodic boundary conditions, which may be true for the turbulent field. 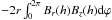For a symmetric or an antisymmetric field with respect to the galaxy’s plane, we have −2r∫02πBr(h)Bz(h)dϕ\hbox{$ - 2 r \int_{0}^{2\pi}{B_r(h) B_z(h){\rm d}\varphi}$} which always contributes with a negative sign for an X-shaped structure as is seen in many edge-on galaxies (Krause 2014).

We note that Bz = 0 implies Br ∝ r-1 in the axisymmetric case and Eq. (12) agrees with Eq. (3). For a given radial distribution of an axisymmetric Br, the radial distribution of the vertical flux from the disc is fixed by divB = 0. Consequently, we can set the vertical field at the disc surface 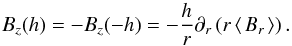Bz(h)=−Bz(−h)=−hr∂r(r⟨Br⟩).\begin{equation} B_z(h)=-B_z(-h)=-\frac{h}{r} \partial_r \left(r \avg{B_r}\right). \end{equation}(13)Here we consider only a symmetric field with respect to the plane. For an antisymmetric field Bz is an independent variable.

The left-hand side of Eq. (12) refers to the total magnetic energy of the three field components, which can be estimated from the synchrotron emission under the assumption of equipartition with cosmic rays. For the cross correlation term at least the sign is known. A flat radial profile of the azimuthal field contributes to an inward-directed Lorentz force, but radial magnetic fields are not negligible in galaxies. For a constant pitch angle, the magnetic force from the azimuthal field will be reduced by the contribution of the radial component. For pitch angles at about 20°, the force will be reduced by 14%; for an angle of 35°, the effect will amount to about 50%. This effect only occurs for anti-parallel fields, in contrast to a uniform regular field, where the radial component has no influence. The turbulent magnetic field also contributes to the Lorentz force as a pressure term to the momentum equation for isotropic fields (cf. Eq. (14)). For anisotropic turbulence (i.e. 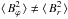⟨Bϕ2⟩≠⟨Br2⟩\hbox{$\avg{B_{\varphi}^2} \not= \avg{B_{r}^2}$}), we may also get tension effects similar to the regular fields.

Defining vM2=1μ⟨ρ⟩[(⟨Bϕ2⟩+r2∂r⟨Bϕ2⟩)−(⟨Br2⟩+r2∂r⟨Br2⟩) −r4πh∫02π( Br(h)Bz(h)−Br(−h)Bz(−h) ) dϕ\begin{eqnarray} \vv_{M}^{ 2 } & = &\frac { 1 }{ \mu \avg{\rho}} \left[\; \left( \avg{B_{\varphi}^2} + \frac{r}{2}\partial _{ r }\avg{B_{\varphi}^2} \right) \right. - \left( \avg{B_{r}^2} + \frac{r}{2}\partial _{ r }\avg{B_{r}^2} \right) \nonumber \\ & &\quad- \frac{r}{4\pi h} \int_{0}^{2\pi}{ \left(\, B_r(h) B_z(h) - B_r(-h) B_z(-h) \,\right)\,{\rm d}\varphi} \nonumber \\ && \quad \left. + \frac{r}{2}\partial _{r}\avg{B_{z}^2} \;\right] \label{eq5} \end{eqnarray}(14)and the rotation velocity vG balancing the gravitational force we get the circular velocity 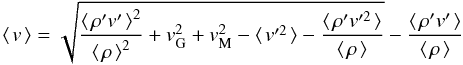⟨v⟩=⟨ρ′v′⟩2⟨ρ⟩2+vG2+vM2−⟨v′2⟩−⟨ρ′v′2⟩⟨ρ⟩−⟨ρ′v′⟩⟨ρ⟩\begin{equation} \!\avg{\vv} = \sqrt{\frac{\avg{\rho'\vvp}^2}{\avg{\rho}^2} + \vv_{\rm G}^2 + \vv_{\rm M}^2 - \avg{\vvp^2} - \frac{\avg{\rho'\vvp^2}}{\avg{\rho}}} - \frac{\avg{\rho'\vvp}}{\avg{\rho}} \label{eq6} \end{equation}(15)by applying Reynolds rules to the term ⟨ρv2⟩. Here we neglect all effects of velocity and density fluctuations including the asymmetric drift term ⟨v′2⟩. We finally obtain the circular velocity supported by gravitation and magnetic fields, 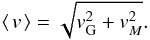⟨v⟩=vG2+vM2.\begin{equation} \avg{\vv} = \sqrt{\vv_{\rm G}^2 + \vv_{M}^2}. \label{eq7} \end{equation}(16)It is easy to see that vM coincides with the magnetic velocity vmag defined in Eq. (3). In contrast, Eq. (14) serves as an alternative formulation for the magnetic velocity with energy densities of the total magnetic field components, which allows a better interpretation of the observed data.

3. Observed radial profiles of magnetic fields and gas in galaxies

The radial profiles of the total and linearly polarised radio synchrotron intensities in nearby galaxies can be well fitted by exponential distributions. The exponential scale lengths for grand-design spirals are typically 5 kpc for the polarised and about 4 kpc for the total synchrotron emission, for instance in NGC 6946 (see Walsh et al. 2002).

The scale length of the total magnetic field Btot follows from that of the total synchrotron emission, assuming equipartition between the total magnetic and cosmic ray energy densities (see below). The scale length of the regular magnetic field Breg follows from that of the total synchrotron emission and the degree of linear polarisation. As the degree of polarisation generally increases with increasing radius, the scale length of Breg is larger than that of Btot, but has a larger uncertainty. We note that the anisotropic field component also contributes to the polarised intensity, but it would affect the magnetic velocity in a similar way to the turbulent field, where the effect of the azimuthal field is reduced for non-zero pitch angles (cf. Eq. (14)).

Under the equipartition assumption and assuming a radio synchrotron spectral index of about −1, 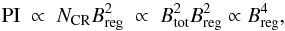PI∝NCRBreg2∝Btot2Breg2∝Breg4,\begin{equation} {\rm PI} \;\propto\; N_{\rm CR} B_{\rm reg}^2 \;\propto\; B_{\rm tot}^2 B_{\rm reg}^2 \;{\propto}\; B_{\rm reg}^4, \end{equation}(17)and hence 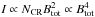I∝NCRBtot2∝Btot4\hbox{$I \propto N_{\rm CR} B_{\rm tot}^2 \propto B_{\rm tot}^4$} (Beck 2007), the scale length of the total magnetic field is about four times larger than that of the total synchrotron emission. The profile of the regular field is described as Breg = Breg,0exp( − r/RB reg) and that of the turbulent field Btur = Btur,0exp( − r/RB tur). The observed synchrotron scale lengths correspond to a typical scale length of the regular field of RBreg ≃ 20 kpc and a scale length of the total field of RBtot ≃ 16 kpc. These values vary with the size of the galaxies and do strongly scatter. Synchrotron scale lengths for M 83 (Harnett 1987; Neininger et al. 1993) and the Milky Way are about 2.5 kpc and may reach 7 kpc for M101 (Hummel 1990) and NGC 6753 (Harnett 1987).

Mean-field αΩ dynamo models also show an exponential radial profile of the magnetic field, but mostly with shorter scale lengths of the order of 5 kpc for grand design spirals (Gressel et al. 2013). In the cosmological simulations of Beck et al. (2012), the field strength in protogalactic halos approximately follows a 1 /r profile.

The total field has two components: regular and turbulent. The turbulent field may be anisotropic, where the extreme case of a vanishing radial and vertical component would still contribute to polarised emission. Hence, the exponential scale length of the total field is a weighted mean of the individual field components. As the turbulent field dominates (Beck 2007; Tabatabaei et al. 2013), we assume a typical scale length of the turbulent field of RBtur ≃ 15 kpc for spiral galaxies.

The synchrotron scale lengths of dwarf galaxies are smaller than in spirals, for instance 0.6 kpc in NGC 4214 (Kepley et al. 2011). The corresponding scale length of the total and turbulent fields is about 3 kpc. Polarised emission has been detected only for dwarf galaxies with a high star formation rate, like NGC 4449 (Chyży et al. 2000), for which we assume a typical scale length of the regular field of RBreg ≃ 4 kpc.

The strength of the turbulent field Btur depends on the star formation rate. At r = 0, Btur,0 ≃ 20 μG is typical for a grand-design spiral like NGC 6946 (Beck 2007), while for galaxies with lower star formation rates we assume Btur,0 ≃ 10 μG. The strongly star-forming dwarf galaxy NGC 4449 has Btur,0 ≃ 15 μG (Chyży et al. 2000), while weakly star-forming dwarfs reveal Btur,0 ≃ 3 μG (Chyży et al. 2011).

The strength of the regular field Breg does not show a clear dependence on a single parameter of the host galaxy. We assume a ratio of Breg,0/Btur,0 = 0.4 for spiral galaxies, corresponding to a mean degree of polarisation of 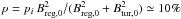p=pi Breg,02/(Breg,02+Btur,02)≃10%\hbox{$p = p_i \, B_{\rm reg,0}^2/(B_{\rm reg,0}^2 + B_{\rm tur,0}^2) \simeq 10\%$}. This value increases with radius R because of the larger scale length of Breg. Dwarf galaxies have weaker regular fields even if the star formation rate is high (Breg,0 ≃ 3 μG). No regular fields have been detected so far in dwarf galaxies with a low star formation rate.

Typical parameters of the magnetic field strengths near the centre (r = 0) and the magnetic scale lengths are given in Table 1 for different galaxy types. We also include values for the Milky Way (Kalberla & Dedes 2008; Ferriere 1998; Clemens 1985; Burton & Gordon 1978), NGC 6946 (Walsh et al. 2002; Boomsma et al. 2008) and M 31 (Beck & Gräve 1982). In the last column we give estimates for the Alfvén velocity of the total field near the centre.

Table 1

Observational parameters for typical spiral and dwarf galaxies (see text for details).

All non-magnetic effects like gravitational forces (stellar disc, gas disc, dark matter, etc.) or thermal and turbulent gas pressure are represented by the circular velocity which we prescribe by a Brandt law 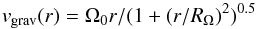vgrav(r)=Ω0r/(1+(r/RΩ)2)0.5\begin{equation} \vv_{\rm grav}(r) = \Omega_0 r/ (1+(r/R_\Omega)^2)^{0.5} \end{equation}(18)with the inner circular frequency Ω0 and the turnover radius RΩ where the rotation becomes flat. This simple approximation does not really reflect the universal rotation law of galaxies (Salucci et al. 2007), but will be sufficient for a comparison with the magnetic influence on the rotation.

The ionisation fraction in the neutral gas component is still high enough to treat the total gas as a single fluid. Bigiel & Blitz (2012) found a universal exponential radial scaling of the total gas surface density for nearby, non-interacting disc galaxies, with a scale length of about Rgas ≃ 0.6 r25 ≃ 10 kpc. Furthermore we add a constant value of 10-29 g cm-3 for the intergalactic medium. Typical parameters of the scale length Rgas are given in Table 1 for different galaxy types. With the exception of gas-stripped galaxies with a much reduced central density of ρgas = 1 cm-3, the density is ρgas = 15 cm-3 at r = 0. We include the case of a spiral galaxy for which the gas has been stripped by tidal interaction, but the magnetic field is still unchanged. Such a scenario may occur in the early phase of interaction (Vollmer et al. 2012).

The scale length of the total gas density is in many cases similar to half of the scale length for the regular field, in accordance with a constant Alfvén velocity, but again with a large scatter. The most extreme deviation could be M 101 with 28 kpc scale length for the total field and 7 kpc for the gas scale length (Hummel 1990; Bigiel et al. 2010). Here the Alfvén velocity is exponentially but slowly increasing with a huge scale length of 28 kpc. So far there is no evidence that the magnetic field strength follows such a law even at distances of more than 28 kpc. For M 83 we have Rgas = 7 kpc and RB total = 10 kpc (Bigiel et al. 2010; Neininger et al. 1993).

There is not always a single scale length, in particular for interacting galaxies, such as M 51, with about Rgas = 5.5 kpc and RB total = 18 kpc (derived from radio data at 151 MHz, assuming equipartition) between 2−10 kpc radius; these values change in the outer disc to become about Rgas = 2 kpc and RB total = 8 kpc in the range 10−18 kpc (Bigiel et al. 2010; Mulcahy et al. 2014). Here we have the case for a slowly growing Alfvén velocity reaching about 100 km s-1 at a distance of 40 kpc, but the small exponential scale in the outer part allows only an outward directed Lorentz force. Tabatabaei et al. (2013) found 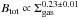Btot∝Σgas0.23±0.01\hbox{$B_{\rm tot}\propto\Sigma_{\rm gas}^{0.23\pm0.01}$} in NGC 6946 (where Σgas is the gas surface density), based on many small regions within the bright star-forming regions of the galaxy. The magnetic field distribution was derived via the equipartition assumption from that of the synchrotron intensity, which is known to be smoother than that of the gas, due to diffusion of cosmic-ray electrons (Berkhuijsen et al. 2013). Hence, the exponent of the above relation should be regarded as a lower limit and does not question our assumption of a constant Alfvén velocity on large scales.

A scaling of Breg ∝ ρ0.5 is also in agreement with an equipartition field strength for the more or less constant velocity dispersion. For the typical field strength of several μG and a density of 1 cm-3, the Alfvén velocity is of the order of 10−20 km s-1, which is too small to cause a significant change of a 200 km s-1circular velocity.

The estimates for the density are derived from observations of surface densities. For a constant vertical scale height of the gas disc, the scale length is the same for the midplane densities. For a flaring disc such as in the Milky Way, the scale length for the midplane density will be smaller. In the case that the magnetic field extends with the same scale length outside the optical radius (which is still not observed) the Lorentz force would not be negligible anymore.

Grand-design spiral galaxies usually have a regular field strengths between 4 μG and 8 μG for low and high star formation rates, respectively (Fletcher 2010). The exponential scale length for the regular magnetic field turns out to be twice the scale length of the HI density, which means a constant Alfvén speed of around 10 km s-1up to the outer parts of the gaseous disc. This value can be lower in the central region because of high molecular gas density. Therefore the magnetic energy is roughly in equipartition with the turbulent energy of the gas in the midplane. With such low values of the Alfvén velocity, we exclude any influence of the magnetic field on the gas rotation independent of the radial magnetic field distribution. A similar situation is found for flocculent galaxies. For extensively star-forming dwarf galaxies, the magnetic scale is only slightly larger than the density scale length, which leads to a radially decreasing Alfvén velocity of at most 10% of the rotational velocity.

4. Effect on rotation for idealised radial profiles

We model the total magnetic field as the sum of the regular and turbulent field. Because of the unknown contribution of the anisotropic turbulent field to the polarised emission, we model that part of the field as a regular field only. We assume instead some anisotropy for the turbulent field. Prescribing the radial profile of the regular Bϕ and the radial profile of the pitch angle fixes the components Br and Bz for a symmetric regular field. For the turbulent field we prescribe the radial profile of 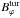Bϕtur\hbox{$B_\varphi^{\rm tur}$} and the degree of anisotropy ( 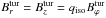Brtur=Bztur=qisoBϕtur\hbox{$B_r^{\rm tur}=B_z^{\rm tur}= q_{\rm iso} B_\varphi^{\rm tur}$}). The third term of the right-hand side in Eq. (14) vanishes for the turbulent field. Under the assumptions for the radial profiles of density, regular, and turbulent magnetic field for a typical spiral (cf. Table 1) we plot the circular velocity modified by the magnetic field in Fig. 1. The reduction of the magnetic velocity outside 20 kpc is mainly caused by the pressure of the vertical component of the turbulent field. The anisotropy of the turbulent field appears to be negligible. For an antisymmetric regular field the result is similar for a negligible magnetic flux through the disc.

thumbnail Fig. 1

Typical spiral including a turbulent field. Upper-left panel: the contributions to the magnetic velocity (solid) are from the total field of Bϕ (dotted), Br (dashed), Bz (dash dot dot), and the BrBz term (dash dot) of the regular field only. Upper-right panel: radial dependence of the pitch angle for the regular field (solid) and the anisotropy qiso of the turbulent field (dotted). Lower-left panel: radial profiles of total magnetic field components Bϕ (solid), Br (dotted), and Bz (dashed) (the last two components are almost identical). Lower-right panel: rotation modified by the Lorentz force (solid) and from the gravitation only (dotted).

4.1. Large spirals

Some large galaxies (like M 51) have a truncated gas disc, where a much smaller scale of the density is observed in the outer disc. The corresponding truncation in the radio continuum disc may be ascribed to a lack of star formation and hence of cosmic-ray electrons in the outer disc, while the magnetic field may extend beyond the truncation radius with a constant scale length. In such a case, the Lorentz force may be influential in the outer parts. Neglecting the turbulent field leads to an increase of the rotation velocity by about 20 km s-1at 10 kpc, where the Alfvén speed is 130 km s-1. The situation changes if we also consider the turbulent magnetic field acting as a pressure term only. Now the outward pressure force would be in equilibrium with the gravitation at a radius of 10 kpc, but our assumption of equipartition between magnetic and cosmic-ray energies gives an additional pressure truncating the gaseous disc at a smaller radius. Assuming a polytropic index of γ = 4/3 for the cosmic-ray gas, the cosmic-ray pressure is PCR = (1/3)Pmag, which reduces the truncation to 9 kpc.

We now consider two more or less constrained cases for typical spirals. For NGC 6946 all parameters can be taken from Walsh et al. (2002); Beck (2007); and Boomsma et al. (2008), which will be an example of a large spiral with moderate star formation. Despite the exponential growth of the Alfvén speed in Fig. 2 we see only a weak reduction of the rotation velocity as a result of the Lorentz force. This effect stems from the turbulent magnetic field, which is included here only as a pressure term. This galaxy is one of the extreme cases were the magnetic energy is larger than the turbulent kinetic energy.

thumbnail Fig. 2

NGC 6946: upper panels: dotted lines denote the turbulent magnetic field and dashed lines the regular field. Upper right panel: magnetic velocity vmag for the total field (solid line). Lower right panel: resulting total circular velocity is plotted (solid). The dashed line indicates the rotation velocity neglecting the turbulent field.

4.2. The Milky Way

thumbnail Fig. 3

Milky Way: circular velocity for a distribution of the regular magnetic field with an exponential profile (solid), compared to the profile given by Eq. (7). The exponential scale length is 10 kpc, and rm = 7 kpc. One cannot distinguish the two profile shapes from a measurement of the (normalised) polarised intensity in the inner 10 kpc. The density distribution of Kalberla & Dedes (2008) is marked with crosses.

Observations of the radial profile of the polarised intensity for the Milky Way are less constrained than observations for external galaxies. Estimates for the radial magnetic profile often rely on models for the magnetic field (Sun et al. 2008; Strong et al. 2000). The scale length of the magnetic field is nearly three times as big as the scale length of the gas density, which gives an increase of the Alfvén velocity (cf. Table 1). Here we compare the two basic assumptions for the radial profile of the magnetic field. The first model relies on the assumption of equipartition between magnetic field and cosmic ray energies. The density profile is taken from Kalberla & Dedes (2008). For the second model, we used a magnetic field profile according to Eq. (7), approximating a 1 /r profile at infinity. Assuming equipartition, this would lead to clear contradiction with an exponential law for the polarised emission. On the other hand, for an exponential cosmic ray distribution ρcr = exp( − r/rcr) with a scale length of rcr = 6 kpc, a nearly exponential distribution of the polarised intensity is obtained. Figure 3 shows the magnetic disturbance of the rotation for both assumptions. This leads to an increase in gas rotation for the model of Ruiz-Granados et al. (2012), but a decrease in the exponential magnetic field distribution. However, the effect is still below 10 km s-1at 20 kpc radius in agreement with Sánchez-Salcedo & Santillán (2013), who used an exponential law.

4.3. Field reversals

For the Milky Way, a reversal of the regular magnetic field is a possible interpretation of the data (see Van Eck et al. 2011, for example). For the parameters of a typical spiral (cf. Table 1) with a low star formation rate, we modelled a reversal of the regular field. A sharp field reversal on a length scale below 1 kpc can lead to strong modulations in the rotation curve. For a dominant azimuthal field (i.e., a small pitch angle), the effect leads first to a reduction and then to an increase of the circular velocity (cf. Fig. 4) when moving radially outwards. For larger pitch angles, the reversal of an axisymmetric field also implies a strong vertical field, which results in a local increase of the magnetic pressure. As a consequence, the deviation from the unperturbed rotation curve starts with super-rotation and ends with a weaker rotation (cf. Fig. 5) when moving from smaller to larger radii. For a broader transition zone, the effect becomes negligible.

thumbnail Fig. 4

Milky Way: reversal within 1 kpc and a small pitch angle. Upper-left: regular Bϕ (solid), Br (dotted), Bz (dashed); lower-left: total Bϕ (solid), Br (dotted), Bz (dashed); upper-right: regular Br/Bϕ (solid); lower-right: circular velocity with magnetic force (solid), gravitation only (dotted).

thumbnail Fig. 5

Milky Way: reversal within 3 kpc and a large pitch angle. Upper left: regular Bϕ (solid), Br (dotted), Bz (dashed); lower left: total Bϕ (solid), Br (dotted), Bz (dashed); upper right: regular Br/Bϕ (solid); lower right: circular velocity with magnetic force (solid), gravitation only (dotted).

5. Dynamo model

In this section, we aim to confront the theoretical expectations derived above with a full-blown global simulation of a Milky Way-type galaxy (Gressel et al. 2013), where we modelled a mean-field dynamo in a dynamical fashion by additionally solving the momentum equation in a prescribed static gravitational potential. In this model, we found the action of the supernova-driven αΩ dynamo to be limited to the inner 10−15 kpc. In the outer part, the magnetic field was maintained by the magnetorotational instability. The final magnetic field had a radial exponential scale length of about 10 kpc and a modestly varying Alfvén speed of 10−30 km s-1. Consistent with our preceding estimates, we found only a very weak influence of the Lorentz force on the rotational velocity.

thumbnail Fig. 6

Results from a dynamical dynamo simulation including mean-field effects. Colour-coded lag in the rotation velocity vφ(r,z) averaged over azimuth. Values | δv | > 30 km s-1have been clipped for clarity. Top: Predicted deviation from the initial rotation profile based on the effect of the Lorentz force. Bottom: the actual deviation seen in the simulation, which appears more washed out owing to the effect of the turbulent viscosity but otherwise agrees markedly well (see also the lower panel of Fig. 9 in Gressel et al. 2013, for the actual field distribution).

The deviation in rotation after the magnetic field has grown into saturation is shown in the lower panel of Fig. 6. Here and in the following figure, we plot azimuthally averaged rotation velocities. The colour coding is such that super-rotation is indicated by red hues, sub-rotation corresponds to green hues, and neutral rotation appears in yellow. For reasons of clarity, the data range has been limited to ±30 km s-1, with values exceeding this level being confined to high-latitude regions near the domain boundary. 1 Apart from being of more diffuse appearance, the structure seen in this panel agrees very well with the prediction obtained via Eq. (5), which is displayed in the upper panel of the same figure, and which is based on computing 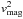vmag2\hbox{$\vv_{\rm mag}^2$} from the Lorentz force encountered in the simulation. It is thus fair to say that the resulting deviations of the rotational velocities in our MHD model can be explained by the acting of magnetic forces.

The most pronounced difference between the two panels of Fig. 6 is that the effect of the Lorentz force (seen in the upper panel) appears negligible in the disc midplane, something that is owed to the higher gas density there and which reduces the relative importance of magnetic forces. This trend is moreover reinforced when going radially inward, where the disc surface density is higher. In contrast to this, the actual rotation profile seen in the simulations shows some local deviations even in the midplane. This may be explained by a coupling of overlying magnetically-affected layers via a viscous drag force mediated by the turbulent viscosity caused by SNe. A potential example for this can be seen around r = 17 kpc, where the rotation appears to be coupled over an extended vertical patch of the disc.

thumbnail Fig. 7

Same as the upper panel in Fig. 6, but comparing the contributions from different field components. Top: effect of the poloidal field Bz(r,z) zˆ+Br(r,z) rˆ\hbox{$B_z(r,z)\,\zz+B_r(r,z)\,\rr$}, which predominantly affects high-latitude layers presumably via magnetic pressure gradients. Bottom: effect of the azimuthal field Bϕ(r,z) component, contributing to super-rotation outside the reversal at r = 10 kpc and providing weak pressure-support in the outer disc away from the midplane.

To facilitate a more detailed interpretation of the various features seen in the rotation cross-section of the disc, we now turn to Fig. 7, where we plot the contributions to 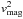vmag2\hbox{$\vv_{\rm mag}^2$} stemming from the poloidal field 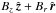Bz zˆ+Br rˆ\hbox{$B_z\,\zz+B_r\,\rr$} (upper panel), and the azimuthal field component Bϕ (lower panel). It can be seen that the poloidal field only affects the very upper layers of the disc. Given the limited vertical extend of our model, we should express some caution in interpreting these features as they may be partly affected by the chosen boundary conditions. Still, the characteristic patches seen near the field reversal at r = 10 kpc actually serve as a nice example that vertical fields enter the force balance via magnetic pressure gradients. Here, a localised region of strong vertical field leads to a pressure support (and hence sub-rotation, green) on its outside, and the opposite effect (red) on the inside. Similar effects are seen farther out in the disc but show a more complex structure. These features outside 10 kpc may be related to the Parker instability also seen in the simulations of Machida et al. (2013).

As can be seen in the lower panel of Fig. 7, the more large-scale variations in vrot are clearly caused by the azimuthal disc field Bϕ. Only the asymmetric rotation of the upper and lower disc inside 6 kpc is due to the combined symmetric radial component of the dynamo and a vertical field going through the disc. This mixed parity of the field is the reason for the antisymmetric change of the rotational velocity arising from the term Bz∂zBr in Eq. (3). The strongest effect causing super-rotation (red) is related to the dynamo mode with A0 parity residing between 8 kpc and 10 kpc, and the combined dynamo and MRI mode located between 10 kpc and 13 kpc. At the interfaces between these modes, the azimuthal field Bϕ vanishes, which leads to local gradients in the Lorentz force. Both of the red regions have green regions adjacent on the outside and the overall picture is again consistent with the dominant effect stemming from magnetic forces. Even though these features appear fairly washed-out in the actual simulation, they are tied to particular field reversals and their character is clearly local.

Because of the A0 parity, the super-rotation near the field reversal (at 10 kpc) does not affect the disc midplane. With the midplane harbouring the peak in the gas density on one hand, and Bφ = 0 on the other hand, this does seem a little surprising. In contrast to the picture based on the j × B alone, the simulation (cf. the lower panel of Fig. 6) does show some weak sub-rotation around (r,z) = (12,0) kpc. Given the long-wavelength vertical modulation, one may be tempted to interpret these fluctuations as low-wavenumber MRI channels, where the effect of field-line tension is complemented by inertial forces. The global tendency of sub-rotation around the midplane outside 10 kpc is consistent with the scale length of 10 kpc for the exponential fit to the magnetic field strength in the model.

The variation of the rotation of the Milky Way, as is shown in Fig. 2 of Ruiz-Granados et al. (2012), may be due to a field reversal between 10 kpc and 15 kpc, mainly caused by the azimuthal field, although the details of the reversal differ in our model. We should remark that the magnetic field strength of the dynamo may still be underestimated and the contribution of the small-scale turbulent field is neglected in this type of model. Therefore one could have slightly stronger changes of the rotation by the action of the Lorentz force in real galaxies.

6. Discussion

From Eq. (14) we obtain the effect of the Lorentz force from the total field strength, supposing we know the fraction of the different components and the vertical field on the surface of the disc. For the regular or an anisotropic field, we can estimate the fraction of radial to azimuthal field by the pitch angle. The vertical component of the regular field near the disc plane is negligible, as seen from polarised emission of edge-on galaxies (e.g. Soida et al. 2011). The surface term (Br(h)Bz(h)) reduces the magnetic velocity for observed X-shaped geometries. For a typical pitch angle of 20°, the field contributing to the polarised emission only acts like an azimuthal field. The other part of the field contributing to the total intensity will act like isotropic turbulence. Therefore the profile of the polarised intensity should be flatter than r-2 for a centripetal force action.

It is observationally unclear how far one can extrapolate the exponential law of the magnetic field strength and how reliable the assumption of energy equipartition between magnetic field and cosmic rays is in the outer disc. In the case of a valid exponential law of the regular magnetic field in the outer disc, a reduction of the circular velocity occurs outside the scale length, that is, where the tension force is dominated by the pressure force of the azimuthal field. Apart from ram pressure stripping, this may be another source for truncations of the gaseous disc. Dynamical simulations of ram pressure stripping suggest this (Ruszkowski et al. 2014). Stars formed within the slower rotating gas will decouple from the magnetic force and migrate inwards.

With the present data we do not find any support for the possibility of attributing flat rotation curves to magnetic forces. This has been claimed previously with the intention of reducing the required dark matter content of galaxies. On the contrary, at large radii the observed flat gas rotation may demand even more extended dark matter profiles because of an additional magnetic pressure support. This is, however, speculative because the observations of extended disc rotation are mainly done for extended gaseous discs, where the Alfvén velocity is still small compared to the rotation velocity. Additional direct measurements of radio emission in the outer discs in the low-frequency range or of Faraday rotation of background radio sources (Beck et al. 2013) will give better constraints than our simple extrapolation of the scale length.

Our dynamo model exhibits nearly no influence of the magnetic field on the rotation in the disc, with a weak sub-rotation outside the radial scale length of the field. Outside the midplane of the disc, variations of the order of 10% of the rotation velocity may be caused by magnetic field reversals. The super-rotation appearing at the outer vertical boundaries caused by the flat radial profile of the azimuthal field may be due to boundary effects and no proper modelling of the halo gas. Another interesting feature seen in our dynamo model is the antisymmetric disturbance of the circular velocity away from the midplane by a symmetric disc field, together with a vertical field threading the disc.

7. Summary

We estimated the effects of the Lorentz force onto the gas rotation of galaxies assuming equipartition of the magnetic field with cosmic ray energy.

The scale length of the regular magnetic field is rather large compared to the optical disc size. The scale for the gas density varies between a quarter and a half of the magnetic scale length. This translates into a constant or slowly growing Alfvén velocity along the disc. Stripped galaxies may be an exception.

An exponential distribution of the magnetic field leads always to a centrifugal force (reduction of the rotational velocity) outside one exponential scale length. The centripetal force (increase of the rotational velocity) inside one exponential scale length is too weak because of the low Alfvén velocity in the disc. A strong turbulent field in the inner region will further reduce the centripetal force. Reversals of the large scale magnetic field on scales below 1 kpc may cause variations of the rotation velocity.

Recent dynamic dynamo models confirm the above findings, independent of the equipartition argument.

1

The departures there are related to strong vertical fields in the disc halo, and simulations with an extended domain should be performed to exclude a spurious origin related to the chosen boundary conditions.

Acknowledgments

Part of this work was supported by the German Deutsche Forschungsgemeinschaft (DFG), project numbers FOR1254 and FG1257. We thank Marita Krause for carefully reading the manuscript and the referee Eduardo Battaner for useful comments.

References

  1. Battaner, E., & Florido, E. 2000, Fundamentals of Cosmic physics, 21, 1 [Google Scholar]
  2. Beck, A. M., Lesch, H., Dolag, K., et al. 2012, MNRAS, 422, 2152 [NASA ADS] [CrossRef] [Google Scholar]
  3. Beck, R. 2007, A&A, 470, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Beck, R., & Gräve, R. 1982, A&A, 105, 192 [NASA ADS] [Google Scholar]
  5. Beck, R., & Wielebinski, R. 2013, Magnetic Fields in Galaxies, eds. T. D. Oswalt, & G. Gilmore (Dordrecht: Springer Science + Buisness Media), 641 [Google Scholar]
  6. Beck, R., Brandenburg, A., Moss, D., Shukurov, A., & Sokoloff, D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
  7. Beck, R., Anderson, J., Heald, G., et al. 2013, Astron. Nachr., 334, 548 [NASA ADS] [CrossRef] [Google Scholar]
  8. Berkhuijsen, E. M., Beck, R., & Tabatabaei, F. S. 2013, MNRAS, 435, 1598 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bigiel, F., & Blitz, L. 2012, ApJ, 756, 183 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bigiel, F., Leroy, A., Walter, F., et al. 2010, AJ, 140, 1194 [NASA ADS] [CrossRef] [Google Scholar]
  11. Boomsma, R., Oosterloo, T. A., Fraternali, F., van der Hulst, J. M., & Sancisi, R. 2008, A&A, 490, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Burton, W. B., & Gordon, M. A. 1978, A&A, 63, 7 [NASA ADS] [Google Scholar]
  13. Chyży, K. T., Beck, R., Kohle, S., Klein, U., & Urbanik, M. 2000, A&A, 355, 128 [NASA ADS] [Google Scholar]
  14. Chyży, K. T., Weżgowiec, M., Beck, R., & Bomans, D. J. 2011, A&A, 529, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Clemens, D. P. 1985, ApJ, 295, 422 [NASA ADS] [CrossRef] [Google Scholar]
  16. Crutcher, R. M., Wandelt, B., Heiles, C., Falgarone, E., & Troland, T. H. 2010, ApJ, 725, 466 [NASA ADS] [CrossRef] [Google Scholar]
  17. Elstner, D., Gressel, O., & Rüdiger, G. 2009, in IAU Symp., 259, 467 [Google Scholar]
  18. Ferriere, K. 1998, ApJ, 497, 759 [NASA ADS] [CrossRef] [Google Scholar]
  19. Fletcher, A. 2010, in eds. R. Kothes, T. L. Landecker, & A. G. Willis, ASP Conf. Ser., 438, 197 [Google Scholar]
  20. Gressel, O., Elstner, D., & Ziegler, U. 2013, A&A, 560, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Gressel, O., Elstner, D., Ziegler, U., & Rüdiger, G. 2008a, A&A, 486, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Gressel, O., Ziegler, U., Elstner, D., & Rüdiger, G. 2008b, Astron. Nachr., 329, 619 [NASA ADS] [CrossRef] [Google Scholar]
  23. Harnett, J. I. 1987, MNRAS, 227, 887 [NASA ADS] [CrossRef] [Google Scholar]
  24. Hummel, E. 1990, in Windows on Galaxies, eds. G. Fabbiano, J. S. Gallagher, & A. Renzini, Astrophys. Space Sci. Lib., 160, 141 [Google Scholar]
  25. Jałocha, J., Bratek, Ł., Pȩkala, J., & Kutschera, M. 2012, MNRAS, 427, 393 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kalberla, P. M. W., & Dedes, L. 2008, A&A, 487, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Kepley, A. A., Zweibel, E. G., Wilcots, E. M., Johnson, K. E., & Robishaw, T. 2011, ApJ, 736, 139 [NASA ADS] [CrossRef] [Google Scholar]
  28. Krause, M. 2014 [arXiv:1401.1317] [Google Scholar]
  29. Machida, M., Nakamura, K. E., Kudoh, T., et al. 2013, ApJ, 764, 81 [NASA ADS] [CrossRef] [Google Scholar]
  30. Mulcahy, D. D., Horneffer, A., Beck, R., et al. 2014, A&A, 568, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Neininger, N., Beck, R., Sukumar, S., & Allen, R. J. 1993, A&A, 274, 687 [NASA ADS] [Google Scholar]
  32. Niklas, S., & Beck, R. 1997, A&A, 320, 54 [NASA ADS] [Google Scholar]
  33. Persic, M., & Salucci, P. 1993, MNRAS, 261, L21 [NASA ADS] [CrossRef] [Google Scholar]
  34. Ruiz-Granados, B., Rubiño-Martín, J. A., Florido, E., & Battaner, E. 2010, ApJ, 723, L44 [NASA ADS] [CrossRef] [Google Scholar]
  35. Ruiz-Granados, B., Battaner, E., Calvo, J., Florido, E., & Rubiño-Martín, J. A. 2012, ApJ, 755, L23 [NASA ADS] [CrossRef] [Google Scholar]
  36. Ruszkowski, M., Brüggen, M., Lee, D., & Shin, M.-S. 2014, ApJ, 784, 75 [NASA ADS] [CrossRef] [Google Scholar]
  37. Salucci, P., Lapi, A., Tonini, C., et al. 2007, MNRAS, 378, 41 [NASA ADS] [CrossRef] [Google Scholar]
  38. Sánchez-Salcedo, F. J., & Santillán, A. 2013, MNRAS, 433, 2172 [NASA ADS] [CrossRef] [Google Scholar]
  39. Sellwood, J. A., & Balbus, S. A. 1999, ApJ, 511, 660 [NASA ADS] [CrossRef] [Google Scholar]
  40. Sofue, Y., & Rubin, V. 2001, ARA&A, 39, 137 [NASA ADS] [CrossRef] [Google Scholar]
  41. Soida, M., Krause, M., Dettmar, R.-J., & Urbanik, M. 2011, A&A, 531, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Strong, A. W., Moskalenko, I. V., & Reimer, O. 2000, ApJ, 537, 763 [Google Scholar]
  43. Sun, X. H., Reich, W., Waelkens, A., & Enßlin, T. A. 2008, A&A, 477, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Tabatabaei, F. S., Schinnerer, E., Murphy, E. J., et al. 2013, A&A, 552, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Van Eck, C. L., Brown, J. C., Stil, J. M., et al. 2011, ApJ, 728, 97 [NASA ADS] [CrossRef] [Google Scholar]
  46. Vollmer, B., Soida, M., Braine, J., et al. 2012, A&A, 537, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Walsh, W., Beck, R., Thuma, G., et al. 2002, A&A, 388, 7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1

Observational parameters for typical spiral and dwarf galaxies (see text for details).

In the text

All Figures

thumbnail Fig. 1

Typical spiral including a turbulent field. Upper-left panel: the contributions to the magnetic velocity (solid) are from the total field of Bϕ (dotted), Br (dashed), Bz (dash dot dot), and the BrBz term (dash dot) of the regular field only. Upper-right panel: radial dependence of the pitch angle for the regular field (solid) and the anisotropy qiso of the turbulent field (dotted). Lower-left panel: radial profiles of total magnetic field components Bϕ (solid), Br (dotted), and Bz (dashed) (the last two components are almost identical). Lower-right panel: rotation modified by the Lorentz force (solid) and from the gravitation only (dotted).

In the text
thumbnail Fig. 2

NGC 6946: upper panels: dotted lines denote the turbulent magnetic field and dashed lines the regular field. Upper right panel: magnetic velocity vmag for the total field (solid line). Lower right panel: resulting total circular velocity is plotted (solid). The dashed line indicates the rotation velocity neglecting the turbulent field.
In the text
thumbnail Fig. 3

Milky Way: circular velocity for a distribution of the regular magnetic field with an exponential profile (solid), compared to the profile given by Eq. (7). The exponential scale length is 10 kpc, and rm = 7 kpc. One cannot distinguish the two profile shapes from a measurement of the (normalised) polarised intensity in the inner 10 kpc. The density distribution of Kalberla & Dedes (2008) is marked with crosses.
In the text
thumbnail Fig. 4

Milky Way: reversal within 1 kpc and a small pitch angle. Upper-left: regular Bϕ (solid), Br (dotted), Bz (dashed); lower-left: total Bϕ (solid), Br (dotted), Bz (dashed); upper-right: regular Br/Bϕ (solid); lower-right: circular velocity with magnetic force (solid), gravitation only (dotted).
In the text
thumbnail Fig. 5

Milky Way: reversal within 3 kpc and a large pitch angle. Upper left: regular Bϕ (solid), Br (dotted), Bz (dashed); lower left: total Bϕ (solid), Br (dotted), Bz (dashed); upper right: regular Br/Bϕ (solid); lower right: circular velocity with magnetic force (solid), gravitation only (dotted).
In the text
thumbnail Fig. 6

Results from a dynamical dynamo simulation including mean-field effects. Colour-coded lag in the rotation velocity vφ(r,z) averaged over azimuth. Values | δv | > 30 km s-1have been clipped for clarity. Top: Predicted deviation from the initial rotation profile based on the effect of the Lorentz force. Bottom: the actual deviation seen in the simulation, which appears more washed out owing to the effect of the turbulent viscosity but otherwise agrees markedly well (see also the lower panel of Fig. 9 in Gressel et al. 2013, for the actual field distribution).
In the text
thumbnail Fig. 7

Same as the upper panel in Fig. 6, but comparing the contributions from different field components. Top: effect of the poloidal field Bz(r,z) zˆ+Br(r,z) rˆ\hbox{$B_z(r,z)\,\zz+B_r(r,z)\,\rr$}, which predominantly affects high-latitude layers presumably via magnetic pressure gradients. Bottom: effect of the azimuthal field Bϕ(r,z) component, contributing to super-rotation outside the reversal at r = 10 kpc and providing weak pressure-support in the outer disc away from the midplane.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.