| Issue |
A&A
Volume 568, August 2014
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201423822 | |
| Published online | 29 August 2014 | |
Nucleosynthesis of elements in gamma-ray burst engines
Center for Theoretical Physics, Polish Academy of Sciences, Al. Lotnikow 32/46, 02-668 Warsaw, Poland
e-mail: agnes@cft.edu.pl
Received: 17 March 2014
Accepted: 28 June 2014
Aims. We consider the gamma-ray burst (GRB) central engine that is powered by the collapse of a massive rotating star or compact binary merger. The engine is a hot and dense accretion disk, which is composed of free nucleons, electron-positron pairs, and helium, and cooled by neutrino emission. A significant number density of neutrons in the inner disk body provide conditions for neutron rich plasma in the GRB outflows or jets. helium is synthesized in the inner disk if the accretion rate is large, and heavy nuclei are also formed in the outer disk at distances above 150−250rg from the black hole. We study the process of nucleosynthesis in the GRB engine, depending on its physical properties.
Methods. The GRB central engine is hydrodynamically modelled in the frame of a dense and hot disk, which accretes with a high rate (up to 1 Solar mass per second) onto a maximally spinning, stellar mass black hole. The synthesis of heavy nuclei up to germanium and gallium is then followed by the nuclear reaction network.
Results. The accretion at high rate onto a Kerr black hole feeds the engine activity and establishes conditions for efficient synthesis of heavy nuclei in the disk. These processes may have important observational implications for the jet deceleration process and heavy elements observed in the spectra of GRB afterglows.
Key words: accretion, accretion disks / nuclear reactions, nucleosynthesis, abundances / gamma-ray burst: general / black hole physics
© ESO, 2014
1. Introduction
Gamma-ray bursts (GRBs) are transient sources of extreme brightness observed on the sky with isotropic distribution. The extreme energetics of the observed bursts, which are detectable from a cosmological distance, implies that they must be connected with a gravitational potential energy released by accretion onto a compact star. The short bursts (T90< 2 s) are likely related with mergers of binary compact star systems, such as binary neutron stars (NS-NS) or black hole-neutron star (BH-NS) binaries, while the long duration events are believed to originate in collapsing massive stars. The typical mass of an accreting, newly born black hole is therefore on the order of a few Solar masses, while the accretion rates might exceed 1 M⊙ s-1.
In the collapsar model, the black hole surrounded by the part of the fallback stellar envelope helps launching relativistic jets (Woosley 1993; MacFadyen & Woosley 1999). These polar jets give rise to gamma rays, which are produced far away from the “engine” in the circumstellar region (see, e.g., the reviews by Zhang & Mészáros 2004; Piran 2004).
The process of nucleosynthesis of heavy elements in the central engines of GRBs has recently been studied in a number of works. The evolution of abundances calculated by Banerjee & Mukhopadhyay (2013) have shown the synthesis of rare elements, such as 31P, 39K, 43Sc, and 35Cl and other uncommon isotopes. These elements, which are produced in the simulations at outer parts of low Ṁ accretion disks (i.e. 0.001−0.01 M⊙ s-1), have been discovered in the emission lines of some long GRB X-ray afterglows; however, they are yet to be confirmed by future observations.
In this article, we consider the nucleosynthesis of elements in the accretion disk itself for higher initial accretion rates, as is appropriate for type I collapsars or neutron star mergers and short GRBs. We account for the neutrino opacities and nuclear equation of state (EOS) in dense matter. For the accretion disk model, we use the EOS that is introduced in Janiuk et al. (2007) and subsequently adopted in Janiuk & Yuan (2010) to describe the disk around a Kerr black hole with an arbitrary spin, a. Contrary to previous work, which analytically accounted for the total pressure that consists of gas, radiation, and completely degenerate electrons (Popham et al. 1999) with subsequent addition of the neutrino pressure (Di Matteo et al. 2002), we compute the EOS of matter numerically from the nuclear reaction balance. Our approach allows for a partial degeneracy of all the species, a partial trapping of neutrinos, and Kerr black hole solutions.
We calculate the profiles of density and temperature, as well as the electron fraction in the converged steady-state model of an accreting torus in the GRB engine. We then follow the nucleosynthesis process, and we determine the abundances of the heavy elements isotopes.
2. Neutronization in the hyperdense matter
The central engines of GRBs are dense and hot enough to allow for the nuclear processes that lead to neutron excess (i.e., neutron to proton number density ratio above 1). The reactions of electron and positron capture on nucleons and neutron decay must establish nuclear equilibrium. These reactions are 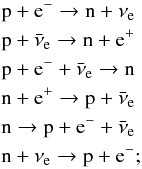 (1)The ratio of protons to nucleons must satisfy the balance between their number densities and reaction rates:
(1)The ratio of protons to nucleons must satisfy the balance between their number densities and reaction rates: 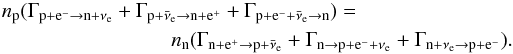 (2)The reaction rates are the sum of forward and backward rates and are given by the following formulae (Reddy et al. 1998; Kohri et al. 2005):
(2)The reaction rates are the sum of forward and backward rates and are given by the following formulae (Reddy et al. 1998; Kohri et al. 2005): 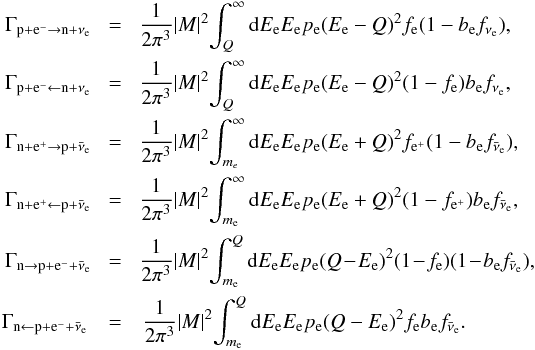 (3)Here Q = (mn − mp)c2 is the (positive) difference between neutron and proton masses and | M | 2 is the averaged transition rate which depends on the initial and final states of all participating particles. For nonrelativistic and noninteracting nucleons,
(3)Here Q = (mn − mp)c2 is the (positive) difference between neutron and proton masses and | M | 2 is the averaged transition rate which depends on the initial and final states of all participating particles. For nonrelativistic and noninteracting nucleons, 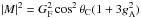 , where GF ≃ 1.436 × 10-49 erg cm3 is the Fermi weak interaction constant, θC(sinθC = 0.231) is the Cabibbo angle, and gA = 1.26 is the axial-vector coupling constant. Here, fe and fνe are the distribution functions for electrons and neutrinos, respectively. The chemical potential of neutrinos is zero for the neutrino transparent matter. When neutrinos are trapped, the factor be reflects the percentage of the partially trapped neutrinos.
, where GF ≃ 1.436 × 10-49 erg cm3 is the Fermi weak interaction constant, θC(sinθC = 0.231) is the Cabibbo angle, and gA = 1.26 is the axial-vector coupling constant. Here, fe and fνe are the distribution functions for electrons and neutrinos, respectively. The chemical potential of neutrinos is zero for the neutrino transparent matter. When neutrinos are trapped, the factor be reflects the percentage of the partially trapped neutrinos.
In addition, two other conditions that need to be satisfied are the conservation of the baryon number, nn + np = nb × Xnuc, and charge neutrality (Yuan 2005), 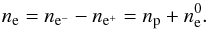 (4)The above condition includes the formation of the helium nuclei. Therefore, the net number of electrons is equal to the number of free protons plus the number of protons in helium, given by
(4)The above condition includes the formation of the helium nuclei. Therefore, the net number of electrons is equal to the number of free protons plus the number of protons in helium, given by 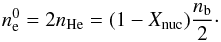 (5)
(5)
2.1. Chemical potential of neutrinos
In the neutrino transparent regime, the neutrinos are not thermalized, and the chemical potential of neutrinos is negligible (see, e.g., Beloborodov 2003). In the neutrino opaque regime when neutrinos are totally trapped, the chemical equilibrium condition yields μe + μp = μn + μν. The chemical potential of neutrinos depends on how many neutrinos and anti-neutrinos are trapped, assuming that the number densities of the trapped neutrinos and anti-neutrinos are the same, where μν = 0.
For the intermediate regime of partially trapped neutrinos, the Boltzmann equation should be solved. To simplify this problem, we use the “gray body” model with a blocking factor b = ∑ i = e,μ,τbi. (Sawyer 2003; Janiuk et al. 2007). The neutrino distribution function is then 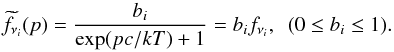 (6)When neutrinos are completely trapped, the blocking factor is bi = 1.
(6)When neutrinos are completely trapped, the blocking factor is bi = 1.
2.2. Electron fraction and nucleosynthesis
In Fig. 1, we show the contours of the constant electron fraction on the temperature-density plane. This value, calculated as 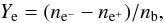 (7)is defined by the net number of electrons, which is equal to the number density difference between electrons and positrons. From the charge neutrality condition, it is equal to the number of free protons plus the number of electrons in helium nuclei if they are formed. Therefore, the electron fraction is modified here by the helium synthesis process.
(7)is defined by the net number of electrons, which is equal to the number density difference between electrons and positrons. From the charge neutrality condition, it is equal to the number of free protons plus the number of electrons in helium nuclei if they are formed. Therefore, the electron fraction is modified here by the helium synthesis process.
The contour of Ye = 0.5 corresponds to the helium number density of nHe = 1/4(nb − 2np). If the neutrons do not dominate over protons, the helium density would vanish here. The top-right region of this figure represents the contours with nHe< 1/4(nb − 2np), where helium abundance is smaller and the electron-positron pairs are produced.
 |
Fig. 1 Electron-fraction contours in the temperature-density plane. The matter is partially opaque to neutrinos. helium nuclei and electron-positron pairs are included in the chemical balance. |
The electron fraction defined above is different from the equilibrium value, defined as Yp = 1/(1 + nn/np), which is given by the ratio of number densities of protons to nucleons. The reason is due to the presence of electron-positron pairs and helium nuclei in the plasma. This “proton fraction” is plotted in Fig. 2. The established chemical balance between the neutronization reactions leads to the neutron excess, therefore, in the temperature and density range shown in the figure; the free proton number density is mostly np< 1/2(np + nn).
 |
Fig. 2 Proton-fraction contours in the temperature-density plane. The values below 0.5 correspond to the excess of free neutrons over protons. |
3. Accretion hydrodynamics
We consider the vertically integrated accretion disk around a black hole of mass M and a dimensionless spin parameter a, (Janiuk & Yuan 2010). The surface density of the disk is Σ = Hρ, where ρ is the baryon density and the height is given by H = cs/ ΩK. Here, the speed of sound is defined by 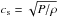 , ΩK = c3/ (GM(a + (r/rg)3/2)) is the Keplerian angular velocity, rg = GM/c2 is the gravitational radius, and P is the total pressure. At very high accretion rates, we note that the disk becomes geometrically “slim” (H ~ − 0.3 − 0.5r) in regions, where neutrino cooling becomes inefficient and advection dominates.
, ΩK = c3/ (GM(a + (r/rg)3/2)) is the Keplerian angular velocity, rg = GM/c2 is the gravitational radius, and P is the total pressure. At very high accretion rates, we note that the disk becomes geometrically “slim” (H ~ − 0.3 − 0.5r) in regions, where neutrino cooling becomes inefficient and advection dominates.
For the disk viscous stress, we use the standard α viscosity prescription of Shakura & Sunyaev (1973), where the stress tensor is proportional to the pressure: 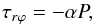 (8)and we take a fiducial value of α = 0.1.
(8)and we take a fiducial value of α = 0.1.
The total pressure is contributed by free nuclei, electron-positron pairs, helium, radiation, and the trapped neutrinos. The fraction of each species is determined by self-consistently solving the balance of the nuclear reaction rates. 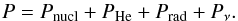 (9)where
(9)where 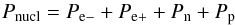 (10)with
(10)with ![\begin{equation} P_{i} = {2 \sqrt{2}\over 3\pi^{2}} {(m_{i}c^{2})^{4} \over (\hbar c)^{3}}\beta_{i}^{5/2} \left[F_{3/2}(\eta_{\rm i},\beta_{\rm i})+{1\over 2} \beta_{\rm i}F_{5/2}(\eta_{\rm i},\beta_{\rm i})\right]. \label{eq:pi} \end{equation}](/articles/aa/full_html/2014/08/aa23822-14/aa23822-14-eq53.png) (11)Here, Fk are the Fermi-Dirac integrals on the order k, and ηe, ηp and ηn are the reduced chemical potentials of electrons, protons and neutrons in units of kT, respectively, where ηi = μi/kT. The reduced chemical potential (or degeneracy parameter) of positrons is ηe + = −ηe − 2 /βe. The relativity parameters of the species i are defined as βi = kT/mic2.
(11)Here, Fk are the Fermi-Dirac integrals on the order k, and ηe, ηp and ηn are the reduced chemical potentials of electrons, protons and neutrons in units of kT, respectively, where ηi = μi/kT. The reduced chemical potential (or degeneracy parameter) of positrons is ηe + = −ηe − 2 /βe. The relativity parameters of the species i are defined as βi = kT/mic2.
The pressure of non-relativistic and non-degenerate helium is given by 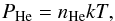 (12)where the density is
(12)where the density is 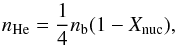 (13)and the fraction of free nucleons scales with density and temperature as
(13)and the fraction of free nucleons scales with density and temperature as 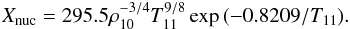 (14)Here, T11 is the temperature in the units of 1011 K, and ρ10 is density in the units of 1010 g cm-3 (Qian & Woosley 1996; Popham et al. 1999; Janiuk et al. 2007).
(14)Here, T11 is the temperature in the units of 1011 K, and ρ10 is density in the units of 1010 g cm-3 (Qian & Woosley 1996; Popham et al. 1999; Janiuk et al. 2007).
The radiation pressure is negligible in comparison with other terms in the GRB central engines. However, when neutrinos are trapped in the disk, the neutrino pressure is non-zero. Following the treatment of photon transport under the two-stream approximation (Popham & Narayan 1995; Di Matteo et al. 2002), we have 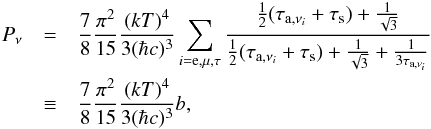 (15)where τs is the scattering optical depth due to the neutrino scattering on free neutrons and protons and τa,νe and τa,νμ are the absorptive optical depths for electron and muon neutrinos. The absorption of electron neutrinos is determined by the reactions inverse to all their production processes: electron-positron capture on nucleons, electron-positron pair annihilation, nucleon bremsstrahlung and plasmon decay. The absorption of muon neutrinos is governed by the rates of pair annihilation and bremsstrahlung reactions, and the contribution from tau neutrinos is the same as that from muon neutrinos. The scattering optical depth is the Rosseland mean opacity,as derived for all the neutrinos from their cross-section of scattering on nucleons (Di Matteo et al. 2002).
(15)where τs is the scattering optical depth due to the neutrino scattering on free neutrons and protons and τa,νe and τa,νμ are the absorptive optical depths for electron and muon neutrinos. The absorption of electron neutrinos is determined by the reactions inverse to all their production processes: electron-positron capture on nucleons, electron-positron pair annihilation, nucleon bremsstrahlung and plasmon decay. The absorption of muon neutrinos is governed by the rates of pair annihilation and bremsstrahlung reactions, and the contribution from tau neutrinos is the same as that from muon neutrinos. The scattering optical depth is the Rosseland mean opacity,as derived for all the neutrinos from their cross-section of scattering on nucleons (Di Matteo et al. 2002).
Throughout the calculations we adopt fiducial values of parameters: black hole mass of M = 3 M⊙, dimensionless spin a = 0.9, and viscosity parameter α = 0.1. We solve the hydrodynamical balance to establish the structure of the accretion disk, by adopting the standard mass, energy, and momentum conservation equations. The viscous heating, Q+ = 3/2αPΩH, is balanced by the advective cooling, Qadv = ΣvrTdS/ dr, photodissociation of alpha particles (if they form) and the radiative and neutrino cooling, Qν. Therefore, we calculate the stationary disk configuration from 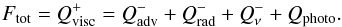 (16)On the left hand side, we have the vertically integrated viscous heating rate per unit area over a half thickness, H, which is given by the global parameters of the model; that is black hole mass and accretion rate,
(16)On the left hand side, we have the vertically integrated viscous heating rate per unit area over a half thickness, H, which is given by the global parameters of the model; that is black hole mass and accretion rate, 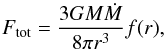 (17)where f(r) denotes the boundary condition around the spinning Kerr black hole (Bardeen et al. 1972; Riffert & Herold 1995).
(17)where f(r) denotes the boundary condition around the spinning Kerr black hole (Bardeen et al. 1972; Riffert & Herold 1995).
In the advective cooling term, the entropy gradient is assumed to be constant with radius and be on the order of unity. The entropy is the sum of four components, which correspond to the pressure terms 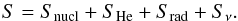 (18)Here,
(18)Here, 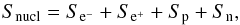 (19)and the contributions from electrons, positrons, protons and neutrons are
(19)and the contributions from electrons, positrons, protons and neutrons are 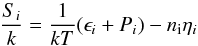 (20)with
(20)with ![\begin{equation} \epsilon_{i} = {2 \sqrt{2}\over 3\pi^{2}} {\left(m_{i}c^{2}\right)^{4} \over (\hbar c)^{3}}\beta_{i}^{5/2} \left[F_{3/2}(\eta_{i},\beta_{i})+\beta_{i}F_{5/2}(\eta_{i},\beta_{i})\right]. \end{equation}](/articles/aa/full_html/2014/08/aa23822-14/aa23822-14-eq88.png) (21)Here Pi is the pressure components of the species, ni the number densities, and ηi the reduced chemical potentials.
(21)Here Pi is the pressure components of the species, ni the number densities, and ηi the reduced chemical potentials.
If the helium nuclei form, their entropy is given by ![\begin{equation} S_{\rm He} = n_{\rm He} \left[{5 \over 2} + {3\over 2} \log \left(m_{\rm He} {kT\over {(\hbar c)^{2}}}{1\over 2\pi}\right)-\log n_{\rm He}\right], \end{equation}](/articles/aa/full_html/2014/08/aa23822-14/aa23822-14-eq92.png) (22)for nHe> 0.
(22)for nHe> 0.
The cooling term due to photodisintegration of α particles has a rate of 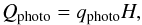 (23)where
(23)where 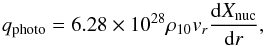 (24)and Xnuc is the mass fraction of free nucleons.
(24)and Xnuc is the mass fraction of free nucleons.
The radiative cooling, 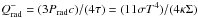 , is in practice a negligible term in comparison with other terms for our assumed global flow parameters. The neutrino cooling rate is high, if only the neutrinos are not completely trapped. In the neutrino optically thick disk, their cooling rate is given by
, is in practice a negligible term in comparison with other terms for our assumed global flow parameters. The neutrino cooling rate is high, if only the neutrinos are not completely trapped. In the neutrino optically thick disk, their cooling rate is given by 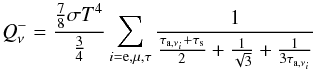 (25)where we include the absorption and scattering optical depths for all three neutrino flavors, following their emission processes, as in Janiuk et al. (2007).
(25)where we include the absorption and scattering optical depths for all three neutrino flavors, following their emission processes, as in Janiuk et al. (2007).
 |
Fig. 3 Mass fraction of free nucleons as a function of distance in the accreting disk. The steady-state models were calculated for Ṁ = 1.0 M⊙ s-1 (top panel) and Ṁ = 0.1 M⊙ s-1 (bottom panel). The radius is in units of rg = GM/c2 and M = 3 M⊙. |
4. Results
4.1. Mass fraction of free nucleons in the inner disk
In Fig. 3, we plot the mass fraction of free nucleons in the accretion disk that power the central engine of GRB. The figure shows two values of accretion rate, Ṁ = 0.1 M⊙ s-1 and Ṁ = 1.0 M⊙ s-1. We adopt the black hole mass of 3 M⊙.
For a given accretion rate, the converged solution for Xnuc is not sensitive to the black hole spin value and its only effect is on the location of marginally stable orbit. The disk is located closer to the black hole gravitational radius, rg = GM/c2, for a large spin value.
Depending on the accretion rate, we find the regions of helium formation in the disk. For a given black hole spin, a = 0.9, the smaller Ṁ = 0.1 M⊙ s-1 solution results in a constant maximum value of Xnuc = 1.0 below the radius of about 100rg. For our assumed mass of the black hole it is about 450 km. Outside this radius, the helium nuclei start forming. Above ~ 300rg, the mass fraction of free nucleons drops to zero and the accreting flow is dominated by helium. For a larger value of accretion rate, Ṁ = 1.0 M⊙ s-1, this outer zone dominated by helium nuclei is shifted outwards to above ~ 630rg; while below ~ 250rg, there is no helium nuclei.
In Fig. 4, we show the number densities of free particles in the disks with two accretion rate values. Free neutrons are dominant species in a large part of the disk up to 40rg for Ṁ = 0.1 M⊙ s-1 and up to 250rg for Ṁ = 1.0 M⊙ s-1. Out from this region, neutrons and protons are synthesizing the helium nuclei, and the electron-positron pairs are still abundant, which keeps the charge neutrality.
For Ṁ = 1.0 M⊙ s-1 in the inner 10rg, the number density of free neutrons is reduced with a flattened radial profile, and the density of protons is smaller. The reason is that protons are more degenerate than neutrons at these density and temperature regime.
 |
Fig. 4 Number density of free particles as a function of distance in the accreting disk, which are plotted for neutrons (solid line), protons (dotted line), electrons (short dashed line), and positrons (long dashed line). The steady-state models were calculated for Ṁ = 1.0 M⊙ s-1 (top panel) and Ṁ = 0.1 M⊙ s-1 (bottom panel). The assumed black hole spin parameter is a = 0.9. |
In Fig. 5, we show the electron fraction Ye, which is calculated as the net number of electrons per baryon (Eq. (7)). The dashed line in this figure compares the “proton fraction”, as derived from the ratio of free neutrons to protons. If the latter is smaller than 0.5, the free neutrons dominate over protons, which is the case in the innermost 50−500 gravitational radii of the disk, depending on its accretion rate. The electron fraction, which is plotted with the solid line, changes due to the formation of helium nuclei. In the outer regions of the disk, the value of electron fraction is saturated at 0.5, while the number densities of neutrons are slightly less than protons, but increase with radius. The efficient neutronization eventually allows for the maximum helium abundance at the outskirts of the disk.
 |
Fig. 5 Electron fraction as a function of distance in the accreting disk. The steady state models were calculated for Ṁ = 1.0 M⊙ s-1 (top panel) and Ṁ = 0.1 M⊙ s-1 (bottom panel). The assumed black hole spin parameter is a = 0.9. Dashed lines show the corresponding proton fraction. |
4.2. Formation of heavy elements in the outer disk
The steady-state models were computed for accretion rates of Ṁ = 1.0 M⊙ s-1 and Ṁ = 0.1 M⊙ s-1 with a black hole dimensionless spin equal to a = 0.9. In these conditions, the density range in the disk, which is up to 1000 gravitational radii, is 3 × 1011 − 106 g cm-3 or 5 × 1011 − 107 g cm-3 for accretion rates of 0.1 and 1.0 M⊙s-1, respectively. The corresponding temperature range is 5 × 1010 − 1.5 × 109 K and 1.2 × 1011 − 2 × 109 K. The innermost temperatures, therefore, may reach 5 or 10 MeV, while the regions, where temperature decreases below 1 MeV, are located in the outer disk parts above 50 or 100 gravitational radii.
To compute the abundances of heavy elements, we used the thermonuclear reaction network code1. The computational methods are described in detail in Seitenzahl et al. (2008) (see also Meyer 1994; Wallerstein et al. 1997; and Hix & Meyer 2006). The code uses the nuceq library to compute the nuclear statistical equilibria established for the thermonuclear fusion reactions. The abundances are calculated under the constraints of nucleon number conservation and charge neutrality. We used the correction function to account for degeneracy of relativistic species here. We used the data downloaded from JINA website2, prepared for studies of the nuclear masses and nuclear partition functions, and for computations of the nuclear statistical equilibria. The reaction data available on JINA reaclib online database provide the currently best determined reaction rates. The nuclide data are merged with reaction data into a network data file, as prepared for astrophysical applications. The network is working well for the temperature ranges about or below 1 MeV, and our method is appropriate for the outer parts of accretion disks in GRBs. For hotter astrophysical plasmas, more advanced computations could be appropriate (Kafexhiu et al. 2012).
Once we have computed the accretion disk model for the GRB central engine, the mass fraction of heavy nuclei was then computed at every radius of the disk, given the profiles of density, temperature and electron fraction. In Figs. 6 and 7, we show the resulting distributions of the most abundant isotopes of heavy elements synthesized in the accretion disk.
 |
Fig. 6 Nucleosynthesis of heavy elements in the accretion disk. The steady-state model is calculated for an accretion rate of Ṁ = 0.1 M⊙ s-1 and a black hole spin a = 0.9. The top panel shows the abundance distribution of free protons and neutrons (dashed lines), as well as helium, and the most abundant isotopes of nickel, iron, and cobalt. The bottom panel shows the distribution of the most abundant isotopes of silicon, sulphur, clorium, argonium, manganium, titatnium, vanadium, and cuprum. |
We first checked for these isotopes, whose mass fraction is greater than 10-4. For the accretion rate of 0.1 M⊙ s-1, the abundance of 4He is large with a value up to 260rg and then decreases throughout the disk; there is some fraction of 3He, Deuterium, and Tritium. The next abundant isotopes are 28Si - 30Si, 31P, 32S - 34S, then 35Cl, and 36Ar - 38Ar. Further, synthesized isotopes are 39K, 40Ca - 42Ca, 44Ti - 50Ti, 47V - 52V, 48Cr - 54Cr, and 51Mn - 56Mn. The most abundant iron isotopes formed in the disk are 52Fe through 58Fe; cobalt is formed with isotopes 54Co through 60Co, and nickel isotopes are 56Ni through 62Ni. The heaviest most abundant isotopes in our disk are 59Cu through 63Cu. Further, there is a smaller fraction of zinc, 60Zn - 64Zn, with a mass fraction above 10-5. These heavy elements are generally produced outside 300−400rg. Inside this radius, the disk consists of mainly free neutrons and protons with some fraction of helium. The mass fraction of free neutrons is smaller than that of protons, and free neutrons disappear above ~ 300rg.
 |
Fig. 7 Nucleosynthesis of heavy elements in the accretion disk. The steady-state model is calculated for an accretion rate of Ṁ = 1.0 M⊙ s-1 and a black hole spin a = 0.9. Top panel: abundance distribution of free protons and neutrons (dashed lines) as well as helium, and most abundant isotopes of nickel, iron and cobalt. Bottom panel: distribution of the most abundant isotopes of argonium, titatnium, cuprum, and zinc. |
For the model with an accretion rate of 1.0 M⊙ s-1, the abundance of 4He is large, up to about 600rg and then decreases. There is also some deuterium and tritium, while the next abundant isotopes are 28Si - 30Si, 31P, 32S - 34S, 35Cl, and 36Ar - 38Ar. Next, there is 39K, 40Ca - 42Ca, 45Sc - 47Sc, 44Ti - 50Ti, and 47V - 52V. Synthesized isotopes include 48Cr - 55Cr, 50Mn - 57Mn, and 52Fe - 59Fe. Further heavy elements are 54Co - 61Co, 56Ni - 63Ni, and 58Cu - 63Cu. The last abundant heavy isotope is 62Zn, while the abundances of 65Ga and 67Ga are about 10-6. In comparison to the model with small accretion rate presented above, the conditions in the larger accretion rate disk are such that the mass fraction of free neutrons is larger than that of free protons inside ~ 200rg and comparable to a proton mass fraction up to ~ 500rg. In both models, the heavy elements dominate above ~ 550rg.
5. Outflows
The outflow of gas from the accretion disk surface may be driven by a centrifugal force or a magnetic field (McKinney 2006; Janiuk et al. 2013). In either case, the flow can be described by a spherical geometry and velocity depending on the distance that computes trajectories of particles (Surman & McLaughlin 2004). The slowly accelerated outflows will produce heavier elements via the triple-alpha reactions up to nickel 56, or, if the entropy per baryon is quite low, the reactions produce nuclei up to iron peak (Woosley 1973). Also, other heavy nuclei such as Sc, Ti, Zi, and Mo, may be produced in the outflows with a moderate abundance (Surman et al. 2006).
For the accretion rate of 0.1 M⊙ s-1, our calculations show the significant proton excess in the disk above ~250rg. The wind ejected at this region may therefore provide a substantial abundance of light elements, Li, Be, and B. The high-accretion rate disk, on the other hand, produces neutron rich outflows and forms heavy nuclei via the r-process. As we show here, the outflows ejected from the innermost 100rg in the high-accretion rate disks are also significantly neutron rich. Therefore these neutron-loaded ejecta, which are accelerated via the black hole rotation, feed the collimated jets at a large distance from the central engine. This has important implications for the observed GRB afterglows, which are induced by the radiation drag (Metzger et al. 2008) and collisions between the proton-rich and neutron-rich shells within the GRB fireball (Beloborodov 2003).
6. Conclusions
We considered the central engine model for GRBs, which result from the massive rotating star collapse or a compact object merger. The two accretion rates invoked as model parameters refer to these two progenitor types, which is usually suggested for long and short GRBs. Our numerical modeling of the accretion flow around a spinning black hole shows that the flow is transparent to neutrinos and free species are only mildly degenerate for moderate accretion rates (~ 0.1 M⊙ s-1). helium nucleosynthesis occurs at the distance of ~ 100 gravitational radii. For large accretion rates above ~ 1 M⊙ s-1, the innermost part of the disk is opaque to neutrinos. Here, the neutrons, protons, and electrons are degenerate. The outflows from this region should be neutron rich. The neutrons, therefore, should be present at large distances within the expanding fireball (i.e. ~ 1017 cm). Their large kinetic energy affects the dynamics of the expanding fireball and leads to interaction with the circumburst medium (Lei et al. 2013).
Our results are in line with those obtained by other groups, who are working on nucleosynthesis models of GRB engines. In particular, Fujimoto et al. (2004) also compute the nuclear synthesis of elements in the accretion disk up to 1000 gravitational radii, and they find more distant layers of dominant oxygen, silicon, and calcium with their abundances enhanced by the α-capture process. With a mass fraction about ~ 1, these elements may be present in large collapsar disks. However, the disk is probably not larger in most progenitors. Nevertheless, we obtain similar results for the isotopes synthesized above ~ 100rg (note that we define rg = GM/c2), and we also find a trend of shifting the layers outward with an increasing accretion rate. We estimate the transition radius for the subsequent layers to be rtr ~ Ṁ-0.28. At the outer parts of the disk, Fujimoto et al. (2004) studied the synthesis of light elements such as 16O, 28Si, and 40Ca, which has mass fractions above 0.0001. We find the mass fraction of 16O to be less than 10-4 inside 1000 gravitational radii, while they are about 0.01 at their peak, at around few hundred rg, for the other two elements . For the heavier elements above the Iron peak, their yields were computed by Surman et al. (2006). Our reaction network results give the isotopes of 74Se, 80Kr, and 84Sr with the abundances of about 10-10, 10-12 and 10-14, respectively, in the case of smaller accretion rate disk. We also found isotopes of 84Rb and 90Zr with mass fractions of 10-12 and 10-14, respectively, for a higher accretion rate disk model.
The main difference among our work, those of Fujimoto et al. (2004) and those of Surman & McLaughlin (2004) results from our model of the accretion disk and detailed treatment of its microphysics, which follows the EOS discussed in detail in Janiuk et al. (2007). In the resulting structure of the disk below ~10rg, we have more neutron-rich material, and the ratio of free neutrons to protons exceeds nn/np = 10 at the inner disk region for Ṁ = 0.1 M⊙ s-1. Outward of ~50rg, the disk is proton rich. For a higher accretion rate, this neutron rich region is shifted outward to >100rg, while we have nn/np ≈ 3 at the inner edge . The electron fraction profiles in our models have the same qualitative trends as the other authors have found and saturate at Ye = 0.5 at the outer disk edge, while they decrease inward to Ye ~ 0.1 due to electron capture. Overall, our profiles are below those found by Fujimoto et al. (2004). We also find a small bump with Ye ~ 0.7 around the radius 160−250rg, depending on accretion rate, located where most of the helium is synthesized. Another small bump, where the electron fraction locally rises to Ye ~ 0.2, is found for high-accretion rate of Ṁ = 1.0 M⊙ s-1.
The effects of photodissociation of helium might have an important effect on its stability properties (Janiuk et al. 2007). This destabilizing process is not suppressed by forces, such as by a magnetic torque that is exerted on the disk by a rotating black hole (Lei et al. 2009; Janiuk & Yuan 2010).
The heavy elements, up to 56Ni, are synthesized efficiently in the outer parts of the disk. These nucleosynthesis processes occur at above ~ 250rg or ~ 500rg, depending on the accretion rate. These elements, such as silicon, phosphorus, sulphur, calcium, argonium, potassium, and the various isotopes, titanium, vanadium, chromium, manganese, iron, and cobalt, are present in wind outflows ejected from the surface of accretion disks. These elements should be observable in the GRB spectra (Reeves et al. 2003), and help constrain the properties of the central engine in the GRB explosions (see, e.g., Margutti et al. 2013).
Moreover, we found non-negligible abundances of elements above nickel, such as isotopes of copper, zinc, gallium, and
germanium, which could be found in the afterglows of short GRBs. The different properties of central engines in the two classes of bursts that determine the nucleosynthesis should therefore also be accounted for in the statistical studies of the observed phenomena (Zhang et al. 2006; Gehrels et al. 2008).
The radioactive decay of certain isotopes should be detectable via the emission lines observed by X-ray satellites. These lines, such as those found in the decay of 44Ti to 40Ca with emission of hard X-ray photons at 68 and 78 keV, have been detected by NuSTAR in the case of supernova remnants. The energy band of this instrument (3−80 keV) should be appropriate to find the X-ray signatures of other elements synthesized in the accretion disks in GRB central engines, like the radioactive isotopes of cuprum, zinc, gallium, cromium, and cobalt. The heavy elements, which were once ejected with a wind outflow from the engine, might also give their imprints in the absorption lines of the GRB optical spectra (Kawai et al. 2006).
Acknowledgments
We thank Irek Janiuk for discussions and help in parallelization of our code. We also thank Carole Mundell and Greg Madejski, and the anonymous referee for helpful comments. This work was supported in part by the grant NN 203 512 638, from the Polish National Science Center. We finally acknowledge inspiration and support by the COST Action MP0905.
References
- Banerjee, I., & Mukhopadhyay, B. 2013, ApJ, 778, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Beloborodov, A. M. 2003, ApJ, 588, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, T., Perna, R., & Narayan, R. 2002, ApJ, 579, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, S.-I., Hashimoto, M.-A., Arai, K., & Matsuba, R. 2004, ApJ, 614, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Barthelmy, S. D., Burrows, D. N., et al. 2008, ApJ, 689, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Hix, W. R., & Meyer, B. S. 2006, Nucl. Phys. A, 777, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Janiuk, A., & Yuan, Y.-F. 2010, A&A, 509, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janiuk, A., Yuan, Y., Perna, R., & Di Matteo, T. 2007, ApJ, 664, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Janiuk, A., Mioduszewski, P., & Moscibrodzka, M. 2013, ApJ, 776, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Kafexhiu, E., Aharonian, F., & Vila, G. S. 2012, Int. J. Mod. Phys. D, 21, 50009 [Google Scholar]
- Kawai, N., Kosugi, G., Aoki, K., et al. 2006, Nature, 440, 184 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kohri, K., Narayan, R., & Piran, T. 2005, ApJ, 629, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Lei, W. H., Wang, D. X., Zhang, L., et al. 2009, ApJ, 700, 1970 [NASA ADS] [CrossRef] [Google Scholar]
- Lei, W.-H., Zhang, B., & Liang, E.-W. 2013, ApJ, 765, 125 [NASA ADS] [CrossRef] [Google Scholar]
- MacFadyen, A. I., & Woosley, S. E. 1999, ApJ, 524, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Margutti, R., Soderberg, A. M., Wieringa, M. H., et al. 2013, ApJ, 778, 18 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, J. C. 2006, MNRAS, 368, 1561 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D., Thompson, T. A., & Quataert, E. 2008, ApJ, 676, 1130 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, B. S. 1994, ARA&A, 32, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Piran, T. 2004, Rev. Mod. Phys., 76, 1143 [Google Scholar]
- Popham, R., & Narayan, R. 1995, ApJ, 442, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Popham, R., Woosley, S. E., & Fryer, C. 1999, ApJ, 518, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, Y.-Z., & Woosley, S. E. 1996, ApJ, 471, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, S., Prakash, M., & Lattimer, J. M. 1998, Phys. Rev. D, 58, 013009 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, J. N., Watson, D., Osborne, J. P., Pounds, K. A., & O’Brien, P. T. 2003, A&A, 403, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riffert, H., & Herold, H. 1995, ApJ, 450, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Sawyer, R. F. 2003, Phys. Rev. D, 68, 3001 [CrossRef] [Google Scholar]
- Seitenzahl, I. R., Timmes, F. X., Marin-Laflèche, A., et al. 2008, ApJ, 685, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Surman, R., & McLaughlin, G. C. 2004, ApJ, 603, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Surman, R., McLaughlin, G. C., & Hix, W. R. 2006, ApJ, 643, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Wallerstein, G., Iben, Jr., I., Parker, P., et al. 1997, Rev. Mod. Phys., 69, 995 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E. 1973, ApJ, 186, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E. 1993, ApJ, 405, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., & Mészáros, P. 2004, Int. J. Mod. Phys. A, 19, 2385 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., Fan, Y. Z., Dyks, J., et al. 2006, ApJ, 642, 354 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Electron-fraction contours in the temperature-density plane. The matter is partially opaque to neutrinos. helium nuclei and electron-positron pairs are included in the chemical balance. |
| In the text | |
 |
Fig. 2 Proton-fraction contours in the temperature-density plane. The values below 0.5 correspond to the excess of free neutrons over protons. |
| In the text | |
 |
Fig. 3 Mass fraction of free nucleons as a function of distance in the accreting disk. The steady-state models were calculated for Ṁ = 1.0 M⊙ s-1 (top panel) and Ṁ = 0.1 M⊙ s-1 (bottom panel). The radius is in units of rg = GM/c2 and M = 3 M⊙. |
| In the text | |
 |
Fig. 4 Number density of free particles as a function of distance in the accreting disk, which are plotted for neutrons (solid line), protons (dotted line), electrons (short dashed line), and positrons (long dashed line). The steady-state models were calculated for Ṁ = 1.0 M⊙ s-1 (top panel) and Ṁ = 0.1 M⊙ s-1 (bottom panel). The assumed black hole spin parameter is a = 0.9. |
| In the text | |
 |
Fig. 5 Electron fraction as a function of distance in the accreting disk. The steady state models were calculated for Ṁ = 1.0 M⊙ s-1 (top panel) and Ṁ = 0.1 M⊙ s-1 (bottom panel). The assumed black hole spin parameter is a = 0.9. Dashed lines show the corresponding proton fraction. |
| In the text | |
 |
Fig. 6 Nucleosynthesis of heavy elements in the accretion disk. The steady-state model is calculated for an accretion rate of Ṁ = 0.1 M⊙ s-1 and a black hole spin a = 0.9. The top panel shows the abundance distribution of free protons and neutrons (dashed lines), as well as helium, and the most abundant isotopes of nickel, iron, and cobalt. The bottom panel shows the distribution of the most abundant isotopes of silicon, sulphur, clorium, argonium, manganium, titatnium, vanadium, and cuprum. |
| In the text | |
 |
Fig. 7 Nucleosynthesis of heavy elements in the accretion disk. The steady-state model is calculated for an accretion rate of Ṁ = 1.0 M⊙ s-1 and a black hole spin a = 0.9. Top panel: abundance distribution of free protons and neutrons (dashed lines) as well as helium, and most abundant isotopes of nickel, iron and cobalt. Bottom panel: distribution of the most abundant isotopes of argonium, titatnium, cuprum, and zinc. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


