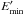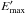| Issue |
A&A
Volume 568, August 2014
|
|
|---|---|---|
| Article Number | A57 | |
| Number of page(s) | 14 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201423761 | |
| Published online | 14 August 2014 | |
Modeling the cross power spectrum of the Sunyaev-Zel’dovich and X-ray surveys
Institut d’Astrophysique Spatiale, CNRS (UMR 8617) and Université Paris-Sud
11,
Bâtiment 121,
91405
Orsay,
France
e-mail:
ghurier@ias.u-psud.fr
Received:
5
March
2014
Accepted:
25
May
2014
The thermal Sunyaev-Zel’dovich (tSZ) effect and X-ray emission from galaxy clusters have been used extensively to constrain cosmological parameters. These constraints are highly sensitive to the relations between cluster masses and observables (tSZ and X-ray fluxes). The cross-correlation of tSZ and X-ray data is thus a powerful tool, in addition of tSZ and X-ray based analysis, for testing our modeling of both tSZ and X-ray emission from galaxy clusters. We chose to explore this cross-correlation because both emissions trace the hot gas in galaxy clusters and thus constitute one of the easiest correlations that can be studied. We present a complete modeling of the cross-correlation between tSZ effect and X-ray emission from galaxy clusters and focus on the dependencies with cluster scaling laws and cosmological parameters. We show that current knowledge of cosmological parameters and scaling-law parameters leads to uncertainties of 48% on the overall normalization of the tSZ-X cross-correlation power spectrum. We present the expected signal-to-noise ratio for the tSZ-X cross-correlation angular power spectrum and consider the sensitivity of actual tSZ and X-ray surveys from Planck-like data and ROSAT. We demonstrate that this signal-to-noise can reach 31.5 in a realistic situation, leading to a constraint on the amplitude of tSZ-X cross-correlation up to 3.2%, which is ten times better than actual modeling limitations. Consequently, using it in addition to other probes of cosmological parameters and scaling relations, we show that the tSZ-X is a powerful probe that constrains the cosmological parameters of scaling relations.
Key words: galaxies: clusters: general / X-rays: galaxies: clusters / submillimeter: general / large-scale structure of Universe / galaxies: clusters: intracluster medium
© ESO, 2014
1. Introduction
Galaxy clusters are the largest virialized structures. They can be observed through X-ray, via the bremsstrahlung emission produced by the ionized intracluster medium (see, e.g., Bohringer et al. 2000; Ebeling et al. 2000, 2001). This hot intracluster medium also produces a distortion of the cosmic microwave background (CMB) black-body emission via the thermal Sunyaev-Zel’dovich (tSZ) effect (Sunyaev & Zeldovich 1969, 1972). This effect was observed toward a large number of clusters by Planck (Planck Collaboration VIII 2011; Planck Collaboration XXIX 2014), ACT (Marriage et al. 2011), and SPT (Reichardt et al. 2013).
The number of galaxy clusters is extremely sensitive to cosmological parameters, especially to the normalization of the matter power spectrum, σ8, and to the matter density, Ωm. It is thus possible to use galaxy cluster catalogs to constraint cosmological parameters (Vanderlinde et al. 2010; Sehgal et al. 2011; Planck Collaboration XX 2014) through a halo mass-function formalism.
We now have access to a full sky coverage for both X-ray emission with the ROSAT all sky survey (RASS) and tSZ emission with Planck (Planck Collaboration VIII 2011). Consequently, beyond tSZ clusters catalogs analysis, it is possible to perform tSZ angular power spectrum analysis. This process allows to consider all clusters on the covered sky without any selection function (see, e.g., Planck Collaboration VIII 2011), contrary to catalog-based analysis. This allows to catch the signals from higher redshift and lower mass objects that are not detected individually. Such measurement is limited by the contamination produced by other astrophysical components, mainly the cosmic infrared background (CIB, Puget et al. 1996; Fixsen et al. 1998).
It is difficult to perform the same power spectrum analysis with X-ray surveys. The X-ray photons, at low energy (<0.5 keV), are absorbed by neutral hydrogen of our Galaxy and, at higher energy, the X-ray sky power is dominated by the emission from active galactic nuclei (AGN). Consequently, X-ray surveys are most commonly used to constraint the AGN spatial clustering (Krumpe et al. 2010; Miyaji et al. 2011; Krumpe et al. 2012).
In addition to auto-correlation power spectrum analysis, the cross power spectrum between tSZ effect and X-ray emission can be used. This cross-correlation is one of the easiest correlations to study, since both signals are produced by the same hot gas of electrons. Using such an approach allows the contamination to be minimized by other astrophysical components and suppresses the instrumental noise contribution to the power spectrum.
The tSZ-X cross spectrum is sensitive to both X-ray and tSZ scaling relations (see, e.g, Benson et al. 2013; Planck Collaboration XI 2011; Arnaud et al. 2010, for present constraints on scaling relations). This sensitivity limits the determination of cosmological parameters. However, it offers another possibility for constraining tSZ and X-ray scaling laws.
The utilization of the tSZ-X correlation has already been discussed in the literature. Diego et al. (2003) has attempted to directly compare theoretical predictions with the measured cross power spectrum between WMAP temperature anisotropy maps and ROSAT All Sky Survey (RASS). The limited sensitivity and resolution of the WMAP experiment leads to upper limits on the tSZ-X correlation. More recently, Hajian et al. (2013) have performed the measurement of the cross-correlation between the tSZ sky and an X-ray based catalog of clusters. From their analysis they derive σ8(Ωm/ 0.30)0.26 = 0.80 ± 0.02.
We present an up-to-date modeling of the tSZ/X-ray cross-correlation. In Sect. 2, we present our modeling of the tSZ-X cross-correlation. We give particular attention to the distribution in mass and redshift of the tSZ-X power. In Sect. 3, we explore the variations in the tSZ-X spectrum with respect to cosmological and scaling-law parameters. We also discuss modeling uncertainties considering our knowledge on cosmological and scaling law parameters and present the main limitations for the tSZ-X correlation measurement using simulated Planck-like data. Finally in Sect. 4, we predict the expected signal-to-noise for the tSZ-X correlation from simulations of Planck-like tSZ survey and ROSAT All Sky Survey, and we present the associated constraints on cosmological, scaling-law, and profile parameters.
Throughout the paper, we used the Planck-CMB best-fitting cosmology (Planck Collaboration XVI 2014) as our fiducial cosmological model, unless otherwise specified. Thus, we consider H0 = 67.1 ± 1.4 km/s/Mpc, σ8 = 0.834 ± 0.027, and Ωm = 0.317 ± 0.020.
2. Modeling tSZ-Xray cross-correlation
2.1. The tSZ effect from galaxy clusters
The tSZ effect consists of a small spectral distortion of the CMB black body (Sunyaev & Zeldovich 1969, 1972), and its intensity is related to the integral of the pressure
across the line of sight via the Compton parameter. This parameter in a given direction of
the sky reads as 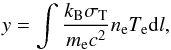 (1)where dl is the distance along
the line-of-sight, and ne and Te are the
electron number density and the temperature, respectively.
(1)where dl is the distance along
the line-of-sight, and ne and Te are the
electron number density and the temperature, respectively.
In units of CMB temperature, the contribution of the tSZ effect to the submillimeter sky
intensity for a given observation frequency ν is given by
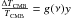 . Neglecting relativistic
corrections, we have
. Neglecting relativistic
corrections, we have ![\hbox{$g(\nu) = \left[ x {\rm coth} \left(\frac{x}{2}\right) - 4\right]$}](/articles/aa/full_html/2014/08/aa23761-14/aa23761-14-eq13.png) , with
x =
hν/
(kBTCMB).
This function is equal to 0 around 217 GHz and is negative at lower frequencies and positive for higher
frequencies. Thus the spectral distortion induced by the hot gas of baryons provides a
characteristic signal allowing the pressure distribution to be directly measured in galaxy
clusters. In the context of a ΛCDM cosmology, this spectral distortion is known to be independent of
the redshift. This has been tested and validated for a redshift range from 0 to 1 (Hurier et al. 2014). This characteristic spectral
distortion can be used to separate the tSZ from other emissions of the microwave sky to
derive Compton parameter map (see, e.g, Remazeilles et al.
2011; Hurier et al. 2013; Planck Collaboration VIII 2011).
, with
x =
hν/
(kBTCMB).
This function is equal to 0 around 217 GHz and is negative at lower frequencies and positive for higher
frequencies. Thus the spectral distortion induced by the hot gas of baryons provides a
characteristic signal allowing the pressure distribution to be directly measured in galaxy
clusters. In the context of a ΛCDM cosmology, this spectral distortion is known to be independent of
the redshift. This has been tested and validated for a redshift range from 0 to 1 (Hurier et al. 2014). This characteristic spectral
distortion can be used to separate the tSZ from other emissions of the microwave sky to
derive Compton parameter map (see, e.g, Remazeilles et al.
2011; Hurier et al. 2013; Planck Collaboration VIII 2011).
2.2. The X-ray emission from galaxy clusters
The ionized gas in the intracluster medium produces an X-ray emission via Bremsstrahlung.
This radiation is proportional to the square of the electronic density. The energy
spectrum of the X-ray emission from galaxy clusters depends mainly on the temperature,
T500, of the intracluster medium and„ to a
lesser extent on the metallicity, Z, of the gas. To model the metallicity evolution
history, we follow Andreon (2012) using the relation
derived from the analysis of 130 galaxy clusters in a redshift range from 0.1 to 1.3,
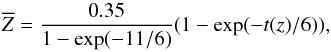 (2)with
t(z) the age of the universe at a
redshift z.
(2)with
t(z) the age of the universe at a
redshift z.
From an observational point of view, the X-ray spectrum depends on the redshift, z. X-ray photons are also absorbed by the neutral hydrogen in our Galaxy. This absorption is particularly significant for photons with E < 0.5 keV. Consequently, the observed count rate depends on the column density of neutral hydrogen, nH, on the line of sight.
To estimate the X-ray flux from each cluster, we computed an unabsorbed X-ray spectrum,
φunabs =
dnγ/
dE, with nγ the number of
emitted photons by the cluster inside a radius of R500, using a
MEKAL model (Mewe et al. 1985). To do this, we used
a relation between the physical properties of the cluster, mass, and redshift and the
temperature. These relations are presented in Sect. 2.5. Then, we computed the absorbed spectrum,φabs, as
![\begin{equation} \phi_{\rm abs}(E) = \phi_{\rm unabs}(E)\, {\rm exp}\left[-n_{\rm H} \sigma(E)\right], \end{equation}](/articles/aa/full_html/2014/08/aa23761-14/aa23761-14-eq28.png) (3)with σ(E) the
photoelectric cross section. The unabsorbed luminosity, L500, in a given
energy bin [
Emin,Emax
] of a cluster reads
as
(3)with σ(E) the
photoelectric cross section. The unabsorbed luminosity, L500, in a given
energy bin [
Emin,Emax
] of a cluster reads
as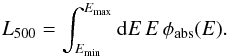 (4)Finally, the expected
number count in a given energy bin
(4)Finally, the expected
number count in a given energy bin ![\hbox{$[E'_{\rm min},E'_{\rm max}]$}](/articles/aa/full_html/2014/08/aa23761-14/aa23761-14-eq33.png) is computed as
is computed as
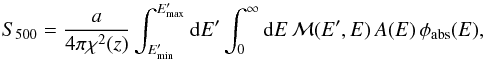 (5)where
χ(z) is the comoving angular
distance at redshift z, a the scale factor, A(E) the
effective area of the detector as a function of the energy, ℳ(E′,E) is the energy
redistribution matrix, E and E′ are the photon energy1 and the measured value of photon energy, respectively.
(5)where
χ(z) is the comoving angular
distance at redshift z, a the scale factor, A(E) the
effective area of the detector as a function of the energy, ℳ(E′,E) is the energy
redistribution matrix, E and E′ are the photon energy1 and the measured value of photon energy, respectively.
We define the flux to count-rate conversion factor as CR(z,Z,nH,T500)
=
S500/L500.
However, clusters can be located at any position on the sky, so we have to convolve the
CR factor
by the distribution of nH on the sky:
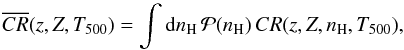 (6)where
(6)where
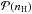 is the probability to have a column density of hydrogen nH on the line
of sight.
is the probability to have a column density of hydrogen nH on the line
of sight.
2.3. The tSZ-Xray cross power spectra
Decomposing both the tSZ Compton parameter map and X-ray count-rate map, we define
 Thus,
the power spectra of both tSZ effect and X-ray can be written as
Thus,
the power spectra of both tSZ effect and X-ray can be written as
 and
the angular cross power spectrum of tSZ effect and X-ray count-rate map reads
as
and
the angular cross power spectrum of tSZ effect and X-ray count-rate map reads
as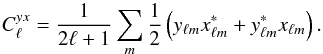 (11)To model this
cross-correlation or the auto correlation power spectra, we assume the following general
expression
(11)To model this
cross-correlation or the auto correlation power spectra, we assume the following general
expression 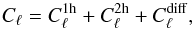 (12)where
(12)where
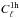 is
the Poissonian contribution,
is
the Poissonian contribution, 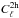 is
the two-halo term that accounts for correlation in the spatial distribution of clusters
over the sky, and
is
the two-halo term that accounts for correlation in the spatial distribution of clusters
over the sky, and 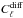 is
produced by the warm-hot intergalactic medium (WHIM). In the following, considering the
low density and the low temperature of the WHIM, we assume
is
produced by the warm-hot intergalactic medium (WHIM). In the following, considering the
low density and the low temperature of the WHIM, we assume
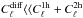 , and
thus we neglect his contribution to the total power spectrum.
, and
thus we neglect his contribution to the total power spectrum.
The Poissonian term can be computed by assuming the Fourier transform of tSZ and X-ray
projected profiles weighted by the mass function, presented in Sect. 2.4, and the fluxes for tSZ effect and X-ray count rate (see, e.g, Komatsu & Seljak 2002, for a derivation of the
tSZ angular power spectrum): 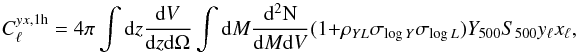 (13)
(13)
Scaling-law parameters and error budget for both Y500 − M500 (Planck Collaboration XX 2014), L500 − M500 (Arnaud et al. 2010), and Y500 − T500 (Planck Collaboration XX 2014) relations.
where 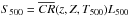 ,
,
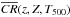 the flux to count-rate
conversion factor described in Sect. 2.2,
the flux to count-rate
conversion factor described in Sect. 2.2,
 the clusters mass function described in Sect. 2.4,
and
the clusters mass function described in Sect. 2.4,
and  the element of comoving volume. The term (1 +
ρYLσlog
Yσlog
L) accounts for extra power produced by the
scatter in the scaling relations described at Sect. 2.5.
the element of comoving volume. The term (1 +
ρYLσlog
Yσlog
L) accounts for extra power produced by the
scatter in the scaling relations described at Sect. 2.5.
The Fourier transform of the 3D profile projected across the line of sight on the sphere
reads as 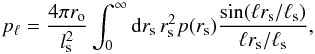 (14)where p(rs) is either the tSZ
3D profile or the X-ray count-rate 3D profile, and rs =
r/ro,
ℓs =
DA(z)
/ro, ro is the scale
radius of the profile.
(14)where p(rs) is either the tSZ
3D profile or the X-ray count-rate 3D profile, and rs =
r/ro,
ℓs =
DA(z)
/ro, ro is the scale
radius of the profile.
The contribution of the two-halo term corresponds to large scale fluctuations in the
matter power spectrum, which induce correlation in the cluster distribution over the sky.
It can be computed as (see, e.g, Taburet et al.
2011, and references therein)
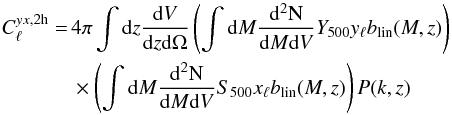 (15)with
P(k,z) the matter power spectrum
computed using CLASS (Lesgourgues
2011), and blin(M,z) the time
dependent linear bias factor that relates P(k,z) to the power spectrum of
the cluster distribution over the sky. Following Mo
& White (1996) and Komatsu &
Kitayama (1999), we adopt blin(M,z) = 1 +
(ν2(M,z) − 1)
/δc(z),
with
(15)with
P(k,z) the matter power spectrum
computed using CLASS (Lesgourgues
2011), and blin(M,z) the time
dependent linear bias factor that relates P(k,z) to the power spectrum of
the cluster distribution over the sky. Following Mo
& White (1996) and Komatsu &
Kitayama (1999), we adopt blin(M,z) = 1 +
(ν2(M,z) − 1)
/δc(z),
with ![\hbox{$\nu(M,z) = \delta_{\rm c}(z)/\left[D_{\rm g}(z) \sigma(M)\right]$}](/articles/aa/full_html/2014/08/aa23761-14/aa23761-14-eq89.png) ,
Dg(z) is the linear
growth factor, and δc(z) is the
overdensity threshold for spherical collapse.
,
Dg(z) is the linear
growth factor, and δc(z) is the
overdensity threshold for spherical collapse.
2.4. Mass function
Our computation of the tSZ-X correlation assumes the mass function calibrated on a
numerical simulation from Tinker et al. (2008):
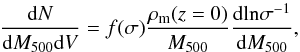 (16)with
(16)with
![\begin{equation} f(\sigma) = A_0\left[ 1+ \left( \frac{\sigma}{A_1}\right)^{A_2}\right] {\rm exp}\left(-\frac{A_3}{\sigma^2} \right), \end{equation}](/articles/aa/full_html/2014/08/aa23761-14/aa23761-14-eq93.png) (17)and ρm(z =
0) the mean matter density today. The coefficients A0,
A1, A2, and
A3 are given in Tinker et al. (2008) for various overdensities, Δmean, with respect to the
redshift-dependent mean cosmic density. These coefficients are interpolated to match
Δcritical defined
with respect to the critical density. The relation between Δcritical and Δmean is given by Δmean = Δcritical/
Ωm(z), with Ωm(z) the matter
density parameter at redshift z. The standard deviation of the density
perturbation in a sphere or radius R, σ, is computed in linear perturbation theory.
(17)and ρm(z =
0) the mean matter density today. The coefficients A0,
A1, A2, and
A3 are given in Tinker et al. (2008) for various overdensities, Δmean, with respect to the
redshift-dependent mean cosmic density. These coefficients are interpolated to match
Δcritical defined
with respect to the critical density. The relation between Δcritical and Δmean is given by Δmean = Δcritical/
Ωm(z), with Ωm(z) the matter
density parameter at redshift z. The standard deviation of the density
perturbation in a sphere or radius R, σ, is computed in linear perturbation theory.
2.5. tSZ and X-ray fluxes
A key step in the modeling of the cross-correlation between tSZ and X-ray is to relate the mass, M500, and the redshift, z, of a given cluster to tSZ flux, Y500, and X-ray luminosity L500 in the [Emin − Emax] keV energy band2 in the rest frame of the cluster. The cross-correlation between tSZ effect and X-ray emission is thus highly dependent on the M500 − Y500 and the M500 − L500 relations in terms of normalization and slope. Consequently, we need to use the relations derived from a representative sample of galaxy clusters, with careful propagation of statistical and systematic uncertainties. We stress that for power spectrum analysis, the intrinsic scatter of such scaling laws has to be considered, because it will produce extra power that has to be accounted for in order to avoid biases.
We used the M500 −
Y500 scaling laws presented in Planck Collaboration XX (2014), ![\begin{equation} E^{-\beta_{\rm sz}}(z) \left[ \frac{D^2_{\rm ang}(z) {Y}_{500}}{10^{-4}\,{\rm Mpc}^2} \right] = Y_\star \left[ \frac{h}{0.7} \right]^{-2+\alpha_{\rm sz}} \left[ \frac{(1-b) M_{500}}{6 \times 10^{14}\,{M_{\odot}}}\right]^{\alpha_{\rm sz}}, \label{szlaw} \end{equation}](/articles/aa/full_html/2014/08/aa23761-14/aa23761-14-eq108.png) (18)with
E(z) =
Ωm(1 + z)3 + ΩΛ.
The coefficients Y⋆, αsz, and
βsz from Planck Collaboration XX (2014), are given in Table 1. We used b
= 0.2 for the bias between X-ray estimated mass and effective mass of
the clusters. To model the L500 − M500
relation, we used the relation derived by Arnaud et al.
(2010) from the REXCESS sample (Böhringer et al.
2007):
(18)with
E(z) =
Ωm(1 + z)3 + ΩΛ.
The coefficients Y⋆, αsz, and
βsz from Planck Collaboration XX (2014), are given in Table 1. We used b
= 0.2 for the bias between X-ray estimated mass and effective mass of
the clusters. To model the L500 − M500
relation, we used the relation derived by Arnaud et al.
(2010) from the REXCESS sample (Böhringer et al.
2007): ![\begin{equation} \left[h E(z)\right]^{-\beta_{\rm x}}\left(\frac{{L}_{500}}{{10^{44}}\,{\rm erg\,s^{-1}}}\right) = L_\star \left[ \frac{M_{{\rm x},500}}{3 \times 10^{14}\,{M_{\odot}}}\right]^{\alpha_{\rm x}}, \end{equation}](/articles/aa/full_html/2014/08/aa23761-14/aa23761-14-eq112.png) (19)where
Mx,500 is the cluster
mass estimated from X-ray observations. It is related to the true mass M500 through
Mx,500 = (1 −
b)M500. The coefficients
L⋆, αx, and
βx are given in Table 1.
(19)where
Mx,500 is the cluster
mass estimated from X-ray observations. It is related to the true mass M500 through
Mx,500 = (1 −
b)M500. The coefficients
L⋆, αx, and
βx are given in Table 1.
The evolution of the M500 − L500 relation suffers from large uncertainties (Reichert et al. 2011). Consequently, we fixed βx to a self-similar value of 7/3. However, we verified that variations from 2 to 3 do not change our results with respect to other sources of uncertainties on the M500 − L500 relation. Indeed, X-ray signal is dominated by low redshift clusters, and thus presents small variations with the redshift evolution of the M500 − L500 relation.
The two relations, M500 − Y500
and M500 −
L500, have intrinsic scatters,
σlog
Y = 0.075 and σlog L =
0.183, respectively. These scatters will contribute to the total power
measured on the sky. Indeed, the quantity ⟨
Y2500 ⟩ is equal to
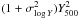 , and
⟨
L2500 ⟩ is equal to
, and
⟨
L2500 ⟩ is equal to
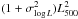 . The
cross-correlation power spectrum of tSZ and X-ray can be affected by the same effect.
However, for a cross-correlation this scatter bias depends on the correlation between the
scatters of the M500 − Y500
and the M500 −
L500 scaling relations. This question is
addressed in Sect. 3.2.
. The
cross-correlation power spectrum of tSZ and X-ray can be affected by the same effect.
However, for a cross-correlation this scatter bias depends on the correlation between the
scatters of the M500 − Y500
and the M500 −
L500 scaling relations. This question is
addressed in Sect. 3.2.
We also need to have an estimate of the cluster temperature, T500. In this
work, we used the scaling law from Planck Collaboration XI
(2011): ![\begin{equation} E(z)^{-\beta_{\rm T}} {Y}_{500} = T_{\star} \left[ \frac{{T}_{500}}{6\,{\rm keV}} \right]^{\alpha_{\rm T}}, \end{equation}](/articles/aa/full_html/2014/08/aa23761-14/aa23761-14-eq126.png) (20)where the
coefficients T⋆, αT and
βT are given in Table 1. This relation also presents an intrinsic scatter
σlog
T = 0.14 ± 0.02. We verified that this
scatter has no significant impact on the tSZ-X cross power-spectrum amplitude with respect
to the scatter from M500 − Y500
and M500 −
L500 relations.
(20)where the
coefficients T⋆, αT and
βT are given in Table 1. This relation also presents an intrinsic scatter
σlog
T = 0.14 ± 0.02. We verified that this
scatter has no significant impact on the tSZ-X cross power-spectrum amplitude with respect
to the scatter from M500 − Y500
and M500 −
L500 relations.
2.6. Pressure and density profiles
The tSZ effect is directly proportional to the pressure integrated across the line of
sight. In this work, we model the galaxy cluster pressure profile by a generalized Navarro
Frenk and White (GNFW, Navarro et al. 1997; Nagai et al. 2007) profile of the form
![\begin{equation} {\mathbb P}(r) = \frac{P_0}{\left(c_{500} r\right)^\gamma \left[1 + (c_{500} r)^\alpha \right]^{(\beta-\gamma)/\alpha}}\cdot \end{equation}](/articles/aa/full_html/2014/08/aa23761-14/aa23761-14-eq129.png) (21)For the parameters
c500, α, β, and γ, we used the best-fitting
values from Arnaud et al. (2010) presented in Table
1. The absolute normalization of the profile
P0 is set assuming the scaling laws
Y500 −
M500 presented in Sect. 2.5.
(21)For the parameters
c500, α, β, and γ, we used the best-fitting
values from Arnaud et al. (2010) presented in Table
1. The absolute normalization of the profile
P0 is set assuming the scaling laws
Y500 −
M500 presented in Sect. 2.5.
To model the X-ray emission, we need both the density, ne(r), and the
temperature, Te(r), profiles. Thus,
we assume a polytropic equation of state (see, e.g., Komatsu & Seljak 2001), P(r) =
ne(r)Te(r),
with ne(r) ∝
Te(r)δ
where δ is
the polytropic index. Considering that the X-ray emission varies with
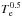 and
and
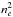 , the X-ray
brightness profile is proportional to P(r)ϵp,
where
, the X-ray
brightness profile is proportional to P(r)ϵp,
where 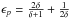 ranges from 1.5 to 2.0 for 1.0
< δ <
∞.
ranges from 1.5 to 2.0 for 1.0
< δ <
∞.
For the X-ray flux to count-rate conversion factor, we only assume an averaged
temperature T500, and then the X-ray flux is directly
proportional to 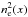 . The overall normalization of
the X-ray emission profile is deduced from the scaling law L500 −
M500 presented in Sect. 2.5.
. The overall normalization of
the X-ray emission profile is deduced from the scaling law L500 −
M500 presented in Sect. 2.5.
 |
Fig. 1 tSZ-Xray cross-correlation for the 1-halo term in blue and for the 2-halo term in red, considering the ROSAT hard band from 0.5 to 2.0 keV. The dashed lines represent the 1σ level considering variations in scaling-relation power laws. This cross-correlation spectrum has been predicted using our fiducial cosmological model. |
3. Results
3.1. The tSZ-X power spectrum
In Fig. 1, we present the angular cross power
spectrum between tSZ and X-rays (assuming a 0.5−2.0 keV energy band for the ROSAT experiment). The power spectrum is
predicted for our fiducial cosmological model. We observe that the tSZ-X power spectrum is
dominated by the one-halo term throughout the entire range of multipole, from
ℓ = 0 to
ℓ = 10 000.
For low multipoles (ℓ < 1000), the tSZ-X power spectrum follows a power law
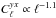 .
.
The correlation factor between tSZ and X-ray surveys,
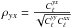 ,
as a function of ℓ presents a slow variation from 0.8 at low
ℓ to 0.6 at
high ℓ. The
smaller correlation factor on small scales highlight the difference in slopes in tSZ and
X-ray profiles in the core of the cluster, as the tSZ profile decreases with
Tene and the
X-ray profile with
,
as a function of ℓ presents a slow variation from 0.8 at low
ℓ to 0.6 at
high ℓ. The
smaller correlation factor on small scales highlight the difference in slopes in tSZ and
X-ray profiles in the core of the cluster, as the tSZ profile decreases with
Tene and the
X-ray profile with 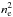 .
.
3.2. The scaling-relation scatter bias
The amplitude of the one-halo term of tSZ-X power spectrum is sensitive to the scatter of scaling relations, which produce an excess of power. The two-halo term is not affected by the scatter. For the tSZ auto-correlation power spectrum, the scatter produces a negligible bias of 0.5%. For the X-ray power spectrum, the effect reach 3.3%.
The bias on tSZ-X cannot be estimated as easily. Indeed the correlation between M500 − Y500 and M500 − L500 scatters has to be known. The quantity ⟨ Y500L500 ⟩ is equal to (1 + ρYLσlog Yσlog L)Y500L500, where ρYL is the correlation between the M500 − Y500 and M500 − L500 scatters. Consequently, the bias is zero for a 0 correlation and maximum for a full correlation.
Using the Y500 −
L500 scatter, σlog YL = 0.14
± 0.02 (Planck Collaboration XI
2011), it is possible to estimate ρYL through
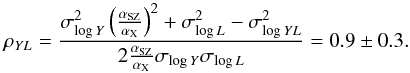 (22)This finding is
consistent with an almost full correlation between M500 −
Y500 and M500 −
L500 scatters. This value for
ρYL leads to a bias of
1.4% for the amplitude of
the tSZ-X power spectrum. Finally, we note that the M500 −
Y500 and M500 −
L500 scatters account for the profile
scatter from cluster to cluster.
(22)This finding is
consistent with an almost full correlation between M500 −
Y500 and M500 −
L500 scatters. This value for
ρYL leads to a bias of
1.4% for the amplitude of
the tSZ-X power spectrum. Finally, we note that the M500 −
Y500 and M500 −
L500 scatters account for the profile
scatter from cluster to cluster.
3.3. Redshift and mass distribution of the tSZ-Xray cross correlation
In Figs. 2 and 3, we present the distribution of the tSZ-Xray cross correlation power spectrum as a function of the redshift and the mass for various values of ℓ from 20 to 10 000 for our fiducial model. We observe that the power below ℓ = 100 is dominated by a local object at redshifts below 0.2. Whereas at high multipole values, ℓ = 10 000, we are sensitive to structures up to z = 1.5. We observe that the small and large angular scales of the power spectrum sample distinct populations in terms of redshift.
Unlike the redshift distribution, we observe that the mass dependency presents small variations for ℓ ranging from 20 to 2000. For these multipoles, the power is dominated by objects with M500 above 1014M⊙. Lower mass objects only make significant contributions to the total power for a very high multipole value ℓ ≃ 10 000.
 |
Fig. 2 Redshift distribution of the contribution to the total tSZ/Xray cross-correlation power for several values of ℓ. In black for ℓ = 20, in dark blue for ℓ = 100, in light blue for ℓ = 200, in green for ℓ = 1000, in orange for ℓ = 2000, and in red for ℓ = 10 000. |
 |
Fig. 3 Mass distribution of the contribution to the total tSZ/Xray cross-correlation power for several values of ℓ. In black for ℓ = 20, in dark blue for ℓ = 100, in light blue for ℓ = 200, in green for ℓ = 1000, in orange for ℓ = 2000, and in red for ℓ = 10 000. |
The mass function predicts a number of objects above a given mass M500 that drastically increases when M500 decreases. Similarly, the comoving volume increases with increasing redshift (below z ≃ 2). The two-halo term presented in Sect. 2.3 is proportional to the number of clusters, which contributes significantly to the total power, to the square, unlike the one-halo terms that are linearly related to this quantity.
This explains the relative small amplitude of the two-halo term with respect to the one-halo term for the tSZ-X power spectrum. Indeed, the low-redshift depth and the high mass sensitivity of the tSZ-X power spectrum imply that the total power is dominated by a small number of objects.
Consequently, low values of αx or αsz promote the two-halo term with respect to the one-halo term. The two-halo term becomes significant at low-ℓ for αx + αsz < 3. However, such values are excluded by existing constraints on the M500 − Y500 and the M500 − L500 relations (see Table 1 for the allowed uncertainty range and Fig. 1 for the impact on tSZ-X cross power spectrum of these uncertainties).
3.4. tSZ-X cross-correlation dependencies with modeling parameters
Our modeling is affected both by cosmological and scaling law parameters. First, we focus
on cosmological parameters, with a particular attention to H0,
Ωm, and
σ8. In Fig. 4, we present the variation in the tSZ-X cross spectrum as a function of
H0 from 60 to 80 km s-1 Mpc-1 in steps of 1
km s-1 Mpc-1, Ωm from 0.2 to 0.4 in steps of 0.01, and σ8 from 0.7 to
0.9 in steps of 0.01. In the most general case, those variations depend on the multipole
ℓ, as
presented in Figs. 2 and 3. Each multipole is sensitive to different regions of the mass function
and thus present different sensitivities to the cosmological parameters: 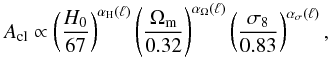 (23)where
Acl is the amplitude of the tSZ-X power
spectrum. However as shown in Fig. 4, we do not
observe a significant distortion of the shape of the cross-correlation with a variation in
the cosmological parameters.
(23)where
Acl is the amplitude of the tSZ-X power
spectrum. However as shown in Fig. 4, we do not
observe a significant distortion of the shape of the cross-correlation with a variation in
the cosmological parameters.
Similar expressions can be used for tSZ and X-ray auto-correlation spectra. In Table 2 we present the values of αH(ℓ), αΩ(ℓ), and ασ(ℓ) for each spectra, tSZ-X, tSZ-auto, X-auto.
 |
Fig. 4 Theoretical tSZ-Xray cross-correlation power spectra, as a function of, from top to bottom, H0, Ωm, and σ8. From blue to red for 21 values of H0, Ωm, and σ8, starting at 60 km s-1 Mpc-1, 0.2, and 0.7 in steps of 1 km s-1 Mpc-1, 0.01, and 0.01, respectively. |
In Fig. 5, we present the power law index variations
with respect to ℓ. For the tSZ auto-correlation we observe
αH ≃
0; however, both the X-ray auto-spectrum and the X-tSZ cross spectrum
present significant variations with H0, with
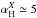 and
and
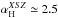 .
These dependency variation are produced by the L500 − M500
scaling relation. We also observe that αΩ ranges from 2.8 to 3.8 and
ασ from 7 to 9. These
variations in spectral indices with respect to ℓ are small.
.
These dependency variation are produced by the L500 − M500
scaling relation. We also observe that αΩ ranges from 2.8 to 3.8 and
ασ from 7 to 9. These
variations in spectral indices with respect to ℓ are small.
In Table 2, we provide fitting formula for each
power law index with respect to ℓ using the following parametric formula:
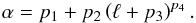 (24)Values for
p1, p2,
p3, p4 are provided
in Table 2. We note that the power law indices are
also functions of the cosmological parameters. Consequently, we stress that the formula
given above has been estimated for cosmological parameters (H0,
Ωm,
σ8) =
(67,0.32,0.83), and thus can only
be considered accurate for 10% variations around these parameters.
(24)Values for
p1, p2,
p3, p4 are provided
in Table 2. We note that the power law indices are
also functions of the cosmological parameters. Consequently, we stress that the formula
given above has been estimated for cosmological parameters (H0,
Ωm,
σ8) =
(67,0.32,0.83), and thus can only
be considered accurate for 10% variations around these parameters.
In addition to the sensitivity to cosmological parameters, the tSZ-X correlation is highly sensitive to the scaling relations described in Sect. 2.5 and cluster profiles described in Sect. 2.6, both of which are related. Consequently for the present work, we consider the profile from Arnaud et al. (2010) that has been used to estimate the Y500 − M500 scaling relation. However, we verified that the tSZ-X cross spectrum varies by 10% at most for various pressure profiles, as Arnaud et al. (2010), Planck Collaboration Int. V (2013), and Sayers et al. (2013) and for various polytropic indices from 1 to ∞ (isothermal case).
A variation in the scaling-relation normalization translates into a variation in the amplitude of the cross spectrum. However, the scaling law power law indices will produce a modification of the shape of the tSZ-X correlation.
In the following, we model the deviation from our reference scaling laws presented in
Sect. 2.5 as  where
δαsz and
δαx represent the
deviations from the reference scaling law indices, αsz and
αx, for M500 −
Y500 and M500 −
L500, respectively.
where
δαsz and
δαx represent the
deviations from the reference scaling law indices, αsz and
αx, for M500 −
Y500 and M500 −
L500, respectively.
In Fig. 6, we present the variation in the tSZ-X,
X-ray, and tSZ power spectra with the scaling law indices, αsz and
αx, insteps of 0.025 for each index and
0.05 for their sum. We note that the tSZ-X power spectrum is only sensitive to the sum of
the indices, αsz +
αx. In terms of amplitude, the tSZ-X
power spectrum follows 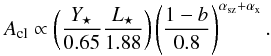 (27)
(27)
 |
Fig. 5 Power law index variation as a function of ℓ for in black the X-tSZ cross-correlation, in red the tSZ auto-correlation, and in blue the X-ray auto-correlation. From top to bottom for αH(ℓ), αΩ(ℓ), and ασ(ℓ). |
 |
Fig. 6 From top to bottom: variation in the theoretical tSZ-X, tSZ-tSZ, and X-X power spectra as a function of αsz + αx, αsz and αx, in steps of 0.05, 0.025, and 0.025, respectively. |
We observe in Fig. 6 that increasing the value of αsz and αx increases the power at low-ℓ where high-mass objets dominate the signal and decreases the power at high ℓ, that is dominated by low-mass objects. However, the shape distortion of the power spectra occurs at high-ℓ. The impact of scaling law indices start to be significant at ℓ > 1000, ℓ > 800, and ℓ > 2000 for tSZ-X, tSZ, and X power spectra, respectively. We observe that the X-ray power spectrum presents the lowest sensitivity in terms of shape with respect to δαx.
We can infer a global dependence of the tSZ-X cross-correlation amplitude for fixed
scaling-law indices and fixed profiles, 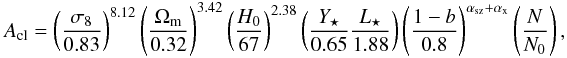 (28)where N is a normalization
parameter for the mass function.
(28)where N is a normalization
parameter for the mass function.
Modeling error budget for the tSZ-X cross spectrum and the X and SZ auto spectra.
3.5. Modeling uncertainties
Uncertainties on the predicted spectrum are produced by uncertainties on galaxies cluster properties and uncertainties on the cosmology. We used the uncertainties on cluster properties listed in Table 1 and propagated them to predict the power spectra. For the mass function, we assumed an overall uncertainty of 10% (Evrard et al. 2002) and for the bias, b, we assumed an uncertainty of 10% (e.g, Piffaretti & Valdarnini 2008). For the uncertainties on cosmological parameters, we consider two different sets of cosmological parameters, our fiducial model named cosmo 1, and a second model based on the best fit from Planck Collaboration XX (2014) named cosmo 2. For both sets of parameter, we propagated the uncertainties to the tSZ-X power spectra. We carefully account for correlation between uncertainties between parameters for each set.
We notice that the propagation of the uncertainty on αSZ,X depends on the multipole, consequently we provide a range for the uncertainty for 0 < ℓ < 2000.
In Table 3, we present the modeling uncertainties on the tSZ-X cross correlation. We stress that these uncertainties translate into an overall normalization of the spectrum. We also provide the uncertainty levels for the tSZ and X-ray auto correlation spectra. Assuming a fixed cosmology, we noted that the error budget is limited by our knowledge of b, leading to an uncertainty of about 35% on the amplitude of the tSX power spectrum. If we propagate the uncertainties on cosmological parameters to the tSZ-X power spectrum, we derived an uncertainty of 31% for the cosmo 1 and an uncertainty of 27% for cosmo 2. Cosmo 2 allows us to obtain slightly lower uncertainties for the tSZ-X prediction, because the degeneracy between cosmological parameters is similar for tSZ and tSZ-X spectra, unlike for cosmo 1 cosmology, which presents different degeneracies.
We finally note that for the tSZ-X cross power spectrum, the error budget from cluster properties and cosmological parameters have the same order of magnitude. The total uncertainty that includes both contributions reaches 48%.
4. Prediction of the tSZ-Xray spectrum measurement
To estimate the tSZ-Xray cross correlation, it is possible to use several approaches. One of them relies on the cross-correlation of frequency maps of the microwave sky with an X-ray map, see Sects. 4.3 and 4.4. Another one consists in using a recovered tSZ map (see, e.g., Hurier et al. 2013) and an X-ray map, see Sect. 4.5. In the following, we discuss the advantages and drawbacks of each approach.
Measurement of the tSZ-X correlation is limited by both instrumental characteristics and contaminating astrophysical emissions. To estimate the constraints that can be reached on the tSZ-X power spectrum, we predicted the expected signal-to-noise ratio assuming the Planck nominal mission characteristics (i.e., noise and beams Planck Collaboration I 2014) for the microwave observations and the RASS (Voges et al. 1999) for X-rays.
4.1. The micro-wave and X-ray skies
 |
Fig. 7 From left to right and top to bottom: predicted sensitivity to the tSZ-X cross correlation by computing the cross power spectra between the RASS hard band and the Planck channels from 70 to 545 GHz. The dark-blue, blue, and light-blue shaded regions show the uncertainties levels at 1, 2, and 3 σ for multipole bins Δℓ = 40. The absolute value of the theoretical tSZ-X cross angular power spectrum is displayed as a red line. |
To simulate the sky emission at microwave frequencies with the appropriate level of noise, we used the Planck Sky Model (PSM, see Delabrouille et al. 2013, and references therein). At microwave frequencies, the main astrophysical emissions are the diffuse Galactic free-free, synchrotron, thermal dust emissions, the anomalous microwave emission, the emission from Galactic and extragalactic point sources, the CIB, the Zodiacal light emission, and the tSZ effect in clusters of galaxies.
To account for the signal from the X-ray sky, we used the RASS data in the energy range [0.5, 2.0] keV, degraded at an angular resolution of FWHM = 2′, and projected again in the HEALpix pixelization (Górski et al. 2005) following a nearest neighbor interpolation. There are several types of astrophysical objects that emit in the X-rays: extragalactic ones such as galaxy clusters, black holes in AGN, the combination of unresolved X-ray emitting objects producing the X-ray background (Freyberg et al. 1992), but also galactic sources, mainly supernova remnants and stars.
In addition to the signal from galaxy clusters, there are other astrophysical emissions that are also correlated between the X-ray and the microwave skies. This is the case of the radio-loud AGNs and the CIB. Both AGN and CIB present a different frequency dependence than the tSZ effect and consequently can, in principle, be separated from the galaxy clusters’ contribution to the tSZ-X cross correlation. In addition, AGNs are point-like at Planck and ROSAT angular resolutions, and thus can be separated from the clusters’ contribution by the shape of the power spectrum.
The emission from our galaxy is also present on sky at microwave frequencies (synchrotron, Free-Free, and thermal dust) and in ROSAT energy bands (nH absorption and galactic X-ray emissions). However, considering only the ROSAT hard band (0.5−2.0 keV) reduces the effect of the nH absorption, and utilizing a galactic mask reduces the contamination by galactic foregrounds. As for the contamination by extragalactic point sources, such contamination will present a frequency dependence that differs from a tSZ spectrum, and thus can be distinguished using multifrequency analysis.
4.2. Statistical and systematic uncertainties
We can estimate the statistical uncertainties, on the tSZ-X correlation, using
-
our prediction for a tSZ-X cross-correlation power spectrum from the galaxy cluster,
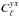 ;
; -
our prediction for tSZ and X-ray auto-correlation power spectra from the galaxy cluster,
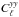 and
and
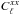 ;
;
-
the measured cross-correlation,
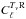 , between the microwave sky from the PSM, denoted
T
ν
for frequency
ν
, and the X-ray sky from RASS data, denoted
R;
, between the microwave sky from the PSM, denoted
T
ν
for frequency
ν
, and the X-ray sky from RASS data, denoted
R;
-
the measured auto correlations,
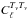 and
and
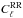 , of the microwave and X-ray skies;
, of the microwave and X-ray skies;
-
the measured cross correlation,
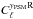 , between the tSZ map constructed from the PSM, denoted
y
PSM
, and the X-ray sky from RASS data, denoted
R;
, between the tSZ map constructed from the PSM, denoted
y
PSM
, and the X-ray sky from RASS data, denoted
R;
-
the measured auto correlation,
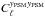 of the tSZ map.
of the tSZ map.
The expression uncertainties for each tSZ-X detection method is presented in Sects. 4.3, 4.4, and 4.5.
Our estimation of uncertainties through simulations of the microwave sky does not allows an estimate of the systematic uncertainties. To account for systematics uncertainties, we considered three cases for describing the measured tSZ-X cross correlation.
-
Case 1: considering only the contribution of galaxy clusters to thetSZ-X correlation.
-
Case 2: considering the contributions from galaxy clusters and AGNs to tSZ-X correlation.
-
Case 3: considering galaxy clusters, AGNs, and CIB-X contributions.
The complete description of the cross power spectrum for Case 3 reads as
![\begin{equation} C_\ell = \left[A_{\rm cl}\, g(\nu) + A_{\rm CIB}\, F_{\rm CIB}(\nu)\right] C^{yx}_\ell + A_{\rm AGN} \, F_{\rm AGN}(\nu), \end{equation}](/articles/aa/full_html/2014/08/aa23761-14/aa23761-14-eq231.png) (29)with FCIB the CIB SED
(Gispert et al. 2000), FAGN(ν) a typical
radio-loud AGN SED assuming a spectral index of −0.7 in intensity units, Acl (see Eq. (28)), ACIB, and
AAGN are the parameters of the model and
account for galaxy clusters, CIB-X, and AGN contributions to the tSZ-X cross power
spectrum, respectively. Case 1 assumes ACIB = 0 and
AAGN =
0 and Case 2 assumes ACIB = 0.
(29)with FCIB the CIB SED
(Gispert et al. 2000), FAGN(ν) a typical
radio-loud AGN SED assuming a spectral index of −0.7 in intensity units, Acl (see Eq. (28)), ACIB, and
AAGN are the parameters of the model and
account for galaxy clusters, CIB-X, and AGN contributions to the tSZ-X cross power
spectrum, respectively. Case 1 assumes ACIB = 0 and
AAGN =
0 and Case 2 assumes ACIB = 0.
This modeling assumes that the CIB-X correlation presents a similar shape, as a function of ℓ, to the clusters’ contribution to the tSZ-X cross spectrum and assumes that the AGN contribution is Poissonian, since the AGN clustering can be neglected.
In the following, we consider the multipole range 40 < ℓ < 2000 for our signal-to-noise ratio prediction.
4.3. Cross correlation spectrum from frequency maps
The tSZ-X cross correlation can be directly estimated from the correlation between X-ray
maps and microwave full-sky observations at a given frequency, denoted
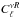 . We estimate
the expected level of uncertainties when correlating the RASS hard-band and microwave maps
at frequency ν. We mask 30% of the sky by applying a cut on the
thermal dust emission intensity. Then, we estimate the uncertainties following
. We estimate
the expected level of uncertainties when correlating the RASS hard-band and microwave maps
at frequency ν. We mask 30% of the sky by applying a cut on the
thermal dust emission intensity. Then, we estimate the uncertainties following
![\begin{align} \label{eqcl} \left(\Delta C^{\nu R}_\ell \right)^2 =& \frac{g(\nu)^2 \left[ \left(C^{yx}_\ell \right)^2 + C^{yy}_\ell C^{xx}_\ell \right]}{(2\ell +1)f_{\rm sky}} \nonumber \\ &+ \frac{\left(C^{T_{\nu} {\rm R}}_\ell \right)^2}{(2\ell +1)f_{\rm sky}} \\ &+ \frac{\left(C^{T_{\nu} T_{\nu}}_\ell + g(\nu)^2 C^{yy}_\ell \right) \left(C^{\rm RR}_\ell - C^{xx}_\ell \right)}{(2\ell +1)f_{\rm sky}}, \nonumber \end{align}](/articles/aa/full_html/2014/08/aa23761-14/aa23761-14-eq240.png) (29)where
(29)where
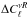 is the
uncertainties on the cross power spectrum between microwave and X-ray skies, and
fsky is the sky fraction used for the
analysis. The first term in Eq. (29)
corresponds to the cosmic variance of the tSZ-X cross correlation, and the other terms
account for the uncertainties produced by foreground emissions.
is the
uncertainties on the cross power spectrum between microwave and X-ray skies, and
fsky is the sky fraction used for the
analysis. The first term in Eq. (29)
corresponds to the cosmic variance of the tSZ-X cross correlation, and the other terms
account for the uncertainties produced by foreground emissions.
In Fig. 7, we present the resulting uncertainty level at 1, 2, and 3σ as a function of the frequency. We also present the expected absolute value of the tSZ-X cross correlation for our fiducial model. All spectra are displayed in units of KCMB cts s-1 arcmin-2sr. Each spectrum has been corrected for the mask effect (see Tristram et al. 2005) and the beam effects. We chose to present the uncertainty for multipole bins with Δℓ = 40.
Detection signal-to-noise of the tSZ-X cross power spectrum frequency per frequency from 30 to 857 GHz considering values of ℓ from 40 to 2000.
For the lowest frequencies, below 70 GHz, the signal is completely dominated by the instrumental noise contribution. For intermediate frequencies from 70 to 217 GHz, the main uncertainty is the CMB contamination, and the uncertainty level clearly shows the CMB features, mainly the first three acoustic pics. Above 353 GHz, the uncertainties are dominated by the thermal dust contamination.
We note that at 217 GHz the tSZ emission is not rigorously zero; however, the tSZ transmission in this channel is faint (Hurier et al. 2014). Consequently, this channel can be used to check systematic effects.
In Table 4, we present the expected signal-to-noise for tSZ-X correlation as a function of frequency. The signal-to-noise is provided assuming Cases 1 and 2. We observe that in Case 3, we reach a signal-to-noise above six for only two channels, 100 and 143 GHz. However, the main limitation in that case is the astrophysical emission from the microwave sky, such as CMB and thermal dust emission. These emissions are correlated from one frequency to another.
4.4. Cross power spectrum from cleaned frequency maps
 |
Fig. 8 From left to right and top to bottom: predicted sensitivity to the tSZ-X cross correlation for the cleaned cross power spectra between the RASS hard band and the Planck channels at 70, 100, 143, 353, and 545 GHz, respectively. The dark-blue, blue, and light-blue shaded regions show the uncertainty levels at 1, 2, and 3σ for multipole bins Δℓ = 40. The absolute value of the theoretical tSZ-X cross angular power spectrum is displayed as a red line. |
Detection signal-to-noise of the tSZ-X cross power spectrum frequency per frequency after cleaning at 70, 100, 143, 353, and 545 GHz considering values of ℓ from 40 to 2000.
To increase the signal to noise of the tSZ-X detection, we combine the different
frequencies to remove the contribution from CMB and thermal dust. This cleaning is
performed by subtracting the 217 GHz spectrum to other spectra to remove CMB contamination
and decorrelating each channel from the 857 GHz map to reduce thermal dust contamination.
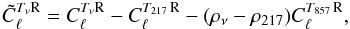 (31)where
ρν is the correlation
factor between the map at the frequency ν and the map at 857 GHz. This factor is computed
on the area of the sky that is not masked. We computed these cleaned angular power spectra
at 70, 100, 143, 353, and 545 GHz.
(31)where
ρν is the correlation
factor between the map at the frequency ν and the map at 857 GHz. This factor is computed
on the area of the sky that is not masked. We computed these cleaned angular power spectra
at 70, 100, 143, 353, and 545 GHz.
We propagate the uncertainties considering the correlation between cross spectra,
![\begin{align} \langle C^{\nu {\rm R}}_\ell,C^{\nu' {\rm R}}_\ell \rangle =& \frac{g(\nu)g(\nu') \left[ \left(C^{yx}_\ell \right)^2 + C^{yy}_\ell C^{xx}_\ell \right]}{(2\ell +1)f_{\rm sky}} \nonumber \\ &+ \frac{ C^{T_{\nu} {\rm R}}_\ell C^{T_{\nu'} {\rm R}}_\ell }{(2\ell +1)f_{\rm sky}} \\ &+ \frac{ \left( C^{T_{\nu} T_{\nu'}}_\ell + g(\nu)g(\nu') C^{yy}_\ell \right) \left(C^{\rm RR}_\ell - C^{xx}_\ell \right)}{(2\ell +1)f_{\rm sky}}\cdot \nonumber \end{align}](/articles/aa/full_html/2014/08/aa23761-14/aa23761-14-eq246.png) (32)
(32)
In Fig. 8, we present the obtained power spectrum. We observe that the uncertainties at low-ℓ are dominated by foreground residuals. Indeed, the decorrelation from the 857 GHz assuming a single scaling coefficient ρν does not account for thermal dust SED variation across the sky and thus leads to residual emission that dominates the uncertainties on those scales. At high-ℓ the uncertainties are dominated by the instrumental noise. In Fig. 8, we also observe that our cleaning is particularly efficient on intermediate scales from ℓ = 100 to ℓ = 1000, owing to CMB contamination removal.
In Table 5 we present the expected signal-to-noise of the tSZ-X cross power spectrum signal in the multipole range 40 < ℓ < 2000. We provide the results in the three cases described in Sect. 4.2.
For Case 2, we performed the adjustment of AAGN individually per frequency. For Case 3, we performed the estimation of the expected signal-to-noise ratio per frequency and considered all frequencies. We note that for both adjustments, the parameters ACIB and AAGN are fit considering all frequencies. This adjustment is performed considering the global covariance matrix of all spectra.
This procedure explains the increase in signal-to-noise between Cases 2 and 3. As for Case 3, we consider the multifrequency information of the tSZ-X cross correlation for the fit of our foreground model.
In a realistic case, Case 3, we reach a signal-to-noise of 13.4 for the tSZ-X cross correlation at 143 GHz. Considering all five frequencies, we obtain a global signal-to-noise of 17.5.
4.5. Cross-correlation from Compton parameter maps
We construct a tSZ map from the PSM simulations of microwave sky observations from 100 to
857 GHz using the MILCA method (Hurier et al.
2013). Then, we estimate the uncertainties on the cross power spectrum,
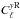 ,
between a tSZ map and an X-ray map as
,
between a tSZ map and an X-ray map as
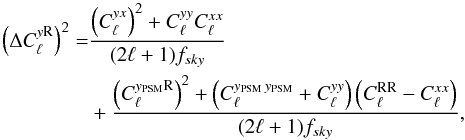 (33)where
yPSM corresponds to the tSZ map
constructed from the PSM simulations.
(33)where
yPSM corresponds to the tSZ map
constructed from the PSM simulations.
In Fig. 9, we present the obtained levels of uncertainties. The tSZ-X power spectrum for our fiducial model is above 2σ for each bin of Δℓ = 40 from ℓ = 40 to 2000. The main limitations are the instrumental noise and CIB residuals that cannot be removed by a linear combination. If we do not consider contamination by correlated astrophysical emissions such as radio-loud AGNs and CIB, we obtain an overall signal-to-noise of 62.3 from ℓ = 40 to ℓ = 2000. If we consider contamination by AGNs and CIB we obtain a signal-to-noise of 31.5.
We note in Sect. 3.5 that the modeling derived from present constraints leads to about a 48% uncertainty on the amplitude of the tSZ-X cross correlation. Considering Case 3 and a signal-to-noise of 31.5, the amplitude of the tSZ-X cross-correlation can be obtained at 3.2% precision. As a consequence, the utilization of a tSZ map allows to set the tighter constraints on the tSZ-X cross-correlation and to increase our knowledge of cosmological and astrophysical parameters in the related degeneracy space by a factor of 15.
4.6. Constraints on astrophysical and cosmological parameters
The amplitude of the tSZ-X cross correlation can be constraints at a precision of 3.2%.
However, this amplitude is sensitive to several parameters from both cosmology and scaling
laws, see Eq. (28). The expected
constraints on the tSZ-X cross correlation normalization reads
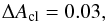 (34)in the case of the
correlation between a tSZ map and an X-ray map considering the contamination by both AGN
and CIB emissions.
(34)in the case of the
correlation between a tSZ map and an X-ray map considering the contamination by both AGN
and CIB emissions.
To obtain the uncertainty over a single parameter, it is necessary for it to carefully propagate the uncertainties from other parameters considering the global covariance matrix of all parameters. Beyond the amplitude of the tSZ-X cross-correlation, if we fix the profiles of galaxy clusters, the expected high level of significance of the tSZ-X cross correlation should allow us to constrain the scaling-law spectral indices.
 |
Fig. 9 Predicted sensitivity to the tSZ-X cross-correlation for the cross power spectra between the RASS hard band and a MILCA tSZ-map. The dark-blue, blue, and light-blue shaded regions show the uncertainties levels at 1, 2, and 3σ for multipole bins Δℓ = 40. The absolute value of the theoretical tSZ-X cross angular power spectrum is displayed as a red line. |
 |
Fig. 10 Likelihood function as a function of the deviation from scaling law indices δαsz and δαx derived from tSZ auto-correlation power spectrum and tSZ-X cross power spectrum. |
In Fig. 10, we present the constraints from our simulated data. The tSZ-X cross correlation is only sensitive to the sum δαx + δαsz for fixed density and temperature profiles. To distinguish the two indices, we used the tSZ auto-correlation power spectrum assuming uncertainty levels from Planck Collaboration VIII (2011).
This measurement is limited by the multipole range accessible, for example, by Planck and ROSAT, ℓ ≤ 2000. In that case, we obtained Δ(δαsz) = 0.10 and Δ(δαsz) = 0.16 for the scaling law index deviation parameters. If we add a measurement of tSZ spectrum at ℓ = 3000, considering tSZ data at higher resolution from SPT-like (Shirokoff et al. 2011) or ACT-like (Sievers et al. 2013) experiments, we can reach Δ(δαsz) = 0.08 and Δ(δαx) = 0.14. These constraints on the scaling-law slopes with respect to the cluster mass are competitive with constraints from the scaling-law-dedicated analyses presented in Table 1.
Finally, we estimated the degeneracy between profile and scaling-relation parameters
considering the tSZ-X cross power spectrum. For small variations (up to 10%) around the
Arnaud et al. (2010) profile, we can express the
degeneracy relation as 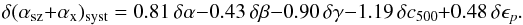 (35)From this result, we
observed that the shape of the tSZ-X cross spectrum is highly sensitive to both
scaling-relation and profile parameters. Consequently, the tSZ-X spectrum is a powerful
probe to simultaneously test the combination of scaling laws and profiles.
(35)From this result, we
observed that the shape of the tSZ-X cross spectrum is highly sensitive to both
scaling-relation and profile parameters. Consequently, the tSZ-X spectrum is a powerful
probe to simultaneously test the combination of scaling laws and profiles.
5. Conclusion
We have presented a complete up-to-date modeling of the tSZ, X-ray, and tSZ-X power spectra. We have carefully studied the sensitivity to cosmological and astrophysical parameters, completing a previous analysis on the topic (Diego et al. 2003). For the variations in the tSZ-X cross-correlation, tSZ, and X-ray auto-correlation with H0, Ωm, and σ8, we provided accurate analytical fitting formulae in the range 0 < ℓ < 10 000.
Then, we carefully propagated the uncertainties on the cosmological and scaling law parameters of our modeling to the predicted power spectra, leading to an overall uncertainty on the normalization of the tSZ-X power spectrum by about 48%. This result highlights our limited knowledge of this cosmological probes.
We note that the contributions to the total uncertainty from clusters’ scaling relations and cosmological parameters are at same order of magnitude. The main contributions to the total uncertainty are produced by the bias b, 35%, and cosmological parameters, 27%. These large uncertainties illustrate the importance of an accurate measurement of the tSZ-X cross angular spectrum to set constraints on both cluster properties and cosmological parameters.
We stress that most of our modeling parameters act on the tSZ-X power spectrum as an overall amplitude factor. This leads to high degeneracy between those parameters, and thus the tSZ-X cross correlation needs to be used in addition of other probes to break the degeneracies. We note that our prediction cannot be directly compared to the measurement recently performed by Hajian et al. (2013), since their measurement concerned the cross-correlation between tSZ maps and X-ray catalogs, and consequently, it presents difference dependencies with cosmological parameters.
We predicted the expected signal-to-noise that can be reached using a simulated microwave sky and ROSAT data for the X-ray sky. We considered three approaches to extracting the tSZ-X cross power spectrum. We demonstrate that in the case of the cross-correlation between a tSZ map and an X-ray map, we reach a signal-to-noise of 31.5. In this case, we can reach a measurement of the tSZ-X cross correlation amplitude at about 3%, improving the actual constraints (from our knowledge of cosmological parameters and scaling laws) on the predicted spectrum by about a factor of 10.
We also studied the possibility of constraining the slope of the tSZ and X-ray scaling laws and the parameters of a GNFW profile using the shape of the tSZ-X cross spectrum. We conclude that scaling-law and profile parameters are highly degenerated. Thus, constraints from tSZ-X spectrum allows the global consistency of scaling laws and profiles to be checked.
Future experiment at high resolution and high sensitivity for tSZ surveys and X-ray measurements will, in the near future, allow the increase of the expected constraints, especially by providing a wider range of multipoles, higher sensitivity, and more frequencies.
Acknowledgments
We acknowledge the support of the French Agence Nationale de la Recherche under grant ANR-11-BD56-015. We are grateful to an anonymous referee for his/her comments and suggestions. We also thank M. Arnaud, J. B. Melin, E. Pointecouteau, and G. Pratt for useful discussions related to this work. This research has made use of the ROSAT all-sky survey data which have been processed at MPE. We acknowledge the use of HEALPix package (Górski et al. 2005).
References
- Andreon, S. 2012, A&A, 546, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benson, B. A., de Haan, T., Dudley, J. P., et al. 2013, ApJ, 763, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Bohringer, H., Voges, W., Huchra, J. P., et al. 2000, VizieR Online Data Catalog, J/MNRAS/318/333 [Google Scholar]
- Böhringer, H., Schuecker, P., Pratt, G. W., et al. 2007, A&A, 469, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delabrouille, J., Betoule, M., Melin, J.-B., et al. 2013, A&A, 553, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diego, J. M., Silk, J., & Sliwa, W. 2003, MNRAS, 346, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Allen, S. W., et al. 2000, VizieR Online Data Catalog, J/ApJS/129/435 [Google Scholar]
- Ebeling, H., Edge, A. C., & Henry, J. P. 2001, ApJ, 553, 668 [Google Scholar]
- Evrard, A. E., MacFarland, T. J., Couchman, H. M. P., et al. 2002, ApJ, 573, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Fixsen, D. J., Dwek, E., Mather, J. C., Bennett, C. L., & Shafer, R. A. 1998, ApJ, 508, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Freyberg, M. J., Snowden, S. L., Plucinsky, P. P., & Schmitt, J. H. M. M. 1992, in Astronomische Gesellschaft Abstract Series, 7, ed. G. Klare, 26 [Google Scholar]
- Gispert, R., Lagache, G., & Puget, J. L. 2000, A&A, 360, 1 [NASA ADS] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Hajian, A., Battaglia, N., Spergel, D. N., et al. JCAP, 11, 064 [Google Scholar]
- Hurier, G., Macías-Pérez, J. F., & Hildebrandt, S. 2013, A&A, 558, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurier, G., Aghanim, N., Douspis, M., & Pointecouteau, E. 2014, A&A, 561, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Komatsu, E., & Kitayama, T. 1999, ApJ, 526, L1 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Komatsu, E., & Seljak, U. 2001, MNRAS, 327, 1353 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., & Seljak, U. 2002, MNRAS, 336, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Krumpe, M., Miyaji, T., & Coil, A. L. 2010, ApJ, 713, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Krumpe, M., Miyaji, T., Coil, A. L., & Aceves, H. 2012, ApJ, 746, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lesgourgues, J. 2011, unpublished [arXiv:1104.2932] [Google Scholar]
- Marriage, T. A., Acquaviva, V., Ade, P. A. R., et al. 2011, ApJ, 737, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Mewe, R., Gronenschild, E. H. B. M., & van den Oord, G. H. J. 1985, A&AS, 62, 197 [NASA ADS] [Google Scholar]
- Miyaji, T., Krumpe, M., Coil, A. L., & Aceves, H. 2011, ApJ, 726, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Mo, H. J., & White, S. D. M. 1996, MNRAS, 282, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, D., Kravtsov, A. V., & Vikhlinin, A. 2007, ApJ, 668, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Piffaretti, R., & Valdarnini, R. 2008, A&A, 491, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VIII. 2011, A&A, 536, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2011, A&A, 536, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. V. 2013, A&A, 550, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321529 [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321591 [Google Scholar]
- Planck Collaboration XX. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321521 [Google Scholar]
- Planck Collaboration XXIX. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321523 [Google Scholar]
- Puget, J.-L., Abergel, A., Bernard, J.-P., et al. 1996, A&A, 308, L5 [NASA ADS] [Google Scholar]
- Reichardt, C. L., Stalder, B., Bleem, L. E., et al. 2013, ApJ, 763, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Reichert, A., Böhringer, H., Fassbender, R., & Mühlegger, M. 2011, A&A, 535, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Remazeilles, M., Delabrouille, J., & Cardoso, J.-F. 2011, MNRAS, 410, 2481 [NASA ADS] [CrossRef] [Google Scholar]
- Sayers, J., Czakon, N. G., Mantz, A., et al. 2013, ApJ, 768, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Sehgal, N., Trac, H., Acquaviva, V., et al. 2011, ApJ, 732, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Shirokoff, E., Reichardt, C. L., Shaw, L., et al. 2011, ApJ, 736, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Sievers, J. L., Hlozek, R. A., Nolta, M. R., et al. 2013, Cosmol. Astropart. Phys., 10, 60 [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1969, Nature, 223, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comments Astrophys. Space Phys., 4, 173 [NASA ADS] [EDP Sciences] [Google Scholar]
- Taburet, N., Hernández-Monteagudo, C., Aghanim, N., Douspis, M., & Sunyaev, R. A. 2011, MNRAS, 418, 2207 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Tristram, M., Macías-Pérez, J. F., Renault, C., & Santos, D. 2005, MNRAS, 358, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Vanderlinde, K., Crawford, T. M., de Haan, T., et al. 2010, ApJ, 722, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
All Tables
Scaling-law parameters and error budget for both Y500 − M500 (Planck Collaboration XX 2014), L500 − M500 (Arnaud et al. 2010), and Y500 − T500 (Planck Collaboration XX 2014) relations.
Modeling error budget for the tSZ-X cross spectrum and the X and SZ auto spectra.
Detection signal-to-noise of the tSZ-X cross power spectrum frequency per frequency from 30 to 857 GHz considering values of ℓ from 40 to 2000.
Detection signal-to-noise of the tSZ-X cross power spectrum frequency per frequency after cleaning at 70, 100, 143, 353, and 545 GHz considering values of ℓ from 40 to 2000.
All Figures
 |
Fig. 1 tSZ-Xray cross-correlation for the 1-halo term in blue and for the 2-halo term in red, considering the ROSAT hard band from 0.5 to 2.0 keV. The dashed lines represent the 1σ level considering variations in scaling-relation power laws. This cross-correlation spectrum has been predicted using our fiducial cosmological model. |
| In the text | |
 |
Fig. 2 Redshift distribution of the contribution to the total tSZ/Xray cross-correlation power for several values of ℓ. In black for ℓ = 20, in dark blue for ℓ = 100, in light blue for ℓ = 200, in green for ℓ = 1000, in orange for ℓ = 2000, and in red for ℓ = 10 000. |
| In the text | |
 |
Fig. 3 Mass distribution of the contribution to the total tSZ/Xray cross-correlation power for several values of ℓ. In black for ℓ = 20, in dark blue for ℓ = 100, in light blue for ℓ = 200, in green for ℓ = 1000, in orange for ℓ = 2000, and in red for ℓ = 10 000. |
| In the text | |
 |
Fig. 4 Theoretical tSZ-Xray cross-correlation power spectra, as a function of, from top to bottom, H0, Ωm, and σ8. From blue to red for 21 values of H0, Ωm, and σ8, starting at 60 km s-1 Mpc-1, 0.2, and 0.7 in steps of 1 km s-1 Mpc-1, 0.01, and 0.01, respectively. |
| In the text | |
 |
Fig. 5 Power law index variation as a function of ℓ for in black the X-tSZ cross-correlation, in red the tSZ auto-correlation, and in blue the X-ray auto-correlation. From top to bottom for αH(ℓ), αΩ(ℓ), and ασ(ℓ). |
| In the text | |
 |
Fig. 6 From top to bottom: variation in the theoretical tSZ-X, tSZ-tSZ, and X-X power spectra as a function of αsz + αx, αsz and αx, in steps of 0.05, 0.025, and 0.025, respectively. |
| In the text | |
 |
Fig. 7 From left to right and top to bottom: predicted sensitivity to the tSZ-X cross correlation by computing the cross power spectra between the RASS hard band and the Planck channels from 70 to 545 GHz. The dark-blue, blue, and light-blue shaded regions show the uncertainties levels at 1, 2, and 3 σ for multipole bins Δℓ = 40. The absolute value of the theoretical tSZ-X cross angular power spectrum is displayed as a red line. |
| In the text | |
 |
Fig. 8 From left to right and top to bottom: predicted sensitivity to the tSZ-X cross correlation for the cleaned cross power spectra between the RASS hard band and the Planck channels at 70, 100, 143, 353, and 545 GHz, respectively. The dark-blue, blue, and light-blue shaded regions show the uncertainty levels at 1, 2, and 3σ for multipole bins Δℓ = 40. The absolute value of the theoretical tSZ-X cross angular power spectrum is displayed as a red line. |
| In the text | |
 |
Fig. 9 Predicted sensitivity to the tSZ-X cross-correlation for the cross power spectra between the RASS hard band and a MILCA tSZ-map. The dark-blue, blue, and light-blue shaded regions show the uncertainties levels at 1, 2, and 3σ for multipole bins Δℓ = 40. The absolute value of the theoretical tSZ-X cross angular power spectrum is displayed as a red line. |
| In the text | |
 |
Fig. 10 Likelihood function as a function of the deviation from scaling law indices δαsz and δαx derived from tSZ auto-correlation power spectrum and tSZ-X cross power spectrum. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.