| Issue |
A&A
Volume 567, July 2014
|
|
|---|---|---|
| Article Number | A131 | |
| Number of page(s) | 4 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201423886 | |
| Published online | 29 July 2014 | |
Research Note
Particle energisation in a collapsing magnetic trap model: the relativistic regime
School of Mathematics and Statistics, University of St
Andrews,
St. Andrews
KY16 9SS,
UK
e-mail: se11@st-andrews.ac.uk; tn3@st-andrews.ac.uk
Received:
26
March
2014
Accepted:
18
June
2014
Context. In solar flares, a large number of charged particles is accelerated to high energies. By which physical processes this is achieved is one of the main open problems in solar physics. It has been suggested that during a flare, regions of the rapidly relaxing magnetic field can form a collapsing magnetic trap (CMT) and that this trap may contribute to particle energisation.
Aims. In this Research Note we focus on a particular analytical CMT model based on kinematic magnetohydrodynamics. Previous investigations of particle acceleration for this CMT model focused on the non-relativistic energy regime. It is the specific aim of this Research Note to extend the previous work to relativistic particle energies.
Methods. Particle orbits were calculated numerically using the relativistic guiding centre equations. We also calculated particle orbits using the non-relativistic guiding centre equations for comparison.
Results. For mildly relativistic energies the relativistic and non-relativistic particle orbits mainly agree well, but clear deviations are seen for higher energies. In particular, the final particle energies obtained from the relativistic calculations are systematically lower than the energies reached from the corresponding non-relativistic calculations, and the mirror points of the relativistic orbits are systematically higher than for the corresponding non-relativistic orbits.
Conclusions. While the overall behaviour of particle orbits in CMTs does not differ qualitatively when using the relativistic guiding centre equations, there are a few systematic quantitative differences between relativistic and non-relativistic particle dynamics.
Key words: Sun: corona / Sun: activity / Sun: flares / acceleration of particles
© ESO, 2014
1. Introduction
Collapsing magnetic traps (CMTs) have been suggested as one of the mechanisms that might contribute to particle energisation in solar flares (e.g. Somov & Kosugi 1997). The basic idea behind CMTs is that charged particles will be trapped on the magnetic field lines below the reconnection region of a flare. The magnetic field will evolve into a state of lower energy, resulting in (a) a shortening of the field line length and (b) an increase in the overall field strength. Owing to the vast difference in length and time scales between the particle motion and the magnetic field evolution, the particle motion can be described with very good accuracy by the guiding centre theory. The conservation of a particle’s magnetic moment and the bounce invariant (e.g. Grady et al. 2012) give rise to the possibility of increase in the particle’s kinetic energy by betatron acceleration and by first-order Fermi acceleration (e.g. Somov & Kosugi 1997; Bogachev & Somov 2005). Several studies have focused on particle energisation and motion in CMT models with varying degrees of detail and have treated different aspects of the physical processes (e.g. Bogachev & Somov 2001, 2005, 2007, 2009; Kovalev & Somov 2002; Somov & Bogachev 2003; Karlický & Kosugi 2004; Giuliani et al. 2005; Karlický & Bárta 2006; Grady & Neukirch 2009; Minoshima et al. 2010, 2011; Grady et al. 2012; Filatov et al. 2013; Eradat Oskoui et al. 2014).
In this Research Note we used the relativistic guiding centre equations (see e.g. Northrop 1963) to extend to the relativistic regime the investigations of a specific analytic CMT model carried out with the non-relativistic guiding centre equations by Giuliani et al. (2005) and Grady et al. (2012). We compare particle motion and energisation in the relativistic case with the non-relativistic case. In Sect. 2 we outline of the CMT model of Giuliani et al. (2005) and introduce the relativistic guiding centre equations. In Sect. 3 we present the results obtained from the relativistic particle orbit calculations by considering the effect of different initial conditions. These relativistic results are compared with results obtained from non-relativistic particle orbit calculations, in particular those reported by Grady et al. (2012). We present a summary of our results in Sect. 4.
2. Background
Giuliani et al. (2005) developed the basic theory for the construction of kinematic CMT models, and for brevity we refer the reader to their paper for a detailed discussion. We used the same coordinate system as in Giuliani et al. (2005) and Grady et al. (2012): the x and z coordinates run parallel to the solar surface, and y represents the height above the solar surface. We assumed that the z-components of the magnetic field and the velocity field vanish. The magnetic field can then be described by a time-dependent flux function A(x,y,t), with B(x,y,t) = ∇A × ez.
A CMT model is then defined by choosing a form for the flux function A∞(x,y) for time t → ∞, and by specifying a flow field v(x,y,t). Instead of defining the flow field directly, it is given implicitly in the theory of Giuliani et al. (2005) by choosing a time-dependent transformation between Lagrangian and Eulerian coordinates, which facilitates solving the kinematic MHD equations.
We used the same magnetic field model and transformation as Giuliani et al. (2005), Grady et al. (2012)
and Eradat Oskoui et al. (2014), that is,
![\begin{eqnarray} \label{defA0}A_\infty &= & c_1\left[ \arctan\left(\frac{y_\infty+d_1}{x_\infty+w} \right) - \arctan\left(\frac{y_\infty+d_2}{x_\infty-w} \right) \right], \\ \label{x_infinity} x_\infty &=& x,\\ y_\infty &=& (at)^{b} \ln\left[ 1 + \frac{y}{(at)^{b}}\right] \left\lbrace \frac{1+ \tanh\left[ (y - L_v ) a_1\right]}{2}\right\rbrace \nonumber \\ \label{y_infinity} && + \left\lbrace \frac{1- \tanh\left[ (y - L_v ) a_1\right]}{2}\right\rbrace y. \end{eqnarray}](/articles/aa/full_html/2014/07/aa23886-14/aa23886-14-eq9.png) The
parameter values are the same as in Giuliani et al.
(2005), Grady et al. (2012) and Eradat Oskoui et al. (2014), namely w = 0.5, d1 = d2
= 1.0, a =
0.4, b =
1.0, Lv = 1.0 and
a1 =
0.9. Here all length scale are normalised to L = 107 m. The
meaning of these parameters is explained in Giuliani et al.
(2005).
The
parameter values are the same as in Giuliani et al.
(2005), Grady et al. (2012) and Eradat Oskoui et al. (2014), namely w = 0.5, d1 = d2
= 1.0, a =
0.4, b =
1.0, Lv = 1.0 and
a1 =
0.9. Here all length scale are normalised to L = 107 m. The
meaning of these parameters is explained in Giuliani et al.
(2005).
Because of the large difference between the time and length scales on which the electromagnetic fields of CMT model change compared with typical Larmor frequencies and radii of charged particle orbits, the guiding centre approximation can be used to calculate particle orbits. We used the relativistic guiding centre equations as given by Northrop (1963):
Here, m,
q, and
c are the
particle rest mass, particle charge, and the speed of light, respectively, R denotes the
guiding centre position, E and B the electric
and magnetic fields at the guiding centre position, 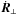 is the guiding centre
velocity perpendicular to the magnetic field direction, and v∥ is the guiding
centre velocity parallel to the magnetic field direction. b denotes the
unit vector along magnetic field lines, s is the coordinate (arc length) along magnetic field
lines, uE =
E ×
b/B is
the E ×
B drift velocity, and μr =
m(γv⊥)2/
2B is the relativistic magnetic moment, with
v⊥
the perpendicular particle velocity associated with its gyration around the magnetic field
lines.
is the guiding centre
velocity perpendicular to the magnetic field direction, and v∥ is the guiding
centre velocity parallel to the magnetic field direction. b denotes the
unit vector along magnetic field lines, s is the coordinate (arc length) along magnetic field
lines, uE =
E ×
b/B is
the E ×
B drift velocity, and μr =
m(γv⊥)2/
2B is the relativistic magnetic moment, with
v⊥
the perpendicular particle velocity associated with its gyration around the magnetic field
lines.
In practice, the CMT model provides the expressions for the electric and the magnetic field and their spatial and temporal derivatives. The guiding centre Eqs. (4)–(6) are then used to calculate the particle trajectories in the CMT model. Because the electric field in our CMT model is derived from the ideal Ohm’s law it only has a component perpendicular to the magnetic field, and E⊥ ≪ cB because the flow velocities in the CMT model are well below the speed of light. We do not state the non-relativistic guiding centre equations here (see e.g. Northrop 1963; Giuliani et al. 2005; Grady et al. 2012), but they can in principle be recovered from the relativistic Eqs. (4) and (5) letting γ → 1 and (E⊥/cB)2 → 0 in expressions that contain this term.
To discuss the energy gain experienced by particles in the CMT we used the following
expressions for the kinetic energy: in the relativistic regime, the kinetic energy of the
particle is given by 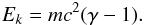 (7)The
rest mass energy of electrons is mc2 ≈ 511 keV. We recall
that v⊥2 =
2μrB/
(mγ2); therefore
gyro-averaged Lorentz factor can be expressed as
(7)The
rest mass energy of electrons is mc2 ≈ 511 keV. We recall
that v⊥2 =
2μrB/
(mγ2); therefore
gyro-averaged Lorentz factor can be expressed as
![\begin{eqnarray} \gamma(t) = \sqrt{\frac{1 + [2 \mu_r B(t)]/c^2}{1- [v_{\parallel}^2(t) + u_{E}^2(t)]/c^2}}\cdot \end{eqnarray}](/articles/aa/full_html/2014/07/aa23886-14/aa23886-14-eq38.png) (8)The
Lorentz factor changes in time because the electromagnetic fields and v∥ are time
dependent. As we describe below, the Lorentz factor increases on average with time in a CMT.
(8)The
Lorentz factor changes in time because the electromagnetic fields and v∥ are time
dependent. As we describe below, the Lorentz factor increases on average with time in a CMT.
For comparison, the non-relativistic kinetic energy EK is given by
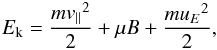 (9)where
mv∥2/
2 is the parallel energy of the particle, μB is the energy associated
with the gyrational motion, and muE2/
2 is the energy associated with the main perpendicular drift of the
guiding centre, which is usually very small compared to the other terms (see e.g. Grady et al. 2012).
(9)where
mv∥2/
2 is the parallel energy of the particle, μB is the energy associated
with the gyrational motion, and muE2/
2 is the energy associated with the main perpendicular drift of the
guiding centre, which is usually very small compared to the other terms (see e.g. Grady et al. 2012).
3. Particle trajectories and energy gain
We first investigated a typical particle orbit and the evolution of its kinetic energy. We chose an orbit starting at the initial position (x,y) = (0,4.2), an initial pitch angle 160.4°, and an initial energy 5.5 keV. These initial condition were chosen because they are very similar to one of the examples discussed in Grady et al. (2012). We then compared this with an orbit with the same initial position and pitch angle, but with an an already mildy relativistic initial energy of 200 keV.
 |
Fig. 1 Particle orbits and energy evolution for test particle orbits starting at (x,y) = (0,4.2). The turquoise curves represent the relativistic calculations, the black curves represent the non-relativistic calculation. Panels a) and c) show the particle trajectories, panels b) and d) the energy evolution for initial energies 5.5 keV (panels a) and b)) and 200 keV (panels c) and d)). |
The results of the particle orbit calculations are shown in Fig. 1. As previously discussed by, for example, Grady et al. (2012) and Eradat Oskoui et al. (2014), the E × B-drift is by far the dominant drift in this CMT model, and thus particles remain on the same field line at all times. This explains the spatial overlap of the relativistic and non-relativistic trajectories. Note, however, that this does not necessarily imply that the non-relativistic and relativistic trajectory are always at the same position at the same time.
Panel (b) in Fig. 1 shows the time evolution of the kinetic energy. Obviously, both graphs start at 5.5 keV, but then begin to move apart. The final shown energy of the non-relativistic orbit is about 15.02 keV, whereas the final energy for the relativistic case is about 14.61 keV, giving a difference of about 0.41 keV or 2.7%. The particle velocity at the final time shown is roughly 0.2c.
As is to be expected the relativistic kinetic energy curve lies systematically below the non-relativistic kinetic energy curve. Another way to express this fact would be to say that in the relativistic case it takes a longer time to reach the same energy than in the non-relativistic case. In both cases, one can see the step-like pattern in the energy curves, which is particularly prominent in the initial phases. In the non-relativistic case, this pattern has been associated with changes in the parallel energy due to the curvature-related terms in the equation for the parallel velocity (e.g. Giuliani et al. 2005; Grady et al. 2012). In the relativistic case, it is difficult to split the kinetic energy into parallel and perpendicular components, but the process seems to operate in the same way.
The case with a starting energy of 5.5 keV shows only very weak relativistic effects. However, when the initial energy is increased to the already mildly relativistic value of 200 keV, the discrepancies between the relativistic calculation and the non-relativistic calculation become much more pronounced. We would like to emphasise that the non-relativistic calculation was made only for comparison purposes. With an initial value of γ = 1.39 giving v = 0.695c, it is clear that only a fully relativistic particle orbit calculation can yield physically correct results.
We show the results for this orbit in the lower two panels of Fig. 1 (panels c and d). For this case, even changes in the particle orbits are visible (Fig. 1c). The relativistic orbit has systematically higher mirror points than the non-relativistic orbit. We also found this behaviour for other orbits and discuss the reasons for this below.
Since the initial kinetic energy Einit is now already mildly relativistic, a much larger difference between the energy graphs can be seen in panel d of Fig. 1. At the final time of the calculation, the kinetic energy in the non-relativistic case is about 546 keV, whereas the kinetic energy of the relativistic case it is about 339 keV. This is a discrepancy of about 207 keV or roughly 38%. This is a significant difference in energy compared with the case with Einit = 5.5 keV. The final Lorentz factor and the particle velocity for the relativistic case are γ = 1.664 and v = 0.799c, which again corroborates the need for a relativistic calculation.
From our case studies, we found two main differences between the relativistic and non-relativistic orbit calculations. Firstly, the final particle energy calculated using the relativistic equations is always lower than the non-relativistic case. This is easily explained because the Lorentz factor grows nonlinearly when the particle velocity approaches c, which diminishes the energy gain in the relativistic regime. Secondly, we found that the mirror points in the relativistic cases are systematically higher than the non-relativistic cases. At first sight, this seems counterintuitive because the mirror term in Eq. (5) scales with γ-1 and therefore one would expect mirror points to be lower for higher values of γ. However, a careful investigation of the terms in Eq. (5) reveals that the terms associated with field line curvature also decrease with increasing γ. These terms are responsible for increasing the parallel velocity component, and if this process becomes less efficient with increasing γ, the mirror points are expected to be higher in the CMT than for the corresponding non-relativistic case.
 |
Fig. 2 Snapshot of the particle position at the final time of the calculation. The colour code indicates the kinetic energy at that time. Top: the non-relativistic case; bottom: the relativistic case. |
Our previous findings were based on the single case studies presented above. However, we calculated particle orbits for a whole range of initial conditions, similar to the non-relativistic investigation by Grady et al. (2012). The conclusion from the case studies are qualitatively similar, although there are of course quantitative differences depending on initial conditions. A key result found by Grady et al. (2012) was that the particle orbits that gain the most energy during the collapse of the trap have initial pitch angles close to 90° and remain trapped at the field line apex (loop top). The particles with the highest energy gain have initial positions in a weak magnetic field region in the middle of the trap. We found the same result when we used the same set of initial conditions for the relativistic case. For comparison, we show in Fig. 2 the positions of a number of particle orbits at the final time of the calculation with the colour code indicating their kinetic energy at that time. The range of final energies in the non-relativistic case is approximately 4.98–317 keV, whereas it is 4.98–255 keV, in the relativistic case, consistent with our previous findings that lower energies are reached in the relativistic case.
4. Summary and conclusions
In this Resarch Note we have extended previous investigations of particle energisation in the CMT model of Giuliani et al. (2005) to the relativistic regime, using the relativistic guiding centre equations. Qualitatively, the particle orbits obtained using
the relativistic guiding centre equations are very similar to the results obtained by Grady et al. (2012) with the non-relativistic guiding centre equations, in particular regarding the trapping of the particle orbits with the strongest increase in energy in the centre of the CMT. We found two main differences between the relativistic and non-relativistic results, in particular for larger initial energies.
The final particle energy calculated using the relativistic approximation is always lower than in the non-relativistic case. In general, the difference in final energy grows with increasing initial energy. This is due to the Lorentz factor, which reduces the size of the terms in the equation of motion that contribute to energy gain. It should be borne in mind, however, that the non-relativistic equations cease to be accurate for higher energies and were presented here only for comparison.
In the relativistic case the mirror points of the particle orbits are located systematically higher than in the corresponding the non-relativistic case. We explained this by investigating the size of the terms that are related to curvature in the equation for the parallel velocity, which decrease with increasing γ factor. This seems to have a stronger effect on the mirror point location than the change of the actual mirror term, which also decreases with increasing γ factor.
Acknowledgments
The authors acknowledge financial support by the UK’s Science and Technology Facilities Council through a Doctoral Training Grant (SEO) and Consolidated Grant ST/K000950/1 (SEO and TN).
References
- Bogachev, S. A., & Somov, B. V. 2001, Astron. Rep., 45, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Bogachev, S. A., & Somov, B. V. 2005, Astron. Lett., 31, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Bogachev, S. A., & Somov, B. V. 2007, Astron. Lett., 33, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Bogachev, S. A., & Somov, B. V. 2009, Astron. Lett., 35, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Eradat Oskoui, S., Neukirch, T., & Grady, K. J. 2014, A&A, 563, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Filatov, L. V., Melnikov, V. F., & Gorbikov, S. P. 2013, Geomagnetism and Aeronomy, 53, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Giuliani, P., Neukirch, T., & Wood, P. 2005, ApJ, 635, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Grady, K. J., & Neukirch, T. 2009, A&A, 508, 1461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grady, K. J., Neukirch, T., & Giuliani, P. 2012, A&A, 546, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karlický, M., & Bárta, M. 2006, ApJ, 647, 1472 [NASA ADS] [CrossRef] [Google Scholar]
- Karlický, M., & Kosugi, T. 2004, A&A, 419, 1159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovalev, V. A., & Somov, B. V. 2002, Astron. Lett., 28, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Minoshima, T., Masuda, S., & Miyoshi, Y. 2010, ApJ, 714, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Minoshima, T., Masuda, S., Miyoshi, Y., & Kusano, K. 2011, ApJ, 732, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Northrop, T. G. 1963, The Adiabatic Motion of Charged Particels (New York: Wiley) [Google Scholar]
- Somov, B. V., & Bogachev, S. A. 2003, Astron. Lett., 29, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Somov, B. V., & Kosugi, T. 1997, ApJ, 485, 859 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Particle orbits and energy evolution for test particle orbits starting at (x,y) = (0,4.2). The turquoise curves represent the relativistic calculations, the black curves represent the non-relativistic calculation. Panels a) and c) show the particle trajectories, panels b) and d) the energy evolution for initial energies 5.5 keV (panels a) and b)) and 200 keV (panels c) and d)). |
| In the text | |
 |
Fig. 2 Snapshot of the particle position at the final time of the calculation. The colour code indicates the kinetic energy at that time. Top: the non-relativistic case; bottom: the relativistic case. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{eqnarray} && \dot{{\vec R}}_{\perp} = {{\frac{{{\vec b}}}{B(1 - {{{E}_{\perp}}^{2}/c^2B^{2}})}}} \times \Bigg\lbrace {{- \left( 1-{\frac{{E_{\perp}}^2}{c^2B^2}} \right){{\vec E}}}} \nonumber \\ &&\hspace*{7mm}+\, \left. \frac{\mu_{r}}{\gamma q} \nabla \left[ B\left( 1-{\frac{{E_{\perp}}^2}{c^2B^2}}\right)^{1/2} \right] + \frac{m \gamma }{q}\left( v_{\parallel} \frac{{\rm d}{{\vec b}}}{{\rm d}t} + \frac{{\rm d}{\vec u}_{E}}{{\rm d}t} \right) \right. \nonumber \\ \label{dvperpdt}&&\hspace*{7mm}+ \, \frac{v_{\parallel}E_{\parallel}}{c^{2}}{{\vec u}_{E}} + \frac{\mu_{r}}{\gamma q}\frac{{{\vec u}}_{E}}{c^2}\frac{\partial}{\partial t}\left[ B\left( 1-{\frac{{E_{\perp}}^2}{c^2B^2}}\right)^{1/2} \right] \Bigg\rbrace, \\ &&m\frac{{\rm d}(\gamma {v}_{\parallel})}{{\rm d} t} = \frac{{\rm d}{p}_{\parallel}}{{\rm d}t} = {q{E}_{\parallel}} - {{\frac{\mu_{r}}{\gamma} \frac{\partial}{\partial s}\left[ B\left( 1-\frac{{E_{\perp}}^2}{c^2B^2} \right)^{1/2} \right]}} \nonumber \\ \label{dvpardt}&& \hspace*{15mm} + \, {{m \gamma {{\vec u}}_{E} \cdot \left(\frac{\partial {{\vec b}}}{\partial t} + \frac{{v}_{\parallel}}{\gamma}\frac{\partial {{\vec b}}}{\partial s} + {{\vec u}}_{E} \cdot \nabla{{\vec b}}\right)}}, \\ \label{eqn_dgammadt}&& \frac{{\rm d} \gamma}{{\rm d}t} = \frac{q}{m c^2}(\dot{{\vec R}}_{\perp} + v_{\parallel}){{\vec b}}\cdot{{\vec E}} + \frac{\mu_{r}}{mc^2 \gamma} \frac{\partial B}{\partial t}\cdot \end{eqnarray}](/articles/aa/full_html/2014/07/aa23886-14/aa23886-14-eq17.png)