| Issue |
A&A
Volume 566, June 2014
|
|
|---|---|---|
| Article Number | A23 | |
| Number of page(s) | 10 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201322979 | |
| Published online | 02 June 2014 | |
Near-Earth asteroid binaries in close encounters with the Earth
Universidade Estadual Paulista, Grupo de Dinâmica Orbital e Planetologia,
CEP,
12516-410
Guaratinguetá,
Brazil
e-mail:
ran.araujo@gmail.com
Received: 4 November 2013
Accepted: 1 April 2014
The asteroids that may cross, or approach, the orbit of the terrestrial planets compose the NEAs population. In the present work we studied the effects of close encounters between hypothetical NEAs’ binaries and the Earth to determine the limiting stability of their satellites as a function of the encounter conditions. We were able to estimate the frequency of such encounters, thus, the expected lifetime of the NEAs binaries. Through numerical simulations, all the encounters between asteroids and the Earth that were closer than 100 Earth radii were recorded. The next step consisted of simulating a representative sample of those encounters considering the Earth, and the asteroid with a cloud of non-interacting satellites around it. The largest radial distance for which all the satellites survive (no collision or disruption) was defined as the critical radius RC. We present a statistical analysis of the recorded encounters, and the critical radius given as a function of the impact parameter and of the relative velocity, defining the stable and unstable encounter conditions for the NEAs satellites. In all these simulations and analyses three distinct satellite masses were considered: massless satellites, satellites with ten percent of the asteroid mass, and satellites with the same mass of the asteroid. We found that the close encounters that are able to remove the most internal satellites are quite frequent. For the NEAs of the sample initially belonging to the Atens group, we found that ≈93% of them suffer an encounter with such characteristics within 10 Myr and that 50% of these encounters happen within approximately 330 thousand years. Our results confirm that, in fact, the close encounter of binaries with the Earth is a powerful mechanism for disrupting these systems and that their lifetimes are strongly influenced by the planetary close encounters.
Key words: celestial mechanics / minor planets, asteroids: general
© ESO, 2014
1. Introduction
The asteroids that may cross, or approach, the orbit of the terrestrial planets compose the population of near-Earth asteroids (NEAs). They are classified into four groups: Atens (Q > 0.983 AU, a < 1.0 AU), Amor (1.017 <q < 1.3 AU, a > 1.0 AU), Apollo (q < 1.017 AU, a > 1.0 AU), and IEO – interior to the Earth orbit (Q < 0.983 AU, a < 1.0 AU), where Q, q, and a, are the aphelion, perihelion, and semi-major axis of the asteroid, respectively.
The close encounters of NEAs with the terrestrial planets are very frequent. It is well known that such close encounters perturb the heliocentric orbit of the asteroid, resulting in a chaotic evolution (Tancredi 1998; Freistetter 2009). The additional perturbations in the NEAs due to such encounters have also been investigated.
According to Solem & Hills (1996), the NEAs imaged by Earth-based radar in the middle nineties present elliptical or “potato” shapes. They analyzed how the close encounters change the shape of these bodies. Considering that the asteroids are rubble piles and using an N-body code, they determined the elongation resulting in an asteroid due to tidal encounters with the Earth, as a function of the impact parameter and relative velocity. They showed that this mechanism is capable of producing the typical elongation observed on NEAs at that time. However, more recent data coming from radar observations and light curve analysis show that actually many of the objects in this population, especially the primaries of binary NEAs, seem to be composed of fast-rotating spherical or oblate asteroids (Richardson & Walsh 2006).
The rotation rates of asteroid influenced by the close planetary encounters has also been analyzed. Scheeres et al. (2000) considered the mutual perturbation between asteroids (interaction with the parent body after a disruption) and the interaction between asteroids and planets during a hyperbolic Flyby, in order to determine the role of such interactions on the spin states of the asteroids. They demonstrated that the close encounters can change the spin state of the asteroids, significantly increasing or decreasing their angular momentum and, consequently, leading to a completely new rotation state. Knowing that the planetary encounters play an important role in the rotation rates of the asteroids, Scheeres et al. (2004) performed a study to analyze the relevance of this mechanism, i.e., how much the planetary encounters change the spin state of the asteroids when compared to its “primordial” state. They found out that, in fact, this is a significant mechanism in the scenario of rotation rates of NEAs.
The binaries and multiple systems compose an interesting subgroup of NEA populations. Examination of doublet craters on Earth and Venus led Bottke & Melosh (1996a) to suggest that about 15% of the asteroids that cross the orbit of Earth are binaries. Currently, there are about 46 known multiple systems in the group of NEAs (JPL/NASA): 44 binaries and 2 triple systems, 2001 SN263 (Nolan et al. 2008) and 1994 CC (Brozovic et al. 2009).
The problem of multiple systems under the influence of gravitational encounters was considered by Chauvineau et al. (1991). They analyzed the stability of binary asteroids perturbed by a passing asteroid. They demonstrated that the collisions process are more effective in the destruction of the binaries, while the approaches of a passing asteroid do not have any significant influence. Chauvineau & Farinella (1993) considered the problem of close encounters with terrestrial planets and discuss the role of close encounters with the Earth analyzing the orbital energy changing and the effects of the encounter on the separation of the bodies of the binary system.
It was also demonstrated that the planetary close encounters also have influence on the process of formation of those systems. Considering that the NEAs are rubble piles, Bottke & Melosh (1996b) show that the tidal forces experienced during close encounters with the Earth can generate binary asteroids. Walsh & Richardson (2006) characterized the formation of binaries NEAs associated with tidal force acting on the asteroid when it has close encounters with Earth. They based their study on simulations of the N-body problem.
The YORP effect is also recognized as a mechanism that may contribute to forming binaries. Bottke et al. (2002) propose that the YORP effect increases the rotation rate of the asteroid, thereby transferring material to the equator of the primary, until it reaches the breakup limit. Ćuk (2007) considers this process of binary formation and shows that, for the NEAs, the close planetary encounters would increase the separation of the bodies until the complete disruption of the system.
Walsh & Richardson (2008) analyzed the role of the tidal disruption in a steady-state model of NEAs binaries. Following Walsh & Richardson (2006), they discuss the problem of the formation and disruption of NEAs binaries from close planetary encounters. They also discuss the expected orbital and physical distribution of the binaries formed through this mechanism, and other possible sources that would explain the observed binary population in the NEAs region, such as the migration of binaries from the Main Belt population. They concluded that the tidal disruption provides only a small fraction of the observed NEAs binaries population, so that other mechanisms or sources are required to explain the characteristics of this population.
Fang et al. (2011) explain the eccentricity values and the nonzero mutual inclinations of the satellites of the triple systems 2001 SN263 and 1994 CC, also considering the effects of the close planetary encounters suffered by these multiple systems. They find that close encounters are able to generate the observable excitation in e and I for the satellites of both systems. Fang & Margot (2012) present a more general study of how the close encounters perturb the orbit of the satellites of the binaries. They considered a sample of binaries, including seven known NEAs binaries, and simulated close encounters of those binaries with the Earth. Only the stable encounters (encounters that did not result in disruption or collision) were analyzed. They discuss the effects of such encounters on the binary’s satellites in terms of variations in semi-major axis, eccentricity, and inclination. They also present the timescales of the close encounters with the Earth for seven well characterized NEAs binaries, as a function of impact parameters.
In the present work we also analyze the gravitational perturbations suffered by the NEA binaries owing to close encounters with Earth, but now considering not just the stable cases, but also the unstable cases – close encounters able to disrupt the binary. Our goal was to determine the stability of the satellites of the NEA binaries as a function of the encounter conditions (impact parameter and relative velocity). In addition, knowing the conditions that led to the loss (by disruption or collisions) of the most internal satellites, we were able to estimate the frequency of such encounters, and thus, estimate the lifetime of the NEA binaries according to their dynamical group (Atens, Apollo, or Amor).
The structure of this paper is as follows. In Sect. 2, we discuss the registered close encounters experienced by the NEAs with the Earth. In Sect. 3, we present the study of the stability of the NEAs satellites. We discuss the particles and massive satellites cases. We determined the stable and unstable condition, giving them as a function of the encounter conditions. In both sections we present the initial considerations and the method adopted and discuss the results. A tentative analytical approach is also presented. In Sect. 4, we discuss the frequency of the close encounters able to remove the most internal satellites of the binaries and how this is related with the current scenario of binaries on the population of NEAs. In Sect. 5 are the final comments.
2. NEAs and Earth: close encounters
The first step of the work consisted on selecting the close encounters of the NEAs with the Earth. We selected the encounters through numerical integration of a system composed by the Sun, the eight planets of the solar system, and a representative sample of asteroids belonging to the group of NEAs.
According to Morbidelli et al. (2002), the known population of NEOs is consistently supplied by asteroids that escape from the Main Belt through resonant mechanisms acting in that region. They reach orbits that allow them to cross the orbits of the terrestrial planets. The three most important known sources of NEAs are the ν6 secular resonance with Saturn, the 3:1 mean-motion resonance with Jupiter, and the Mars-crossing regions. Bottke et al. (2006) show that the thermal Yarkovsky effect moves small bodies from the Main Belt into the resonances at that region. Thus, it indirectly contributes to the replenishment of the NEAs population.
Once belonging to the NEAs population, the frequent close encounters of the asteroids with the terrestrial planets make their orbits move from one group to another. It is well known that the NEAs have a chaotic orbital evolution mainly due to the planetary close encounters (Tancredi 1998; Freistetter 2009), but also owing to the presence of resonances in the inner solar system (Michel 1997; Michel & Froeschle 1997). Such events change the orbits of the NEAs making them transit between Amor, Apollo and Atens groups before being removed from the region of NEAs.
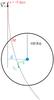 |
Fig. 1 Every time that the distance between the Earth and any of the asteroids of the sample is smaller than 100 Earth radii (100 R⊕), we considered that there was an encounter at time te. We integrate 5 days in the past to obtain the initial conditions of the encounter. In this figure, d is the impact parameter, V∞ the relative velocity of the encounter, q the minimum distance of the encounter, and Vq the relative velocity at this point. |
Based on these characteristics, we follow a methodology similar to the adopted by Gladman et al. (2000) in their study of the lifetime of NEAs. We considered a bigger representative sample of NEAs with perihelion q < 1.3 AU by definition, and distributed in the Amor, Apollo, and Atens groups. A sample of 2100 known NEAs was considered with 700 initially belonging to the Atens group (approximately 100% of the population), 700 initially belonging to the Amor group (approximately 18% of the population), and 700 initially belonging to the Apollo group (approximately 12% of the population). Classifying our sample in these groups helps us make some assumptions on the orbital evolution of a given NEA binary when it is discovered or to explain what we currently know about the observable population of the NEAs’ binaries population. This discussion is presented better in the Sect. 4.1.
The sample of asteroids were randomly chosen from the database of JPL/NASA. They were considered the orbits of these asteroids for the epoch MJD 56 200. The orbital elements for the planets were obtained through JPL’s Horizons system for the same epoch. The numerical integrations were performed using the hybrid sympletic/Bulirsch-Stoer algorithm from Mercury (Chambers 1999), for a time span of 10 Myr, which is the predicted lifetime of the NEAs according to Gladman et al. (2000).
Along the numerical integrations we registered all close encounters with Earth closer than 100 Earth radii (see Fig. 1). When an asteroid crosses the 100 Earth radii limit, at the time of encounter te, we have the position and the velocity of the asteroid and of the Earth relative to the Sun at that moment. We then integrate five days to the past considering the three-body problem (Sun-Earth-asteroid) to obtain the initial conditions of the encounter when the perturbation from the Earth is not significant yet.
 |
Fig. 2 Percentage of close encounters as a function of the encounter velocity V∞. The medians are indicated by the green lines. The histogram d) has a larger bin to better compare our results with the results presented by (Walsh & Richardson 2006) and (Fang & Margot 2012). |
 |
Fig. 3 a) Representation of a typical orbit of an NEA belonging to the Amor group. b) Perturbed orbit of the asteroid with an increase in the eccentricity – the orbits cross and the encounters are possible. c) Perturbed orbit – extreme case with a high increase in eccentricity. In all three cases, it was considered a fixed semi-major axis. |
The parameters that describe the close encounter are the relative velocity V∞ and the impact parameter d. The relative velocity is defined as V∞ = Va − Vp, where Va and Vp are the velocity of the asteroid and of the Earth, relative to the Sun. Through a sum of vectors, is possible to demonstrate that the relative velocity is also given by 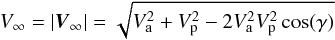 (1)where γ is the angle between Va and Vp.
(1)where γ is the angle between Va and Vp.
From the hyperbolic orbit theory comes the impact parameter definition, given by 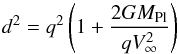 (2)where q is the minimum distance of the close encounter, G the gravitational constant, MPl the mass of the planet, and V∞ the modulus of the relative velocity, as previously defined.
(2)where q is the minimum distance of the close encounter, G the gravitational constant, MPl the mass of the planet, and V∞ the modulus of the relative velocity, as previously defined.
As a result of the numerical integration, were registered 251 129 encounters for the sample of asteroids initially belonging to Atens group, 92 952 encounters for the sample of Apollo and 29 292 encounters for the Amor group, with a total of 373 373 encounters within 10 Myr for the whole sample of NEAs. The asteroids of the Atens group suffer more encounters since they cross the orbit of the Earth and have a shorter orbital period. Moreover, the asteroids of the Amor group suffer fewer encounters. This is a predicted result since the asteroids of the Amor group initially do not cross the orbit of the Earth. They have to suffer external perturbations to increase the eccentricity of their orbits, and then cross the orbit of the planet.
 |
Fig. 4 Stable radial limit of the satellites of NEAs as a function of the impact parameter (d) and of the relative velocity (V∞), for the particles case (M2 = 0). a) Resulting from the numerical simulation. b) Generated through the fit (Eq. (3)). The color-coded scales correspond to the critical initial orbital radius RC, given in the primary’s Hill radius. The white lines delimit three basic regimes: weak, moderate, and extreme disruption limits from right to left, respectively. |
In the histograms of Fig. 2 we present the percentage of encounters as a function of the relative velocity V∞, for Amor, Apollo, and Atens, and for the entire dataset. They indicate that the asteroids of the Atens group suffer encounters with a slightly higher relative velocity, while the asteroids of the Amor group perform the encounters with lower relative velocities. Such behavior is related to the orbital characteristics of the bodies when belonging to each of those group, as discussed below.
-
Amor: as mentioned before, by definition, the asteroids initially belonging to the Amor group do not cross the orbit of the Earth. However, the asteroids suffer external perturbations during their orbital evolution, such as the secular perturbation due to the interaction with the planets or to passages through their region of influence. Such external perturbations may increase the eccentricities of the asteroids, so the crossing orbits become possible. Figure 3 illustrates this process. In Fig. 3a it is shown the orbit of an asteroid belonging to the Amor group, as expected. In Fig. 3b we represent a perturbed case, with a small increase in eccentricity, and in Fig. 3c we represent the extreme cases, with a high increase in eccentricity. In these figures we represent the angle γ, and it is seens that the values for this angle increase with eccentricity. Thus, higher eccentricities result in higher values for γ and, according to Eq. (1), higher relative velocities, while lower eccentricities result in lower values for γ and lower relative velocities. Owing to the nature of the external perturbations, the intermediate case (3b) is more probable to happen, justifying the concentration of encounters with lower relative velocities found for the Amor group. Only extreme cases (less probable) result in the higher velocities seen in the histogram in Fig. 2c.
-
Apollo and Atens: the asteroids initially belonging to the Apollo and Atens groups already have an initial eccentricity that allows them to cross the orbit of the Earth. Therefore, the probability of an encounter occurring with higher eccentricity and, consequently, with higher relative velocity is greater when compared with the encounters of the asteroids of the Amor group, as can be seen by comparing Fig. 2a–c. The distribution for the Apollos has a longer tail when compared to the distribution for the Atens. This is related to the limited semi-major axis of the Atens (a < 1.0 AU).
3. Binaries’ close encounters
Now that we have discussed the close encounters of the NEAs with the Earth, we analyze the effects of such encounters on NEAs binaries. The goal is to determine the stable and unstable encounter conditions for the satellites of the binaries.
Following we present the adopted methodology and the discussion of the results.
3.1. The method
Based on the results of the previous section, we considered a representative sample of about 6000 encounters of the NEAs with the Earth, distributed in the range: 0.02 ≤ d ≤ 0.40 (Earth’s Hill radius1) and 5 ≤ V∞ ≤ 35 km s-1. The impact parameter range was defined by the condition of encounter limited to 100 Earth radii. The method consisted of numerically simulating those encounters, considering binaries now instead of a single asteroid. The binary consisted of a spherical primary with radius Rp = 0.5 km and with a typical rubble pile density of 2 g/cm3, which led to a calculated mass of Mp ≈ 1.1 × 1012 kg.
We considered satellites with radial distribution going from ≈0.02 to ≈0.4 primary’s Hill radius (2 km to 34 km)2, taken every 0.012 primary’s Hill radius (1 km) and with circular orbits. The upper limit for the radial distribution was chosen taking the predicted limit of stability into account, about 0.5 Hill’s radius, since it is expected that the Sun starts to destabilize the system for higher values of orbital radius (Domingos et al. 2006). For each orbital radius 100 satellites were considered with random values for the inclination, longitude of the ascending node, and true anomaly. Thus, for the same encounter we have a cloud of 3300 noninteracting satellites around the primary asteroid.
We performed the numerical integrations of the encounters with the Gauss-Radau integrator (Everhart 1985) for a time span of ten days, step size of one hour and precision of 10-12. From the procedure described in the previous section the initial conditions was obtained for the encounter, for Earth-asteroid distances smaller than 100 Earth radii. We numerically integrate the encounter to the past in order to ensure that the complete effects due to the encounter were being taken into account. The position and velocity of the asteroid and planet for t = −5 days were then considered as the initial conditions for the simulations of the encounter of the binaries (see Fig. 1).
Throughout the close encounters with the Earth, the satellite of the binary could collide with the primary asteroid or be ejected, disrupting the system. The collision was defined by the physical radius of the bodies. The ejection was monitored through the energy of the two-body problem (primary and satellite). When the initially negative energy becomes positive we consider that there was a binary rupture.
We define the critical radius RC, as the largest radial distance for which all satellites survive to the encounter (no collision or disruption). This is considered a border separating the stable conditions from the unstable ones.
3.2. Results: the test particle case
In the diagram of Fig. 4a, we present the results found for the particles case (M2 = 0). The grid shows the range of the encounter conditions and the critical radius found for each one of them. The color-coded scale on the right corresponds to the critical radius values, RC, going from ≈0.02 to ≈0.4 Hill’s radius of the primary (corresponding to 2 km to 34 km for the physical parameters of the binaries considered here). The points in this diagram passed through a smoothing process.
From this diagram we see that approximately all satellites survived for encounters with d > 0.3 Earth’s Hill radius (≈70 Earth radii), independently of the relative velocity of the encounter. When the impact parameter becomes smaller, the most external satellites start being significantly affected by the encounter, and the binary is disrupted. The net effect of such encounters depends on the combination of the encounter parameters: d and V∞, in such way that a binary performing a close encounter with a given d will be less or more influenced depending on the relative velocity. The satellites that suffer encounters with higher relative velocity will be less affected than those that have encounters with lower relative velocities. This can be observed easily in the diagram of Fig. 4a, for d = 0.15 Earth’s Hills radius, for instance. We see that depending on the relative velocity, the critical radius can go from ≈0.15 to 0.4 primary’s Hill radius, passing to intermediate values. Similar analysis can be done by fixing a relative velocity and varying the impact parameter. A better discussion on how the significant gravitational influence of a body during a close encounter depends on the relative velocity and on the impact parameter of the encounter is found in Araujo et al. (2008).
Figure 4a delimits three basic regimes that we classify as weak, moderate, and extreme disruption limits, represented from the right to the left on the diagram by the white lines. The weak disruption limit is given by the close encounters’ conditions beyond which the critical radius is greater than ≈0.36 Hill’s radius of the primary, meaning that the binary is weakly perturbed by the close encounter. The moderate disruption limit is given by the close encounters’ conditions beyond which the critical radius is greater than ≈0.2 Hill’s radius of the primary. The extreme disruption limit is given by the close encounter conditions beyond which the critical radius is greater than ≈0.1 Hill’s radius of the primary. Within this limit we have unstable encounter conditions, meaning that the binary is strongly perturbed by the close encounter. These limits are given by a combination of the relative velocity and of the impact parameter of the encounter. In our model, with Rp = 0.5 km and ρ = 2 g/cm3, those limits correspond to a binary component separation of 30 km for the weak disruption limit, 15 km for the moderate disruption limit, and 5 km for the extreme disruption limit. In the following section we present a more complete analysis where the critical radius is estimated considering the encounter parameters.
The shape of the primary component of the binary influences the dynamic of the satellite. As cited before, the NEA binaries are expected to have oblate shape. For simplicity, here we considered spherical primaries. A known effect observed when the oblateness of the primary is considered is the precession of the pericenter and of the longitude of the ascending node of the orbit of the secondary body. This precession tend to stabilize the orbit of the secondary body, especially those closer to the primary (Winter et al. 2009). Based on this, it is expected that the satellites within the extreme disruption limit would present an increase in the critical radius if an oblate primary was considered.
3.2.1. Critical radius as a function of the encounter conditions
From our results we obtained a function that gives the critical radius RC, as a function of the impact parameter d and of the relative velocity V∞. We did it through linear and quadratic fits. First, the critical radius was given as a function of the impact parameter, considering constant values for the relative velocity. The second fit consisted in obtaining the coefficients of such functions taking the relative velocity into account. We then found that the function that gives the critical radius as a function of the impact parameter and of the relative velocity has the form: 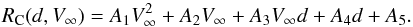 (3)The values of the coefficients Ai are given in Table 1. In this function d is given in Earth’s Hill radius and V∞ in km s-1. As a result we obtain the critical radius of the binary expressed as a fraction of the primary’s Hill radius. This helps us generalize our results for primaries with different sizes.
(3)The values of the coefficients Ai are given in Table 1. In this function d is given in Earth’s Hill radius and V∞ in km s-1. As a result we obtain the critical radius of the binary expressed as a fraction of the primary’s Hill radius. This helps us generalize our results for primaries with different sizes.
The function RC(d,V∞) is valid for 0.02 ≤ d ≤ 0.42 (Earth’s Hill radius), 5 ≤ V∞ ≤ 35 (km s-1), and 0.02 ≤ RC ≤ 0.4 (Primary’s Hill radius). Values for RC lower than the lower limit means that all the satellites are removed (collision or disruption). On the other hand, values for RC greater than the upper limit mean that all the satellites survived. Remembering that for distances greater than ≈0.5 Hill’s radius of the asteroid, the Sun starts to destabilize the satellites orbits.
Given the conditions of a close encounter, the function given in Eq. (2) allows us to predict the stability, or the instability, of a binary going through it. Besides that, knowing the combination d,V∞ that leads to the lost of the most internal satellites we might be able to estimate the frequency of such encounters for the population of NEA, and so estimate their lifetime. This discussion is presented in Sect. 4.
This function reproduces the grid obtained through the numerical integrations with a great concordance, as can be seen by comparing Figs. 4a and b.
 |
Fig. 5 Stable radial limit of the satellites of NEAs as a function of the impact parameter (d) and of the relative velocity (V∞), for the massive satellites case: a) M2 = 0.1M1; b) M2 = M1. The color-coded scales correspond to the critical initial orbital radius RC. The white lines delimit three basic regimes: weak, moderate and extreme disruption limits, from right to left, respectively. |
3.3. Massive satellites
In the previous section we discussed the NEAs satellites stability for the particles case. Now we analyze what changes when massive satellites are considered. We applied the same method described in Sect. 3.1, but now for binaries systems with mass ratios M2 = 0.1M1 (mass of the satellite equal to 10% of the mass of the primary) and M2 = M1. There were considered noninteracting satellites, and the numerical integrator was modified in order to avoid that the satellites were indirectly perturbed by the interaction of the primary with the other satellites.
In the diagrams of Fig. 5a and b, we present the results for the massive cases. These diagrams show that the stable and unstable encounter conditions found for the massive cases are similar when compared with each other and with the particles case (Fig. 4a).
We found that the range of stable encounter conditions are slightly wider for the binaries with higher mass ratio. This can be better visualized in the graph of Fig. 6, by considering the weak disruption limit. Nevertheless, we see that this difference is not significant.
3.4. Comments on a tentative analytical approach
In this section we discuss the difficulties of using an analytical approach to problems involving close encounters of binaries with planets. We focus on an analytical approach that is presented by Agnor & Hamilton (2006) in their work on Neptune’s capture of its moon Triton in a binary-planet gravitational encounter. This approach was also adopted in a work on the capture of the irregular satellites of Jupiter (Philpott et al. 2010). Assuming that the disruption of a binary system is instantaneous (impulse approximation), it was estimated that the distance of the close encounter at which tidal disruption of the binary occurs (rtd), is given by 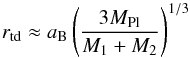 (4)where aB is the semi-major axis of the binary, MPl the mass of the planet, and M1 and M2 are the masses of the binary’s components. The tidal disruption limit given by this equation comes from the definition of Hill’s radius. It corresponds to the distance of encounter at which the primary’s Hill radius with respect to the planet is no longer larger than the separation of the binary itself.
(4)where aB is the semi-major axis of the binary, MPl the mass of the planet, and M1 and M2 are the masses of the binary’s components. The tidal disruption limit given by this equation comes from the definition of Hill’s radius. It corresponds to the distance of encounter at which the primary’s Hill radius with respect to the planet is no longer larger than the separation of the binary itself.
The analytical disruption limits are obtained for each d and V∞ combination through Eq. (2), considering that at the moment of the closest approach q = rtd. We considered aB = 5,15,30 km (separation of the binary for circular orbits), which coincide with the critical radius values RC, obtained numerically for a primary with RP = 0.5 km, and ρ = 2 g/cm3. These limits are those represented in Figs. 4 and 5. In the current analysis we consider M2 as a massless particle.
 |
Fig. 6 Comparison of the weak disruption limit for the particles and massive cases, as a function of the impact parameter (d) and of the relative velocity (V∞). |
The graph in Fig. 7 shows the limits found numerically and analytically for the particles case. We see that there is no agreement between those two approaches. The analytical approach presents a limit that is almost constant as V∞ increases, while the numerical approach clearly shows a significant dependence on this parameter. That is mainly because the analytical approach takes the definition of Hill’s sphere into account, which does not depend on the velocity of the encounter Vq (Fig. 1). It is a statistical model where the relative motion of the planet and of the primary body is not considered in determining the disruption limit.
Araujo et al. (2008) has shown that the encounter velocity, Vq, determines how significantly this body will be disturbed by the close encounter. For instance, for the same encounter distance q (Fig. 1), a body can be strongly perturbed if Vq is low, while for a very high Vq, the body may not even feel the perturbation due to the encounter. Thus, an analytical model that represents this problem must take the velocity of the encounter into account.
 |
Fig. 7 Comparison of the stability limits RC (numerical) and rtd (analytical) for NEAs binaries, for the particles case. Three values were considered for the separation of components of the binaries aB = 5,15,30 km. |
 |
Fig. 8 Timescale for encounters within extreme disruption limits for the sample of 2100 asteroids of the Atens, Apollo, and Amor groups. The color-coded scale gives the time in millions of years. The black lines designate the borders between the groups, according to their definition. |
4. Frequency of encounters
Now that we have determined the limits of the encounter conditions that result in the conservation or loss of the satellites of binaries, we are going to analyze how often those encounters occurs, and thus estimate the lifetime of such binaries.
Walsh & Richardson (2008) present the idea that the NEAs binaries have a shorter lifetime than the lifetime of the asteroids of this population. They statistically estimate the binaries’ lifetimes by taking a set of initial conditions into account for the binaries and for the planetary encounter. They considered the statistical encounter probability with the Earth (Bottke et al. 1994) and the static model for the disruption of the binary (Agnor & Hamilton 2006). They present the result for a specific set of initial conditions, and the other values were used as a parameter in the development of their method. Considering encounters with the Earth with V∞ = 16 km s-1 and a mass ratio of 0.1 fot the binary, they estimated that the lifetime of binaries with separations of approximately 4 or 6 primary’s radius is on the order of about 2 or 1.6 Myr.
Here we present our analysis which also aims to estimate the lifetime of NEAs. It was done based on the results obtained through the numerical integrations of the dynamical systems considered in Sects. 2 and 3. We estimate the lifetimes of the NEAs binaries according to the group that they initially belong to.
We concentrate our analysis on the more extreme cases, i.e., on the encounters capable of removing the satellites closer to the primary asteroid. For this, the disruption limit of RC = 0.1 Primary’s Hill radius was considered (see Fig. 4). We then look for the encounters performed within such conditions in terms of d and V∞, among all the registered encounters for the Amor, Apollo, and Atens groups with the Earth, discussed in Sect. 2.
We found from our initial sample of NEAs that approximately 93% of the asteroids that started the numerical integrations in the Atens group experience an encounter within the extreme disruption limit in the time span of 10 Myr. For the group Apollo, this percentage corresponds to ≈60%, and ≈25% for the Amor group. There is agreement between these results and the results presented in Sect. 2. It was seen that the asteroids of the Atens group experience more close encounters with the Earth than the asteroids of the other groups, and so the probability of encounters within the extreme disruption limit is higher. On the other hand, the asteroids of the Amor group have fewer encounters with the Earth, so the encounters are less probable in such conditions.
Knowing in what proportion such encounters happen, the question that arises is how often those encounters are? To answer this question, we identified how long it took for each of the asteroids in our sample to suffer the first encounter within the extreme disruption limit. The diagram shown in Fig. 8 provides such information for the whole sample of 2100 asteroids. The color-coded scale gives the time in millions of years. According to this code, the yellow dots correspond to asteroids that did not experience encounters within the extreme disruption limit during the whole period of 10 Myr. Since the asteroids of the Amor group suffer fewer encounters in such condition, it is then understandable that this group presents more yellow dots in the diagram.
Considering only the encounters’ cases (not yellow dots), we analyze the frequency of the encounters. We found that the mean and the standard deviation of the time of the first encounter for each group was 1.0 × 106 ± 1.6 × 106 years for the Atens group, 1.5 × 106 ± 1.9 × 106 years for the Apollo group, and 3.0 × 106 ± 2.8 × 106 years for the Amor group. We see that the standard deviation is too high, indicating a high variance in the distribution of the data. Nevertheless, these numbers show that the asteroids of the Atens group suffer close encounters, on average, in smaller intervals of time, while it takes a longer interval for the asteroids of the Amor group. We then analyzed the distribution of the data. This is presented in the histograms shown in Fig. 9.
It is interesting to note the high percentage of encounters performed before 1 Myr, especially for the Atens and Apollo groups. For the Atens, the calculated median is 332 500 years, meaning that 50% of the encounters occurred before that period. In fact, the histogram in Fig. 9a shows that ≈25% of the encounters of the asteroids of the Atens group occur within 100 000 years. For the Apollos, the calculated median is 665 384 years, meaning that 50% of the asteroids of this group are expected to suffer a strong enough encounter to remove the satellites closer to the primary asteroid in about 700 000 years. For the Amor group, this period is much longer, about 2.2 Myr. As discussed before, owing to orbital characteristics of the asteroids of this group, the close encounters with the Earth are not as frequent as for Apollo and Atens. Thus, a longer period is expected for encounters within the extreme disruption limit.
The distinct characteristic of encounters of NEAs with the Earth, discussed above, may influence what we currently know about binaries in the NEAs population. This is discussed in the following section.
 |
Fig. 9 Timescale distribution of close encounters within the extreme disruption limit for a) Atens, b) Apollo, and c) Amor. The medians are indicated by the green lines. |
4.1. The current scenario of binaries NEAs
Recent data from JPL/NASA1 indicate that there are 46 multiple systems in the NEAs population. Johnston2 lists 47 of these multiple systems in the population of NEAs at present. These numbers are constantly updated.
The diagram in Fig. 10 shows the distribution of 37 of such systems as a function of the primary radius and of the separation of the bodies, classified by Atens, Apollo, and Amor. The limit of a 5 km separation between the primary and the satellite is indicated in the diagram, and it is given as a function of the primary’s radius. It is seen that the majority of the known multiple systems have satellites with separations smaller than 5 km. This agree with our work since it was seen that the encounters that would disrupt systems with more separated satellites are very frequent in this population.
We see from this diagram that some of the primaries have radii greater than 0.5 km (physical radius of the primary considered in this work). We therefore represented the separation of 5 km in terms of the primary’s Hill radius. This procedure helps us generalize our results to the multiple systems of different sizes. The calculated Hill’s radius of the primary with physical radius of 0.5 km, ρ = 2 g/cm3 and at 1 AU from the Sun is ≈84 km, in such a way that a separation of 5 km between the massless satellite and the primary corresponds to a separation of ≈0.06 primary’s Hill radius. Considering the same density for the other bodies and their physical radii, we calculated their Hill radius at 1 AU, and so, the separation of their satellite in terms of the primary’s Hill radius.
 |
Fig. 10 Multiple systems in the NEA population, classified according to their group, as a function of the primary radius and of the separation of the bodies (JPL/NASA). Currently, there are about 46 known multiple systems, where 2 of them are triple systems (tagged with the letter “T”). In the diagram the data of 37 multiple systems are presented. For the other binaries, the separations of the bodies were not determined well yet. In the label on the top is the percentage of asteroids of each group related to the total of bodies considered in the diagram – 37 asteroids. For the triple systems the position of the most external satellite was considered. The black line indicates the limit of 0.06 primary’s Hill radius, which corresponds to the 5 km limit of separation between the primary and the satellite. |
It is interesting to note that there is a concentration of the observed multiple systems with the primary/satellite separation smaller than 0.06 primary’s Hill radius (or 5 km). According to the present work, it was estimated that the close encounters able to remove satellites with separation greater than 0.06 primary’s Hill radius are very frequent, in such a way that binaries with satellites with separations greater than this would be rapidly disrupted by the close encounters with the Earth, so less likely to be observed. This may justify the characteristics of the current observable multiple systems in the NEAs population, represented in Fig. 10.
Furthermore, we see that some of the binaries, including the triple systems 1994 CC and 2001 SN263, have the most external satellites beyond the 0.06 primary’s Hill radius limit. The classification of our sample in the Atens, Apollo, and Amor groups helps us make some assumptions about those binaries or about any other multiple system that might be observed in the future. For instance, the discovery of a binary belonging to the Apollo group with a satellite separation greater than 0.06 primary’s Hill radius means that this system has probably not yet suffered a close encounter that would remove such satellite, i.e., an encounter inside the extreme disruption limit. Thus, based on our results, we evaluate that this system is new in the Apollo group or that the binary has a recent formation (less than 700 000 years for the Apollos). Similar analysis can be done for the other groups.
The close encounters of the multiple systems of the NEAs population with the Earth is thus confirmed as a powerful mechanism of disruption of such systems. It may even explain the current observable NEA multiple systems population.
5. Final comments
In this work we investigated the role of close encounters with the Earth on the stability of NEA satellites. Initially we characterized the close encounters suffered by the NEAs with the Earth. As expected, we found that the close encounters of the asteroids of the Atens group with the Earth are much more frequent than the encounters of the asteroids of the Apollo and Amor groups.
We found that the asteroids of the Atens group suffer close encounters with a slightly higher relative velocity, although the majority of the encounters happens approximately in the interval 1 ≤ V∞ ≤ 40 km s-1, independently of the group that they belong to.
Taking a representative sample of the registered close encounters with the Earth, we simulated those encounters performed by hypothetical binaries. For this we built a cloud of noninteracting satellites around the primary, with a radial and angular distribution of the satellites. It was considered massless satellites (particles case) and two cases with massive satellites: M2 = 0.1M1 and M1 = M2.
Through this procedure we characterized the stable (and unstable) encounter conditions for NEA binaries’ satellites. This was presented in diagrams of the stable radial limit of the satellites, given as a function of the impact parameter and of the relative velocity of the encounter. As expected, we found that the close encounters performed closer to the planet and/or with lower relative velocity led to the unstable cases, meaning that any satellite or only the most internal satellites survive the encounter. On the other hand, close encounters performed with high relative velocity and/or farther to the planet lead to the stable encounters, meaning that most of the satellites survive the encounter and that any satellites or only the most external ones are lost. Throughout the paper we discuss the role of the distance and of the relative velocity of the encounter in the net effect of the encounter in the binary. This relation was also presented as a relevant point to be considered in an analytical approach for this problem.
The diagrams of the stable radial limit of the satellites clearly show distinct regions, defined by the critical radius as a function of the encounter conditions. We classified these regions as weak, moderate, and extreme disruption limits, and we obtained a math function to calculate the critical radius as a function of d and V∞. Given the conditions of a close encounter of an NEA binary with the Earth, we are now able to predict the effects of such an encounter on the binary.
We found that there is a slight difference in the range of stable encounter conditions depending on the mass of the bodies. There is an increase in the stable conditions for the systems with higher mass-ratio, but we conclude that this difference is not significant.
After having determined the encounter conditions that led to the loss of the most internal satellites, and so, for the disruption of the binary we estimated the frequency of such encounters for the NEAs belonging to the Atens, Apollo, and Amor groups, and consequently estimated their lifetimes. For the Atens group we estimated that the asteroids may suffer an encounter within the extreme disruption limit with the Earth in about 330 000 years. For the Apollo group we estimated that the asteroids of this group may suffer such close encounters in about 700 000 years and the asteroids of the Amor group in about 2.2 Myr. Thus, the lifetime of the NEA binaries was proved to be strongly influenced by the planetary close encounters and shorter than the predicted lifetime of the NEAs.
We discussed the current population of NEAs multiple system and the role of the close planetary encounters with the Earth in this scenario. We showed that the characteristic of the observed population can be explained by just taking this mechanism into account. The concentration of observable satellites with separation smaller than 0.06 primary’s Hill radius would be explained by the fact that systems with greater separation of satellites are rapidly disrupted, and so, less likely to be observed. On the other hand, under this approach, the multiple systems that have more separated satellites, including the only two triple systems 1994 CC and 2001 SN263 are supposed to have a recent history in the NEAs population.
Available at http://echo.jpl.nasa.gov/~lance/binary.neas.html
Available at http://www.johnstonsarchive.net/astro/asteroidmoons.html
Acknowledgments
This work was funded by INCT – Estudos do Espaço, CNPq and FAPESP – Proc. 201108171-3. This support is gratefully acknowledged. We also thank Ernesto Vieira Neto for his contribution with the numerical integrator.
References
- Agnor, C. B., & Hamilton, D. P. 2006, Nature, 441, 192 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Araujo, R. A. N., Winter, O. C., Prado, A. F. B. A., & Vieira Martins, R. 2008, MNRAS, 391, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke, W. F., & Melosh, H. J. 1996a, Icarus, 124, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke, W. F., & Melosh, H. J. 1996b, Nature, 381, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke, W. F., Jr., Nolan, M. C., Greenberg, R., & Kolvoord, R. A. 1994, in Hazards due to comets and asteroids eds. T. Gehrels, & M. S. Matthews (Tucson: Univ. of Arizona Press), 337 [Google Scholar]
- Bottke, W. F., Jr., Vokrouhlick, D., Rubincam, D. P., & Broz, M. 2002, in The Effect of Yarkovsky Thermal Forces on the Dynamical Evolution of Asteroids and Meteoroids, Asteroids III, eds. W. F. Bottke Jr., A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: Univ. of Arizona Press), 395 [Google Scholar]
- Bottke, W. F., Vokrouhlick, D., Rubincam, D. P., & Nesvorn, D. 2006, Annu. Rev. Earth Planet. Sci., 34, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brozovic, M., Benner, L. A. M., Nolan, M. C, et al. 1994, CC. IAU Circ., 9053, 2 [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chauvineau, B., & Farinella, P. 1993, A&A, 279, 251 [NASA ADS] [Google Scholar]
- Chauvineau, B., Mignard, F., & Farinella, P. 1991, Icarus, 94, 299 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ćuk, M. 2007, ApJ, 659, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Domingos, R. C., Winter, O. C., & Yokoyama, T. 2006, MNRAS, 373, 1227 [NASA ADS] [CrossRef] [Google Scholar]
- Everhart, E. 1985, An efficient integrator that uses Gauss-Radau spacings, in Dynamics of comets: Their origin and evolution, eds. A. Carusi, & G. B. Valsecchi (D. Reidel Publishing Company), 185 [Google Scholar]
- Fang, J., & Margot, J. L. 2012, AJ, 143, 154 [Google Scholar]
- Fang, J., Margot, J.-L., Brozovic, M., et al. 2011, AJ, 141, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Freistetter, F. 2009, Celest. Mech. Dyn. Astron., 104, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Gladman, B., Michel, P., & Froeschle, C. 2000, Icarus, 146, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, P. 1997, Icarus, 129, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, P., & Froeschle, C. 1997, Icarus, 128, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Bottke, W. F., Jr., Froeschlé, Ch., & Michel, P. 2002, Origin and Evolution of Near-Earth Objects, Asteroids III, eds. W. F. Bottke Jr., A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: University of Arizona Press), 409 [Google Scholar]
- Nolan, M. C., et al. 2008, BAAS, 33, 1120 [NASA ADS] [Google Scholar]
- Philpott, C. M., Hamilton, D. P., & Agnor, C. B. 2010, Icarus, 208, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, D. C., & Walsh, K. J. 2006, Ann. Rev. Earth Planetary Sci., 34, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Scheeres, D. J., Ostro, S. J., Werner, R. A., Asphaug, E., & Hudson, R. S. 2000, Icarus, 147, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Scheeres, D. J., Marzari, F., & Rossi, A. 2004, Icarus, 170, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Solem, J. C., & Hills, J. C. 1996, AJ, 111, 1382 [Google Scholar]
- Tancredi, G. 1998, Celest. Mech. Dyn. Astron., 70, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, K. J., & Richardson, D. C. 2006, Icarus, 180, 201 [Google Scholar]
- Walsh, K. J., & Richardson, D. C. 2008, Icarus, 193, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Winter, O. C., Boldrin, L. A. G., Vieira Neto, E., et al. 2009, MNRAS, 395, 218 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Every time that the distance between the Earth and any of the asteroids of the sample is smaller than 100 Earth radii (100 R⊕), we considered that there was an encounter at time te. We integrate 5 days in the past to obtain the initial conditions of the encounter. In this figure, d is the impact parameter, V∞ the relative velocity of the encounter, q the minimum distance of the encounter, and Vq the relative velocity at this point. |
| In the text | |
 |
Fig. 2 Percentage of close encounters as a function of the encounter velocity V∞. The medians are indicated by the green lines. The histogram d) has a larger bin to better compare our results with the results presented by (Walsh & Richardson 2006) and (Fang & Margot 2012). |
| In the text | |
 |
Fig. 3 a) Representation of a typical orbit of an NEA belonging to the Amor group. b) Perturbed orbit of the asteroid with an increase in the eccentricity – the orbits cross and the encounters are possible. c) Perturbed orbit – extreme case with a high increase in eccentricity. In all three cases, it was considered a fixed semi-major axis. |
| In the text | |
 |
Fig. 4 Stable radial limit of the satellites of NEAs as a function of the impact parameter (d) and of the relative velocity (V∞), for the particles case (M2 = 0). a) Resulting from the numerical simulation. b) Generated through the fit (Eq. (3)). The color-coded scales correspond to the critical initial orbital radius RC, given in the primary’s Hill radius. The white lines delimit three basic regimes: weak, moderate, and extreme disruption limits from right to left, respectively. |
| In the text | |
 |
Fig. 5 Stable radial limit of the satellites of NEAs as a function of the impact parameter (d) and of the relative velocity (V∞), for the massive satellites case: a) M2 = 0.1M1; b) M2 = M1. The color-coded scales correspond to the critical initial orbital radius RC. The white lines delimit three basic regimes: weak, moderate and extreme disruption limits, from right to left, respectively. |
| In the text | |
 |
Fig. 6 Comparison of the weak disruption limit for the particles and massive cases, as a function of the impact parameter (d) and of the relative velocity (V∞). |
| In the text | |
 |
Fig. 7 Comparison of the stability limits RC (numerical) and rtd (analytical) for NEAs binaries, for the particles case. Three values were considered for the separation of components of the binaries aB = 5,15,30 km. |
| In the text | |
 |
Fig. 8 Timescale for encounters within extreme disruption limits for the sample of 2100 asteroids of the Atens, Apollo, and Amor groups. The color-coded scale gives the time in millions of years. The black lines designate the borders between the groups, according to their definition. |
| In the text | |
 |
Fig. 9 Timescale distribution of close encounters within the extreme disruption limit for a) Atens, b) Apollo, and c) Amor. The medians are indicated by the green lines. |
| In the text | |
 |
Fig. 10 Multiple systems in the NEA population, classified according to their group, as a function of the primary radius and of the separation of the bodies (JPL/NASA). Currently, there are about 46 known multiple systems, where 2 of them are triple systems (tagged with the letter “T”). In the diagram the data of 37 multiple systems are presented. For the other binaries, the separations of the bodies were not determined well yet. In the label on the top is the percentage of asteroids of each group related to the total of bodies considered in the diagram – 37 asteroids. For the triple systems the position of the most external satellite was considered. The black line indicates the limit of 0.06 primary’s Hill radius, which corresponds to the 5 km limit of separation between the primary and the satellite. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


