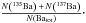| Issue |
A&A
Volume 565, May 2014
|
|
|---|---|---|
| Article Number | A51 | |
| Number of page(s) | 13 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201423432 | |
| Published online | 05 May 2014 | |
Explaining the Ba, Y, Sr, and Eu abundance scatter in metal-poor halo stars: constraints to the r-process⋆
Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482, Potsdam, Germany
e-mail: cescutti@aip.de
Received: 15 January 2014
Accepted: 28 March 2014
Context. Thanks to the heroic observational campaigns carried out in recent years we now have large samples of metal-poor stars for which measurements of detailed abundances exist. In particular, large samples of stars with metallicities −5 < [Fe/H] <−1 and measured abundances of Sr, Ba, Y, and Eu are now available. These data hold important clues on the nature of the contribution of the first stellar generations to the enrichment of our Galaxy.
Aims. We aim to explain the scatter in Sr, Ba, Y, and Eu abundance ratio diagrams unveiled by the metal-poor halo stars.
Methods. We computed inhomogeneous chemical evolution models for the Galactic halo assuming different scenarios for the r-process site: the electron-capture (EC) supernovae and the magnetorotationally driven (MRD) supernovae scenarios. We also considered models with and without the contribution of fast-rotating massive stars (spinstars) to an early enrichment by the s-process. A detailed comparison with the now large sample of stars with measured abundances of Sr, Ba, Y, Eu, and Fe is provided (both in terms of scatter plots and number distributions for several abundance ratios).
Results. The scatter observed in these abundance ratios of the very metal-poor stars (with [Fe/H] <−2.5) can be explained by combining the s-process production in spinstars, and the r-process contribution coming from massive stars. For the r-process we have developed models for both the EC and the MRD scenarios that match the observations.
Conclusions. With the present observational and theoretical constraints we cannot distinguish between the EC and the MRD scenarios in the Galactic halo. Independently of the r-process scenarios adopted, the production of elements by an s-process in spinstars is needed to reproduce the spread in abundances of the light neutron capture elements (Sr and Y) over heavy neutron capture elements (Ba and Eu). We provide a way to test our suggestions by means of the distribution of the Ba isotopic ratios in a [Ba/Fe] or [Sr/Ba] vs. [Fe/H] diagram.
Key words: Galaxy: evolution / Galaxy: halo / stars: abundances / stars: massive / stars: rotation / nuclear reactions, nucleosynthesis, abundances
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
The site for the production of the heaviest elements built via rapid neutron captures (the so-called r-process) is still unclear, and has been driving large theoretical efforts (e.g. Goriely et al. 2013; Nakamura et al. 2013; Wanajo 2013; Qian 2012; Winteler et al. 2012; Arcones & Martínez-Pinedo 2011; Thielemann et al. 2011). The r-process requires high neutron fluxes (i.e., the high neutron-to-seed ratios needed for the r-process to occur). The site of the r-process must also reproduce the abundance patterns seen in strongly r-process-enhanced metal-poor stars (which match the solar r-process pattern in a wide range of elements), and hence enrich the interstellar medium (ISM) on short timescales.
In our latest work (Cescutti et al. 2013), we studied the impact on the chemical evolution of the Galactic halo of the s-process generated by massive fast-rotating metal-poor stars (spinstars). We showed that spinstars can explain the long-standing problem of the [Sr/Ba] spread in the Galactic halo (for alternative scenarios see Arcones & Montes 2011; Aoki et al. 2013b). However, to achieve this, it was necessary to consider the contribution of an r-process to the chemical enrichment. In Cescutti et al. (2013), we followed the scenario described by Wanajo et al. (2009), where the r-process occurs in a relative narrow mass range (8−10 M⊙). We underline that these assumptions on the r-process did not influence our main result, which was to show how spinstars can explain the Sr/Ba ratios.
In the present work we verify this by testing other r-process scenarios. First, this offers the opportunity to confirm the important role of spinstars not only in the chemical evolution of the light elements such as C and N (Chiappini et al. 2006, 2008), but also for the heavier elements (Pignatari et al. 2008; Chiappini et al. 2011; Frischknecht et al. 2012). Second, we aim to find observational constraints on the nature of the r-process by studying chemical evolution models of the earliest phases of the chemical enrichment of our Galaxy.
In the present work we compute a new chemical evolution model that includes the site of production of r-process recently suggested by Winteler et al. (2012). These authors suggested that magnetorotationally driven supernovae might be the source of the r-process in the early Galaxy. These SNe explode in a rare progenitor configuration that is characterized by a high rotation rate and a strong magnetic field necessary for the formation of bipolar jets. The findings of Winteler et al. (2012) suggest that the second and third peaks of the solar r-process distribution can be reproduced well. Here, we test whether this site for the r-process provides an enrichment for the earliest phases of the Galactic chemical evolution consistent with the abundances observed in metal-poor halo stars.
We anticipate that the results we obtain in the Galactic halo for the Winteler scenario cannot clearly be distinguished from the r-process scenario based on electron-capture SNe used in Cescutti et al. (2013), at least not before a substantial improvement in the number of stars measured in the Galactic halo has provided stronger constraints. Therefore, spinstars play a key role in this scenario as well, and the oldest halo stars are formed from an ISM enriched by both r- and s-processes.
A clear prediction of both models is that EMP stars with a high [Sr/Ba] ratio should be almost entirely enriched by the s-process. This prediction is original and differs from the other possible scenarios in which the spread in [Sr/Ba] ratio is explained by a weak r-process (Arcones & Montes 2011) or a truncated r-process (Aoki et al. 2013b). A way to distinguish in this mixture between s-process and r-process in the early phase of the Galaxy formation is to examine the prediction of our models for the Ba isotopes.
The s-process preferentially produces even isotopes, whereas the r-process produces approximately the same amount of odd and even isotopes. According to nucleosynthesis calculations (Arlandini et al. 1999), it is expected that an odd fraction of Ba isotopes (fodd) = 0.11 ± 0.01 occurs in the case of a pure s-process, and an fodd = 0.46 ± 0.06 in the case of pure r-process. Magain (1995) measured for the first time the isotopic ratio of a very bright halo star, HD 140283, finding an s-process signature ([Sr/Ba] = 0.9), which agrees with our theoretical results. However, his results have been challenged and still need to be confirmed (Lambert & Allende Prieto 2002; Collet et al. 2009; Gallagher et al. 2010). The biggest challenge is to correctly take into account the 3D effects on the line formation. More recently, Gallagher et al. (2012) have again attempted to measure isotopic ratios in other metal-poor stars, but all their candidates are expected to be s-process dominated. Although the measurement of the Ba isotopic ratio is not trivial, it is feasible, and we intend to provide our results to compare them with future measurements, which will provide an important test for our models.
The paper is organized as follows: in Sect. 2 we describe the observational data; Sect. 3 describes the chemical model and the adopted stellar yields. In Sect. 4 our results are presented, and in Sect. 5 we summarize our conclusions.
2. Observational data
For the halo we employed the same data as presented in Cescutti et al. (2013), where we have adopted observational abundance ratios from the literature; the data for the neutron capture elements and for the α-elements are those compiled by Frebel (2010)1, labeled as halo stars2. To this sample, we added the very recent data measured by Aoki et al. (2013a). Among the halo stars collected, we differentiate the normal stars from the carbon-enhanced metal-poor (CEMP) stars. Around 20% of stars with [Fe/H] <−2.0 are CEMP stars (Lucatello et al. 2006). We followed the definition given by Masseron et al. (2010), where a CEMP star is defined as having [C/Fe] > 0.9. The important distinction in the present work is made between CEMP-s (including CEMP-rs) and CEMP-no (including CEMP-r), that is, we distinguished whether a strong signature of s-process is present.
Indeed, CEMP-s (and CEMP-rs) stars most likely stem from binary mass transfer from a previous asymptotic giant branch companion (Bisterzo et al. 2012; Lugaro et al. 2012), and for this reason CEMP-s (and CEMP-rs) do not reflect the chemical evolution of the ISM. We therefore opted to exclude the CEMP-s (and CEMP-rs) stars from our figures and included only the CEMP-no and the CEMP-r stars; in the compilation by Frebel and in the data reported by Aoki et al. (2013a) there is also an large portion of stars without carbon measurements. For these stars we cannot establish whether they are CEMP stars or not; still, since they represent a large portion we decided to include them in our plots, but to distinguish them graphically from the confirmed normal stars.
Because the data come from different authors, the methods, instruments and quality of the spectra are not homogenous. Nevertheless, the number of metal-poor stars for which detailed abundances are available is still impressive: we have found measurements of Ba abundances for 774 stars in the literature. For 459 of these, carbon abundances have also been determined, and 67 of the objects are classified as CEMP stars. Of these 67 stars, 21 are classified as CEMP-no, and one as a CEMP-r star.
Our sample is clearly biased toward extremely low metallicity: there are more stars (with carbon measurement) with an [Fe/H] <−2.5 than with an higher ratio, which is at odds with the metallicity distribution function of the Galactic halo. This simply reflects the observational strategies; typically, the most metal-poor candidates are selected a priori using low-resolution spectra or photometry, and then these stars are followed-up with time-consuming high-resolution observations. Other biases can also play a role; for example, a preferential selection toward high (or low) abundance ratios for neutron capture elements. Indeed, for certain elements (such as Eu) the lines tend to be very weak and only upper limit detections are available if the abundance is below a certain threshold value (which is also a function of the signal-to-noise ratio of the spectra). We kept these biases in mind when presenting our results.
3. Chemical evolution model
The chemical evolution model presented here is the same as in Cescutti et al. (2013). Therefore, we describe its main characteristics only briefly.
We considered the same chemical evolution model as adopted in Cescutti & Chiappini (2010), which is based on the inhomogenous model developed by Cescutti (2008) and on the homogeneous model of Chiappini et al. (2008). The halo consists of many independent regions, each with the same typical volume, and each region does not interact with the others. Accordingly, the dimension of the volume is expected to be large enough to allow us to neglect the interactions between different volumes, at least as a first approximation. For typical ISM densities, a supernova remnant becomes indistinguishable from the ISM – that is, merges with the ISM – before reaching ~50 pc (Thornton et al. 1998) therefore, we decided to have a typical volume with a radius of roughly 90 pc, and the number of assumed volumes is 100 to ensure good statistical results. We did not use larger volumes because we would lose the stochasticity we are looking for; in fact, larger volumes produce more homogeneous results.
In each region, we assumed the same law for the infall of the gas with primordial composition, following the homogeneous model by Chiappini et al. (2008): 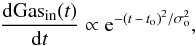 (1)where to is set to 100 Myr and σo is 50 Myr. Similarly, the star formation rate (SFR) is defined as
(1)where to is set to 100 Myr and σo is 50 Myr. Similarly, the star formation rate (SFR) is defined as 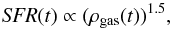 (2)where ρgas(t) is the density of the gas mass inside the volume under consideration. Moreover, the model takes an outflow from the system into account:
(2)where ρgas(t) is the density of the gas mass inside the volume under consideration. Moreover, the model takes an outflow from the system into account: 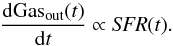 (3)Knowing the mass that is transformed into stars in a time-step (hereafter,
(3)Knowing the mass that is transformed into stars in a time-step (hereafter, 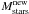 ), we therefore assigned the mass to one star with a random function, weighted according to the initial mass function (IMF) of Scalo (1986) in the range between 0.1 and 100 M⊙. We then extracted the mass of another star and repeated this cycle until the total mass of newly formed stars exceeded
), we therefore assigned the mass to one star with a random function, weighted according to the initial mass function (IMF) of Scalo (1986) in the range between 0.1 and 100 M⊙. We then extracted the mass of another star and repeated this cycle until the total mass of newly formed stars exceeded 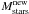 . In this way, the
. In this way, the 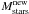 is the same, in each region at each time-step, but the total number and mass distribution of the stars are different. We thus know the mass of each star contained in each region, when it is born, and when it will die, assuming the stellar lifetimes of Maeder & Meynet (1989). At the end of its lifetime, each star enriches the ISM with its newly produced chemical elements and with the elements locked in that star when it was formed, excluding the fractions of the elements that are permanently locked in the remnant.
is the same, in each region at each time-step, but the total number and mass distribution of the stars are different. We thus know the mass of each star contained in each region, when it is born, and when it will die, assuming the stellar lifetimes of Maeder & Meynet (1989). At the end of its lifetime, each star enriches the ISM with its newly produced chemical elements and with the elements locked in that star when it was formed, excluding the fractions of the elements that are permanently locked in the remnant.
Yields for Fe are the same as in François et al. (2004). The model considers the production by s-process from 1.5 to 3 M⊙ stars and SNIa enrichment, as in Cescutti et al. (2006).
As shown in Cescutti et al. (2013), our model is able to reproduce the MDF measured for the halo by Li et al. (2010); the results by Li et al. (2010) are based on main-sequence turn-off stars from the data of the Hamburg/ESO objective-prism survey (HES; Christlieb et al. 2008). This comparison shows that the timescale of enrichment of the model is compatible with that of the halo stars in the solar vicinity. Moreover, our model predicts a small spread for the α-elements Ca and Si, compatible with the observational data. In addition, our model predicts a slight increase in the scatter in the very metal-poor regime. Interestingly, inhomogeneous models, as the one shown here, do predict a few outliers with low values of [α/Fe] (see Fig. 2 of Cescutti et al. 2013).
3.1. Stellar yields for heavy elements
3.1.1. Empirical yields for the r-process
We considered two scenarios for the r-process. The first is the same as the r-process scenario assumed in Cescutti et al. (2013): the stellar mass range contributing to the r-process is from 8 to 10 M⊙. This scenario is similar to the one proposed by theoretical models of electron-capture supernovae (EC SNe). We call this model EC+s. We added +s to the names of all models to indicate that we included the contribution by spinstars (discussed in the next section). The yields are calculated with the following approach (see also Cescutti et al. 2006): we computed a homogeneous chemical evolution model where the yields of Ba were chosen so as to reproduce the mean trend of [Ba/Fe] versus [Fe/H], see Fig. 3 in Cescutti et al. (2013).
The second scenario follows the idea described in Winteler et al. (2012). According to these authors, a small percentage of massive stars end their lives as magnetorotationally driven (MRD) supernovae. To implement this scenario into our chemical evolution model, we assumed that only 10% of all the simulated massive stars contribute to the r-process. This percentage is higher than the rough estimate of 1% of the massive stars mentioned in Woosley & Heger (2006) at solar metallicity, which is the reference of Winteler et al. (2012), but this number is expected to increase toward lower metallicity (Woosley & Heger 2006).
Similarly to the EC SNe scenario, for the MRD SNe scenario there is no prediction of the ejected mass in each r-process event. On these grounds we used the constraints computed for the EC SNe scenario on the basis of observational data; we present two cases for the r-process yields of the MRD SNe scenario:
-
MRD+s A: in this case we made the sim-plest assumption that 10% of all the stars with massesbetween 10 M⊙ and80 M⊙ generate an r-processthat produces a fixed mass. We determined the ejected mass ofBa for each event in such a way that MRD+s Aproduces the same amount of Ba as the EC+s model in astellar generation. The resulting yield of r-process Ba is8.0 × 10-6M⊙; the other chemical elements were simply scaled using the solar system r-process contribution as determined by Simmerer et al. (2004).
-
MRD+s B: in this case we took into account the possibility that the amount of mass ejected as r-process varies. Since the variation is unknown, we assumed this range: the minimum is 1% of the fixed value in the previous model and the maximum is twice the same value. Since the total production should be conserved, the ejected mass for n- star (r-process producer) in the model MRD+s B can be described by the following equation:
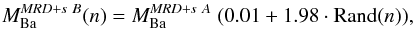 (4)where Rand(n) is a uniform random distribution in the range [0, 1].
(4)where Rand(n) is a uniform random distribution in the range [0, 1].
The models EC+s, MRD+s A and MRD+s B are summarized in Table 1.
Nucleosynthesis prescriptions for the three cases analyzed for strontium.
The difference between the r-process ratio observed in metal-poor r-process-rich stars (see Sneden et al. 2008) and the solar system r-process contribution as determined by Simmerer et al. (2004) seriously affects on the Y ratio, which is 0.5 dex lower in the observational case. Therefore, we computed other two models with the only difference that we assumed the r-process ratio observed in metal-poor r-process-rich stars (see Sneden et al. 2008), instead of the solar system r-process contribution determined by Simmerer et al. (2004) as in the previous scenarios. The models are denoted
-
EC+s 2: the model based on the EC+s scenariowith the observed r-process ratios in r-process-rich stars,
-
MRD+s B2: the model based on the MRD+s B scenario with the observed r-process ratios in r-process-rich stars.
These two models and the comparison model EC+s are summarized in Table 2.
Nucleosynthesis prescriptions for the three cases analyzed for yttrium.
We do not show these models for the Sr, since the difference in this case would be only of ~0.1 dex, that is, lower than the typical error of the observational data.
3.1.2. Contribution of spinstars
We assumed for all our models the same contribution by s-process as in the fs-model of Cescutti et al. (2013). However, we show here results for yttrium which was not treated in the previous paper, therefore we recall that for the yields at3Z = 10-5 we considered the stellar yields obtained by Frischknecht et al. (2012) after decreasing the reaction rate for 17O(α,γ) from Caughlan & Fowler (1988) by a factor of 10, which enhances the s-process production. Unfortunately, we have results with this reaction rate only for a single mass (25 M⊙) at Z = 10-5, and we used the scaling factor obtained for the whole range of masses (see Cescutti et al. 2013). Indeed, there are no nucleosynthesis calculations for spinstars currently carried out with a reduced value of the 17O(α,γ) rate for a metallicity higher than Z = 10-5, and we adopted those computed with the standard value given by Caughlan & Fowler (1988). We need to keep this caveat in mind when interpreting our theoretical predictions for the intermediate metallicity range. Finally, we note that in the spinstars framework, Eu is produced in negligible amounts.
 |
Fig. 1 Stellar distribution. From the left [Ba/Fe], [Sr/Fe] and [Sr/Ba] vs. [Fe/H] in the halo; the density plot is the distribution of simulated long-living stars for our models, see bar below the main figure for the color scale; superimposed, we show the abundances ratios for halo stars (data from Frebel 2010; Aoki et al. 2013a). The symbols for the Frebel (2010) data are black dots for normal stars, cyan dots for CEMP-no, a red x marker for the CEMP-r star, and black open circle for stars without carbon measurement; for the Aoki et al. (2013a) data we adopt the same symbols, but instead of dots we used squares. |
4. Results
4.1. Stellar distribution for strontium and barium
Figure 1 summarizes our results for the stellar distribution of strontium and barium in the Milky Way halo. In the first row we reproduce the results obtained for the fs-model of Cescutti et al. (2013; see their Fig. 5), in which the r-process is assumed to be produced by stars in a narrow mass range (the EC scenario). In the second row, we present the MRD+s A model, which assumes an MRD scenario for r-process. In particular, this model is computed with the assumption that 10% of all the massive stars contribute to the r-process enrichment. The s-process production remains the same as in the model above.
Overall, the comparison with the results of the EC+s model does not reveal significant differences. One main feature is a gap in the stellar distribution in the [Ba/Fe] vs. [Fe/H] diagram. This gap is due to the significant difference we assumed between the production of Ba in spinstars and in the r-process events; this gap is absent from the [Sr/Fe] plot for which the two stellar yields are of the same order of magnitude. The fact that a gap is not seen in the data suggests that our assumption that the amount of mass produced by the r-process is independent of the stellar mass or any other parameter (for instance, magnetic field and rotation) is too simplistic.
In model MRD+s B we relaxed the assumption of a constant yield for the r-process, and allowed a variation in the total amount of r-process production (see third row in Fig. 1). In this case, the gap in the [Ba/Fe] distribution disappears. In addition, model MRD+s B predicts a slightly more pronounced spread in the [Ba/Fe] distribution at intermediate metallicities (−2 < [Fe/H] < − 1).
We now focus on the comparison between MRD+s B and the EC+s models (first and third rows in Fig. 1). The two models give very similar results. In other words, the observational constraints displayed in this figure cannot distinguish between these two scenarios. In both scenarios the time delay in the r-process production is short: the first star (r-process producer) in the MRD scenario explodes after 3−4 Myr (lifetime of a 80 M⊙ star), whereas in the case of the EC scenario this occurs after 20 Myr (lifetime of a 10 M⊙ star). These timescales coupled with the star formation of the Galactic halo do not produce any appreciable difference. We expect, however, that in a system with a more intense star formation history the small differences in the time delay of these two cases can lead to differences in the predicted distributions for the heavy element abundance ratios that might in principle be testable through observations. We will explore this possibility when studying the halo versus bulge chemical enrichment, in a forthcoming paper.
In Fig. 1, some of the observational data present a [Sr/Ba] ratio that is lower than our model predictions. The reason for this is that our models only include the r-process contribution (as given by the solar system pattern) and the s-process contribution by spinstars. The spinstars contribution (with the current stellar yields taken from Frischknecht et al. 2012, at the end of the pre-SN phase) produces [Sr/Ba] ratios higher than the solar system value. The situation can be more complex, however, as shown in Chiappini et al. (2011), where stellar yields were computed at two different phases of He-burning (see their Fig. 2), showing that there might be situations where spinstars produce a negative [Sr/Ba] ratio. More detailed stellar yields are needed to investigate this point in more detail. In addition, the scaled r-process contribution adopted here is a simplified approach (see discussion on the [Y/Ba] ratio). Finally, some objects might still have a small contribution from AGB mass-transfer, which would again decrease the [Sr/Ba] ratios. The AGB mass-transfer contribution is not taken into account in our models. However, only very few data points show negative [Sr/Ba] ratios (see also Fig. 5). It is encouraging that with only two nucleosynthesis sites for Sr and Ba, our results agree so well with the metal-poor data.
4.2. Isotopic distribution of Ba
 |
Fig. 2 Barium isotopic ratio. From the left [Ba/Fe], [Sr/Fe] and [Sr/Ba] vs. [Fe/H] in the halo. The density plot is the distribution of the isotopic ratio of Ba according to the models, see the bar below the main figure. The data are the same as in Fig. 1. |
In Fig. 2, we present our model predictions for the isotopic ratio of Ba in Galactic halo stars for the same models as presented in Fig. 1. This is the first time these results have been computed, and even though the measurement of the Ba isotopic ratio is challenging, it provides an important method to test our model predictions. We are also interested in investigating whether the Ba isotopic ratio might help in distinguishing the two scenarios for r-process production studied here.
The color code in Fig. 2 indicates the fraction of odd isotopes of Ba4 in the simulated stars. The ratio of odd isotopes can be used as an indicator for the presence of the r-process production (blue color) or the s-process production (red) in our simulated stars. Solid nucleosynthesis results indeed indicate that the s-process preferentially produces even isotopes, thus generating a low odd fraction of Ba isotopes (0.11 according to Arlandini et al. 1999); conversely the r-process has no preferential production between odd and even isotopes, thus generating an odd fraction of about 0.5 (0.46 according to Arlandini et al. 1999).
 |
Fig. 3 Stellar distribution. From the left [Y/Fe], [Y/Ba] and [Sr/Y] vs. [Fe/H] in the halo; the density plot is the distribution of simulated long-living stars for our halo models, see bar below Fig. 1 for the color scale; the data are the same as in Fig. 1. |
In the three first plots in the first row, we show the results for the EC+s r-process site. As expected, there is a strong r-process signature in the stars with a high [Ba/Fe] (or [Sr/Fe]), whereas a strong s-process signature marks the stars with low [Ba/Fe] ([Sr/Fe]). The two populations are present and rather distinct up to [Fe/H] ~ − 2.5, above which the r-process signature becomes dominant. This is due to the larger mass produced by the r-process compared with s-process by spinstars. As soon as an r-process event enriches the simulated volume, the isotopic ratio tends to be r-process-like. At the very end of the simulation, the production of s-process by low-intermediate mass stars moves the isotopic ratio toward an intermediate situation with an odd fraction of ~0.3. For the [Sr/Fe] case, where the yields are of the same order, this effect is less pronounced. Indeed, the larger production of Sr by spinstars (compared to Ba) explains why there are extremely metal-poor stars with a strong s-process signature at [Sr/Fe] > 0 in the [Sr/Fe] diagram (in contrast to what is seen for the [Ba/Fe] ratio). In this area an intermediate isotopic ratio is displayed as well; this is due to stars with s-process and r-process signatures that share the same locus on the graph and not to a real mixture in each star.
The situation is different for the [Sr/Ba] plot. In this case the stars dominated by r-process nucleosynthesis lie on the r-process ratio assumed for our empirical yields, whereas the stars above it exhibit an enrichment by spinstars and are thus s-process-rich (i.e., with a low fraction of odd Ba isotopes). This plot clearly shows the impact of spinstars on promoting the [Sr/Ba] scatter observed in the observational data.
 |
Fig. 4 Stellar distribution. From the left [Eu/Y], [Eu/Fe] and [Eu/Ba] vs. [Fe/H] in the halo; the density plot is the distribution of simulated long-living stars for our halo models, see bar below Fig. 1 for the color scale; the data are the same as Fig. 1. |
The second- and third-row models MRD+s A and MRD+s B − show very similar results in this figure as well. Therefore, we underline the differences between the MRD+s B and the EC+s models. The different r-processes considered lead to only small differences in the fraction of s-process-dominated loci in all the plots. This means that it is not possible to use the Ba isotopic ratio to distinguish between the two possibilities.
In summary, the main result is that in the spinstars framework we expect a large portion of extremely metal-poor stars to show a clear s-process signature. The latter tends to be quickly erased by the larger injection of r-process material as soon as their sites become fully operative (in scales on the order of 10 Myrs). This is a robust prediction regardless of the nature of the site for the r-process production.
4.3. Stellar distribution for yttrium
In Fig. 3 we show our results for another light neutron capture element for which observational data are present in literature: Y. The comparison with a new element is important because we can further test our theory by verifying whether our results for the new element agree with the observational data using the same nucleosynthesis hypothesis.
The comparison of the EC+s model with the observational data for [Y/Fe] and [Y/Ba] is not satisfactory. In this case we adopted the same ingredients for s- and r-process as for the Sr EC+s model. We note that for [Fe/H] > − 2, where the model result distribution is no longer affected by a strong spread, the model results appear to be roughly 0.5 dex above the observational data; this is particularly visible in the [Y/Ba] ratio. In this regime, as we have learned from the isotopic distribution of Ba, the dominant contributor to the chemical evolution is the r-process. On the other hand, we recall that we assumed the solar system r-process pattern of Simmerer et al. (2004) for the ratios between Ba (which is fixed empirically), Y and Sr.
To estimate the solar system r-process contribution Simmerer et al. (2004) removed the s-process contribution produced by low-intermediate mass stars from the solar abundances. In addition to possible uncertainties in accounting for the s-process contribution by low-mass stars (and the integration to find the solar abundances), other contributors such as spinstars, might be hidden in the so-called r-process residual when this method is adopted. An alternative way to infer the r-process pattern is to use the observed ratio between Sr and Ba in r-process-rich stars (Sneden et al. 2008). This method is affected by observational errors, which are kept low by averaging five of the known r-process-rich stars. With the observational fraction the Y/Ba is subject to a displacement of −0.5 dex. The effect of this different method is shown in the second row of Fig. 3, which displays the results obtained with the EC+s 2 model in which we assumed the observed r-process signature (see also Table 2). For the EC+s 2 model our results agree very well with the observational data. Finally, for Y we predict a slightly smaller spread than for [Sr/Fe] (and [Ba/Fe]). The same is shown by the observational data. This result arises naturally from the higher amount of Y theoretically predicted by s-process in spinstars compared with Sr (and Ba).
In the third row we show the results obtained with the model MRD+s B2 (we do not show the results for model MRD+s B because it suffers from the same offset we discussed when presenting the EC+s model results). Our conclusions here do not differ from those indicated when we described the results for Sr. Note also that for yttrium we cannot easily distinguish between the MRD+s and the EC+s scenarios, and again the MRD+s scenario presents a slightly larger spread at [Fe/H] > − 2.
4.4. Stellar distribution for europium
In Fig. 4 we present the results for the neutron capture elements Eu compared with Y, Fe, and Ba. The element Eu is a heavy neutron capture element (its stable isotopes have atomic masses 151 and 153) and peculiar in that it is produced almost entirely by the r-process (typically less than 5% is believed to be produced through the s-process at solar metallicity). The Eu lines are weak, and in the literature we found only upper limits for the stars at [Fe/H] <−3.
Although Eu is not produced by spinstars according to the current models, this element can be important to distinguish between the r-process scenarios because it is uncontaminated by other production sites. Moreover, it can be useful as a reference element, instead of iron.
For the r-process production, the [Eu/Fe] ratio shows the largest discrepancy between the two scenarios (see the central column of Fig. 4). To have enough spread at extremely low metallicity, we need to have a large r-process production (and thus Eu) in each event of EC SN (plot above). At intermediate metallicity this produces a too high ratio of [Eu/Fe]. The MRD+s scenario appears to agree better with the [Eu/Fe] ratio of halo stars.
The plots in the left column in Fig. 4 display the ratio [Eu/Y] for the EC+s 2 and MRD+s B2 models. This ratio is interesting because Y is the element most affected by spinstars s-process production among the investigated elements, whereas we do not consider any production of Eu by spinstars. On the other hand, this ratio does not help to highlight different features between the different r-process scenarios because we assumed the same r-process pattern in both cases. The spread that we predict for the two models agrees very well with the spread observed in halo stars. The trend toward higher metallicity is slightly different between the two models: the MRD+s scenario tends to keep a larger spread in the [Eu/Y] ratio even at metallicities above −2.5. Both models show a smooth decrease of the [Eu/Y] ratio toward solar (at around metallicities [Fe/H] = −1) because of the s-process production in intermediate-mass stars. Although the data also show a decreasing [Eu/Y] ratio toward higher metallicities, the observations are systematically lower than the model predictions. How important this discrepancy is, is difficult to access because for this metallicity range, there is no information on the carbon abundance in these stars (as illustrated by the open symbols). Therefore, we cannot exclude that the abundances observed in some of these stars are contaminated by a binary star; in this case, material enriched in Y (and other elements predominantly produced in the s-process) coming from the binary star can change the original ratio of the chemical elements so that the observed ratio of [Eu/Y] is expected to be lower than the predictions from our chemical evolution models.
The same lack of carbon measurements also afflicts the plots for [Eu/Ba] (last column of Fig. 4). To a first approximation, the same as discussed above for Y applies for Ba; though for Ba the spread in the [Eu/Ba] for the models is relatively small, in agreement with the measured halo stars, again both models appear to predict a too high ratio for [Eu/Ba] at intermediate metallicities (−2 < [Fe/H] < − 1). At these metallicities the MRD+s scenario presents a slightly higher spread. The general trend of both models does not satisfactorily reproduce the observations, suggesting that a higher production of Ba by spinstars probably also takes place at these intermediate metallicities to improve the match between the predicted and observed [Eu/Ba] ratios. We recall that we adopted the spinstar nucleosynthesis prescriptions computed with a decreased 17O(α,γ) reaction rate only for Z< 10-5; since the decrease of the reaction rate would promote the s-process production, we can expect to produce more Ba and to alleviate this problem. Unfortunately, we can only speculate upon this option because for higher metallicities we do not have nucleosynthesis results with the decreased reaction rate at the moment.
4.5. Distribution functions
 |
Fig. 5 Distribution functions of observed (blue histograms) and simulated stars in the range [Fe/H] < − 2.5. We consider nine different chemical abundance ratios. Three different models are plotted: EC+s (black line), MRD+s B2 (red line) and MRD-s B2 (without contribution of spinstars, dashed red line). |
 |
Fig. 6 Distribution functions of observed (blue histograms) and simulated stars in the range [Fe/H] < − 2.5. We consider nine different chemical abundance ratios. In this case we plot the MRD+s B2 (solid red line) and a comparison model in which we assume a rate of 5% among massive stars for MRD SNe (dashed magenta line). |
The comparison of our chemical evolution model predictions (computed with different nucleosynthesis prescriptions) with the observed abundances in metal-poor stars (Figs. 1−4) provides not only very useful constraints to the chemical enrichment of the Galactic halo, but also to the nucleosynthetic process itself. Here we can go a step further. Tighter constraints can be obtained by comparing the predicted and observed distribution functions of the number of stars with a certain value of the different studied abundance ratios. In the present section we carry out, for the first time, to the best of our knowledge, such a comparison (except for the work of Cescutti & Chiappini 2010, where a similar attempt was carried out for CNO elements).
Thanks to the efforts in recent years of many observers, the number of stars measured at this extremely low metallicity regime has increased considerably. It is now possible to obtain the distribution (in number) of observed stars as a function of different key chemical species with a significant statistic and compare it with model results. However, one has to be aware of the strong biases contained in the halo star samples (where detailed abundances are usually obtained for the confirmed most metal-poor stars with 8−10 m class telescopes). Hence we carried out this comparison only for metallicities [Fe/H] < − 2.5 where the biases are certainly less important. In addition, the selection of this metallicity range meets our goal, which is to extract the information contained in the scatter (or lack thereof) in the abundance ratios. The observed spread becomes more important below [Fe/H] ~ − 2.5.
In Figs. 5 and 6 we present nine abundance ratios for the four neutron capture elements we studied Ba, Sr, Y and Eu: the four elements compared with H and all the possible combination among them (except [Eu/Sr]). In Fig. 5 we present the results obtained with three different nucleosynthesis models: the EC+s 2, the MRD+s B2 (the best two models for the two possible scenarios), and the MRD-s B2 model (which is the MRD+s B2, but without the contribution of spinstars). The latter model then shows the predictions for the case where only the r-process is at play.
Before discussing the comparison with the observational data, we note that the EC+s 2 and the MRD+s B2 model are quite similar, and in a distribution with a bin of 0.4 dex, there are tiny differences between them for [Fe/H] < − 2.5 (note that the choice of the bin size was made because we needed to have enough measurements and hence statistically meaningful results per bin). Furthermore, the observational uncertainties can be on this order for the n-capture elements considered in the present work.
We first focus on the absolute abundances (with respect to hydrogen) of Ba, Sr, and Y (these are shown in the first row of Fig. 5). The two models MRD+s B2 and EC+s 2 appear to agree well with the observations: our predictions for [Ba/H] and [Y/H] match the peaks of the distributions remarkably well, whereas for Sr there is a small offset. We remark that the peaks are determined by the r-process contribution, and only the Ba yields for the r-process have been empirically determined, whereas those for Sr and Y were simply scaled using the observation of r-process-rich stars for these models. The fact that the peaks are set by the r-process is also illustrated by the comparison with the model MRD-s (without the s-process contribution by spinstars): it is clear that the peaks do not move when the contribution from spinstars is switched off. It is also clear that after the spinstar contribution is turned off, the predicted distribution for the [Ba/H] becomes worse because the model now severely underestimates the number of stars with very low [Ba/H] ratios (the same occurs for Sr, although in this case the effect is minor). For Y the peak position is also changed slightly. Finally, for [Ba/H] we also note that the models with contributions from spinstars predict a double-peaked distribution, which is not present in the data.
In the second row of Fig. 5, the plots for the [Sr/Ba] and [Y/Ba] ratios all share similar features. The models are able to match the dispersion observed for these ratios thanks to the contribution from spinstars; this result was already seen in our previous figures. From these figures the role of spinstars in explaining the spread for these chemical ratios is clear. It is also clear that the r-process production by itself is unable to explain the observed spread. We also note that the shapes of the model predictions do not match the observational data perfectly. In particular for [Sr/Ba] and [Y/Ba] our models predict a peak at the r-process ratio with a more extended tail toward high [Sr/Ba] or [Y/Ba] ratios, whereas the data have a peak at a relatively higher ratio with more symmetric tails. For [Sr/Y] observations confirm the model predictions that the scatter should be small because in this case both elements are produced in similar ratios by r-process and s-process.
Finally, in the third row Fig. 5 we present the results for abundance ratios involving europium. It is interesting that here the predicted and observed [Eu/Y] ratios match very well. For this ratio the (predicted and observed) spread is smaller than that obtained for [Sr/Ba] and [Y/Ba]. However, for [Eu/Y] there is still the tendency to have too many modeled stars closer to the r-process signature (which is shown by the peak of the MRD+s model without spinstars). For [Eu/H] we are also able to match the peak and the spread; for this element models with and without spinstars show the same results because spinstars do not contribute Eu. It is interesting to note that in this plot the spread for [Eu/H] is less pronounced than for [Ba/H]. For [Eu/Ba] the spread expected by the model is smaller than the dimensions of the assumed bin because of the dominant role of the r-process production compared with s-process contribution by spinstars. The lack of dispersion in the [Eu/Ba] ratio is also confirmed by the data. More measurements for Eu are clearly needed.
The purpose of Fig. 6 is to illustrate the potential of our approach for constraining the site of the r-process. In this figure we show our MRD+s B2 model compared with a similar model in which we decreased the probability of having a r-process event from 10% to 5%. In the latter model, to conserve the average production of the r-process by a stellar generation, we have increased the amount of r-process material ejected by each event by a factor of two. This change does not affect considerably the comparison of the model results and data in a stellar density plot similar to the one shown in Fig. 1. This is illustrated in the appendix in Fig. A.1. In the diagrams shown in Fig. 6, the difference between the two models can be easily appreciated. A lower probability for the r-process contribution implies that the distribution of stars will be more influenced by the contribution from spinstars. This is the case in all the diagrams of Fig. 6. From this figure the danger of using biased samples also becomes clear. Indeed, any biases toward, for instance, r-process-rich stars can provoke a deformation of the observed distributions and erroneously favor a given scenario or different rates. Accounting for the observational biases will be mandatory in the future of very metal-poor research if one wishes to use their precious information to better constrain chemical evolution models and the nucleosynthesis of the r- and s-processes.
5. Conclusions
We have developed inhomogeneous chemical evolution models for the Milky Way halo. We adopted different hypotheses for the site of the r-process, and also included an early production of the s-process by fast-rotating massive stars (spinstars). We compared our predictions for Ba, Y, Sr, and Eu with the abundance patterns of very metal-poor stars for these elements. Our main conclusions can be summarized as follows:
-
Independently of the r-process scenarios adopted, the spinstars production of s-process is needed to reproduce the spread in the light neutron capture elements (Sr and Y) over the heavy neutron capture elements (Ba and Eu).
-
Our two best models based on two different r-process scenarios when coupled with the spinstars s-process production are able to reproduce the observational data for a set of four neutron capture elements (Sr, Y, Ba, and Eu).
-
The r-process scenarios are not clearly distinguishable with the present data for the Galactic halo. Both scenarios reproduce the fraction of r-process-rich stars fairly well. The abundance measurements of [Eu/Fe] at intermediate metallicity −2 < [Fe/H] < − 1 tend to favor the MRD scenario. More data at this intermediate metallicity might provide an important constraint.
-
We predict the contribution of spinstars to be more pronounced in specific zones in the chemical abundance ratios, for example, at high [Sr/Ba] at [Fe/H] < −2 or at low [Ba/Fe] for the same metallicity range. In these zones the stars are expected to present an s-process signature in the Ba isotopic ratios, leading to low odd isotopic ratios possibly measurable by the hyperfine splitting of the Ba lines (in particular, the line at 455.4 nm).
-
The change of the rate of MRD SNe produces differences in the predictions of the model that can be distinguished using the distribution functions. This comparison confirms that the rate we have chosen produces results that better agree with the observational data. There is also a caveat, since we can conclude this only by assuming no bias in the observational data depending on the abundance of neutron capture elements; so not only a greater number of measured stars but also observational data without (or with known) bias are needed to proceed a step forward in the understanding of the sources of the r-process.
Finally, we would like to point out that a possible method to distinguish between these two scenarios might be to apply these same r-process nucleosynthesis prescriptions to another Galactic component. A different star formation history provides new constraints because a fast evolution of the metallicity can help to enhance the differences in the timescales between the two scenarios considered here. We will study this possibility in a future work by comparing our model predictions for the halo and the bulge.
Online material
 |
Fig. A.1 Stellar distribution. As Fig. 1, but in this case the MRD+s models have 5% as a rate of MRD SNe. |
The list of authors we use from the collection are McWilliam et al. (1995), McWilliam (1998), Westin et al. (2000), Aoki et al. (2002, 2005, 2006, 2007), Cowan et al. (2002), Ivans et al. (2003), Honda et al. (2004), Barklem et al. (2005), Ivans et al. (2006), Masseron et al. (2006), Preston et al. (2006), François et al. (2007), Lai et al. (2007, 2008), Cohen et al. (2008), Roederer et al. (2008), Bonifacio et al. (2009), Hayek et al. (2009).
Acknowledgments
We acknowledge the heroic efforts of all the very metal-poor star hunters as well as those of all the stellar modelers without whom this work would not have been possible. We are grateful to P. Creasey for carefully reading the manuscript.
References
- Aoki, W., Ando, H., Honda, S., et al. 2002, PASJ, 54, 427 [NASA ADS] [Google Scholar]
- Aoki, W., Honda, S., Beers, T. C., et al. 2005, ApJ, 632, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Frebel, A., Christlieb, N., et al. 2006, ApJ, 639, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Honda, S., Beers, T. C., et al. 2007, ApJ, 660, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Beers, T. C., Lee, Y. S., et al. 2013a, AJ, 145, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Suda, T., Boyd, R. N., Kajino, T., & Famiano, M. A. 2013b, ApJ, 766, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Arcones, A., & Martínez-Pinedo, G. 2011, Phys. Rev. C, 83, 5809 [Google Scholar]
- Arcones, A., & Montes, F. 2011, ApJ, 731, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Arlandini, C., Käppeler, F., Wisshak, K., et al. 1999, ApJ, 525, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., Christlieb, N., Beers, T. C., et al. 2005, A&A, 439, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., & Käppeler, F. 2012, MNRAS, 422, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Bonifacio, P., Spite, M., Cayrel, R., et al. 2009, A&A, 501, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caughlan, G. R., & Fowler, W. A. 1988, Atomic Data and Nuclear Data Tables, 40, 283 [Google Scholar]
- Cescutti, G. 2008, A&A, 481, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., & Chiappini, C. 2010, A&A, 515, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., François, P., Matteucci, F., Cayrel, R., & Spite, M. 2006, A&A, 448, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., Chiappini, C., Hirschi, R., Meynet, G., & Frischknecht, U. 2013, A&A, 553, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Hirschi, R., Meynet, G., et al. 2006, A&A, 449, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Ekström, S., Meynet, G., et al. 2008, A&A, 479, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Frischknecht, U., Meynet, G., et al. 2011, Nature, 472, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Christlieb, N., Schörck, T., Frebel, A., et al. 2008, A&A, 484, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cohen, J. G., Christlieb, N., McWilliam, A., et al. 2008, ApJ, 672, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Collet, R., Asplund, M., & Nissen, P. E. 2009, PASA, 26, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, J. J., Sneden, C., Burles, S., et al. 2002, ApJ, 572, 861 [NASA ADS] [CrossRef] [Google Scholar]
- François, P., Matteucci, F., Cayrel, R., et al. 2004, A&A, 421, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- François, P., Depagne, E., Hill, V., et al. 2007, A&A, 476, 935 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frebel, A. 2010, Astron. Nachr., 331, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Frischknecht, U., Hirschi, R., & Thielemann, F.-K. 2012, A&A, 538, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallagher, A. J., Ryan, S. G., García Pérez, A. E., & Aoki, W. 2010, A&A, 523, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallagher, A. J., Ryan, S. G., Hosford, A., et al. 2012, A&A, 538, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goriely, S., Sida, J.-L., Lemaître, J.-F., et al. 2013, Phys. Rev. Lett., 111, 242502 [Google Scholar]
- Hayek, W., Wiesendahl, U., Christlieb, N., et al. 2009, A&A, 504, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Honda, S., Aoki, W., Kajino, T., et al. 2004, ApJ, 607, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Ivans, I. I., Sneden, C., James, C. R., et al. 2003, ApJ, 592, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Ivans, I. I., Simmerer, J., Sneden, C., et al. 2006, ApJ, 645, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, D. K., Johnson, J. A., Bolte, M., & Lucatello, S. 2007, ApJ, 667, 1185 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, D. K., Bolte, M., Johnson, J. A., et al. 2008, ApJ, 681, 1524 [NASA ADS] [CrossRef] [Google Scholar]
- Lambert, D. L., & Allen de Prieto, C. 2002, MNRAS, 335, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Li, H. N., Christlieb, N., Schörck, T., et al. 2010, A&A, 521, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucatello, S., Beers, T. C., Christlieb, N., et al. 2006, ApJ, 652, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaro, M., Karakas, A. I., Stancliffe, R. J., & Rijs, C. 2012, ApJ, 747, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 1989, A&A, 210, 155 [NASA ADS] [Google Scholar]
- Magain, P. 1995, A&A, 297, 686 [NASA ADS] [Google Scholar]
- Masseron, T., van Eck, S., Famaey, B., et al. 2006, A&A, 455, 1059 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masseron, T., Johnson, J. A., Plez, B., et al. 2010, A&A, 509, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McWilliam, A. 1998, AJ, 115, 1640 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., Preston, G. W., Sneden, C., & Searle, L. 1995, AJ, 109, 2757 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, K., Kajino, T., Mathews, G. J., Sato, S., & Harikae, S. 2013, Int. J. Mod. Phys. E, 22, 30022 [Google Scholar]
- Pignatari, M., Gallino, R., Meynet, G., et al. 2008, ApJ, 687, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Preston, G. W., Sneden, C., Thompson, I. B., Shectman, S. A., & Burley, G. S. 2006, AJ, 132, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, Y.-Z. 2012, in AIP Conf. Ser. 1484, eds. S. Kubono, T. Hayakawa, T. Kajino, et al., 201 [Google Scholar]
- Roederer, I. U., Frebel, A., Shetrone, M. D., et al. 2008, ApJ, 679, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Scalo, J. M. 1986, Fundamentals of Cosmic Physics, 11, 1 [Google Scholar]
- Simmerer, J., Sneden, C., Cowan, J. J., et al. 2004, ApJ, 617, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C., Cowan, J. J., & Gallino, R. 2008, ARA&A, 46, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thielemann, F.-K., Arcones, A., Käppeli, R., et al. 2011, Prog. Part. Nucl. Phys., 66, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Thornton, K., Gaudlitz, M., Janka, H.-T., & Steinmetz, M. 1998, ApJ, 500, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Wanajo, S. 2013, ApJ, 770, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Wanajo, S., Nomoto, K., Janka, H.-T., Kitaura, F. S., & Müller, B. 2009, ApJ, 695, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Westin, J., Sneden, C., Gustafsson, B., & Cowan, J. J. 2000, ApJ, 530, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Winteler, C., Käppeli, R., Perego, A., et al. 2012, ApJ, 750, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Heger, A. 2006, ApJ, 637, 914 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Stellar distribution. From the left [Ba/Fe], [Sr/Fe] and [Sr/Ba] vs. [Fe/H] in the halo; the density plot is the distribution of simulated long-living stars for our models, see bar below the main figure for the color scale; superimposed, we show the abundances ratios for halo stars (data from Frebel 2010; Aoki et al. 2013a). The symbols for the Frebel (2010) data are black dots for normal stars, cyan dots for CEMP-no, a red x marker for the CEMP-r star, and black open circle for stars without carbon measurement; for the Aoki et al. (2013a) data we adopt the same symbols, but instead of dots we used squares. |
| In the text | |
 |
Fig. 2 Barium isotopic ratio. From the left [Ba/Fe], [Sr/Fe] and [Sr/Ba] vs. [Fe/H] in the halo. The density plot is the distribution of the isotopic ratio of Ba according to the models, see the bar below the main figure. The data are the same as in Fig. 1. |
| In the text | |
 |
Fig. 3 Stellar distribution. From the left [Y/Fe], [Y/Ba] and [Sr/Y] vs. [Fe/H] in the halo; the density plot is the distribution of simulated long-living stars for our halo models, see bar below Fig. 1 for the color scale; the data are the same as in Fig. 1. |
| In the text | |
 |
Fig. 4 Stellar distribution. From the left [Eu/Y], [Eu/Fe] and [Eu/Ba] vs. [Fe/H] in the halo; the density plot is the distribution of simulated long-living stars for our halo models, see bar below Fig. 1 for the color scale; the data are the same as Fig. 1. |
| In the text | |
 |
Fig. 5 Distribution functions of observed (blue histograms) and simulated stars in the range [Fe/H] < − 2.5. We consider nine different chemical abundance ratios. Three different models are plotted: EC+s (black line), MRD+s B2 (red line) and MRD-s B2 (without contribution of spinstars, dashed red line). |
| In the text | |
 |
Fig. 6 Distribution functions of observed (blue histograms) and simulated stars in the range [Fe/H] < − 2.5. We consider nine different chemical abundance ratios. In this case we plot the MRD+s B2 (solid red line) and a comparison model in which we assume a rate of 5% among massive stars for MRD SNe (dashed magenta line). |
| In the text | |
 |
Fig. A.1 Stellar distribution. As Fig. 1, but in this case the MRD+s models have 5% as a rate of MRD SNe. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.