| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | L14 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201423734 | |
| Published online | 11 April 2014 | |
Stochastic pulsations in the subdwarf-B star KIC 2991276
1 Instituut voor Sterrenkunde, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
e-mail: roy@ster.kuleuven.be
2 Department of Physics, Astronomy, and Materials Science, Missouri State University, Springfield MO 65804, USA
3 Uniwersytet Pedagogiczny w Krakowie, ul. Podchorążych 2, 30-084 Kraków, Poland
4 Nordic Optical Telescope, Rambla José Ana Fernández Pérez 7, 38711 Breña Baja, Spain
Received: 28 February 2014
Accepted: 25 March 2014
The subdwarf-B star KIC 2991276 was monitored with the Kepler spacecraft for nearly three years. Two pulsation modes with periods of 122 and 132 s are clearly detected in the Fourier spectrum, as well as a few weaker modes with periods ranging from 118 to 216 s. Unlike the other subdwarf-B pulsators with similar high-quality Kepler lightcurves, the modes in KIC 2991276 do not display long-term coherency. Rather, their pulsation amplitudes vary substantially in amplitude and phase on timescales of about a month, sometimes disappearing completely. Thus, while the pulsations are seen to have amplitudes of up to 1.4% in individual months, the amplitude spectrum of the full lightcurve shows a broad, messy peak with an amplitude of only 0.23%. Such stochastic oscillations are normal in the Sun and other cool stars with solar-like pulsations and have been suspected for V361-Hya pulsators, but thanks to the exceptional coverage of Kepler data, this is the first unambiguous case established for a hot subdwarf.
Key words: subdwarfs / stars: oscillations / stars: individual: KIC 2991276
© ESO, 2014
1. Introduction
Extreme horizontal branch (EHB) stars are the helium-burning cores of stars that have shed their envelope while ascending the red giant branch, most likely because of interaction with a companion star or massive planets. For a detailed review of EHB stars, see Heber (2009).
The Kepler spacecraft spent four years monitoring a 105 deg2 field in the Cygnus-Lyrae region, with the primary goal of detecting transiting planets (Borucki et al. 2011). The high-quality lightcurves that the spacecraft produces reveal a host of variable stars, providing a treasure trove for asteroseismic studies (Gilliland et al. 2010).
In the first quarters of the Kepler mission, a survey for pulsating stars was made, and a total of 113 compact-pulsator candidates were checked for variability in Østensen et al. (2010c, 2011). This very successful survey revealed one clear V361-Hya pulsator (Kawaler et al. 2010b) and a total of thirteen V1093-Her stars (Reed et al. 2010; Kawaler et al. 2010a; Baran et al. 2011), including an sdB+dM eclipsing binary in which the hot primary shows an exceptionally rich pulsation spectrum (Østensen et al. 2010a). Another three V1093-Her pulsators have been identified in the open cluster NGC 6791 (Pablo et al. 2011; Reed et al. 2012), bringing the total to 18. A detailed analysis of a 15-month dataset of the V361-Hya pulsator KIC 10139564 was presented by Baran et al. (2012), and an extended analysis based on 27 months of data was presented by Baran & Østensen (2013). Detailed analysis of datasets containing months or years of near-continuous data that the Kepler spacecraft gathered during the long-term monitoring phase of seven of the V1093-Her pulsators have also been presented (Charpinet et al. 2011; Baran 2012; Telting et al. 2012; Baran & Winans 2012; Pablo et al. 2012; Reed et al. 2014; Østensen et al. 2014).
The target presented here, KIC 2991276, was included in the first survey and classified as a transient short-period pulsator in Østensen et al. (2010c), where a single pulsation mode at 122 s was found to decrease in amplitude from ~1 mma1 to the detection limit over the one-month span of the survey observations (Q2.1; the first month of the second quarter of Kepler observations). Since then, KIC 2991276 has been observed throughout Q6 to 11 and Q13 to the end of the mission midway through Q17, which is the data we analyse in this Letter. We also present new spectroscopic observations that show that KIC 2991276 does not display significant radial velocity variations, and is therefore most likely a single sdB star.
 |
Fig. 1 Field images for KIC 2991276 = SDSS J192709.14+381026.3. The image on the left is from the SDSS DR9 (Stoughton et al. 2002) and covers 2.5×2.5 arcminutes. The same section from a Kepler full-frame image is shown on the right, with a thin outline showing the pixels used in a typical quarter. |
 |
Fig. 2 FT of the full Kepler dataset of KIC 2991276 (upper). Magnifications of the regions for the most significant peaks are shown in the panels on the lower left. The 5σ level is plotted as a line in each panel, and the Lorentzian fit for the most significant modes are shown as curves. In the lower right-hand panels, the amplitude and phase for the two main modes are plotted for consecutive 20-day chunks. For the amplitude/phase fits, the frequency was kept constant, and points with amplitudes of less than 1.5 mma were dropped. |
2. Kepler photometry
KIC 2991276 is a 17th-mag star whose proximity to a pair of 14–15 mag stars makes the Kepler photometry suffer from heavy contamination that varies from quarter to quarter, depending on the positioning of the spacecraft photometer’s 4′′-sized pixels. Figure 1 shows a field image and the corresponding section of a Kepler full-frame image.
We used the optimally-extracted lightcurves provided by the Kepler pipeline and detrended them using low-order polynomials for each continuous lightcurve segment, removing only trends on month-long timescales. In a final step, data from individual quarters were decontaminated. This was done by using the contamination factors provided by the Kepler pipeline as a starting point, and subsequently adjusting them to get matching count levels between all quarters. After removing the contaminating signal the lightcurve was normalised so that the resulting Fourier amplitudes are intrinsic to the target. We experimented with extracting custom apertures from the Kepler pixel data, but found no significant improvements in the overall results, so reverted to using the standard extraction. The resulting lightcurve appears unimpressive since the scatter is too high to reveal any obvious pulsation signal. However, Fourier transforms (FTs) of month-long lightcurves easily reveal pulsations with amplitudes that occasionally reach as high as 14%.
The full lightcurve contains 1.3 million one-minute samples, and spans 1051.5 days. The frequency resolution is 0.011 μHz so that the full FT contains 772 000 independent frequencies up to the Nyquist limit of 8496 μHz. At this resolution, a normal distribution of peaks implies that one would expect to find ~50 peaks above a Gaussian 4σ limit. Thus, we choose a stricter 5σ limit in order to have reasonable confidence that a given peak represents a real signal. We measure the mean level in the Fourier transform to be σFT = 0.0574 mma, so we set our detection threshold to 0.287 mma. In the upper part of Fig. 2, we show the FT of KIC 2991276 for the high-frequency region, where all significant peaks are found. The comb of artefacts associated with the read-out cycle are marked with black bars. The eight highest possible pulsation peaks are labelled, and their frequency and amplitude are listed in Table 1. Only the first five are significant according to the 5σ threshold. The six highest peaks are shown in the right half of Fig. 2. The top two show a triplet structure, with a mean splitting of δf = 1.84 μHz, indicating that they are most likely the components of ℓ = 1 triplets. Since the Ledoux constant is small for low-order acoustic modes, this splitting would imply a rotation period of Prot ≈ 1/δf = 6.3 days.
 |
Fig. 3 Sliding FT for the strongest pulsations in KIC 2991276 computed for 20-day chunks of data. The horizontal lines reflect data gaps. |
In Fig. 3 we show the sliding FT (sFT) of our dataset. The lightcurve was chopped into chunks, to visualise the time variability of the three most significant modes. The highest amplitude detected for each peak in any 20-day chunk is listed in Table 1. The peak amplitudes are much higher here: up to 14 mma in the highest peaks as opposed to only 2.5 mma in the full FT. The real amplitude is even higher than this, since 8201 μHz is very close to the Nyquist frequency. As shown in Østensen et al. (2010c), at this frequency the FT can recover only ~66% of the pulsation amplitude. Thus, on two occasions the f1 peak of KIC 2991276 has a pulsation amplitude higher than 2%, which makes it comparable in amplitude and frequency, as well as Teff and log g, to the most powerful V361-Hya pulsators such as QQ Vir (Silvotti et al. 2002). One can also note from the sFT that the sidelobes of the two triplets only show up when the central peak is at its strongest. Magnifying these details reveals that when the middle peak drifts in frequency, the sidelobes follow. This is surprising if the three modes were excited randomly, since they should be independent modes. Similar sFTs are shown in Baran & Østensen (2013) and Reed et al. (2014), where multiplet components seem to behave independently of each other.
Regions of pulsation power detected in KIC 2991276.
Pulsations that are stochastically driven, i.e. that suffer persistent cycles of damping and re-excitations, have long been observed in the Sun and similar stars, where they are known as solar-like oscillations. The peaks in the Fourier spectra of time-series observations of such stochastic pulsations are very different from that of stable pulsators. As subsequent periods of re-exitation do not retain the phase of earlier periods, the FT of long datasets suffers from partial cancellation effects, which produces a forest of peaks with a broad profile. Under certain assumptions, including an exponential growth and dampening with a characteristic timescale, the power spectrum creates a forest of peaks that will have a Lorentzian distribution (e.g. Beck et al. 2011) 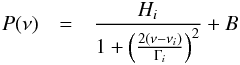 where Hi is the Lorentzian height, νi the central frequency of the mode, and Γi the width that is inversely proportional to the lifetime of the mode. The bias term, B, accounts for the white-noise component. When fitting Lorentzian profiles to regions of power excess in the FT we find Γ = ~0.22 μHz for f1 and ~0.09 for f2. This corresponds to mode lifetimes of ~12 and ~30 days when using the proportionality factor that follows from a turbulent motion assumption (Eq. (5.56) in Aerts et al. 2010). That the mode lifetime is longer for f2 than for f1 can also be discerned visually in the lower right-hand panels of Fig. 2. The amplitudes corresponding to the Lorentzian heights are given in Table 1, and the fits are plotted as curves in Fig. 2.
where Hi is the Lorentzian height, νi the central frequency of the mode, and Γi the width that is inversely proportional to the lifetime of the mode. The bias term, B, accounts for the white-noise component. When fitting Lorentzian profiles to regions of power excess in the FT we find Γ = ~0.22 μHz for f1 and ~0.09 for f2. This corresponds to mode lifetimes of ~12 and ~30 days when using the proportionality factor that follows from a turbulent motion assumption (Eq. (5.56) in Aerts et al. 2010). That the mode lifetime is longer for f2 than for f1 can also be discerned visually in the lower right-hand panels of Fig. 2. The amplitudes corresponding to the Lorentzian heights are given in Table 1, and the fits are plotted as curves in Fig. 2.
3. Spectroscopy
In addition to the spectrum obtained with the William Herschel Telescope (WHT) in 2009, we obtained three spectra with the Nordic Optical Telescope (NOT) in 2011. All spectra were processed and extracted using standard IRAF tasks. Radial velocities (RVs) were computed with fxcor, by cross-correlating with a synthetic template derived from a mean spectrum of the target. While the NOT spectra have rather low signal-to-noise ratios (S/Ns), the observations demonstrate that KIC 2991276 is not in a close binary with a white dwarf, unless the orbit is seen at an unfavourable inclination. Table 2 lists the observations with their mid-exposure dates, resolution, S/N, and RV and associated error from fxcor. Values for Teff and log g relative to the LTE grid of Heber et al. (2000), computed for the mean of the NOT spectra agrees well with the values found from the WHT spectrum as reported in Østensen et al. (2010c); Teff = 33 900 ± 200 K and log g = 5.82 ± 0.04 dex.
Spectroscopic radial-velocity observations.
4. Conclusions
Amplitude variability has been detected in a number of sdB stars, and stochasticity has been suspected (Reed et al. 2007; Kilkenny 2010). However, the limitations of ground-based observations has meant that up to now the stochastic nature of such variability could not be proved unambiguously. With the essentially uninterrupted lightcurve from the Kepler spacecraft studied here, we have shown that the pulsations in KIC 2991276 lose coherence on timescales longer than ~60 days and are therefore stochastic in nature.
The spectroscopic parameters of KIC 2991276 places it right in the middle of the V361-Hya instability region, so driving of the pulsations should be effective provided that the star is not too young to have built up a sufficiently strong iron-opacity bump in the driving region (Fontaine et al. 2006). The pulsation frequencies in KIC 2991276 are short, but within the range observed in other V361-Hya stars at the high-gravity end of the EHB. Thus, the stochastically excited modes that we observe are the same as the low-order acoustic modes observed in those pulsators. Coherent pulsations that show phase stability over many years have been demonstrated for a few V361-Hya stars, most spectacularly in Silvotti et al. (2007), where close to a decade of observations revealed periodic phase variations that betrayed an orbiting planet with a period of 3.2 years. Why the pulsations in KIC 2991276 are not coherent, while other stars with similar atmospheric parameters are, is not clear but may well be related to the long-standing question of why only ~10% of stars in the instability strip are seen to pulsate (Østensen et al. 2010b). A further hint that the stochastic behaviour is related to events in the driving zone comes from our observations that all triplet components simultaneously disappear, rather than behaving independently. A possible explanation for this might come from invoking thermohaline convection (Théado et al. 2009), in which the accumulation of iron-group elements into the Z-bump that is responsible for driving the pulsations in these stars (Charpinet et al. 1997), develops local instabilities due to the buildup of an inverse μ-gradient. When this happens, blobs of iron-rich material may temporarily sink out of the driving zone and quash pulsations until radiative levitation restores the Z-bump and driving resumes. Since the different triplet components all probe approximately the same driving region, they would be equally
sensitive to a temporary drop in Z-bump opacity induced by thermohaline convection. An alternative interpretation for the coherent sidelobes in the triplet components is that they are phase modulations caused by orbital effects. If we use Eqs. (3) and (6) from Telting et al. (2012) we can compute the RV amplitude required to produce the observed sidebands, K = 16.3 km s-1, which is below the detection limit. An orbital period of 6.3 days is not unusual for a white dwarf companion, but the low RV amplitude would require the orbit to be seen at a very low inclination angle. Unfortunately, because of low-frequency signals associated with the contaminating stars, we were unable to reliably detect an orbital Doppler-beaming signal that could have confirmed this possibility.
Acknowledgments
The authors gratefully acknowledge the Kepler team and everybody who has contributed to making this mission possible. Funding for the Kepler mission is provided by NASA’s Science Mission Directorate. The research leading to these results has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007–2013)/ERC grant agreement No. 227224 (prosperity), and from the Research Council of KU Leuven grant agreement GOA/2008/04. Funding for this research was also provided by the US National Science Foundation grants #1009436 and #1312869, and the Polish National Science Centre under project No. UMO-2011/03/D/ST9/01914. The spectroscopic observations used in this work were collected at the Nordic Optical Telescope (NOT) at the Observatorio del Roque de los Muchachos (ORM) on La Palma, operated jointly by Denmark, Finland, Iceland, Norway, and Sweden, and the William Herschel Telescope (WHT) also at ORM, operated by the Isaac Newton Group.
References
- Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Springer) [Google Scholar]
- Baran, A. S. 2012, Acta Astron., 62, 179 [NASA ADS] [Google Scholar]
- Baran, A. S., & Østensen, R. H. 2013, Acta Astron., 63, 79 [NASA ADS] [Google Scholar]
- Baran, A. S., & Winans, A. 2012, Acta Astron., 62, 343 [NASA ADS] [Google Scholar]
- Baran, A. S., Kawaler, S. D., Reed, M. D., et al. 2011, MNRAS, 414, 2871 [NASA ADS] [CrossRef] [Google Scholar]
- Baran, A. S., Reed, M. D., Stello, D., et al. 2012, MNRAS, 424, 2686 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, P. G., Bedding, T. R., Mosser, B., et al. 2011, Science, 332, 205 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Borucki, W. J., Koch, D. G., Basri, G., et al. 2011, ApJ, 736, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., et al. 1997, ApJ, 483, L123 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., et al. 2011, Nature, 480, 496 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fontaine, G., Brassard, P., Charpinet, S., & Chayer, P. 2006, Mem. Soc. Astron. It., 77, 49 [NASA ADS] [Google Scholar]
- Gilliland, R. L., Brown, T. M., Christensen-Dalsgaard, J., et al. 2010, PASP, 122, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Heber, U. 2009, ARA&A, 47, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Heber, U., Reid, I. N., & Werner, K. 2000, A&A, 363, 198 [NASA ADS] [Google Scholar]
- Kawaler, S. D., Reed, M. D., Østensen, R. H., et al. 2010a, MNRAS, 409, 1509 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaler, S. D., Reed, M. D., Quint, A. C., et al. 2010b, MNRAS, 409, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D. 2010, Ap&SS, 329, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Østensen, R. H., Green, E. M., Bloemen, S., et al. 2010a, MNRAS, 408, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Østensen, R. H., Oreiro, R., Solheim, J., et al. 2010b, A&A, 513, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Østensen, R. H., Silvotti, R., Charpinet, S., et al. 2010c, MNRAS, 409, 1470 [NASA ADS] [CrossRef] [Google Scholar]
- Østensen, R. H., Silvotti, R., Charpinet, S., et al. 2011, MNRAS, 414, 2860 [NASA ADS] [CrossRef] [Google Scholar]
- Østensen, R. H., Telting, J. H., Reed, M. D., Baran, A. S., & Kiaeerad, F. 2014, A&A, in press [Google Scholar]
- Pablo, H., Kawaler, S. D., & Green, E. M. 2011, ApJ, 740, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Pablo, H., Kawaler, S. D., Reed, M. D., et al. 2012, MNRAS, 422, 1343 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, M. D., O’Toole, S. J., Terndrup, D. M., et al. 2007, ApJ, 664, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, M., Kawaler, S. D., Østensen, R. H., et al. 2010, MNRAS, 409, 1496 [Google Scholar]
- Reed, M. D., Baran, A., Østensen, R. H., Telting, J., & O’Toole, S. J. 2012, MNRAS, 427, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, M. D., Foster, H., Telting, J. H., et al. 2014, MNRAS, in press [Google Scholar]
- Silvotti, R., Østensen, R., Heber, U., et al. 2002, A&A, 383, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silvotti, R., Schuh, S., Janulis, R., et al. 2007, Nature, 449, 189 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stoughton, C., Lupton, R. H., Bernardi, M., et al. 2002, AJ, 123, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Telting, J. H., Østensen, R. H., Baran, A. S., et al. 2012, A&A, 544, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Théado, S., Vauclair, S., Alecian, G., & Le Blanc, F. 2009, ApJ, 704, 1262 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Field images for KIC 2991276 = SDSS J192709.14+381026.3. The image on the left is from the SDSS DR9 (Stoughton et al. 2002) and covers 2.5×2.5 arcminutes. The same section from a Kepler full-frame image is shown on the right, with a thin outline showing the pixels used in a typical quarter. |
| In the text | |
 |
Fig. 2 FT of the full Kepler dataset of KIC 2991276 (upper). Magnifications of the regions for the most significant peaks are shown in the panels on the lower left. The 5σ level is plotted as a line in each panel, and the Lorentzian fit for the most significant modes are shown as curves. In the lower right-hand panels, the amplitude and phase for the two main modes are plotted for consecutive 20-day chunks. For the amplitude/phase fits, the frequency was kept constant, and points with amplitudes of less than 1.5 mma were dropped. |
| In the text | |
 |
Fig. 3 Sliding FT for the strongest pulsations in KIC 2991276 computed for 20-day chunks of data. The horizontal lines reflect data gaps. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


