EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 564 (April 2014) A&A, 564 (2014) A98 Full HTML
Free Access
Issue
A&A
Volume 564, April 2014
Article Number A98
Number of page(s) 8
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201423377
Published online 11 April 2014

© ESO, 2014

1. Introduction

Hot subdwarfs (sdBs) are core helium-burning stars with very thin hydrogen envelopes that are not able to sustain hydrogen-shell burning (Heber 2009). To form such objects, the progenitor has to lose almost all of its hydrogen envelope. The high percentage of 50% of close binaries (Maxted et al. 2001; Napiwotzki et al. 2004) suggests that these sdBs are formed via binary evolution, which is responsible for the required large mass loss on the red giant branch (RGB). These sdB binaries are formed via a common envelope phase or by stable Roche lobe overflow. The other half of sdB stars, however, appears to be single. Hence, binary evolution seems to be irrelevant at first glance. Nevertheless, is it possible to form a single star through merging of the components of a binary star. To form a helium core burning object like an sdB star, two helium white dwarfs need to merge and ignite helium burning. The binary components are driven into a merger by gravitational wave radiation (Webbink 1984; Iben & Tutukov 1984). The merged object is expected to rotate rapidly. However, rotation velocities of single sdB stars are very slow (<=10 km s-1, Geier & Heber 2012), which is in contradiction with the merger scenario. Therefore, the merger scenario may explain a few cases of exceptionally fast rotators (Geier et al. 2011a, 2013). Moreover, binary population synthesis predicts a wide mass distribution around 0.52 M⊙ for the sdBs, which result from the merger channel (Han et al. 2002, 2003). The empirical mass distribution derived by asteroseismology (Fontaine et al. 2012; Van Grootel et al. 2013b), however, shows a sharp peak at 0.47 M⊙ for single sdB stars, which is inconsistent with the prediction of the merger scenario.

An alternative scenario proposes the engulfment and possible destruction of a substellar object within a common envelope (CE) as formation channel for single sdB stars (Soker 1998; Nelemans & Tauris 1998). Close binary sdB stars with very low-mass stellar companions are known for decades (Kilkenny et al. 1978; Menzies & Marang 1986). When eclipsing, such systems are named HW Vir stars. Most of the dozen known HW Vir systems have periods as short as 0.1 days. Hence, they must have undergone a common envelope and spiral-in phase. Binary population synthesis shows that sdBs in these post-common envelope systems should have masses around 0.47 M⊙, also known as canonical mass (Han et al. 2002, 2003). The companions in HW Vir type binaries have masses close to, but usually exceeding the nuclear-burning limit of ≃0.08 M⊙, and are, therefore, very late M-dwarf stars.

Whether a substellar companion would also be able to contribute enough energy and angular momentum to unbind a common envelope has been under debate. The discovery of a brown dwarf orbiting an sdB star in the HW Vir type binary SDSS J082053.53+000843.4 demonstrated that substellar companions are able to form an sdB (Geier et al. 2011d). The subsequent discoveries of two Earth-sized bodies orbiting a single pulsating sdB, which might be the remnants of one or two more massive companion evaporated in the CE-phase (Charpinet et al. 2011; Bear & Soker 2012), provide further evidence that substellar companions play an important role in the formation of close binary and single sdB stars alike. One of the open questions is, how massive the companion has to be to trigger the mass loss of the red giant to form an sdB star.

Here, we report on the discovery of a short period eclipsing hot subdwarf binary with a substellar companion in the course of the MUCHFUSS project. The project, Massive Unseen Companions to Hot Faint Underluminous Stars from SDSS (MUCHFUSS), aims to find sdBs with compact companions, such as massive white dwarfs (M> 1.0 M⊙), neutron stars, or black holes. Details about target selection and the scope of the project can be found in Geier et al. (2011b). As one of two selection criteria, sdBs with radial velocity (RV) variations on timescales of half an hour or less were selected from the Sloan Digital Sky Survey (SDSS). These targets are either sdBs with compact, massive companions and comparatively long orbital periods, or short-period binaries with low-mass companions, such as the system described here.

To distinguish low-mass stellar or substellar companions from white dwarfs and other more compact objects, we also started a photometric follow-up. As HW Vir systems have characteristic lightcurves, this turned out to be the ideal approach to find such binaries. A low-mass, cool companion can be identified due to the so-called reflection effect, which results from the large difference in temperature of both components. The companion is heated up on one side, and, therefore, a sinusoidal variation of the flux with the phase can be observed, as the heated hemisphere emits more flux. This effect is also visible at rather low inclinations, where no eclipses are observed. If eclipses are present, a combined spectroscopic and photometric analysis allows us to put tight constraints on the binary parameters. In the course of the MUCHFUSS project, we already discovered three new HW Vir systems (Geier et al. 2011d; Schaffenroth et al. 2013a) and a pulsating sdB in a reflection-effect binary (Østensen et al. 2013).

In this paper, we present the observations and analysis of a HW Vir star, discovered by the MUCHFUSS project. We describe the spectroscopic and photometric observations in Sect. 2 and their analysis in Sects. 3 (spectroscopy) and 4 (photometry). Evidence for the brown dwarf nature of the companion is given in Sect. 5 and the lack of synchronisation of the sdB star is discussed in Sect. 6. Finally, we conclude and present suggestions on how to improve the mass determination.

2. Observations

2.1. Spectroscopy

The SDSS spectra of SDSS J162256.66+473051.1 (J1622 for short, also known as PG 1621+476, g′ = 15.96 mag) showed a radial velocity shift of 100 km s-1 within 1.45 h. Therefore, the star was selected as a high priority target for follow-up. The 18 spectra were taken with the ISIS instrument at the William Herschel Telescope on La Palma, from 24 to 27 August 2009 at medium resolution (R ~ 4000). Additional 64 spectra with the same resolution were obtained with the TWIN spectrograph at the 3.5 m telescope at the Calar Alto Observatory, Spain, from 25 to 28 May 2012. Moreover, ten higher resolution spectra (R ~ 8000) were observed with ESI at the Keck Telescope, Hawaii, on 13 July 2013. The TWIN and ISIS data were reduced with the MIDAS package distributed by the European Southern Observatory (ESO). The ESI data was reduced with the pipeline Makee1.

2.2. Photometry

When the RV-curve from the ISIS spectra showed a short period of only 0.069 d, a photometric follow-up was started. The object J1622 was observed with the Bonn University Simultaneous Camera (BUSCA) at the 2.2 m telescope at the Calar Alto Observatory. The instrument BUSCA (Reif et al. 1999) can observe in four bands simultaneously. We did not use any filters but we used instead the intrinsic transmission curve given by the beam splitters, which divides the visible light into four bands UB, BB, RB, and IB (and means no light loss). Four sets of lightcurves, each covering one orbit of J1622, were obtained on 12 June 2010, 29 September 2010, 28 February 2011, and 1 June 2011. They were reduced by using the aperture photometry package of IRAF. As the comparison stars have different spectral types, we observed a long-term trend in the lightcurve with changing air mass due to the different wavelength dependency of atmospheric extinction, which cannot be corrected.

thumbnail Fig. 1

Phased BUSCA lightcurve in BB and RB of J1622. The solid line demonstrates the best-fit model. In the bottom panel, the residuals can be seen.

3. Spectroscopic analysis

3.1. Radial velocity curve

The radial velocities were measured by fitting a combination of Gaussians, Lorentzians, and polynomials to the Balmer and helium lines of all spectra and are given in Table A1. Since the phase-shift between primary and secondary eclipses in the phased lightcurve (see Fig. 1) is exactly 0.5, we know that the orbit of J1622 is circular. Therefore, sine curves were fitted to the RV data points in fine steps over a range of test periods. For each period, the χ2 of the best-fit sine curve was determined (see Geier et al. 2011c). All three datasets were fit together. The orbit is well covered. Figure 2 shows the phased RV curve with the fit of the best solution. It gives a semi-amplitude of K = 47.2 ± 2.0 km s-1, a system velocity of γ = −54.7 ± 1.5 km s-1, and a period of 0.0696859 ± 0.00003 d. The period is consistent with the period from the photometry (see Sect. 4) and is the second shortest ever measured for an sdB binary.

thumbnail Fig. 2

Radial velocity plotted against orbital phase of J1622. The radial velocity was determined from the SDSS, ISIS, TWIN, and ESI spectra. All spectra were fitted together. The stars mark the SDSS spectra, the dots the TWIN spectra, the filled squares the ISIS spectra, and the open squares the ESI spectra. The errors are formal 1σ uncertainties. The lower panel shows the residuals.

3.2. Atmospheric parameters

The atmospheric parameters were determined by fitting synthetic spectra, which were calculated using local thermodynamical equilibrium model atmospheres with solar metallicity and metal line blanketing (Heber et al. 2000), to the Balmer and helium lines using SPAS (Hirsch 2009). For some of the HW Vir stars and similar non-eclipsing systems, it was found that the atmospheric parameters seemed to vary with the phase (e.g. Schaffenroth et al. 2013b), as the contribution of the companion to the spectrum varies with the phase. Therefore, all spectra were fit separately. Figure 3 shows the effective temperature and the surface gravity determined from the TWIN spectra plotted against orbital phase. No change with the orbital phase can be seen. Therefore, we co-added all 64 TWIN spectra and derived the atmospheric parameters (Teff = 29 000 ± 600 K, log g = 5.65 ± 0.06, log y = −1.87 ± 0.05). In Fig. 4 the best fit to the Balmer and helium lines of the co-added spectrum is shown.

In Fig. 5, the position of J1622 in the Teff-log g diagram is compared to those of the known HW Vir systems and other sdB binaries. It is worthwhile to note that all of the HW Vir systems, but two, which have evolved off the EHB, have very similar atmospheric parameters. Those systems cluster in a distinct region of the Teff-log g diagram. Unlike the HW Vir stars, other sdB binaries are distributed more or less uniformly across the extreme horizontal branch (see Fig. 5). In this respect, J1622 turns out to be a typical HW Vir system.

Due to their higher resolution, the ESI spectra are suitable to measure the rotational broadening of spectral lines of the sdB. We co-added all 10 spectra and determined the projected rotational velocity of the sdB primary by adding a rotational profile to the fit of the Balmer and helium lines. The other atmospheric parameters were kept fixed to the values determined from the TWIN spectra. The best fit for vrotsini = 71 ± 7 km s-1 is displayed in Fig. 6. Surprisingly, the projected rotational velocity is only about two thirds of the one expected for tidally locked rotation of the hot subdwarf primary. This issue is further discussed in Sect. 6.

thumbnail Fig. 3

Effective temperature and surface gravity plotted over the phase of J1622. Teff and log g were determined from the TWIN spectra. The errors are statistical 1σ errors. The lines represent the parameters from the co-added spectrum with the errors.

thumbnail Fig. 4

Fit of the Balmer and helium lines in the co-added TWIN spectrum. The solid line shows the measurement, and the dashed line shows the best fitting synthetic spectrum.

thumbnail Fig. 5

Teff − log  g diagram of the HW Vir systems. The solid lines are evolutionary tracks by Dorman et al. (1993) for an sdB mass of 0.471, 0.473, and 0.475 M⊙. The positions of J1622 and J0820 are indicated with crosses. The other squares mark the position of other HW Vir-like systems (Van Grootel et al. 2013a; Drechsel et al. 2001; For et al. 2010; Geier et al. 2011d; Maxted et al. 2002; Klepp & Rauch 2011; Østensen et al. 2008, 2010; Wood & Saffer 1999; Almeida et al. 2012; Barlow et al. 2013). The open dots represent other sdB binaries from the literature.

thumbnail Fig. 6

Fit of the helium lines in the co-added ESI spectrum. The solid line shows the measurement and the dashed line shows the best fitting synthetic spectrum. The dotted line shows the line-broadening, if we assume synchronisation.

4. Photometric analysis

The BUSCA lightcurves clearly show a strong reflection effect and grazing eclipses, as can be seen in Fig. 1. Unfortunately, the signal-to-noise of the UB and IB lightcurves is insufficient, so that only the BB and RB lightcurves are used for the analysis. The ephemeris was determined from the BUSCA lightcurves by fitting parabolas to the cores of the primary eclipses. The period was derived with the help of the Lomb-Scargle Algorithm (Press & Rybicki 1989).

The ephemeris of the primary minimum is given by

HJD = 2 455 359.58306(2) + 0.0697885(53)·E (thereby E is the eclipse number, see Drechsel et al. 2001).

Table 1

Adopted lightcurve solution.

Table 2

Parameters of J1622.

The phased lightcurves are shown in Fig. 1. The lightcurve analysis was performed by using MORO (MOdified ROche Program, see Drechsel et al. 1995), which calculates synthetic lightcurves, which were fitted to the observation. This lightcurve solution code is based on the Wilson-Devinney approach (Wilson & Devinney 1971) but uses a modified Roche model that considers the radiative pressure of hot binaries. More details of the analysis method are described in Schaffenroth et al. (2013b).

The main problem of the lightcurve analysis is the high number of parameters. To calculate the synthetic lightcurves, 12 + 5n (n is the number of lightcurves) parameters that are not independent are used. Therefore, strong degeneracies exist, in particular in the mass ratio, which is strongly correlated with the other parameters. The mass ratio is, therefore, fixed, and solutions for different mass ratios are calculated. To resolve this degeneracy, it is, moreover, important to constrain as many parameters as possible from the spectroscopic analysis or theory.

From the spectroscopic analysis, we derive the effective temperature and the surface gravity of the sdB primary. Due to the early spectral type of the primary star, the gravity darkening exponent can be fixed at g1 = 1, as expected for radiative outer envelopes (von Zeipel 1924). For the cool convective companion, g2 was set to 0.32 (Lucy 1967). The linear limb darkening coefficients were extrapolated from the table of Claret & Bloemen (2011).

To determine the quality of the lightcurve fit, the sum of the deviations from each point to the synthetic curve is calculated, and the solution with the smallest sum is supposed to be the best solution. The difference between the solutions for the different mass ratios is unfortunately small, as expected. Therefore, we cannot determine a unique solution from the lightcurve analysis alone and adopted the solution closest to the canonical mass for the sdB star. The corresponding results of the lightcurve analysis are given in Table 1 with errors determined with the bootstrapping method. The lightcurves in the BB and RB band are displayed in Fig. 1 with the best-fit models for these parameters. The apparent asymmetries of the observed lightcurve can not be modelled, but we are not sure if this effect is real or is due to uncorrected long-term trends in the photometry (see Sect. 2.2). The parameters of the system resulting from the adopted solution with the mass function are summarised in Table 2. The errors result from error propagation of the errors of K,P, and i.

thumbnail Fig. 7

Comparison of the photometric and spectroscopic surface gravity for the solutions with different mass ratio q = 0.11−0.19 (marked by the error cross). The spectroscopic surface gravity with uncertainty is given by the shaded area.

5. The brown dwarf nature of the companion

From the semi-amplitude of the radial velocity curve and the orbital period, we can derive the masses and the radii of both components for each mass ratio. To constrain the solutions further, we first compared the photometric surface gravity, which can be derived from the mass and the radius, to the spectroscopic surface gravity. This is displayed in Fig. 7. The spectroscopic surface gravity is consistent with the lightcurve solution for sdB masses from 0.25 to 0.6 M⊙. It is, therefore, possible to find a self-consistent solution. This is not at all a matter of course, because gravity derived from photometry was found to be inconsistent with the spectroscopic result in other cases, such as AA Dor (Vučković et al. 2008).

We also compared the radius of the companion to theoretical mass-radius relations for low-mass stars and brown dwarfs with ages of 1, 5, and 10 Gyr, respectively (Baraffe et al. 2003). As can be seen from Fig. 8, the measured mass-radius relation is well matched by theoretical predictions for stars ≳3 Gyr for companion masses between 0.055 M⊙ and 0.075 M⊙. The corresponding mass range for the sdB star is from 0.39 M⊙ to 0.63 M⊙, which is calculated from the mass ratio.

However, the companion is exposed to intense radiation of a luminous hot star that is only 0.58 R⊙ away, which could lead to an underestimate of the radius, if compared to non-irradiated models (Baraffe et al. 2003). Such inflation effects have been found in the case of hot Jupiter exoplanets (e.g. Udalski et al. 2008) but also in the MS+BD binary CoRoT-15b (Bouchy et al. 2011). We can estimate the maximum inflation effect from theoretical mass-radius relations shown in Fig. 8. As can be seen from Fig. 8, inflation by more than 10% can be excluded because none of the theoretical mass-radius relations otherwise would match the measured one, even if the star was as old as 10 Gyr (the age of the Galactic disk).

If we assume an inflation of 5–10%, the mass-radius relation for the companion would be in perfect agreement with the lightcurve solution for a companion with a mass of 0.064 M⊙ and a radius of 0.085 R⊙, and an age of ~5–10 Gyr. The corresponding mass of the sdB is close to the canonical sdB mass, which we therefore adopt for the sdB throughout the rest of the paper. As we calculated solutions for discrete q and, hence, discrete masses for the sdB and the companion, we adopted the solution closest to the canonical mass, which is also marked in Fig. 8.

thumbnail Fig. 8

Comparison of theoretical mass-radius relations of brown dwarfs by Baraffe et al. (2003) for an age of 1 Gyr (filled triangles), 5 Gyr (triangles) and 10 Gyr (diamond) to results from the lightcure analysis. Each error cross represents a solution from the lightcurve analysis for a different mass ratio (q = 0.11−0.19). The dashed vertical lines mark different values of the corresponding sdB masses. The solid lines mark the solution closest to the canonical mass for the sdB star of 0.47 M⊙ that was adopted.

6. Synchronisation

Most HW Vir systems have orbital separations as small as one solar radius. Hence, it is reasonable to expect that the rotation of both components is tidally locked to the orbit. Indeed the rotation rates of HW Vir and other objects of the class with similarly short periods (0.1d) are found to be synchronised. It is worthwhile to note that the system PG 1017−036, a reflection-effect binary with almost the same parameters as J1622 (P = 0.072 d, K = 51 km s-1, Teff = 30 300 K, log g = 5.61), has a measured vrotsini = 118 km s-1 (Maxted et al. 2002), which is fully consistent with synchronised rotation. However, J1622 (P = 0.0698 d, K = 47 km s-1, Teff = 29 000 K, log g = 5.65) rotates with vrotsini = 71 km s-1. With an inclination of 72.33°, this results in a rotational velocity of 74 km s-1, which is only about two thirds of the rotational velocity expected for a synchronous rotation (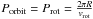Porbit=Prot=2πRvrot\hbox{$P_{\rm orbit}=P_{\rm rot}=\frac{2\pi R}{v_{\rm rot}}$}).

The physical processes leading to synchronisation are not well understood particularly for stars with radiative envelopes, such as sdB stars and rivalling theories (Zahn 1977; Tassoul & Tassoul 1992), predict very different synchronisation timescales (for details see Geier et al. 2010). The synchronisation timescales increase strongly with orbital separation, hence with the orbital period of the system. Actually the objects J1622 and PG 1017−036 have the shortest periods and the highest probability for tidally locked rotation amongst all known HW Vir systems. Therefore, it is surprising that J1622 apparently is not synchronised, while PG 1017−036 is. Calculations in the case of the less efficient mechanism (Zahn 1977) predict that the synchronisation should be established after 105 yr, a time span much shorter than the EHB lifetime of 108 yr.

Evidence for a non-synchronous rotation of sdB stars in reflection-effect binaries was presented recently by Pablo et al. (2011, 2012), who measured the rotational splittings of pulsation modes in three reflection-effect sdB binaries observed by the Kepler space mission, which reveals that the subdwarf primaries rotate more slowly than synchronised. However, those binaries have rather long periods (~0.5 d), and predicted synchronisation timescales are much longer than for J1622 and even exceed the EHB life time if the least efficient synchronisation process (see Fig. 19 in Geier et al. 2010) is adopted. Hence, unlike for J1622, the non-synchronisation of those systems is not in contradiction with synchronisation theory.

It is quite unlikely that J1622 is too young for its rotation to be tidally locked to the orbit. Hence, we need to look for an alternative explanation. Tidal forces leading to circularisation and synchronisation may lead to stable configurations, in which the rotational and the orbital periods are in resonance; that is, their ratio is that of integer numbers as observed for Mercury. Comparing the observed rotational period of J1622 to the orbital one, we find that the ratio is 0.607 ± 0.065, hence close to a 2 to 3 resonance. However, J1622 must have undergone a spiral-in phase through the common-envelope phase and it must be investigated, whether such a resonant configuration can persist through that dynamical phase.

7. Conclusions

We performed a spectroscopic and photometric analysis of the eclipsing hot subdwarf binary J1622, which was found in the course of the MUCHFUSS project. The atmospheric parameters of the primary are typical for an sdB star in a HW Vir system. Mass-radius relations were derived for both components. The mass of the sdB star is constrained from spectroscopy (surface gravity) to 0.28 M⊙ to 0.64 M⊙. The mass of the companion can be constrained by theoretical mass-radius relations to lie between 0.055 M⊙ and 0.075 M⊙, which implies that the sdB mass is between 0.39 M⊙ and 0.63 M⊙.

Assuming small corrections of about 5–10% to the radius due to the inflation of the companion by the strong irradiation from the primary, a companion mass of 0.064 M⊙ appears to be the most plausible choice that results in a mass of the sdB close to the canonical mass of 0.47 M⊙ star. Accordingly, the companion is a substellar object. This is the second time that a brown dwarf is found as a close companion to an sdB star. The object J1622 provides further evidence that substellar objects are able to eject a common envelope and form an sdB star. Finding more of these systems helps to constrain theoretical models (Soker 1998; Nelemans & Tauris 1998).

An important result of the spectral analysis is that the sdB star is rotating slower than expected, if its rotation was locked to its orbit, as observed for the very similar system PG 1017−036. The non-synchronous rotation of J1622 is in contradiction with the predictions of tidal interaction models unless the sdB star is very young. The ratio of the rotational to the orbital period is close to a resonance of 2 to 3. However, it has to be investigated further, if such a configuration can survive the common envelope phase.

Future investigations should aim at the detection of spectral lines from the secondary to measure its radial velocity, which turns the system into an double-lined spectroscopic binary that would allow to pin down the mass ratio. Emission lines of the companion’s irradiated atmosphere have been detected in the sdOB system AA Dor (Vučković et al. 2008) and also for the prototype HW Vir (Vučković et al. 2013) most recently. Since J1622 is quite compact and the irradiation of the companion strong, such emission lines might be detectable in high-resolution spectra of sufficient quality. Accurate photometry is needed to confirm or disprove any asymmetries in its lightcurve, which hints at flows at the surface of the companion.

Online material

Appendix A: Radial velocity table

Table A1

Radial velocities with errors of J1622.

Acknowledgments

Based on observations collected at the Centro Astronómico Hispano Alemán (CAHA), operated jointly by the Max-Planck Institut für Astronomie and the Instituto de Astrofisica de Andalucia (CSIC) with BUSCA at 2.2 m telescope, and with TWIN at the 3.5 m telescope. Based on observations made with the William Herschel Telescope operated on the island of La Palma by the Isaac Newton Group in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. Based on observations obtained at the W.M. Keck Observatory, which is operated as a scientific partnership among the California Institute of Technology, the University of California, and the National Aeronautics and Space Administration. The Observatory was made possible by the generous financial support of the W.M. Keck Foundation. The authors wish to recognise and acknowledge the very significant cultural role and reverence that the summit of Mauna Kea has always had within the indigenous Hawaiian community. We are most fortunate to have the opportunity to conduct observations from this mountain. V.S. acknowledges funding by the Deutsches Zentrum für Luft- und Raumfahrt (grant 50 OR 1110) and by the Erika-Giehrl-Stiftung. T.K. acknowledges support from the Netherlands Research School of Astronomy (NOVA).

References

  1. Almeida, L. A., Jablonski, F., Tello, J., & Rodrigues, C. V. 2012, MNRAS, 423, 478 [NASA ADS] [CrossRef] [Google Scholar]
  2. Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Barlow, B. N., Kilkenny, D., Drechsel, H., et al. 2013, MNRAS, 430, 22 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bear, E., & Soker, N. 2012, ApJ, 749, L14 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bouchy, F., Deleuil, M., Guillot, T., et al. 2011, A&A, 525, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Charpinet, S., Fontaine, G., Brassard, P., et al. 2011, Nature, 480, 496 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  7. Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Dorman, B., Rood, R. T., & O’Connell, R. W. 1993, ApJ, 419, 596 [CrossRef] [Google Scholar]
  9. Drechsel, H., Haas, S., Lorenz, R., & Gayler, S. 1995, A&A, 294, 723 [NASA ADS] [Google Scholar]
  10. Drechsel, H., Heber, U., Napiwotzki, R., et al. 2001, A&A, 379, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Fontaine, G., Brassard, P., Charpinet, S., et al. 2012, A&A, 539, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. For, B.-Q., Green, E. M., Fontaine, G., et al. 2010, ApJ, 708, 253 [NASA ADS] [CrossRef] [Google Scholar]
  13. Geier, S., & Heber, U. 2012, A&A, 543, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Geier, S., Heber, U., Podsiadlowski, P., et al. 2010, A&A, 519, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Geier, S., Classen, L., & Heber, U. 2011a, ApJ, 733, L13 [NASA ADS] [CrossRef] [Google Scholar]
  16. Geier, S., Hirsch, H., Tillich, A., et al. 2011b, A&A, 530, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Geier, S., Maxted, P. F. L., Napiwotzki, R., et al. 2011c, A&A, 526, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Geier, S., Schaffenroth, V., Drechsel, H., et al. 2011d, ApJ, 731, L22 [Google Scholar]
  19. Geier, S., Heber, U., Heuser, C., et al. 2013, A&A, 551, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Han, Z., Podsiadlowski, P., Maxted, P. F. L., Marsh, T. R., & Ivanova, N. 2002, MNRAS, 336, 449 [NASA ADS] [CrossRef] [Google Scholar]
  21. Han, Z., Podsiadlowski, P., Maxted, P. F. L., & Marsh, T. R. 2003, MNRAS, 341, 669 [NASA ADS] [CrossRef] [Google Scholar]
  22. Heber, U. 2009, ARA&A, 47, 211 [NASA ADS] [CrossRef] [Google Scholar]
  23. Heber, U., Reid, I. N., & Werner, K. 2000, A&A, 363, 198 [NASA ADS] [Google Scholar]
  24. Hirsch, H. 2009, Ph.D. Thesis, Friedrich Alexander Universität Erlangen Nürnberg [Google Scholar]
  25. Iben, Jr., I., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kilkenny, D., Hilditch, R. W., & Penfold, J. E. 1978, MNRAS, 183, 523 [NASA ADS] [CrossRef] [Google Scholar]
  27. Klepp, S., & Rauch, T. 2011, A&A, 531, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Lucy, L. B. 1967, Zeitschrift für Astrophysik, 65, 89 [Google Scholar]
  29. Maxted, P. f. L., Heber, U., Marsh, T. R., & North, R. C. 2001, MNRAS, 326, 1391 [NASA ADS] [CrossRef] [Google Scholar]
  30. Maxted, P. F. L., Marsh, T. R., Heber, U., et al. 2002, MNRAS, 333, 231 [NASA ADS] [CrossRef] [Google Scholar]
  31. Menzies, J. W., & Marang, F. 1986, in Instrumentation and Research Programmes for Small Telescopes, eds. J. B. Hearnshaw, & P. L. Cottrell, IAU Symp., 118, 305 [Google Scholar]
  32. Napiwotzki, R., Karl, C. A., Lisker, T., et al. 2004, Ap&SS, 291, 321 [NASA ADS] [CrossRef] [Google Scholar]
  33. Nelemans, G., & Tauris, T. M. 1998, A&A, 335, L85 [NASA ADS] [Google Scholar]
  34. Østensen, R. H., Oreiro, R., Hu, H., Drechsel, H., & Heber, U. 2008, in Hot Subdwarf Stars and Related Objects, eds. U. Heber, C. S. Jeffery, & R. Napiwotzki, ASP Conf. Ser., 392, 221 [Google Scholar]
  35. Østensen, R. H., Green, E. M., Bloemen, S., et al. 2010, MNRAS, 408, L51 [NASA ADS] [CrossRef] [Google Scholar]
  36. Østensen, R. H., Geier, S., Schaffenroth, V., et al. 2013, A&A, 559, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Pablo, H., Kawaler, S. D., & Green, E. M. 2011, ApJ, 740, L47 [NASA ADS] [CrossRef] [Google Scholar]
  38. Pablo, H., Kawaler, S. D., Reed, M. D., et al. 2012, MNRAS, 422, 1343 [NASA ADS] [CrossRef] [Google Scholar]
  39. Press, W. H., & Rybicki, G. B. 1989, ApJ, 338, 277 [NASA ADS] [CrossRef] [Google Scholar]
  40. Reif, K., Bagschik, K., de Boer, K. S., et al. 1999, in SPIE Conf. Ser. 3649, eds. M. M. Blouke, & G. M. Williams, 109 [Google Scholar]
  41. Schaffenroth, V., Geier, S., Barbu-Barna, I., et al. 2013a, ASP Conf. Ser., in press [Google Scholar]
  42. Schaffenroth, V., Geier, S., Drechsel, H., et al. 2013b, A&A, 553, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Soker, N. 1998, AJ, 116, 1308 [NASA ADS] [CrossRef] [Google Scholar]
  44. Tassoul, M., & Tassoul, J.-L. 1992, ApJ, 395, 604 [NASA ADS] [CrossRef] [Google Scholar]
  45. Udalski, A., Pont, F., Naef, D., et al. 2008, A&A, 482, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Van Grootel, V., Charpinet, S., Brassard, P., Fontaine, G., & Green, E. M. 2013a, A&A, 553, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Van Grootel, V., Fontaine, G., Charpinet, S., Brassard, P., & Green, E. M. 2013b, in Eur. Phys. J. Web Conf., 43, 4007 [Google Scholar]
  48. von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
  49. Vučković, M., Østensen, R., Bloemen, S., Decoster, I., & Aerts, C. 2008, in Hot Subdwarf Stars and Related Objects, eds. U. Heber, C. S. Jeffery, & R. Napiwotzki, ASP Conf. Ser., 392, 199 [Google Scholar]
  50. Vučković, M., et al. 2013, ASP Conf. Ser., in press [Google Scholar]
  51. Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
  52. Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 [NASA ADS] [CrossRef] [Google Scholar]
  53. Wood, J. H., & Saffer, R. 1999, MNRAS, 305, 820 [NASA ADS] [CrossRef] [Google Scholar]
  54. Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]

All Tables

Table 1

Adopted lightcurve solution.

In the text
Table 2

Parameters of J1622.

In the text
Table A1

Radial velocities with errors of J1622.

In the text

All Figures

thumbnail Fig. 1

Phased BUSCA lightcurve in BB and RB of J1622. The solid line demonstrates the best-fit model. In the bottom panel, the residuals can be seen.
In the text
thumbnail Fig. 2

Radial velocity plotted against orbital phase of J1622. The radial velocity was determined from the SDSS, ISIS, TWIN, and ESI spectra. All spectra were fitted together. The stars mark the SDSS spectra, the dots the TWIN spectra, the filled squares the ISIS spectra, and the open squares the ESI spectra. The errors are formal 1σ uncertainties. The lower panel shows the residuals.
In the text
thumbnail Fig. 3

Effective temperature and surface gravity plotted over the phase of J1622. Teff and log g were determined from the TWIN spectra. The errors are statistical 1σ errors. The lines represent the parameters from the co-added spectrum with the errors.
In the text
thumbnail Fig. 4

Fit of the Balmer and helium lines in the co-added TWIN spectrum. The solid line shows the measurement, and the dashed line shows the best fitting synthetic spectrum.
In the text
thumbnail Fig. 5

Teff − log  g diagram of the HW Vir systems. The solid lines are evolutionary tracks by Dorman et al. (1993) for an sdB mass of 0.471, 0.473, and 0.475 M⊙. The positions of J1622 and J0820 are indicated with crosses. The other squares mark the position of other HW Vir-like systems (Van Grootel et al. 2013a; Drechsel et al. 2001; For et al. 2010; Geier et al. 2011d; Maxted et al. 2002; Klepp & Rauch 2011; Østensen et al. 2008, 2010; Wood & Saffer 1999; Almeida et al. 2012; Barlow et al. 2013). The open dots represent other sdB binaries from the literature.
In the text
thumbnail Fig. 6

Fit of the helium lines in the co-added ESI spectrum. The solid line shows the measurement and the dashed line shows the best fitting synthetic spectrum. The dotted line shows the line-broadening, if we assume synchronisation.
In the text
thumbnail Fig. 7

Comparison of the photometric and spectroscopic surface gravity for the solutions with different mass ratio q = 0.11−0.19 (marked by the error cross). The spectroscopic surface gravity with uncertainty is given by the shaded area.
In the text
thumbnail Fig. 8

Comparison of theoretical mass-radius relations of brown dwarfs by Baraffe et al. (2003) for an age of 1 Gyr (filled triangles), 5 Gyr (triangles) and 10 Gyr (diamond) to results from the lightcure analysis. Each error cross represents a solution from the lightcurve analysis for a different mass ratio (q = 0.11−0.19). The dashed vertical lines mark different values of the corresponding sdB masses. The solid lines mark the solution closest to the canonical mass for the sdB star of 0.47 M⊙ that was adopted.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.