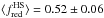EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 564 (April 2014) A&A, 564 (2014) L3 Full HTML
Free Access
Issue
A&A
Volume 564, April 2014
Article Number L3
Number of page(s) 8
Section Letters
DOI https://doi.org/10.1051/0004-6361/201323272
Published online 26 March 2014

© ESO, 2014

1. Introduction

The study of globular cluster (GC) systems in galaxies is one of the keystones for understanding the processes at the base of the formation and evolution of galaxies (Ashman & Zepf 1992; Brodie & Strader 2006). Recently, the interpretation of one of the most intriguing properties of GC systems in early-type galaxies, the nearly universal presence of two distinct peaks in the optical color distribution, has inspired a vigorous and prolific debate (Yoon et al. 2006, 2011; Kundu & Zepf 2007; Chies-Santos et al. 2012; Blakeslee et al. 2012; Usher et al. 2012; Vanderbeke et al. 2014).

The importance of GC bimodality was recognized before it was a commonly observed property in early-type galaxies (ETGs, Schweizer 1987). Historically, the bimodal GC color in optical bands has been equated to metallicity ([Fe/H]) bimodality, implying a fundamental constraint on GC and galaxy formation scenarios. Metallicity bimodality requires two distinct epochs or mechanisms of formation, or both, for the blue (metal-poor) and red (metal-rich) GC subpopulations.

There are various proposed explanations for the GC color bimodality in ETGs: dissipational merging of spirals, in which a merger-formed population of red, metal-rich GCs is assumed to appear distinct from the blue, metal-poor GCs of the progenitor spirals (Ashman & Zepf 1992); the dry hierarchical assembly, which begins with a massive “seed” ETG that has a unimodal metal-rich GC distribution, and in which it is possible to produce a bimodal metallicity distribution through dissipationless accretion of many early-type dwarfs (Côté et al. 1998); and the insitu formation scenario (Forbes et al. 1997). Most of these proposed mechanisms, though, have assumed a simple linear conversion between [Fe/H] and color, which seemed justified from the small fractional age variations among the GCs (Cohen et al. 1998; Kuntschner et al. 2002; Puzia et al. 2005). However, this assumption became the subject of debate when three independent works, using observations and stellar population models, pointed out non-negligible nonlinearities in the color-metallicity relations of GCs (Peng et al. 2006; Richtler 2006; Yoon et al. 2006). In particular, Yoon and colleagues and Richtler demonstrated that these nonlinearities naturally produce bimodal color histograms from nonbimodal [Fe/H] distributions. This interpretation, dubbed the projection effect, provided an alternative explanation based on stellar evolution for the ubiquity of bimodal GC color distributions.

In this regard, Cantiello & Blakeslee (2007) suggested the use of multicolor GC histograms to verify the consistency of [Fe/H] distributions derived from different colors. These authors highlighted the role of optical to near-infrared (NIR) colors to distinguish between genuine bimodality in [Fe/H] and projected bimodality in color. If the nonlinear projection is at work, then the [Fe/H] distributions inferred from linear inversion of different color indices for the same GC sample will show some degree of inconsistency (discordant [Fe/H] peaks and/or fractions of GCs in each [Fe/H] component). The analysis of optical-to-NIR GC colors in various ETGs, as well as u to z photometry in some Virgo cluster members, indicates that the nonlinear projection effect is present at some level in these galaxies (Blakeslee et al. 2012; Chies-Santos et al. 2012; Yoon et al. 2011, 2013).

At the same time, the results of the SLUGGS survey1, which collected spectra of ~ 1000 GCs in 11 galaxies and derived [Fe/H] from the calcium II triplet index, CaT, support true [Fe/H] bimodality in at least some galaxies in addition to the Milky Way. Usher et al. (2012) found evidence for bimodal CaT distributions in six of eight galaxies with sufficient numbers of GC spectra. Nevertheless, the spectroscopically and photometrically derived [Fe/H] distributions show non-negligible differences in several galaxies of the SLUGGS sample, thus lacking the aforementioned multi-index coherence. However, the case of NGC 3115, an isolated lenticular galaxy at a distance of ~ 10 Mpc (Tonry et al. 2001), revealed highly consistent [Fe/H] and color distributions, leading the authors to present this galaxy as a critical test of [Fe/H] bimodality (Brodie et al. 2012). Previous optical VLT FORS2 spectroscopy for 17 GCs in NGC 3115 showed hints of both a bimodal metallicity distribution and color or spectral index nonlinearity (Kuntschner et al. 2002), but it was limited by sample size.

In this Letter, we combine new NIR photometry with literature data to investigate the consistency of the bimodality in the optical, NIR, optical-NIR colors, and CaT, of the GCs in NGC 3115.

2. Observations

To analyze the properties of the GC system in NGC 3115, we took advantage of NIR observations with VLT/HAWK-I, HST/ACS optical photometry from Jennings et al. (2013) and spectroscopy from the SLUGGS survey (Usher et al. 2012).

All photometry is corrected for Galactic foreground-reddening using the Schlegel et al. (1998) maps, with recalibration from Schlafly & Finkbeiner (2011). To compare all data in the same photometric system, magnitudes were converted to AB mag using the zero points derived using the SYNPHOT task of IRAF/STSDAS and the spectrum of Vega from the Kurucz (1993) atlas of stellar atmosphere models.

2.1. VLT/HAWK-I near-infrared data

We used HAWK-I science verification data. The observations were carried out in very good seeing conditions, with \hbox{$\textit{FWHM}\la 0\farcs5$} in all three bands. The science observations centered on NGC 3115 were interleaved with sky exposures of equal exposure time. The total on-source exposure times were 480 s in J, 960 s in H, and 1620 s in Ks.

A series of custom IDL scripts was used to carry out the data reduction. Briefly, this consisted of subtracting dark exposures, producing super-sky flats from the stacked, unregistered sky exposures, and applying the derived flats to the individual science and sky exposures. Finally, individual exposures were registered and coadded.

Because it is difficult to model the disk component of the galaxy, we adopted the approach described in Jordán et al. (2004). After taking the logarithm of the galaxy image, we fitted two-dimensional bicubic splines to the brightness distribution using SExtractor (Bertin & Arnouts 1996). We then took the inverse logarithm of this model and subtracted it from the original image.

The photometry was then obtained from a second run of SExtractor on the residual image. Because of the very strong SBF signal (Tonry et al. 1990), we added the galaxy model times a filter-dependent constant to the SExtractor input rms map to avoid detecting surface brightness fluctuations as sources (see Jordán et al. 2004)2. To derive the absolute calibration, we compared our photometry catalogs with the 2MASS point source catalog. A total of 15 point sources in the JH frames, and 11 in Ks were used to derive the zero points, providing zpJ = 25.75 ± 0.06 mag, zpH = 26.03 ± 0.06 mag, and zpKs = 25.03 ± 0.09 mag. The list of matched sources is reported in Table 2.

2.2. Optical photometry and spectroscopy

We compared the NIR data with ACS optical photometry and with the SLUGGS data. The literature catalogs were selected on the basis of either the radial velocity or the spatial extent of the source or for both quantities. This allowed us to obtain GC catalogs with negligible contamination from fore- or background sources.

The SLUGGS survey is based on Subaru Suprime-Cam gi photometry and Keck/Deimos Ca II triplet measurements. The final sample of matched sources includes NGC = 88 GCs (HS sample hereafter).

The ACS catalog consists of deep gF475W and zF850LP photometry. We paired our NIR catalog with the ACS one, which produced a sample of NGC = 264 GC candidates (HA sample).

Finally, we also considered the sample of objects obtained by matching all three of the catalogs, which includes 74 GCs (HSA sample).

We analyzed the color and CaT distributions for the above three samples using the Gaussian mixture modeling code (GMM, Muratov & Gnedin 2010). This uses the likelihood-ratio test to compare the goodness of fit for double Gaussians versus a single Gaussian. For the best-fit double model, it estimates the means and widths of the two components, their separation DD in terms of combined widths, and the kurtosis kurt of the overall distribution. It also provides uncertainties based on bootstrap resampling.

thumbnail Fig. 1

Color-CaT and a selection of color–color diagrams for the HS sample (sel#1, full gray circles). Open circles mark GC candidates rejected by the adopted selection criteria. SPoT SSP models for [Fe/H]  =  −2.3 (pink), −1.3 (red), −0.7 (yellow), −0.3 (cyan), 0.0 (blue) and + 0.3 (green) dex are also shown. The age range is 2 ≤ t(Gyr) ≤ 14, at fixed metallicity younger ages have bluer color. Histograms, and nonparametric density estimates for histograms are also shown with arbitrary scale. (This figure is available in color in electronic form.)

3. Analysis of the color distributions

We analyzed the three samples mentioned in Sect. 2.2 by adopting the two different selection criteria described below. First, to coherently compare our results with the recent analysis by Brodie et al. (2012), we selected all GC candidates with CaT measurements with a signal-to-noise ratio > 12 Å-1 (sel#1 hereafter3). Second, for a consistent comparison of our analysis with a similar study of NGC 1399 GCs (Blakeslee et al. 2012), we selected only GCs within the magnitude range 20.5 ≤ mi(mag) ≤ 22.5, and photometric uncertainty on color Δ  color ≤ 0.07 mag (sel#2).

thumbnail Fig. 2

Similar to Fig. 1, but for the HSA sample. The solid black lines show linear least-squares fits to the GCs with gF475W − zF850LP < 1.1 and 1.2 < gF475W − zF850LP < 1.6, respectively; the dotted nearly horizontal black line connects the endpoints of these fits. (This figure is available in color in electronic form.)

The results of the GMM tests on the three GC samples with the two different selection criteria are reported in Tables 3–4 and can be summarized as follows:

  • i)

    HS sample (sel#1) – The color–color andcolor-CaT diagrams for this sample and selection are shown inFig. 1. In general, the GMM resultsagree well for the various indices. However, for the purelyNIR colors, the likelihood ratio test,p(χ2), is consistent with a bimodal distribution in J − Ks and H − Ks, while the p-values for the peak separation and kurtosis do not significantly favor bimodality.

  • ii)

    HA sample (sel#1) – Although the sample is nearly twice as large as the HS sample, the relevance of color bimodality in optical and optical-to-NIR data, and the lack of a strong evidence of bimodality in NIR colors is nearly identical to the previous case.

  • iii)

    HSA sample – The sample, contains 58 GC candidates in the case of sel#1 and returns GMM values consistent with the two previous samples (Fig. 2).

  • iv)

    sel#1 versus sel#2 – As expected, the results of GMM obtained using sel#1 or sel#2 are very similar for the HS and HSA samples. This is mostly a consequence of the small difference between the catalogs obtained when adopting one selection or the other. However, the similarity between selections #1 and #2 is also true for the HA sample, which is twice as large as sel#2, meaning that it reaches NGC up to four times higher than some other samples or selections.

  • v)

    Although the values for the fraction of red GCs fred derived from different samples, or selection, or colors are largely consistent, closer inspection shows the systematic nature of fred with respect to galactocentric distance RGC, that is, the radial gradient in mean GC color. In particular, for sel#1 we find 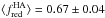⟨fredHA⟩=0.67±0.04\hbox{$\langle f_{\rm red}^{\rm HA}\rangle=0.67\pm0.04$}, while 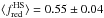⟨fredHS⟩=0.55±0.04\hbox{$\langle f_{\rm red}^{\rm HS}\rangle=0.55\pm0.04$}4. Because the mean RGC of the HA sample is smaller than that of the HS (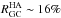RGCHA~16%\hbox{$R_{\rm GC}^{\rm HA}\sim 16\%$} smaller), the difference in fred for the two samples reflects the known tendency of red GCs to be more centrally concentrated than blue ones (Kissler-Patig 1997; Larsen & Brodie 2003).

A summary of Tables 3, 4 is reported in Table 1. The table gives the averaged p-values from the different samples, obtained from coupling all the optical colors (e.g. g − i; the column Ncol gives the number of colors used for the average), all the optical-to-NIR (e.g. g − H), and all the NIR colors (e.g. J − Ks). The most profound result here, again, is the coherence between optical and optical-to-NIR colors, and the already mentioned lack of bimodality in NIR colors based on peak separation and kurtosis statistics.

Table 1

Average results of GMM tests.

Table 2

Matched HAWK–I JHKs photometry for all detected sources.

Before moving on, we note that in some cases the GMM analysis indicates that three Gaussians are preferred to (or as good as) the double Gaussians model. The results of GMM fits with three components are reported in Table 5. Only cases where the least populated peak contains at least ~ 10% of the total population are considered. Although some colors for some samples are well fit with three Gaussians, we stress the lack of coherence in these tri-modal models for different colors.

4. Comparison with population models

Figures 1, 2 show the integrated colors for simple stellar population (SSP) models from the SPoT group (Raimondo 2009; Raimondo et al. 2005)5. The model grid ranges from 2 to 14 Gyr in SSP age, and from −2.3 to + 0.3 dex in [Fe/H]. Interpretation of integrated colors is hindered by the age-metallicity degeneracy (Worthey 1994). In this case, though, the broad wavelength coverage of the data and the higher sensitivity to [Fe/H] of optical-to-NIR colors compared with purely optical colors allows one to set more robust constraints on the stellar populations from the full set of color–color diagrams (Georgiev et al. 2012). Overall, the SSP models and the data agree well in general, and it is evident that the GC system covers almost the full metallicity range of the models.

In Fig. 2 we show a color–color diagram for the HSA sample (sel#1). The sample from matching the three catalogs is smaller than the others considered above. However, the features observed in other samples are preserved, with lower scatter. Among these we highlight first, the absence of a GC component with t ≤ 8 Gyr and [Fe/H]  ≤  − 2.3 dex, or even the complete lack of clusters with this or a lower metallicity. Second, on the high-metallicity regime, some GC candidates (gF475W − zF850LP ≥ 1.5 and i − H ≥ 0.9 mag) are consistent with [Fe/H]  ≥  + 0.3 dex. The fraction of high-metallicity GC candidates is ~ 5 − 10%. Other color–color diagrams also show a similar fraction of GCs above the [Fe/H]  = 0.3 dex limit6.

Furthermore, while the bluer GCs appear to match the locus of SSP models for ages t > 10 Gyr, the red clusters are more consistent with t < 10 Gyr. However, the age sensitivity of the models is weak, and uncertainties in evolutionary and atmosphere models of AGB stars – such as low temperature opacity, the prescriptions for mass loss and dust – as well as the presence of extreme horizontal branch stars, might lead to artificial age differences. Nonetheless, the suggested trend agrees with other studies that found the metal-poor GCs to be 1–2 Gyr older than metal-rich ones (Puzia et al. 2005; Woodley et al. 2010).

An additional interesting feature of Fig. 2 is the nonlinear shape of the color–color relation: at blue colors, i − H increases steeply with gF475W − zF850LP; the dependence flattens at intermediate colors before becoming steep again. This is similar to the behavior found by Blakeslee et al. (2012) and resembles the quasi-inflection point present in color-metallicity relations, possibly indicating the shift in HB morphology around i − H ~ 0.5 mag (Yoon et al. 2006; Cantiello & Blakeslee 2007).

Finally, with regard to the dip in the color distributions, there is general agreement among the various color indices for a deficit of GCs in the −1.2 ≲  [Fe/H]  ≲  −0.4 dex range. This confirms the results from the CaT index (Brodie et al. 2012) and indicates that CaT provides metallicity estimates consistent with integrated colors (when interpreted with the above models), at least at this intermediate [Fe/H] regime.

5. Discussion and conclusions

Our analysis of the GC system in NGC 3115 provides additional definitive proof of GC [Fe/H] bimodality in this S0 galaxy, the first to be firmly established beyond the Milky Way. Various studies have noted that to rule out the possibility that nonlinearities project a nonbimodal [Fe/H] distribution into a bimodal color distribution, one must recover consistent [Fe/H] distributions from multiple different photometric indices. In particular, Cantiello & Blakeslee (2007) showed that optical-to-NIR colors are the most useful in constraining the underlying metallicities. This is in part because the broad color baselines imply a lower sensitivity to the detailed shape of the index-metallicity relation; for the converse reason, bimodal [Fe/H] distributions may not be evident in the purely NIR colors. The present study confirms these expectations: i) the optical and optical-to-NIR colors are clearly bimodal and consistent with each other in terms of proportions of red and blue GCs; and ii) the pure NIR distributions give ambiguous results, in the sense that different colors and/or statistical indicators show the presence or lack of bimodality.

The comparison of GC colors with SSP models confirms earlier results (Brodie et al. 2012), using CaT as a proxy for metallicity, which derived a bimodal [Fe/H] distribution with a dip at −1.3 ≲  [Fe/H]  ≲  − 0.3 dex. The model comparison also suggests that the metal-rich GCs have slightly younger ages than the blue/metal-poor ones. Although this conclusion is subject to model uncertainties, the size of the age difference is consistent with that found between the metal-rich and metal-poor GCs in the Milky Way (VandenBerg et al. 2013).

Some previous studies of optical-to-NIR GC colors in giant ellipticals have found significantly different optical versus optical-to-NIR color distributions. For instance, using HST ACS and WFC3/IR data, Blakeslee et al. (2012) showed that while the optical color distributions of the Fornax giant elliptical NGC 1399 are clearly bimodal (supporting earlier results from Forte et al. 2005), the V − H and I − H distributions are not, or they imply significantly different bimodal breakdowns than found for the optical alone. Similarly, Chies-Santos et al. (2012) studied the gzK color distributions of 14 elliptical galaxies, mainly in the Virgo cluster, and reported that double-peaked color distributions are more common in g − z than in the optical-NIR colors. Both studies found significant nonlinearity between the purely optical and optical-to-NIR colors, and both concluded that bimodal optical color distributions are not necessarily indicative of underlying bimodality in metallicity.

The lack of consistency between the purely optical and optical-NIR colors for NGC 1399 and some Virgo ellipticals contrasts strongly with the coherent color bimodality observed in NGC 3115, for which the metallicities are also clearly bimodal. In light of this contrast, and with the evidence for nonlinear color–color relations, the inconsistent optical and optical-NIR color bimodalities in some galaxies imply that nonlinearities do indeed play an important role in shaping the GC color distributions in those galaxies. Thus, while our multicolor photometric analysis confirms the [Fe/H] bimodality of NGC 3115 GCs, we conclude that the nonlinear projection effect remains a viable explanation for the ubiquity of optical color bimodality and is the most likely cause in cases where the optical-NIR colors lack obvious bimodality.

In summary: i) optical and optical-to-NIR colors and CaT indices of GCs in NGC 3115 are bimodal; ii) the bimodal distributions derived for different photometric and spectroscopic indices show good consistency; iii) evidence for bimodality is weak or absent for purely NIR colors; iv) our results agree with model predictions for GC systems with truly bimodal [Fe/H] distributions, which provides definitive proof of [Fe/H] bimodality in NGC 3115, perhaps the first galaxy beyond the Local Group for which this is the case; v) comparison with SSP models confirms earlier metallicity results based on CaT indices; vi) despite the consistency of the color distributions, we also observe color–color nonlinearities, most clearly in the case of i − H versus g − z.

Thus, the metallicity distributions of extragalactic GC systems and, more specifically, the existence or lack of a universal bimodality of [Fe/H] in ETGs, remains a matter of debate. Indirectly, when taken in the broader context of previous work,

our analysis indicates that optical GC color bimodalities have different causes in different galaxies, with nonlinear color-metallicity relations playing an important role for some previously studied giant ellipticals. Finally, our study shows the effectiveness of optical-to-NIR colors as an unambiguous test for underlying metallicity bimodality.

Online material

Table 3

Results of GMM runs on GCs selected using criterion #1 (based on ΔCaT, see text).

Table 4

Results of GMM runs on GCs selected using criterion #2 (based on Δ  color and magnitude, see text).

Table 5

Results of GMM runs for the three Gaussian model with GCs selected using criterion #1.

2

The constants were chosen to minimize the number of false detections. However, spurious objects are also removed when matching the NIR with optical photometric and spectroscopic catalogs (Sect. 2.2).

3

Since the HA sample lacks the CaT measurements used to define the sample sel#1, in this case we chose to include only matching sources with Δ  mag ≤ 0.05 in all HAWK-I and ACS passbands.

4

For the selection #2 we find ⟨fredHA⟩=0.56±0.09\hbox{$\langle f_{\rm red}^{\rm HA} \rangle = 0.56\pm0.09$}, and ⟨fredHS⟩=0.52±0.06\hbox{$\langle f_{\rm red}^{\rm HS}\rangle=0.52\pm0.06$}.

6

Larger fractions, up to ~ 15%, are implied by the z − J or z − H colors. The data-to-model mismatch might in part results from the uncertainty in high-[Fe/H] SSP models for these colors that is caused by the partial overlap or proximity of the passbands and uncertainties in stellar atmosphere models in this wavelength regime. However, a similar fraction of GCs with [Fe/H]  ≳ 0.3 dex was also found by Brodie et al. (2012) – we transformed their [Z/H] in [Fe/H] assuming the results of Tantalo et al. (1998), with [α/Fe]  = 0.35 (Pietrinferni et al. 2006). Moreover, these higher metal-rich fractions are for the HA sample, which is the most centrally concentrated of the considered samples (item (iv), Sect. 3), and would therefore have the highest proportion of metal-rich GCs.

Acknowledgments

Support for this work was provided by the FIRB-MIUR 2008 (P.I. G. Imbriani), INAF-PRIN/2010 (P.I. G. Clementini) and INAF-PRIN/2011 (P.I. M. Marconi).

References

  1. Ashman, K. M., & Zepf, S. E. 1992, ApJ, 384, 50 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Blakeslee, J. P., Cho, H., Peng, E. W., et al. 2012, ApJ, 746, 88 [NASA ADS] [CrossRef] [Google Scholar]
  4. Brodie, J. P., & Strader, J. 2006, ARA&A, 44, 193 [NASA ADS] [CrossRef] [Google Scholar]
  5. Brodie, J. P., Usher, C., Conroy, C., et al. 2012, ApJ, 759, L33 [NASA ADS] [CrossRef] [Google Scholar]
  6. Cantiello, M., & Blakeslee, J. P. 2007, ApJ, 669, 982 [NASA ADS] [CrossRef] [Google Scholar]
  7. Chies-Santos, A. L., Larsen, S. S., Cantiello, M., et al. 2012, A&A, 539, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Cohen, J. G., Blakeslee, J. P., & Ryzhov, A. 1998, ApJ, 496, 808 [NASA ADS] [CrossRef] [Google Scholar]
  9. Côté, P., Marzke, R. O., & West, M. J. 1998, ApJ, 501, 554 [NASA ADS] [CrossRef] [Google Scholar]
  10. Forbes, D. A., Brodie, J. P., & Grillmair, C. J. 1997, AJ, 113, 1652 [NASA ADS] [CrossRef] [Google Scholar]
  11. Forte, J. C., Faifer, F., & Geisler, D. 2005, MNRAS, 357, 56 [NASA ADS] [CrossRef] [Google Scholar]
  12. Georgiev, I. Y., Goudfrooij, P., & Puzia, T. H. 2012, MNRAS, 420, 1317 [NASA ADS] [CrossRef] [Google Scholar]
  13. Jennings, Z. G., Strader, J., Romanowsky, A. J., et al. 2013, AJ, submitted [Google Scholar]
  14. Jordán, A., Blakeslee, J. P., Peng, E. W., et al. 2004, ApJS, 154, 509 [NASA ADS] [CrossRef] [Google Scholar]
  15. Kissler-Patig, M. 1997, A&A, 319, 83 [NASA ADS] [Google Scholar]
  16. Kundu, A., & Zepf, S. E. 2007, ApJ, 660, L109 [NASA ADS] [CrossRef] [Google Scholar]
  17. Kuntschner, H., Ziegler, B. L., Sharples, R. M., Worthey, G., & Fricke, K. J. 2002, A&A, 395, 761 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Kurucz, R. L. 1993, CD-ROM N° 15 (Cambridge, Mass.: Smithsonian Astrophysical Observatory) [Google Scholar]
  19. Larsen, S. S., & Brodie, J. P. 2003, ApJ, 593, 340 [NASA ADS] [CrossRef] [Google Scholar]
  20. Muratov, A. L., & Gnedin, O. Y. 2010, ApJ, 718, 1266 [NASA ADS] [CrossRef] [Google Scholar]
  21. Peng, E. W., Jordán, A., Côté, P., et al. 2006, ApJ, 639, 95 [NASA ADS] [CrossRef] [Google Scholar]
  22. Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef] [Google Scholar]
  23. Puzia, T. H., Kissler-Patig, M., Thomas, D., et al. 2005, A&A, 439, 997 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Raimondo, G. 2009, ApJ, 700, 1247 [NASA ADS] [CrossRef] [Google Scholar]
  25. Raimondo, G., Brocato, E., Cantiello, M., & Capaccioli, M. 2005, AJ, 130, 2625 [NASA ADS] [CrossRef] [Google Scholar]
  26. Richtler, T. 2006, Bull. Astron. Soc. Ind., 34, 83 [Google Scholar]
  27. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
  28. Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
  29. Schweizer, F. 1987, in Nearly Normal Galaxies. From the Planck Time to the Present, Proc. Eighth Santa Cruz Summer Workshop in Astronomy and Astrophysics, Santa Cruz (New York: Springer Verlag), ed. S. M. Faber, 18 [Google Scholar]
  30. Tantalo, R., Chiosi, C., & Bressan, A. 1998, A&A, 333, 419 [NASA ADS] [Google Scholar]
  31. Tonry, J. L., Ajhar, E. A., & Luppino, G. A. 1990, AJ, 100, 1416 [NASA ADS] [CrossRef] [Google Scholar]
  32. Tonry, J. L., Dressler, A., Blakeslee, J. P., et al. 2001, ApJ, 546, 681 [NASA ADS] [CrossRef] [Google Scholar]
  33. Usher, C., Forbes, D. A., Brodie, J. P., et al. 2012, MNRAS, 426, 1475 [NASA ADS] [CrossRef] [Google Scholar]
  34. VandenBerg, D. A., Brogaard, K., Leaman, R., & Casagrande, L. 2013, ApJ, 775, 134 [NASA ADS] [CrossRef] [Google Scholar]
  35. Vanderbeke, J., West, M. J., De Propris, R., et al. 2014, MNRAS, 437, 1734 [NASA ADS] [CrossRef] [Google Scholar]
  36. Woodley, K. A., Harris, W. E., Puzia, T. H., et al. 2010, ApJ, 708, 1335 [NASA ADS] [CrossRef] [Google Scholar]
  37. Worthey, G. 1994, ApJS, 95, 107 [NASA ADS] [CrossRef] [Google Scholar]
  38. Yoon, S.-J., Yi, S. K., & Lee, Y.-W. 2006, Science, 311, 1129 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  39. Yoon, S.-J., Sohn, S. T., Lee, S.-Y., et al. 2011, ApJ, 743, 149 [NASA ADS] [CrossRef] [Google Scholar]
  40. Yoon, S.-J., Sohn, S. T., Kim, H.-S., et al. 2013, ApJ, 768, 137 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Average results of GMM tests.

In the text
Table 2

Matched HAWK–I JHKs photometry for all detected sources.

In the text
Table 3

Results of GMM runs on GCs selected using criterion #1 (based on ΔCaT, see text).

In the text
Table 4

Results of GMM runs on GCs selected using criterion #2 (based on Δ  color and magnitude, see text).

In the text
Table 5

Results of GMM runs for the three Gaussian model with GCs selected using criterion #1.

In the text

All Figures

thumbnail Fig. 1

Color-CaT and a selection of color–color diagrams for the HS sample (sel#1, full gray circles). Open circles mark GC candidates rejected by the adopted selection criteria. SPoT SSP models for [Fe/H]  =  −2.3 (pink), −1.3 (red), −0.7 (yellow), −0.3 (cyan), 0.0 (blue) and + 0.3 (green) dex are also shown. The age range is 2 ≤ t(Gyr) ≤ 14, at fixed metallicity younger ages have bluer color. Histograms, and nonparametric density estimates for histograms are also shown with arbitrary scale. (This figure is available in color in electronic form.)
In the text
thumbnail Fig. 2

Similar to Fig. 1, but for the HSA sample. The solid black lines show linear least-squares fits to the GCs with gF475W − zF850LP < 1.1 and 1.2 < gF475W − zF850LP < 1.6, respectively; the dotted nearly horizontal black line connects the endpoints of these fits. (This figure is available in color in electronic form.)
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.