| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A116 | |
| Number of page(s) | 14 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201323147 | |
| Published online | 16 April 2014 | |
A new catalog of H i supershell candidates in the outer part of the Galaxy⋆
1 Instituto Argentino de Radioastronomía (IAR), CC 5, 1894 Villa Elisa, Argentina
e-mail: lasuad@iar.unlp.edu.ar
2 Facultad de Ingeniería, Universidad de Buenos Aires, C.A.B.A., C117AAZ, Buenos Aires, Argentina
3 Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, 1900 La Plata, Argentina
4 Instituto de Astronomía y Física del Espacio (IAFE), Ciudad Universitaria, C.A.B.A, 1428 Buenos Aires, Argentina
Received: 28 November 2013
Accepted: 17 February 2014
Aims. The main goal of this work is to a have a new neutral hydrogen (H i) supershell candidate catalog to analyze their spatial distribution in the Galaxy and to carry out a statistical study of their main properties.
Methods. This catalog was carried out making use of the Leiden-Argentine-Bonn (LAB) survey. The supershell candidates were identified using a combination of two techniques: a visual inspection plus an automatic searching algorithm. Our automatic algorithm is able to detect both closed and open structures.
Results. A total of 566 supershell candidates were identified. Most of them (347) are located in the second Galactic quadrant, while 219 were found in the third one. About 98% of a subset of 190 structures (used to derive the statistical properties of the supershell candidates) are elliptical with a mean weighted eccentricity of 0.8 ± 0.1, and ~70% have their major axes parallel to the Galactic plane. The weighted mean value of the effective radius of the structures is ~160 pc. Owing to the ability of our automatic algorithm to detect open structures, we have also identified some “galactic chimney” candidates. We find an asymmetry between the second and third Galactic quadrants in the sense that in the second one we detect structures as far as 32 kpc, while for the 3rd one the farthest structure is detected at 17 kpc. The supershell surface density in the solar neighborhood is ~8 kpc-2, and decreases as we move farther away form the Galactic center. We have also compared our catalog with those by other authors.
Key words: ISM: bubbles / ISM: structure / methods: data analysis / techniques: image processing / radio lines: ISM
Full table is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/564/A116
© ESO, 2014
1. Introduction
When viewed in the neutral hydrogen (H i) line emission (λ = 21 cm), the interstellar medium (ISM) reveals a complex structuring that manifests itself by the presence of a plethora of structures such as shells, supershells, filaments, arcs, cavities, worms, and loops. In particular, H i shells and supershells are detected in a given radial velocity range as voids in the H i emission distribution that are surrounded completely, or partially, by walls of enhanced H i emission.
The physical processes usually invoked to explain the formation of H i shells and supershells are the combined action of strong winds from massive stars upon the surrounding ISM, and their ultimate explosion as supernovae. Other alternative mechanisms have also been proposed to explain their creation, such as gamma-ray bursts (Efremov et al. 1998; Loeb & Perna 1998) and the infall of high velocity clouds (Tenorio-Tagle & Bodenheimer 1988).
Several catalogs of shells and supershells have already been constructed with a variety of different techniques such as visual identification (Heiles 1979, 1984; McClure-Griffiths et al. 2002) and automatic identification algorithms (Ehlerová & Palouš 2005; Daigle et al. 2007; Ehlerová & Palouš 2013).
Based on a visual inspection of photographic representations of the H i emission distribution derived from the H i survey of Weaver & Williams (1973), a first catalog of H i shells and supershells was constructed by Heiles (1979), who defines as supershells to those structures requiring at least 3 × 1052 erg for their creation. A total of 63 structures were identified. Later, using the 21 cm database of Heiles & Habing (1974) for | b | > 10°, Hu (1981) discovered 50 new shells. In a subsequent work, Heiles (1984) combined the surveys of Weaver & Williams (1973) and Heiles & Habing (1974) in order to eliminate the boundary problems at | b | = 10°, in this way finding a total of 42 new structures. Afterwards, McClure-Griffiths et al. (2002) report the discovery of 19 new H i shells, using the Southern Galactic Plane Survey (SGPS; McClure-Griffiths et al. 2001).
On the other hand, applying a fully automatic method to the H i Leiden-Dwingeloo survey (Hartmann & Burton 1997), Ehlerová & Palouš (2005) searched for regions having a local minimum in the H i emissivity that were completely encircled by regions of higher emissivity. Later on, the same authors (Ehlerová & Palouš 2013) used the Leiden-Argentine-Bonn (LAB) survey (Kalberla et al. 2005) to conduct an all-sky search for H i shells, employing an automatic procedure that is slightly different from the one described in Ehlerová & Palouš (2005). Using an artificial neural network and the H i database of the Canadian Galactic Plane Survey (CGPS; Taylor et al. 2003), Daigle et al. (2007) identified a large number of small expanding H i shells in the Perseus arm.
Bearing in mind that different identification techniques applied to the same database (see Ehlerová & Palouš 2005, 2013) provide different results and that quite different structures are identified in the same region of the sky when different identification criteria and databases are used (see feature GSH 263+00+47 of McClure-Griffiths et al.2002 and GS 263-02+45 of Arnal & Corti2007), we believe that it is worth making the effort to unveil the presence of these structures (shells and supershells) by using a relatively different approach for their identification.
In particular, in this paper we deal solely with the identification of the so-called H i supershells located in the outer part of the Galaxy by using a novel procedure that combines both visual and automatic algorithms of identification. The constraint of only analyzing the second and third Galactic quadrants stems from the fact that toward this part of the Galaxy the radial velocity-distance relationship only has a single value, a fact that strongly simplifies determination of the physical sizes of the detected structures.
The paper is organized as follows. In Sect. 2 we briefly describe the database used in constructing the catalog of H i supershell candidates, while in Sect. 3 the identification techniques are described in some detail. Section 4 describes the selection effects of our catalog. The statistical properties of the supershell candidates are presented in Sect. 5, and a comparison with previous catalogs is made in Sect. 6.
2. Observations
Neutral hydrogen (H i) data were retrieved from the Leiden-Argentine-Bonn (LAB) survey (Kalberla et al. 2005) to explore the H i emission distribution. This database, well suited to a study of large scale structures, has an angular resolution of 34′, a velocity resolution of 1.3 km s-1, and a channel separation of 1.03 km s-1, and it covers the velocity range from − 400 to + 450km s-1. The entire database has been corrected for stray radiation (Kalberla et al. 2005).
3. catalog of H i supershell candidates
3.1. Selection criteria
In this work a given H i structure will be cataloged as a candidate object to be a supershell, if it simultaneously fulfills the following set of conditions:
-
a) It must have, in a given velocity range, a well defined low brightness temperature region, which is surrounded, partially or completely, by a ridge of higher H i emissivity.
-
b) The H i minimum must be observable in at least five consecutive velocity channels.
-
c) The overall structure (minimum + surrounding ridge) must have a minimum angular size of 2°.
-
d) At the kinematic distance of the H i structure, its linear size must be larger than 200 pc.
Condition b) is set in order to assure the persistence of the structure along a minimum velocity range of ~6 km s-1. With this criterion, on the one hand, we seek to avoid picking up structures that may arise from the turbulent nature of the ISM, and on the other, we keep the chance of detecting slowly expanding structures. Condition c) is related to the angular resolution of the HI survey we are working with, and it implies that the feature is, angularly speaking, fully resolved. Finally, criteria d) is imposed to ensure identification of only large scale features.
3.2. catalog elaboration
To construct a catalog of structures satisfying the above criteria, a four-stage procedure was followed, namely:
-
1.
A visual search of the supershell candidates;
-
2.
A learning phase of the automatic detection algorithm;
-
3.
Running the automatic detection algorithm in a blind way;
-
4.
A new visual inspection of the structures found in the previous step.
In the following sections we describe each step in some detail.
To reach a balance between data-cube size and the computational resources needed to run the algorithm on a reasonable timescale, the individual H i data cubes used in this work were (Δl,Δb) = (50° × 60°) in size. In Galactic latitude the region −50° ≤ b ≤ 50° was covered, while our search covered 80° ≤ l ≤ 290° in Galactic longitude. Every individual H i cube overlaps 10° in Galactic longitude and 20° in Galactic latitude, with the neighboring one.
3.2.1. Visual search
The main goal of this step is to identify by eye the most conspicuous structures likely to be classified as H i supershells. This method, “due to the ability of the human eye to combine disconnected features into a single shape” (Ehlerová & Palouš 2005) is very efficient at unveiling either complete or incomplete large angular size features. To this end, a visual inspection of the H i data cubes covering the Galactic longitude ranges of 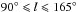 and
and 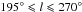 for
for 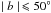 was performed. The region between
was performed. The region between 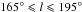 around the Galactic anti-center was not surveyed because along these lines of sight Galactic rotation models provide very unreliable kinematic distances.
around the Galactic anti-center was not surveyed because along these lines of sight Galactic rotation models provide very unreliable kinematic distances.
The visual search was made using the software KARMA1, which is a visualization software package that contains several visualization and analysis tools. In this work we have used the module kvis to visualize the H i data cubes. Since with kvis the position-position images can be seen as movies of the data cube, it allows us to detect the continuity of a structure at different velocity channels.
It is important to mention that the visual search was independently made by three of us (Suad, L.A.; Cichowolski, S.; and Arnal, E.M.). The identifications made by each of us were compared with the others. Only when a given structure was detected by at least two of us was it incorporated in the listing of the visual catalog. In this way, a total of 149 features were listed. Using a classical minimum mean squared error technique (MMSE) an ellipse was fitted to each structure.
3.2.2. Automatic search: “Learning” phase
Since the algorithm developed to carry out an automatic search requires setting up different thresholds to run in an efficient way, a pilot run of this algorithm was made in the same data cubes as are used to construct the visual catalog. By iteratively running the algorithm with starting points set at the centers of the available structures in the initial visual catalog, the different thresholds were tuned in order to guarantee a maximum rate of detection and, at the same time, to maximize the similarity between the detected surrounding walls and their associated ellipses defined in the initial visual catalog.
In the following section, STEP 2, the threshold parameters are precisely defined. It is noted that, a fine tuning of these thresholds allowed us to detect a maximum of approximately 80% of those features listed in the visual catalog.
3.2.3. Automatic search: Blind running phase
The automatic search for H i supershell candidates was carried out in the following steps:
-
STEP 1: to search for local minima pixels in averaged channel maps.
Since we need to find structures observed in at least five velocity channel maps, instead of working on single slices at a given velocity, we average five consecutive channel maps. More specifically, at every velocity channel v0, we compute the average by using slices at velocities v = v0 + nδv with n = −2, −1,0, +1, +2 and δv = 1.031km s-1 (channel separation). In every averaged map we identify those pixels that belong to a local minimum, i.e., a set of pixels whose surrounding pixels have a higher value of brightness temperature.
-
STEP 2: To find surrounding walls.
At each detected local minimum pixel, and for different position angles θ, the algorithm computes the brightness temperature profile Tb(r,θ) along radial lines having their origin at the corresponding minimum pixel (see Fig. 1b). A total of 100 radial lines being separated by
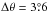 , are analyzed for every local minimum pixel. Along each Tb(r,θ) a maximum (or peak) is present if the following conditions are simultaneously fulfilled:
, are analyzed for every local minimum pixel. Along each Tb(r,θ) a maximum (or peak) is present if the following conditions are simultaneously fulfilled: -
1.
Along each Tb(r,θ), a “big slope point” is found at a point r = rslp, if the slope at that point exceeds a predetermined slope threshold (Tslp) (i.e. if
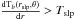 , see Fig. 1b). From the “learning phase”, the threshold slope was set to Tslp = 0.2 K/px.
, see Fig. 1b). From the “learning phase”, the threshold slope was set to Tslp = 0.2 K/px. -
2.
At a certain point r = rM (rM>rslp), Tb(rM,θ) reaches a local maximum. This local maximum is defined in such a way that its brightness temperature Tb(rM,θ) exceeds by at least a threshold δT the brightness temperature of both Tb(rM − 1,θ) and Tb(rM + 1,θ); i.e., Tb(rM,θ) >Tb(rM ± 1,θ) + δT. This criterion is set to avoid misidentifying of the local maximum due to noise fluctuations (see Fig. 1b). The value of δT = 0.4 K was set during the “learning phase”. It should be noted that this value is five times higher than the rms noise of the LAB survey (0.07−0.09 K) (Kalberla et al. 2005).
-
3.
To avoid detecting structures that may be mostly the consequence of the algorithm picking up pixels whose peak temperature is only a few times the local confusion level in brightness temperature (Tconf), which arises from the normal structuring of the ISM, (e.g., fake structures), the maximum temperature Tb(rM,θ) of each brightness temperature radial profile must always exceed the brightness temperature at the local minimum pixel Tb(0,θ) by a certain threshold (e.g., Tb(rM,θ) − Tb(0,θ) >TM(l,b,v)). The value of TM(l,b,v) depends on the position of the pixel within the H i data cube. At low Galactic latitudes TM(l,b,v) should be higher than at higher ones, because the confusion levels are higher in the Galactic plane. Since an analytical form of TM(l,b,v) is not available, during the “learning phase” we have computed the optimal value of TM(l,b,v) corresponding to the location of each feature listed in the initial visual catalog by maximizing the similarity between the detected walls and the associated known structure. Since the structures found in the visual catalog are mostly confined to the central part of the HI data cubes, the obtained values of TM(l,b,v) cannot be used outside the region defined by the structures belonging to the visual catalog. Thus, to estimate TM(l,b,v) in these locations, new data cubes were created having the same coverage in Galactic longitude than before but covering 100° in Galactic latitude (− 50° ≤ b ≤ 50°). Then, for each of these data cubes, six square regions of 2° in size were selected and used to compute Tconf. Since we need to estimate Tconf at the boundaries of the data cubes, the center of each of the six regions are located at Galactic longitudes ll + 1° and lh − 1° and at Galactic latitudes bl + 1°, bh − 1°, and b = 0°, where the subscripts l and h refer to the lowest and highest values (for a given data cube), respectively. Then, for three different velocity channels (two corresponding to the extreme velocities of the data cube and the third one at an intermediate value) within each region, we compute the standard deviation (σ) of the brightness temperature and adopt Tconf = σ and TM(l,b,v) = 3 Tconf. Therefore, the corresponding threshold TM(l,b,v) at any position (l,b,v) is obtained by a 3D interpolation of all available estimates, i.e., those corresponding to structures available in the visual catalog plus those derived for the boundaries of the data cube. For every detected structure, it is desirable that the points defining the H i “wall” are “well behaved”. It means they should follow a more or less ordered pattern (i.e., the distance of a given point of the H i wall to the center of the structure should not drastically differ from the distance of the precedent or posterior). Under this assumption, the algorithm requires that all the points defining the H i wall should be located at a distance such that dn (the distance of the n-point) must verify that
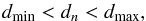 (1)where the parameters dmin and dmax are defined for every object by performing a principal component analysis (PCA) on the complete set of local maxima defining the H i wall of a particular structure. Using PCA the algorithm finds both the direction along which the set of H i maxima points defining the wall achieve their maximum variance, and its orthogonal direction. We denote by σ1 and σ2 the standard deviations along these directions. By fine-tuning the relationship between dmin, dmax, σ1 and σ2 during the “learning phase” of the algorithm, it was found that dmin ~ 0.5σ2 and dmax ~ 2σ1. After each cycle all points that do not fulfill condition 1 are dropped from the original set of points defining the H i wall. The PCA iteration cycle stops when all remaining points fulfill condition 1.
(1)where the parameters dmin and dmax are defined for every object by performing a principal component analysis (PCA) on the complete set of local maxima defining the H i wall of a particular structure. Using PCA the algorithm finds both the direction along which the set of H i maxima points defining the wall achieve their maximum variance, and its orthogonal direction. We denote by σ1 and σ2 the standard deviations along these directions. By fine-tuning the relationship between dmin, dmax, σ1 and σ2 during the “learning phase” of the algorithm, it was found that dmin ~ 0.5σ2 and dmax ~ 2σ1. After each cycle all points that do not fulfill condition 1 are dropped from the original set of points defining the H i wall. The PCA iteration cycle stops when all remaining points fulfill condition 1.
Finally, the algorithm will assume that it has found anH i wall around a brightnesstemperature minimum when at least 50 individualH i peaks have beenidentified, which corresponds to half of the total radial directions,even in the case where they do not belong to consecutive radiallines.

Fig. 1 Example of a shell detected on the average of five contiguous velocity channels a) centered at the systemic velocity (− 57.7km s-1), and one corresponding temperature profile (black straight line in a) panel) where the big slope and the local maximum points are identified b).
-
1.
-
STEP 3: To unify multiple local minima observed at the same velocity interval.
Sometimes, several local minima are found inside a given supershell candidate. To avoid multiple listings of the “same” structure with slightly different central pixels, the algorithm compares the HI “walls” associated with every central pixel and keeps the minimum among all the central pixels. To measure the “discrepancy” between the two sets of points, let us say S1 = {x1,x2,...,xN} and S2 = {y1,y2,...,yM}, where N and M are the number of points in S1 and S2, respectively (N ≤ M); for each point xi in S1, we measure the Euclidean distance to its closer point in S2 denoted by d(xi,S2) and compute the mean discrepancy between S1 and S2 as follows
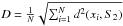 . We decide that the two sets of points are assumed to belong to the same structure if D is smaller than a threshold that was empirically set equal to 0.2. In case of coincidence, only the structure with the minimum central pixel is kept.
. We decide that the two sets of points are assumed to belong to the same structure if D is smaller than a threshold that was empirically set equal to 0.2. In case of coincidence, only the structure with the minimum central pixel is kept. -
STEP 4: Ellipse fit.
In this step the algorithm fits an ellipse to the entire set of points defining the H i walls, by using a classical MMSE technique. Every ellipse is characterized by the following set of parameters: i) the coordinates of the centroid (le,be); ii) the major (a) and minor (b) semi-axes; and iii) the inclination angle (φ) between the Galactic plane and the major axis. This angle is measured counterclockwise from the Galactic plane.
-
STEP 5: Selection of structures according to their sizes.
Finally, based on the value of the major axis derived in the previous step and assuming the Galactic rotation model of Fich et al. (1989), the linear size of the major axis is derived. Only those structures having a major axis larger than 200 pc are retained in our catalog.
Supershell candidates (Excerpt).
3.2.4. Final visual inspection
To obtain the final set of structures, after implementing the automatic search, we made a new visual inspection (again using the package kvis of KARMA) of all the detected structures. Considering that a structure will change its shape as one steps through different velocity channels, the structure will be seen in a (l,b) diagram as a set of concentric rings at different radial velocities, in the ideal case of a symmetric expansion. At the systemic velocity, vo, the ring should attain its maximum dimensions, while the H i emission distribution should look like a cap at extreme velocities. According to this, we expect a change in the shape of the structures and a continuity in the walls of the observed features at different velocity channels. Though this ideal behavior is usually not observed, in this final visual check we discard those features whose behavior strongly departs from the one described above.
As an example, we mention structures whose centers in consecutive channel maps “jump” from one position to another in a random pattern, or structures whose angular diameters vary in an unrealistic physical way. At the end of this last stage of the catalog elaboration, we cataloged a total of 566 supershell candidates, 347 in the second Galactic quadrant and 219 in the third one.
For all these structures, the velocity extent (Δv) are determined by visual inspection. Under the assumption of a symmetric expansion, the expansion velocity (vexp) of a shell is estimated as half of the velocity extent of the shell vexp = Δv/ 2. The systemic velocity (v0) of each structure is determined as the central velocity channel over the velocity extent. The effective radius of the structures are derived as the geometrical mean of the semi-major (a) and semi-minor (b) axes of the fitted ellipse, 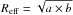 .
.
Table 1, available at the CDS2, contains all the parameters of the detected supershell candidates. The information is given as follows: Column 1: the name of the supershell candidate using the code, GS ll ± bb ± v0, where GS stands for Galactic shell, ll and bb are the Galactic longitude and latitude of the center of the fitted ellipse, respectively, and v0 is the systemic velocity of the structure. Columns 2 and 3: the Galactic longitude and latitude of the center of the fitted ellipse, in degrees. The uncertainty in the values estimated for the centroid of the ellipses is about ± 0.2°. Column 4: the systemic velocity (v0) in units of km s-1. The uncertainty of this velocity is equal to the velocity resolution of the data (± 1.3km s-1). Column 5: the heliocentric distance, in kpc. The mean weight distance error for all the sample is about 21%. Columns 6 and 7: the Galactic longitude and Galactic latitude (in degrees) of the local minimum. Columns 8 and 9: the major and minor semi-axes, in degrees. The uncertainties in the semi-axes are about 10%. Column 10: the inclination angle (φ) (major axis inclination relative to the Galactic plane, this angle is measured counterclockwise form the Galactic plane). See Sect. 5.3.2 for uncertainties in φ. Column 11: the effective radius (Reff) of the structures, in pc. The uncertainties in these values come from the uncertainties in the distances and angular semi-axes, and are around 16%. Column 12: the velocity extension (Δ v), in km s-1, of the structures. The uncertainty is about 2.6km s-1. Column 13: the total number of full quadrants: i.e., each structure has been divided, from the center of the fitted ellipse, into four quadrants. We counted the number of quadrants that present H i emission related to the wall of the structure (full quadrants). See Sect. 5.1.
An excerpt from the table is shown in Table 1.
4. Selection effects
Due to the location of the Sun (our observing place) within the Milky Way, our catalog suffers from distance dependence. Our criteria for identifying candidate features introduce selection effects in the calatog that must be taken into account when attempting to derive their large scale properties.
As a consequence of the selection criterion c) (the structure must have a minimum angular diameter of 2°), there will be structures that, even when having diameters greater than 200 pc, will not be detected by the algorithm if at their corresponding distances the angular diameters are lower than 2°. For instance, a structure with a diameter of 200 pc located at 5.7 kpc from the Sun will be in the limit of detection, with an angular size of 2°. In Fig. 2 the region that suffers for this effect is labeled as “non-detection zone”. As can be inferred, beyond 5.7 kpc from the Sun, the catalog of H i supershell candidates will not be complete.
On the one hand, large linear size features located close to the Sun will have large angular diameters and will be missed by the detection algorithm because they are too big compared to the field size of the data cube where the algorithm is run. In other words, structures with linear sizes larger than 1 kpc that are closer to the Sun than 1.1 kpc will have angular dimensions greater than ~50° and will not be detected by our algorithm. Besides, at 2 kpc away from the Sun, a structure having the minimum required size (200 pc) to be cataloged as a supershell candidate will have a large angular diameter of 5.7°, raising the possibility of having in its interior a lot of small scale structures. As a consequence, our algorithm may fail to identify large angular structures.
 |
Fig. 2 Scheme showing selection effects. The black dashed dotted line shows 2° angular size structures at different distances from the Sun. The full horizontal line represents structures with linear sizes of 200 pc. The gray line at 5.7 kpc from the Sun marks the limit of detection of a 2° structure. The area marked with black dashed lines shows the non-detection region. The area marked with dotted lines shows the detection zone. |
5. General properties of the supershell candidates
As mentioned before, after following all the steps described in Sect. 3, we have detected a total of 347 structures in the second Galactic quadrant (90°<l< 165°) and 219 in the third one (195°<l< 270°). In the following we analyze each quadrant separately.
 |
Fig. 3 Supershell candidates in a Hammer-Aitoff projection, centered on (l,b) = (180°,0°). |
5.1. Supershells morphology
One characteristic that makes our algorithm different from other automatic implementations (e.g., Ehlerová & Palouš 2005, 2013) is that it is able to detect structures that are not completely surrounded by walls of H i emission. To decide whether a supershell candidate is completely “closed” or not (“open”), we divided each supershell candidate into four quadrants centered on the center of the fitted ellipse and determine how many quadrants show H i emission (local maxima). To tag a given quadrant as “full” or “empty”, our algorithm counts how many local maxima points (npts) are present in each quadrant. We named the maximum number of points among the four quadrants as nptsm. Afterwards, for each structure, the quadrant having the highest number of local maxima points is selected. Then, a quadrant is considered “full” if the number of local maxima (npts) in that quadrant is greater than nptsm − 3σ, where 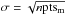 . Otherwise the quadrant will be considered “empty”.
. Otherwise the quadrant will be considered “empty”.
A careful inspection of all the structures (347 in total) found in the second Galactic quadrant reveals that 182 (~52% of the total) are completely closed structures, 120 have one quadrant empty, 32 present two quadrants empty, and 13 have all quadrants empty but one. As for the third Galactic quadrant, 126 (~58% of the total) out of the 219 detected structures are completely closed structures, 62 have one quadrant empty, 24 have two of the quadrants empty, and only 7 have one of the quadrants full.
Open structures may play an important role in the Galaxy because it is believed that these structures, when open towards the Galactic halo, may play a role in injecting material from the Galactic plane into the Galactic halo. These structures, open towards high Galactic latitudes may represent candidates features to be identified as “Galactic chimneys”. To look for these features among all the detected supershell candidates, we selected those having one quadrant “empty” and analyzed whether it is open toward the halo or toward the Galactic plane.
To this end, we have only taken those structures into account that have a galactocentric distance lower than 15 kpc. This restriction is imposed because beyond 15 kpc, the warp of the Galactic plane becomes important and complicates the identification of the structures whose opening is mostly directed away from the Galactic plane defined in the classical way (b = 0°). Structures with two or three “empty” quadrants are not taken into account because they only represent a very small fraction (~13 − 14%) of the overall number of the structures present in the catalog.
A total of 120 structures were found to have one quadrant “empty” and a kinematic galactocentric distance smaller than 15 kpc. Among them about 67% are open towards the Galactic halo, and may be classified as “Galactic chimney” candidates. They are identified in Table 1 with an asterisk after the supershell’s name. As an example see the excerpt of Table 1. On the other hand, we have found that 21% of all detected structures having galactocentric distances lower than 15 kpc are classified as “Galactic chimney” candidates.
5.2. Distribution in the sky
The fitted ellipses of the supershell candidates are plotted in Fig. 3 in a Hammer-Aitoff projection. As expected, most of the structures are located near the Galactic plane. Figure 4 shows all the centroids of the cataloged features in a polar diagram. The Sun is located at position (X, Y) = (0, 0). Clearly enough, within 1.5−2 kpc from the Sun, the number of cataloged structures is much smaller than beyond this distance (see Fig. 4 bottom panel). Very likely this reflects a limitation (or selection effect) of our identification algorithm (see Sect. 4).
Towards the anti-center (l = 180°), the Galactic rotation models predict a very small gradient of the radial velocity with distance. Furthermore, non-circular motions may be comparable to the supershell radial velocities. Since both facts will make the kinematic distances of the supershell candidates quite uncertain, those structures whose centroids fall between 165° ≤ l ≤ 195° are not listed in our catalog. The straight lines having their origin at (X, Y) = (0, 0) mark these boundaries.
Figure 4 also shows that supershell candidates are identified at large distances (~32 kpc) from the Sun in the second Galactic quadrant, while in the third quadrant there are not supershell candidates located beyond 17 kpc from the Sun. This finding agrees with Ehlerová & Palouš (2013). The explanation of this effect is far from clear. This striking difference between both quadrants is unexpected if both quadrants were similar from a geometrical point of view. Certainly, in regards to the H i supershells, a more thorough study of the external part of the Milky Way is needed.
 |
Fig. 4 Distribution of the supershell candidates in a polar diagram. Dots correspond to all the structures detected. Top panel: the 2 kpc ring around the Sun is marked by a continuous black line semi-circumference. The 5.7 kpc and 17 kpc rings are marked by dashed and dashed-dot semi-circumferences, respectively. The ± 15° region around the anti-center is delimited by straight black lines. Bottom panel: zoom of the area delimited by the rectangle in the top panel. |
5.3. Statistics
In the following, to derive the statistical properties of the supershell candidates we only use a subset of the detected structures to minimize the selection effects present in the catalog. We have only considered structures that fulfill the following conditions: i) that are located at distances smaller than 5.7 kpc from the Sun (see Sect. 4); and ii) that are completely closed or have only one quadrant “empty”. A total of 190 structures out of the 566 cataloged meet these criteria, 93 in the second Galactic quadrant and 97 in the third one.
Even though we have mentioned before that most of the structures having distances less than 2 kpc will be missed by our detection algorithm. Bearing in mind that the number of these structures represents only 5% of the cataloged structures having d< 5.7 kpc, we have included them in all our statistical analysis, except those related to the galactocentric distribution analysis (see Sect. 5.3.5).
5.3.1. Size distribution
As mentioned above, kinematic distances (d) and physical sizes of the supershell candidates are determined after using the rotation curve of Fich et al. (1989). In Fig. 5 (upper and lower panels) the Reff distribution is shown for the second and third Galactic quadrants, respectively. The weighted mean value of Reff in the second Galactic quadrant is 158 pc with a dispersion of 47 pc, and is 163 pc with a dispersion of 49 pc for the third one. The lack of structures with effective radius less than 100 pc is a consequence of our selection criteria.
 |
Fig. 5 Distribution of the effective radius of the supershell candidates in the 2nd Galactic quadrant (upper panel) and in the 3rd Galactic quadrant (lower panel). |
5.3.2. Distribution of the position angles (φ)
Figure 6 shows the distribution of the inclination angles φ of the supershell major axes relative to the Galactic plane. The error in the value of φ has a strong dependence on φ and a minor dependence on the major semi-axis a, according to the following relation:
![$$ \sigma_\phi^2 = \frac{1}{(a\, \sin(\phi))^2} \left[\left(\frac{1}{|1-2\,\sin(\phi)^2|} + \cos(\phi)^2 \right)\, \sigma_a^2 + \sigma_{l_0}^2 \right], $$](/articles/aa/full_html/2014/04/aa23147-13/aa23147-13-eq139.png) where l0 is the Galactic longitude of the center of the fitted ellipse and σl0 = 0.2. The error in φ diverges for φ = 0° and for φ = 45°.
where l0 is the Galactic longitude of the center of the fitted ellipse and σl0 = 0.2. The error in φ diverges for φ = 0° and for φ = 45°.
 |
Fig. 6 Relative Galactic distribution of the inclination angles (φ) between the major axes of the H i supershell candidates and the Galactic plane for the 2nd Galactic quadrant (upper panel) and the 3rd Galactic quadrant (lower panel). |
 |
Fig. 7 2D histogram with φ in degrees and the Galactic plane height (z) in pc. The color bar indicates the number of structures in each bin. |
Given that the H i density varies with the Galactic plane height (z) such that the H i density decreases as z increases (Dickey & Lockman 1990, they found a scale height of 403 pc), we would expect that structures expand more rapidly in the direction perpendicular to the Galactic plane than along it. In this context, in case the Galactic density gradient was playing a major role in determining the overall shape of the expanding structures, one would expect the major axis to be mostly perpendicular to the Galactic plane. To analyze this hypothesis, we study the distribution of the angles φ. We consider that the major axis is parallel to the Galactic plane if φ< 45° and otherwise if φ> 45°. Bearing in mind the errors involved in determining φ, and taking a 5σφ confidence level into account, those structures having 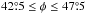 were not considered (these structures are the ones located in the bin centered at 45° in Fig. 6), because in these cases a structure considered parallel could also be perpendicular taking into account the involved errors.
were not considered (these structures are the ones located in the bin centered at 45° in Fig. 6), because in these cases a structure considered parallel could also be perpendicular taking into account the involved errors.
In this way, roughly 70% of the structures have their major axes parallel to the Galactic plane for both quadrants. This result agrees with the one found by Ehlerová & Palouš (2005, 2013) where they state that the majority of the detected structures are elongated in the longitude direction rather than in latitude.
To detect a difference in the orientation of the major axis according to the location of the structures with respect to z, we made a 2D histogram (see Fig. 7). There, it is shown that most of the structures have their major axes oriented parallel to the Galactic plane, independently of the value of z, i.e. structures with the major axis oriented parallel to the Galactic plane are distributed in a wide range of z. From the 2D histogram we can conclude that there is not a significant change in φ when z increases.
It is important to mention that the magnetic fields could play an important role in the evolution of the supershells. Taking magnetic fields and the density stratification in the Galactic disk into account, a 3D numerical magnetohydrodynamical simulation has been done by Tomisaka (1998) where the author concludes that a magnetic field running parallel to the Galactic disk has the effect of preventing the structure from expanding in the direction perpendicular to the field when the magnetic field has a larger scale height than the density. On the other hand, Tomisaka (1998) has developed a model where the magnetic field strength decreases in the halo as the square root of the density, and found that in this case the structure may eventually blow out.
Based on these findings, the dynamical evolution of the supershell candidates seems to be less affected by the H i density gradient present in the direction perpendicular to the Galactic plane than by the Galactic magnetic fields running parallel to the Galactic disk.
5.3.3. Eccentricity of the supershell candidates
The eccentricity of the structures was calculated from
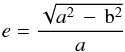 where a and b are the major and minor semi-axes, respectively, of the fitted ellipse. Figure 8 shows the distributions of the eccentricities for the second and third Galactic quadrants. The error associated with the eccentricity varies for different values of e. A mean error bar corresponding to different values of e is plotted in Fig. 8. It can be seen that about 98% of the structures are elliptical with mean weighted eccentricities of 0.8 ± 0.1 for both quadrants.
where a and b are the major and minor semi-axes, respectively, of the fitted ellipse. Figure 8 shows the distributions of the eccentricities for the second and third Galactic quadrants. The error associated with the eccentricity varies for different values of e. A mean error bar corresponding to different values of e is plotted in Fig. 8. It can be seen that about 98% of the structures are elliptical with mean weighted eccentricities of 0.8 ± 0.1 for both quadrants.
 |
Fig. 8 Distribution of the eccentricities of the supershell candidates in the 2nd Galactic quadrant (upper panel) and in the 3rd Galactic quadrant (lower panel). Error bars are plotted for each bin, and a parametric form of the error shows that it is about σe = 0.6 for e = 0.1 and σe = 0.02 for e = 0.9. |
5.3.4. Distribution of the structures relative to z
The distribution of the centroids of the structures with respect to z is shown in Fig. 9. Taking the location of the centroids into account, we calculated that 42% and 39% of the structures from the second and third Galactic quadrants, respectively, are confined to z ≤ 500 pc. This result agrees, within the uncertainties, with the result obtained by Ehlerová & Palouš (2005), in the sense that these authors found that half of all their shells lie in a 1-kpc thick layer.
 |
Fig. 9 Distribution of the centroids of the structures relative to z in the 2nd Galactic quadrant (upper panel) and in the 3rd Galactic quadrant (lower panel). |
Parameters used to estimate the density of supershell candidates in the areas Aa + Aac.
5.3.5. Galactocentric distribution
To attempt to derive the distribution of the supershell candidates with respect to the galactocentric distance, the number of structures identified in our catalog has to be corrected for at least two limitations, namely, a) the ±15° zone of avoidance around l = 180°; and b) the failure of our algorithm to detect structures closer than 2 kpc to the Sun.
Bearing the above set of restrictions in mind, the number of candidate features observed to be H i supershells must be multiplied by four different “incompleteness factors” before attempting to derive their large scale properties (on Galactic scale). To derive the different correction factors, we divide the Galaxy into a set of concentric rings centered on the Galactic center. Each ring will have an inner radius of Ri kpc and an outer radius Re, where Re = Ri + 1 kpc. Since we are looking for structures in the outer part of the Galaxy, the first ring we have to deal with has Ri = 8.5 kpc and Re = 9.5 kpc. For a given ring, we define the area between 165° ≤ l ≤ 195° as Aac (see Fig. 10). Furthermore, we let the area for those rings having Ri ≥ 10.5 kpc, outside 165° ≤ l ≤ 195° but within the 5.7 kpc solar semi-circle, be referred to as Aa. For those rings having Ri equal to 8.5 kpc and 9.5 kpc, the area comprised between the heliocentric semi-circles of radius 2 and 5.7 kpc and the straight line joining l = 90° and l = 270° will be denoted A2 (see again Fig. 10), and the area delimited by the zone of “avoidance” around l = 180° and the heliocentric semi-circle of radius 2 kpc will be referred to as A3. The values of the mentioned areas are listed in Table 2.
Considering the above definitions, and assuming that the supershell candidates density (number of supershell candidates per unit area) is constant within a given galactocentric ring, we defined the correction factors Fa as those to be applied in order to attempt to correct the observed structures for those that should fall within ± 15° zone of avoidance around l = 180°. We also defined the correction factors Fb as those to be applied in order to attempt to correct for those features that should be located between the straight lines defining the boundaries of the mentioned zone of avoidance and the semicircle with radius of 2 kpc centered on the solar location. The correction factors are the following: 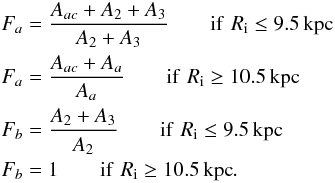 To derive the correct number of H i supershell candidates in the Galaxy for a given galactocentric ring (Nc, given in the ninth column of Table 2), the observed number of such features (N0, given in the seventh column of Table 2) must therefore be multiplied by a correction factor,
To derive the correct number of H i supershell candidates in the Galaxy for a given galactocentric ring (Nc, given in the ninth column of Table 2), the observed number of such features (N0, given in the seventh column of Table 2) must therefore be multiplied by a correction factor, 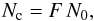 where F = FaFb.
where F = FaFb.
Finally, the surface density of H i supershell candidates for a given galactocentric ring is defined as the ratio between the corrected number of supershell candidates (Nc) and the area of the ring in the outer part of the Galaxy. The corresponding values are listed in Table 2. Figure 11 shows the H i supershell candidates surface density as a function of the galactocentric distance.
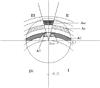 |
Fig. 10 Scheme of some of the areas Aa (between rings of radius Ri = 11.5 kpc and Re = 12.5 kpc, in diagonal black lines), Aac (between rings of radius Ri = 12.5 kpc and Re = 13.5 kpc, in gridded), A2 (between rings of radius Ri = 9.5 kpc and Re = 10.5 kpc, in gray), and A3 (between rings of radius Ri = 9.5 and Re = 10.5 kpc, in straight black lines). G.C. marks the position of the Galactic center. |
 |
Fig. 11 Surface supershell density as a function of galactocentric distance. |
Following Ehlerová & Palouš (2013), but assuming that the supershell surface density, Σ(R), follows a Gaussian distribution with galactocentric distance R given by ![\begin{equation} \label{sigma} \Sigma (R) = \Sigma_0 \times {\rm e}^{-[(R-R_0)/\sigma_{\rm GS}]^2} \qquad [\mathrm {kpc^{-2}}], \end{equation}](/articles/aa/full_html/2014/04/aa23147-13/aa23147-13-eq226.png) (2)where Σ0 is the supershell density in the solar neighborhood, σGS is the galactocentric scale length, and R and R0 are the supershell’s and Sun’s galactocentric distances, respectively. Fitting Eq. (2) to the surface density given in Table 2 (see last column), we derive Σ0 = 7.4 ± 0.5 kpc-2 and σGS = 4.4 ± 0.3 kpc. The galactocentric radial scale length is comparable to the one found in previous works (see Ehlerová & Palouš 2005, and references therein), but the estimated surface density of Hi supershells in the solar neighborhood is a factor ~2 greater than previous estimates (Ehlerová & Palouš 2013). This higher surface density may well be explained by the ability of our procedure to also identify structures that are not completely closed. In this context, we would like to point out that the total number of supershells that are either completely closed or have one quadrant “empty” (see Sect. 5.1) is almost a factor of 2 larger than the total number of closed features.
(2)where Σ0 is the supershell density in the solar neighborhood, σGS is the galactocentric scale length, and R and R0 are the supershell’s and Sun’s galactocentric distances, respectively. Fitting Eq. (2) to the surface density given in Table 2 (see last column), we derive Σ0 = 7.4 ± 0.5 kpc-2 and σGS = 4.4 ± 0.3 kpc. The galactocentric radial scale length is comparable to the one found in previous works (see Ehlerová & Palouš 2005, and references therein), but the estimated surface density of Hi supershells in the solar neighborhood is a factor ~2 greater than previous estimates (Ehlerová & Palouš 2013). This higher surface density may well be explained by the ability of our procedure to also identify structures that are not completely closed. In this context, we would like to point out that the total number of supershells that are either completely closed or have one quadrant “empty” (see Sect. 5.1) is almost a factor of 2 larger than the total number of closed features.
 |
Fig. 12 Effective radius versus expansion velocity. Triangles and circles show the supershell candidates in the second and third Galactic quadrants, respectively. Black dashed straight lines show the curves of constant expansion time. Black solid lines correspond to constant values of Lw/n (Lw is the wind mechanical luminosity and n is the interstellar medium density). Black dashed and solid lines were computed using the model of Weaver et al. (1977). |
5.3.6. Filling factors
The filling factors of the supershell candidates are defined as the area (f2d) or volume (f3d) occupied by the supershells in a given area or volume, respectively. The area considered was calculated in a semicircle of 5.7 kpc from the Sun, except for the area of ±15° around l = 180°, and the volume was calculated considering the same area and a Galactic plane height of ±0.5 kpc.
To estimate f2d filling factor, the structures should be projected in the mentioned area. The estimated filling factors in the outer part of the Galaxy are f2d = 0.5 ± 0.1 and 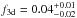 . These values, within the errors, agree with those derived by Ehlerová & Palouš (2005), f2d = 0.4 and f3d = 0.05. Since the filling factors are dominated by larger shells, and bearing in mind that our method is not able to detect them when located close to the Sun (see Sect. 4), the quoted filling factors may be regarded as lower limits.
. These values, within the errors, agree with those derived by Ehlerová & Palouš (2005), f2d = 0.4 and f3d = 0.05. Since the filling factors are dominated by larger shells, and bearing in mind that our method is not able to detect them when located close to the Sun (see Sect. 4), the quoted filling factors may be regarded as lower limits.
5.3.7. Effective radius versus expansion velocity
The relationship between the effective radius of the supershell candidates and their expansion velocities is shown in Fig. 12. We recall that the expansion velocity of the supershell candidates is calculated as 0.5 Δv, where Δv is the velocity range where the structure is detected, and the effective radius is defined as 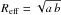 , where a and b are the major and minor semi-axes, respectively, of the fitted ellipse. Bearing in mind that one of the possible origins for these structures may be the cumulative action of the stellar winds for a high number of massive stars, in Fig. 12 we have also plotted lines of constant dynamical age and constant ratio Lw/n, where Lw is the wind mechanical luminosity and n the ISM density. Following the analytical solution of Weaver et al. (1977), the dynamical age is derived from
, where a and b are the major and minor semi-axes, respectively, of the fitted ellipse. Bearing in mind that one of the possible origins for these structures may be the cumulative action of the stellar winds for a high number of massive stars, in Fig. 12 we have also plotted lines of constant dynamical age and constant ratio Lw/n, where Lw is the wind mechanical luminosity and n the ISM density. Following the analytical solution of Weaver et al. (1977), the dynamical age is derived from
![$$ t_{\rm dyn}= 0.55 \, \frac{R_{\rm eff}}{v_{\rm exp}} \qquad [\mathrm{Myr}] $$](/articles/aa/full_html/2014/04/aa23147-13/aa23147-13-eq243.png) where Reff is expressed in units of pc, and vexp is given in km s-1. The constant 0.55 represents a mean value for the energy and momentum conserving models. To derive a mean dynamical age for the supershells, we need to know the dominant mechanism at work for their creation. Since this process (or processes) have not been pinned down yet, under the assumption that stellar winds and supernova explosions are the main formation agent, we use a mean value of the constant just for illustrative purposes.
where Reff is expressed in units of pc, and vexp is given in km s-1. The constant 0.55 represents a mean value for the energy and momentum conserving models. To derive a mean dynamical age for the supershells, we need to know the dominant mechanism at work for their creation. Since this process (or processes) have not been pinned down yet, under the assumption that stellar winds and supernova explosions are the main formation agent, we use a mean value of the constant just for illustrative purposes.
In Fig. 12 lines of constant dynamical age (in units of 106 yr) and lines for constant Lw/n (in units of 1036 erg/s cm-3) are shown. Were this mechanism at work for the genesis of most of the structures listed in our catalog, it would imply that most of the structures have dynamical ages between (5 − 50) × 106 yr, with only three structures younger than 5 × 106 yr. This result agrees with the findings of Ehlerová & Palouš (2005, 2013). On the other hand, most of the structures are between 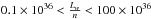 erg/s cm-3. Under the assumption of a stellar origin, such structures cannot be created by the action of only one star.
erg/s cm-3. Under the assumption of a stellar origin, such structures cannot be created by the action of only one star.
It is important to mention that the model of Weaver et al. (1977) does not consider the supernova explosions (SNe), which are the dominant energy source at later evolutionary stages. For illustrative purposes, following McCray & Kafatos (1987) and assuming a density of n = 1 cm-3 and an age t = 5 × 106 yr to create a structure having Reff = 150 pc, roughly 70 OB stars with masses ≳7 M⊙ would be needed, approximately seven of which should have experienced a supernova explosion.
6. Comparison with other catalogs
In this section we compare our catalog with the catalogs of Heiles (1979, 1984), McClure-Griffiths et al. (2002), Ehlerová & Palouš (2005 and 2013), because they used similar databases with comparable angular resolution to the one used in this work.
It is worth mentioning that only the catalogs of Heiles (1979, 1984) deal with H i supershells. The other catalogs may contain a mixture of structures having small and moderate lineal dimensions (usually called “shells”), and those having large sizes or requiring a large amount of energy for their creation. The latter are usually termed “supershells”.
To carry out the comparison with the above catalogs, we only considered those structures fulfilling our selection criteria. With the aim of identifying the structures that meet our selection criterion d), we recalculated the distances and the linear sizes of those structures whose distances were obtained with a different Galactic rotation model than the one used in this paper.
Structures in common with other catalogs.
Structures cataloged by Heiles (1979, 1984) that were detected by our algorithm.
Structures of the McClure-Griffiths et al. (2002) catalog detected by our algorithm.
Structures of the Ehlerová & Palouš (2005) catalog detected by our algorithm.
Structures of Ehlerová & Palouš (2013) catalog detected by our algorithm.
We have defined that a simultaneous detection exists between structures belonging to our catalog and the ones of other catalogs when the following conditions are simultaneously met:
-
1.
The angular difference of their central coordinates is lower than the 50% of the effective radius of the supershell candidate cataloged in this work.
-
2.
The difference between their systemic velocities is lower than 8 km s-1.
A concise summary of the comparison among our catalog and those mentioned above is given in Table 3. There, the first column identifies the catalog we are comparing with, the second gives the total number (N0) of structures listed in the catalog, the third one provides the number (N1) of objects of the catalog cited in the first column that meet our selection criteria and are located within the Galactic longitude range analyzed by us. The fourth column gives the number (N2) of structures common to both surveys (the one listed in the first column and ours). The fifth column gives the percentage (%) of the common detected structures between the different catalogs and ours. Finally, the last column provides the table number listing the structures common to both surveys. In Tables 4−7, the first column always gives the name of the H i supershell candidate as quoted in our catalog. The second and third columns depict the angular extent of the feature in Galactic longitude and Galactic latitude, and the extent of the velocity range along which the feature is seen, in a format like (Δl/ 2 × Δb/ 2 × Δv). When performing the comparison with the catalog of Ehlerová & Palouš (2005), we have only considered those features classified by them as having the maximum confidence level (index 1 in their nomenclature).
Undetected structures in our catalog.
After carrying out the comparisons, we found that the lack of detection in our catalog of a given feature listed in other catalog may be due to a series of facts that can be summarized as follows:
-
Case A: the structure does not have a clearly definedH i centralminimum. In this case all non-detected structuresshow scatter HI emission peaks towards theircentral areas. For this reason our algorithm may detect featuressmaller than 2°, or it may detect HI maxima that though at first “glance” look like they belong to an HI wall, in the end they are too dispersed in position along the radial lines, and do not follow the expected pattern for a shell-like feature.
-
Case B: the wall of the detected structure has a low brightness temperature along most of its perimeter. In this case, the H i maxima defining the supershell wall have a peak brightness temperature lower than the Trms(l, b, v) threshold set by our algorithm.
-
Case C: the structures being compared have a good positional coincidence, but the difference in their systematic radial velocities is greater than 8 km s-1.
-
Case D: the structures being compared have a good positional correspondence, but the angular diameter of the structure detected by our algorithm is smaller than 2°.
-
Case E: the structure is detected by our algorithm, but it is discarded in the final visual revision step.
7. Conclusions
A new catalog of H i supershell candidates has been constructed using a combination of an automatic detection algorithm plus a visual one. It is known that pure visual identification methods are difficult and very time consuming mainly because the dynamic range has to be adjusted quite often to make structures visible. However, the eye is an incredibly powerful instrument, especially when images are irregular, since it is able to combine disconnected patterns. Our algorithm was trained on an initial visual catalog and then applied to the whole dataset. At the end of this process, all the detected structures were again carefully inspected by eye to do the final selection. In other words, in our method, we have combined the power of visual inspection, together with the power of a computer-based algorithm working in a supervised (semi-automatic) mode to optimize the time required to analyze a huge amount of data. A total of 566 candidate structures has been detected, 347 in the second Galactic quadrant and 219 in the third one.
From the distribution of the detected structures in the sky, it can be seen that for the second Galactic quadrant, we have detected structures with distances up to 32 kpc form the Sun, while for the third quadrant all the structures have distances less than 17 kpc from the Sun. The explanation of this effect is far from clear. It shows that the outer part of the Galaxy deserves a thorough study.
Owing to our selection criteria, the catalog suffers from selection effects. Bearing this in mind only features closer to the Sun than 5.7 kpc were used to derive their statistical properties.
The estimated mean weighted effective radius is about 160 pc for both Galactic quadrants. The derived eccentricities indicate that about 98% of the supershells are elliptical. The mean weighted eccentricity is 0.8 ± 0.1 for both Galactic quadrants.
An inspection of the orientation angle values (e.g., the angle between the Galactic plane and the feature’s major semi-axis) shows that most of the supershell candidates are elongated parallel to the Galactic plane, in agreement with the conclusions of other researchers. Based on this finding, it is believed that the Galactic density gradient plays a minor, if any, role in the time evolution of these structures. On the other hand, the magnetic field running parallel to the Galactic disk could be the responsible for the observed effect. Otherwise, the major axes of the structures should be predominantly perpendicular to the Galactic plane.
The distribution of the centroid of the structures relative to the Galactic plane shows that roughly ~40% of the supershells are confined to z ≤ 500 pc. After applying correction factors owing to the incompleteness of our sample, we derived the surface density of H i supershells. Though it decreases as the galactocentric distance increases, in close agreement with the findings of other researchers, the actual surface density in the solar neighborhood is almost a factor of 2 higher, 7.4 kpc-2, than the one derived before by Ehlerová & Palouš (2013). This could be a direct consequence of the “ability” of our method to identify incomplete features. In line with this, we would like to point out that roughly only half of the supershell candidates are found to be completely closed. The decrease in the surface density with galactocentric distance is well fit by a Gaussian function with a radial scale length of 4.4 ± 0.3 kpc. The surface (f2D) and volume (f3D) filling factors are f2D = 0.5 ± 0.1 and 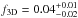 . As mentioned above, because our algorithm is able to detect incomplete structures, we have, as a byproduct, a catalog of “Galactic chimney” candidates, which contains 80 structures.
. As mentioned above, because our algorithm is able to detect incomplete structures, we have, as a byproduct, a catalog of “Galactic chimney” candidates, which contains 80 structures.
A clear relationship between the effective radius of the structures and their expansion velocities is not detected in our catalog. Under the assumption that their genesis is mostly consequence of the action of massive stars (stellar winds and supernova explosions), the dynamic age of the structures are between 5−50 Myr and most of the structures fall between values of Lw/n of (0.1−100) ×1036 erg/s cm-3.
A comparison with the structures listed in our catalog with those given in other shell/supershell catalogs, shows that we identify, on average, 57% of the structures listed elsewhere. The lowest correspondence is with the catalog of Heiles (1979) (~36%), and the highest is with McClure-Griffiths et al. (2002) (~75%).
Centre de Données astronomiques de Strasbourg. http://cdsweb.u-strasbg.fr/
Acknowledgments
This work was partially supported by the grants PIP01299/2008 and 11/G091 of the Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET) of Argentina, and Universidad Nacional de La Plata (UNLP), respectively. We acknowledge Dr. Ariel Chernomoretz for having produced Fig. 3. We would like to thank an anonymous referee for constructive and useful comments that helped us to considerably improve the quality of the original paper.
References
- Arnal, E. M., & Corti, M. 2007, A&A, 476, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daigle, A., Joncas, G., & Parizeau, M. 2007, ApJ, 661, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Efremov, Y. N., Elmegreen, B. G., & Hodge, P. W. 1998, ApJ, 501, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Ehlerová, S., & Palouš, J. 2005, A&A, 437, 101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ehlerová, S., & Palouš, J. 2013, A&A, 550, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fich, M., Blitz, L., & Stark, A. A. 1989, ApJ, 342, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, D., & Burton, W. B. 1997, Atlas of Galactic Neutral Hydrogen (Cambridge: Cambridge University Press) [Google Scholar]
- Heiles, C. 1979, ApJ, 229, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C. 1984, ApJS, 55, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C., & Habing, H. J. 1974, A&AS, 14, 1 [NASA ADS] [Google Scholar]
- Hu, E. M. 1981, ApJ, 248, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loeb, A., & Perna, R. 1998, ApJ, 503, L35 [NASA ADS] [CrossRef] [Google Scholar]
- McClure-Griffiths, N. M., Green, A. J., Dickey, J. M., et al. 2001, ApJ, 551, 394 [NASA ADS] [CrossRef] [Google Scholar]
- McClure-Griffiths, N. M., Dickey, J. M., Gaensler, B. M., & Green, A. J. 2002, ApJ, 578, 176 [NASA ADS] [CrossRef] [Google Scholar]
- McCray, R., & Kafatos, M. 1987, ApJ, 317, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. R., Gibson, S. J., Peracaula, M., et al. 2003, AJ, 125, 3145 [NASA ADS] [CrossRef] [Google Scholar]
- Tenorio-Tagle, G., & Bodenheimer, P. 1988, ARA&A, 26, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Tomisaka, K. 1998, MNRAS, 298, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, H., & Williams, D. R. W. 1973, A&AS, 8, 1 [NASA ADS] [Google Scholar]
- Weaver, R., McCray, R., Castor, J., Shapiro, P., & Moore, R. 1977, ApJ, 218, 377 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Parameters used to estimate the density of supershell candidates in the areas Aa + Aac.
Structures of the McClure-Griffiths et al. (2002) catalog detected by our algorithm.
All Figures
 |
Fig. 1 Example of a shell detected on the average of five contiguous velocity channels a) centered at the systemic velocity (− 57.7km s-1), and one corresponding temperature profile (black straight line in a) panel) where the big slope and the local maximum points are identified b). |
| In the text | |
 |
Fig. 2 Scheme showing selection effects. The black dashed dotted line shows 2° angular size structures at different distances from the Sun. The full horizontal line represents structures with linear sizes of 200 pc. The gray line at 5.7 kpc from the Sun marks the limit of detection of a 2° structure. The area marked with black dashed lines shows the non-detection region. The area marked with dotted lines shows the detection zone. |
| In the text | |
 |
Fig. 3 Supershell candidates in a Hammer-Aitoff projection, centered on (l,b) = (180°,0°). |
| In the text | |
 |
Fig. 4 Distribution of the supershell candidates in a polar diagram. Dots correspond to all the structures detected. Top panel: the 2 kpc ring around the Sun is marked by a continuous black line semi-circumference. The 5.7 kpc and 17 kpc rings are marked by dashed and dashed-dot semi-circumferences, respectively. The ± 15° region around the anti-center is delimited by straight black lines. Bottom panel: zoom of the area delimited by the rectangle in the top panel. |
| In the text | |
 |
Fig. 5 Distribution of the effective radius of the supershell candidates in the 2nd Galactic quadrant (upper panel) and in the 3rd Galactic quadrant (lower panel). |
| In the text | |
 |
Fig. 6 Relative Galactic distribution of the inclination angles (φ) between the major axes of the H i supershell candidates and the Galactic plane for the 2nd Galactic quadrant (upper panel) and the 3rd Galactic quadrant (lower panel). |
| In the text | |
 |
Fig. 7 2D histogram with φ in degrees and the Galactic plane height (z) in pc. The color bar indicates the number of structures in each bin. |
| In the text | |
 |
Fig. 8 Distribution of the eccentricities of the supershell candidates in the 2nd Galactic quadrant (upper panel) and in the 3rd Galactic quadrant (lower panel). Error bars are plotted for each bin, and a parametric form of the error shows that it is about σe = 0.6 for e = 0.1 and σe = 0.02 for e = 0.9. |
| In the text | |
 |
Fig. 9 Distribution of the centroids of the structures relative to z in the 2nd Galactic quadrant (upper panel) and in the 3rd Galactic quadrant (lower panel). |
| In the text | |
 |
Fig. 10 Scheme of some of the areas Aa (between rings of radius Ri = 11.5 kpc and Re = 12.5 kpc, in diagonal black lines), Aac (between rings of radius Ri = 12.5 kpc and Re = 13.5 kpc, in gridded), A2 (between rings of radius Ri = 9.5 kpc and Re = 10.5 kpc, in gray), and A3 (between rings of radius Ri = 9.5 and Re = 10.5 kpc, in straight black lines). G.C. marks the position of the Galactic center. |
| In the text | |
 |
Fig. 11 Surface supershell density as a function of galactocentric distance. |
| In the text | |
 |
Fig. 12 Effective radius versus expansion velocity. Triangles and circles show the supershell candidates in the second and third Galactic quadrants, respectively. Black dashed straight lines show the curves of constant expansion time. Black solid lines correspond to constant values of Lw/n (Lw is the wind mechanical luminosity and n is the interstellar medium density). Black dashed and solid lines were computed using the model of Weaver et al. (1977). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


