| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 5 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322723 | |
| Published online | 15 April 2014 | |
Dust temperature maps of the Galactic plane: The Herschel spectral energy distribution fitting with Cloudy predictions⋆,⋆⋆
1
National Astronomical Observatories,
20A Datun Road, Chaoyang District,
100012
Beijing,
PR China
e-mail:
mhuang@nao.cas.cn
2
University of Chinese Academy of Sciences,
100049
Beijing, PR
China
Received:
21
September
2013
Accepted:
11
February
2014
Context. Dust grains absorb the interstellar far ultra-violet and visible photons and re-emit them in far-infrared (FIR) wavebands. The dust FIR continuum can be predicted by a grid of models using various values of the interstellar radiation field.
Aims. We analyze the dust continuum emission in two Hi-GAL science-demonstration phase (SDP) fields using both the radiative transfer code, Cloudy, and the DustEM dust model, to explore the effect of radiative transfer on dust temperature. The 500 μm sub-millimeter excess emission and the very small grain (VSG) contribution to the 70 μm intensity are investigated by spectral energy distribution (SED) fitting using the Cloudy model.
Methods. By comparing the observation with the model prediction, we derive dust temperature maps of the two SDP fields by fitting the dust SED with 4-band data (SPIRE bands plus PACS 160 μm) using both Cloudy and DustEM models. Considering radiative transfer and grain physics simultaneously, we investigate the existence of a 500 μm excess and estimate the VSG contribution to the 70 μm intensity by fitting the dust SED with 3-band data (160, 250, and 350 μm) and 5-band data (SPIRE and PACS bands), respectively.
Results. We confirm that the field with star formation activities have a higher temperature (18.7 ± 0.9 K) than the quiescent region (15.2 ± 0.6 K). We find that the radiative transfer affects the FIR SED of the SDP fields and results in a higher temperature distribution than the dust-only model fit. There is no significant detection of a 500 μm excess in the two SDP fields. The relative contribution from the VSGs to the 70 μm intensity can be up to 50%.
Key words: ISM: general / dust, extinction / infrared: ISM / methods: data analysis
Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.
Reduced Herschel maps (FITS) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/564/A111
© ESO, 2014
1. Introduction
Interstellar dust particles are size distributed. Mathis et al. (1977) developed a power-law grain-size distribution on the basis of the observed interstellar extinction from infrared to ultraviolet wavelengths: n(a) ∝ a-3.5, where n(a) is the number density of grains with radius <a (0.005 μm <a< 0.25μm). The emission from dust grains with different sizes dominates far-infrared (FIR) emission in different wavelength ranges. Small grains (≲0.005μm) radiate at λ ≲ 50μm by cooling after they are heated by single starlight photons (Draine 2003). Big grains (BGs; ≳0.01μm) are at thermal equilibrium, emitting FIR continuum at λ ≳ 50μm.
To derive the equilibrium temperature of BGs in the interstellar radiation field (ISRF), there have been mainly two methods to analyze FIR spectral energy distributions (SED) of dust grains. One is fitting the SED with a modified blackbody (i.e., gray body; e.g., Paradis et al. 2010). The other is fitting the SED with FIR continuum emission calculated by dust models, such as DustEM (Compiègne et al. 2010).
In the gray body method, the temperature of big grains is approximated by
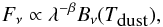 (1)where
Fν is the observed flux,
Bν is the blackbody
emission, Tdust is dust temperature, and
β is the
emissivity spectral index that modifies the blackbody emission. Boulanger et al. (1996) found that β = 2 for the solar
neighborhood derived from diffuse FIR emission, which is measured by Diffuse InfraRed
Background Experiment (DIRBE) and Far InfraRed Absolute Spectrophotometer (FIRAS) at high
Galactic latitudes, while Paradis et al. (2010)
showed variations of the spectral emissivity spectral index in the range 1.8 ~ 2.6 for the Galactic plane. This method
assumes that the dust abundance does not vary and dust grains are single size grains.
(1)where
Fν is the observed flux,
Bν is the blackbody
emission, Tdust is dust temperature, and
β is the
emissivity spectral index that modifies the blackbody emission. Boulanger et al. (1996) found that β = 2 for the solar
neighborhood derived from diffuse FIR emission, which is measured by Diffuse InfraRed
Background Experiment (DIRBE) and Far InfraRed Absolute Spectrophotometer (FIRAS) at high
Galactic latitudes, while Paradis et al. (2010)
showed variations of the spectral emissivity spectral index in the range 1.8 ~ 2.6 for the Galactic plane. This method
assumes that the dust abundance does not vary and dust grains are single size grains.
In the second method, DustEM is used to predict the emission of dust grains with specified grain types and grain size distributions. This method is more physical than using a gray body fit, since it considers the grain size distribution. Bernard et al. (2010) derived dust temperature maps of the Galactic plane using the DustEM code as a modeling tool. The DustEM code does not include any radiative transfer calculation. For dust and gas near hot OB stars, it is more physical to consider both the gas and grain absorption of radiation. To do that, calculation of full radiative transfer is needed.
The Cloudy code (Ferland et al. 2013) includes grain models into self-consistent radiative transfer calculation, which produces the continuum and line emission of gas and dust in equilibrium condition. In this paper, we compare the predicted dust emission of Cloudy models for various values of ISRF with Hi-GAL (Molinari et al. 2010) science-demonstration phase (SDP) data to derive dust temperature maps of SDP fields. The SDP fields are two 2° × 2° images centered at l = 30°, b = 0°, and l = 59°, b = 0°.
We introduce the observation data and analysis method in Sect. 2. Results of 4-band (160, 250, 350, and 500 μm) fits and the comparison between Cloudy and DustEM results are presented in Sect. 3. In Sect. 4, we present the results of 3-band (160, 250, and 350 μm) fits for Cloudy models and the calculation of the 500 μm excess. The contribution from very small grains to the 70 μm intensity is estimated in Sect. 5. We summarize in Sect. 6.
2. The observation and analysis method
The Herschel (Pilbratt et al. 2010) Hi-GAL images provide data with extraordinary spatial, wavelength, and dynamic range coverage for studying the FIR emission of dust grains in the Galactic plane. The Hi-GAL SDP fields are products of the Hi-GAL program, which are observed with PACS (Poglitsch et al. 2010) 70 μm and 160 μm channels and SPIRE (Griffin et al. 2010) 250, 350, and 500 μm channels on board Herschel. The Hi-GAL data processing and map making are described in Molinari et al. (2010). Since the GLS map-making technique is known to introduce artifacts in the maps, namely crosses and stripes in correspondence of the brightest sources, a weighted post-processing of the GLS maps (WGLS, Piazzo et al. 2012) has been applied to finally obtain images in which artifacts are removed or heavily attenuated. The SDP images used in this article are the latest version released to the Hi-GAL consortium. The data have been absolutely calibrated. For more information of the absolute calibration of the Hi-GAL pipeline, we refer the reader to Elia et al. (2013).
The very small grains (VSGs, radius <0.005 μm) are stochastically heated. The contribution from the VSGs to the PACS 70 μm channel can be up to ~50% (Compiègne et al. 2010). To focus on equilibrium temperature of BGs, we exclude the 70 μm emission in our SED fitting to derive the temperature maps. The adopted absolute calibration uncertainty is 20% for PACS bands (Bernard et al. 2010) and 15% for SPIRE bands (Paradis et al. 2010). We exclude the higher latitude areas (| b | > 0.9°), where the data could be less reliable. Maps of all five channels are smoothed to the same resolution as SPIRE 500 μm channel with the convolution kernels given by Karl Gordon1.
We adopt the build-in ISM dust grains and ISM gas abundance of Cloudy. This grain set has two components, graphite and silicate. The size distribution of ISM dust grains is given by Mathis et al. (1977). This grain set generally reproduces the observed overall extinction properties for RV = 3.1, or the average Milky Way extinction (Fitzpatrick 2004). The size of adopted ISM grains ranges from 0.005 μm to 0.25 μm with a dust-to-gas mass ratio, D/G = 6.362 × 10-3. PAHs are included in our calculation with a power-law size distribution, as described in Abel et al. (2008). The geometry is plane-parallel.
With input parameters specified above, we use Cloudy to pre-calculate the dust FIR SED for
the gas column density, N(H) =
1020 H cm-2, for various values of ISRF. The SED of ISRF is
described in Black (1987). The scaling factor
U in Cloudy
scales the intensity of ISRF. We have U = 1.04 G0 in Habing
field unit (1.6 ×
10-3 erg cm-2 s-1; Habing 1968). In
the calculations, U is set to range from 10-2 to 102 with 0.02 dex steps. The gas
density n is
fixed at 10 cm-3. We
test the effect of gas density by comparing the predicted FIR SED for varying gas density,
which ranges from 1 cm-3 to 103 cm-3 with 1 dex steps, when the logarithmic value of
U is set to
range from –2 to 2 with 1 dex steps. For a certain G0, tests show
that the difference between the resulted SED of the FIR continuum at n = 10 cm-3 and at other value of gas
density is less than 0.2% when
N(H) is fixed
to 1020 H
cm-2. Thus, we
ignore the effects of gas density. For every map pixel, we compare the observed fluxes with
model predictions by computing a chi-square statistic using equation, 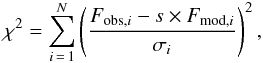 (2)where
Fobs,i is the observed
flux of waveband i, Fmod,i is the model
predicted flux of waveband i, and σi is the calibration
uncertainty of waveband i. In this equation, s is the scaling factor
chosen to minimize the χ2 between observation and model
prediction. The value N is the number of band, and the degrees of freedom of
χ2
distribution is N −
M, where M is the number of free parameters determining the
model prediction. In our case, G0 and s are the varying parameters.
(2)where
Fobs,i is the observed
flux of waveband i, Fmod,i is the model
predicted flux of waveband i, and σi is the calibration
uncertainty of waveband i. In this equation, s is the scaling factor
chosen to minimize the χ2 between observation and model
prediction. The value N is the number of band, and the degrees of freedom of
χ2
distribution is N −
M, where M is the number of free parameters determining the
model prediction. In our case, G0 and s are the varying parameters.
We minimize the χ2 to recover the best fit G0 for every pixel. The parameter G0 determines the SED of dust FIR continuum. We estimate dust temperature using the formula Td = 17.5 K(G0)1/(4 + β) (Bernard et al. 2010; Boulanger et al. 1996; Compiègne 2010) with a dust emissivity index β = 2. For both fields, we fit the dust SED with 4-band data using Cloudy. When the scaling factor s is held fixed, we estimate the 68% confidence interval of G0 by increasing the minimized value of χ2 by 1 for every pixel (Avni & Bahcall 1976).
To explore the effect of radiative transfer, we also fit the SED with 4-band data using the DustEM model. Following the same procedures as 4-band fits for Cloudy models, we first use the DustEM code to pre-calculate the dust FIR SED for various values of ISRF. The SED of ISRF, the dynamic range and the increment step of G0, and the grain set used in DustEM models are the same as what we adopt in the SED fitting for Cloudy models. The pre-calculated dust FIR SED is then compared with the observation. We adjust G0 and the scaling factor s in Eq. (2) to fit the SED of every map pixel and compute the χ2 using Eq. (2). We find the best fit G0 by minimizing the χ2 of every pixel and then estimate dust temperature using the formula Td = 17.5 K(G0)1/(4 + β).
To investigate the existence of a 500 μm excess, we use the same procedures to fit the SED with 3-band data (160, 250, and 350 μm) using the Cloudy code and compare them to results of 4-band fits for Cloudy models. We also fit the SED with 5-band data using Cloudy to estimate the contribution from the VSGs to the 70 μm intensity by comparing the results of 5-band fits with 4-band fits for Cloudy models.
3. Results of 4-band fits for Cloudy and DustEM models
 |
Fig. 1 Temperature maps and χ2 maps of the l = 30° field. Upper panel: the temperature map. Lower panel: χ2 map. |
 |
Fig. 2 Temperature maps and χ2 maps of the l = 59° field. Upper panel: the temperature map. Lower panel: χ2 map. |
In this section, we compare the results for Cloudy models with DustEM models to explore the effects of radiative transfer. We present the temperature maps and χ2 distribution of 4-band fits for Cloudy results in Figs. 1, and 2 and summarize results in Table 1. We show the temperature histograms in Fig. 3. For the l = 30° field, the average temperature is 18.7 K with the root mean square (RMS) value 0.9 K. For the l = 59° field, the average temperature is 15.2 K with the RMS 0.6 K. For both fields, the percentages of pixels with χ2> 2 are both 0.015%.
To explore the effects of radiative transfer, we overlay histograms of Cloudy results on DustEM results and present them in Fig. 4. For both fields, the derived maximum and average temperatures of DustEM results (Table 1) are lower than Cloudy results. Comparing histograms in the upper panels of Fig. 4, we find that the temperature distributions of DustEM results shift toward lower value of temperature. The difference between results for Cloudy and DustEM models is better shown in the lower panels of Fig. 4. We plot the temperature of every pixel for Cloudy and DustEM models in the lower panels of Fig. 4 and overlay the 68% confidence interval of Cloudy results on the two plots. A black dot indicates the temperatures of every pixel for DustEM (TDustEM, the value of y axis) and Cloudy results (TCloudy, the value of x axis); two red lines indicate the 68% confidence interval of dust temperature for Cloudy results. A black line of y = x is also plotted. If TCloudy equals to TDustEM, the black dot would fall on the black line; if TDustEM is consistent with TCloudy within the 68% confidence interval, the black dot would fall between the two red lines. As shown in the lower panels of Fig. 4, most black dots fall outside the area between the two red lines. To find the degree of inconsistency, we count the number of black dots outside the area between the two red lines. For the l = 30° field, 99.9% of all pixels for DustEM results are inconsistent with Cloudy results within the 68% confidence interval. For the l = 59° field, the temperature of all pixels for DustEM results are inconsistent with Cloudy results within the 68% confidence interval. This high degree of inconsistency between DustEM and Cloudy results indicates that 1) the radiative transfer has an effect on FIR SED compared to predictions using the dust model only; 2) the effect is pronounced in both the hotter region and the colder region and makes the temperature distribution shift toward higher value of temperature.
Results of 4-band fits.
 |
Fig. 3 Temperature histograms for 4-band fits. Black line: the histogram of the l = 30° field. Red line: the histogram of the l = 59° field. |
 |
Fig. 4 Comparison of DustEM and Cloudy results. Upper panels: the overlay of histograms; black line is the result of Cloudy; red line is the result of DustEM. Lower panels: the function of the black line: y = x; black dot indicates the temperatures of every pixel for DustEM results and for Cloudy results; red lines indicate the 68% confidence interval of Cloudy results. |
4. Results of 3-band fits for Cloudy models
Using Cloudy models, we fit the dust SED using 160, 250, and 350 μm data to investigate the influence of 500 μm data points in the SED fitting and the existence of a 500 μm excess.
To investigate the influence of 500 μm data point in the SED fitting, we compare the results of 3-band and 4-band fits for Cloudy models. We overlay the temperature histograms of 3-band fits on the histograms of 4-band fits in Fig. 5. The properties of 3-band fits for both fields are listed in Table 2. For both fields, part of histograms of 3-band fits and 4-band fits are overlapped.
 |
Fig. 5 Comparison of 3-band and 4-band fits for Cloudy models. Left panel: the histograms of the l = 30° field. Right panel: the histograms of the l = 59° field. Black line is the result of 3-band fits for Cloudy models; red line is the result of 4-band fits for Cloudy models. |
Results of 3-band fits for the Cloudy model
 |
Fig. 6 500 μm excess. Left panel: excess histograms of the l = 30° field. Right panel: excess histograms of the l = 59° field. |
For the l =
30° field, 99.5% of all pixels of 3-band fits are consistent with 4-band fits
within the confidence interval of 4-band fits. For the l = 59° field,
98.3% of all pixels of 3-band
fits are consistent with 4-band fits within the confidence interval. The high degree of
consistency indicates that 500 μm data point has little influence on the results of
SED fitting, and there is no significant excess of a 500 μm emission. More
specifically, we calculate the 500 μm excess by the equation,
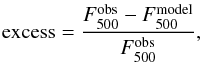 (3)where
(3)where
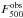 is the
observed 500 μm
intensity and
is the
observed 500 μm
intensity and 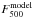 is the
model predicted intensity. Histograms of the 500 μm excess is presented in Fig. 6. The pixel distribution of excess for both fields skew toward positive
values, and the average excess with and without negative values is 1% and 2% for both
fields. Thus, there is no detection of any notable 500 μm excess in the Hi-GAL SDP
fields.
is the
model predicted intensity. Histograms of the 500 μm excess is presented in Fig. 6. The pixel distribution of excess for both fields skew toward positive
values, and the average excess with and without negative values is 1% and 2% for both
fields. Thus, there is no detection of any notable 500 μm excess in the Hi-GAL SDP
fields.
Our calculation of the 500 μm excess is consistent with the results of Paradis et al. (2012). With respect to the predictions of a modified black-body model, Paradis et al. (2012) reported that the 500 μm excess in the peripheral parts of the Galactic plane can be up to 16% to 20%. Nevertheless, they found the median value of the 500 μm excess is only 1% and 3% in the l = 30° field and the l = 59° field, respectively.
5. The VSG contribution to the 70 μm intensity
Based on the results of 4-band fits for Cloudy models, we include the 70 μm data in the SED fitting to estimate the VSG contribution to the 70 μm intensity. In the 5-band fits, the scaling factor s in Eq. (2) is the same as in the 4-band fits for Cloudy models, and G0 is the only free parameter.
Since the VSG contributes to the 70 μm emission, we should subtract the contribution from the VSG when we fit the SED using 5-band data to derive the equilibrium temperature of the BGs. We assume that VSGs contribute x% to the 70 μm intensity. After subtracting x% of the 70 μm intensity coming from the VSGs, we fit the SED using 5-band data.
We compare the results of 5-band fits with 4-band fits for x = 0, 10, 20, 30, 40, 45, 48, 50, and 60, and derive the consistency, or the percentage of pixels whose temperature of 5-band fits are consistent with 4-band fits within the 68% confidence interval of 4-band fits. Since about 10% of all pixels in the l = 59° field have negative values of the 70 μm emission, which might be caused by improper calibration in this waveband, we only analyze the l = 30° field here.
 |
Fig. 7 Consistency of 5-band and 4-band fits for Cloudy models. |
The histogram of consistency is presented in Fig. 7. The value of consistency increases from 88% to 98% when the VSG contribution increases from 0% to 30%. When the VSG contribution is more than 30%, the value of consistency decreases with the increasing contribution. The consistency is 52% and 44% when the contribution is 48% and 50%, respectively. Thus, the
VSG contribution to the 70 μm intensity can be from 0% up to 50%. The temperature distributions of the 5-band fits are most consistent (consistency >95%) with the 4-band fits when the contribution is 20% to 30%. Our estimation of 70 μm contribution from the VSGs is consistent with Compiègne et al. (2010), who found that the VSG contribution goes from 10% up to 50% with a median value of 27% in a diffuse region of the l = 59° field.
6. Summary
We derive temperature maps of the BGs in the fields of l = 30° and l = 59° by considering radiative transfer and grain physics at the same time. The dust temperatures of the l = 30° field range from a minimum 10.9 K in diffuse regions to a maximum 32.8 K with an average value of 18.7 ± 0.9 K. For the l = 59° field, the dust temperatures range from 12.8 K to 29.4 K with an average value of 15.2 ± 0.6 K. Compared to results for dust-only models, we find that the radiative transfer affects the FIR SED and makes the temperature distribution shift toward higher value of temperature.
We explore the 500 μm excess by fitting the dust SED without the 500 μm waveband and find that there is no significant excess of a 500 μm emission in the two SDP fields. The SED fitting of 5-band data is performed to estimate the VSG contribution to the 70 μm intensity. The VSGs can contribute up to 50% of the observed 70 μm intensity.
Acknowledgments
We thank the anonymous referee for helpful comments. This study is supported by funding KJCX2-YW-T20 of Chinese Academy of Science.
References
- Abel, N. P., van Hoof, P. A. M., Shaw, G., Ferland, G. J., & Elwert, T. 2008, ApJ, 686, 1125 [Google Scholar]
- Avni, Y., & Bahcall, N. A. 1976, ApJ, 209, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard, J.-P., Paradis, D., Marshall, D., et al. 2010, A&A, 518, L88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Black, J. H. 1987, Astrophys. Space Sci. Lib., 134, 731 [Google Scholar]
- Boulanger, F., Abergel, A., Bernard, J. -P., et al. 1996, A&A, 312, 256 [NASA ADS] [Google Scholar]
- Compiègne, M. 2010, ASP Conf. Ser., 438, 55 [NASA ADS] [Google Scholar]
- Compiègne, M., Flagey, N., Noriega-Crespo, A., et al. 2010, ApJ, 724, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Elia, D., Molinari, S., Fukui, Y., et al. 2013, ApJ, 772, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mex. Astron. Astrophys., 49, 137 [Google Scholar]
- Fitzpatrick, E. L. 2004, in Astrophysics of Dust, eds. A. N. Witt, G. C. Clayton, & B. T. Draine (San Francisco, CA: ASP), ASP Conf. Ser. 309, 33 [Google Scholar]
- Griffin, M. J., Paladini, R., Noriega-Crespo, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Habing, H. J. 1968, Bull. Astron. Inst. Netherlands, 19, 421 [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Riedinger, J. R., & Passvogel, T. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paradis, D., Veneziani, M., Noriega-Crespoet, A., et al. 2010, A&A, 520, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paradis, D., Paladini, R., Noriega-Crespo, A., et al. 2012, A&A, 537, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piazzo, L., Ikhenaode, D., Natoli, P., et al. 2012, IEEE Trans. Image Process., 21, 3687 [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Temperature maps and χ2 maps of the l = 30° field. Upper panel: the temperature map. Lower panel: χ2 map. |
| In the text | |
 |
Fig. 2 Temperature maps and χ2 maps of the l = 59° field. Upper panel: the temperature map. Lower panel: χ2 map. |
| In the text | |
 |
Fig. 3 Temperature histograms for 4-band fits. Black line: the histogram of the l = 30° field. Red line: the histogram of the l = 59° field. |
| In the text | |
 |
Fig. 4 Comparison of DustEM and Cloudy results. Upper panels: the overlay of histograms; black line is the result of Cloudy; red line is the result of DustEM. Lower panels: the function of the black line: y = x; black dot indicates the temperatures of every pixel for DustEM results and for Cloudy results; red lines indicate the 68% confidence interval of Cloudy results. |
| In the text | |
 |
Fig. 5 Comparison of 3-band and 4-band fits for Cloudy models. Left panel: the histograms of the l = 30° field. Right panel: the histograms of the l = 59° field. Black line is the result of 3-band fits for Cloudy models; red line is the result of 4-band fits for Cloudy models. |
| In the text | |
 |
Fig. 6 500 μm excess. Left panel: excess histograms of the l = 30° field. Right panel: excess histograms of the l = 59° field. |
| In the text | |
 |
Fig. 7 Consistency of 5-band and 4-band fits for Cloudy models. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


