| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A81 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201322628 | |
| Published online | 11 April 2014 | |
Deep optical observations of the γ-ray pulsar J0357+3205⋆,⋆⋆
1
Ioffe Physical-Technical Institute,
Politekhnicheskaya 26,
194021
St. Petersburg,
Russia
e-mail: aida.astro@mail.ioffe.ru; danila@mail.ioffe.ru; shib@mail.ioffe.ru, pshternin@gmail.com; da.zyuzin@gmail.com
2
St. Petersburg State Polytechnical University,
Politekhnicheskaya 29,
195251
St. Petersburg,
Russia
3
Observatorio Astronómico Nacional SPM, Instituto de Astronomía,
Universidad Nacional Autónomia de Mexico, Ensenada, BC, Mexico
e-mail:
zhar@astrosen.unam.mx
Received: 8 September 2013
Accepted: 6 February 2014
Context. A middle-aged radio-quiet pulsar J0357+3205 was discovered in gamma rays with Fermi and later in X-rays with Chandra and XMM-Newton observatories. It produces an unusual thermally emitting pulsar wind nebula that is observed in X-rays.
Aims. Deep optical observations were obtained to search for the pulsar optical counterpart and its nebula using the Gran Telescopio Canarias (GTC).
Methods. The direct imaging mode in the Sloan g′ band was used. Archival X-ray data were reanalysed and compared with the optical data.
Results. No pulsar optical counterpart was detected down to g′ 28
28 1. No pulsar nebula was identified in the optical either. We confirm early results that the X-ray spectrum of the pulsar consists of a nonthermal power-law component of the pulsar magnetospheric origin dominating at high energies and a soft thermal component from the neutron star surface. Using magnetised, partially ionised hydrogen atmosphere models in X-ray spectral fits, we found that the thermal component can come from the entire surface of the cooling neutron star with a temperature of 36
1. No pulsar nebula was identified in the optical either. We confirm early results that the X-ray spectrum of the pulsar consists of a nonthermal power-law component of the pulsar magnetospheric origin dominating at high energies and a soft thermal component from the neutron star surface. Using magnetised, partially ionised hydrogen atmosphere models in X-ray spectral fits, we found that the thermal component can come from the entire surface of the cooling neutron star with a temperature of 36 eV, making it one of the coldest among cooling neutron stars known. The surface temperature agrees with the standard neutron star cooling scenario. The optical upper limit does not put any additional constraints on the thermal component, however it does imply a strong spectral break for the nonthermal component between the optical and X-rays as is observed in other middle-aged pulsars.
eV, making it one of the coldest among cooling neutron stars known. The surface temperature agrees with the standard neutron star cooling scenario. The optical upper limit does not put any additional constraints on the thermal component, however it does imply a strong spectral break for the nonthermal component between the optical and X-rays as is observed in other middle-aged pulsars.
Conclusions. The thermal emission from the entire surface of the neutron star very likely dominates the nonthermal emission in the UV range. Observations of PSR J0357+3205 in this range are promising to put more stringent constraints on its thermal properties.
Key words: stars: neutron / pulsars: general
Based on observations made with the Gran Telescopio Canarias (GTC), instaled in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias, in the island of La Palma under Programme GTC3-12BMEX.
The reduced optical imaging data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/564/A81
© ESO, 2014
1. Introduction
Gamma-ray pulsars are considered as one of the main targets of the Fermi mission. For its five years of activity, the Large Area Telescope (LAT) has discovered numerous such sources previously observed in the radio band. But, apart from the ability to detect many known radio pulsars in γ-rays, Fermi LAT also affords the opportunity to discover pulsars independently in so-called blind searches (cf. Saz Parkinson et al. 2009). These blind searches were quite successful by leading to discovery of about three dozen pulsars in γ-rays (see e.g. Saz Parkinson & Fermi LAT Collaboration 2013; Pletsch et al. 2012). Further multiwavelength investigations of these objects are crucial for unveiling the pulsar emission nature. Because Fermi pulsars are typically nearby and energetic (Saz Parkinson & Fermi LAT Collaboration 2013), they, in particular, appear to be promising targets for studies in the X-ray and optical domains.
A middle-aged radio-quiet PSR J0357+3205 with period P = 444 ms, magnetic field B = 2.3 × 1012 G, and characteristic age P/2Ṗ = 5.4 × 105 yr has been discovered in one of the Fermi LAT blind frequency searches (Abdo et al. 2009). The distance to the pulsar of about 500 pc was estimated by De Luca et al. (2011) based on the γ-ray “pseudo-distance” relation (see e.g. Saz Parkinson et al. 2010). First X-ray observations of the pulsar field with Chandra revealed a faint X-ray counterpart of the object with an extended (9 arcmin) X-ray tail (De Luca et al. 2011). Subsequent XMM-Newton observations have shown clearly that emission from the pulsar itself is generally nonthermal with a soft thermal component (Marelli et al. 2013). The pulsar field was also observed in the optical and near-infrared bands with 2.5–4 m class telescopes. No counterpart was found down to V ≳ 26 7 (De Luca et al. 2011).
7 (De Luca et al. 2011).
To search for an optical counterpart of PSR J0357+3205 and/or its tail at a higher sensitivity level, we performed deep optical observations with the 10.4 m GTC. The details of observations and data reduction are described in Sect. 2. Our results, together with reanalysis of the archival X-ray data, are presented in Sect. 3 and are discussed in Sect. 4.
 |
Fig. 1 Left panel: GTC/OSIRIS ~51′′× 51′′ Sloan g′-image fragment of the PSR J0357+3205 field. The circle shows 3σ X-ray pulsar position uncertainty for the optical observations epoch (see text for details). The 15′′× 15′′ pulsar vicinity within the dashed rectangle is enlarged in the right panel and smoothed with a one-pixel Gaussian kernel. The sources discussed in the text are labelled by numbers |
2. GTC data
Log of the GTC/OSIRIS observations of PSR J0357 +3205.
2.1. Observations and data reduction
The observations of the pulsar field were carried out in the Sloan g′ band with the Optical System for Imaging and low-intermediate Resolution Integrated Spectroscopy (OSIRIS1) at the GTC in a queue-scheduled service mode in 2012 December and 2013 January. With the image scale of 0 254/pixel (2 × 2 binning) and unvignetted field size of 7.́8 × 7.́8 available with the OSIRIS detector consisting of a mosaic of two CCDs, we obtained four sets of 700 s dithered exposures in a grey time. The pulsar was exposed on CCD1. The observing conditions were photometric, with seeing varying from 0
254/pixel (2 × 2 binning) and unvignetted field size of 7.́8 × 7.́8 available with the OSIRIS detector consisting of a mosaic of two CCDs, we obtained four sets of 700 s dithered exposures in a grey time. The pulsar was exposed on CCD1. The observing conditions were photometric, with seeing varying from 0 8 to 1
8 to 1 0 (see Table 1).
0 (see Table 1).
Standard data reduction, including bias subtraction, flat-fielding, cosmic-ray removal, and bad pixel correction, was performed with IRAF and MIDAS tools. Subsequent data inspection showed that each single exposure was significantly contaminated by a nonuniform background. This was caused by the fact that OSIRIS detector filter wheels are inclined at an angle of 10 5 with respect to the incident light. For this reason, the central wavelength of the filter moves slightly bluewards from CCD1 to CCD2 of the OSIRIS focal plane. For the broad-band filters, this effect is small2, but becomes visible in case of a high background as on our images obtained during grey time. To eliminate the contamination, we performed illumination correction for each observational set.
5 with respect to the incident light. For this reason, the central wavelength of the filter moves slightly bluewards from CCD1 to CCD2 of the OSIRIS focal plane. For the broad-band filters, this effect is small2, but becomes visible in case of a high background as on our images obtained during grey time. To eliminate the contamination, we performed illumination correction for each observational set.
Finally, using a set of unsaturated stars, we aligned all the corrected individual exposures to the best one obtained in the highest quality seeing conditions. The alignment accuracy was ≲0.1 pixel. As a result, we obtained a combined image with mean seeing of 0 9, mean airmass of 1.12, and total integration time of 9.8 ks.
9, mean airmass of 1.12, and total integration time of 9.8 ks.
2.2. Astrometric referencing and photometric calibration
To perform a precise astrometric referencing, we used the positions of the astrometric standards from the USNO-B1 astrometric catalogue3. A set of ten isolated unsaturated stars was selected on the combined image. Precise pixel coordinates of these stars were obtained using the IRAF task imcenter with an accuracy of ≲0.003 pixel. For the astrometric transformation we applied the IRAF task ccmap. Formal rms uncertainties of the astrometric fit were ΔRA ≲ 0 123 and ΔDec ≲ 0
123 and ΔDec ≲ 0 155, which is consistent with the nominal catalogue uncertainty of ≈0
155, which is consistent with the nominal catalogue uncertainty of ≈0 2. The resulting conservative 1σ referencing uncertainty for the combined images is ≲0
2. The resulting conservative 1σ referencing uncertainty for the combined images is ≲0 23 for RA and ≲0
23 for RA and ≲0 25 for Dec.
25 for Dec.
For photometric calibration we used the G158-100 Sloan standard (Smith et al. 2002) observed the same nights as our target. The atmospheric extinction coefficient for g′ taken from the OSIRIS user manual is 0.16(1) mag airmass-1. The determined magnitude zero point for our g′ image is 28.64(5).
3. Results
Best-fit parameters of the pulsar X-ray spectrum with three models.
3.1. Pulsar field
In the left-hand panel of Fig. 1 we present the resulting GTC g′ image fragment that contains PSR J0357+3205. The circle is centred on the expected pulsar position with RA = 03:57:52.293 and Dec = +32:05:20.970 (l = 162.76° and b = −16.01°) for the GTC observation epoch. It was estimated using the X-ray pulsar position obtained in the Chandra 2009 observations (see De Luca et al. 2011) and accounting for the pulsar proper motion of 0 165 ± 0
165 ± 0 030 yr-1 (De Luca et al. 2013) at ~3.2 yr time base between the Chandra 2009 and GTC 2012–2013 observations. The circle radius of ~1
030 yr-1 (De Luca et al. 2013) at ~3.2 yr time base between the Chandra 2009 and GTC 2012–2013 observations. The circle radius of ~1 1 corresponds to the 3σ pulsar position uncertainty in the optical image, which accounts for the optical astrometric referencing, proper motion, and pulsar X-ray position uncertainties4.
1 corresponds to the 3σ pulsar position uncertainty in the optical image, which accounts for the optical astrometric referencing, proper motion, and pulsar X-ray position uncertainties4.
The pulsar vicinity is enlarged in the right-hand panel of Fig. 1. In this region using the IRAF task daofind we find five compact sources detected at ≳3σ significance, they are labelled by numbers. Source “1” has a g′ magnitude of 26 6(1) and is the closest object to the pulsar. However, it is located 2
6(1) and is the closest object to the pulsar. However, it is located 2 2 away from the X-ray position, implying the offset significance of ~6σ. Such a high displacement rules out this object as a pulsar optical counterpart. Based on its spatial brightness profile, we cannot firmly distinguish whether it is a point source or a bright part of an extended structure immediately SW of the pulsar. Objects “2” and “3” with magnitudes of 26
2 away from the X-ray position, implying the offset significance of ~6σ. Such a high displacement rules out this object as a pulsar optical counterpart. Based on its spatial brightness profile, we cannot firmly distinguish whether it is a point source or a bright part of an extended structure immediately SW of the pulsar. Objects “2” and “3” with magnitudes of 26 4(1) and 26
4(1) and 26 8(2), respectively, are likely point-like sources. They are even more distant from the pulsar position and are certainly unrelated objects. Finally, extended sources “4” and “5” with magnitudes 25
8(2), respectively, are likely point-like sources. They are even more distant from the pulsar position and are certainly unrelated objects. Finally, extended sources “4” and “5” with magnitudes 25 9(1) and 26
9(1) and 26 3(1) are probably galaxies or irrelevant blended stellar objects. A compact flux enhancement is seen within the 3σ pulsar position error circle. However, it does not exceed the background fluctuations in this area much, so currently we do not have any strong arguments for proposing this as a real object.
3(1) are probably galaxies or irrelevant blended stellar objects. A compact flux enhancement is seen within the 3σ pulsar position error circle. However, it does not exceed the background fluctuations in this area much, so currently we do not have any strong arguments for proposing this as a real object.
Therefore, based on our optical data, we can only give a conservative estimation of the optical flux upper limit from the pulsar. Following a standard procedure (e.g. Zharikov & Mignani 2013) we obtained the point source 3σ flux upper limit of ≲0.023 μJy (g′ ≳ 28 1). This is currently the most stringent constraint on the optical flux of the pulsar.
1). This is currently the most stringent constraint on the optical flux of the pulsar.
We did not detect any reliable (≳3σ) extended emission except the feature around the source “1” immediately SW of the pulsar. This feature cannot be associated with the long SE tail behind the pulsar detected in X-rays. However, the brightest parts of the tail in X-rays are outside the GTC field of view. The nature of the extended SW feature is unclear. It could be an interstellar cloud in the pulsar vicinity partially ionised by the pulsar emission and emitting in [OIII]5007/4969 Å lines which fall within the g′ bandpass. Observations in other broad and/or narrow bands would be useful for understanding the origin of the source.
3.2. Reanalysis of the X-ray spectrum
To evaluate how informative the pulsar flux upper limit is, it is useful to compare it with X-ray spectral data. To do that, we performed an independent X-ray data analysis. We retrieved all the available archival X-ray data obtained with Chandra5 and XMM-Newton6. To extract the pulsar spectra, we used 2′′ and 30′′ apertures centred on the pulsar position, which enclose ≳90% of the pulsar emission in the Chandra and XMM-Newton data, respectively. The CIAO v.4.5 specextractand SAS 13.0 especgettools were used for the extraction, resulting in ~3500 XMM-Newton/EPIC and ~1000 Chandra/ACIS source counts. Using the XSPEC v.12.8.1 , we then fitted the spectra in the 0.3−10 keV range by an absorbed spectral model containing power-law (PL) and thermal emission components originating in the magnetosphere and the surface of the neutron star (NS), respectively. We used the XSPEC photoelectric absorption model phabs with default abundances angr (Anders & Grevesse 1989) and cross-sections bcmc (Balucinska-Church & McCammon 1992). We also tried other abundances and cross-sections available in XSPEC 7, but this did not significantly change fit statistics (χ2) and fit parameters remained within their confidence intervals. For the thermal component we used either blackbody (BB) or magnetised neutron star hydrogen atmosphere NSA and NSMAX models (Pavlov et al. 1995; Ho et al. 2008), which provided equally acceptable fits.
The best-fit parameters for the absorbed BB+PL, NSA+PL, and NSMAX+PL models are presented in Table 2 where errors are at the 90% confidence. For the NSA model we fixed NS mass M, circumferential radius R, and surface magnetic field B at 1.4 M⊙, 13 km, and 1012 G, respectively. For the NSMAX model we fixed the redshift parameter 1 + z at the value of 1.21, which corresponds to the same M and R. We selected the model 1200 from NSMAX family, which represents the atmosphere with B = 1012 G. Owing to the space-time curvature near the NS, its apparent radius is R(1 + z) = 15.73 km. The values of temperatures T∞ and thermally emitting area radii R∞ (in units of d500 pc km) are given as measured by a distant observer. For all models, R∞ is derived from the model normalisation.
The BB emitting area is much smaller than the entire surface of the NS, but is consistent with a canonical pulsar polar cap size (Sturrock 1971) of about 0.32 km derived for the 13 km NS with the period of 444 ms. At the same time, both NSA and NSMAX models give emitting area radii, which are much larger than the cap size, but agree well with the standard apparent NS size (10−20 km), especially accounting for the distance uncertainties (see below). This is also demonstrated by the T∞ − R∞ confidence contours presented in Figs. 2 and 3. Moreover, if the normalisations for both hydrogen atmosphere models are fixed according to apparent emitting area radius of the 15.73 km at 500 pc distance, the fit is still statistically acceptable (third and fifth rows in Table 2). While both NSA and NSMAX models give comparable best-fit parameters (see Table 2), the NSMAX results appear to be more plausible, since this model accounts for the partial ionisation of atmosphere plasma. The latter is essential for magnetised hydrogen atmospheres with effective temperatures less than 90 eV (Potekhin et al. 1999).
We also estimated an upper limit on the star entire surface temperature for the BB+PL model following the procedure used by Weisskopf et al. (2011) for the Crab pulsar. We added an additional BB component to this model, which is not required to describe the data and does not affect the initial best fit. The upper limit is then derived from the upper boundary of the R∞ − T∞ confidence contours for the new component. Respective contours for 90% and 99% confidence are shown in Fig. 4. Here the R∞ scale corresponds to a reasonable range of the NS radii accounting for uncertainties of the distance to the pulsar (see below). For the R∞ = 15.73 d500 pc km, the entire NS surface temperature upper limit is 40 eV (at 99% confidence).
 |
Fig. 2 68%, 90%, and 99% ( |
Our results for the BB+PL model are similar to those of Marelli et al. (2013). However, the results for the NSA+PL model and for the upper limit on the surface temperature in the blackbody model are different. The reason for the former is in the different value of magnetic field used. We checked that for B = 1013 G our results agree with Marelli et al. (2013). In our spectral fits we use B = 1012 G, which is closer to the value inferred from the spindown measurements. The blackbody upper limit reported by Marelli et al. (2013) is 38 eV for the NS radius of 10 km and distance of 500 pc. According to Fig. 4, the upper limit for these parameters (R∞ ≈ 13 km for 1.4 M⊙ NS) should be 42 eV. Unfortunately, Marelli et al. (2013) do not describe the method for obtaining their value, and the reason for this discrepancy is unclear.
 |
Fig. 4 90% and 99% ( |
It is important to stress that the hydrogen atmosphere and blackbody models have equal rights to be considered as the interpretation of the thermal component of the emission. The blackbody model can mimic the emission from the iron atmosphere or from the condensed surface of the NS (see e.g. van Adelsberg et al. 2005, and references therein). Deeper X-ray observations allowing for a phase-resolved spectral analysis will enable us to distinguish between the models. The parameters of the PL component, dominating at energies ≳1 keV, are almost independent of the type of the thermal component involved into the combined model (Table 2).
Finally, any reasonable single spectral model is not acceptable. For instance, absorbed PL, BB, and NSA models give reduced χ2/(d.o.f.) of 1.30/(246), 2.52/(246), and 2.22/(246), respectively. Any combined model with the PL replaced by a second thermal component, which may represent the emission from two areas of the NS with different temperatures, is not acceptable either: e.g., an absorbed BB+BB, NSA+NSA, and NSMAX+NSMAX give χ2/(d.o.f.) = 1.27/(244), 1.68/(244), and 2.50/(244), respectively.
4. Discussion
From three statistically acceptable X-ray models, BB+PL, NSA+PL, and NSMAX+PL, considered in the previous section, the last two result in similar parameters of the pulsar thermal emission. However, the NSMAX model is more justified for the physical reasons. Therefore in what follows we omit the NSA+PL model for simplicity.
To compare the X-ray data and the optical upper limit, the latter must be corrected for the interstellar extinction AV. The standard AV − NH relation (Predehl & Schmitt 1995) can be used to estimate AV. The BB+PL and NSMAX+PL X-ray spectral fits suggest NH in a range of (1.0−2.3) × 1021 cm-2 (Table 2). This corresponds to the AV range of 0.6−1.4. However, AV can hardly exceed the entire Galactic extinction in this direction of 0.8, which was recently estimated by Schlafly & Finkbeiner (2011). Therefore, we accept 0.8 as a conservative extinction value for dereddening the optical upper limit. At the same time, the actual NH value can be higher than 1.4 × 1021 cm-2 which corresponds to this AV. For instance, Marelli et al. (2013) estimate entire Galactic NH = (2.1 ± 0.2) × 1021 cm-2 from the spectral analysis of extra-galactic sources in the pulsar field.
Considering the half-thickness of ~100 pc for the Galactic gaseous disk responsible for the extinction, the pulsar latitude b = −16°, and the minimal AV = 0.6 (NH = 1021 cm-2), we obtain the minimum distance to the pulsar of ~270 pc. This value is derived assuming the uniform AV scaling with distance within the disk. The upper limit on the distance of ~900 pc was estimated by Marelli et al. (2013) based on an assumption that the pulsar intrinsic γ-ray luminosity cannot exceed its spin-down energy loss rate. The 500 pc distance accepted in Sect. 3.2 is consistent with these limits.
 |
Fig. 5 Unabsorbed spectrum of PSR J0357+3205 in the optical-X-ray range. The GTC g′-band flux upper limit is indicated by the bar with an arrow. The XMM-Newton and Chandra data points are shown by grey bars8. The thick solid line is the best-fit BB+PL model to the X-ray data. The thin dotted line with the dark-grey filled region is the PL component with 90% uncertainties. The thick dotted line is the BB hot spot component. The thin/thick dash-dotted and dashed lines are the best-fit NSA and NSMAX components with variable/fixed normalisations. The upper limit on the thermal spectral flux from the entire surface of the NS obtained with the BB+PL+BB model is shown by the light-grey filled region. The extrapolation of the γ-ray Fermi spectrum with its uncertainties is shown by the thin solid line with a hatched region. |
At the distance of 500 pc, the optical (in the V band) and nonthermal X-ray (in the range of 2−10 keV) luminosities of the pulsar are LV ≲ 1.1 × 1027 erg s-1 and LX = 6.0 × 1029 erg s-1. Accounting for the spin-down luminosity Ė = 5.8 × 1033 erg s-1 (Abdo et al. 2009), they yield the optical and X-ray efficiencies of the pulsar LV/Ė ≲ 10-6.7 and LX/Ė ≈ 10-4.0. These values are compatible with the empirical X-ray luminosity and efficiency vs. age dependencies demonstrated by the pulsars detected in the optical and X-rays (e.g. Zharikov et al. 2006; Zharikov & Mignani 2013). This also supports the distance estimate of 500 pc.
In Fig. 5 we compare the unabsorbed X-ray and γ-ray spectra of the pulsar with the optical upper limit of 0.052 μJy derived from the GTC observations and dereddened with AV = 0.8. The optical upper limit is two orders of magnitude lower than would be expected from the extrapolation of the PL spectral component to the optical range. According to Sect. 3.2, the PL component is essential to describe the high-energy tail of the pulsar X-ray spectrum. This suggests a spectral break in the PL component between the optical and X-rays, as observed for all middle-aged pulsars detected in both domains (Shibanov et al. 2006). The extrapolation of the γ-ray PL spectrum of the pulsar (see Fig. 5) lies well below the optical upper limit.
The best-fit NSMAX spectral components with variable and fixed normalisations are shown in Fig. 5. For completeness we also show the NSA spectral components. As seen, to significantly constrain the NS thermal emission in these models, one has to go as deep as ~30 0 in the optical, which is not feasible with the current instrumentation. The BB hot spot spectral component derived from the X-ray data with the BB+PL model cannot be currently reached in the optical/UV either. The light-grey region in Fig. 5 contains all possibilities for the soft thermal component in the BB+BB+PL model for allowed R∞ range in accordance with the 99% confidence contour of Fig. 4. We may conclude that the optical upper limit does not put any additional constraints on thermal emission from the NS surface.
0 in the optical, which is not feasible with the current instrumentation. The BB hot spot spectral component derived from the X-ray data with the BB+PL model cannot be currently reached in the optical/UV either. The light-grey region in Fig. 5 contains all possibilities for the soft thermal component in the BB+BB+PL model for allowed R∞ range in accordance with the 99% confidence contour of Fig. 4. We may conclude that the optical upper limit does not put any additional constraints on thermal emission from the NS surface.
However, according to Fig. 5, the entire surface thermal spectral component can be reached in UV. It can also dominate the PL component there, if the PL component has an approximately flat spectral slope from the optical to the UV, as observed for other middle-aged pulsars. The latter would be better constrained at longer optical wavelengths, and less affected by the interstellar extinction. Therefore, UV observations of J0357+3205 would be useful for constraining its surface temperature. There are only few pulsars with thermal emission detected in the UV range namely PSR B0656+14 (Durant et al. 2011), PSR B1055−52 (Mignani et al. 2010), PSR J0437−4715 (Kargaltsev et al. 2004), and Geminga (Kargaltsev et al. 2005). In addition, Kaplan et al. (2011) report detecting UV thermal emission from a few isolated neutron stars. In all these cases the UV data on thermal emission were a good complement to the X-ray data.
Accounting for the direction of the pulsar proper motion and the spindown age, we find its likely birth place in the λ-Orionis cluster, a 5 Myr active star-forming region located in ~32° from the pulsar and in ~450 ± 50 pc from Earth (Mayne & Naylor 2008). Several authors have proposed that an expanding molecular ring surrounding the cluster is a supernova remnant left by a Type II supernova explosion of a massive companion of the O-type λ Ori star about 1 Myr ago (see e.g., Cunha & Smith 1996; Dolan & Mathieu 2002). By adopting this birth place, we independently constrained the pulsar age of 0.2−1.3 yr, accounting for the pulsar proper motion uncertainties, and the cluster and the pulsar distance ranges. This is consistent with its spindown age of 0.54 Myr.
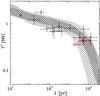 |
Fig. 6 Measured entire surface temperatures T∞ as seen by a distant observer (filled circles) for NSs of different ages t in comparison with the cooling theory predictions (hatched regions). The dense hatched region corresponds to the standard cooling theory, while the sparse hatched region shows the minimal cooling theory predictions. The bold star with error bars show the PSR J0357+3205 surface temperature. |
After accepting this age range and the NS effective temperature of 36 eV derived from the NSMAX+PL fit, we could compare these with the NS cooling theory predictions. The J0357+3205 position on the temperature–age plane is shown in Fig. 6. The data for other isolated neutron stars are taken from Shternin et al. (2011). It is seen that J0357+3205 is among the coldest cooling NSs known. The figure shows the range of the NS temperatures that can be obtained by the standard cooling theory where the modified Urca processes are considered as the main neutrino emission mechanism (e.g. Yakovlev & Pethick 2004). The J0357+3205 position agrees well with the standard cooling theory. However, as seen from Fig. 6 the standard cooling theory is insufficient to reproduce the data on all cooling NSs; therefore, we show the range of cooling curves obtained within the minimal cooling scenario (Gusakov et al. 2004; Page et al. 2004, 2009), which takes the presence of the baryon superfluidity inside neutron stars into account. In this scenario the specific process of the neutrino emission due to a Cooper pair formation cools the star more effectively than the modified Urca process. To date, the parameters of the superfluidity can be plausibly adjusted to fit all the data on the observed NSs temperatures (Gusakov et al. 2004), including the likely rapidly cooling NS in Cas A (Shternin et al. 2011). Obviously, J0357+3205 agrees with the minimal cooling scenario as well.
eV derived from the NSMAX+PL fit, we could compare these with the NS cooling theory predictions. The J0357+3205 position on the temperature–age plane is shown in Fig. 6. The data for other isolated neutron stars are taken from Shternin et al. (2011). It is seen that J0357+3205 is among the coldest cooling NSs known. The figure shows the range of the NS temperatures that can be obtained by the standard cooling theory where the modified Urca processes are considered as the main neutrino emission mechanism (e.g. Yakovlev & Pethick 2004). The J0357+3205 position agrees well with the standard cooling theory. However, as seen from Fig. 6 the standard cooling theory is insufficient to reproduce the data on all cooling NSs; therefore, we show the range of cooling curves obtained within the minimal cooling scenario (Gusakov et al. 2004; Page et al. 2004, 2009), which takes the presence of the baryon superfluidity inside neutron stars into account. In this scenario the specific process of the neutrino emission due to a Cooper pair formation cools the star more effectively than the modified Urca process. To date, the parameters of the superfluidity can be plausibly adjusted to fit all the data on the observed NSs temperatures (Gusakov et al. 2004), including the likely rapidly cooling NS in Cas A (Shternin et al. 2011). Obviously, J0357+3205 agrees with the minimal cooling scenario as well.
At the same time, according to Fig. 4, the entire surface temperature in the blackbody spectral model is poorly constrained, when taking the uncertainties in the NS radius and distance to the pulsar into account. Thus it is not possible to extract any valuable information from comparison of the BB+BB+PL fit results with the cooling theories.
To summarise, our deep optical observations of PSR J0357+3205 allowed us to constrain the pulsar nonthermal emission, suggesting a strong spectral break in this emission between the optical and X-rays. Reanalysis of X-ray data allowed us to constrain the NS thermal spectrum and to measure the effective temperature of the NS surface T∞ = 36 eV. Comparing the optical upper limit with the NS thermal spectrum, we conclude that the thermal emission from the entire surface of the NS can be feasibly examined in the UV range and that it very likely dominates there over the nonthermal emission and the emission from pulsar hot spot(s). This makes J0357+3205 a promising target for UV observations.
eV. Comparing the optical upper limit with the NS thermal spectrum, we conclude that the thermal emission from the entire surface of the NS can be feasibly examined in the UV range and that it very likely dominates there over the nonthermal emission and the emission from pulsar hot spot(s). This makes J0357+3205 a promising target for UV observations.
For instrument features see http://www.gtc.iac.es/instruments/osiris/
It leads to a displacement of as much as 30 Å for the Sloan g′ filter, see OSIRIS user manual for details: http://www.gtc.iac.es/instruments/osiris/media/OSIRIS-USER-MANUAL_v2.1.pdf
We used the Chandra pulsar positional error of 0 25 from De Luca et al. (2011).
25 from De Luca et al. (2011).
The data were unfolded and unabsorbed by applying the factor (unfolded unabsorbed model)/(folded absorbed model) in each spectral bin, assuming the best-fit BB+PL model. This procedure is analogous to how an unfolded spectrum is plotted by the Xspec plot ufspec command. The data points obtained this way are model-dependent and for different models will follow the respective best-fit lines.
Acknowledgments
We are grateful to the anonymous referee for useful comments allowing us to improve the paper and to Alexander Potekhin and Dmitriy Barsukov for helpful discussions. We also thank Antonio Cabrera Lavers for the discussion on the GTC data reduction. The work was partially supported by CONACYT 151858 projects, the Russian Foundation for Basic Research (grants 13-02-12017-ofi-m, 14-02-00868-a), and RF Presidential Programme MK-2837.2014.2.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, Science, 325, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Balucinska-Church, M., & McCammon, D. 1992, ApJ, 400, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, K., & Smith, V. V. 1996, A&A, 309, 892 [NASA ADS] [Google Scholar]
- De Luca, A., Marelli, M., Mignani, R. P., et al. 2011, ApJ, 733, 104 [NASA ADS] [CrossRef] [Google Scholar]
- De Luca, A., Mignani, R. P., Marelli, M., et al. 2013, ApJ, 765, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Dolan, C. J., & Mathieu, R. D. 2002, AJ, 123, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Durant, M., Kargaltsev, O., & Pavlov, G. G. 2011, ApJ, 743, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Gusakov, M. E., Kaminker, A. D., Yakovlev, D. G., & Gnedin, O. Y. 2004, A&A, 423, 1063 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ho, W. C. G., Potekhin, A. Y., & Chabrier, G. 2008, ApJS, 178, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Kaplan, D. L., Kamble, A., van Kerkwijk, M. H., & Ho, W. C. G. 2011, ApJ, 736, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Kargaltsev, O., Pavlov, G. G., & Romani, R. W. 2004, ApJ, 602, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Kargaltsev, O. Y., Pavlov, G. G., Zavlin, V. E., & Romani, R. W. 2005, ApJ, 625, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Marelli, M., De Luca, A., Salvetti, D., et al. 2013, ApJ, 765, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Mayne, N. J., & Naylor, T. 2008, MNRAS, 386, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Mignani, R. P., Pavlov, G. G., & Kargaltsev, O. 2010, ApJ, 720, 1635 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D., Lattimer, J. M., Prakash, M., & Steiner, A. W. 2004, ApJS, 155, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D., Lattimer, J. M., Prakash, M., & Steiner, A. W. 2009, ApJ, 707, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlov, G. G., Shibanov, Y. A., Zavlin, V. E., & Meyer, R. D. 1995, in The Lives of the Neutron Stars, eds. M. A. Alpar, U. Kiziloglu, & J. van Paradijs (Dordrecht: Kluwer Academic), 71 [Google Scholar]
- Pletsch, H. J., Guillemot, L., Allen, B., et al. 2012, ApJ, 744, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y., Chabrier, G., & Shibanov, Y. A. 1999, Phys. Rev. E, 60, 2193 [NASA ADS] [CrossRef] [Google Scholar]
- Predehl, P., & Schmitt, J. H. M. M. 1995, A&A, 293, 889 [NASA ADS] [Google Scholar]
- Saz Parkinson, P. M., & Fermi LAT Collaboration 2013, in IAU Symp., 291, 81 [Google Scholar]
- Saz Parkinson, P. M., Dormody, M., & Ziegler, M. (for the LAT Collaboration) 2009, Proc. of the 31st ICRC, Lodz, Poland [arXiv:0908.1243] [Google Scholar]
- SazParkinson, P. M., Dormody, M., Ziegler, M., et al. 2010, ApJ, 725, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Shibanov, Y. A., Zharikov, S. V., Komarova, V. N., et al. 2006, A&A, 448, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shternin, P. S., Yakovlev, D. G., Heinke, C. O., Ho, W. C. G., & Patnaude, D. J. 2011, MNRAS, 412, L108 [NASA ADS] [Google Scholar]
- Smith, J. A., Tucker, D. L., Kent, S., et al. 2002, AJ, 123, 2121 [Google Scholar]
- Sturrock, P. A. 1971, ApJ, 164, 529 [NASA ADS] [CrossRef] [Google Scholar]
- van Adelsberg, M., Lai, D., Potekhin, A. Y., & Arras, P. 2005, ApJ, 628, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Weisskopf, M. C., Tennant, A. F., Yakovlev, D. G., et al. 2011, ApJ, 743, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Yakovlev, D. G., & Pethick, C. J. 2004, ARA&A, 42, 169 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Zharikov, S., & Mignani, R. P. 2013, MNRAS, 435, 2227 [NASA ADS] [CrossRef] [Google Scholar]
- Zharikov, S., Shibanov, Y., & Komarova, V. 2006, Adv. Space Res., 37, 1979 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left panel: GTC/OSIRIS ~51′′× 51′′ Sloan g′-image fragment of the PSR J0357+3205 field. The circle shows 3σ X-ray pulsar position uncertainty for the optical observations epoch (see text for details). The 15′′× 15′′ pulsar vicinity within the dashed rectangle is enlarged in the right panel and smoothed with a one-pixel Gaussian kernel. The sources discussed in the text are labelled by numbers |
| In the text | |
 |
Fig. 2 68%, 90%, and 99% ( |
| In the text | |
 |
Fig. 3 Same as in Fig. 2 but for the absorbed NSMAX+PL model. |
| In the text | |
 |
Fig. 4 90% and 99% ( |
| In the text | |
 |
Fig. 5 Unabsorbed spectrum of PSR J0357+3205 in the optical-X-ray range. The GTC g′-band flux upper limit is indicated by the bar with an arrow. The XMM-Newton and Chandra data points are shown by grey bars8. The thick solid line is the best-fit BB+PL model to the X-ray data. The thin dotted line with the dark-grey filled region is the PL component with 90% uncertainties. The thick dotted line is the BB hot spot component. The thin/thick dash-dotted and dashed lines are the best-fit NSA and NSMAX components with variable/fixed normalisations. The upper limit on the thermal spectral flux from the entire surface of the NS obtained with the BB+PL+BB model is shown by the light-grey filled region. The extrapolation of the γ-ray Fermi spectrum with its uncertainties is shown by the thin solid line with a hatched region. |
| In the text | |
 |
Fig. 6 Measured entire surface temperatures T∞ as seen by a distant observer (filled circles) for NSs of different ages t in comparison with the cooling theory predictions (hatched regions). The dense hatched region corresponds to the standard cooling theory, while the sparse hatched region shows the minimal cooling theory predictions. The bold star with error bars show the PSR J0357+3205 surface temperature. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




