| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201322622 | |
| Published online | 01 April 2014 | |
Kepler-210: An active star with at least two planets⋆
1 Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
e-mail: pioannidis@hs.uni-hamburg.de
2 Centre for Astrophysics and Planetary Science, School of Physical Sciences (SEPnet), The University of Kent, Canterbury, CT2 7NH, UK
3 Dept. of Astronomy, Box 351580, University of Washington, Seattle WA 98195, USA
Received: 6 September 2013
Accepted: 31 January 2014
We report the detection and characterization of two short-period, Neptune-sized planets around the active host star Kepler-210. The host star’s parameters derived from those planets are (a) mutually inconsistent and (b) do not conform to the expected host star parameters. We furthermore report the detection of transit timing variations (TTVs) in the O–C diagrams for both planets. We explore various scenarios that explain and resolve those discrepancies. A simple scenario consistent with all data appears to be one that attributes substantial eccentricities to the inner short-period planets and that interprets the TTVs as due to the action of another, somewhat longer period planet. To substantiate our suggestions, we present the results of N-body simulations that modeled the TTVs and that checked the stability of the Kepler-210 system.
Key words: planetary systems / methods: data analysis / stars: individual: Kepler 210
Tables 5–8 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/564/A33
© ESO, 2014
1. Introduction
Since the launch of the Kepler Mission in 2009, a large number of planetary candidates has been found using the transit method in the high precision Kepler lightcurves. Specifically, 2321 planetary candidates in 1790 hosts stars have been reported, from which about one third are actually hosted in multiple systems (Batalha et al. 2013). The majority of these Kepler planetary candidates are expected to be real planets (Lissauer et al. 2012) and therefore those stars present an excellent opportunity for a more detailed study and characterization through the method of transit timing variations (TTVs). Ever since the first proposals of the method by Agol et al. (2005) and Holman & Murray (2005), TTVs have been widely used to search for smaller, otherwise undetectable planets in systems containing already confirmed planets. In multiple systems this method can be applied in order to confirm the physical validity of the system along with a rough estimate of the components’ mass, which can otherwise be obtained only through radial velocity data. For the Kepler candidates the Kepler team has carried out and reported this kind of analysis for 41 extrasolar planet systems. For the last announcement of the series see Steffen et al. (2013).
 |
Fig. 1 Lomb-Scargle periodogram for the raw lightcurve as logarithmic power (on y axis) vs. period. A polynomial fit was applied to remove systematics related to the rotation of the telescope. |
In this paper we present our in-depth analysis and results for a particular system, Kepler-210 (=KOI-676), which was previously identified and listed as a planet host candidate in the catalog by Borucki et al. (2011). The specific characteristics of Kepler-210 that enticed us to perform a detailed study of this candidate system were the high activity of its host star coupled with the fact that the system harbors two transiting planets, which we validate using spectral and TTVs analysis, as well as stability tests.
The plan of our paper is as follows. In the first section we describe the methods used to determine the stellar and planetary properties. In the second section we discuss various scenarios to explain the detected discrepancies in the orbital elements of the planets. Furthermore, we describe the results of our TTVs analysis for both planets, and finally, we summarize with what we believe is the most probable scenario.
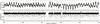 |
Fig. 2 Fraction of the Kepler-210 lightcurve. Top: part of the raw lightcurve demonstrating the activity of Kepler-210. Bottom: the transits of planet a (green) and b (red) for that particular time, with the stellar activity removed by using the kepflatten routine of the Pyke package for pyraf. |
2. Data analysis
2.1. Stellar activity
The Kepler data of Kepler-210 were obtained from the STDADS archive and contain the data recorded in the quarters Q1 to Q12. To achieve better temporal coverage we used both long and short cadence data. We decided to use the SAP data for our analysis to avoid any artifacts introduced by the use of SAP_PDC data, given the obvious complexity of the Kepler-210 lightcurve (cf., Fig. 2). Clearly, the host star of the Kepler-210 system is of particular interest by itself.
To give an impression of the activity of Kepler-210, a part of the overall Kepler lightcurve of Kepler-210 covering 500 days is shown in Fig. 2. Peak-to-peak variations on the order of 2% can easily be identified on time scales of a few days, and in addition, variations on longer time scales are also visible. To assess the dominant time scales of variability we computed a Lomb-Scargle periodogram over the full available data set, which we show in Fig. 1. Two peaks are clearly observable in the resulting periodogram. We interpret the most significant peak at 12.33 ± 0.15 days as the rotation period of the star, while the second, smaller peak at 6.15 ± 0.047 days is interpreted as an alias from the 12.33 day rotation period. We further note that both peaks are quite broad, with significant power residing at frequencies near the peak frequency.
 |
Fig. 3 Demonstration of stellar activity removal procedure; see text for details. |
Stellar parameters of Kepler-210 taken from Batalha et al. (2013).
MCMC analysis transit model fit results and their “1σ” errors.
2.2. Data preparation
For our transit and TTVs analysis we must remove all effects of stellar activity as much as possible. In order to rectify the Kepler lightcurve of Kepler-210 we proceed as follows: for each transit of each planet we select some part of the lightcurve centered at the estimated mid-transit time, including data points before and after ingress and egress, respectively (see Fig. 3, upper left). The obvious transit points are then removed (Fig. 3, upper right) and a second order polynomial fit is applied to the remaining data points (see Fig. 3 lower left). Finally, all selected data points including those obtained during transit are divided by the result of the polynomial fit (see Fig. 3 lower right) and we obtain a rectified lightcurve, normalized to unity for the data prior to the first and after the fourth contact. In this fashion we prepare the transit data for both planets for an application of our transit model fit; we consider only transits by one planet and exclude any simultaneous transits from our analysis.
2.3. Model fitting
The effects of the host star’s stellar activity are clearly visible also in the transit lightcurves, which are twofold: (see Fig. 2): star spots occulted by the planet on the one hand lead to bumps in the lightcurve as shown by Wolter et al. (2009), while star spots on the unocculted face of the star on the other hand lead to variable transit depths. Thus, both effects increase the dispersion of the transit data and the incorrect normalization leads to incorrect stellar and planetary parameters. In order to minimize the effects of stellar activity we therefore decided to use transits, following the following two rules:
-
1.
We select those transits occurring close to maximum flux in the activity modulations, which corresponds to smaller spot coverage of the stellar surface.
-
2.
We model each transit separately, isolated the transit data and measure the χ2-test statistics. Only the transits with acceptable fits are selected.
Thus, for the transit model fit of the inner planet 89 transits were used, while for the outer planet a total of 10; we rejected 154 transits by the inner planet and 41 transits by the outer planet for this analysis. To determine the best fit model we used the analytical transit lightcurve model by Mandel & Agol (2002) and Markov-chain Monte-Carlo (MCMC) sampling1 for the computation of the fit parameters and their errors. In this process we used the limb darkening coefficients for the model as calculated by integrating the values of the Claret catalog (Claret et al. 2012) for the parent star’s nominal parameters Teff, log g and [Fe/H] listed in Table 1 .
2.4. Fit results
 |
Fig. 4 Folded lightcurve of planet b, using the total number of transits and the best fit model. The lower diagram shows the model residuals binned, which in this case is less obvious than in case of planet c (see Fig. 5). |
In Figs. 4 and 5 we show the full sample of the derived mean normalized Kepler transit lightcurves and our best fit model (red line; upper panel), the fit residuals for all data points (middle panel) and the mean values of the individual residuals as well as for blocks of twenty adjacent phase points (lower panel). The physical parameters derived from our transit analysis are listed in Table 2; note that the inner, shorter period planet is smaller than the outer planet.
3. Transit timing variations
3.1. Timing variation analysis
 |
Fig. 5 Folded lightcurve of planet c, using the total number of transits and the best fit model. The transit profile is affected by spots during and after ingress. |
After completion of the transit model fit procedure and the determination of the global parameters for each planet, we recalculated the mid-transit times for all transits of each planet, i.e., also those that had been rejected for the best model fit. To that end we reapplied the MCMC fitting algorithm for every transit separately, keeping all model parameters fixed except for the individual mid-transit times tMT,ii = 1,N. From the observed mid-transit times tMT,i, their errors σi and the integer transit epochs Ni we derived a mean period P and time reference T0, by minimizing the expression 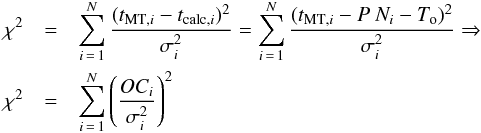 (1)with respect to P and T0; the thus resulting O–C diagrams for planets b and c are shown in Fig. 6; the appropriate data for the creation of those diagrams are available at the CDS.
(1)with respect to P and T0; the thus resulting O–C diagrams for planets b and c are shown in Fig. 6; the appropriate data for the creation of those diagrams are available at the CDS.
3.2. TTVs results
While in the O–C diagram of planet b (Fig. 6) some modulation is visible, no clear variation is apparent for planet c. In order to assess to what extent TTVs might be caused by stellar activity, as for example the observed anomaly in the ingress of the transit of planet b (Fig. 4), we calculated the transit times using two different approaches, additional to the one described in 3.1:
-
–
We recalculated the transit times using the methoddescribed in 3.1, but by excluding the affected areas of thetransit phase.
-
–
We used the analysis described by Carter & Winn (2009) in order to remove the spot anomalies, considering them as red noise.
Null hypothesis χ2 results with their P-values for the long cadence alone (left column) vs. the short cadence alone (middle column) and the combined long and short cadence data (right column) for unbinned and binned data. In the square brackets are listed the degrees of freedom.
 |
Fig. 6 O–C diagrams of planet b (upper panel) and c (lower panel), along with the best fit models. The dashed line discriminates the long from the short cadence data. |
In order to quantify the significance of the observed O–C variations, we carried out a χ2-analysis on the null hypothesis that there are no timing variations, on the long and short cadence data separately and on the joined long and short cadence data. We also carried out the same analysis by averaging the measured O–C values over ten consecutive epochs; the respective χ2-values and the derived significance levels are listed in Table 3.
An inspection of Table 3 shows that the unbinned long cadence data show no evidence for any non-zero O–C values, while the short cadence data do; binning does greatly increase the significance of the non-zero O–C values.
Since the values of the χ2-test statistics sensitively depend on the measurement errors σi, we carefully checked the errors of the derived mid-transit times by using two independent methods and convinced ourselves of the internal consistency of our error determination. In addition we checked that the derived χ2-values are not produced by a few individual outliers. As a result we are confident that the observed TTVs are statistically significant.
4. Discussion
4.1. Examination of stellar properties
In order to better determine the stellar parameters of Kepler-210, a high resolution spectrum was acquired, using the CAFE instrument on the 2.2 m telescope of the Calar Alto Observatory in Spain. For our analysis we also used two spectra of Kepler-210, taken from the CFOP2 web page. We specifically inspected the spectra for a second set of lines indicating the existence of a close unresolved companion but found none. For the same purpose we also examined the pixel area around the star using the Kepler target fits frames, but found again no evidence of any variable star in the vicinity of the central star that could create a contaminating signal.
To measure the color index B − V, we observed Kepler-210 together with with two standard stars (HD 14827 and HD 195919), using the 1.2 m Oskar-Lühning-Telescope (OLT) from Hamburg Observatory and found B − VKepler − 210 = 1.131 ± 0.064, consistent with the color derived from CFOP (1.088 ± 0.037) and other sources; thus the spectral type of Kepler-210 is in the late K range.
We then proceeded to estimate the stars age using the gyrochronology expression 2 derived by Barnes (2007)![\begin{eqnarray} \label{age} \log(t_{\rm gyro}) &=& {1\over n}\{\log(P)-\log(\alpha)-[\beta \cdot \log(B-V-0.4)]\}, \end{eqnarray}](/articles/aa/full_html/2014/04/aa22622-13/aa22622-13-eq35.png) (2)where t is in Myr, B − V is the measured color, P (in days) is the rotational period, n = 0.5189, α = 0.7725 ± 0.011 and β = 0.601 ± 0.024. By using Eq. (2) with P = 12.33 days and the B − V=1.131, we estimate an age of 350 ± 50 Myrs for Kepler-210; this estimate appears reasonable given its high degree of activity.
(2)where t is in Myr, B − V is the measured color, P (in days) is the rotational period, n = 0.5189, α = 0.7725 ± 0.011 and β = 0.601 ± 0.024. By using Eq. (2) with P = 12.33 days and the B − V=1.131, we estimate an age of 350 ± 50 Myrs for Kepler-210; this estimate appears reasonable given its high degree of activity.
4.2. Mean stellar density
When a planet is transiting in front of its parent star, we have the opportunity to accurately derive the ratio between the stellar radius R⋆ and the orbital semimajor axis a (cf., Table 2). Combining this information with Kepler’s third law, we can compute an expression for the mean density ρmean of the host star through 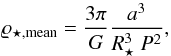 (3)with G denoting the gravitational constant in addition to the terms containing only the observed quantities a/R⋆ and period P. The value for a/R⋆ is derived from the transit modeling, given the large number of transits, for both planets, the values of a/R⋆ and P can be estimated with relatively high accuracy. Carrying out this computation using the observed parameters for planets b and c (cf., Table 2) we obtain densities of ϱ⋆ ,b = 0.27 ± 0.004 g/cm3 and ϱ⋆ ,c = 0.46 ± 0.038 g/cm3, respectively for the host. On the other hand, based on the nominal stellar parameters of the host star we expect a mean density of ϱo ≈ 2.6 g/cm3. Thus the mean host star densities derived from planets b and c are, first, inconsistent with each other, and second, differ by almost an order of magnitude from the expected host star density. Since we firmly believe in Kepler’s third law, there must be a physical explanation for both discrepancies.
(3)with G denoting the gravitational constant in addition to the terms containing only the observed quantities a/R⋆ and period P. The value for a/R⋆ is derived from the transit modeling, given the large number of transits, for both planets, the values of a/R⋆ and P can be estimated with relatively high accuracy. Carrying out this computation using the observed parameters for planets b and c (cf., Table 2) we obtain densities of ϱ⋆ ,b = 0.27 ± 0.004 g/cm3 and ϱ⋆ ,c = 0.46 ± 0.038 g/cm3, respectively for the host. On the other hand, based on the nominal stellar parameters of the host star we expect a mean density of ϱo ≈ 2.6 g/cm3. Thus the mean host star densities derived from planets b and c are, first, inconsistent with each other, and second, differ by almost an order of magnitude from the expected host star density. Since we firmly believe in Kepler’s third law, there must be a physical explanation for both discrepancies.
 |
Fig. 7 Contour plot of eccentricity versus true anomaly during the mid-transit (φ). For a circular system (e = 0) the density should equal ϱo ⋍ 2.6 g/cm3, as can be calculated for the given values of R⋆ and M⋆. The TBD derived from the a/R⋆ values of ϱ⋆ for the planets Kepler-210b (black line) and Kepler-210c (gray line) can be explained for eccentricities ≳0.4 and ≳0.51 respectively, depending on the true anomaly of the planet during the mid-transit. The dashed lines represent the uncertainty limits. |
4.2.1. Ellipticity of planetary orbits
 |
Fig. 8 Variation of inclination, R⋆ and Rp, assuming third light interference F3 for Kepler-210c. |
So far our analysis has implicitly assumed circular orbits for both planets. For elliptical orbits the orbital speed and hence the transit duration change during the orbit and therefore there is no unique relation between transit duration and stellar and planetary dimensions. Assuming that the orbital velocity is constant during the actual transit, Tingley & Sackett (2005) relate the transit duration Dell to the period P and the impact parameter b of a transit through the expression 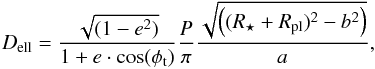 (4)where φt denotes the true anomaly at the mid-transit, while R⋆, Rpl and a, denote stellar and planetary radii and semi-major axis respectively. Consequently, the transit duration Dell of an elliptical orbit scales with the transit duration Dcirc of a circular orbit (for the same system geometry and the same period) through
(4)where φt denotes the true anomaly at the mid-transit, while R⋆, Rpl and a, denote stellar and planetary radii and semi-major axis respectively. Consequently, the transit duration Dell of an elliptical orbit scales with the transit duration Dcirc of a circular orbit (for the same system geometry and the same period) through 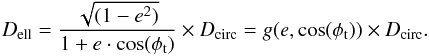 (5)It is straightforward to convince oneself that the derived sizes for star and planet scale with the scaling function g(e,cos(φt)) introduced in Eq. (5). Since the mean stellar density scales with
(5)It is straightforward to convince oneself that the derived sizes for star and planet scale with the scaling function g(e,cos(φt)) introduced in Eq. (5). Since the mean stellar density scales with 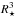 , we find
, we find 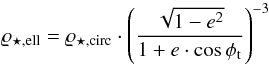 (6)with ϱ⋆ ,circ = ϱ⋆ ,mean from Eq. (3). Hence the discrepant stellar densities can be explained by introducing suitable eccentricities and true transit anomalies. By solving 6 for different values of e and φt it is thus possible to to constrain the range of permissible eccentricities as well as values for φt, for which the derived stellar density becomes equal to the density expected for the spectral type of the star for both planets; the corresponding curves are shown in Fig. 7, where we plot for each planet the combination of e and φt resulting in a nominal stellar density of 2.7 g cm-3. Figure 7 shows that eccentricities of 0.4 (for planet b) and 0.5 (for planet c) are required to produce the expected stellar densities.
(6)with ϱ⋆ ,circ = ϱ⋆ ,mean from Eq. (3). Hence the discrepant stellar densities can be explained by introducing suitable eccentricities and true transit anomalies. By solving 6 for different values of e and φt it is thus possible to to constrain the range of permissible eccentricities as well as values for φt, for which the derived stellar density becomes equal to the density expected for the spectral type of the star for both planets; the corresponding curves are shown in Fig. 7, where we plot for each planet the combination of e and φt resulting in a nominal stellar density of 2.7 g cm-3. Figure 7 shows that eccentricities of 0.4 (for planet b) and 0.5 (for planet c) are required to produce the expected stellar densities.
4.2.2. Second (third) light scenario
 |
Fig. 9 Derived stellar density versus assumed third light contribution F3. |
Despite the fact that neither the optical spectrum nor the centroid analysis of the Kepler data have shown any evidence for a companion or blend, it might still be possible that some third object in the background or foreground with flux F3 contributes to the system flux in a way that the observed total flux Fobs is given by 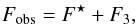 (7)where F⋆ is the desired planet host’s flux, which has to be used for the transit modeling. If this hypothetical third light contribution F3 is substantial, the true transit depth dtrue would be underestimated and an incorrect radius for the Kepler-210 host star would be derived. Assuming that the limb darkening coefficients are identical and equal to the values presented in Table 1 for all system sources, we calculate the influence of the third light source on the derived stellar density (as shown in Fig. 9), considering the following non-linear system of equations, which allows computing the stellar and planetary radii (each scaled by the semi-major axis)
(7)where F⋆ is the desired planet host’s flux, which has to be used for the transit modeling. If this hypothetical third light contribution F3 is substantial, the true transit depth dtrue would be underestimated and an incorrect radius for the Kepler-210 host star would be derived. Assuming that the limb darkening coefficients are identical and equal to the values presented in Table 1 for all system sources, we calculate the influence of the third light source on the derived stellar density (as shown in Fig. 9), considering the following non-linear system of equations, which allows computing the stellar and planetary radii (each scaled by the semi-major axis) 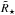 and
and 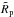 and, i, the inclination of the orbit normal with respect to the line of sight, given the observed period P, the observed time between the first and forth contact, T14, the time between the second and third contact, T23 and the observed (relative) transit depth at mid-transit dobs.
and, i, the inclination of the orbit normal with respect to the line of sight, given the observed period P, the observed time between the first and forth contact, T14, the time between the second and third contact, T23 and the observed (relative) transit depth at mid-transit dobs. 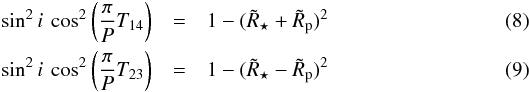 and
and 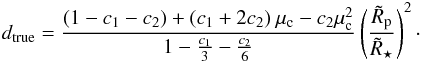 (10)Here c1 and c2 denote the quadratic limb darkening coefficients and μc denotes the expression
(10)Here c1 and c2 denote the quadratic limb darkening coefficients and μc denotes the expression 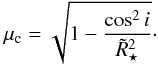 (11)We clearly need the true transit depth dtrue to compute the values of
(11)We clearly need the true transit depth dtrue to compute the values of 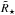 ,
, 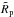 and i, yet only the observed transit depth dobs is available; the two depths are related, however, through
and i, yet only the observed transit depth dobs is available; the two depths are related, however, through 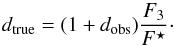 (12)Therefore, given the observed values of dobs, T14 and T23 and the observed periods P for both planets, the derived values for
(12)Therefore, given the observed values of dobs, T14 and T23 and the observed periods P for both planets, the derived values for 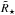 and hence ϱ⋆ will depend on the assumed third light contribution F3/F⋆. The resulting system of equation is quite non-linear. In order to provide a feeling on how sensitive the solutions depend on the third light contribution F3/F⋆, we plot in Fig. 8 the variation of the derived values for the inclination and stellar and planetary radii (for the planet Kepler-210c), relative to the case of no third light. As is clear from Fig. 8, the inclination increases only slightly (it cannot exceed 90 degrees), while the stellar radius decreases (as desired) and the planetary radius increases. Finally, we can derive the stellar density, for which our results are shown in Fig. 9, where we plot the derived stellar densities for both planets as a function of the assumed third light contribution
and hence ϱ⋆ will depend on the assumed third light contribution F3/F⋆. The resulting system of equation is quite non-linear. In order to provide a feeling on how sensitive the solutions depend on the third light contribution F3/F⋆, we plot in Fig. 8 the variation of the derived values for the inclination and stellar and planetary radii (for the planet Kepler-210c), relative to the case of no third light. As is clear from Fig. 8, the inclination increases only slightly (it cannot exceed 90 degrees), while the stellar radius decreases (as desired) and the planetary radius increases. Finally, we can derive the stellar density, for which our results are shown in Fig. 9, where we plot the derived stellar densities for both planets as a function of the assumed third light contribution 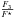 . As is clear from Fig. 9, the third light contribution would have to be substantial, and in fact the third light would have to dominate the total system flux in order to obtain values of ϱ⋆ c as expected for stars on the main sequence in the relevant spectral range. Yet, the two planets still yield discrepant densities of their host, so one would have to introduce yet another host for the second planet, which appears at least a little contrived. Therefore we conclude that the introduction of a third light source does not lead to a satisfactory solution of inconsistency in the derived stellar parameters.
. As is clear from Fig. 9, the third light contribution would have to be substantial, and in fact the third light would have to dominate the total system flux in order to obtain values of ϱ⋆ c as expected for stars on the main sequence in the relevant spectral range. Yet, the two planets still yield discrepant densities of their host, so one would have to introduce yet another host for the second planet, which appears at least a little contrived. Therefore we conclude that the introduction of a third light source does not lead to a satisfactory solution of inconsistency in the derived stellar parameters.
4.2.3. Inflated star
Another possible scenario explaining the Kepler observations of Kepler-210 would be the assumption that the host is not on the main sequence, but rather evolved and in fact a giant or sub-giant. Such stars are usually not active, however, there are some classes of evolved stars which are quite active, for example, variables of the FK Com type. Those stars are highly active G-K type sub-giant stars with surface gravities log(g) of ~3.5. They show strong photometric rotational modulations caused by a photosphere covered with inhomogeneously distributed spots. An other important characteristic of these objects is their rapid rotation. Generally the vsini derived from their spectra is between ~50 and 150 km s-1 (Berdyugina 2005). In the case of Kepler-210 vsini is ~4 km s-1, and thus we believe that a FK-com scenario does not provide a suitable explanation for the observed density discrepancy.
4.3. Kepler-210 TTVs
As described in Sect. 3, TTVs are detected in both planets. In order to further examine the properties of these variations we searched for any periodicities in the O–C data by constructing a Lomb-Scargle periodogram on every set. For the outer and larger planet, the Lomb-Scargle periodogram shows a leading period of about 690 days, which is apparent in the modulation of the O−C curve in Fig. 6, while for the inner and smaller planet the periodicity results remain ambiguous, most probably due to the large scatter in its O–C diagram.
χ2 results of the model for 2 eccentric planets hypothesis, 3 non eccentric planets and 3 eccentric planets.
What would be a physical scenario consistent with these O–C diagrams? We first note that the orbital period ratio of the system is very close to a 13/4, if we consider that the errors in periods in Table 2 are also affected by the TTVs. This ratio is not close to any low order mean motion resonance so the amplitude of any TTVs is expected to be relatively small for both planets (Agol et al. 2005).
In order to verify this and to model the TTVs we use the N-body code as presented in the same paper. The N-body code requires the planetary masses which are unknown. Assuming ad hoc that the planetary densities are below 5 g/cm3, it is clear that the masses of the two planets are substantially below 0.5 MJ. Furthermore, in order to roughly estimate the planetary masses below that limit, we use a general mass vs. radius law as described by Lissauer et al. (2011) in the form 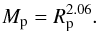 (13)With the masses thus specified, we first considered only the two transiting planets for our TTVs simulations. Assuming non-eccentric orbits resulted in TTVs of less than a minute, which is far from the observed variations for both planets. The TTVs would remain in that state even if we assume higher masses, under the limit of 12 MJ. As discussed in detail by Lithwick et al. (2012), the TTVs amplitude can also be affected by eccentricity. Implementation of eccentric orbits for both planets, Kepler-210b and Kepler-210c, improved the fit substantially; the modeled TTVs together with the data are shown in Fig. 10, the fit results in terms of fit quality measured through χ2 are given in Table 4.
(13)With the masses thus specified, we first considered only the two transiting planets for our TTVs simulations. Assuming non-eccentric orbits resulted in TTVs of less than a minute, which is far from the observed variations for both planets. The TTVs would remain in that state even if we assume higher masses, under the limit of 12 MJ. As discussed in detail by Lithwick et al. (2012), the TTVs amplitude can also be affected by eccentricity. Implementation of eccentric orbits for both planets, Kepler-210b and Kepler-210c, improved the fit substantially; the modeled TTVs together with the data are shown in Fig. 10, the fit results in terms of fit quality measured through χ2 are given in Table 4.
Clearly, also the TTVs analysis supports a scenario of two planets with rather eccentric orbits similar to our discussion in 4.2.1. However, in order to produce the observed TTVs the system configuration must be such that the true anomaly, of both planets at the time of transit, φt, should exceed 40°, while also the difference in true anomaly Δφt should be ~60°, However, this configuration appears impossible due to the physical constraints in Fig. 7. Furthermore, our stability tests, which performed with the swift_rmvs3 algorithm (Levison & Duncan 1994), show that this configuration is unstable on time scales in excess of ~1 Myear. Finally we note that the probability of observing a transit is higher for small values of true anomaly, i.e., for the times near periastron passage.
We therefore conclude that a scenario with only two planets with eccentric orbits is unlikely and introduce a third, hypothetical planet KOI-676.03 in order to stabilize the system. We consider both eccentric and non-eccentric orbits for Kepler-210b and Kepler-210c. In order to determine period, mass and eccentricity for the hypothetical planet KOI-676.03, we considered several possible system configurations.
We emphasize that we cannot derive a unique solution for the physical parameters of this hypothetical planet. Most importantly, we need to assume a mass for this planet, which controls the strength of the gravitational interaction with the observed planets Kepler-210b and Kepler-210c. Thus, given the observed TTVs amplitude and given the assumed mass of KOI-676.03, a certain value of semi-major axis and hence period is derived. The higher the assumed mass, the longer the resulting period, and thus there is more than one configuration to account for the detected TTVs signal.
In order to produce possible candidate systems, we carried out simulations assuming some given mass for KOI-676.03, considering periods between 20 to 300 days, masses in the range M03 ~ 0.1–0.6 MJ and eccentricities e ≃ 0.1–0.3. A particularly promising configuration, but by no means unique solution, consistent with all Kepler data, has a period P ≃ 63 days; in Fig. 11 and again Table 4 (for the case with zero eccentricity) and in Fig. 12 and Table 4 (for the eccentric case) we show that such a scenario provides results consistent with the available Kepler data. As is clear from Figs. 11 and 12, as well as Table 4, the difference between the non-eccentric and eccentric case is marginal at best, while (statistically) preferable over a two planets scenario. In addition, the eccentricities of the planets Kepler-210b and Kepler-210c give a high frequency TTVs signal, which might better explain the higher dispersion of the TTVs in Kepler-210b. In that case the model also suggests φt values around zero with Δφ < 30°, which are in line with Fig. 7. Also the system’s stability exceeds 107 years.
 |
Fig. 10 TTVs expected for two planets assuming eccentric orbits with eb = 0.44 and ec = 0.50. |
 |
Fig. 11 TTVs expected for three planets with non-eccentric orbits for all components of the system. The third planet’s period for that case is P03 = 63.07 days. |
 |
Fig. 12 TTVs expected for three planets assuming eccentric orbits with eb = 0.45, ec = 0.51 and e03 = 0.23. The Third planet’s period for that case is P03 = 63.29 days. |
In the case of non eccentric orbits the system would reach fatal instability once masses above 5 MJ are chosen. For eccentric orbits the upper limit for the masses of the system becomes lower. While this fact suggests a planetary nature of the system components, it also introduces an additional factor of concern about the long term stability of the system. We do point out that this third stabilizing planet does produce a radial velocity signal in the system. For our nominal case we plot in Fig. 13 the expected RV signal in a synthetic radial velocity diagram, which shows peak-to-peak variations in excess of 60 m/s; clearly such RV variations ought to be detectable despite the high activity level of the host star, and therefore, the detection of a RV-signal would significantly constrain the possible configuration space of the system.
5. Summary
We report the detection and characterization of two transiting Neptune-sized planets, Kepler-210b and Kepler-210c with periods of 2.4532 days and 7.9723 days respectively around a presumably quite young and active K-type dwarf. These objects were first listed as planetary candidates by the Kepler team. We show that the transits of both planets are affected by spots. From the observed transit parameters and in particular from the observed value of a/R⋆ it is possible to calculate the mean density of the host star using the Kepler’s 3rd law. Interestingly, the two planets yield discrepant mean host star densities, which in addition are inconsistent with the densities expected for a K-type dwarf. Having explored various scenarios we conclude that the assumption of quite eccentric orbits for both planets provides the currently most probable scenario.
 |
Fig. 13 Predicted, synthetic, radial velocity diagram for the system Kepler-210 for P03 = 63 days, M03 = 0.4 Mj, e03 = 0.23 and i03 = 60°. |
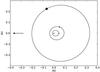 |
Fig. 14 Suggested system configuration. The earth is at the direction of the arrow. |
In addition, both planets show transit timing variations. Using N-body simulations we constructed possible system configurations consistent with the Kepler data. While it is possible to explain the observed TTVs with a two planet scenario,
such a scenario requires a very special geometrical configuration and is unstable on time scales of 106 years. As a result we believe that there exists a third planet, KOI-676.03, with a mass between ~0.3–0.6 MJ in a slightly eccentric (e ≃ 0.2) orbit with period ~63 days, which stabilizes the whole Kepler-210 planetary system.
Different configurations are also possible, yet this stabilizing hypothetical planet should produce a detectable RV signal. We therefore suggest RV monitoring of Kepler-210, which is likely to provide a substantially increased insight into the Kepler-210 planetary system.
Acknowledgments
P.I. and C.v.E. acknowledge funding through the DFG grant RTG 1351/2 “Extrasolar planets and their host stars”. The results of this publication are based on data collected by the NASA’s Kepler satellite. We would like to thank the director and the Calar Alto Observatory staff for the approval and execution of a DDT proposal. Finally we acknowledge the exceptional work by the CFOP team which was essential for this publication.
References
- Agol, E., Steffen, J., Sari, R., & Clarkson, W. 2005, MNRAS, 359, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, S. A. 2007, ApJ, 669, 1167 [NASA ADS] [CrossRef] [Google Scholar]
- Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2013, ApJS, 204, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V. 2005, Liv. Rev. Sol. Phys., 2, 8 [Google Scholar]
- Borucki, W. J., Koch, D. G., Basri, G., et al. 2011, ApJ, 736, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, J. A., & Winn, J. N. 2009, ApJ, 704, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A., Hauschildt, P. H., & Witte, S. 2012, VizieR Online Data Catalog, J/A+A/546/A14 [Google Scholar]
- Holman, M. J., & Murray, N. W. 2005, Science, 307, 1288 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Levison, H. F., & Duncan, M. J. 1994, Icarus, 108, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J., Ragozzine, D., Fabrycky, D. C., et al. 2011, ApJS, 197, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J., Marcy, G. W., Rowe, J. F., et al. 2012, ApJ, 750, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Lithwick, Y., Xie, J., & Wu, Y. 2012, ApJ, 761, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, J. H., Fabrycky, D. C., Agol, E., et al. 2013, MNRAS, 428, 1077 [NASA ADS] [CrossRef] [Google Scholar]
- Tingley, B., & Sackett, P. D. 2005, ApJ, 627, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Wolter, U., Schmitt, J. H. M. M., Huber, K. F., et al. 2009, A&A, 504, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Null hypothesis χ2 results with their P-values for the long cadence alone (left column) vs. the short cadence alone (middle column) and the combined long and short cadence data (right column) for unbinned and binned data. In the square brackets are listed the degrees of freedom.
χ2 results of the model for 2 eccentric planets hypothesis, 3 non eccentric planets and 3 eccentric planets.
All Figures
 |
Fig. 1 Lomb-Scargle periodogram for the raw lightcurve as logarithmic power (on y axis) vs. period. A polynomial fit was applied to remove systematics related to the rotation of the telescope. |
| In the text | |
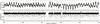 |
Fig. 2 Fraction of the Kepler-210 lightcurve. Top: part of the raw lightcurve demonstrating the activity of Kepler-210. Bottom: the transits of planet a (green) and b (red) for that particular time, with the stellar activity removed by using the kepflatten routine of the Pyke package for pyraf. |
| In the text | |
 |
Fig. 3 Demonstration of stellar activity removal procedure; see text for details. |
| In the text | |
 |
Fig. 4 Folded lightcurve of planet b, using the total number of transits and the best fit model. The lower diagram shows the model residuals binned, which in this case is less obvious than in case of planet c (see Fig. 5). |
| In the text | |
 |
Fig. 5 Folded lightcurve of planet c, using the total number of transits and the best fit model. The transit profile is affected by spots during and after ingress. |
| In the text | |
 |
Fig. 6 O–C diagrams of planet b (upper panel) and c (lower panel), along with the best fit models. The dashed line discriminates the long from the short cadence data. |
| In the text | |
 |
Fig. 7 Contour plot of eccentricity versus true anomaly during the mid-transit (φ). For a circular system (e = 0) the density should equal ϱo ⋍ 2.6 g/cm3, as can be calculated for the given values of R⋆ and M⋆. The TBD derived from the a/R⋆ values of ϱ⋆ for the planets Kepler-210b (black line) and Kepler-210c (gray line) can be explained for eccentricities ≳0.4 and ≳0.51 respectively, depending on the true anomaly of the planet during the mid-transit. The dashed lines represent the uncertainty limits. |
| In the text | |
 |
Fig. 8 Variation of inclination, R⋆ and Rp, assuming third light interference F3 for Kepler-210c. |
| In the text | |
 |
Fig. 9 Derived stellar density versus assumed third light contribution F3. |
| In the text | |
 |
Fig. 10 TTVs expected for two planets assuming eccentric orbits with eb = 0.44 and ec = 0.50. |
| In the text | |
 |
Fig. 11 TTVs expected for three planets with non-eccentric orbits for all components of the system. The third planet’s period for that case is P03 = 63.07 days. |
| In the text | |
 |
Fig. 12 TTVs expected for three planets assuming eccentric orbits with eb = 0.45, ec = 0.51 and e03 = 0.23. The Third planet’s period for that case is P03 = 63.29 days. |
| In the text | |
 |
Fig. 13 Predicted, synthetic, radial velocity diagram for the system Kepler-210 for P03 = 63 days, M03 = 0.4 Mj, e03 = 0.23 and i03 = 60°. |
| In the text | |
 |
Fig. 14 Suggested system configuration. The earth is at the direction of the arrow. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


