| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 5 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201322555 | |
| Published online | 28 March 2014 | |
Research Note
pFoF: a highly scalable halo-finder for large cosmological data sets
1 Laboratoire Univers et Théories, UMR 8102, CNRS, Observatoire de Paris, Université Paris Diderot, 5 place Jules Janssen, 92195 Meudon Cedex, France
e-mail: fabrice.roy@obspm.fr; vincent.bouillot@obspm.fr; yann.rasera@obspm.fr
2 Centre for Astrophysics, Cosmology & Gravitation, Department of Mathematics & Applied Mathematics, University of Cape Town, 7701 Cape Town, South Africa
Received: 28 August 2013
Accepted: 2 February 2014
We present a parallel implementation of the friends-of-friends algorithm and an innovative technique for reducing complex-shaped data to a user-friendly format. This code, named pFoF, contains an optimized post-processing workflow that reduces the input data coming from gravitational codes, arranges them in a user-friendly format and detects groups of particles using percolation and merging methods. The pFoF code also allows for detecting structures in sub- or non-cubic volumes of the comoving box. In addition, the code offers the possibility of performing new halo-findings with a lower percolation factor, useful for more complex analysis. In this paper, we give standard test results and show performance diagnostics to stress the robustness of pFoF. This code has been extensively tested up to 32768 MPI processes and has proved to be highly scalable with an efficiency of more than 75%. It has been used for analysing the Dark Energy Universe Simulation: Full Universe Runs (DEUS-FUR) project, the first cosmological simulations of the entire observable Universe, modelled with more than half a trillion dark matter particles.
Key words: dark matter / large-scale structure of Universe / methods: numerical
© ESO, 2014
1. Introduction
Owing to the huge volume of forthcoming cosmological surveys (e.g. LSST, EUCLID or SKA), the need for larger and larger cosmological N-body simulations is greater than ever. With the ever-increasing memory and computing power of supercomputers, recent simulations are able to handle as many as one trillion particles or resolution elements (Alimi et al. 2012; Habib et al. 2012). While this provides access to new scientific questions, a drawback lies in the generation of petabytes of data. The large amount of data produced during such runs is thus becoming a critical problem and needs a highly scalable efficient post-processing workflow. An effective physically motivated way of reducing those data is to detect structures in the underlying continuous dark matter (DM) density field and save properties of those groups of particles instead of saving all of the numerical information. Obviously, this reduction requires the use of an optimized and flexible tool to avoid the complete loss of valuable cosmological information near under-dense or unstructured regions. Moreover, a very generic method is needed to perform such a detection since it represents a major issue in gravitational physics: indeed, no unique way of defining collapsed objects in the sampling of a continuous matter field in a reasonable time has been found.
Although many different methods have been proposed in the past decades (for an extensive review see Knebe et al. 2011, 2013 and references therein), those detection techniques are usually divided into two main families:
-
Methods based on an integrated density criterion. Those methodsare related to the spherical overdensity (SO) algorithmintroduced by Press & Schechter (1974) andfurther developed by Lacey & Cole (1994).
-
Methods related to local density estimation. Those approaches derive from the friends-of-friends (FoF) algorithm introduced in astrophysics by Davis et al. (1985).
Since those classes of algorithm are complementary, the choice of algorithm is mainly driven by the physics we want to probe. For instance, SO haloes have a spherical geometry that is closely related to the observational definition of haloes, whereas FoF haloes are unstructured. From a purely algorithmic point of view, each method has its advantages and drawbacks. FoF is a local algorithm and is thus more adapted to a distributed parallelization than SO, which uses integrated densities over a spherical volume to identify dark matter haloes. Finally, FoF avoids the overlapping of DM haloes and may enclose all the particles of a simulation in haloes.
In order to analyse the very large data sets produced by the DEUS consortium, we have developed an MPI-based parallel halo-finder code built on the FoF algorithm: pFoF. One of the reasons for this choice is that a halo detection based upon FoF grants a better following of the non-linear dynamics of the matter field and thus tends to improve the universality of the mass function that is expected in Einstein-de-Sitter for scale-free or nearly scale-free cosmologies (Courtin et al. 2011).
In principle, pFoF can be applied to any cosmological code, such as ART (Kravtsov 1999), GADGET (Springel 2005), CUBE-P3M (Harnois-Deraps et al. 2013), etc. The generality of the implementation makes it very easy to perform a halo-finding analysis to any of those dynamical codes, provided their data are distributed in a compact form. In the scope of this paper, the gravitational code following the dynamics of the dark matter particles in an expanding Universe is RAMSES (Teyssier 2002).
In Sect. 2, we introduce the basics of the FoF algorithm and develop the parallelization strategy. We also describe the format of the I/O data, stressing the simplicity of the outputs, and some additional features implemented in the code. In Sect. 3, some results and several performance diagnostics up to a large number of cores are described. Finally, we conclude and discuss perspectives in Sect. 4.
2. Friends-of-friends algorithm and parallel implementation
pFoF is a fully distributed code which relies on a domain decomposition: the simulation box is divided into p cubic domains, where p is the number of processes used by pFoF1. The code first finds groups of particles in parallel in each domain, each process using a FoF algorithm on its local cubic data and then merges haloes that extend across multiple cubes.
2.1. RAMSES data and reading strategy
Optimizing the reading strategy is a critical step for two main reasons: (1) the input data are usually ordered along a space-filling curve which is not user-friendly; (2) in state-of-the-art simulations, large amount of data has to be read which can be prohibitive in terms of computing time.
To overcome those problems, we chose to implement two different reading methods that can be used equally. Particles must be distributed between the pFoF processes so that each process knows the properties of each particles located in the cubic domain it deals with. The first strategy implies that each pFoF process reads every RAMSES output file that contains at least one of its particles. In the second strategy, one RAMSES output file is read by one pFoF process which then uses MPI Remote Memory Access functions to send the particle properties to the right process in the cubic splitting.
The pFoF code can then write the particles properties distributed along the cubic domains and create one file for each domain. These cubic domains are much more user-friendly than the distribution along the Peano-Hilbert curve for further analyses, such as fast correlation function computations.
2.2. The Friends-of-Friends algorithm and its parallel implementation
As explained in the introduction, the FoF algorithm is widely used to detect haloes in cosmological simulations. The principle of FoF is to link particles that are close to each other in coordinate space in its standard version. It could be extended to higher dimensional phase spaces (Behroozi et al. 2013; Diemand et al. 2006). In the standard picture, particles p1 and p2 located at positions x1 and x2 in a simulation with mean inter-particle distance λ are considered to belong to the same group of particles if they are separated by a distance d(p1,p2) less than the percolation length b times λ so that 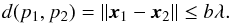 (1)The percolation factor value typically used for cosmological simulations is b = 0.2, which corresponds roughly to an integrated overdensity Δ = 200, which itself is close to the spherical collapse expectation in an Einstein-de-Sitter Universe. Several authors (Lukić et al. 2009; Courtin et al. 2011) describe the physical processes acting on the link between the integrated density Δ and the percolation factor b. Since this link poses several fundamental questions in cosmology and since we want to avoid introducing new free parameters, we chose not to implement a complex 6D phase-space halo-finder.
(1)The percolation factor value typically used for cosmological simulations is b = 0.2, which corresponds roughly to an integrated overdensity Δ = 200, which itself is close to the spherical collapse expectation in an Einstein-de-Sitter Universe. Several authors (Lukić et al. 2009; Courtin et al. 2011) describe the physical processes acting on the link between the integrated density Δ and the percolation factor b. Since this link poses several fundamental questions in cosmology and since we want to avoid introducing new free parameters, we chose not to implement a complex 6D phase-space halo-finder.
For a given MPI process, each halo is built through this linking procedure until no additional particle is close enough to any of the particles already linked. The construction of a new halo then begins with a non-linked particle. The linking process is sped up thanks to a priori knowledge of the spatial positions of DM groups of particles using linked lists of particles distributed in cubic cells with one list for each cell.
The parallel implementation of FoF relies on two steps. The first step consists in a local halo detection done by each process in their local domain. But haloes can extend across several cubic domains and then have to be merged. This merging phase is the second step. If a particle is separated from the face of the local cube by a distance less than the linking length b used by FoF, it means that there may be another particle on the other side of this face that should be linked to it (see Fig. 1). The pFoF code flags every particle located near one face of a cube. Each process sends the positions of these flagged particles to its neighbours and receives positions of flagged particles from its neighbours. For example flagged particles located near the bottom face of a cube are then compared with particles received from the bottom neighbour and pairs of particles that should be linked together (i.e. particles are separated by a distance less than the percolation length) are saved.
Once pairs of particles representing a link between two parts of a same halo are found for the six faces of the local cubic domain, pFoF applies the same halo identifier to both halo parts, using the minimum value of the two halo ID from before the merging began. This merging process is performed iteratively for the six faces of the cubes until no merging operation is done during a cycle over the six faces.
 |
Fig. 1 Illustration of the merging procedure. Each MPI process detects its own halo and triggers a merging process if a halo detected in the neighbouring process is less distant than the linking length b. The particular case of a single particle at a distance less than b in one of the process is included by calling halo a single particle before the merging procedure. |
2.3. Output from pFoF
Prior to halo detection, each pFoF process can generate a “cube file” that contains the properties (position, velocity, and id) of all the particles organized along the cubic splitting instead of the original space decomposition. This output format can be used as a start for further halo detections, thus avoiding conserving both pFoF “cube files” and RAMSES original outputs.
Two kinds of output files are produced by pFoF, thus corresponding to two files per process. “Mass file” contains a list of the haloes gathered in the process and, for each halo, the id, mass, and position of the centre of mass. “Structure file” contains, for each halo gathered on the process, the mass and the properties of all the particles inside the halo.
2.4. Additional features
The pFoF code could also be run on “structure files” pre-computed with a given value of the percolation length using a lower value. It uses the convenient property of an FoF halo-finder, namely that a halo detected with a given b is entirely part of a halo detected with larger b. Eventually, this function is able to split the initial group of particles into many haloes or sub-haloes depending on the value of the percolation factor. The algorithm consists in using a serial FoF algorithm for each halo that we want to analyse with a smaller percolation length. Each pFoF process then deals with a fraction of the total haloes to be re-analysed.
This feature is particularly interesting for probing smaller linking length and therefore higher enclosed overdensity. A physical application of this option can be found in Bouillot et al. (2014) with the study of the occurrence of closely interacting massive DM halo pairs. In this analysis, the requirement is to obtain the same virial mass at z = 0 as derived from a SO overdensity Δ = 200 at redshift z = 0.5. Such a requirement imposes the use of a b = 0.15 percolation factor.
Another specific feature of pFoF consists in detecting groups of particles in complex volumes, going from cubic sub-volumes of the computational box to cone-shaped or spherical volumes. The former shapes are ideal for building up merger trees, whereas the latter geometries are considered to mimic the geometry of observational surveys in redshift space. RAMSES provides those two types of outputs ordered along a convolution of the space-filling curve and the desired complex shape. In both cases, since we are handling sub-volumes of the original computational box, we require that there are no periodic boundary conditions.
3. Results and performance
3.1. Numerical results
The pFoF code has been widely tested on reference data sets. Results have been compared to those produced by the sequential algorithm. The haloes are identical, with one noteworthy exception: if two halo parts are linked through two particles separated by an edge or a vertex separating two domains dealt with by two different pFoF processes, then these two parts are not linked by pFoF, while they would have been linked using the sequential algorithm. We choose not to correct this difference because we consider that a halo consisting of two “sub-haloes” linked through a single bridge between two particles is not a physically justified halo. It could arise just because of the Poisson noise and therefore these fine bridges would be cut by any unbinding process. Moreover, an upper bound on the fraction of missing DM haloes is 1.7 × 10-5 in the case of a simulation of 10243 particles sliced by 32 768 processes (i.e. the most penalizing case dealt with in this paper). This shows that the increased time consumption of going from six (only through faces) to twenty-six communications (through faces, edges, and vertices) per cycle between a pFoF process and its neighbours to handle this situation is not counterbalanced by the gain in accuracy.
The pFoF code has been compared to other halo-finder codes during the Haloes Going Mad Workshop (Knebe et al. 2011, 2013). In this context, a reference N-body simulation was used to detect collapsed structures in the DM field using numerous halo-finders and to verify their consistency through the derivation of four main cosmological observables. The conclusion is that the main properties of pFoF haloes are statistically in good agreement with the ones issued from other codes. More in detail, pFoF haloes give competitive measurements of the DM halo mass function with a maximum difference of 8.5% on the entire mass range. The measured halo two-point correlation function and the cumulative vmax function have a maximum difference of ~10%. Finally, the bulk velocities of pFoF-detected haloes differ by a 3.7% factor. These differences are not related to some errors of implementation; on the contrary, they are related to the various halo definitions considered by each halo-finder.
The pFoF code also proved to be a highly efficient analysis tool, for instance, it has been used to analyse the DEUS-FUR (Alimi et al. 2012) simulations (81923 particles) using 32 768 processes, showing good scalability and low memory use during the “Grand Challenge” test phase of the Curie supercomputer. Finally as seen in the following, the I/O step is efficient but could probably be optimized. The pFoF code has been designed as a post-processing tool for organizing the data in the most user-friendly manner, and the I/O step has been implemented to favour this characteristic. However, we could probably improve the I/O performance by gathering the output data on a subset of the processes and writing fewer files.
3.2. Strong scaling
We have analysed the output of a 10243 particles 2625 h-1 Mpc box ΛCDM RAMSES simulation with 64, 512, 4096, and 32 768 pFoF processes on the Curie Thin Nodes supercomputer in a strong scaling configuration. The data was read from 64 cubic domain files, not from the RAMSES output files. The results of this strong scaling test, normalized against the perfect linear case, are plotted in Fig. 2.
A general remark is that the speed-up is linear up to 4096 processes for the initialization, the local FoF, and the MPI merging phases. The speed-up drops slightly for 32 768 pFoF processes for each phase and for 4096 processes for the output phase.
The speed-up of the MPI merging process is linear from 64 to 4096 pFoF processes, but it drops strongly for 32 768 processes. This poor performance can be explained by the ratio between the mean radius of the haloes detected by pFoF for this precise simulation and the size of the pFoF cubic domains with 32 768 processes. Indeed, in the latter case, the mean radius of the haloes and the size of the domains have the same order of magnitude. The reason for that sudden decrease is thus linked with the numerous haloes extending over several cubic domains. It triggers an increase in the volume of communications required by the merging phase in the case of 32 768 processes compared to the one needed with fewer processes.
The output phase of the code also presents lower performances for 4096 and 32 768 processes. Results of the DEUS-FUR simulations show that the I/O bandwidth of the Curie supercomputer is saturated by 4096 processes writing at the same time (Alimi et al. 2012). This supercomputer-dependent feature explains the low speed-up for high number of processes.
 |
Fig. 2 Strong scaling performance test on a 10243 DM particles simulation using from 64 to 32 768 pFoF processes. The normalized computing time (speed-up) is plotted against the number of pFoF processes used. The computing times for 64, 512, and 4096 processes are the median computing times issued from 20 different runs. The pFoF analysis with 32 768 processes was performed only once. |
3.3. Weak scaling
In the same spirit, we performed a weak scaling performance test using 8, 64, 512, 4096, and 32 768 processes. Table 1 shows the numerical characteristics of each simulation used for this weak-scaling test. The cosmological simulations are done in a standard Λ cold dark matter framework, where dark energy is supposed to be a cosmological constant with an equation of state w = −1.
The efficiency of the different phases of pFoF for this test is plotted in Fig. 3.
Characteristics of the test run simulations in weak-scaling configuration.
The efficiency for the initialization, the local FoF, and the MPI merging phases are very good (more than 75%) even with 32768 processes. The slow performance degradation can be explained by the increasing number of communications implied by the increasing number of processes. Concerning the local FoF efficiency, the reason of the slow deterioration of the performance comes from a slight increase in the number of particles dealt with by some pFoF process compared to the reference case.
The efficiency for the output phase is much lower. However, such a measurement depends on many parameters inherent to the supercomputer. Indeed, since the I/O bandwidth of the Curie file system is almost saturated for more than 512 processes writing at the same time, and since the size of our output files was not specifically tuned to this file system, the efficiency decreases when the number of processes increases. With 4096 and 32 768 processes, a ticket system is triggered to achieve better efficiency: only a fraction of the total number of processes writes its output files at any given time. As expected, this allows better use of the total I/O bandwidth and results in increased efficiency. However, this step could be improved by gathering data before the writing step.
 |
Fig. 3 Weak scaling performance test from 5123 particles on 64 pFoF processes to 81923 particles on 32 768 processes. The efficiency is plotted against the number of pFoF processes used. Due to the low number of communications, the performance of the halo detection remains above 75%. An effort should be made on the outputs. The computing times for 8, 64, 512, and 4096 processes are the median values of 20 different runs. The error bars are related to the dispersion of the timings of the 20 different runs. The pFoF analysis with 32 768 processes was performed only once. |
4. Conclusion and perspectives
To reduce, manage, and analyse petabytes of data generated by upcoming N-body cosmological simulations, we develop an efficient halo-finder named pFoF. This code built on a standard three-dimensional Friends-of-Friends algorithm allows to detect haloes. It is parallelized using a domain decomposition and making numerous calls to local FoF halo detection followed by the merging of the haloes extending across several domains. Particular attention has been paid to optimize the reading methods and tune it according to the performance of the supercomputer. Effort will be needed to further optimize the outputs of the code (e.g. using MPI/IO) without impacting their simple and compact forms. We present several additional features of the code, such as the detection of structures performed on halo previously detected with another percolation factor or the halo-finding in non-cubic geometries (e.g. light-cones).
The pFoF code has been tested against a sequential version of FoF for single haloes and has successfully detected the same structures. The results of pFoF have been statistically proved against other halo-finder techniques and agree with usual cosmological quantities up to 10%. The code demonstrates a good scalability for large number of processes (up to 32 768 with an efficiency above 75%). The conclusion is that pFoF allows us to analyse large sets of data in a quick and efficient manner.
In the future, we plan to merge pFoF and the RAMSES code to avoid I/O problems, both time and disk consuming. Moreover, the integration of pFoF into RAMSES would allow us to find haloes at many more different cosmological times. A major motivation for such a call is to acquire DM haloes merger trees on the fly. We also plan to implement an unbinding process to remove particles that are not gravitationally linked with the detected haloes.
Acknowledgments
We would like to thank Jean-Michel Alimi for useful discussions and Patrick Hennebelle for his ideas about the parallelization of halo-finders. This code is based upon a sequential version of the FoF algorithm by E. Audit. This work was granted access to the HPC resources of TGCC under the allocation x2013042287 made by GENCI (Grand Équipement National de Calcul Intensif). V. R. Bouillot was supported by funding from the ERC-StG EDECS 365782 grant. V. R. Bouillot is supported by the South African National Research Foundation.
References
- Alimi, J.-M., Bouillot, V., Rasera, Y., et al. 2012, Supercomputing 2012 Conf. [arXiv:1206.2838] [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., & Wu, H.-Y. 2013, ApJ, 762, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Bouillot, V., Alimi, J.-M., Rasera, Y., & Corasaniti, P.-S. 2014, MNRAS, submitted [Google Scholar]
- Courtin, J., Rasera, Y., Alimi, J.-M., et al. 2011, MNRAS, 410, 1911 [NASA ADS] [Google Scholar]
- Davis, M., Efstathiou, G., Frenk, C. S., & White, S. D. M. 1985, ApJ, 292, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Diemand, J., Kuhlen, M., & Madau, P. 2006, ApJ, 649, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Habib, S., Morozov, V., Finkel, H., et al. 2012, in Int. Conf. for High Performance Computing, Networking, Storage and Analysis, 1 [Google Scholar]
- Harnois-Deraps, J., Pen, U.-L., Iliev, I. T., et al. 2013, MNRAS, 436, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Knebe, A., Knollmann, S. R., Muldrew, S. I., et al. 2011, MNRAS, 415, 2293 [NASA ADS] [CrossRef] [Google Scholar]
- Knebe, A., Pearce, F. R., Lux, H., et al. 2013, MNRAS, 435, 1618 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V. 1999, Ph.D. thesis, New Mexico state university [Google Scholar]
- Lacey, C., & Cole, S. 1994, MNRAS, 271, 676 [Google Scholar]
- Lukić, Z., Reed, D., Habib, S., & Heitmann, K. 2009, ApJ, 692, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Illustration of the merging procedure. Each MPI process detects its own halo and triggers a merging process if a halo detected in the neighbouring process is less distant than the linking length b. The particular case of a single particle at a distance less than b in one of the process is included by calling halo a single particle before the merging procedure. |
| In the text | |
 |
Fig. 2 Strong scaling performance test on a 10243 DM particles simulation using from 64 to 32 768 pFoF processes. The normalized computing time (speed-up) is plotted against the number of pFoF processes used. The computing times for 64, 512, and 4096 processes are the median computing times issued from 20 different runs. The pFoF analysis with 32 768 processes was performed only once. |
| In the text | |
 |
Fig. 3 Weak scaling performance test from 5123 particles on 64 pFoF processes to 81923 particles on 32 768 processes. The efficiency is plotted against the number of pFoF processes used. Due to the low number of communications, the performance of the halo detection remains above 75%. An effort should be made on the outputs. The computing times for 8, 64, 512, and 4096 processes are the median values of 20 different runs. The error bars are related to the dispersion of the timings of the 20 different runs. The pFoF analysis with 32 768 processes was performed only once. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


