| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 10 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201322931 | |
| Published online | 27 February 2014 | |
Spectral properties of a few F-like ions
Theoretical Physics Division, Physical Research Laboratory, 380009 Ahmedabad, India
e-mail: dillip@prl.res.in
Received: 29 October 2013
Accepted: 24 December 2013
Aims. We intend to provide accurate data for the oscillator strengths, transition probabilities, lifetimes, and hyperfine shifts of the atomic energy levels in the fluorine (F)- like Ti, V, Cr, Mn, Co, Ni, Cu, Zn, and Mo ions for the diagnostic of the astrophysical plasma. Furthermore, we propose these ions for probing possible variation in the fine structure constant (αe) by observing their transition lines from the distant astronomical objects.
Methods. We have employed an all-order perturbative method in the relativistic coupled-cluster framework using the Dirac-Coulomb Hamiltonian for calculating the atomic wave functions in the considered F-like ions. We adopted the Fock-space formalism to account for the correlation effects among the occupied electrons by allowing all possible singly and doubly excited configurations in two steps: first considering the correlations between the electrons in a closed-shell configuration, and second constructing the open-shell configurations of the first three low-lying states in the considered atomic systems by removing the respective electron from the core orbitals. This procedure enormously simplifies the computational complexity and overcomes the need to select important configuration state functions in determining the atomic state functions in contrast to a truncated configuration interaction method. Moreover, corrections from the frequency-independent Breit interaction and the lowest order quantum electrodynamic effects are incorporated self-consistently.
Results. We present the calculated ionization potential energies of the electrons that are detached to form the above considered F-like ions. The correctness of our estimated results are ensured by comparing them with the available experimental values and other calculations. From these calculations, we evaluate the relativistic sensitivity coefficients that we propose here to be used for probing possible temporal variation of the fine structure constant (αe) through the precise astrophysical observation of the spectral lines of the transitions involving the above low-lying states. The accuracies of these sensitivity coefficients are appraised from the comparison of our calculated energies with the experimental values. We also present the line strengths by calculating the reduced matrix elements of the allowed transitions and of the M1 and E2 forbidden transitions. By combining our calculated line strengths with the observed wavelengths, we determine the oscillator strengths, transition probabilities, and lifetimes of the first two excited states of the above ions and compare them with the other theoretical calculations. The hyperfine splittings of the states are also presented by calculating their magnetic dipole and electric quadrupole hyperfine structure constants.
Key words: atomic data / relativistic processes / methods: numerical / quasars: absorption lines
© ESO, 2014
1. Introduction
It is a well known fact that the composition of the matter in the universe is non-isotropic and inhomogeneous. Most of it is filled with very hot plasma that is generally in thermal non-equilibrium states (Benz 2002). These objects are enriched with the highly charged ions of different elements. To characterize the hot plasma it is essential to acquire precise knowledge of the spectral properties of these highly charged ions. On the other-hand, investigating characteristics related to the solar plasma is very useful since the plasma of the Sun, whose structure has been studied extensively (Benz 2002; Antonucci et al. 2004; Graham et al. 2011), and it is an easily accessible astronomical object. It may be possible to generalize the physical phenomenon observed in solar plasma for analyzing other astrophysical hot plasma. The physical conditions of the outer atmosphere of the Sun can be explored by analyzing the extreme ultraviolet (EUV) spectral lines of various abundant elements observed from its transition region and corona (Peter 2001; Del Zanna et al. 2002).
In 2006, these regions were observed using the EUV imaging spectrometer (EIS) onboard the Hinode mission by the national astronomical observatory of Japan (Culhane et al. 2007). This mission successfully observed the solar EUV spectra, monochromatic images of possibly non-ionization-equilibrium plasma in the solar transition region and corona at two-wavelength bands of width 170–210 Å and 250–290 Å (Culhane et al. 2007; Watanabe 2009). Analysis from these observations provides spectral lines of F-like Fe ion, along with the other multiple charged ions of the lighter elements (Watanabe 2009). A spectral line with wavelength 974 Å of Fe XVIII has also been observed prominently in flaring and solar plasma (Doschek et al. 1975) and in the spectrum of the star Capella (Young et al. 2001).
The characteristics of the astronomical objects are typically inferred by scrutinizing the line spectra of the atomic and molecular systems present in the interstellar mediums that emit radiations by absorbing photons coming out of these astronomical objects. In this way, we also gain information regarding the structure and the evolution processes of the cosmic objects. For extracting such information, we need input related to the electron-impact-excitation, photo-ionization, radiative recombination, dielectric-recombination, etc., processes of the atomic ions. The physical quantities of interest from these mechanism are the electron collisional rate coefficients, electron-ion recombination rate coefficients, photo-ionization cross-sections, etc. Determining these properties requires knowledge of effective collisional strengths that are related to the line strengths of different electromagnetic transitions (Nahar 2005; Tayal 2012). Moreover, other transition properties such as radiative decay rates, and lifetimes of the atomic states. are also the vital ingredients for deriving useful structural information about the astronomical objects (Young et al. 2003). As an example, Foster et al. (1994) have determined cross-sections and rate coefficients for the 2s22p5 2P3/2 → 2s22p5 2P1/2 transition in the Ti XIV, Ni XX, Zn XXII, and Mo XXXIV ions by considering the proton, deuteron, trition and α particles impact by using the calculated radiative decay rates in the closed-coupling method. Also, observations of the spectral lines due to both the allowed and forbidden transitions of the Fe XVIII and Ni XX ions are reported (Suckewer & Hinnov 1979; Doyle 1983; Stratton et al. 1985; Acton et al. 1985; Wang et al. 1988). Precise values of the transition probabilities for the highly charged ions that are due to the forbidden channels are of particular interest to physicists for diagnosing the low-density magnetically confined high temperature laboratory plasma generated in tokamak (Currell 2003). In this process, the ions are injected into the plasma to find its temperature and to investigate the rotation and transport dynamics of the plasma impurities (Currell 2003; Davis et al. 1977). These transition probabilities are also useful for determining the intensity diagnostic ratios to ascertain the electron density in the plasma approaching the Boltzmann equilibrium (Keenan et al. 1987).
Furthermore, absorption lines from the quasi-stellar objects (QSO) are used for laboratory testing the temporal variation of the fine structure constant (αe = e2/ħc) on the cosmological time scale (Webb et al. 2011; King et al. 2012; Chand et al. 2008; Levshakov et al. 2008b,a; Molaro et al. 2008). The ground state of the considered ions have the fine structure splitting and the next excited s- state will decay to these fine-structure levels by the allowed transition. The ratio of the transition frequencies between the fine structure splitting and one of these allowed transitions has one leading-order relativistic correction in 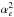 rather than the ratio of the transition frequencies between both the allowed transitions. For this reason, we would like to propose precise observations of the frequencies of these transition lines in the considered ions, from which possible signature of the temporal variation of αe can be inferred by comparing the observed frequencies with their laboratory values as carried out in the earlier studies (Chand et al. 2008; Webb et al. 2011; Thong et al. 2010). Primary objectives for carrying out these studies are to argue for theories that predict violation of the Einstein’s equivalence principle and to support models such as superstring theory and Kaluza-Klein’s five-dimensional model that attempt to unify the gravity with the other three fundamental interactions of nature (Damour & Polyakov 1994; Kaluza 1921; Klein 1926; Mbelek & Lachièze-Rey 2002).
rather than the ratio of the transition frequencies between both the allowed transitions. For this reason, we would like to propose precise observations of the frequencies of these transition lines in the considered ions, from which possible signature of the temporal variation of αe can be inferred by comparing the observed frequencies with their laboratory values as carried out in the earlier studies (Chand et al. 2008; Webb et al. 2011; Thong et al. 2010). Primary objectives for carrying out these studies are to argue for theories that predict violation of the Einstein’s equivalence principle and to support models such as superstring theory and Kaluza-Klein’s five-dimensional model that attempt to unify the gravity with the other three fundamental interactions of nature (Damour & Polyakov 1994; Kaluza 1921; Klein 1926; Mbelek & Lachièze-Rey 2002).
Considering the many-multiplet (MM) methods in the observation of the absorption spectra coming out of the high red-shifted quasars, variation in αe can be probed (Murphy et al. 2004; Dzuba et al. 1999). In this procedure, the velocity profile of the absorber situated closer to the quasars can be analyzed at different red-shifts that are related to the emission frequencies of the spectral lines coming out of the quasars. As is known, these objects correspond to the remote past in the cosmological time scale. Comparing these frequencies against the laboratory results, their unusual differences can be interpreted as a change in the αe value.
A recent international program “The UVES Large Program for testing Fundamental Physics” is being launched by Molaro et al. (2013). It project the main focus towards the improvement of the systematic miscalibration of quasar wavelength scale. In this program, nearly 12 bright quasars with about 25 absorbers along the line of sight are considered for further investigation of the variation in αe with the precision better than ~10 ppm by enhancing the signal-to-noise ratio of the observational data. Since this observation and analysis involves a wide variety of quasars and absorbing systems containing many metallic transition lines, the present study in this context may provide useful input into this program. Nevertheless, transition lines in the considered ions can also be observed using other telescopes around the world. Therefore, it is imperative to provide accurate theoretical data of αe sensitive coefficients and other transition properties prior to their observations in the considered ions. This may also encourage the astrophysicists to plan for their observations by considering these theoretical investigations.
It is also important to take the hyperfine interactions in the observational profiles into account for analyzing the strengths of the stellar absorption lines (Booth et al. 1983). Transition lines from the hyperfine levels in the highly charged ions can facilitate observations of the hot rarefied astrophysical plasma (Sunyaev & Docenko 2007). For their tiny magnitudes, high resolution detectors are required for their observations from the astronomical objects. Additionally, transition lines among the hyperfine levels can be separately investigated for yielding the signature of variation in αe with accurate knowledge of their splittings. In this work, we present hyperfine splittings for the first three low-lying states of the considered ions, taking the dominant magnetic dipole and electric quadrupole interactions between the electrons and the respective atomic nuclei into account.
2. Theory and calculation method
The relation between the transition probabilities and the line strengths for the electromagnetic radiations mediated through the electric-dipole (E1), magnetic-dipole (M1), and electric-quadrupole (E2) channels are given by (Sobelman 2006) 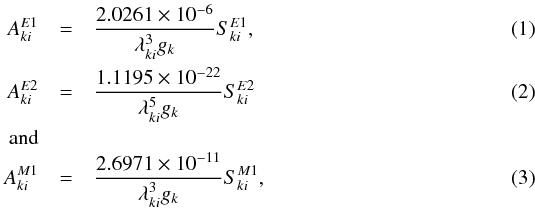 where the quantity
where the quantity 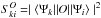 is known as the line strength of a transition for a corresponding reduced matrix element of the radiative operator O (given in atomic unit (au)), gk = 2Jk + 1 is the degeneracy factor of the transition state with angular momentum Jk, and λki is the transition wavelength to the lower state denoted by the index i (used in cm). The evaluated transition probabilities As are given here in s-1.
is known as the line strength of a transition for a corresponding reduced matrix element of the radiative operator O (given in atomic unit (au)), gk = 2Jk + 1 is the degeneracy factor of the transition state with angular momentum Jk, and λki is the transition wavelength to the lower state denoted by the index i (used in cm). The evaluated transition probabilities As are given here in s-1.
Similarly, the emission (absorption) oscillator strength fki (fik) due to the above transitions is given by 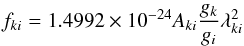 (4)with the weighted oscillator strengths satisfying the relation gifik = −gkfki.
(4)with the weighted oscillator strengths satisfying the relation gifik = −gkfki.
The lifetime of an excited state denoted by the index k is given by 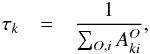 (5)where the sum over i indicates all possible lower states and over O means all the radiative operators obeying the Fermi-Golden selection rules.
(5)where the sum over i indicates all possible lower states and over O means all the radiative operators obeying the Fermi-Golden selection rules.
The relativistic correction to the energy level of a multi-electron atomic system with a single valence electron can be expressed as (Murphy 2002) ![\begin{eqnarray} \Delta E=-\frac{E_{\rm NR}}{\nu}(Z\alpha_e)^2 \left [ \frac{1}{j+1/2}-C(Z,j,l) \right ], \end{eqnarray}](/articles/aa/full_html/2014/03/aa22931-13/aa22931-13-eq23.png) (6)where ENR is the non-relativistic value of the atomic energy level, ν the effective principal quantum number of the valence electron, l and j are its orbital and total angular momenta, and the factor C(Z,j,l) accounts the many-body correlation effects among the electrons. The change in transition frequency between two states in this system with respect to an arbitrary variation in αe can be given by
(6)where ENR is the non-relativistic value of the atomic energy level, ν the effective principal quantum number of the valence electron, l and j are its orbital and total angular momenta, and the factor C(Z,j,l) accounts the many-body correlation effects among the electrons. The change in transition frequency between two states in this system with respect to an arbitrary variation in αe can be given by 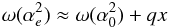 (7)where α0 is the laboratory value of αe and
(7)where α0 is the laboratory value of αe and 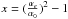 . Considering dx = x1 − x2 for two different values of x as x1 and x2, the relativistic sensitivity coefficient is expressed as
. Considering dx = x1 − x2 for two different values of x as x1 and x2, the relativistic sensitivity coefficient is expressed as 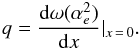 (8)For the numerical determination of this quantity, we use x1 = x and x2 = −x, which leads to
(8)For the numerical determination of this quantity, we use x1 = x and x2 = −x, which leads to 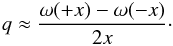 (9)We have chosen x = 0.025 in the present calculation.
(9)We have chosen x = 0.025 in the present calculation.
The relation that is generally used in the MM method for finding Δαe (change in αe) is 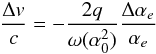 (10)where Δv corresponds to the relative velocity of the absorber along the line of sight of the detection with respect to the observer.
(10)where Δv corresponds to the relative velocity of the absorber along the line of sight of the detection with respect to the observer.
When considering only up to the quadrupole interaction and neglecting the off-diagonal interactions (Schwartz 1955), the energy shift for the total angular momentum F = I + J due to the hyperfine interaction is given by 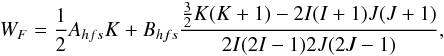 (11)where K = F(F + 1) − I(I + 1) − J(J + 1) with I, J, and F as the nuclear spin and angular momentum of the atomic state. Ahfs and Bhfs are, respectively, known as the magnetic dipole and electric quadrupole structure constants, which are given by
(11)where K = F(F + 1) − I(I + 1) − J(J + 1) with I, J, and F as the nuclear spin and angular momentum of the atomic state. Ahfs and Bhfs are, respectively, known as the magnetic dipole and electric quadrupole structure constants, which are given by 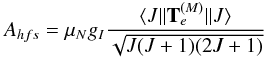 (12)and
(12)and ![\begin{eqnarray} B_{hfs}=Q_{\rm nuc}\left [\frac{8J(2J-1)}{(2J+1)(2J+2)(2J+3)}\right]^{1/2}\langle J||{\bf T}_{\rm e}^{(Q)}||J\rangle \end{eqnarray}](/articles/aa/full_html/2014/03/aa22931-13/aa22931-13-eq53.png) (13)where μN, gI and Qnuc are the magnetic moment, gyromagnetic ratio and quadrupole moment of the atomic nucleus, and
(13)where μN, gI and Qnuc are the magnetic moment, gyromagnetic ratio and quadrupole moment of the atomic nucleus, and 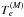 and
and 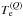 are the tensors representing the electronic functions of the magnetic dipole and electric quadrupole hyperfine interactions.
are the tensors representing the electronic functions of the magnetic dipole and electric quadrupole hyperfine interactions.
Using the relativistic coupled-cluster (RCC) theory, we express the interested atomic state functions (ASFs) in the considered ions as 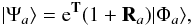 (14)where | Φa ⟩ is the reference state, T and Ra are the RCC excitation operators that excite only the spin-paired core electrons and spin-paired core electrons along with the unpaired single valence electron, respectively. In our calculation, we consider the Dirac-Coulomb (DC) Hamiltonian given by
(14)where | Φa ⟩ is the reference state, T and Ra are the RCC excitation operators that excite only the spin-paired core electrons and spin-paired core electrons along with the unpaired single valence electron, respectively. In our calculation, we consider the Dirac-Coulomb (DC) Hamiltonian given by ![\begin{eqnarray} {\bf H}=\sum_i \left [ c{\boldsymbol\alpha}_i\cdot \textbf{p}_i+(\beta_i -1)c^2+ V_{\rm nuc}(r_i) + \sum_{j>i} \frac{1}{r_{ij}} \right ] , \label{dch} \end{eqnarray}](/articles/aa/full_html/2014/03/aa22931-13/aa22931-13-eq62.png) (15)where αi and βi are the Dirac matrices, the Vnuc(r) is the nuclear potential obtained using the Fermi charge distribution and rijs are the interelectronic distances. Contributions from the frequency independent Breit interaction are estimated by adding the potential given by
(15)where αi and βi are the Dirac matrices, the Vnuc(r) is the nuclear potential obtained using the Fermi charge distribution and rijs are the interelectronic distances. Contributions from the frequency independent Breit interaction are estimated by adding the potential given by 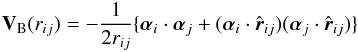 (16)with the DC Hamiltonian (referred as DCB Hamiltonian). Similarly, quantum electrodynamic effects are added in two steps. First we consider the lower order vacuum polarization effects incorporating the Uehling (VUhl(r)) and Wichmann-Kroll (VWK(r)) potentials given by (Flambaum & Ginges 2005)
(16)with the DC Hamiltonian (referred as DCB Hamiltonian). Similarly, quantum electrodynamic effects are added in two steps. First we consider the lower order vacuum polarization effects incorporating the Uehling (VUhl(r)) and Wichmann-Kroll (VWK(r)) potentials given by (Flambaum & Ginges 2005) 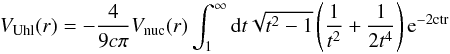 (17)and
(17)and 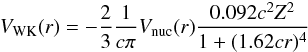 (18)along with the DCB Hamiltonian (referred as DCBV Hamiltonian). In the next step, we account the lowest order self-energy correction to the DCBV Hamiltonian (referred to as DCBVS Hamiltonian) considering the additional potential (Flambaum & Ginges 2005)
(18)along with the DCB Hamiltonian (referred as DCBV Hamiltonian). In the next step, we account the lowest order self-energy correction to the DCBV Hamiltonian (referred to as DCBVS Hamiltonian) considering the additional potential (Flambaum & Ginges 2005) ![\begin{eqnarray} V_{\rm SE}(r)&=&-\frac{1}{4 c^2 \pi } {\boldsymbol\gamma}.{\boldsymbol\nabla} \left [V_{\rm nuc}(r)\left (\int^{\infty}_{1}{\rm d}t \frac{{\rm e}^{-2ctr}}{\sqrt{t^2-1}}\right)\right] \nonumber \\ &&-A(Z,r)\frac{1}{c\pi}V_{\rm nuc}(r) \int^{\infty}_1 {\rm d}t \frac{{\rm e}^{-2ctr}}{\sqrt{t^2-1}}\Bigg[\left( 1-\frac{1}{2t^2}\right)\nonumber \\ &&\times \{\ln(t^2-1)+4 \ln(c/Z+0.5)\}-\frac{3}{2}+\frac{1}{t^2}\Bigg]\nonumber \\ && - B(Z) \frac{Z^4}{c^3} {\rm e}^{-Zr}, \end{eqnarray}](/articles/aa/full_html/2014/03/aa22931-13/aa22931-13-eq72.png) (19)where A(Z,r) = [1.071 − 1.97((Z − 80)/c)2 − 2.128((Z − 80)/c)3 + 0.169((Z − 80)/c)4] cr/(cr + 0.07Z2/c2) and B(Z) = 0.074 + 0.35Z/c with Z as atomic number of the ion.
(19)where A(Z,r) = [1.071 − 1.97((Z − 80)/c)2 − 2.128((Z − 80)/c)3 + 0.169((Z − 80)/c)4] cr/(cr + 0.07Z2/c2) and B(Z) = 0.074 + 0.35Z/c with Z as atomic number of the ion.
In our formalism, we treat ASF of the [2p6] configuration as | Ψ0 ⟩, and the annihilation operator aa corresponds to a core electron either from the 2s or 2p1/2,3/2 orbitals that is detached to obtain the corresponding ASF, | Ψa ⟩, of the considered ions. This procedure includes correlations among all the core electrons from the [2p6] configuration through the T excitation operator using the RCC ansatz 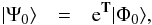 (20)where | Φ0 ⟩ is the mean-field wave function for the [2p6] configuration that is calculated using the Dirac-Hartree-Fock (DHF) method. Then, we remove the extra correlation effects accounted for the electron that is detached from | Ψ0 ⟩ by defining the new DHF wave function as | Φa ⟩ = aa | Φ0 ⟩ and introducing the RCC operator Ra.
(20)where | Φ0 ⟩ is the mean-field wave function for the [2p6] configuration that is calculated using the Dirac-Hartree-Fock (DHF) method. Then, we remove the extra correlation effects accounted for the electron that is detached from | Ψ0 ⟩ by defining the new DHF wave function as | Φa ⟩ = aa | Φ0 ⟩ and introducing the RCC operator Ra.
Since the considered ions only have nine electrons, all possible configurations generated by the excitations and de-excitations due to one electron and two electrons (referred to as CCSD method) from the reference states will be reasonable enough for calculating of the ASFs. This, therefore, corresponds to the singly and doubly excited configurations from | Φ0 ⟩ for the T operator and replacement of one core electron and, along with this process, excitation of a core electron from | Φa ⟩ for the Ra operator.
In the second quantization notation, we express the same as 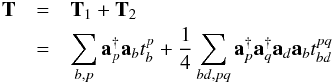 (21)and
(21)and 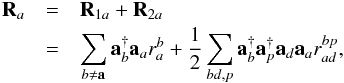 (22)where b,d and p,q represent electrons from all the core orbitals and from the virtual orbitals, respectively, with the amplitudes denoted by t and r carrying the appropriate indices. Considering further important triple excitation configurations in the calculations of the CCSD operator amplitudes in a self-consistent manner (referred to as the CCSD(T) method), we also raise the quality of the results. The detailed working equations for evaluating the above RCC amplitudes can be found elsewhere (Nandy & Sahoo 2013).
(22)where b,d and p,q represent electrons from all the core orbitals and from the virtual orbitals, respectively, with the amplitudes denoted by t and r carrying the appropriate indices. Considering further important triple excitation configurations in the calculations of the CCSD operator amplitudes in a self-consistent manner (referred to as the CCSD(T) method), we also raise the quality of the results. The detailed working equations for evaluating the above RCC amplitudes can be found elsewhere (Nandy & Sahoo 2013).
Ionization potentials of the 2s22p5 2P3/2, 2s22p5 2P1/2, and 2s2p6 2S1/2 states (in cm-1) in the considered F-like ions.
After obtaining the ASFs with a valence electron in the 2p3/2, 2p1/2, and 2s orbitals of these ions, we calculate transition matrix element of an operator O between two considered states | Ψf ⟩ and | Ψi ⟩ by 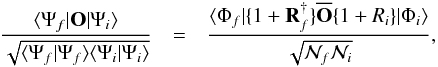 (23)where
(23)where 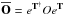 and
and 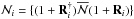 with
with 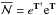 . The evaluation procedure of these terms are described elaborately in (Nandy & Sahoo 2013). The hyperfine structure constants of a given state | Ψa ⟩ are calculated by equating | Ψi ⟩ = | Ψf ⟩ = | Ψa ⟩ in the above expression.
. The evaluation procedure of these terms are described elaborately in (Nandy & Sahoo 2013). The hyperfine structure constants of a given state | Ψa ⟩ are calculated by equating | Ψi ⟩ = | Ψf ⟩ = | Ψa ⟩ in the above expression.
3. Results and discussion
In Table 1, we present the ionization potentials (IPs) of the electrons from the 2p3/2, 2p1/2, and 2s orbitals in the calculations of the 2s22p5 2P3/2, 2s22p5 2P1/2, and 2s2p6 2S1/2 states from the closed-shell [2p6] configuration. The results are given using the DHF method and from the CCSD(T) method considering the DC, DCB, DCBV, and DCBVS Hamiltonians. The results are finally compared with the tabulated values given in the national institute of science and technology (NIST) database (Kramida et al. 2013) in the same table. Most of these data are compiled in (Sugar & Corliss 1985; Sugar & Musgrove (1990, 1988, 1995), and Shirai et al. 2000) and obtained either from the tokamak plasma experiments or from the Dirac-Fock calculations.
Comparing these results from the above table, it shows that the DHF method overestimates the results, and the CCSD(T) method brings the results down close to the experimental values. In most of the cases, including of the higher order relativistic corrections improves the results to give very good agreement with the NIST data. This implies that, apart from the incorporation of the all-order correlation effects, it is also important to consider the higher order relativistic effects for accurate calculations of the atomic wave functions because the considered systems are highly charged ions. Our final results using the DCBVS Hamiltonian are below 0.5% in all the ions; given as δ in the above table. We expect that the results can improve further by accounting the quantum electrodynamic corrections in a more rigorous treatment than the present work.
Taking the differences between the IPs obtained using the CCSD(T) method, we determine excitation energies (EEs) of the first three transitions in the considered F-like ions and present them in Table 2. The purpose of giving the EEs explicitly from the IPs is to justify the accuracies of the relativistic sensitive coefficients that are estimated from these quantities. Also, there are other calculations of EEs available that employ the multiconfiguration Dirac-Fock (MCDF) method (Jönsson et al. 2013). We compared our results with the MCDF results and NIST database in the same table and find a reasonable agreement between them. Likewise, the above MCDF method also includes higher order relativistic corrections. The advantage of this calculation is that the numerical orbitals are used in contrast to our analytical orbitals constructed from the Gaussian type of orbitals (GTOs) in the CCSD(T) method. However, our CCSD(T) method automatically picksup all possible configuration state functions (CSFs) by its formulation. The absence of enough triply excited CSFs may be another reason why the CCSD(T) results seem to be incompatible with the above MCDF results. Nevertheless, the achieved accuracy using the CCSD(T) method is good enough to provide valid relativistic sensitive coefficients for probing possible temporal variation of the fine structure constant.
Excitation energies (in cm-1) of the 2s22p5 2P3/2 → 2s22p5 2P1/2 and 2s22p5 2P3/2 → 2s2p6 2S1/2 transitions in the considered F-like ions obtained with the CCSD(T) method.
Relativistic sensitivity coefficients q (in cm-1) of the first three low-lying transitions in the considered F-like ions.
Line strengths (S in au), transition rates (A in s-1), weighted oscillator strengths (gf), and lifetimes (τ in s) of the first two excited states in the considered ions.
Magnetic dipole hyperfine structure constant (Ahyp), electric quadrupole hyperfine structure constant (Bhyp), and hyperfine energy splittings for different angular momenta F in the 2s22p5 2P3/2, 2s22p5 2P1/2, and 2s2p6 2S1/2 states of the 49Ti XIV, 51V XV, 53Cr XVI, 55Mn XVII, 57Fe XVIII, 59Co XIX, 61Ni XX, 65Cu XXI, 67Zn XXII, and 95Mo XXXIV ions. Results are given in MHz.
From the calculation procedure of EEs as described above and varying the velocity of light value c in Eq. (15), we extract the relativistic sensitive coefficients qs that are given in Table 3. To understand the passage of the relativistic effects in the evaluation of the q factors and to compare its trend with respect to the calculated energies, we present the q parameters at different level of approximations in the atomic Hamiltonian in the same table. It can be noted from the differences in these values using the DCB and DC Hamiltonians and using the DCBVS and DC Hamiltonians for both the quantities that the relativistic effects in the determination of q parameters are greater than in the calculations of the corresponding IPs and EEs. The reason for this could be attributed to the fact that the relativistic sensitivity coefficients are the functions of 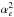 and do not carry any non-relativistic contributions, whereas the non-relativistic contributions are the main factors in evaluating of the energies. We show in Fig. 1 the scale where the q parameters are enhanced with respect to the atomic numbers of the ions for different transitions.
and do not carry any non-relativistic contributions, whereas the non-relativistic contributions are the main factors in evaluating of the energies. We show in Fig. 1 the scale where the q parameters are enhanced with respect to the atomic numbers of the ions for different transitions.
We now present the transition properties of the first two excited states in the ions treated in Table 4. The given line strengths due to both the allowed and M1 and E2 forbidden channels are obtained using the DCBVS Hamiltonian. With these values and wavelengths determined from the excitation energies given in the NIST database (Kramida et al. 2013), we evaluated the transition probabilities and present them in the same table. Instead of using energies from the CCSD(T) method, we considered the experimental energies in order to reduce the uncertainties in the estimated transition probabilities. We also give the weighted oscillator strengths and the lifetimes of the excited states in the same table. We compare our results with the two other calculations (Jönsson et al. 2013; Kaufman & Sugar 1986). Since the radiative transition amplitudes known to converge faster with the CSFs when the length gauge expressions are used, we give results only from the length gauge calculations in this table. In fact, transition probabilities and oscillator strengths are calculated using both the length and velocity gauge expressions in Jönsson et al. (2013) showing excellent agreement. The results reported in Kaufman & Sugar (1986) are combinations of the observed wavelengths with the matrix elements obtained from the mean-field calculations.
As can be seen, our transition probabilities match other calculations reasonably well. The differences between the results could be because we used the experimental wavelengths to estimate these quantities, while Jönsson et al. (2013) give the ab initio values, including uncertainties from their calculated energies. The M1 transition probabilities seem to be the dominant ones among the fine structure transitions and are solely responsible for determining the lifetimes of the corresponding fine structure states. Among the allowed transitions, the transition probability from the 2s2p6 2S1/2 state to the ground state 2s22p5 2P3/2 is the largest one in all the ions. The estimated branching ratios of the 2s2p6 2S1/2 → 2s22p5 2P1/2 transition and the 2s2p6 2S1/2 → 2s22p5 2P3/2 transition are about 30% and 70%, respectively.
The reported oscillator strengths for both the allowed and forbidden transitions could be very useful for astrophysical studies as mentioned in the introduction. Compared to the allowed transitions, the oscillator strengths of the forbidden transitions are smaller in magnitude. We plot the transition probabilities due to the allowed and the dominant forbidden M1 transitions in Figs. 2 and 3, respectively, against the atomic number of the ions to find out their trends. These figures clearly indicate that the transition probabilities due to the M1 channel increase rapidly with the atomic number of the ions whereas the E1 transition probabilities grow slowly especially for the 2s2p6 2S1/2 → 2s22p5 2P3/2 transition.
 |
Fig. 1 Scaling of q parameters against the atomic numbers of the considered ions. |
 |
Fig. 2 Trends followed by the forbidden M1 transition probabilities with respect to the atomic numbers of the considered ions. |
 |
Fig. 3 Behavior of the allowed transition probabilities with respect to the atomic numbers of the considered ions. |
We also present the results for the magnetic dipole and electric quadrupole hyperfine structure constants of the 49Ti XIV, 51V XV, 53Cr XVI, 55Mn XVII, 57Fe XVIII, 59Co XIX, 61Ni XX, 65Cu XXI, 67Zn XXII, and 95Mo XXXIV ions of the stable isotopes using the DCBVS Hamiltonian in Table 5. It can be noted that these values in other isotopes of these ions can be estimated approximately by multiplying it with the appropriate nuclear gyromagnetic ratios. There are no other experimental or theoretical results available for comparison. Using these values we estimated the hyperfine energy splittings for different angular momenta F, which are given in the same table. Owing to the negative values of the nuclear moments, the Ahyp values of the Ti XIV, Cr XIV, Ni XX, and Mo XXXIV ions are negative in all three states considered. For the same reason, the Bhyp value of the 2s22p5 2P3/2 state in these ions is also negative. There are only two hyperfine splittings possible for the 2s22p5 2P1/2 and 2s2p6 2S1/2 states and four for the ground state in all the ions because of their possible F angular momenta. It is also observed that the hyperfine energy splittings in the 2s2p6 2S1/2 state are large, followed by the 2s22p5 2P1/2 state, and they are much bigger in the Co XIX and Cu XXI ions owing to their large nuclear magnetic moments and higher degree of ionization compared to other ions. Although the degree of ionization for the 67Zn XXII and 95Mo XXXIV ions is higher than 59Co XIX and 65Cu XXI, their small nuclear magnetic moments give narrow hyperfine splittings.
4. Conclusions
We have reported the relativistic sensitivity coefficients for the possible detection of the temporal variation in the fine structure constant by observing low-lying transition lines in the considered F-like highly charged ions. The accuracies of these quantities are expected to be similar to the calculated energies reported in this work using the relativistic coupled-cluster method with the singly and doubly excited configurations. We also determined the transition probabilities and the weighted oscillator strengths due to the allowed and forbidden transitions using the line strengths evaluated by employing this method. These results were compared with the other reported values. Using our reported transition probabilities, we also estimate the lifetimes of the first two lower excited states in the considered ions. All the investigated atomic properties could be very useful for the astrophysical plasma analysis.
Acknowledgments
The computations were carried out using the PRL 3TFLOP HPC cluster, Ahmedabad.
References
- Acton, L. W., Bruner, M. E., Brown, W. A., et al. 1985, ApJ, 291, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, E., Dodero, M. A., Giordano, S., Krishnakumar, V., & Noci, G. 2004, A&A, 416, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benz, A. 2002, Astrophys. Space Sci. Lib., 279, Plasma Astrophysics, 2nd edn (Kluwer: Academic Publishers) [Google Scholar]
- Booth, A. J., Shallis, M. J., & Wells, M. 1983, MNRAS, 205, 191 [NASA ADS] [Google Scholar]
- Chand, H., Srianand, R., Petitjean, P., & Aracil, B. 2008, in Precision Spectroscopy in Astrophysics, Proc. ESO/Lisbon/Aveiro Conf. held in Aveiro, Portugal, eds. N. C. Santos, L. Pasquini, A. C. M. Correia, & M. Romaniello, 101 [Google Scholar]
- Culhane, J. L., Harra, L. K., James, A. M., et al. 2007, Sol. Phys., 243, 19 [Google Scholar]
- Currell, F. J. 2003, The Physics of multiply and highly charged ions (Kluwer Academic) [Google Scholar]
- Damour, T., & Polyakov, A. M. 1994, Nucl. Phys. B, 423, 532 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Davis, J., Jacobs, V. L., Kepple, P. C., & Blaha, M. 1977, J. Quant. Spectr. Rad. Transf., 17, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Del Zanna, G., Landini, M., & Mason, H. E. 2002, A&A, 385, 968 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Doschek, G. A., Dere, K. P., Sandlin, G. D., et al. 1975, ApJ, 196, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Doyle, J. G. 1983, Sol. Phys., 89, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Dzuba, V. A., Flambaum, V. V., & Webb, J. K. 1999, Phys. Rev. Lett., 82, 888 [Google Scholar]
- Flambaum, V. V., & Ginges, J. S. 2005, Phys. Rev. A, 72, 052115 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, V. J., Keenan, F. P., & Reid, R. H. G. 1994, Atom. Data Nucl. Data Tables, 58, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, D. R., Fletcher, L., & Hannah, I. G. 2011, A&A, 532, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jönsson, P., Alkauskas, A., & Gaigalas, G. 2013, Atom. Data Nucl. Data Tables, 99, 431 [Google Scholar]
- Kaluza, T. 1921, Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften (Berlin), Seite, 966 [Google Scholar]
- Kaufman, V., & Sugar, J. 1986, J. Phys. Chem. Ref. Data, 15, 321 [Google Scholar]
- Keenan, F. P., Mohan, M., Baluja, K. L., Berrington, K. A., & Hibbert, A. 1987, Phys. Lett. A, 122, 170 [NASA ADS] [CrossRef] [Google Scholar]
- King, J. A., Webb, J. K., Murphy, M. T., et al. 2012, MNRAS, 422, 3370 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, O. 1926, Z. Phys., 37, 895 [Google Scholar]
- Kramida, A., Yu. Ralchenko, Reader, J., & NIST ASD Team. 2013, NIST Atomic Spectra Database (ver. 5.1), http://physics.nist.gov/asd, October 28, National Institute of Standards and Technology, Gaithersburg, MD [Google Scholar]
- Levshakov, S. A., Molaro, P., Lopez, S., et al. 2008a, in Precision Spectroscopy in Astrophysics, eds. N. C. Santos, L. Pasquini, A. C. M. Correia, & M. Romaniello (Springer Verlag), 105 [Google Scholar]
- Levshakov, S. A., Reimers, D., Kozlov, M. G., Porsev, S. G., & Molaro, P. 2008b, A&A, 479, 719 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mbelek, J. P., & Lachièze-Rey, M. 2002, Int. J. Mod. Phys. A, 17, 4317 [NASA ADS] [CrossRef] [Google Scholar]
- Molaro, P., Reimers, D., Agafonova, I. I., & Levshakov, S. A. 2008, EPJ. Spec. Top., 163, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molaro, P., Centurión, M., Whitmore, J. B., et al. 2013, A&A, 555, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, M. T. 2002, Ph.D. Thesis, Institute of Astronomy, University of Cambridge [Google Scholar]
- Murphy, M. T., Flambaum, V. V., Webb, J. K., et al. 2004, in Astrophysics, Clocks and Fundamental Constants, eds. S. G. Karshenboim, & E. Peik (Berlin: Springer Verlag), Lect. Notes Phys., 648, 131 [Google Scholar]
- Nahar, N. S. 2005, ApJ, 156, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Nandy, D. K., & Sahoo, B. K. 2013, Phys. Rev. A, 88, 052512 [NASA ADS] [CrossRef] [Google Scholar]
- Peter, H. 2001, A&A, 374, 1108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwartz, C. 1955, Phys. Rev., 97, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Shirai, T., Sugar, J., Musgrove, A., & Wiese, W. L. 2000, Spectral Data for Highly Ionized Atoms: Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Kr, and Mo (AIP) [Google Scholar]
- Sobelman, I. I. 2006, Theory of Atomic Spectra (Alpha Science International Ltd) [Google Scholar]
- Stratton, B. C., Moos, H. W., Suckewer, S., et al. 1985, Phys. Rev. A, 31, 2534 [NASA ADS] [CrossRef] [Google Scholar]
- Suckewer, S., & Hinnov, E. 1979, Phys. Rev. A, 20, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Sugar, J., & Corliss, C. 1985, Atomic energy levels of the iron-period elements: Potassium through Nickel (Washington: American Chemical Society) [Google Scholar]
- Sugar, J., & Musgrove, A. 1988, J. Phys. Chem. Ref. Data, 17, 155 [Google Scholar]
- Sugar, J., & Musgrove, A. 1990, J. Phys. Chem. Ref. Data, 19, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Sugar, J., & Musgrove, A. 1995, J. Phys. Chem. Ref. Data, 24, 1803 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Docenko, D. O. 2007, Astron. Lett., 33, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Tayal, S. S. 2012, A&A, 541, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thong, L. D., Hung, T. V., Nguyen, T. T. H., & Bang, H. H. 2010, Astrophysics, 53, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J.-S., Griem, H. R., Hess, R., & Rowan, W. L. 1988, Phys. Rev. A, 38, 4761 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, T. 2009, J. Phys, Conf. Ser., 163, 012002 [NASA ADS] [CrossRef] [Google Scholar]
- Webb, J. K., King, J. A., Murphy, M. T., et al. 2011, Phys. Rev. Lett., 107, 191101 [NASA ADS] [CrossRef] [Google Scholar]
- Young, P. R., Dupree, A. K., Wood, B. E., et al. 2001, ApJ, 555, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Young, P. R., Del Zanna, G., Landi, E., et al. 2003, ApJS, 144, 135 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Ionization potentials of the 2s22p5 2P3/2, 2s22p5 2P1/2, and 2s2p6 2S1/2 states (in cm-1) in the considered F-like ions.
Excitation energies (in cm-1) of the 2s22p5 2P3/2 → 2s22p5 2P1/2 and 2s22p5 2P3/2 → 2s2p6 2S1/2 transitions in the considered F-like ions obtained with the CCSD(T) method.
Relativistic sensitivity coefficients q (in cm-1) of the first three low-lying transitions in the considered F-like ions.
Line strengths (S in au), transition rates (A in s-1), weighted oscillator strengths (gf), and lifetimes (τ in s) of the first two excited states in the considered ions.
Magnetic dipole hyperfine structure constant (Ahyp), electric quadrupole hyperfine structure constant (Bhyp), and hyperfine energy splittings for different angular momenta F in the 2s22p5 2P3/2, 2s22p5 2P1/2, and 2s2p6 2S1/2 states of the 49Ti XIV, 51V XV, 53Cr XVI, 55Mn XVII, 57Fe XVIII, 59Co XIX, 61Ni XX, 65Cu XXI, 67Zn XXII, and 95Mo XXXIV ions. Results are given in MHz.
All Figures
 |
Fig. 1 Scaling of q parameters against the atomic numbers of the considered ions. |
| In the text | |
 |
Fig. 2 Trends followed by the forbidden M1 transition probabilities with respect to the atomic numbers of the considered ions. |
| In the text | |
 |
Fig. 3 Behavior of the allowed transition probabilities with respect to the atomic numbers of the considered ions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


