| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 35 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322446 | |
| Published online | 28 February 2014 | |
Complex organic molecules in protoplanetary disks⋆
1 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
e-mail: cwalsh@strw.leidenuniv.nl
2 Astrophysics Research Centre, School of Mathematics and Physics, Queen’s University Belfast, University Road, Belfast BT7 1NN, UK
3 Department of Astronomy, Graduate School of Science, Kyoto University, 606-8502 Kyoto, Japan
4 National Astronomical Observatory of Japan, Osawa, Mitaka, Tokyo 181-8588, Japan
5 Department of Earth and Planetary Sciences, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, 152-8551 Tokyo, Japan
6 Departments of Physics, Chemistry and Astronomy, The Ohio State University, Columbus OH 43210, USA
7 Departments of Chemistry, Astronomy, and Physics, University of Virginia, Charlottesville VA 22904, USA
8 Department of Chemistry, Emory University, Atlanta GA 30322, USA
9 Department of Earth and Planetary Sciences, Kobe University, 1-1 Rokkodai-cho, Nada, 657-8501 Kobe, Japan
10 Department of Chemistry, University of Virginia, Charlottesville VA 22904, USA
11 Visiting Scientist, Ural Federal University, 620075 Ekaterinburg, Russia
Received: 5 August 2013
Accepted: 7 December 2013
Context. Protoplanetary disks are vital objects in star and planet formation, possessing all the material, gas and dust, which may form a planetary system orbiting the new star. Small, simple molecules have traditionally been detected in protoplanetary disks; however, in the ALMA era, we expect the molecular inventory of protoplanetary disks to significantly increase.
Aims. We investigate the synthesis of complex organic molecules (COMs) in protoplanetary disks to put constraints on the achievable chemical complexity and to predict species and transitions which may be observable with ALMA.
Methods. We have coupled a 2D steady-state physical model of a protoplanetary disk around a typical T Tauri star with a large gas-grain chemical network including COMs. We compare the resulting column densities with those derived from observations and perform ray-tracing calculations to predict line spectra. We compare the synthesised line intensities with current observations and determine those COMs which may be observable in nearby objects. We also compare the predicted grain-surface abundances with those derived from cometary comae observations.
Results. We find COMs are efficiently formed in the disk midplane via grain-surface chemical reactions, reaching peak grain-surface fractional abundances ~10-6–10-4 that of the H nuclei number density. COMs formed on grain surfaces are returned to the gas phase via non-thermal desorption; however, gas-phase species reach lower fractional abundances than their grain-surface equivalents, ~10-12–10-7. Including the irradiation of grain mantle material helps build further complexity in the ice through the replenishment of grain-surface radicals which take part in further grain-surface reactions. There is reasonable agreement with several line transitions of H2CO observed towards T Tauri star-disk systems. There is poor agreement with HC3N lines observed towards LkCa 15 and GO Tau and we discuss possible explanations for these discrepancies. The synthesised line intensities for CH3OH are consistent with upper limits determined towards all sources. Our models suggest CH3OH should be readily observable in nearby protoplanetary disks with ALMA; however, detection of more complex species may prove challenging, even with ALMA “Full Science” capabilities. Our grain-surface abundances are consistent with those derived from cometary comae observations providing additional evidence for the hypothesis that comets (and other planetesimals) formed via the coagulation of icy grains in the Sun’s natal disk.
Key words: protoplanetary disks / astrochemistry / ISM: molecules / stars: formation
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Protoplanetary disks are crucial objects in star formation. They dissipate excess angular momentum away from the protostellar system, facilitate the accretion of matter from the natal cloud onto the new star, and contain all the material, dust and gas, which will likely go on to form a surrounding planetary system (for a review, see, e.g., Williams & Cieza 2011). The study of the detailed chemistry of these objects has gained impetus in recent years driven by the impending completion of the Atacama Large Millimeter/Submillimeter Array (ALMA). ALMA, with its unprecedented sensitivity and spatial and spectral resolution, will reveal, for the first time, the composition of protoplanetary disks on ~milliarcsecond scales, probing material ≲10 AU of the parent star in objects relatively close to Earth (≈140 pc). This spatial resolution will be achievable using the most extended configuration (with maximum baseline, B ≈ 16 km) at its highest operational frequencies (ν > 275 GHz). This will allow the study of the detailed composition of the cold molecular material within the “planet-forming” region of nearby disks, which will advance our understanding of the process of planetary system formation, and help answer questions regarding the morphology and composition of our own solar system.
The molecules observed in protoplanetary disks have thus far been restricted to small species and associated isotopologues due to their relatively high abundance and simple rotational spectra leading to observable line emission. The sources in which these molecules have been detected are also limited to a handful of nearby, and thus well-studied, objects. Molecules have been observed at both infrared (IR) and (sub)mm wavelengths with the IR emission originating from the inner warm/hot material (T ≳ 300 K, R ≲ 10 AU) and the (sub)mm emission originating from the outer cold disk (T < 300 K, R ≳ 10 AU). The molecules detected at (sub)mm wavelengths include CO, HCO+, CN, HCN, CS, N2H+, SO and C2H (see, e.g., Kastner et al. 1997; Dutrey et al. 1997; van Zadelhoff et al. 2001; Thi et al. 2004; Fuente et al. 2010; Henning et al. 2010). Also detected are several isotopologues of the listed species, e.g., 13CO, C18O, H13CO+, DCO+ and DCN (see, e.g., van Dishoeck et al. 2003; Thi et al. 2004; Qi et al. 2008). Several relatively complex molecules have also been observed: H2CO (Dutrey et al. 1997; Aikawa et al. 2003; Thi et al. 2004; Öberg et al. 2010, 2011), HC3N (Chapillon et al. 2012), and c-C3H2 (Qi et al. 2013b). Line emission in the (sub)mm can be observed from the ground and such observations have historically been conducted using single-dish telescopes, e.g., the James Clerk Maxwell Telescope (JCMT), the Caltech Submillimeter Observatory (CSO), the Institut de Radioastronomie Millimétrique (IRAM) 30 m telescope, and the Atacama Pathfinder Experiment (APEX). More recently, several interferometers have been available, e.g., the Submillimeter Array (SMA), Combined Array for Research in Millimeter-wave Astronomy (CARMA), and Plateau-de-Bure Interferometer (PdBI). These latter facilities have enabled spatially-resolved mapping of very nearby objects including the archetypical protoplanetary disk, TW Hydrae, located at a distance of ≈56 pc (Öberg et al. 2010, 2011; Hughes et al. 2011; Qi et al. 2011). Due to its proximity, TW Hydrae was observed during ALMA Science Verification which utilised between six and nine antennae working in conjunction to map the line emission from this source (Öberg et al. 2012; Rosenfeld et al. 2012). Early results from ALMA also include the first detection of the location of the CO snowline1in the disk around HD 163296 using DCO+ line emission (Mathews et al. 2013), and in the disk around TW Hydrae using N2H+ line emission (Qi et al. 2013c).
The launch of the Herschel Space Observatory allowed the first detection of ground-state transitions of ortho- and para-H2O (at 557 GHz and 1113 GHz, respectively) in the disk of TW Hydrae (Hogerheijde et al. 2011). Bergin et al. (2013) also report the first detection of HD in TW Hydrae using Herschel, allowing, for the first time, a direct determination of the disk mass without relying on analysis of dust thermal emission or CO rotational line emission. Bergin et al. (2013) determine a disk mass <0.05 M⊙ confirming that TW Hydrae, although considered a rather old system (~10 Myr), contains sufficient material for the formation of a planetary system. Also detected in the far-IR using Herschel, is the molecular ion, CH+, in the disk of the Herbig Be star, HD 100546 (Thi et al. 2011), and multiple lines of OH and warm H2O have also been detected in numerous sources (Fedele et al. 2012; Meeus et al. 2012; Riviere-Marichalar et al. 2012).
Most detections of line emission in the mid-IR have been conducted with the Spitzer Space Telescope and molecules observed include OH, H2O, C2H2, HCN, CO, and CO2 (Lahuis et al. 2006; Carr & Najita 2008; Salyk et al. 2008; Pontoppidan et al. 2010; Bast et al. 2013). Species detected at IR wavelengths are also limited to abundant, small, simple molecules with strong rovibrational transitions and/or vibrational modes, which are able to survive the high temperatures encountered in the inner disk. Mandell et al. (2012) also report the detection of near-IR emission lines of C2H2 and HCN, for the first time, using ground-based observatories (CRIRES on the Very Large Telescope and NIRSPEC on the Keck II Telescope).
The greatest chemical complexity (outside of our solar system) is seen in massive star-forming regions towards the Galactic centre (e.g., Sgr B2(N), Turner 1991) and in objects called “hot cores” and “hot corinos”, considered important stages in high-mass (M∗ ≳ 10 M⊙) and low-mass (M∗ ≲ 10 M⊙) star formation, respectively (see, e.g., Herbst & van Dishoeck 2009). Hot cores are remnant, often clumpy, cloud material left over from the explosive process of high-mass star formation which is heated by the embedded massive star. They are warm (T ~ 100 K), dense (n ≳ 106 cm-3), relatively large (R ~ 0.1 pc) objects which are heavily shielded by dust from both the internal stellar radiation and the external interstellar radiation (Av ~ 100 mag). Hot corinos, considered the equivalent early stage of low-mass star formation, possess similar densities and temperatures to hot cores, yet, are much less massive and smaller in spatial extent (typically, R ~ 100 AU). The line emission from the hot corino arises from a very compact region on the order of 1′′ in size for a source at the distance of Taurus (140 pc). Hence, we are limited to studying a handful of nearby sources (see, e.g., Ceccarelli 2005). Nevertheless, hot corinos are certainly as chemically complex as their more massive counterparts (if not more so), attested by the detection of glycolaldehyde, HOCH2CHO, in IRAS 16293+2422 during ALMA Science Verification (Jørgensen et al. 2012).
Hot cores and corinos are typified by the detection of rotational line emission from complex organic molecules (henceforth referred to as COMs), the formation of which remains one of the great puzzles in astrochemistry. The generally accepted mechanism is that simple ices formed on grain surfaces in the molecular cloud at 10 K, either via direct freezeout from the gas phase or via H-addition reactions on the grain (e.g., CO, H2O, H2CO, CH3OH), undergo warming to ≈30 K where they achieve sufficient mobility for grain-surface chemistry to occur via radical-radical association to create more complex ice mantle species (e.g., HCOOCH3). The grain-surface radicals necessary for further molecular synthesis are thought to be produced by dissociation via UV photons created by the interaction of cosmic rays with H2 molecules. Dissociation and/or ionisation via energetic electrons, created along the impact track as a cosmic ray particle penetrates a dust grain, is an alternative scenario (see, e.g., Kaiser & Roessler 1997). Further warming to T ≳ 100 K allows the removal of these more complex species from the ice mantle via thermal desorption thus “seeding” the gas with gas-phase COMs. Typically, the observed rotational line emission is characterised by a gas temperature of ≳100 K with COMs observed at abundances ~10-10 to ~10-6 times that of the H2 number density (see, e.g., Herbst & van Dishoeck 2009).
Comparing the physical conditions in hot cores/corinos with those expected in the midplane and molecular regions of protoplanetary disks, it appears a similar chemical synthesis route to COMs may be possible; however, to date, targeted searches for gas-phase COMs in nearby protoplanetary disks have been unsuccessful (see, e.g., Thi et al. 2004; Öberg et al. 2010, 2011). The possible reasons for this are severalfold: (i) gas-phase COMs are relatively abundant in disks; however, due to their more complex spectra and resulting weaker emission and the small intrinsic size of disks, existing telescopes are not sufficiently sensitive to detect line emission from COMs on realistic integration time scales; (ii) gas-phase COMs are relatively abundant in disks; however, previous targeted searches have not selected the best candidate lines for detection with existing facilities; and (iii) gas-phase COMs achieve negligible abundances in disks. The latter reason may be related to the major difference between hot cores/corinos and disks: the presence of external UV and X-ray radiation. Certainly, observations using ALMA, with its superior sensitivity and spectral resolution, will elucidate which scenario is correct. The confirmation of the presence (or absence) of COMs in disks is of ultimate astrobiological importance; is it possible for prebiotic molecules to form in the disk and survive assimilation into planets and other objects such as comets and asteroids? Looking at our own solar system, it appears possible. Many relatively complex molecules have been observed in the comae of multiple comets: H2CO, CH3OH, HCOOH, HC3N, CH3CN, C2H6 (see, e.g., Mumma & Charnley 2011, and references therein). The brightest comet in modern times, Hale-Bopp, displayed immense chemical complexity with additional detections of CH3CHO, NH2CHO, HCOOCH3, and ethylene glycol, (CH2OH)2 (Crovisier et al. 2004a,b). In addition, the simplest amino acid, glycine (NH2CH2COOH), was identified in samples of cometary dust from comet 81P/Wild 2 returned by the Stardust mission (Elsila et al. 2009). The detection of gas-phase glycine is considered one of the “holy grails” of prebiotic chemistry; however, thus far, searches for gas-phase glycine towards hot cores have been unsuccessful (see, e.g., Snyder et al. 2005).
In Walsh et al. (2010) and Walsh et al. (2012), henceforth referred to as WMN10 and WNMA12, we calculated the chemical composition of a protoplanetary disk using a gas-phase chemical network extracted from the UMIST Database for Astrochemistry (Woodall et al. 20072), termed “Rate06”, and the grain-surface chemical network from Hasegawa et al. (1992) and Hasegawa & Herbst (1993). We included the accretion of gas-phase species onto dust grains and allowed the removal of grain mantle species via both thermal and non-thermal desorption. In WMN10, our aim was to study the effects of cosmic-ray-induced desorption, photodesorption, and X-ray desorption on the chemical structure of the disk, whereas, in WNMA12, we extended our investigations to cover the importance of photochemistry and X-ray ionisation on disk composition. In both works, we focussed our discussions on species detected in disks, the most complex of which, at that time, was formaldehyde, H2CO.
Rate06 includes several gas-phase COMs, including methanol (CH3OH), formaldehyde (H2CO), formic acid (HCOOH), methyl formate (HCOOCH3), dimethyl ether (CH3OCH3) and acetone (CH3COCH3). These represent the most simple alcohol, aldehyde, carboxylic acid, ester, ether and ketone, respectively. The network also includes several larger members of these families, e.g., ethanol (C2H5OH) and acetaldehyde (CH3CHO). In WMN10 and WNMA12, we adopted the grain-surface network of Hasegawa et al. (1992) and Hasegawa & Herbst (1993) which includes the grain-surface synthesis of several of these more complex species. However, this network concentrates on simple atom-addition reactions, more likely to occur at the lower temperatures encountered in dark clouds. Hence, to date, the grain-surface chemistry that has been included is by no means comprehensive regarding the grain-surface synthesis of COMs.
In this work, we study the efficiency of the synthesis of COMs in protoplanetary disks using a chemical network typically used for hot core and hot corino chemical models. In Sect. 2, we describe our protoplanetary disk model (Sect. 2.1) and chemical network (Sect. 2.2). In Sects. 3 and 4, we present and discuss our results, respectively, and in Sect. 5 we state our conclusions.
 |
Fig. 1 Gas temperature (top left panel), H nuclei number density (top right panel), integrated UV flux (bottom left panel), and integrated X-ray flux (bottom right panel) as a function of disk radius, R, and disk height, Z/R. The contours in the top left panel represent the dust temperature. |
2. Protoplanetary disk model
2.1. Physical model
Our protoplanetary disk physical structure is calculated according to the methods outlined in Nomura & Millar (2005) with the addition of X-ray heating as described in Nomura et al. (2007). We model an axisymmetric disk in Keplerian rotation about a typical classical T Tauri star with mass, M∗ = 0.5 M⊙, radius, R∗ = 2 R⊙ and effective temperature, T∗ = 4000 K (see, e.g., Kenyon & Hartmann 1995). The surface density distribution is determined by the central star’s mass and radius and assuming a constant disk mass accretion rate, Ṁ, (see, e.g., Pringle 1981) and we parameterise the kinematic viscosity, ν, using the α-disk model of Shakura & Sunyaev (1973). We use a viscous parameter, α = 0.01, and a mass accretion rate, Ṁ = 10-8 M⊙ yr-1, typical values for accretion disks around classical T Tauri stars. We self-consistently solve the equation of hydrostatic equilibrium in the vertical direction and the local thermal balance between the heating and cooling of the gas to model the gas temperature, dust temperature, and density structure of the disk. The heating mechanisms included are grain photoelectric heating by UV photons and heating due to hydrogen ionisation by X-rays. We include gas-grain collisions and line transitions as cooling mechanisms.
The UV field in our disk model has two sources: the central star and the interstellar medium. The central star’s UV radiation field has three components: black-body radiation at the star’s effective temperature, hydrogenic bremsstrahlung emission, and strong Ly-α line emission. The latter two components are necessary for accurately modelling the excess UV emission often observed towards T Tauri stars, which is thought to arise from an accretion shock as material from the disk impinges upon the stellar surface (see, e.g., Johns-Krull et al. 2000). For the UV extinction, we include absorption and scattering by dust grains. The combined UV spectrum originating from the T Tauri star is displayed in Fig. C.1 in Nomura & Millar (2005) and replicated in Fig. 1 in WNMA12. The total UV luminosity is LUV ~ 1031 erg s-1.
We model the X-ray spectrum of the T Tauri star by fitting the XMM-Newton spectrum observed towards the classical T Tauri star, TW Hydrae, with a two-temperature thin thermal plasma model (see, e.g., Liedahl et al. 1995, MEKAL model). The best-fit parameters for the temperatures are kT1 = 0.8 keV and kT2 = 0.2 keV. For the foreground interstellar hydrogen column density, we find N(H2) = 2.7 × 1020 cm-2. For the X-ray extinction, we include attenuation due to all elements and Compton scattering by hydrogen. The resulting X-ray spectrum is shown in Fig. 1 in Nomura et al. (2007) and is replicated in Fig. 11 in WNMA12. The total X-ray luminosity of the star is LX ~ 1030 erg s-1.
We assume the dust and gas in the disk are well mixed, and we adopt a dust-grain size distribution which reproduces the extinction curve observed in dense clouds (Weingartner & Draine 2001). The dust grains are assumed to consist of silicate and carbonaceous material, and water ice. The resulting wavelength-dependent dust absorption coefficient is shown in Fig. D.1 in Nomura & Millar (2005). We acknowledge that this is a simplistic treatment of the dust-grain distribution in protoplanetary disks since it is thought that gravitational settling and grain coagulation (grain growth) will perturb the dust size and density distribution from that observed in dense clouds (see, e.g., Dullemond & Dominik 2004, 2005; D’Alessio et al. 2006). To keep the chemical calculation computationally tractable, we adopt average values for the dust grain size and density that are consistent with the dust model adopted in the disk structure calculation (see, e.g., Bergin 2011).
In Fig. 1, to guide the discussion in the paper, we present the resulting gas temperature (top left panel), total H nuclei number density, nH (top right panel), integrated UV flux (bottom left panel), and integrated X-ray flux (bottom right panel), as a function of disk radius, R, and height, Z/R. The contours in the top left panel represent the dust temperature. Here, we do not discuss the resulting disk structure in detail as this is covered in a series of previous publications (Walsh et al. 2010, 2012). In WMN10, we also present the two-dimensional gas and dust temperatures and gas number density, with supporting material and comprehensive discussions in the Appendix of that paper. In WNMA12, we display and discuss the incident UV and X-ray spectra and the resulting two-dimensional wavelength-integrated UV and X-ray fluxes.
The physical conditions throughout the disk cover many different regimes that generally differ from the conditions typical of dark clouds and hot cores and corinos. The gas temperature ranges from ≈17 K in the outer disk midplane to >6000 K in the inner disk surface. The H nuclei number density in the dark disk midplane spans many orders of magnitude from ~107 cm-3 in the outer disk (R ≈ 300 AU) to ~1014 cm-3 in the inner disk (R ~ 1 AU). We also remind the reader that protoplanetary disks around T Tauri stars are irradiated by X-rays in addition to cosmic rays and UV photons; hence, the ionisation rates and induced photodestruction rates in the molecular regions of protoplanetary disks can reach values much higher than those experienced in molecular clouds and hot cores and corinos (see Fig. 1).
2.2. Chemical model
We include various processes in our chemical network: gas-phase two-body reactions, photoreactions, cosmic-ray and X-ray reactions, gas-grain interactions, grain-surface two-body reactions, grain-surface photoreactions, and grain-surface cosmic-ray-induced and X-ray induced photoreactions. The latter three processes allow the chemical processing of grain-surface material by the radiation field present in the disk. The gas-phase chemistry (including the photochemistry and cosmic-ray chemistry) is from Laas et al. (2011) which is based on the OSU chemical network3 and which includes new possible routes to the formation of methyl formate and its structural isomers. To render the network suitable for protoplanetary disk chemistry, we have added reactions and rate coefficients applicable at higher temperatures (Harada et al. 2010, 2012). We include the direct X-ray ionisation of elements and calculate the X-ray ionisation rate throughout the disk using the prescription outlined in WNMA12. To simulate the X-ray chemistry, we duplicate the set of cosmic-ray-induced photoreactions and scale the rates by the X-ray ionisation rate. We also include the explicit calculation of the photochemical rates using the UV spectrum at each point in the disk for those species for which photodissociation and photoionisation cross sections exist (around 60 species, see van Dishoeck et al. 20064). In the absence of cross-sectional data, we approximate the rate by scaling the expected interstellar rate by the ratio of the integrated UV flux to that of the ISRF (≈1.6 × 10-3 erg cm-2 s-1).
For gas-grain interactions, we include accretion from the gas onto dust grains (i.e., freezeout) and desorption from grain surfaces back into the gas phase. For calculating the gas accretion and thermal desorption rates, we use the theory of Hasegawa et al. (1992) as in our previous work (see Eqs. (2)–(4) in WMN10). We assume, for simplicity, that the grains are negatively charged compact spheres with a radius, a = 0.1 μm, and a constant fractional abundance (relative to the H nuclei number density) of ~10-12, equivalent to a gas-to-dust mass ratio of ~100. We assume a sticking coefficient, S ~ 1, for all species. We model the grain-surface formation of molecular hydrogen by assuming the rate of H2 formation equates to half the rate of arrival of H atoms on the grain surface and use a reduced sticking coefficient for atomic hydrogen (S ~ 0.3). We adopt binding energies from the work of Laas et al. (2011) which originate from Garrod & Herbst (2006) and Garrod et al. (2008) and references therein (also see Table 1). Garrod & Herbst (2006) assume the value for the molecule measured in water ice (which makes up the largest component of the ice mantle) and we maintain this convention (see, e.g., Collings et al. 2004). We include the dissociative recombination of cations on grain surfaces with the products returned to the gas phase. We adopt the same branching ratios as for the equivalent gas-phase dissociative recombination reaction. Note that in the densest regions of the disk (n ≳ 1010 cm-3), the assumption of negatively charged grains becomes invalid and explicit grain-charging reactions should be included. Umebayashi & Nakano (2009) found that neutral grains dominate the grain population in the midplane in the inner disk (R < 1.5 AU). In this region, we are likely overestimating the recombination of cations on grain surfaces where n(G0)/n(G−) is of the order of a factor of a few. Because we are concerned with the chemistry occurring in the outer disk (R ≫ 1 AU), the neglect of explicit grain charging will not affect the discussion and conclusions presented in this work.
Initial fractional abundances (with respect to nH) and molecular binding (desorption) energies, ED (K).
In addition to thermal desorption, we include photodesorption, cosmic-ray-induced desorption (via heating), and reactive desorption. For the photodesorption rates, we use the most recent experimental values for the photodesorption yields (Öberg et al. 2009a,b). In this model, we include a “coverage” factor, θs, accounting for recent experimental results which suggest that photodesorption occurs from the top few monolayers only (Bertin et al. 2012). For molecules which do not have constrained photodesorption yields, Yi, we use the early experimental value determined for water ice by Westley et al. (1995) of 3 × 10-3 molecules photon-1 (see Table 1 and Eq. (1) in WNMA12). The photodesorption rate for species i, 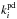 , is thus given by
, is thus given by 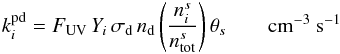 where FUV (photons cm-2 s-1) is the wavelength-integrated UV photon flux, σd (cm2) is the dust-grain cross section, nd is the number density of dust grains,
where FUV (photons cm-2 s-1) is the wavelength-integrated UV photon flux, σd (cm2) is the dust-grain cross section, nd is the number density of dust grains, 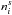 (cm-3) is the number density of species i on the grain, and
(cm-3) is the number density of species i on the grain, and 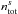 (cm-3) is the total number density of grain surface species. The surface coverage factor, θs is given by
(cm-3) is the total number density of grain surface species. The surface coverage factor, θs is given by 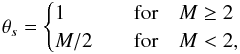 where M is the total number of monolayers per grain. We include photodesorption by both external and internal UV photons, the latter of which are produced by the interaction of cosmic rays with H2. We adopt a value for the integrated cosmic-ray-induced UV photon flux equal to ~104 photons cm-2 s-1 (Prasad & Tarafdar 1983). In regions where cosmic rays are attenuated, we scale the internal UV photon flux by the corresponding cosmic-ray ionisation rate. In WMN10, we investigated the influence of X-ray desorption on molecular abundances in protoplanetary disks and found it a potentially very powerful mechanism for returning grain-surface molecules to the gas phase. We used the theoretical framework of Léger et al. (1985), Najita et al. (2001), and Dwek & Smith (1996) to estimate the X-ray absorption cross sections and desorption rates. However, the interaction of X-ray photons with ice is still not well understood and indeed, recent experiments suggest that the picture is somewhat complicated with soft X-rays inducing chemistry in the ice via the production of ionic fragments (see, e.g., Andrade et al. 2010; Jiménez-Escobar et al. 2012). In general, there is a significant lack of quantitative data on X-ray induced desorption of astrophysical ices, hence, we choose not to include this process explicitly in this work and instead, we treat X-ray photodesorption as we treat UV photodesorption. Note that we also allow X-rays to dissociate and ionise grain mantle material in line with that seen in experiments (see discussion below).
where M is the total number of monolayers per grain. We include photodesorption by both external and internal UV photons, the latter of which are produced by the interaction of cosmic rays with H2. We adopt a value for the integrated cosmic-ray-induced UV photon flux equal to ~104 photons cm-2 s-1 (Prasad & Tarafdar 1983). In regions where cosmic rays are attenuated, we scale the internal UV photon flux by the corresponding cosmic-ray ionisation rate. In WMN10, we investigated the influence of X-ray desorption on molecular abundances in protoplanetary disks and found it a potentially very powerful mechanism for returning grain-surface molecules to the gas phase. We used the theoretical framework of Léger et al. (1985), Najita et al. (2001), and Dwek & Smith (1996) to estimate the X-ray absorption cross sections and desorption rates. However, the interaction of X-ray photons with ice is still not well understood and indeed, recent experiments suggest that the picture is somewhat complicated with soft X-rays inducing chemistry in the ice via the production of ionic fragments (see, e.g., Andrade et al. 2010; Jiménez-Escobar et al. 2012). In general, there is a significant lack of quantitative data on X-ray induced desorption of astrophysical ices, hence, we choose not to include this process explicitly in this work and instead, we treat X-ray photodesorption as we treat UV photodesorption. Note that we also allow X-rays to dissociate and ionise grain mantle material in line with that seen in experiments (see discussion below).
For the calculation of the cosmic-ray-induced thermal desorption rates we use the method of Hasegawa & Herbst (1993) (see Eq. (5) in WMN10). Here, we also include the process of reactive desorption for the first time. We follow the method of Garrod et al. (2007) and assume, for each grain-surface reaction which leads to a single product, a proportion of the product will be released into the gas phase. This assumes a probability that, upon reaction, a proportion of the energy released goes into desorbing the molecule from the grain surface. Investigations into the efficacy of reactive desorption in dark cloud models by Garrod et al. (2007) constrain the value for the probability of desorption to Prd = 0.01 and we adopt this value in our work. Recently, Vasyunin & Herbst (2013) suggested reactive desorption from grain surfaces followed by radiative association in the gas phase as a potential mechanism for the production of several complex molecules recently detected in dark clouds and prestellar cores (Bacmann et al. 2012; Cernicharo et al. 2012). The species detected include the methoxy radical (CH3O), ketene (CH2CO), acetaldehyde (CH3CHO), methyl formate (HCOOCH3), and dimethyl ether (CH3OCH3). Certainly, the detection of gas-phase complex molecules in regions with a temperature ≲15 K was unexpected and further adds to the puzzle regarding the chemical origin of COMs. In addition, recent experiments have investigated grain-surface chemistry induced by the irradiation of a single monolayer of O2 ice by a beam of D atoms (Dulieu et al. 2013). These experiments suggest that reactive desorption is particularly efficient for the reformation of doubly-deuterated water (D2O) and O2 via the surface reactions, s-D + s-OD and s-O + s-O, respectively. Dulieu et al. (2013) find these reactions release D2O and O2 into the gas phase with efficiencies, >90% and ≈60%, respectively We discuss the sensitivity of our results to the assumed probability for reactive desorption in Appendix A.
Our grain-surface network is also from Laas et al. (2011) which itself is derived from Garrod & Herbst (2006) and Garrod et al. (2008) with the grain-surface reaction rates calculated according to Hasegawa et al. (1992). We assume a density of surface sites equal to ≈1.5 × 1015 cm-2 and for the barrier between surface sites, Eb ≈ 0.3ED, where ED is the binding (desorption) energy to the grain surface of the reactant of interest. We discuss the sensitivity of our results to the assumed diffusion barrier in Appendix A. For light reactants i.e., H and H2, the diffusion rate is replaced with the quantum tunnelling rate assuming a barrier thickness of 1 Å (10-8 cm). Whether or not there is a quantum component in the diffusion rate of H atoms on grain surfaces remains a controversial topic. Analysis of experimental work on H2 formation on bare grain surfaces concluded there was no quantum diffusion component (Pirronello et al. 1997, 1999; Katz et al. 1999). A reanalysis of this experimental work determined a quantum component is necessary to explain the rate of formation of HD observed in the experiments (Cazaux & Tielens 2004). More recent experiments on H atom diffusion on amorphous solid water (ASW) have proved inconclusive (see, e.g., Watanabe et al. 2010). Here, since the bulk of our ice mantle is composed of water ice, we choose the “optimistic” case and allow quantum tunnelling for H and H2.
The dissociation and ionisation of grain-surface species via UV photons (originating both externally and internally via cosmic rays) and X-rays are new processes, not included in our previous work. The importance of UV processing for building chemical complexity in interstellar ice analogues has been known for some time (see, e.g., Allamandola et al. 1988). An example of a grain-surface photoreaction is the photodissociation of grain-surface methanol, s-CH3OH, into its constituent radicals, s-CH3 and s-OH, which are then available on the grain to take part in further surface-association reactions. Note that grain-surface (ice) species are prefixed with “s-”. For these reactions, we assume the rate of the equivalent gas-phase reaction. This is supported by recent estimates of the grain-surface photodestruction of pure methanol ice which also show that photochemistry occurs deep within the bulk ice (Öberg et al. 2009c). The various reaction channels possible are estimated by assuming a grain-surface molecule will likely dissociate into its functional group components (as demonstrated above for methanol), i.e., allowing no rearrangement of the constituent atoms, and allowing reactions involving destruction of the weaker bonds to have higher branching ratios (Garrod et al. 2008). For each ionisation event, we assume that the cation dissociatively recombines with the electron, and the excess energy in the products lost via translation energy on the grain mantle, i.e., the products remain on the grain surface (Garrod et al. 2008). We adopt the same branching ratios for the equivalent gas-phase dissociative recombination reaction. For X-ray induced dissociation and ionisation of grain-surface species, we follow the same formulation as that adopted for the gas-phase X-ray reactions: we duplicate the set of cosmic-ray-induced photoreactions and scale the reaction rates by the X-ray ionisation rate calculated in the disk. In line with experiments, we allow X-ray and UV photodissociation and ionisation to occur throughout the ice mantle (see, e.g. Öberg et al. 2009c; Andrade et al. 2010; Jiménez-Escobar et al. 2012).
In addition to cosmic-ray-induced photoreactions, the direct impact of cosmic ray particles, which, in the Galaxy, consist predominantly of protons and stripped nuclei (≈98%, see, e.g. Simpson 1983) can penetrate the dust grain and induce cascades of up to 102 suprathermal atoms along the impact track. These atoms, in turn, ionise the molecular material within the ice mantle also creating energetic electrons (~keV) which also dissociate ionise the ice mantle material (see, e.g., Kaiser & Roessler 1997; Bennett & Kaiser 2007; Bennett et al. 2011). Here, we simulate this process in the ice by also adopting the direct cosmic-ray ionisation rates for the equivalent gas-phase reaction.
Our complete chemical network has ≈9300 reactions involving ≈800 species and is one of the most complex chemical models of a protoplanetary disk constructed to date.
2.3. Molecular line emission
In order to compare our model results with current observations and select potential molecules and line transitions which may be observable in protoplanetary disks, we have calculated the molecular line emission from the disk to determine rotational line transition intensities for molecules of interest in this work.
For simplicity, we assume the disk is “face-on”, i.e., has an inclination of 0°, and that local thermodynamic equilibrium (LTE) holds throughout. The former assumption allows us to quickly and efficiently calculate the line emission without worrying about geometrical effects due to disk inclination, whilst the latter assumption makes the calculation more computationally tractable and allows us to compute an entire spectrum of a particular molecule in a single calculation. This is important for COMs, in particular, which typically have many energy levels and transitions and thus, relatively complex spectra. In order to perform a non-LTE calculation, we require accurate collisional rate coefficients which are only available for a handful of molecules (see, e.g., the Leiden Atomic and Molecular Database or LAMDA5). For molecules considered in this work, collisional data for H2CO, CH3OH, HC3N and CH3CN only are available. We expect the disk conditions to depart from LTE mainly in the outer, colder, more diffuse regions of the disk. However, we also only expect our LTE disk-integrated line intensities to deviate from those calculated assuming non-LTE conditions by no more than a factor of a few (see, e.g., Pavyluchenkov et al. 2007). Since this work is exploratory in nature, the line intensities we calculate are still very useful for determining which transitions in which molecules may be detectable using ALMA.
There are numerous caveats when assuming LTE. The intense background thermal radiation in warm regions of the disk may radiatively pump particular transitions leading to weakly (or possibly, strongly) masing lines (Trot>Tk). Formaldehyde (H2CO) and methanol (CH3OH) masers have been observed in the local interstellar medium and are commonly associated with massive star forming regions (see, e.g., Elitzur 1992). Indeed, there have been suggestions that methanol masers trace the protoplanetary disk material around massive embedded protostars (see, e.g., Norris et al. 1998). Certainly, the potential for observable maser emission from formaldehyde and methanol in disks around low-mass stars should be explored in future work.
The disk-integrated line flux density, Fν, is determined by integrating the solution of the radiative transfer equation in the vertical direction and summing over radial sections of the disk, i.e., 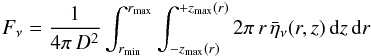 (1)where D is the distance to source and
(1)where D is the distance to source and 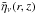 is the emissivity at a grid point (r,z) times the absorption in the upper disk, i.e.,
is the emissivity at a grid point (r,z) times the absorption in the upper disk, i.e., ![\begin{eqnarray} \bar{\eta}_\nu(r,z) = n_\mathrm{u}(r,z)\, A_\mathrm{ul} \, \phi_\nu \frac{h\nu}{4\pi} \exp{\left[ -\tau_\nu(r,z)\right ]}. \end{eqnarray}](/articles/aa/full_html/2014/03/aa22446-13/aa22446-13-eq102.png) (2)Here, nu is the abundance in the upper energy level of the transition, Aul is the Einstein coefficient for spontaneous emission from the upper level, u, to the lower level, l, φν is the value of the line profile function at the frequency, ν (assumed to be Gaussian in shape), and h is Planck’s constant. The optical depth, τν(r,z), is
(2)Here, nu is the abundance in the upper energy level of the transition, Aul is the Einstein coefficient for spontaneous emission from the upper level, u, to the lower level, l, φν is the value of the line profile function at the frequency, ν (assumed to be Gaussian in shape), and h is Planck’s constant. The optical depth, τν(r,z), is 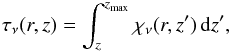 (3)where the absorption coefficient, χν, is given by
(3)where the absorption coefficient, χν, is given by 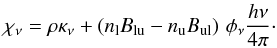 (4)Here, ρ is the dust mass density (g cm-3), κν is the dust mass absorption coefficient (cm2 g-1), nl is the abundance in the lower energy level of the transition and Blu and Bul are the Einstein coefficients for absorption and stimulated emission, respectively.
(4)Here, ρ is the dust mass density (g cm-3), κν is the dust mass absorption coefficient (cm2 g-1), nl is the abundance in the lower energy level of the transition and Blu and Bul are the Einstein coefficients for absorption and stimulated emission, respectively.
Since we assume LTE holds throughout, our level populations are given by the Boltzmann distribution, i.e., the population of an energy level, i, is determined using 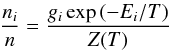 (5)where ni is the number density in level i, n is the total number density of the molecule (∑ ini), gi is the degeneracy of the level, Ei is the energy (in units of K) and T is the gas temperature. We explicitly calculate the rotational partition function, Zrot(T), by summing over populated energy levels in colder regions, i.e., Zrot(T) = ∑ igiexp( − Ei/T), and swapping to the high temperature approximation once the higher energy levels become sufficiently populated, that is,
(5)where ni is the number density in level i, n is the total number density of the molecule (∑ ini), gi is the degeneracy of the level, Ei is the energy (in units of K) and T is the gas temperature. We explicitly calculate the rotational partition function, Zrot(T), by summing over populated energy levels in colder regions, i.e., Zrot(T) = ∑ igiexp( − Ei/T), and swapping to the high temperature approximation once the higher energy levels become sufficiently populated, that is, 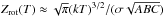 , where, k is Boltzmann’s constant, σ is the symmetry factor, i.e., the number of indistinguishable rotational orientations of the molecule, and A, B, and C are the rotational constants in energy units. In the inner regions of the disk, the gas temperature is sufficiently high that molecules can become vibrationally excited. COMs, in particular, can be vibrationally excited at relatively moderate temperatures, ≈300 K; hence, we also include the vibrational partition function in our determination of the total partition function, Z(T) = Zvib(T) × Zrot(T), where
, where, k is Boltzmann’s constant, σ is the symmetry factor, i.e., the number of indistinguishable rotational orientations of the molecule, and A, B, and C are the rotational constants in energy units. In the inner regions of the disk, the gas temperature is sufficiently high that molecules can become vibrationally excited. COMs, in particular, can be vibrationally excited at relatively moderate temperatures, ≈300 K; hence, we also include the vibrational partition function in our determination of the total partition function, Z(T) = Zvib(T) × Zrot(T), where 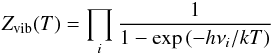 (6)with νi representing the set of characteristic vibrational frequencies for each molecule. Typically, i ≫ 1 for complex molecules, e.g., methanol has 12 characteristic frequencies of vibration.
(6)with νi representing the set of characteristic vibrational frequencies for each molecule. Typically, i ≫ 1 for complex molecules, e.g., methanol has 12 characteristic frequencies of vibration.
We use the molecular rotational line lists from either the Cologne Database for Molecular Spectroscopy (CDMS, Müller et al. 20056) or the Jet Propulsion Laboratory (JPL) molecular spectroscopic database (Pickett et al. 19987) and molecular constants (rotational constants and vibrational frequencies) from CDMS, JPL, and the NIST database8,9. For line lists from CDMS, we use internally generated Einstein A coefficients provided by the database. For JPL, we convert the listed line intensities, Sν, to transition probabilities using the partition function provided by the database at the reference temperature, 300 K (see Eq. (9) in Pickett et al. 1998). We have benchmarked our partition functions with those provided by CDMS and JPL. Our results for H2CO and CH3OH at low temperatures (T ≤ 37.5 K) agree with those provided by the databases to >3 significant figures. At higher temperatures, our results agree to within ≈15% of the database values over the temperature range applicable to our disk model (T ≲ 150 K, see Fig. 1).
In our calculations, we assume a distance to source, D = 140 pc, the distance to the Taurus molecular cloud complex where many well-studied protoplanetary disks are located. To convert line flux densities to sources at other distances, one must simply scale the values by the square of the ratio of the distances, e.g., for a source at 400 pc, for example, the Orion molecular cloud, the line flux density is reduced by a factor, (140/400)2 = 0.123, whilst for a source at 56 pc, for example, TW Hya, the line flux density is enhanced by a factor, (140/56)2 = 6.25.
3. Results
We determine the chemical structure of the disk by calculating the time-dependent chemical evolution at each grid point in our model. Firstly, we investigate the influence of different chemical processes by running a reduced grid at a fixed radius in the outer disk (R = 305 AU). Secondly, we present results from our full disk model, i.e., by running the entire grid (≈10 000 points) as a series of single-point models. We calculate the chemical structure between a radius of ≈1 AU and ≈305 AU. We concentrate our results and discussions on the outer cold disk (T ≲ 100 K) where sufficient freezeout allows grain-surface synthesis to occur. We map the chemical structure of the disk at a time of 106 yr, the typical age of classical T Tauri stars.
3.1. Initial abundances
Our initial abundances are extracted from the results of a simple time-dependent dark cloud model with constant physical conditions (n = 105 cm-3, T = 10 K, Av = 10 mag) at a time of 105 yr. We use the same chemical network for the generation of the initial abundances as in our full disk model. Our initial elemental abundance ratios for H:He:O:C:N:S:Na:Mg:Si:Cl:Fe are 1:9.75(−2):1.76(−4):7.3(−5):2.14(−5):2(−8):3(−9):3(−9): 3(−9):3(−9):3(−9) where a(b) represents a × 0b (Graedel et al. 1982).
The initial abundances for a selection of gas-phase and grain-surface (ice) molecules are shown in Table 1 along with their corresponding grain-surface binding energies. The species are ordered by mass and we list the initial fractional abundances and binding energies of the complex molecules of interest in this work separately.
The calculations begin with appreciable fractional abundances (relative to total H nuclei number density, nH = n(H) + 2n(H2)) of relatively simple ices, such as, s-H2O (≈1 × 10-4), s-CO (≈3 × 10-5), s-CH4 (≈3 × 10-5), s-NH3 (≈1 × 10-5), and s-N2 (≈4 × 10-6). Formaldehyde (s-H2CO), methylamine (s-CH3NH2), methanol (s-CH3OH), formamide (s-NH2CHO), and ethane (s-C2H6) also achieve relatively high fractional abundances on the grains (≳10-8). These species are efficiently formed via atom-addition reactions at 10 K. s-C3H4 also reaches an appreciable fractional abundance (≈2 × 10-6). In this network we do not distinguish between isomers of C3H4. Because propyne has the lower zero-point energy and also possesses a rotational spectrum, we choose to treat C3H4 as propyne (CH3CCH) as opposed to allene (CH2CCH2).
Under dark cloud conditions, methanol and formaldehyde are formed on the grain via the sequential hydrogenation of CO ice, 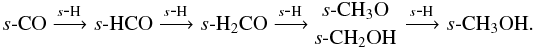 Methylamine is formed via the hydrogenation of s-CH2NH,
Methylamine is formed via the hydrogenation of s-CH2NH, 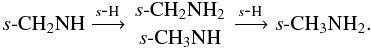 s-CH2NH has multiple formation pathways originating from atom addition to small hydrocarbon radicals,
s-CH2NH has multiple formation pathways originating from atom addition to small hydrocarbon radicals, 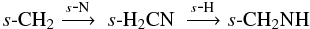 and
and 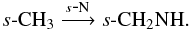 Propyne, s-CH3CCH, forms via successive hydrogenation of s-C3 and s-C3H, both of which form readily in the gas phase and subsequently freeze out onto the dust grains. Grain-surface formamide originates from s-OCN e.g.,
Propyne, s-CH3CCH, forms via successive hydrogenation of s-C3 and s-C3H, both of which form readily in the gas phase and subsequently freeze out onto the dust grains. Grain-surface formamide originates from s-OCN e.g., 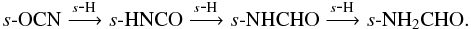 s-OCN can form either on the grain via the reactions
s-OCN can form either on the grain via the reactions 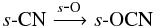 and
and 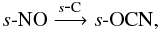 or in the gas phase via atom-radical and radical-radical reactions, such as,
or in the gas phase via atom-radical and radical-radical reactions, such as,  and
and  whence it can freeze out onto dust grains. Ethane, s-C2H6, forms on the grain in a similar manner to propyne, via the sequential hydrogenation of s-C2 and s-C2H. Note that radicals, such as, CH3O and CH2OH, can also be formed via the photodissociation of larger species, in this case, CH3OH, as well as on the grain and via ion-molecule chemistry.
whence it can freeze out onto dust grains. Ethane, s-C2H6, forms on the grain in a similar manner to propyne, via the sequential hydrogenation of s-C2 and s-C2H. Note that radicals, such as, CH3O and CH2OH, can also be formed via the photodissociation of larger species, in this case, CH3OH, as well as on the grain and via ion-molecule chemistry.
 |
Fig. 2 Physical conditions as a function of disk height at a radius, R = 305 AU. Number density of H nuclei (cm-3) and gas and dust temperature (K) are shown in the left-hand panel (solid red lines, solid blue lines, and dashed blue lines, respectively). UV and X-ray radiative fluxes (erg cm-2 s-1) and X-ray and cosmic-ray ionisation rates (s-1) are shown in the right-hand panel (solid red lines, dashed red lines, dashed blue lines, and dotted blue lines, respectively). |
 |
Fig. 3 Fractional abundance (with respect to H nuclei number density) of gas-phase molecules as a function of disk height, Z at a radius, R = 305 AU. The chemical complexity in the model increases from Model 1 to Model 5 (see Sect. 3.2 for details). |
3.2. Vertical abundance profiles at R = 305 AU
Here, we present results from a series of reduced grids to investigate the particular chemical processes responsible for the production and destruction of COMs in the outer disk. We calculated the chemical evolution over a 13-point grid in a single vertical slice of the disk at a fixed radius of 305 AU. The physical conditions in this slice are presented in Fig. 2. The H nuclei number density decreases from a maximum value of ≈5 × 107 cm-3 in the disk midplane to ≈6 × 105 cm-3 at the surface and the gas temperature increases from a minimum of ≈16 K in the midplane to ≈42 K at the disk surface. The gas and dust temperatures at the disk surface decouple above a height of ≈150 AU such that the dust temperature on the disk surface reaches a maximum value of ≈28 K. The disk midplane is heavily shielded from both UV and X-ray photons; however, cosmic rays are able to penetrate the entire disk. As expected, the disk surface is heavily irradiated with the UV and X-ray fluxes reaching a value ~10-2 erg cm-2 s-1, an order of magnitude stronger than the integrated interstellar UV flux (1.6 × 10-3 erg cm-2 s-1).
We present results from five different models which increase incrementally in complexity from Model 1 through to Model 5. Model 1 is the most simple and includes gas-phase chemistry, freezeout onto dust grains, and thermal desorption. In Model 2, we add cosmic-ray-induced thermal desorption and photodesorption by internal and external UV photons and X-ray photons. In Model 3, we include grain-surface chemistry and in Model 4, we also add the cosmic-ray, X-ray, and UV photoprocessing of ice mantle material. The most complex model, Model 5, also includes reactive desorption (see Sect. 2.2).
In Figs. 3 and 4 we present the fractional abundance (relative to H nuclei number density) as a function of disk height, Z, at a radius, R = 305 AU, of a selection of gas-phase and grain-surface (ice) COMs, respectively10. Note that we have used the same scale for the abundance of each gas-phase molecule and analogous grain-surface species to ease the comparison between plots.
3.2.1. Model 1: freezeout and thermal desorption
In Model 1 (red lines in Figs. 3 and 4), where we include freezeout and thermal desorption only, a handful of molecules achieve an appreciable fractional abundance (≳10-11) in the disk molecular layer: H2CO, HC3N, CH3CN, and CH3NH2. These species are depleted in the disk midplane below a height of ≈100 AU due to efficient freezeout onto dust grains. Higher in the disk, gas-phase formation replenishes molecules lost via freezeout onto grain surfaces. These species generally retain a similar peak fractional abundance as that achieved under dark cloud conditions. The exception to this is acetonitrile (CH3CN) which increases from an initial fractional abundance of ~10-12 to reach a peak value of ~10-10 at Z ≈ 200 AU. The fractional abundances decrease towards the disk surface due to increasing photodestruction. None of the other gas-phase species achieve significant peak fractional abundances in the molecular layer (≲10-11), even those which begin with an appreciable initial abundance, i.e., CH3OH and CH3CCH. The fractional abundance of gas-phase CH3OH remains ≲10-14 throughout the disk height. For these species, freezeout onto dust grains wins over gas-phase formation. The more complex molecules, which cannot form in the gas-phase under dark cloud conditions, are also unable to form under the conditions in the outer disk, in the absence of grain-surface chemistry.
Regarding the grain-surface results for Model 1 (Fig. 4), due to the higher binding energies of most species, thermal desorption alone is unable to remove significant fractions of the grain mantle. Hence, the ice remains abundant throughout the vertical extent of the disk with most species retaining their initial fractional abundance. We see enhancements in the fractional abundances of s-H2CO, s-HCOOH, s-HC3N and s-CH3CN around 100 AU. All four species have gas-phase routes to formation; however, under the conditions beyond Z ≈ 100 AU, additional molecules created in the gas phase can accrete onto dust grains thereby increasing their abundance on the grain mantle.
3.2.2. Model 2: non-thermal desorption
In Model 2 (green lines in Figs. 3 and 4), we have added cosmic-ray-induced thermal desorption and photodesorption due to external and internal UV photons and X-ray photons. Non-thermal desorption has a powerful effect on both the gas-phase and grain-surface abundances as we also concluded in our previous work (WMN10). There are several noticeable effects: (i) the gas-phase abundances of many molecules are enhanced towards the disk midplane, relative to the results for Model 1, due to cosmic-ray-induced thermal desorption and photodesorption; (ii) the abundances of grain-surface molecules drop significantly towards the disk surface due to photodesorption by external UV photons; and (iii) there is a shift in the position of the gas-phase “molecular layer” towards the midplane. This latter effect is due to a combination of non-thermal desorption and enhanced gas-phase formation lower in the disk, and enhanced destruction higher in the disk due to the release of a significant fraction of the grain mantle back into the gas phase. Non-thermal desorption effectively “seeds” or replenishes the gas with molecules that otherwise would remain bound to the grain, e.g., H2O and its protonated form, H3O+, which then go on to take part in gas-phase reactions which can form (destroy) molecules which would otherwise be depleted (abundant).
The fractional abundance of gas-phase H2CO is enhanced to ~10-12 in the disk midplane. However, its fractional abundance in the molecular layer and disk surface reaches values similar to that in Model 1 (~10-10–10-9). CH3OH reaches a peak abundance of ~10-10 around a height of ≈100 AU corresponding to the height where photodesorption by external photons begins to have an effect. Once released from the grain, methanol is efficiently destroyed under the conditions in the upper disk since methanol does not have efficient gas-phase routes to formation at low temperatures. Methanol is also significantly enhanced in the disk midplane by cosmic-ray-induced desorption, reaching a fractional abundance, ~10-13. Other gas-phase species enhanced in the midplane and molecular layer due to non-thermal desorption and reaching appreciable fractional abundances (≳10-11) include HCOOH, HC3N, CH3CN, CH3CCH, and CH3NH2.
3.2.3. Model 3: grain-surface chemistry
In Model 3 (blue lines in Figs. 3 and 4), we have added thermal grain-surface chemistry (Hasegawa et al. 1992). Grain-surface chemistry is a very important process for building chemical complexity in the ice mantle under the conditions in the outer disk. There are several reasons for this. In addition to reactions involving atoms and other neutrals, which are well known in ice chemistry at 10 K, it appears that a reasonably high abundance of radicals, such as, s-OH and s-HCO, can be achieved without radiation processing of the ice mantle. They form via association reactions on the grain, e.g, s-H + s-CO, or accrete from the gas phase where they are formed via gas-phase chemistry or via the photodissociation of larger species. These radicals can diffuse and react at the dust temperatures in the outer disk (17−30 K).
The major effect of the addition of thermal grain-surface chemistry is that the gas-phase fractional abundances of all molecules we consider in this section are enhanced (relative to the results for Model 1 and Model 2). We see around an order of magnitude increase in the peak abundance of formaldehyde in the molecular layer of the disk, from ~10-9 to ~10-8. Gas-phase methanol is enhanced throughout the molecular layer and disk surface also reaching a peak fractional abundance of ~10-8 at a height of ≈150 AU. We see a corresponding rise in the ice abundance indicative that grain-surface formation of methanol is replenishing the grain mantle molecules lost to the gas by non-thermal desorption. Formic acid, HCOOH, reaches a peak abundance of ~10-8 in the molecular layer. We see a dramatic rise in the fractional abundance of s-HCOOH throughout the disk height. s-HCOOH can be formed at low temperatures (≈20 K) on grain surfaces via the barrierless reactions, 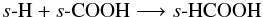 and
and 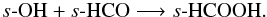 The former reaction requires s-COOH to be sufficiently abundant and this is formed on grain-surfaces via s-OH + s-CO which has a high reaction barrier (≈3000 K). Thus, the latter reaction is the main route to formation in the cold midplane. Although the mobility of both s-OH and s-HCO is relatively low at ≈20 K, the long lifetime of the disk, ~106 years, and the high density in the midplane, ~107 cm-3, allows the sufficient buildup of formic acid ice via this reaction.
The former reaction requires s-COOH to be sufficiently abundant and this is formed on grain-surfaces via s-OH + s-CO which has a high reaction barrier (≈3000 K). Thus, the latter reaction is the main route to formation in the cold midplane. Although the mobility of both s-OH and s-HCO is relatively low at ≈20 K, the long lifetime of the disk, ~106 years, and the high density in the midplane, ~107 cm-3, allows the sufficient buildup of formic acid ice via this reaction.
Gas-phase HC3N experiences a order-of-magnitude enhancement in Model 3 relative to Model 2, reaching a peak fractional abundance of ~10-9. However, we see a drop in the fractional abundance of grain-surface s-HC3N below a height, Z ≲ 150 AU, relative to the results for Model 2. s-HC3N can be sequentially hydrogenated up to s-C2H5CN (propionitrile).
We also see enhancements, related to grain-surface chemistry, in gas-phase CH3CN, CH3CCH, CH3CHO, NH2CHO, and CH3NH2 in the molecular layer and disk surface, reaching peak fractional abundances of ~10-10–10-8. s-CH3CN is formed via successive hydrogenation of s-C2N, 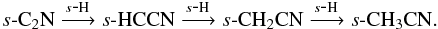 In turn, s-C2N can form via s-C + s-CN and s-N + s-C2, or freeze out from the gas phase, where it is formed via ion-molecule and radical-radical reactions. In warmer regions, s-CH3CN can also form via the radical-radical reaction, s-CN + s-CH3. Intermediate species in the above hydrogenation sequence can also form via grain-surface association reactions, e.g.,
In turn, s-C2N can form via s-C + s-CN and s-N + s-C2, or freeze out from the gas phase, where it is formed via ion-molecule and radical-radical reactions. In warmer regions, s-CH3CN can also form via the radical-radical reaction, s-CN + s-CH3. Intermediate species in the above hydrogenation sequence can also form via grain-surface association reactions, e.g., 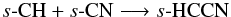 and
and 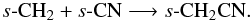 s-CH3CCH, forms via the successive hydrogenation of s-C3 and s-C3H, and in warmer gas can also form via the barrierless radical-radical reaction,
s-CH3CCH, forms via the successive hydrogenation of s-C3 and s-C3H, and in warmer gas can also form via the barrierless radical-radical reaction, 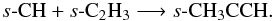 In turn, s-C2H3, has several grain-surface formation routes, in addition to the hydrogenation of s-C2H2, e.g., s-C + s-CH3 and s-CH + s-CH2. Acetaldehyde (s-CH3CHO) can form via the association of s-CH3 and s-HCO or via s-CH3CO which, in turn, forms on the grain via s-CH3 + s-CO. This latter reaction has a barrier of ≈3500 K and can only proceed on sufficiently warm grains. The formation of formamide (s-NH2CHO) and methylamine (s-CH3NH2) via atom-addition reactions was discussed previously in relation to dark cloud chemistry (see Sect. 3.1). In warmer regions, again, there are formation routes via the association of the amine and formyl radicals (s-NH2 + s-HCO), and the methyl and amine radicals (s-CH3 + s-NH2), respectively. In all cases, these precursor radicals are either formed on the grain via atom-addition reactions, or they form in the gas phase via ion-molecule chemistry or photodissociation and freeze out onto dust grains.
In turn, s-C2H3, has several grain-surface formation routes, in addition to the hydrogenation of s-C2H2, e.g., s-C + s-CH3 and s-CH + s-CH2. Acetaldehyde (s-CH3CHO) can form via the association of s-CH3 and s-HCO or via s-CH3CO which, in turn, forms on the grain via s-CH3 + s-CO. This latter reaction has a barrier of ≈3500 K and can only proceed on sufficiently warm grains. The formation of formamide (s-NH2CHO) and methylamine (s-CH3NH2) via atom-addition reactions was discussed previously in relation to dark cloud chemistry (see Sect. 3.1). In warmer regions, again, there are formation routes via the association of the amine and formyl radicals (s-NH2 + s-HCO), and the methyl and amine radicals (s-CH3 + s-NH2), respectively. In all cases, these precursor radicals are either formed on the grain via atom-addition reactions, or they form in the gas phase via ion-molecule chemistry or photodissociation and freeze out onto dust grains.
Moving on to the more complex species, we see much the same effect as for those already discussed; gas-phase abundances are enhanced when grain-surface chemistry is included. Each gas-phase species reaches a peak abundance of ~10-12 − 10-10 in the molecular layer, which correlates with enhancements in the grain-surface abundances and hence are directly due to synthesis via grain-surface chemistry and subsequent release to the gas phase via non-thermal desorption. The peak fractional abundance attained by the more complex species on the grain surface ranges between ~10-9 − 10-7. For those complex species for which we begin with negligible abundances on the grain (≲10-13), i.e., s-C2H5OH, s-CH3OCH3, s-CH3COCH3, s-CH3COOH, s-HCOOCH3, and s-HOCH2CHO, grain-surface chemistry is absolutely necessary for their formation. These species form predominantly via radical-radical association routes and, thus, require significant abundances of precursor radicals. For example, methyl formate (s-HCOOCH3) can form on the grain via the association reaction, 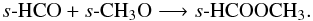 Both reactants are steps on the ladder of the sequential hydrogenation of CO to form CH3OH. Similarly,
Both reactants are steps on the ladder of the sequential hydrogenation of CO to form CH3OH. Similarly,
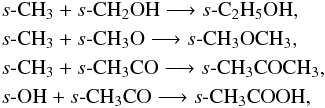 and,
and,  Note that the isomers, s-HCOOCH3 and s-HOCH2CHO (methyl formate and glycolaldehyde), are relatively abundant in the disk midplane. Both species are formed via reactants which are products of the hydrogenation of s-CO. In contrast, the third member of this family, s-CH3COOH, is formed on the grain via s-CH3CO which is formed via the association of s-CH3 and s-CO. This reaction has a barrier of around 3500 K and so cannot proceed at the low temperatures in the disk midplane. Radicals, such as, CH2OH and CH3O, are also formed in the gas via the photodissociation of larger molecules, e.g., CH3OH.
Note that the isomers, s-HCOOCH3 and s-HOCH2CHO (methyl formate and glycolaldehyde), are relatively abundant in the disk midplane. Both species are formed via reactants which are products of the hydrogenation of s-CO. In contrast, the third member of this family, s-CH3COOH, is formed on the grain via s-CH3CO which is formed via the association of s-CH3 and s-CO. This reaction has a barrier of around 3500 K and so cannot proceed at the low temperatures in the disk midplane. Radicals, such as, CH2OH and CH3O, are also formed in the gas via the photodissociation of larger molecules, e.g., CH3OH.
3.2.4. Model 4: radiation processing of ice
In Model 4 we added cosmic-ray, X-ray and UV photo-processing of ice mantle material. The behaviour of ice under irradiation is still very uncertain with only a handful of quantitative experiments conducted. Experiments on UV-irradiated pure methanol ice show that chemistry is induced by the process with many gas-phase products, other than methanol, observed (see e.g., Gerakines et al. 1996; Hudson & Moore 2000; Öberg et al. 2009c). Experiments investigating soft X-ray irradiated ice also show a rich chemistry as discussed earlier in the context of X-ray desorption (see e.g., Andrade et al. 2010; Ciaravella et al. 2012; Jiménez-Escobar et al. 2012). Experiments have also been performed to simulate the chemical consequences of the direct impact of cosmic-ray particles on ice-covered dust grains (see, e.g, Kaiser & Roessler 1997; Bennett & Kaiser 2007; Bennett et al. 2011). High energy cosmic rays can fully penetrate dust grains creating suprathermal atoms which, in turn, transfer energy to the ice mantle and ionise molecules creating high-energy electrons (~keV) which induce a further cascade of secondary electrons. Bennett & Kaiser (2007) simulate this effect by irradiating astrophysical ices (consisting of s-CO and s-CH3OH) with energetic electrons and find that complex molecules, such as glycolaldehyde and methyl formate, can efficiently form, reaching relative abundances commensurate with those observed in hot cores.
The radiation processing of grain mantle material should provide an additional means for complex species to build up on the grain since the process allows the replenishment of grain-surface atoms and radicals to take part in further reactions. Indeed, to reproduce the observed abundances of gas-phase COMs in hot cores (~10-8 − 10-6), models need to include radiative processing of ice to produce the necessary precursor molecules (see e.g., Garrod et al. 2008). For example, instead of s-CH3OH effectively becoming the “end state” of s-CO via hydrogenation, cosmic-rays, X-rays, and UV photons can break apart s-CH3OH into s-CH3 and s-OH which are then available to either reform methanol or form other species such as s-CH3CN (s-CH3 + s-CN) or s-HCOOH (s-OH + s-HCO). More complex molecules can also be synthesised by the association of surface radicals; a most important case in hot cores is the association of the s-HCO and s-CH3O radicals to form methyl formate (s-HCOOCH3). Laas et al. (2011) found that the gas-phase formation of methyl formate contributes, at most, to 1.6% of the total abundance in hot cores. Another case is the surface formation of dimethyl ether (s-CH3OCH3) via the association of the surface radicals s-CH3 and s-CH3O. These and many other cases are discussed in Sect. 3.2.3 and in further detail in Garrod et al. (2008).
The results for Model 4 are represented by the yellow-orange lines in Figs. 3 and 4. In general, we see drops in abundances of gas-phase molecules in the molecular layer and disk surface (≳100 AU) which correlates with drops in the abundances of grain-surface molecules at a similar height. Conversely, in the disk midplane (≲100 AU), we see an increase in the abundances of gas-phase and grain-surface species. This is most noticeable for those species which otherwise are unable to form efficiently on the grain at low temperatures: s-CH3CHO, s-C2H5OH, s-CH3OCH3, s-CH3COCH3, and, s-CH3COOH. The grain-surface fractional abundances of these species are enhanced by between four (e.g., s-CH3CHO) and nine orders of magnitude (e.g., s-CH3COCH3) to values ~10-10 − 10-6 (relative to the results from Model 3). However, this dramatic increase in grain-surface abundance in the disk midplane does not necessarily translate to an “observable” gas-phase fractional abundance (~10-17–10-13).
 |
Fig. 5 Fractional abundance (with respect to H nuclei number density) of s-CO2 as a function of disk height, Z at a radius, R = 305 AU. The chemical complexity in the model increases from Model 1 to Model 5 (see Sect. 3.2 for details). |
The internal cosmic-ray-induced photons help to build chemical complexity on the ice in the midplane by breaking apart the more simple species, e.g., methanol, generating radicals which can go on to create more complex species. However, the increasing strength of external UV photons and X-rays towards the disk surface acts to break down this complexity and the grain-surface chemistry favours the production of more simple ice species, e.g., s-CO2 and s-H2O. In fact, we find that the main repository of carbon and oxygen in the molecular layer is s-CO2. In Fig. 5 we present the fractional abundance of s-CO2 as a function of disk height for our reduced grid at R = 305 AU for each of our chemical models. In Model 4, s-CO2 reaches a peak fractional abundance of ~10-4 at a height of ≈150 AU, which corresponds to the point where there is a sharp decrease in the abundance of other C- and O-containing complex molecules.
s-CO2 is formed on grain-surfaces via the reaction,  (7)We find that the rate for this reaction, under the physical conditions in the molecular layer, is marginally faster than the rate for the rehydrogenation of s-OH. Over time, s-CO2 grows at the expense of s-CO and s-H2O, and indeed, other O- and C-containing species. CO2 has a smaller cross-section for photodissociation than H2O at longer wavelengths (>1200 Å, van Dishoeck et al. 2006) and so is more photostable in the molecular layer of the disk where the UV radiation field is softer than that in the upper disk. Historically, the above reaction has been included in chemical networks with a small reaction barrier of ≈80 K based on the gas-phase reaction potential energy surface (see, e.g., Smith 1988; Ruffle & Herbst 2001; Garrod et al. 2008; Garrod & Pauly 2011). Recent experiments suggest the effective barrier for this reaction is closer to ≈400 K (Noble et al. 2011) and we have adopted the higher barrier in the work presented here. Lowering the barrier to 80 K further increases the production of s-CO2, further decreasing the abundances of other O- and C-containing species. CO2 ice has been observed in many different environments with a typical abundance ~30% that of water ice; however, its exact formation mechanism under cold interstellar conditions remains a puzzle. Recently, Poteet et al. (2013) observed CO2 ice in absorption towards the low-mass protostar, HOPS-68, and analysis of their data revealed the CO2 was contained within an ice matrix consisting of almost pure CO2 ice (≈90%). The authors postulate that HOPS-68 has a flattened envelope morphology, with a high concentration of material within ≈10 AU of the central star, thereby explaining the lack of primordial hydrogen-rich ices along the line of sight. They also propose a scenario where an energetic event has led to the evaporation of the primordial grain mantle and subsequent cooling and recondensation has led to the production of CO2 ice in a H-poor ice mantle. Certainly, our results suggest that the reprocessing of ice species by UV photons may play a role in driving the production of CO2 ice at the expense of other typical grain mantle species, such as, CO and H2O.
(7)We find that the rate for this reaction, under the physical conditions in the molecular layer, is marginally faster than the rate for the rehydrogenation of s-OH. Over time, s-CO2 grows at the expense of s-CO and s-H2O, and indeed, other O- and C-containing species. CO2 has a smaller cross-section for photodissociation than H2O at longer wavelengths (>1200 Å, van Dishoeck et al. 2006) and so is more photostable in the molecular layer of the disk where the UV radiation field is softer than that in the upper disk. Historically, the above reaction has been included in chemical networks with a small reaction barrier of ≈80 K based on the gas-phase reaction potential energy surface (see, e.g., Smith 1988; Ruffle & Herbst 2001; Garrod et al. 2008; Garrod & Pauly 2011). Recent experiments suggest the effective barrier for this reaction is closer to ≈400 K (Noble et al. 2011) and we have adopted the higher barrier in the work presented here. Lowering the barrier to 80 K further increases the production of s-CO2, further decreasing the abundances of other O- and C-containing species. CO2 ice has been observed in many different environments with a typical abundance ~30% that of water ice; however, its exact formation mechanism under cold interstellar conditions remains a puzzle. Recently, Poteet et al. (2013) observed CO2 ice in absorption towards the low-mass protostar, HOPS-68, and analysis of their data revealed the CO2 was contained within an ice matrix consisting of almost pure CO2 ice (≈90%). The authors postulate that HOPS-68 has a flattened envelope morphology, with a high concentration of material within ≈10 AU of the central star, thereby explaining the lack of primordial hydrogen-rich ices along the line of sight. They also propose a scenario where an energetic event has led to the evaporation of the primordial grain mantle and subsequent cooling and recondensation has led to the production of CO2 ice in a H-poor ice mantle. Certainly, our results suggest that the reprocessing of ice species by UV photons may play a role in driving the production of CO2 ice at the expense of other typical grain mantle species, such as, CO and H2O.
 |
Fig. 6 Fractional abundance of gas-phase molecules with respect to total H nuclei number density as a function of disk radius, R, and height, Z. |
 |
Fig. 8 Column density (cm-2) as a function of radius, R, for gas-phase (red lines) and grain-surface (blue lines) molecules. The corresponding data can be found in Tables A.2 and A.3. |
Concerning commonly observed gas-phase species in disks, we find the inclusion of radiation processing of ice has an effect mainly on those species for which precursor species remain frozen out at this radius. For CO, we do not see a strong effect because CO does not rely on grain-surface chemistry for its formation. In the molecular and surface layers of the disk, CO exists predominantly in the gas phase as it is able to thermally desorb from grain surfaces. We see a small decrease in the CO abundance (on the order of a factor of a few) in Model 4 relative to Model 3 between a height of 50 AU and 150 AU as CO is driven into s-CO2(discussed above). We also do not see a strong effect on the abundance of carbon monosulphide, CS, since this species reaches its peak fractional abundance (~10-8) in the surface layers of the disk (above a height of 150 AU) only.
In contrast, for CN (and its precursor species, HCN), we do see a similar drop in abundance around 150 AU in Model 4 (compared with Model 3) since HCN mainly exists as ice on the grain at this disk radius. The ethynyl radical, C2H exhibits a similar behaviour to CN which is related to acetylene, C2H2, also existing primarily as ice, albeit at a lower abundance than for more abundant ice species, such as s-HCN and s-H2O. s-C2H2 can be hydrogenated on the grain to form s-C2H3 (and beyond).
3.2.5. Model 5: reactive desorption
In Model 5 we also include reactive desorption and the results are represented by the gray lines in Figs. 3 and 4. In general, we find reactive desorption helps release further gas-phase COMs in the disk midplane leading to an enhancement of around one to two orders of magnitude. However, this enhancement is not necessarily sufficient to increase the molecular column density to an observable value. For example, acetaldehyde (CH3CHO) is enhanced from a fractional abundance of ~10-13 in Model 4 to ≈2 × 10-12 in Model 5. We also see a slight increase (around a factor of a few) in the grain-surface abundances of several species in the disk midplane; s-CH3CHO, s-CH3NH2, s-C2H5OH, s-CH3OCH3, s-CH3COCH3, and s-CH3COOH. At heights Z ≳ 100 AU, the results from Model 4 and Model 5 are similar.
The inclusion of reactive desorption also helps increase the abundance of gas-phase CS, CN, HCN, and C2H in the disk midplane. However, this enhancement is not sufficient to significantly increase the observable column density. This is because these species can form in the gas phase and thus are not reliant on grain-surface association reactions. For CO, reactive desorption is unimportant as, again, grain-surface chemistry does not contribute significantly to the formation of CO on the grain. In the disk midplane, cosmic-ray-induced desorption is the primary mechanism for releasing s-CO into the gas phase.
3.3. Full disk model
In Figs. 6 and 7, we display the fractional abundances of COMs (relative to total number density) as a function of disk radius, R, and height, Z/R, for gas-phase and grain-surface (ice mantle) species, respectively. In Fig. 8, we display the vertical column densities of gas-phase (red lines) and grain-surface (blue lines) species as a function of disk radius, R.
Figures 6 to 8 show that the grain-surface (ice mantle) abundances and resulting column densities are consistently higher than those of the corresponding gas-phase species. Most of the grain-surface COMs reach maximum fractional abundances of ~10-6 to 10-4 relative to the local number density and are confined to a layer in the midplane, whereas, we see a large spread in the maximum fractional abundances of gas-phase species from ~10-12 to ~10-7. The grain-surface molecules also reach their peak abundance over a much larger region in the disk than their gas-phase analogues. The exceptions to this are formaldehyde, H2CO, cyanoacetylene, HC3N, and acetonitrile, CH3CN, all of which can be formed readily via gas-phase chemistry. These species are abundant throughout most of the upper regions of the disk, whereas, the more complex species reach their peak abundance in the outer disk only in a layer bounded below by freezeout and above by destruction via photodissociation and ion-molecule reactions. Generally, the more complex the molecule, the less abundant it is in the gas phase, and the smaller the extent over which the molecule reaches an appreciable abundance. This indicates that species which can form in the gas phase, e.g., H2CO and HC3N, are less sensitive to the variation in disk physical conditions than the more complex species, such as, HCOOCH3 and HOCH2CHO, which can only form via grain-surface chemistry. Given that the abundance of gas-phase complex species relies on efficient photodesorption and limited photodestruction over a narrow range of the disk, one can imagine that a small increase/decrease in UV flux or X-ray flux in the disk may either inhibit or enhance the abundance of gas-phase complex molecules to a much more significant degree than for the simpler species. In addition, the evolution of dust grains may also be important. Dust-grain settling (or sedimentation) towards the disk midplane can lead to the increased penetration of UV radiation, whereas dust-grain coagulation (or grain growth) leads to bigger grains and a smaller grain-surface area available for the absorption of UV photons (see, e.g., D’Alessio et al. 2001, 2006; Dullemond & Dominik 2004). We discuss this issue further in Sect. 4. We intend to explore the effects of dust evolution in future work.
Several of the grain-surface species (s-CH3OH, s-HC3N, s-CH3CN, s-CH3CCH, s-CH3NH2, s-C2H5OH, and s-CH3COOH) remain frozen out down to ≈2 AU. These species have desorption or binding energies higher than ≈4500 K and so we would expect their snow lines to reside at a similar radius to that for water ice (≈2 AU). s-HCOOH, s-NH2CHO, s-HCOOCH3, and s-HOCH2CHO also possess high binding energies (≳4000 K); however, these species have snow lines at ≈5 AU. Within 5 AU, the dust temperature is >70 K and radical-radical association reactions are more important than atom-addition reactions due to the fast desorption rates of atoms at these temperatures. Grain-surface species which depend on atom-addition routes to their formation are not formed as efficiently on warm grains. For example, s-HCOOCH3 is formed either via the hydrogenation of s-COOCH3 or via the reaction between s-HCO and s-CH3O. These latter two species, in turn, are formed via hydrogenation of s-CO on the grain. s-CH3O is also formed via the photodissociation of s-CH3OH by cosmic-ray-induced photons. The radical-radical formation routes of s-HCOOH, s-NH2CHO, and s-HOCH2CHO all rely on the formation of s-HCO which, in turn, is formed mainly via the hydrogenation of s-CO. In contrast, at warmer temperatures, s-CH3OH can efficiently form via the association of s-CH3 and s-OH rather than via the hydrogenation of s-CO. Both these radicals can form in the gas and accrete onto grains, or they are formed via the cosmic-ray induced photodissociation of grain-mantle molecules. A similar argument holds for s-CH3CN (s-CH3 + s-CN), s-CH3CCH (s-C2H3 + s-CH), s-CH3NH2 (s-CH3 + s-NH2), s-C2H5OH (s-CH3 + s-CH2OH), s-CH3COOH (s-CH3 + s-CH3CO). s-CH2OH and s-CH3CO also have radical-radical association formation routes, i.e., s-CH2 + s-OH and s-CH3 + s-CO.
Column density (cm-2) of gas-phase and grain-surface organic molecules at radii of 10, 30, 100, and 305 AU from our full disk model.
 |
Fig. 9 Disk-integrated line spectra (Jy) for H2CO (left) and CH3OH (right). The grey boxes indicate the frequency coverage of ALMA “Full Science” receivers: band 3 (84 to 116 GHz), band 4 (125 to 163 GHZ), band 6 (211 to 275 GHz), band 7 (275 to 373 GHz), band 8 (385 to 500 GHz), band 9 (602 to 720 GHz), and band 10 (787 to 950 GHz). |
In Fig. 8, we display the column density of gas-phase (red lines) and grain-surface (blue lines) species as a function of radius, R. In Table 2, we also display the calculated column densities at radii of 10, 30, 100, and 305 AU. An expanded version of Table 2 which includes all data used to plot Fig. 8 is available in Appendix A (Tables A.2 and A.3).
Most of the gas-phase molecules reach values ≳1012 cm-2 throughout most of the outer disk (R ≳ 50 AU). The exceptions are HC3N and the more complex species considered here, i.e., C2H5OH, CH3OCH3, HCOOCH3, CH3COCH3, HOCH2CHO, and CH3COOH. Most of these species achieve a column density ~1011 cm-2 throughout the outer disk. CH3COCH3 peaks around 100 AU before decreasing towards larger radii and CH3COOH reaches a peak column density of ~1010 cm-2 between ≈25 and 50 AU before steadily decreasing towards larger radii. Both these species form via s-CH3CO which, in turn, forms on the grain via s-CH3 + s-CO. This latter reaction has an appreciable reaction barrier (≈3500 K) and can only proceed on sufficiently warm grains.
We produce very similar gas-phase and grain-surface column densities for the structural isomers, glycolaldehyde (HOCH2CHO) and methyl formate (HCOOCH3), which are formed primarily via the grain-surface association routes, s-CH2OH + s-HCO and s-CH3O + s-HCO, respectively. These species have been detected in the gas phase in the hot core, Sgr B2(N), and in the low-mass protostar, IRAS 16293+2422 (see, e.g., Hollis et al. 2000; Jørgensen et al. 2012). In both sources, methyl formate is more than a factor of 10 more abundant than glycolaldehyde. In this work, we have assumed a branching ratio of 1:1 for the production of CH3O and CH2OH via the photodissociation of gas-phase and grain-surface methanol. Hence, the formation rates of both radicals via this mechanism are similar leading to similar abundances of methyl formate and glycolaldehyde. Laas et al. (2011) investigated various branching ratios for methanol photodissociation in hot cores and concluded that branching ratios for grain-surface cosmic-ray-induced photodissociation have an influence on the resulting gas-phase abundances. They found that models including ratios favouring the methoxy channel (s-CH3O) agreed best with observed abundances of methyl formate; however, ratios favouring the methyl channel (s-CH3) agreed best with the observed gas-phase abundance of glycolaldehyde. This is in contrast with laboratory experiments which show that formation of the hydroxymethyl radical (s-CH2OH) is the dominant channel (Öberg et al. 2009c).
The mobilities of the s-CH2OH and s-CH3O radicals can also influence the production rates of grain-surface methyl formate and glycolaldehyde. Here, we have followed Garrod et al. (2008) and assumed that s-CH2OH is more strongly bound to the grain mantle than s-CH3O (ED = 5080 K and 2250 K, respectively) due to the -OH group which allows hydrogen bonding with the water ice. Hence, we expect s-CH3O to have higher mobility than s-CH2OH. However, the reaction rates for the grain-surface formation of methyl formate and glycolaldehyde at the temperatures found in the disk midplane are dominated by the mobility of the s-HCO radical. This radical has a significantly lower binding energy to the grain mantle (ED = 1600 K) leading, again, to similar grain-surface formation rates for methyl formate and glycolaldehyde.
3.4. Line spectra
In Fig. 9 we display our disk-integrated line spectra for H2CO and CH3OH up to a frequency of 1000 GHz to cover the full frequency range expected for ALMA “Full Science” operations. We also highlight, in gray, the frequency bands expected to be available at the commencement of “Full Science”: band 3 (84 to 116 GHz), band 4 (125 to 163 GHZ), band 6 (211 to 275 GHz), band 7 (275 to 373 GHz), band 8 (385 to 500 GHz), band 9 (602 to 720 GHz), and band 10 (787 to 950 GHz). In our calculations, we assume a distance to source of 140 pc. We find peak flux densities of ≈160 mJy for H2CO and ≈120 mJy for CH3OH.
Our calculations suggest that reasonably strong lines of H2CO and CH3OH which fall into bands 7, 8, and 9 are good targets for ALMA “Early Science” and “Full Science” capabilities. The strongest methanol line in band 7 is the 312-303 transition of A-CH3OH at 305.474 GHz. The peak line flux density calculated is ≈45 mJy. Using the full ALMA array (50 antennae) and a channel width of 0.2 km s-1, a sensitivity of 5 mJy can be reached in an integration time of ≈30 min. In band 8, a good candidate line is the 212–101 transition of A-CH3OH at 398.447 GHz. The peak line flux density calculated for this transition is ≈60 mJy. Again, using the full ALMA array and a similar channel width, a sensitivity of 10 mJy can be reached in ≈60 min. Observations of weak lines in ALMA band 9 are more challenging due to the increasing influence of the atmosphere11 and the strong continuum emission at higher frequencies. Nevertheless, several methanol line transitions in this band may also be accessible with full ALMA. Under the same conditions, a sensitivity of 25 mJy can be reached in ≈120 mins at a frequency of 665.442 GHz, corresponding to the 524–414 transition of E-CH3OH. We remind the reader that the line intensities calculated here can be considered lower limits to the potential intensities due to the truncation of our disk model at 305 AU. It is possible that methanol has not yet been observed in disks because lower frequency transitions, which we find to be relatively weak, have historically been targeted. A deep search for methanol in nearby well-studied objects should help ascertain whether this species is present: if so, this is a clear indication that our current grain-surface chemistry theory works across different physical regimes and sources.
We also calculated the line spectra for HCOOH, HC3N, CH3CN, CH3CCH, and NH2CHO and found that the line intensities were negligible in all cases (≪10 mJy). For more complex molecules (e.g., HCOOCH3 and CH3OCH3), line detection and identification in nearby protoplanetary disks may prove challenging, even with the superior sensitivity and spatial resolution of ALMA. Also, millimeter and (sub)millimeter observations of molecular line emission from warm, chemically rich sources (for example, hot cores and massive star-forming regions located towards the galactic centre), often suffer from line overlapping (or blending) which can hinder the solid identification of specific COMs (see the discussion in, e.g., Herbst & van Dishoeck 2009).
It is also worth noting here that the Square Kilometre Array (SKA12), due for completion by 2020 and consisting of some 3000 dishes spread over numerous sites around the world, will have high sensitivity in the 70 MHz to 30 GHz frequency range. This may allow detection of line emission/absorption from complex molecules in nearby disks at lower frequencies than those achievable with ALMA (see, e.g., Lazio et al. 2004).
4. Discussion
In this section, we discuss and compare our results with observations of molecular line emission from protoplanetary disks and cometary comae, and with results from other models with similar chemical complexity. We also discuss the astrobiological significance of our work.
H2CO and CH3OH rotational transitions in protoplanetary disks.
4.1. Comparison with observations
Our exploratory calculations suggest that complex organic molecules may be efficiently formed on grain surfaces in protoplanetary disks. However, it is difficult to observe ice species in disks and indeed, this has only been achieved for water ice in a handful of (almost) edge-on systems (see, e.g., Terada et al. 2007). Instead, in the cold outer regions of disks, we are limited to observing gas-phase molecules which possess a permanent dipole moment, only. This also presents difficulties if the gas-phase form of the molecule is not present in sufficient quantities and/or also possesses a complex rotational spectrum.
The only relatively complex molecules detected in disks, to date, are formaldehyde, H2CO, cyanoacetylene, HC3N, and cyclopropenylidene, c-C3H2. Dutrey et al. (1997) detected several rotational lines of H2CO in the disks of DM Tau and GG Tau deriving a column density of ~1012 cm-2. Aikawa et al. (2003) and Thi et al. (2004) present detections of formaldehyde in the disk of LkCa 15 determining column densities of 7.2–19 × 1012 cm-2 and 7.1 − 51 × 1011 cm-2, respectively. The large spread in column density is due to the difficulty in using a simple model to derive column densities from observations, even when several lines of the species are detected. From Fig. 8 and Table 2, we can see the column density in the outer disk i.e., >10 AU (1012 − 1013 cm-2) compares well with those values constrained from observation.
More recently, Öberg et al. (2010, 2011) and Qi et al. (2013a) present detections of H2CO using the SMA in a selection of protoplanetary disks in the well-studied Taurus region and in the Southern sky. They confirmed the previous detections of H2CO in the disks of DM Tau and LkCa 15, and they also present new detections: one line in the disk of AA Tau, two lines in GM Tau, and two lines in TW Hya. They also detected formaldehyde in the disks of IM Lup, V4046 Sgr, and HD 142527. Their detected lines and line intensities towards T Tauri disks are listed in Table 3. Their values range from ~100 mJy km s-1 to ~1 Jy km s-1 depending on the source and transition. The authors do not infer any column densities using their data and explain the difficulties in doing so. Instead, they present integrated intensities with which we can compare our calculated line intensities.
Calculated column densities (cm-2) at R = 250 AU.
We also note here the first detection of HC3N in a selection of T Tauri disks by Chapillon et al. (2012). The authors state that their observations are most sensitive to a radius of around 300 AU and derive column densities of ≲3.5 × 1011 cm-2, ≈8 × 1011 cm-2 and ≈13 × 1011 cm-2 for DM Tau, LkCa 15 and GO Tau, respectively. Comparing this with our calculations at 305 AU in Table 2, we determine a column density of 1 × 1011 cm-2, which is within the upper limit derived for DM Tau, but around one order of magnitude lower than the column densities for the remaining two sources. We also calculated the rotational line spectra for HC3N and found the lines were much weaker than the observed line intensities (≪10 mJy km s-1 versus 60–100 mJy km s-1). We note here that LkCa 15 is a particularly peculiar object: the discovery of a large cavity in continuum emission within a radius of ≈50 AU has reclassified this object as a transition disk (Piétu et al. 2006) in which planet formation is likely at an advanced stage (Kraus & Ireland 2012). Analysis of CO line observations also identified the lack of a vertical temperature gradient in this disk (see, e.g., Piétu et al. 2007). In addition, GO Tau hosts a particularly large, massive molecular disk (RCO ~ 900 AU, Schaefer et al. 2009). Hence, our disk model is likely not a good analogue for both these sources, providing further explanation for the disagreement between our model results and observations.
Recently, Qi et al. (2013b) reported the detection of cyclopropenylidene, c-C3H2, in a protoplanetary disk for the first time. The authors identified several lines of this species in ALMA Science Verification observations of the disk of HD 163296, a Herbig Ae star. This allowed the authors to derive a column density ~1012–1013 cm-2. Herbig Ae/Be stars are more massive and luminous than T Tauri stars, hence, our disk model is not a suitable analogue for this source. However, it is interesting to consider whether this species may also be detectable in disks around T Tauri stars. Our model predicts a column density of ≈1 × 1011 cm-2 at a radius of 100 AU and ≈3 × 1011 cm-2 at 305 AU, around two orders of magnitude lower than that derived for HD 163296.
Gas-phase methanol, CH3OH, has not yet been detected in a protoplanetary disk. However, there have been multiple searches in several well-studied objects giving well-constrained upper limits to the line intensities and column densities. Thi et al. (2004) searched for four lines of methanol (202 − 101 A, 422 − 312 E, 505 − 404 A, 707 − 606 A) in the disks of LkCa15 and TW Hya using the IRAM 30 m and JCMT single-dish telescopes. In all cases, upper limits only were determined, leading to derived upper column densities between ≈1 × 1013 and ≈4 × 1014 cm-2. Again, our calculated column densities agree with these values in that we predict column densities generally lower than the upper limits derived from the observations. Öberg et al. (2010, 2011) also included a line transition of methanol in their SMA line survey of protoplanetary disks. They targeted the 422 − 312 transition of E-type CH3OH at 218.440 GHz in a range of T Tauri and Herbig Ae/Be disks and were unable to detect the line in all cases.
In Table 3, we compare our modelled line intensities with observations towards sources in which H2CO has been detected and in which H2CO and CH3OH upper limits have been determined. We restrict this list to T Tauri stars which possess a substantial gaseous disk. We have rescaled our modelled intensities by the disk size and distance to source using the values listed in Table 3. We have listed the sources roughly in order of decreasing spectral type, from K3 (GM Aur) to M1 (DM Tau). We have converted the IRAM 30 m and JCMT line intensities from Thi et al. (2004) using the standard relation ![\begin{eqnarray} \left ( \frac{T}{1\,\mathrm{K}} \right ) = \left ( \frac{S_\nu}{1\,\mathrm{Jy}\,\mathrm{beam}^{-1}} \right ) \left [ 13.6 \left ( \frac{300\,\mathrm{GHz}}{\nu} \right )^{2} \left ( \frac{1''}{\theta^2} \right ) \right ] \end{eqnarray}](/articles/aa/full_html/2014/03/aa22446-13/aa22446-13-eq237.png) (8)where T is the line intensity in K, Sν is the line intensity in Jy beam-1, ν is the line frequency in GHz and θ is the beam size in arcseconds.
(8)where T is the line intensity in K, Sν is the line intensity in Jy beam-1, ν is the line frequency in GHz and θ is the beam size in arcseconds.
The modelled line intensities for H2CO agree reasonably well (within a factor of three) with most transitions towards most sources. For the hotter stars (GM Tau, LkCa 15, V4046 Sgr, and TW Hya) there is better agreement for the higher frequency transitions than for the lower frequency transitions. For the cooler stars (DM Tau and GG Tau), there is also reasonable agreement with the lower frequency transitions. The change in line intensity ratios moving from hotter stars to cooler stars reflects the change in disk temperature structure and thus excitation conditions. For the lines in which we see poor agreement, the calculations tend to underestimate the observed line intensities. We would not expect absolute agreement with any particular source because we have adopted “typical” T Tauri star-disk parameters in our model. However, the level of agreement between our calculations and observations is sufficient for us to conclude that our model is providing a reasonable description of the formation and distribution of H2CO in protoplanetary disks around T Tauri stars and the resulting line emission expected from these objects.
Comparing the methanol upper limits and calculated line intensities, we see that our calculations fall well within the upper limits for all sources. Our calculations suggest that the lines of methanol targeted in previous surveys of disks are likely too weak to have been observable. However, our calculations also suggest several potential candidate lines we expect to be strong enough for detection with ALMA (see Sect. 3.4 and Fig. 9).
4.2. Comparison with other models
Here, we compare our results with other protoplanetary disk models, concentrating on work which has published lists of column densities or fractional abundances for relatively complex species. Historically, chemical models of disks have concentrated on simple, abundant species (and isotopologues), since these are readily observed in many systems (e.g., CO, HCO+, CN, CS, and HCN). As we enter the era of ALMA, it is likely that the molecular inventory of protoplanetary disks will significantly increase, requiring much more sophisticated complex chemical models, such as that presented here.
In Table 4, we compare column densities of various complex molecules at a radius of ≈250 AU with other protoplanetary disk models of comparable chemical complexity and with similar chemical ingredients. Willacy (2007, W07) presented a chemically complex model of a protoplanetary disk, including a comprehensive deuterium chemistry. We compare our column densities with Model C in that work, which includes both grain-surface chemistry and non-thermal desorption. Semenov & Wiebe (2011, SW11) present results from a disk model which uses a network with a number of chemical reactions (≈7300) approaching the number in the network presented here (≈9300). We compare our results with their “laminar” model in which they neglect turbulent mixing, since we do not consider mixing in this work. We also list the column densities from our most recent paper, WNMA12, which is most similar to the work presented here in that the disk physical model is identical as are the methods used to calculate the chemistry. In WNMA12 we used a chemical network based on “Rate06”, the most recent release of the UMIST Database for Astrochemistry (UDfA) available at that time, whereas, here, our network is derived from the Ohio State University (OSU) network and includes a vastly more comprehensive grain-surface chemical network to simulate the build up of complex molecules. The network used in W07 is also derived from UDfA, albeit an earlier version (Rate95, Millar et al. 1997), whereas, the network used by SW11 is also based on the OSU network. Care must be taken when comparing results from different protoplanetary disk models, as they often differ in physical ingredients as well as the chemistry.
The work presented here generally predicts higher column densities for COMs than those presented in W07 and SW11 despite relatively similar (within an order of magnitude) column densities for CO, H2CO, and HC3N. In this work, we calculate significantly higher column densities for CH3OH, HCOOH, CH3CN, CH3CHO, NH2CHO, HCOOCH3, C2H5OH, CH3OCH3, and CH3COCH3. The network used by SW11 is based on that presented in Garrod & Herbst (2006) which does not contain many pathways to the larger species introduced in Garrod et al. (2008). Also, they adopt Ed = 0.77ED for their grain-surface diffusion rates (which originates from Ruffle & Herbst 2000), where ED is the binding energy of the molecules to the grain surface. This is a rather conservative value and partly explains their much lower abundances of complex species. In addition, they do not consider quantum tunnelling of H atoms on grain surfaces, nor through reaction energy barriers (a full description of the chemical model is provided in Semenov et al. 2010). The neglect of H atom tunnelling through reaction energy barriers explains the particularly low column density of methanol in SW11 (~108 cm-2). W07 include atom-addition grain-surface reactions only and thus neglect radical-radical pathways to form larger COMs.
Comparing our results with those from our previous work (WNMA12), we see a significant increase in the column density of CH3OH, HCOOCH3, CH3OCH3, and CH3COCH3 when using the gas-grain network presented here. The higher column density of grain-surface methanol, s-CH3OH, can be attributed to the higher binding energy of CO adopted here. In previous work, we used the value measured for pure CO ice (855 K) as opposed to the value measured in water ice (1150 K). The binding energy regulates the abundance of s-CO on the grain and thus the amount available for conversion to s-CH3OH, as well as the grain-surface radicals, s-HCO, s-CH3O, and s-CH2OH. Regarding the formation of s-HCOOCH3, the grain-surface association reaction, s-HCO + s-CH3O, is included in both models. The difference in column density is due, again, to the different sets of binding energies adopted. The results from our exploratory calculations presented in Sect. 3.2 demonstrate the importance of radiation processing for the production of s-CH3OCH3 and s-CH3COCH3 in the disk midplane. The midplane is the densest region of the disk and thus contributes significantly to the vertical column density. In previous work we did not include the processing of ice mantle material by UV photons and X-rays. We also see a decrease in the column density of gas phase HC3N, and a corresponding increase in the grain-surface column density, compared with our previous values. This is due to the increased binding energy for HC3N adopted here (4580 K compared with 2970 K). Our previous value shows better agreement with the column densities constrained from observations (~1012 cm-2).
Protoplanetary disks are turbulent environments and the effects of vertical turbulent mixing on disk chemical structure has been investigated by multiple groups (see, e.g., Ilgner et al. 2004; Willacy et al. 2006; Semenov et al. 2006; Aikawa 2007; Heinzeller et al. 2011; Semenov & Wiebe 2011). Semenov & Wiebe (2011) conducted a comprehensive investigation of disk chemical structure with and without turbulent mixing and identified a plethora of species which are sensitive to mixing. Semenov & Wiebe (2011) also used a chemical network including several complex molecules (see Table 4). Of the gas-phase molecules of interest here, they found that the column densities of HCOOH, HC3N, and CH3CN, were significantly affected by the inclusion of turbulent mixing. However, they concentrated their discussions on species which reached column densities ≳1011 cm-2.
In this work, we assume the dust grains are well mixed with the gas and, for the calculation of the chemical structure, we assume the grains are compact spherical grains with a fixed radius. In reality, the dust grains will have both a size distribution and variable dust-to-gas mass ratio caused by gravitational settling towards the midplane and dust-grain coagulation (grain growth). Several groups have also looked at the effects of dust-grain evolution on protoplanetary disk chemistry (see, e.g., Aikawa & Nomura 2006; Fogel et al. 2011; Vasyunin et al. 2011; Akimkin et al. 2013). A parameterised treatment of grain growth affects the geometrical height of the molecular layer but appears to have little effect on the column densities of gas-phase molecules (Aikawa & Nomura 2006). Larger grains may lead to a reduced volume grain-surface area (for a fixed dust-to-gas mass ratio) which will lower the accretion rate of molecules onto dust grains, thereby potentially lowering the formation rate of COMs. However, this effect depends on the assumed morphology and porosity of the grains. Grain coagulation models suggest that the growing dust grains retain a “fluffy” morphology (with a low filling factor, ≪1) such that the volume grain-surface area may not significantly decrease before compression occurs (see, e.g., Ossenkopf 1993; Ormel et al. 2007; Kataoka et al. 2013). Grain settling towards the midplane allows the deeper penetration of UV radiation leading to warmer grains in the disk midplane. This subsequently results in a smaller depletion (freezeout) zone and a larger molecular layer situated closer to the midplane (Fogel et al. 2011). Akimkin et al. (2013) performed a coupled calculation of the structure of a protoplanetary disk including dust evolution and radiative transfer, and subsequently calculated the chemical evolution. They find that the abundances of several species are enhanced in models including dust evolution, including the relatively complex species, NH2CN and HCOOH. We intend to explore the effects of grain evolution on the formation and distribution of COMs in future models.
A final issue to consider is the validity of our set of initial abundances. Disk formation is thought to be a vigorous, energetic, and potentially destructive process. Accretion shocks are thought to occur as material falls from the envelope onto the disk. Heating by the shock may raise the temperature of the dust grains above the sublimation temperature of ices and energised ions may sputter ices from dust grain surfaces (see, e.g., Neufeld & Hollenbach 1994; Tielens et al. 1994). Hence, using initial abundances representative of dark cloud (or prestellar) conditions may not be realistic because dust grains may be stripped of ices as they pass through an accretion shock during the disk formation stage. Visser et al. (2009) studied the 2D chemical evolution during the protostellar collapse phase to determine the chemical history of simple ices contained within the disk at the end of collapse. They concluded that accretion shocks that occur as material falls from the envelope onto the disk are much weaker than commonly assumed. For the outer disk, the main contribution to heating is via stellar heating (see Fig. 3 in Visser et al. 2009). Sputtering of dust grains by energetic ions can also occur. Visser et al. (2009) also considered this and concluded that the shock velocities experienced by the gas, ≈8 km s-1, are not sufficient to energise ions, such as He+, to energies required for the removal of water molecules from grain surfaces. As a result, much of the material contained within the outer disk (≳10 AU) at the end of collapse consists primarily of “pristine” interstellar ice (see Fig. 4 in Visser et al. 2011). Hence, beginning our simulations with initial molecular abundances representative of prestellar conditions is an appropriate assumption.
 |
Fig. 10 Range of abundances of grain-surface complex molecules relative to water ice from our model calculations (red lines) compared with those derived from observations of cometary comae (blue asterisks and lines) and our initial dark cloud ice ratios (green asterisks). The comet data are from Bockelée-Morvan et al. (2004) and Crovisier et al. (2006). The single points and upper limits for the comet ratios represent data derived from observations of comet Hale-Bopp (Crovisier et al. 2004b). |
4.3. Complex molecules in comets
It is generally accepted that minor bodies in the solar system, such as asteroids and comets, likely formed in conjunction with the planets in the Sun’s primordial disk and can be considered remnant material left over from the process of planet formation. When a comet’s orbit is perturbed in such a way that it is injected into the inner solar system, the gradual warming of the nearing Sun evaporates solid surface material and creates an expansive cometary coma of gaseous volatile material enveloping the comet nucleus. Photolysis of the sublimated material (termed “parent” species) and subsequent chemistry creates ions and radicals and new molecules (termed “daughter” species). It is now understood that comets are complex objects composed of ice (mainly H2O, CO2, and CO), refractory material (such as silicates), and organic matter. To date, more than 20 parent molecules have been observed in cometary comae including the relatively complex species, H2CO, CH3OH, HCOOH, CH3CHO, HC3N, CH3CN, NH2CHO, HCOOCH3, and ethylene glycol ((HOCH2)2), which are relevant to this work. Of these species, CH3CHO, NH2CHO, HCOOCH3, and (HOCH2)2 have been observed in only a single object, comet Hale-Bopp, with percentage abundances of 0.02%, 0.015%, 0.08%, and 0.25% (relative to H2O), respectively (see, e.g., Bockelée-Morvan et al. 2004; Crovisier et al. 2004a,b, 2006; Mumma & Charnley 2011).
In Fig. 10 we present the range of calculated abundances for each of these grain-surface species relative to water ice (red lines) and compare these with our initial adopted dark cloud ice ratios (green asterisks) and data derived from cometary comae observations (blue asterisks and lines). The fractional abundances from the disk model are determined by the relative vertical column densities at each radius. We restrict our data to R ≳ 20 AU which corresponds to the radius beyond which grain-surface COMs achieve significant column densities (see Fig. 8). This also correlates with the region where comets are postulated to have originally formed and resided in modern dynamical models of the solar system (see, e.g., Gomes et al. 2005; Walsh et al. 2011). The single points and upper limits for the comet observations refer to data derived from observations of comet Hale-Bopp. We find that our range of calculated abundances (relative to water ice) are consistent with those derived from observations, with some overlap between the two datasets for most species. Exceptions include s-CH3CHO and s-NH2CHO for which a single observation only is available. In both cases, our data range is larger than the observed ratio, with the lower limit of our data within a factor of a few of the measured ratio. Another exception is s-CH3CCH, for which an upper limit towards Hale-Bopp only has been derived (Crovisier et al. 2004b). Again, we find our calculated ratio range is larger than the upper limit. In this case, the lower limit of our data is much further away from that derived from observation, by a factor of ≈30. It is also interesting to compare our range of calculated abundances in the disk model with our initial abundances adopted from a dark cloud model (see Table 1). The s-H2CO/s-CH3OH ratio indicates there is significant chemical processing of the dark cloud grain-surface material within the disk with this ratio decreasing from cloud to disk. For all other species (except s-CH3CCH) the dark cloud abundance is lower than the lower limit reached in the disk model indicating that disk physical conditions are necessary for thermal grain-surface chemistry to efficiently form the complex molecules observed in cometary comae.
It certainly appears that our grain-surface chemistry is appropriate for describing the grain-surface formation of most COMs observed in cometary comae, supporting the postulation that comets are formed via the coagulation and growth of icy dust grains within the Sun’s protoplanetary disk. One outstanding issue is the high abundance of ethylene glycol ((HOCH2)2) observed towards comet Hale-Bopp, with a percentage abundance of 0.25% relative to water ice. This ratio is similar to that observed for H2CO and around an order of magnitude higher than the ratio derived for CH3CHO and NH2CHO. Also, (HOCH2)2 is observed to be at least 5 times more abundant than the chemically-related species, HOCH2CHO (Crovisier et al. 2004b). In this network, we include a single barrierless route to the formation of s-(HOCH2)2 via the grain-surface association of two s-CH2OH radicals. Under the conditions throughout much of the disk, the mobility of this radical is significantly slower than smaller radicals, such as, s-CH3 and s-HCO, due to its significantly larger binding energy to the grain mantle (≈5000 K). The large binding energy is due to the presence of the -OH functional group allowing hydrogen bonding of this species with the bulk water ice (see, e.g., Garrod et al. 2008). Hence, the reaction forming s-(HOCH2)2 cannot compete with other barrierless radical-radical association reactions which form, for example, s-C2H5OH and s-HOCH2CHO. We find a negligible abundance of s-(HOCH2)2 is produced throughout our disk model.
In the network used here, radical-radical association pathways only have been included for the formation of many COMs, in addition to pathways involving sequential hydrogenation of precursor molecules. However, an alternative grain-surface route to the production of (HOCH2)2 (and other COMs) has been proposed by Charnley (1997) involving sequential atom-addition reactions. For example, (HOCH2)2 is postulated to form via the hydrogenation of s-OCCHO, which in turn is formed from s-CO via atom-addition reactions, i.e., 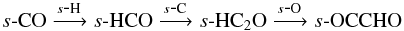 (9)followed by
(9)followed by
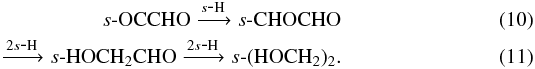 In this sequence, 2s-H implies a barrier penetration reaction by a hydrogen atom followed by the exothermic addition of an additional H atom. This sequence of atom-addition reactions is postulated to lead to different ratios of resultant grain-surface COMs relative to the radical-radical network used here and may provide a route to the formation of s-(HOCH2)2. However, as discussed in Herbst & van Dishoeck (2009), many of these reaction rates and reaction barriers remain unmeasured. The efficacy of this type of formation route to COMs under protoplanetary disk conditions is yet to be studied and we intend to explore this in future work. Of course, it is also possible that significant processing of the cometary surface by UV photons (and potentially, cosmic rays) over the comet’s lifetime may lead to a surface composition which differs from the initial grain mantle composition in the protoplanetary disk. In addition, thermally driven chemical processing of the comet’s interior may occur. This may be caused by heating due to radioactive decay of radionuclides, such as 26Al (see, e.g., Wallis 1980; Prialnik et al. 1987).
In this sequence, 2s-H implies a barrier penetration reaction by a hydrogen atom followed by the exothermic addition of an additional H atom. This sequence of atom-addition reactions is postulated to lead to different ratios of resultant grain-surface COMs relative to the radical-radical network used here and may provide a route to the formation of s-(HOCH2)2. However, as discussed in Herbst & van Dishoeck (2009), many of these reaction rates and reaction barriers remain unmeasured. The efficacy of this type of formation route to COMs under protoplanetary disk conditions is yet to be studied and we intend to explore this in future work. Of course, it is also possible that significant processing of the cometary surface by UV photons (and potentially, cosmic rays) over the comet’s lifetime may lead to a surface composition which differs from the initial grain mantle composition in the protoplanetary disk. In addition, thermally driven chemical processing of the comet’s interior may occur. This may be caused by heating due to radioactive decay of radionuclides, such as 26Al (see, e.g., Wallis 1980; Prialnik et al. 1987).
4.4. Implications for astrobiology
One of the most complex molecules detected to date is aminoacetonitrile, NH2CH2CN, which was observed towards the hot core in the massive star-forming region, Sgr B2(N), with a fractional abundance ~10-9 (Belloche et al. 2008). NH2CH2CN has been postulated as a potential precursor to the simplest amino acid, glycine, NH2CH2COOH. In turn, amino acids are the building blocks of proteins, considered a key component for the commencement of life. Multiple routes to the formation of glycine (and other simple amino acids) under interstellar conditions have been proposed including via Strecker synthesis (see, e.g., Peltzer et al. 1984), UV-irradiated ice mantles (see, e.g., Bernstein et al. 2002; Muñoz Caro et al. 2002), and gas-phase chemistry (see, e.g, Blagojevic et al. 2003).
Recently, Garrod (2013) investigated the formation of glycine in hot cores via grain-surface radical-radical reactions, i.e., an extension to the reaction scheme used here, incorporating the ice chemistry proposed in Woon (2002) to describe the formation of glycine in UV-irradiated ices. Garrod (2013) calculated a peak fractional abundance for gas-phase glycine ~10-10 − 10-8 with the molecule returned to the gas phase at temperatures ≳200 K. He also included gas-phase formation of glycine (Blagojevic et al. 2003) and determined it to have a negligible effect on the resulting abundances. The detection of glycine is considered one of the holy grails of astrochemistry and astrobiology; however, searches for gas-phase glycine, thus far, have been unsuccessful (see, e.g., Snyder et al. 2005). The predictions from Garrod (2013) are consistent with upper limits derived from these observations. He proposes that due to the high binding energy of glycine, the emission from hot cores is expected to be very compact, and thus, an ideal target for detection with ALMA.
Certainly, a similar grain-surface formation route to s-NH2CH2CN and thus, s-NH2CH2COOH, may be possible under protoplanetary disk conditions and should be explored in future models, particularly considering the recent identification of glycine in a sample returned from comet 81P/Wild 2 (Elsila et al. 2009) and the detection of numerous amino acids in meteorites, some of which are either very rare on Earth or, indeed, unknown in terrestrial biochemistry (for an overview, see, e.g., Ehrenfreund & Charnley 2000). Models would help ascertain whether it is possible for simple amino acids to form on dust grains in the Sun’s protoplanetary disk and become incorporated into comets and asteroids. Such models could also provide further evidence for the delivery of prebiotic molecules to Earth via asteroid and/or cometary impact, rather than forming “in situ” early in the Earth’s evolution. However, based on our molecular line emission calculations (see Sect. 3.4), even if such prebiotic molecules were present in quantities similar to that expected in hot cores, the detection of the gas-phase form of these species in protoplanetary disks would be incredibly challenging, if not impossible, even with ALMA full capabilities.
5. Summary
In this work, we have presented the results of exploratory models investigating the synthesis of COMs in a protoplanetary disk around a typical T Tauri star. We used an extensive chemical network, typically adopted in chemical models of hot cores, which includes gas-phase chemistry, gas-grain interactions (freeze out and desorption), grain-surface chemistry, and the irradiation of ice mantle material.
We summarise the main results of this work below.
-
1.
COMs can form efficiently on the grain mantle under the physical conditions in the disk midplane via grain-surface chemical reactions, reaching peak fractional abundances, ~10-6 to ~10-4 that of the H nuclei number density.
-
2.
Gas-phase COMs are released to the gas phase via non-thermal desorption, with photodesorption via external photons being the most important process for increasing the abundances in the “molecular layer”, and cosmic-ray-induced desorption being most important in the disk midplane.
-
3.
This mechanism is different to that in hot core models which require a “warm up” phase in which the temperature increases from 10 K to ≳100 K over a time scale of ≈105 years (see, e.g., Garrod & Herbst 2006).
-
4.
Most gas-phase COMs reside in a narrow region within the “molecular layer” ranging in peak fractional abundance from ~10-12 (e.g., CH3COCH3) to ~10-7 (e.g., HCOOH). Generally, the more complex the species, the lower the peak gas-phase fractional abundance and column density.
-
5.
H2CO, HC3N, and CH3CN, are exceptions to the above statement. These species have gas-phase and grain-surface routes to formation and so are relatively abundant throughout the molecular layer and upper disk.
-
6.
Including the irradiation of ice mantle material allows further complexity to build in the ice mantle through the generation of grain-surface radicals which are available for further molecular synthesis. This process increases the abundances of more complex molecules in the disk midplane, further enhancing the abundance of several COMs, e.g., CH3CHO, C2H5OH, CH3OCH3, CH3COCH3, and CH3COOH. However, this increase in grain-surface abundances does not necessarily translate to an “observable” abundance in the gas phase.
-
7.
Reactive desorption provides an additional means for molecules to return to the gas phase in the disk midplane, e.g., CH3CHO, C2H5OH, and CH3OCH3.
-
8.
The calculated column densities for H2CO and CH3OH are consistent with values and upper limits derived from observations.
-
9.
There is reasonably good agreement between the majority of our calculated line intensities for H2CO and those observed towards nearby T Tauri stars. For the hotter stars, we get better agreement with the higher frequency transitions than the lower frequency transitions. For the cooler stars, we also get reasonable agreement with the lower frequency transitions.
-
10.
There is poor agreement with observed HC3N line intensities towards LkCa 15 and GO Tau, which is attributed to our lower calculated column density for this species. This disagreement may also be due to the particularites of these two sources: LkCa 15 is now considered a transition disk with a large gap in continuum emission within ≈50 AU and GO Tau hosts a particularly large, massive molecular disk (RCO ≈ 900 AU).
-
11.
The predicted line intensities for methanol line emission lie well below the upper limits determined towards all sources. We suggest strong lines of methanol around ≈300 GHz (and higher frequencies) are excellent candidates for observation in nearby protoplanetary disks using ALMA ( for details see Sect. 3.4 and Fig. 9).
-
12.
The molecular line emission calculations put interesting constraints on the observability of COMs in protoplanetary disks. The calculations suggest that the detection of more complex species, especially those typically observed in hot cores, e.g., CH3CN and HCOOCH3, may prove challenging, even with ALMA “Full Science” operations. Detections of COMs of prebiotic significance, e.g., NH2CH2CN and NH2CH2COOH, in protoplanetary disks, may provide additional challenges, remaining beyond the reach of ALMA.
-
13.
Our grain-surface fractional abundances (relative to water ice) for the outer disk (R≳ 20 AU) are consistent with abundances derived for comets, suggesting a grain-surface route to the formation of COMs observed in cometary comae. This lends support to the idea that comets formed via the coagulation and growth of icy grains in the Sun’s natal protoplanetary disk.
Two of the most complex molecules observed in disks, H2CO and HC3N, can both be efficiently synthesised by gas-phase chemistry alone and, thus, are not currently validations of the efficacy of grain-surface chemistry in protoplanetary disks. Observations of molecules which can only be efficiently formed on the grain, e.g., CH3OH, are required in order to determine the degree to which grain-surface chemistry contributes to the chemical content in protoplanetary disks. Methanol is an important molecule in that it is essentially the next “rung” on the “ladder” of molecular complexity following H2CO. It is also a parent molecule of many more complex species. The calculations suggest that the expected line intensities of transitions of methanol lie well below current observational upper limits. Utilising ALMA, with its unprecedented sensitivity and spectral and spatial resolution, and performing a deep search for the strongest transitions of methanol that fall with the observing bands, would confirm whether grain-surface chemistry is an important mechanism in protoplanetary disks.
Online material
Appendix A: On the assumed parameters
In this work, we have used a fixed set of parameters for the calculation of the thermal grain-surface reaction rates and desorption rates. Two parameters which may have a strong influence on the grain-surface abundances and subsequent gas-grain balance are the diffusion barriers between surface sites, Eb, and the probability for reactive desorption, Prd. We assume the grain-surface diffusion barrier for each species is proportional to its binding (desorption) energy to the grain surface, ED. Here, we assume an optimistic value, Eb/ED = 0.3. This value allows the reasonably efficient diffusion of radicals within the grain mantle when T ≳ 15 K, which helps to build chemical complexity in the outer disk. Vasyunin & Herbst (2013) recently explored the effects of the value assumed for Eb/ED in a macroscopic Monte Carlo model of hot core chemistry, using a “layer-by-layer” approach to calculate the grain mantle composition. They explored a range of values for Eb/ED: 0.3 (Hasegawa et al. 1992), 0.5 (Garrod & Herbst 2006), and 0.77 (Ruffle & Herbst 2000). They concluded models using the intermediate value, Eb/ED = 0.5, produced ice compositions in better agreement with observations; however, models with Eb/ED = 0.3 also gave reasonable agreement for the warm-up phase.
In addition, we assume a conservative value for the probability for reactive desorption, Prd = 0.01. This value is that constrained in investigations into the efficacy of reactive desorption in dark cloud chemical models (Garrod et al. 2007). Recently, reactive desorption has been postulated as a potential mechanism for the release of precursor COMs (e.g., H2CO and CH3OH) in cold, dark clouds where they eventually form larger complex organic molecules (e.g., HCOOCH3 and CH3OCH3) in the gas phase via radiative association (Vasyunin & Herbst 2013). In addition, as discussed in the main body of the paper, recent experiments suggest that reactive desorption is particularly efficient for the reformation of doubly-deuterated water (D2O) and O2 via the surface reactions, s-D + s-OD and s-O + s-O, with efficiencies, >90% and ≈60%, respectively (Dulieu et al. 2013).
In this appendix, we present results from additional exploratory models to investigate the effects of a higher diffusion barrier and a higher probability for reactive desorption. In Table A.1, we list the parameters adopted in four models. In Model A, we assume Eb/ED = 0.3 and Prd = 0.01. This model corresponds to our fiducial model, the full results for which are discussed in the main section of this paper. In Model B, we adopt a higher diffusion barrier, Eb/ED = 0.5, and in Model C we adopt a higher probability for reactive desorption, Prd = 0.1. We present results from an additional model, Model D, in which we have adopted the higher values for both parameters.
In Figs. A.1 and A.2 we present the fractional abundances of gas-phase and grain-surface COMs, respectively, relative to the H nuclei number density, as a function of disk radius, R. We show and discuss results for the disk midplane only. This is the region where grain-surface COMs form most efficiently in our fiducial disk model. In Sects. A.1 and A.2, we discuss the effects and importance of the values adopted for the diffusion barrier and the probability for reactive desorption, respectively.
Model parameters.
 |
Fig. A.1 Fractional abundance (with respect to H nuclei number density) of gas-phase molecules as a function of radius, R, along the disk midplane. The differences between Models A to D are described in the text and listed in Table A.1. |
Appendix A.1: Diffusion barrier
In Figs. A.1 and A.2, the red lines represent results from Model A (our fiducial model) in which we have adopted Eb/ED = 0.3 and the green lines represent results from Model B in which we have used Eb/ED = 0.5. There are only minor differences (less than an order of magnitude) between the gas-phase and grain-surface abundances of H2CO, CH3OH, HC3N, and CH3CCH calculated using Model A and Model B. These are species which can form either in the gas phase or which depend on hydrogenation reactions for their formation.
Lower abundances are calculated for Model B relative to Model A in the outer disk for those grain-surface species which require radical-radical association to enhance their abundance above that achieved in dark clouds. In Model B, the fractional abundances attained in the very outer disk midplane, ≈300 AU, for most species are comparable to those achieved under dark cloud conditions (see Table 1 and Fig. 4). We see an enhancement in the fractional abundances of s-C2H5OH, s-CH3OCH3, and s-HCOOCH3 relative to their initial abundances. This is indicative that radical-radical grain-surface chemistry still operates in the outer disk midplane in Model B, albeit significantly slower relative to Model A. Moving inwards along the midplane, the temperature and density both increase and there is a corresponding increase in the fractional abundances of most COMs. This increase is mirrored in the fractional abundances attained by the analogous gas-phase species. s-CH3CHO, s-C2H5OH, s-CH3OCH3, and s-CH3COCH3 exhibit an interesting behaviour between ≈50 and 150 AU. Within this region, the fractional abundances of all four species show a “dip” or minimum around 70 AU. The dust temperature within ≈150 AU in the midplane is ≳22 K allowing thermal desorption of volatile molecules, for example, s-CO (ED = 1150 K). The species showing this minimum all form via grain-surface reactions involving the relatively volatile methyl radical, s-CH3 (ED = 1180 K). In Model B, the grain-surface reaction rates are not sufficiently fast to compete with the thermal desorption of s-CH3 until the dust temperature increases to a value which allows grain-surface thermal chemistry to operate efficiently.
The mobility of grain-surface species is dependent upon exp( − Eb/T) = exp( − χED), where χ = (Eb/ED)/T. In Model A, there is efficient mobility of grain-surface radicals and thus efficient grain-surface synthesis when χ ≳ 0.02. In Model B this value of χ (a measure of the degree of mobility) is attained when T ≳ 28 K which is reached within ≈70 AU in the disk midplane. In Model B, relatively high fractional abundances of grain-surface COMs are attained that are comparable with those from Model A. However, the radial range over which they reach their peak fractional abundance is restricted to regions where T ≳ 28 K and where the temperature is also lower than the desorption temperature of each molecule. Results from Model A and Model B are similar within ≈50 AU of the central star.
Appendix A.2: Reactive desorption
In Figs. A.1 and A.2, the blue lines represent results from Model C in which we have adopted a higher probability for reactive desorption, Prd = 0.1. The increased reactive desorption has little effect on the grain-surface abundances. However, in the outer disk midplane, there is around an order of magnitude enhancement in the gas-phase fractional abundances when using the higher probability. In the inner disk, thermal desorption is the most important mechanism for releasing grain mantle material back into the gas phase so that the results from all models converge at small radii.
There is a similar effect seen when comparing results from Model B and Model D, in which the higher diffusion barrier, Eb/ED = 0.5, has been adopted. Results for Model B and Model D are represented by the green lines and yellow lines, respectively. Again, there is little change in the grain-surface species when the probability for reactive desorption is increased to 0.1. For the gas-phase abundances, in Model D there is the familiar “order-of-magnitude” enhancement when using Prd = 0.1. Note that for the most “optimistic” model, Model C, the gas-phase COMs reach peak fractional abundances between 10-13 and 10-9 in the outer disk midplane (R ≳ 10 AU). This enhancement in fractional abundance will increase the column densities of COMs; however, the main contribution to the COM gas-phase column density remains the photodesorbed material in the molecular layer.
Column densities (cm-2) of gas-phase molecules as a function of radius.
continued.
Column densities (cm-2) of grain-surface (ice) molecules as a function of radius.
Acknowledgments
The authors thank an anonymous referee for his or her useful comments which greatly improved the discussion in the paper. C.W. acknowledges support from the European Union A-ERC grant 291141 CHEMPLAN and financial support (via a Veni award) from the Netherlands Organisation for Scientific Research (NWO). Astrophysics at QUB is supported by a grant from the STFC. E.H. thanks the National Science Foundation for support of his program in astrochemistry. He also acknowledges support from the NASA Exobiology and Evolutionary program through a subcontract from Rensselaer Polytechnic Institute. H.N. acknowledges the Grant-in-Aid for Scientific Research 23103005 and 25400229. She also acknowledges support from the Astrobiology Project of the CNSI, NINS (Grant Number AB251002, AB251012). S.L.W.W. and J.C.L. acknowledge support from S.L.W.W.’s startup funds provided by Emory University. The authors thank K. Öberg and D. Semenov for providing observational data and model calculations for inclusion in this paper.
References
- Aikawa, Y. 2007, ApJ, 656, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Aikawa, Y., & Nomura, H. 2006, ApJ, 642, 1152 [NASA ADS] [CrossRef] [Google Scholar]
- Aikawa, Y., Momose, M., Thi, W.-F., et al. 2003, PASJ, 55, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Akimkin, V., Zhukovska, S., Wiebe, D., et al. 2013, ApJ, 766, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Allamandola, L. J., Sandford, S. A., & Valero, G. J. 1988, Icarus, 76, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Andrade, D. P. P., Rocco, M. L. M., & Boechat-Roberty, H. M. 2010, MNRAS, 409, 1289 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2009, ApJ, 700, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., et al. 2012, ApJ, 744, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Bacmann, A., Taquet, V., Faure, A., Kahane, C., & Ceccarelli, C. 2012, A&A, 541, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bast, J. E., Lahuis, F., van Dishoeck, E. F., & Tielens, A. G. G. M. 2013, A&A, 551, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Menten, K. A., Comito, C., et al. 2008, A&A, 482, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bennett, C. J., & Kaiser, R. I. 2007, ApJ, 661, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. J., Hama, T., Kim, Y. S., Kawasaki, M., & Kaiser, R. I., ApJ, 2011, 727, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A. 2011, in Physical Processes in Circumstellar Disks Around Young Stars, ed. P. Garcia (Chicago: University of Chicago Press) [Google Scholar]
- Bergin, E. A., Cleeves, L. I., Gorti, U., et al. 2013, Nature, 493, 644 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bernstein, M. P., Dworkin, J. P., Sandford, S. A., Cooper, G. W., & Allamandola, L. J. 2002, Nature, 416, 401 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bertin, M., Fayolle, E. C., Romanzin, C., et al. 2012, PCCP, 14, 9929 [Google Scholar]
- Blagojevic, V., Petrie, S., & Bohme, D. K. 2003, MNRAS, 339, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Bockelée-Morvan, D., Crovisier, J., Mumma, M. J., & Weaver, H. A. 2004, in Comets II (Tucson: University of Arizona Press), 391 [Google Scholar]
- Chapillon, E., Dutrey, A., Guilloteau, S., et al. 2012, ApJ, 756, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Carr, J. S., & Najita, J. R. 2008, Science, 319, 1504 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cazaux, S., & Tielens, A. G. G. M. 2004, ApJ, 604, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Ceccarelli, C. 2005, in Astrochemistry: Recent Successes and Current Challenges, eds. D. C. Lis, G. A. Blake, & E. Herbst, IAU Symp., 231, 1 [Google Scholar]
- Cernicharo, J., Marcelino, N., Roueff, E., et al. 2012, ApJ, 759, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Charnley, S. B. 1997, in Astronomical and biochemical origins and the search for life in the universe, eds. C. B. Cosmovici, S. Bowyer, & D. Werthimer, IAU Colloq., 161, 89 [Google Scholar]
- Ciaravella, A., Jiménez-Escobar, A., Muñoz Caro, G. M., et al. 2012, ApJ, 746, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Collings, M. P., Anderson, M. A., Chen, R., et al. 2004, MNRAS, 354, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Crovisier, J. 2006, in Asteroids, Comets, Meteors, eds. L. Daniela, M. Sylvio Ferraz, & F. Julio Angel, IAU Symp., 229, 133 [Google Scholar]
- Crovisier, J., Bockelée-Morvan, D., Biver, N., et al. 2004a, A&A, 418, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crovisier, J., Bockelée-Morvan, D., Colom, P., et al. 2004b, A&A, 418, 1141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuppen, H., & Herbst, E. 2007, ApJ, 668, 294 [Google Scholar]
- D’Alessio, P., Calvet, N., & Hartmann, L. 2001, ApJ, 553, 321 [NASA ADS] [CrossRef] [Google Scholar]
- D’Alessio, P., Calvet, N., Hartmann, L., Franco-Hernández, R., & Servín, H. 2006, ApJ, 638, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Dulieu, F., Congiu, E., Noble, J., et al. 2013, Nat. Sci. Rep., 3, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2004, A&A, 421, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2005, A&A, 434, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dutrey, A., Guilloteau, S., & Guélin, M. 1997, A&A, 317, L55 [NASA ADS] [Google Scholar]
- Dutrey, A., Guilloteau, S., & Guélin, M. 2000, in From Molecular Clouds to Planetary Systems, eds. Y. C. Minh, & E. F. van Dishoeck, IAU Symp., 197, 415 [Google Scholar]
- Dutrey, A., Guilloteau, S., Piétu, V., et al. 2008, A&A, 490, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dwek, E., & Smith, R. K. 1996, ApJ, 459, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M. 1992, ARA&A, 30, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Elsila, J. E., Glavin, D. P., & Dworkin, J. P. 2009, Meteor. Planet. Sci., 44, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenfreund, P., & Charnley, S. B. 2000, ARA&A, 38, 427 [Google Scholar]
- Fedele, D., Bruderer, S., van Dishoeck, E. F., et al. 2012, A&A, 544, L9 [Google Scholar]
- Fogel, J. K. J., Bethell, T. J., Bergin, E. A., Calvet, N., & Semenov, D. 2011, ApJ, 726, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Fuente, A., Cernicharo, J., Agúndez, M., et al. 2010, A&A, 524, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gomes, R., Levison, H. F., Tsiganis, K., & Morbidelli, A. 2005, Nature, 435, 466 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Garrod, R. T. 2013, ApJ, 765, 60 [Google Scholar]
- Garrod, R. T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T., & Pauly, T. 2011, ApJ, 735, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T., Wakelam, V., & Herbst, E. 2007, A&A, 467, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T., Widicus Weaver, S. L., & Herbst, E. 2008, ApJ, 682, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Gerakines, P. A., Schutte, W. A., & Ehrenfreund, P. 1996, A&A, 312, 289 [NASA ADS] [Google Scholar]
- Graedel, T. E., Langer, W. D., & Frerking, M. A. 1982, ApJS, 48, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Guilloteau, S., Dutrey, A., & Simon, M. 1999, A&A, 348, 570 [NASA ADS] [Google Scholar]
- Harada, N., Herbst, E., & Wakelam, V. 2010, ApJ, 721, 1570 [NASA ADS] [CrossRef] [Google Scholar]
- Harada, N., Herbst, E., & Wakelam, V. 2012, ApJ, 756, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 261, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Heinzeller, D., Nomura, H., Walsh, C., & Millar, T. J. 2011, ApJ, 731, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, Th., Semenov, D., Guilloteau, St., et al. 2010, ApJ, 714, 1511 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, E., & van Disheock, E. F. 2009, ARA&A, 47, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Hogerheijde, M. R., Bergin, E. A., Brinch, C., et al. 2011, Science, 334, 338 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hollis, J. M., Lovas, F. J., & Jewel, P. R. 2000, ApJ, 540, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, R. L., & Moore, M. H. 2000, Icarus, 145, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, A. M., Wilner, D. J., Andrews, S. M., Qi, C., & Hogerheijde, M. R. 2011, ApJ, 727, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Ilgner, M., Henning, Th., Markwick, A. J., & Millar, T. J. 2004, A&A, 415, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiménez-Escobar, A., Muñoz Caro, G. M., Ciaravella, A., et al. 2012, ApJ, 751, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Johns-Krull, C. M., Valenti, J. A., & Linsky, J. L. 2000, ApJ, 539, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., Favre, C., Bisschop, S. E., et al. 2012, ApJ, 757, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, R. I., & Roessler, K. 1997, ApJ, 475, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Kastner, J. H., Zuckerman, B., Weintraub, D. A., & Forveille, T. 1997, Science, 277, 67 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kataoka, A., Tanaka, H., Okuzumi, S., & Wada, K. 2013, A&A, 554, A4 [Google Scholar]
- Katz, N., Furman, I., Biham, O., Pirronello, V., & Vidali, G. 1999, ApJ, 522, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler-Silacci, J. 2004, Ph.D. Thesis, California Institute of Technology, USA [Google Scholar]
- Kraus, A. L., & Ireland, M. J. 2012, ApJ, 745, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Laas, J., Garrod, R. T., Herbst, E., & Widicus Weaver, S. L. 2011, ApJ, 728, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Lahuis, F., van Dishoeck, E. F., Boogert, A. C. A., et al. 2006, ApJ, 636, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Lazio, T. J. W., Tarter, J. C., & Wilner, D. J. 2004, New A Rev., 48, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Léger, A., Jura, M., & Omont, A. 1985, A&A, 144, 147 [NASA ADS] [Google Scholar]
- Liedahl, D. A., Osterheld, A. L., & Goldstein, W. H. 1995, ApJ, 438, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Mandell, A. M., Bast, J., van Dishoeck, E. F., et al. 2012, ApJ, 747, 92 [Google Scholar]
- Mathews, G. S., Klaassen, P. D., Juhász, A., et al. 2013, A&A, 557, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meeus, G., Montesinos, B., Mendigutía, I., et al. 2012, A&A, 544, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Millar, T. J., Farquhar, P. R. A., & Willacy, K. 1997, A&AS, 121, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct. 742, 215 [Google Scholar]
- Mumma, M. J., & Charnley, S. B. 2011, ARA&A, 49, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz Caro, G. M., Meierhenrich, U. J., Schutte, W. A., et al. 2002, Nature, 416, 403 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Najita, J., Bergin, E. A., & Ullom, J. N. 2001, ApJ, 561, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., & Hollenbach, D. J. 1994, ApJ, 428, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Noble, J., Dulieu, F., Congui, E., & Fraser, H. J. 2011, ApJ, 735, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Nomura, H., & Millar, T. J. 2005, A&A, 438, 923 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Nomura, H., Aikawa, Y., Tsujimoto, M., Nakagawa, Y., & Millar, T. J. 2007, ApJ, 661, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, R. P., Byleveld, S. E., Diamond, P. J., et al. 1998, ApJ, 508, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., van Dishoeck, E. F., & Linnartz, H. 2009a, A&A, 496, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Öberg, K. I., Linnartz, H., Visser, R., & van Dishoeck, E. F. 2009b, ApJ, 693, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Garrod, R. T., van Dishoeck, E. F., & Linnartz, H. 2009c, A&A, 504, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Öberg, K. I., Qi, C., Fogel, J. K. J., et al. 2010, ApJ, 720, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Qi, C., Fogel, J. K. J., et al. 2011, ApJ, 734, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Qi, C., Wilner, D. J., & Hogerheijde, M. R. 2012, ApJ, 749, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., Spaans, M., & Tielens, A. G. G. M. 2007, A&A, 461, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V. 1993, A&A, 280, 617 [NASA ADS] [Google Scholar]
- Qi, C., Wilner, D. J., Aikawa, Y., Blake, G. A., & Hogerheijde, M. R. 2008, ApJ, 681, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Qi, C., D’Alessio, P., Öberg, K. I., et al. 2011, ApJ, 740, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Qi, C., Öberg, K. I., & Wilner, D. J. 2013a, ApJ, 765, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Qi, C., Öberg, K. I., Wilner, D. J., & Rosenfeld, K. A. 2013b, ApJ, 765, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Qi, C., Öberg, K. I., Wilner, D. J., et al. 2013c, Science, 341, 630 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Panić, O., Hogerheijde, M. R., Wilner, D., & Qi., C. 2009, A&A, 501, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pavlyuchenkov, Ya., Semenov, D., Henning, Th., et al. 2007, ApJ, 669, 1262 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Rad. Transf., 60, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Peltzer, E. T., Bada, J. L., Schlesinger, G., & Miller, S. L. 1984, Adv. Space Res., 4, 69 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Piétu, V., Dutrey, A., Guilloteau, S., Chapillon, E., & Pety, J. 2006, A&A, 460, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piétu, V., Dutrey, A., & Guilloteau, S. 2007, A&A, 467, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pirronello, V., Biham, O., Lui, C., Shen, L., & Vidali, G. 1997, ApJ, 483, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Pirronello, V., Lui, C., Roser, J. E., & Vidali, G. 1999, A&A, 344, 681 [NASA ADS] [Google Scholar]
- Pontoppidan, K. M., Salyk, C., Blake, G. A., et al. 2010, ApJ, 720, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Poteet, C. A., Pontoppidan, K. M., Megeath, S. T., et al. 2013, ApJ, 766, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Prasad, S. S., & Tarafdar, S. P. 1983, ApJ, 267, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Prialnik, D., Bar-Nun, A., & Podolak, M. 1987, ApJ, 319, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E. 1981, ARA&A, 19, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Riviere-Marichalar, P., Ménard, F., Thi, W.-F., et al. 2012, A&A, 538, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodriguez, D. R., Kastner, J. H., Wilner, D., & Qi, C. 2010, ApJ, 720, 1684 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenfeld, K. A., Qi, C., Andrews, S. M., et al. 2012, ApJ, 757, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffle, D. P., & Herbst, E. 2000, MNRAS, 319, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffle, D. P., & Herbst, E. 2001, MNRAS, 324, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Salyk, C., Pontoppidan, K. M., Blake, G. A., et al. 2008, ApJ, 676, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Schaefer, G. H., Dutrey, A., Guilloteau, S., Simon, M., & White, R. J. 2009, ApJ, 701, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Semenov, D., & Wiebe, D. 2011, ApJS, 196, 25 (SW11) [NASA ADS] [CrossRef] [Google Scholar]
- Semenov, D., Wiebe, D., & Henning, Th. 2006, ApJ, 647, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Semenov, D., Hersant, F., Wakelam, V., et al. 2010, A&A, 522, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Simpson, J. A. 1983, Ann. Rev. Nucl. Part. Sci., 33, 323 [Google Scholar]
- Smith, I. W. M. 1988, MNRAS, 234, 1059 [NASA ADS] [Google Scholar]
- Snyder, L. E., Lovas, F. J., Hollis, J. M., et al. 2005, ApJ, 619, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Terada, H., Tokunaga, A. T., Kobayashi, N., et al. 2007, ApJ, 667, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Thi, W.-F., van Zadelhoff, G., & van Dishoeck, E. F. 2004, A&A, 425, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thi, W.-F., Ménard, F., Meeus, G., et al. 2011, A&A, 530, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tielens, A. G. G. M., McKee, C. F., Seab, C. G., & Hollenbach, D. J. 1994, ApJ, 431, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, B. E. 1991, ApJS, 76, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Umebayashi, T., & Nakano, T. 2009, ApJ, 690, 69 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., Thi, W.-F., & van Zadelhoff, G.-J., A&A, 2003, 400, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., Jonkheid, B., & van Hemert, M. C. 2006, Faraday Discussion, 133, 231 [Google Scholar]
- van Zadelhoff, G.-J., van Dishoeck, E. F., Thi, W.-F., & Blake, G. A. 2001, A&A, 377, 566 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasyunin, A. I., & Herbst, E. 2013a, ApJ, 762, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Vasyunin, A. I., & Herbst, E. 2013b, ApJ, 769, 34 [Google Scholar]
- Vasyunin, A. I., Wiebe, D. S., Birnstiel, T., et al. 2011, ApJ, 727, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Visser, R., van Dishoeck, E. F., Doty, S. D., & Dullemond, C. P. 2009, A&A, 495, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Visser, R., Doty, S. D., & van Dishoeck, E. F. 2011, A&A, 534, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wallis, M. K. 1980, Nature, 284, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, C., Millar, T. J., & Nomura, H. 2010, ApJ, 722, 1607 (WMN10) [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, C., Nomura, H., Millar, T. J., & Aikawa, Y. 2012, ApJ, 747, 114 (WNMA12) [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, K. J., Morbidelli, A., Raymond, S. N., O’Brien, D. P., & Mandell, A. V. 2011, Nature, 475, 206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Watanabe, N., Kimura, Y., Kouchi, A., et al. 2010, ApJ, 714, L233 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Westley, M. S., Baragiola, R. A., Johnson, R. E., & Baratta, G. A. 1995, Planet. Space Sci., 43, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Willacy, K. 2007, ApJ, 660, 441 (W07) [NASA ADS] [CrossRef] [Google Scholar]
- Willacy, K., & Langer, W. D. 2000, ApJ, 544, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Willacy, K., Langer, W., Allen, M., & Bryden, G. 2006, ApJ, 644, 1202 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Woodall, J., Agúndez, M., Markwick-Kemper, A. J., & Millar, T. J. 2007, A&A, 446, 1197 [CrossRef] [EDP Sciences] [Google Scholar]
- Woon, D. E. 2002, ApJ, 571, L177 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Initial fractional abundances (with respect to nH) and molecular binding (desorption) energies, ED (K).
Column density (cm-2) of gas-phase and grain-surface organic molecules at radii of 10, 30, 100, and 305 AU from our full disk model.
Column densities (cm-2) of grain-surface (ice) molecules as a function of radius.
All Figures
 |
Fig. 1 Gas temperature (top left panel), H nuclei number density (top right panel), integrated UV flux (bottom left panel), and integrated X-ray flux (bottom right panel) as a function of disk radius, R, and disk height, Z/R. The contours in the top left panel represent the dust temperature. |
| In the text | |
 |
Fig. 2 Physical conditions as a function of disk height at a radius, R = 305 AU. Number density of H nuclei (cm-3) and gas and dust temperature (K) are shown in the left-hand panel (solid red lines, solid blue lines, and dashed blue lines, respectively). UV and X-ray radiative fluxes (erg cm-2 s-1) and X-ray and cosmic-ray ionisation rates (s-1) are shown in the right-hand panel (solid red lines, dashed red lines, dashed blue lines, and dotted blue lines, respectively). |
| In the text | |
 |
Fig. 3 Fractional abundance (with respect to H nuclei number density) of gas-phase molecules as a function of disk height, Z at a radius, R = 305 AU. The chemical complexity in the model increases from Model 1 to Model 5 (see Sect. 3.2 for details). |
| In the text | |
 |
Fig. 4 Same as Fig. 3 for grain-surface (ice) species. |
| In the text | |
 |
Fig. 5 Fractional abundance (with respect to H nuclei number density) of s-CO2 as a function of disk height, Z at a radius, R = 305 AU. The chemical complexity in the model increases from Model 1 to Model 5 (see Sect. 3.2 for details). |
| In the text | |
 |
Fig. 6 Fractional abundance of gas-phase molecules with respect to total H nuclei number density as a function of disk radius, R, and height, Z. |
| In the text | |
 |
Fig. 7 Same as Fig. 6 for grain-surface species. |
| In the text | |
 |
Fig. 8 Column density (cm-2) as a function of radius, R, for gas-phase (red lines) and grain-surface (blue lines) molecules. The corresponding data can be found in Tables A.2 and A.3. |
| In the text | |
 |
Fig. 9 Disk-integrated line spectra (Jy) for H2CO (left) and CH3OH (right). The grey boxes indicate the frequency coverage of ALMA “Full Science” receivers: band 3 (84 to 116 GHz), band 4 (125 to 163 GHZ), band 6 (211 to 275 GHz), band 7 (275 to 373 GHz), band 8 (385 to 500 GHz), band 9 (602 to 720 GHz), and band 10 (787 to 950 GHz). |
| In the text | |
 |
Fig. 10 Range of abundances of grain-surface complex molecules relative to water ice from our model calculations (red lines) compared with those derived from observations of cometary comae (blue asterisks and lines) and our initial dark cloud ice ratios (green asterisks). The comet data are from Bockelée-Morvan et al. (2004) and Crovisier et al. (2006). The single points and upper limits for the comet ratios represent data derived from observations of comet Hale-Bopp (Crovisier et al. 2004b). |
| In the text | |
 |
Fig. A.1 Fractional abundance (with respect to H nuclei number density) of gas-phase molecules as a function of radius, R, along the disk midplane. The differences between Models A to D are described in the text and listed in Table A.1. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1 for grain-surface species. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


