| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 15 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201322136 | |
| Published online | 28 February 2014 | |
Exploring the magnetic field complexity in M dwarfs at the boundary to full convection⋆
1
Institute of Astrophysics, Georg-August University,
Friedrich-Hund-Platz 1,
37077
Göttingen,
Germany
e-mail:
denis.shulyak@gmail.com
2
Department of Physics and Astronomy, Uppsala
University, Box
515, 751 20
Uppsala,
Sweden
Received: 25 June 2013
Accepted: 20 January 2014
Context. Magnetic fields play a pivotal role in the formation and evolution of low-mass stars, but the dynamo mechanisms generating these fields are poorly understood. Measuring cool star magnetism is a complicated task because of the complexity of cool star spectra and the subtle signatures of magnetic fields.
Aims. Based on detailed spectral synthesis, we carry out quantitative measurements of the strength and complexity of surface magnetic fields in the four well-known M dwarfs GJ 388, GJ 729, GJ 285, and GJ 406 that populate the mass regime around the boundary between partially and fully convective stars. Very high-resolution (R = 100 000), high signal-to-noise (up to 400), near-infrared Stokes I spectra were obtained with CRIRES at ESO’s Very Large Telescope covering regions of the FeH Wing-Ford transitions at 1μm and Na i lines at 2.2μm.
Methods. A modified version of the Molecular Zeeman Library (MZL) was used to compute Landé g-factors for FeH lines. We determined the distribution of magnetic fields by magnetic spectral synthesis performed with the Synmast code. We tested two different magnetic geometries to probe the influence of field orientation effects.
Results. Our analysis confirms that FeH lines are excellent indicators of surface magnetic fields in low-mass stars of type M, particularly in comparison to profiles of Na i lines that are heavily affected by water lines and that suffer problems with continuum normalization. The field distributions in all four stars are characterized by three distinct groups of field components, and the data are consistent neither with a smooth distribution of different field strengths nor with one average field strength covering the full star. We find evidence of a subtle difference in the field distribution of GJ 285 compared to the other three targets. GJ 285 also has the highest average field of 3.5 kG and the strongest maximum field component of 7–7.5 kG. The maximum local field strengths in our sample seem to be correlated with rotation rate. While the average field strength is saturated, the maximum local field strengths in our sample show no evidence of saturation.
Conclusions. We find no difference between the field distributions of partially and fully convective stars. The one star with evidence of field distribution different from the other three is the most active star (i.e. with X-ray luminosity and mean surface magnetic field) rotating relatively fast. A possible explanation is that rotation determines the distribution of surface magnetic fields, and that local field strengths grow with rotation even in stars in which the average field is already saturated.
Key words: stars: atmospheres / stars: low-mass / stars: magnetic field
© ESO, 2014
1. Introduction
Low-mass stars of spectral type M are subjects of intensive studies today because of several attractive characteristics. Most important are the high level of activity accompanied by strong X-ray fluxes, appearance of emission lines, and global magnetic fields of a few kilogauss detected in many stars. The last signature is different from what we know about the Sun because such strong magnetic fields can only be found in small localized areas known as solar spots. In the case of M dwarfs we observe magnetic regions that have scales comparable to the size of the stars themselves (see e.g. Morin et al. 2010). Stellar evolution predicts that stars of spectral types later than M3.5 become fully convective and do not host an interface layer of strong differential rotation. Both partially and fully convective stars can host magnetic fields of similar intensities but most likely with different dynamo mechanisms operating in their interiors. All this provides a unique testing ground and a challenge for the theory of stellar evolution and magnetism. In addition, owing to their low mass, M dwarfs are attractive stars for searching for Earth-size planets in the habitable zone since these planets will be relatively close to their central star, will have correspondingly shorter orbital periods, and will induce relatively large radial-velocity signatures.
The first direct measurements of magnetic fields from Zeeman broadened line profiles was done by Saar & Linsky (1985). However, atomic lines are often blended by rich molecular absorption, which complicated the analysis. Johns-Krull & Valenti (1996) applied a relative analysis based on a few atomic lines including the strong Fe iλ8468 line to measure magnetic fields in a number of M dwarfs (Johns-Krull & Valenti 2000; Kochukhov et al. 2009). For dwarfs cooler than mid–M, atomic line intensities decay rapidly and molecular lines of FeH Wing-Ford F4 Δ − X4 Δ transitions around 0.99μm were proposed as alternative magnetic field indicators (Valenti et al. 2001; Reiners & Basri 2006). Some of these lines do show strong magnetic sensitivity, as seen, for instance, in the sunspot spectra (Wallace et al. 1999).
Unfortunately, theoretical attempts to compute Zeeman patterns of FeH lines have not achieved much success. This is because the Born-Oppenheimer approximation, which is usually used in theoretical descriptions of level splitting, fails for the FeH molecule. We refer to works of Asensio Ramos & Trujillo Bueno (2006) and Berdyugina & Solanki (2002) for more details.
A promising solution was then suggested by Reiners & Basri (2006, 2007, hereafter RB07), who estimated the magnetic fields in a number of M dwarfs by simple linear interpolation between the spectral features of two reference stars with known magnetic fields. The reference stars were GJ 873 (EV Lac) with ∑ | Bi | fi = 3.9 kG estimated by Johns-Krull & Valenti (2000) (here f is a filling factor), and the non-magnetic GJ 1002. See Reiners (2012) for a review.
The later attempts tried to combine theoretical and empirical approaches to obtain better estimates of magnetic fields. Afram et al. (2008) made use of a semi-empirical approach to estimate the Landé g-factor of FeH lines in the sunspot spectra. Harrison & Brown (2008) present the empirical g-factors for a number of FeH lines originating in different levels but limited to low magnetic J-numbers.
Finally, Shulyak et al. (2010) present a slightly different semi-empirical approach where Landé g-factors are computed according to the level’s Ω and J quantum numbers. Using sunspot spectra as a reference, these authors show a good consistency between observed and predicted splitting patterns for numerous FeH lines and applied their method to measure magnetic fields in selected M dwarfs. It was found that the magnetic fields needed to fit characteristic magnetic features are by ~15−30% smaller than those reported in previous studies using a FeH molecule. However, throughout the analysis it was assumed that the magnetic field has only one single component, i.e. the corresponding filling factor f = 1.
That surface magnetic fields of M dwarfs can be localized in areas similar to Sun spots and therefore have rather complex geometry that correspond to particular sets of filling factors (i.e. set of surface areas of the star covered by a magnetic field of particular intensity) had already been noted in previous works (see e.g. Johns-Krull & Valenti 2000; Kochukhov et al. 2009). These complex geometries turn out to prohibit narrow cores and wide wings of magnetically sensitive lines to be fit simultaneously with a single magnetic field component.
Spectropolarimetry and Doppler imaging have the potential to reconstruct the true magnetic field geometry in M-stars. However, these techniques are very challenging to apply for such faint objects. Nevertheless, it is still possible to observe the brightest objects and use a least square deconvolution (LSD) method (see Donati et al. 1997) to construct an average line profile based on selected individual atomic lines for which Landé factors are accurately known, as was done in a series of papers by Donati et al. (2006, 2008) and Morin et al. (2008). The authors found the presence of regions with strong magnetic fields that occupy large surface areas in selected M dwarfs, but the field geometry of the majority of them are dominated by the poloidal component, which indicates rather homogeneous magnetic fields. Interestingly, these authors also find a signature of different magnetic field geometry observed in partly and fully convective stars with the former hosting mostly non-axisymmetric toroidal fields while axisymmetric poloidal fields are common for the later. However, new observations show that there are exceptions in both groups (Morin et al. 2010). Because of complicated spectra of M dwarfs and the use of only Stokes V spectra for Doppler mapping (which is only sensitive to large scale magnetic fields) the results of these studies should be reconfirmed with more precise analysis involving at least Stokes I and V spectra, as well as direct synthesis of both atomic and molecular features.
Since the direct detection of strong surface magnetic fields in M dwarfs from magnetically split lines in the mid eighties, there is still no clear understanding about the true geometry of these fields. Because of flaring events that affect fluxes of stars in a dramatic and irregular way, it remains very challenging to confirm the presence of stellar spots via light curve analysis and answer the question of whether the magnetic fields originate in such active regions or if they cover the whole stellar surface. What is known from spectroscopic and spectropolarimetric studies is that the magnetic fields can have complex structures covering a large (≈70−80%) percentage of the stellar surface.
In this work we make use of the very high-resolution infrared spectra of four benchmark M dwarfs GJ 388, GJ 285, GJ 729, and GJ 406 obtained with VLT/CRIRES to measure the complexity of their surface magnetic fields by studying individual line profiles. We attempt to derive distributions of filling factors that provide the best agreement between observed and theoretical spectra and to address the question of whether there are any differences between fully and partly convective stars solely from spectroscopic analysis.
2. Observations
Our study is based on high-resolution, near-infrared spectra obtained with CRIRES, (the CRyogenic high-resolution InfraRed Echelle Spectrograph; Kaeufl et al. 2004), mounted on UT1 at ESO’s VLT. The data were collected between June 2010 and January 2011 under PID 385.D-0273. The CRIRES instrument is the only spectrograph capable of providing a resolving power of R = 100 000 in the near-infrared (1−5 μm). We observed each of our four programme stars in two wavelength regions around 1.0 μm and 2.2 μm, to cover the FeH molecular band and the Na i line. In each wavelength region, two adjacent wavelength settings were observed to bridge the three small gaps in wavelength coverage introduced by the spacing between the four CRIRES detectors. For all observations, we used an entrance slit width of 0.̋2, resulting in a nominal resolving power of R = 105. The adaptive optics system was also utilized to improve throughput. Table 1 contains basic information about observations obtained.
Observations used in the paper.
In addition to the four programme stars, we obtained CRIRES data for another target, GJ 1002, observed over several nights in October 2008 (PID 079.D-0357). These data cover some strong Ti i lines in the 1−1.1 μm interval.
Data reduction of the nodded observations followed mostly standard procedures, where each detector chip is treated separately. Averaged dark frames are created for all the raw frames except for the nodded science frames, from appropriate exposure times. This is an important step in treating the odd-even effect and the amplifier glow inherent to the CRIRES detectors1. To correct for the non-linear detector response, we measured the linearity deviation as a function of flux per pixel as obtained from a series of flat field images with varying illumination levels, recorded close in time to our actual observations. These data also served to identify bad pixels, which are then flagged. The bad pixel mask constructed in this way greatly helps to mask out detector defects and cosmetics. The corrections are applied to all science frames and to their corresponding flat field images. The thus corrected flat fields are averaged and subsequently utilized to calibrate spatial inhomogeneities of the science exposures. Finally, the science frames obtained in two nodding positions along the slit are subtracted, thereby removing the sky background and dark and bias signal in the 2D spectra. We usually obtained eleven pairs of nodded observations per setting, which were then aligned and combined to boost the signal-to-noise ratio (S/N). Lastly, an optimal extraction is performed to retrieve 1D spectra, which have a typical S/N of 50 to 400 depending on the object faintness. A wavelength solution was assigned per chip, based on the comparison with the synthetic spectra (see below).
3. Methods
In our investigation we employed the FeH line list of the Wing-Ford band (F4 Δ − X4 Δ transitions) and molecular constants taken from Dulick et al. (2003)2. Transition probabilities for some of these lines were corrected according to Wende et al. (2010). Transition parameters for atomic lines were extracted from the VALD database (Piskunov et al. 1995; Kupka et al. 1999).
To compute synthetic spectra of atomic and molecular lines in the presence of a magnetic field, we employed the Synmast code (Kochukhov 2007). The code represents an improved version of the Synthmag code described by Piskunov (1999). It solves the polarized radiative transfer equation for a given model atmosphere, atomic and molecular line lists, and magnetic field parameters. Model atmospheres are from MARCS the grid3 (Gustafsson et al. 2008).
To analyse the magnetic field via the spectral synthesis, it is necessary to know the Landé g-factors of upper and lower levels of a particular transition. In the case of atomic lines the necessary information was extracted directly from VALD. As shown by Berdyugina & Solanki (2002), among others, lines of FeH exhibit splitting that is, in most cases, intermediate between a pure Hund’s case (a) and Hund’s case (b) and for which no analytic expression is possible. Therefore, to compute g-factors we implemented an approach described in Shulyak et al. (2010) that is based on numerical libraries from the Molecular Zeeman Library (MZL) package originally written by Leroy (Leroy 2004), and adopted by us for the particular case of FeH.
We tried to measure the intensity and complexity of surface magnetic fields by carrying out a detailed synthetic spectral fitting. The lines of FeH were selected in such a way that their Zeeman patterns are accurately reproduced in the reference sunspot spectra for which both temperature and magnetic field are known independently of the fit to atomic lines, as shown in Shulyak et al. (2010). To fully characterize the magnetic field, one needs to derive a) the surface-averaged field modulus ⟨ Bs ⟩ that affects the magnitude of the splitting between individual Zeeman components of a given line and b) the geometry of the magnetic field that influences the intensity and shape of magnetically split lines. A true and unique picture of the surface magnetic field can be restored by surface imaging techniques like Zeeman Doppler Imaging, which relies on the rotationally modulated signals in polarized light or at least phase-resolved longitudinal magnetic field measurements with subsequent modelling of spectroscopic lines.
Because only unpolarized Stokes I spectra were available to us, however, it was impossible to draw conclusions about the geometry of the surface magnetic field in target stars. That is, no information about vector magnetic field and positions of magnetic areas on stellar surfaces can be derived. Nevertheless, even Stokes I spectra alone contain information about the magnetic field structure or what we call the complexity of the magnetic field, i.e. the minimum number of magnetic field components required to fit the observed line profiles. The latter depend on the geometry of the magnetic field through the intensities of Zeeman π- and σ±-components. This allows one to investigate how complex the magnetic field is compared to the case where it can be described by a single component having a fixed strength. For instance, a homogeneous magnetic field of a fixed strength and a configuration where the field is concentrated only in small surface areas (i.e. spots) would result in line profiles that look different. This can then be described in terms of magnetic filling factors fi, which are nothing but a measure of the area on the stellar surface covered by a magnetic field of intensity | B | i. For a homogeneous field (f = 1), the mean surface magnetic field is ⟨ Bs ⟩ = | B |, while in the case of more complex fields, ⟨ Bs ⟩ = ∑ | Bi | fi. The aims of the present work is to measure the distribution of filling factors by fitting theoretical and observed line profiles and to derive the minimum number of magnetic field components, which provides an acceptable agreement between theory and observation. This approach is similar to those used by, say, Johns-Krull & Valenti (2000) with a difference of using many magnetically sensitive FeH lines instead of only a few atomic lines, as well as of accurately treating thousands of blends in the spectrum synthesis code.
The fitting procedure consists of the following steps. For each spectrum we apply a chi-square Levenberg-Marquardt minimization algorithm with filling factors fi as fit parameters. We consider 21 filling factors that correspond to magnetic fields ranging from 0 kG to 10 kG in steps of 0.5 kG. We sequentially start from two filling factors and then add new ones one-by-one by computing the corresponding χ2 and mean deviation σ between observed and predicted spectra. The whole procedure is applied to different sets of atmospheric parameters: Teff, α(Fe), and υsini. We assume the same surface gravity, log (g) = 5.0, for all M dwarfs. The effect of varying atmospheric parameters on the derived distributions of filling factors is also investigated.
This is an important part of our work since little is known about the surface structure of active M dwarfs: do they exhibit large cool or hot areas similar to sunspots and plage regions observed in the Sun? How is the magnetic field correlated with these regions, etc.? Measurements of stellar magnetic fields from spectroscopy requires that atmospheric parameters are accurately known, which is unfortunately not always the case because of well-known problems in matching spectra of M dwarfs where errors in, say, effective temperatures, and metallicities can be large.
This raises another goal in our investigation, namely to see the impact of choosing different atmospheric parameters on the derived magnetic field and filling factors. Errors in atmospheric parameters are not the only uncertainties that affect the measurements of the magnetic fields. There are other potentially important effects, such as temperature inhomogenities of active regions with bright and dark areas similar to those observed on the Sun, which we ignore in the present study. A more in-depth analysis would be needed to fully account for the complex morphologies of stellar photospheres. We plan to address these questions step-by-step in future calculations, assuming at present that the surface temperatures of sample stars are homogenous and can be accurately derived from magnetically insensitive lines.
The initial values of Teff and υsini for all targets were taken from RB07. The iron abundance was then adjusted to fit magnetically-insensitive FeH lines located at λλ9914–9916, λλ9925–9928, λ9945, λ9957, and λ9999 regions. Because of the high density of FeH lines, magnetically sensitive FeH lines are in most cases found in blends that contain many individual lines. In the present study, the FeH features in the following spectral intervals have been used for the magnetic field measurements: λλ9903.3–9907.0, λλ9908.3–9913.8, λλ9919.0–9921.6, λλ9928.0–9929.0, λλ9931.0–9933.5, λλ9938.5–9939.3, λλ9941.5–9942.6, λλ9945.5–9947.8, λλ9956.1–9958.80, and λ9961.3. These intervals have been used in all calculations presented below and are the same for all stars we studied. As shown by 3D hydrodynamical simulations carried out by Wende et al. (2009), the velocity fields in atmospheres of M dwarfs with temperatures Teff < 3500 K are well below 1 km s-1. This only has a weak impact on line profiles, leaving the Zeeman effect and rotation to be the dominating broadening mechanisms. Therefore we assumed zero micro- and macroturbulent velocities in all calculations.
 |
Fig. 1 Forward simulation of FeH and Na i lines assuming two different distributions of surface magnetic fields. Thick black symbols: simulated observed spectrum; dashed violet line: computation with zero magnetic field; red line: computation with multi-component magnetic field shown on the bottom plots; blue line : computations with homogeneous magnetic field (i.e. f = 1) of the same average intensity as multi-component magnetic field. Columns 1–4 correspond to the assumed S/N of 100 and 500, respectively. Atmospheric parameters are the same for all simulations. Open blue diamonds in the bottom plots show the true distribution of filling factors used to simulate observations. |
To test whether our fitting method is capable of restoring the original solution under conditions where all atmospheric parameters are accurately known, we performed forward calculations of selected FeH and one Na i λ22056 line using two distributions of filling factors: one with only three components of 0 kG (f = 0.5), 4 kG (f = 0.35), and 7 kG (f = 0.15), and another with seven components between 1.5 kG and 4.5 kG with a smooth Gaussian-like distribution of filling factors. The simulated “observed” spectra were computed for Teff = 3400 K and υsini = 0 km s-1, and convolved with R = 100 000. We find that the code always finds a unique distribution of filling factors. However, because of the implicit normalization requirement ∑ fi = 1, the filling factors are highly correlated variables. Therefore, no meaningful estimate of error bars is possible based on the covariance matrix provided by the minimization technique. Instead, we provide estimates of a significance for every magnetic field component. For each magnetic field distribution, the following procedure is applied:
-
1.
Noise is added to the simulated spectra. The noise amplitude (1σ) ranges from 2% to 0.001%, which covers the S/N of the spectra of target stars in our sample.
-
2.
For each simulated spectrum with a given noise level, a distribution of magnetic fields and their filling factors are derived. The spectra computed from these distributions of filling factors are then taken as a reference to compute the significance for each magnetic field component.
-
3.
For each magnetic field component fi > 0, its filling factor is decreased by a chosen amount Δf. At the same time, the filling factor of the field component left of it (e.g. fi − 1) is increased by the same amount so that the condition ∑ fi = 1 always holds.
-
4.
The adjusted distribution of filling factors obtained at the previous step is then used to compute a synthetic spectrum and its deviation from the reference spectrum computed with the best fit distribution in Step 2.
-
5.
The adjustment of a given filling factor is repeated until the maximum deviation from the reference spectrum at any fit point is greater than the 1σ error that was used to generate the simulated spectrum in Step 1.
It is clear that the solution and corresponding error bars strongly depend upon the S/N of observations. As an example, Fig. 1 shows results of two simulations with different distributions of filling factors and S/N values of 100 and 500. The simulations were done by assuming the magnetic field model with a dominating radial field component (see below). Two main conclusions can be drawn. First, the lowest S/N needed to restore the shape of the filling factors distribution is S/N > 300, and the original amplitudes are restored with S/N ≈ 500, as shown in the last two columns of Fig. 1. With S/N = 100, it is challenging to restore a complex distribution of magnetic fields similar to that shown on, e.g., lower left plots of Fig. 1 where many components are localized in a particular range of field strength. However, distributions where only a few field components are present and are well separated from each other are accurately reconstructed, although their significance is small. In other words, the lower plot the second column of Fig. 1 shows that, for insrance, the component of 7 kG strength can be replaced by a component with a 6.5 kG strength and still provide a similar quality of the fit to the line profiles within the error bars of the observations. The only difference is that the 7 kG component provides a smaller deviation between the observed and synthetic spectra. A second thing to note is that the restored mean magnetic field ⟨ Bs ⟩ = ∑ | Bi | fi is always equal to the original value even if the reconstructed amplitudes of filling factors deviate.
Because only unpolarized Stokes I spectra are analysed in this paper, no information about vector magnetic field could be retrieved. Therefore, we made use of a simple magnetic field model described with a few free parameters. The field is homogeneous in the stellar reference frame and is specified by the three vector components: radial Br, meridional Bm, and azimuthal Ba, as reckoned in the spherical coordinate system whose polar axis coincides with the line of sight. Then, the two field components relevant for calculating the Stokes I profiles are given by  (1)for the line of sight component and
(1)for the line of sight component and ![\begin{equation} B_{\rm t} = \left[ (\br\sin{\theta} + \ba\cos{\theta})^2 + \bm^2 \right]^{1/2} \end{equation}](/articles/aa/full_html/2014/03/aa22136-13/aa22136-13-eq97.png) (2)for the transverse component. In practice it is sufficient to adjust Br and Bm, keeping Ba zero.
(2)for the transverse component. In practice it is sufficient to adjust Br and Bm, keeping Ba zero.
This approximation of the magnetic field structure is undoubtedly simplistic and unsuitable for describing four phase-dependent Stokes-parameter profiles of magnetic M dwarfs. Nevertheless, as shown by the previous studies of Zeeman-sensitive lines in cool stars (Johns-Krull & Valenti 1996; Johns-Krull 2007), it is sufficient for modelling unpolarized spectra of M dwarfs and T Tauri stars with strong fields.
In the following we assume that the stellar surface is covered by a dominating radial (RC model, hereafter, Bm = Ba = 0) or meridional (MC model, hereafter, Br = Ba = 0) field component and perform respective calculations for each target star.
 |
Fig. 2 Examples of theoretical fits to selected FeH lines and resulting distributions of filling factors for two spectra of GJ 1002 taken in two different observing runs with CRIRES. Top panels: run 385.D-0273, Teff = 3100 K, α(Fe) = −4.37, υsini = 2.43 km s-1. Middle panels: run 079.D-0357, Teff = 3100 K, υsini = 1.85 km s-1, α(Fe) = −4.47. Bottom panels: same as top panels but adopting atmospheric parameters from the middle panels: implementation of these parameters results in a spurious detection of the magnetic field as illustrated on the corresponding plot of filling factors (see text). Dashed violet line: computation with zero magnetic field; red line: computation with multi-component magnetic field shown on the right hand side; blue line: computations with homogeneous magnetic field (i.e. f = 1) of the same average intensity as multi-component magnetic field. Vertical dashed lines mark the edges of the actual fit region. |
 |
Fig. 3 Same as Fig. 2 but for Ti i in GJ 1002. Top panels: Teff = 3100 K, α(Ti) = −7.24, υsini = 2.43 km s-1. Middle panels: Teff = 3100 K, α(Ti) = −7.24, υsini = 1.85 km s-1. Bottom panels: Teff = 3050 K, α(Ti) = −7.24, υsini = 2.60 km s-1. |
4. Testing molecular and atomic diagnostics
Our observations cover the range of FeH lines at 1μm and strong Na i lines at 2.2μm. Presumably, the magnetic fields derived independently of these two sets of lines must agree, if the atmospheric model structure and/or physical conditions in the line formation depths are accurately predicted by model atmospheres and spectrum synthesis codes. Sadly, we find this is not always the case: one needs noticeably different temperatures to fit FeH and Na lines. In particular, the wide wings of the later demand a lower Teff compared to FeH lines. As a result, magnetic fields derived from best-fit spectra assuming fixed Teff deviate from one another. A good illustration can be seen from the analysis of a non-magnetic M4.5 dwarf GJ 1002. This star shows no detectable X-ray emission, and thus the corresponding surface magnetic field of the star is expected to be nearly zero or absent. The atmospheric parameters were derived from the fit to magnetically insensitive FeH lines and are consistent with estimates from previous independent studies: Teff = 3100 K, α(Fe) = −4.37, υsini = 2.4 km s-1. For instance, Shulyak et al. (2010) used Teff = 3100 K, α(Fe) = −4.37, υsini = 2.5 km s-1. The values of α(Fe) and υsini depend strongly on the effective temperature adopted, but also on the continuum normalization and data quality. For instance, using the same spectra from Shulyak et al. (2010), but a slightly different continuum normalization procedure, yields υsini = 1.85 km s-1, α(Fe) = −4.47. The magnetic field derived from the former set of parameters is only about 100 G (which we consider as no detection within observed error bars, because such a small field causes very insignificant changes in theoretical line profiles compared to precise zero field calculation), while it is zero if the latter set of parameters was used.
Examples of theoretical fits to a few FeH lines assuming the RC model of the magnetic field and resulting distributions of filling factors are illustrated on the first two panels of Fig. 2. The error bars for the filling factors were computed as described in the previous section. Different combinations of atmospheric parameters are allowed as long as they fit the observed magnetically insensitive lines. For instance, one of the unknown parameters in fitting FeH lines is the constant of van der Waals broadening γWaals. It was shown in Shulyak et al. (2010) that, in order to fit FeH lines in GJ 1002 with a given Teff = 3100 K and υsini = 2.5 km s-1, the value of γWaals must be increased by an enhancement factor of f(γWaals) = 3.5 compared to a classical value given in Gray (1992). Different combinations of atmospheric parameters, such as iron abundance, γWaals, and υsini, could provide the same accurate fit to the observed spectra: a change in one of these parameter could be compensated for (to a certain extent) by an opposite change in the others. For example, decreasing f(γWaals) = 1.75 would require α(Fe) = 4.30, υsini ≈ 2.0 for the spectra of GJ 1002 from our run 385.D-0273.
The bottom line of this example is that small inaccuracies in atmospheric parameters, although they might be small when comparing theoretical fits to individual lines, might result in a spurious detection of magnetic fields, in particular for multi-component solutions. An illustrative example is shown in the bottom panel of Fig. 2 where we apply atmospheric parameters derived from the spectra of the two CRIRES runs. In both these cases we detect nearly zero magnetic fields (0.113 kG and 0.022 kG, respectively), as long as we apply individual atmospheric parameters derived from the fit to the magnetic insensitive lines in the spectra of each run, but detect a spurious ⟨ Bs ⟩ = 1.14 kG field when applying atmospheric parameters from one run to fit the spectrum of another. This is a purely numerical artefact because in this particular case, the fitting algorithm increases the Zeeman broadening to compensate for the corresponding differences in υsini and α(Fe) between the runs.
Ideally the atmospheric parameters derived from the two spectra of the same star must be the same. In reality, however, this is not the case mainly because of differences in S/N and continuum normalization that affect the depths of spectroscopic features. This exercise highlights the importance of using magnetically insensitive lines for determining of atmospheric parameters that might need to be adjusted once new data, improved line lists, model atmospheres, etc., are being used. Following this procedure helps avoid false detections of magnetic fields.
The main problem in using a multi-component approach for the magnetic field measurements is its sensitivity to the line shapes that are largely affected by data processing algorithms and inaccuracies in atomic/molecular parameters. In the case of FeH lines, no individual Zeeman components can be seen because of the large number of individual π and σ± components that are relevant to every single transition, which are smeared out and only result in line broadening. This is not the case for all FeH lines is described below, but is true for smaller fields when Zeeman components of nearby strong lines do not overlap. Such broadening can easily be mimicked by an appropriate choice of the rotational velocity. This degeneracy can be removed by the use of magnetically insensitive lines.
The spectrum of GJ 1002 observed with CRIRES in run 079.D-0357 also contains strong Ti i lines in the λλ10 300−10 700 region. We used less blended lines at λ10399, λ10498, and λ10587 to test our method when applied to atomic transitions. Unfortunately, all sets of atmospheric parameters derived from FeH lines are consistent with non-zero magnetic fields. Adjusting α(Ti) for a fixed Teff = 3100 K does not help solve the problem of fitting the wings of Ti lines, which we find to be the main reason for detecting non-zero magnetic field. The top panel of Fig. 3 shows a fit to Ti lines with Teff = 3100 K, υsini = 2.4 km s-1, α(Ti) = −7.24. A υsini = 1.9 km s-1 (adopted from FeH lines) results in line cores that are too deep but almost in the same strength of the magnetic field detected (middle panel of Fig. 3). To obtain a nearly zero magnetic field, one has to decrease the effective temperature to Teff ≈ 3050 K and increase rotational velocity to υsini ≈ 2.6 km s-1, as shown in the bottom panel of Fig. 3. It is seen that in the latter case magnetic field components that are as strong as 10 kG appear, but this is obviously an artefact of the method: such a high component occasionally provides a better fit to line wings, though its impact on the line profiles is very small. A non-detection of the magnetic field is obtained when eassuming υsini = 3 km s-1, and the example of using υsini = 2.6 km s-1 shows that the highest field components may easily result from uncertainties in rotational velocities and instrument resolving power. Finally, the tested Ti lines are not very magnetically sensitive, with effective Landé factors geff ≈ 1, therefore strong fields are needed to mimic small adjustments in the υsini described above.
 |
Fig. 4 Same as Fig. 3 but for Na i lines. Atmospheric parameters are: Teff = 3100 K, α(Na) = −5.87, υsini = 2.43 km s-1. |
Magnetic field measurements in M dwarfs.
No set of atmospheric parameters adopted from the above investigation provides a reasonable fit to Na i lines at 2.2μm. These lines appear to be too wide, and their profiles are strongly affected by stellar water lines to allow for an accurate analysis. That is, there is always an unknown vertical offset if one attempts to synthesize those lines. To improve the quality of the theoretical fit, we used a list of water lines to determine the continuum offset and then shifted each observed spectrum accordingly in such a way that quasi-continuum levels in both observed and theoretical spectra match. The list of water lines is taken from R. Kurucz’s website4. Still, this does not solve the problem completely, most probably because of intrinsic inaccuracies in the water list itself.
Figure 4 illustrates the problem. Even shifting each line vertically in the attempt to account for the unknown continuum level would not help achieve a zero magnetic field detection because lines still remain too wide. The depths and widths of Na lines (as well as Ti lines) are well fit in the spectrum of the solar photosphere, and thus the problem that we encounter for these lines in cool M dwarf spectra do not arise from possibly inaccurate line transition parameters. Therefore we decided not to use Na lines for the magnetic field measurements. This is a disappointing result because Na lines are strong features that probe a wide range of atmospheric depths. However, they can only be used when accurate telluric modelling, improved molecular line lists, and more accurate continuum normalization methods become available.
 |
Fig. 5 Examples of theoretical fits to selected FeH lines and resulting distributions of filling factors for GJ 388 assuming RC (first and second rows) and MC (third and fourth rows) magnetic field models. Atmospheric parameters Teff = 3400 K, α(Fe) = −4.64, υsini = 3 km s-1. Dashed violet line: computation with zero magnetic field; red line: computation with multi-component magnetic field shown in the bottom right plot; blue line: computations with homogeneous magnetic field (i.e. f = 1) of the same intensity as in the multi-component magnetic field. |
5. Results
In this section we present the results of magnetic field determination for individual M dwarfs, which are also combined together in Table 2. As follows from the previous section, the Na i lines can not be used for field measurements, and the region of the Ti i lines (though they appear to be good indicators of atmospheric structure) was not covered by our observational settings. Therefore the results presented in this section are from FeH lines alone.
5.1. GJ 388 (AD Leo)
GJ 388 is an M3.5 star with a rotational velocity of 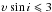 km s-1 Teff = 3400 K and a surface magnetic field of 2.9 kG as estimated in RB07. From magnetically insensitive FeH lines we estimated the iron abundance to be α(Fe) = −4.64. We find that υsini does not influence the determination of the magnetic field if decreased below 3 km s-1. It can always be balanced out by the respective increase in the iron abundance to obtain a similar quality of the fit. The derived mean magnetic field strength matches the value given by RB07, that is, ⟨ Bs ⟩ = 2.9 kG.
km s-1 Teff = 3400 K and a surface magnetic field of 2.9 kG as estimated in RB07. From magnetically insensitive FeH lines we estimated the iron abundance to be α(Fe) = −4.64. We find that υsini does not influence the determination of the magnetic field if decreased below 3 km s-1. It can always be balanced out by the respective increase in the iron abundance to obtain a similar quality of the fit. The derived mean magnetic field strength matches the value given by RB07, that is, ⟨ Bs ⟩ = 2.9 kG.
Figure 5 illustrates the comparison between observed and predicted profiles of some FeH lines. It reveals the strong sensitivity of FeH features to the magnetic field configuration, i.e. to the presence of different magnetic field components. FeH lines at λ9906 and λ9947 are the most illustrative examples of Zeeman broadening, (but see also lines at λ9942 and λ9956).
The distribution of the magnetic field that we recover depends critically upon the assumed magnetic field model used in spectrum synthesis. Employing the RC model results in one strong component of 1.5 kG covering about 50% of the visible stellar surface. There are four other significant field components covering the rest of the surface with intensities spread between 3 kG and 6.5 kG. These components appear because of the necessity to obtain a match between the narrow cores (requiring weak field components) and wide wings (requiring strong field components). There is no significant zero field component, and we do not find any zero-field component when we applied different atmospheric parameters. For instance, using a higher temperature of Teff = 3500 K, υsini = 3 km s-1, and solar α(Fe) = −4.54 results in a similar distribution of filling factors, as well as ⟨ Bs ⟩ value. A zero-field component appears when the MC model is assumed. In addition, the components of 2 kG and 2.5 kG of the same filling factors (f ≈ 0.25) appear. The strongest 6.5 kG component stays similar to what is found in the case of RC model. The detection of a zero-field component is not surprising because Zeeman π-components are deep in MC model compared to the RC one, therefore they immediately provide a good fit to sharp line cores of such features as λ9942 and λ9956.
Although the two magnetic field models result in distributions of filling factors that look different, we always find at least three distinct groups of magnetic field components, and no smooth distributions are ever detected. The derived mean magnetic fields ⟨ Bs ⟩ are very similar, too. By examining individual lines we find that the MC model provides, on average, a better fit to observations.
 |
Fig. 6 Same as Fig. 5 but for GJ 729. Atmospheric parameters Teff = 3400 K, α(Fe) = −4.40, υsini = 4 km s-1. |
5.2. GJ 729
GJ 729 is classified as an M3.5 star, for which RB07 provide υsini ≈ 4 km s-1 and ⟨ Bs ⟩ = 2.2 kG. The best fit between theory and observations was obtained employing atmospheric parameters from RB07 and α(Fe) = −4.40. Assuming solar iron abundance α(Fe) = −4.54 results in a lower effective temperature of Teff = 3300 K in order to obtain the same quality of the fit. The distributions of filling factors look very similar for these two sets of atmospheric parameters. Because the first set formally provides a better fit, we prefer it to the second. Figure 6 illustrates the match between theory and observations. The magnetic field of the star appears to be distributed over three groups of components. For the RC model, we find components with the small 1−1.5 kG, moderate 2.5−3 kG, and strong 5.5 kG intensities. Although errors bars are large, the existence of such distinct features as FeH λ9906 demonstrate that well-separated deep cores only appear with 2.5−3 kG magnetic field components so that their significance is well constrained. A similar three-like component distribution is also recovered when assuming MC model, but as in the previous case of the GJ 388, a strong zero-field component appears (f = 0.4) along with a 2 kG component of similar strength. The mean magnetic fields are also a bit different and amount to ⟨ Bs ⟩ = 2.3 kG and ⟨ Bs ⟩ = 2.1 kG. Finally, we prefer neither of the two cases by looking at individual line profiles.
 |
Fig. 7 Same as Fig. 5 but for GJ 285. Atmospheric parameters Teff = 3300 K, α(Fe) = −4.37, υsini = 6 km s-1. |
5.3. GJ 285 (YZ CMi)
GJ 285 is another very active M4.5 dwarf with rotational velocity of about υsini ≈ 5 km s-1. RB07 derived a lower limit for the mean surface magnetic field of ≈3.9 kG. We find a stable solution for filling factors using an enhanced iron abundance and a faster rotation velocity of υsini = 6 km s-1, as illustrated in Fig. 7. The RC model reveals five significant magnetic field components: one zero field, two components with 3 kG and 3.5 kG field, and two with very strong 7 kG and 7.5 kG fields. In total they give a mean magnetic field of ⟨ Bs ⟩ = 3.6 kG, which is 0.3 kG lower than reported in RB07. Employing υsini = 5 km s-1 results in ⟨ Bs ⟩ = 3.9 kG, but this increase in ⟨ Bs ⟩ is then caused by the appearance of a non-zero 10 kG field component that (as we argued for the case of GJ 1002) is likely spurious because it lowers χ2 by a better match only to the far wings. Using υsini = 6 km s-1 provides the best overall fit between observed and predicted spectra. The MC model gives a very similar distribution of filling factors with a zero field, 4 kG, and 7 kG components. But the resulting mean magnetic field is then 0.2 kG lower compared to RC model, i.e. ⟨ Bs ⟩ = 3.4 kG. From Fig. 7 one can see that the fit to FeH lines is not always accurate. Lines like λ9905 are possibly affected by data reduction problems because they are fit accurately in spectra of GJ 388, for instance. Next, the observed line at λ9947 does not seem to show a doubled profile, but the synthetic spectra predicts one. This may tell us that the intensity of the magnetic field could be even lower than what we have found here. From the comparison of line profiles, it is clear that the RC model provides a better fit to observations. Lines like FeH λ9942 and λ9956 are obviously too strong, and the central feature of λ9947 is not reproduced when using the MC model.
 |
Fig. 8 Same as Fig. 5 but for GJ 406. Atmospheric parameters Teff = 3100 K, α(Fe) = −4.08, υsini = 3 km s-1. |
5.4. GJ 406 (CN Leo)
GJ 406 is a coolest target we analyse in this paper. It has spectral type M5.5 and a slow rotator with υsini = 3 km s-1 (RB07). We find the best fit atmospheric parameters Teff = 3100 K, α(Fe) = −4.08, and υsini = 3 km s-1. Using a solar iron abundance, we were not able to obtain an accurate fit to FeH lines such as λ9942, λ9950, and λ9956, while matching profiles of all other FeH lines. Moreover, the solar iron abundance systematically led to a much lower Teff = 2900 K, which is inconsistent with the assigned spectral type of the star. Therefore we preferred a model with Teff = 3100 K, though with a high iron abundance of α(Fe) = −4.08. Figure 8 demonstrates the fit to the FeH lines and the distribution of filling factors. The latter reveals a strong 1.5 kG component with f = 0.6, two components with 2.5 kG and 3 kG, and two components of 6 kG and 6.5 kG strength when employing the RC model. The mean magnetic field strength is ⟨ Bs ⟩ = 2.6 kG. The MC model leads to a f = 0.3 zero-field component and a strong f = 0.55 component of 2 kG, as well as a weak f = 0.2 component of 6.5 kG. This model gives a mean ⟨ Bs ⟩ = 2.3 kG, i.e. ≈0.3 kG lower compared to the RC case.
6. Discussion
6.1. Indicators of Zeeman splitting
While most previous studies were based on only a few (or one) atomic lines at visual wavelengths, in this work we attempted to extend the spectroscopic investigation of magnetic fields in M dwarfs by using numerous lines of the FeH molecule. We used VLT/CRIRES to obtain high resolution R = 100 000 spectra of four well known M dwarfs in the FeH Wing-Ford band and Na i lines in the K band. Our goal was to measure the complexity of the magnetic fields in these stars by using direct spectrum synthesis and up-to-date models of Zeeman splitting of FeH lines developed and tested in Shulyak et al. (2010). What we mean here by “complexity” of the field is the minimum number of filling factors (each corresponding to a given magnetic field intensity) required to fit the observed line profiles for a given set of atmospheric parameters. The distribution and amplitude of filling factors contain information about the possible structure of surface magnetic fields.
As shown by our forward simulations, the restored distribution of filling factors depends critically on the S/N of the observed spectrum. If the S/N is of the order of 100 the derived amplitude of filling factors may be biased if the real distribution is smooth, that is to say, similar to those presented in the lower left-hand plot of Fig. 1. On the other hand, the value of the average surface magnetic field can be reproduced in all cases. In our sample, GJ 285 and GJ 388 have S/N > 200, while GJ 729 and GJ 406 have S/N ≈ 100−130. Because the shape of the magnetic field distribution is less affected by S/N we do not expect strong changes in the corresponding results if higher S/N observations were available, but we note that comprehensive analysis is only possible with S/N > 300.
We confirm that FeH lines are suitable indicators of magnetic fields because they contain both magnetically very sensitive and magnetically insensitive lines in a ≈100 Å window of the Wing-Ford band. Additionally, there are very few lines of other species in that region except FeH, only some very weak atomic lines; i.e., FeH lines do not suffer blends of other species. Lines at λλ9903−9907 and λ9947 are also excellent diagnostics of the complexity of the magnetic field because of the characteristic behaviour of their line shapes as a function of the field distribution.
On the other hand, we failed to fit lines of Na i even in a presumably non-magnetic reference star GJ 1002. Since this spectral region is known to be crowded by numerous stellar water lines, it is likely that we failed to perform an appropriate continuum normalization of the spectra. Unfortunately, CRIRES only provides data in very narrow wavelengths intervals, about Δλ ≈ 100 Å in that region, which makes a reliable continuum determination very difficult.
As additional check for the consistency between atomic and FeH spectra, we used strong Ti i lines at 1.1μm. Some of these lines are wide features with weak or no detectable blending. In the case where our method detects none or an insignificant magnetic field from FeH lines, it resulted in a detection when only Ti lines were used. This is because of a mismatch between observed and predicted profiles in the wings of the Ti lines. To obtain a solution that is consistent with a field-free situation, we had to decrease Teff of the star by 50 K and slightly increase υsini. Obviously, we do not expect FeH and Ti lines to form under such different physical conditions: the atmosphere of the star should be homogeneous, in particular in the absence of substantial magnetic activity. The difference may partly be explained by atomic and molecular lines being formed at different atmospheric layers, but it is more likely a sign of some missed physics, as seen in e.g. van der Waals broadening of Ti lines at such cool temperatures that differs from the classical treatment that we use in our spectral synthesis.
6.2. Comparison to earlier field measurements
We summarize our magnetic field measurements in Table 2. For each star, we provide the three best-fit solutions, one for our best estimate of Teff and, in addition, two solutions assuming a ± 100 K uncertainity on Teff, which corresponds to roughly 0.5 stellar spectral types. With this assumption, α(Fe) and υsini were determined by least-square fitting to the magnetically insensitive FeH features listed in Sect. 3 before the magnetic field distribution was calculated by including all available spectral features. We note that in most cases the simultaneous least-square fit to all atmospheric parameters did not yield a statistically meaningful solution (the formal reduced χ2 was always much larger than 1), which results in underestimating uncertainties, in particular in the average magnetic field. Therefore, we do not provide formal uncertainties from χ2 intervals but calculate the effect of varying atmospheric parameters, which is the dominating source of error. The difference between the mean magnetic fields for the three solutions in Teff are shown in Table 2, and they can be used as a measure of the uncertainity of the magnetic field measurements. In addition, Cols. 5 and 6 of Table 2 contain values of the cumulative deviation between observed and predicted line profiles computed as: 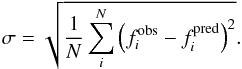 (3)The last two rows of Table 2 list the two sets of atmospheric parameters of GJ 1002 discussed in Sect. 3.
(3)The last two rows of Table 2 list the two sets of atmospheric parameters of GJ 1002 discussed in Sect. 3.
It is interesting to compare our results to measurements of magnetic fields in the literature. First, Saar & Linsky (1985) used five Ti lines in the K band to measure the magnetic field of GJ 388. They found an average | B | = 3.8 kG and f = 0.73 so that (| B | f) = 2.8 kG. Later, Johns-Krull & Valenti (2000) employed a method similar to the one we used to a few atomic lines finding ∑ | Bi | fi = 3.3 kG. This is very close to the ∑ | Bi | fi = 3.2 kG derived by Kochukhov et al. (2009). Using the results from Johns-Krull & Valenti (1996), RB07 report a value of ⟨ Bs ⟩ = 2.9 kG, which is identical to the value we derive here from FeH lines, independent of the magnetic field model used.
For GJ 729 Johns-Krull & Valenti (2000) found ∑ | Bi | fi = 2.0 kG, the corresponding value from RB07 is ⟨ Bs ⟩ = 2.2 kG, again in good agreement with what we find: ⟨ Bs ⟩ = 2.3 kG and ⟨ Bs ⟩ = 2.1 kG when employing RC and MC models, respectively. (Recall that the average surface magnetic field ⟨ Bs ⟩ = ∑ | Bi | fi, where ⟨ Bs ⟩ i runs from 0 kG to 10 kG.)
Next, for GJ 285 Johns-Krull & Valenti (2000) report ∑ | Bi | fi = 3.3 kG, which is much smaller than the lower limit of ⟨ Bs ⟩ > 3.9 kG given by RB07. A recent study by Kochukhov et al. (2009) provides ∑ | Bi | fi = 4.5 kG. Our estimates are ⟨ Bs ⟩ = 3.6 kG and ⟨ Bs ⟩ = 3.4 kG for the RC and MC models, respectively, which fall between the earlier measurements.
For the coolest star in our sample, GJ 406, Reiners et al. (2007) found ⟨ Bs ⟩ = 2.2 kG in a campaign spanning three observing nights. Intra-night magnetic variability was found to be significant at the level of 100 G. We find ⟨ Bs ⟩ = 2.6 kG and ⟨ Bs ⟩ = 2.3 kG by employing RC and MC models, while RB07 derived a value of ⟨ Bs ⟩ = 2.4 kG.
Thus, in general, measurements taken at different times are in good agreement considering the substantial uncertainties reported by all authors and the different spectral indicators used. Nevertheless, it is interesting to note that the highest variability (both absolute and relative) occurs in the most active star GJ 285, which has the strongest mean surface magnetic field and the highest level of x-ray luminosity among other stars in our sample (Schmitt & Liefke 2004). To what extent this reflects the variability of the magnetic fields or differences between measurement techniques remains to be identified.
6.3. Field distributions
For our sample stars, we have determined distributions of magnetic fields rather than average values alone. A great advantage of our method is that it is able to capture the full magnetic field distribution on the surface of a star regardless of the field polarity and geometry. All four stars show distinct groups of different magnetic field strength. We did not find any solutions with homogeneous field distributions (f = 1 for the component that equals the average field), and we did not find any solutions in which different field strengths are equally represented on the stellar surfaces (f = const. for all values of B up to Bmax). This is an interesting result because the average fields on the four stars are close to the maximum field strength we observe in sunspots. This implies that large surface regions contain fields that always resemble those in small scale sunspots. Magnetic field saturation (see Reiners et al. 2009) would then occur because the entire stellar surface is populated with a field strength of the order of 2–3 kG, while the local field strength does not change. Our results and earlier reports for example in Johns-Krull & Valenti (2000) clearly show that this is not the case, but instead local magnetic flux densities occur that are much higher than those found in sunspots, and they co-exist with groups of much lower flux densities.
For our spectrum synthesis calculations we assumed two geometrically different magnetic field models: one with a dominating radial component (RC) and another one with a dominating meridional component (MC). The two cases represent two extreme realizations of field geometries and can provide useful information for estimating the uncertainty in the field distribution introduced by our ignorance of the field geometry. For the RC model, we find that three of the four stars in our sample, GJ 388, GJ 729, and GJ 406 share very similar field distributions. Their surfaces are entirely covered with regions of significant magnetic fields, i.e. they show no zero-field component (f = 0 for ⟨ Bs ⟩ = 0 kG). In them, the weakest field component shows 1−1.5 kG field strength covering the largest fraction of the star (f = 0.35−0.55). There is a lack of field strengths of 2 kG, but a few smaller components with fields between 2.5−4 kG exist (f = 0.1−0.3). These components cover 10% to 30% of the stellar surface. This group is again distinct from the strongest component with a magnetic field between 5.5 and 6.5 kG (f = 0.15−0.20). In the RC case, the field distribution of the fourth star in our sample, GJ 285, consists of three components as well, but this one is different from the other three stars because it shows a significant zero-field component (f = 0.3). The second component has a field strength of the order of 3.5 kG and a comparable size (f ≈ 0.3), and the third component has a very strong magnetic field of 7.5 kG that again covers about a third of the star.
Our second model of the magnetic field geometry, the MC model, leads to very similar field distributions. In all stars, we detect three distinct groups of field components similar to the previous case of the RC model. Their relative strengths are slightly different, while the maximum field strength required for our MC model is the same as for the RC model. In the MC case, a zero-field component is always present (but is not generally the dominating one). GJ 388 shows an additional fourth component of 4.5 kG with a relatively small (yet significant) filling factor of f = 0.15.
It is remarkable that very similar magnetic field distributions are found in all four sample stars and that the distributions are not very affected by the choice of the magnetic field geometry. This suggests that field distributions indeed follow some geometrical order ruled by the parameters of a star and its dynamo. Furthermore, our target stars populate the region around the boundary between partially and fully convective stars: GJ 388 and GJ 729 are on the cool side of this threshold, while GJ 406 and GJ 285 are probably fully convective. Spectropolarimetric observations of stars in this spectral range indicate the existence of two distinct magnetic field geometries (with a few exceptions, see e.g. Morin et al. 2010): partly convective objects seem to harbour non-axisymmetric, toroidal fields, while fully convective objects prefer axisymmetric, poloidal fields. However, if such a dichotomy of geometries exists, we would expect it to affect the distribution of magnetic field components among our sample stars. For instance, large scale axisymmetric poloidal fields would show something like one dominating component, while non-axisymmetric, toroidal fields would have a more uniform distribution of field components. The pattern of the magnetic field distributions we find shows no evidence of any such a transition at the convection boundary. We therefore conclude that our Stokes I measurements of the entire magnetic field cannot confirm a difference in magnetic field geometries between partially and fully convective stars.
While the overall field distribution of the four sample stars is very similar, we find more subtle differences between the distributions of GJ 285 and the other three stars. In GJ 285, we always detect a zero-field component independent of the magnetic field model used. A zero-field component is also found in the MC models of the other stars but not in their RC models. We cannot determine the geometry of the field lines, but this difference is a first hint of a subtle physical difference in the field geometries. Furthermore, the MC model provides a rather poor fit in GJ 285 (see Fig. 7) so that we believe the RC solution is more probable in this case . If the three other stars host a zero-field component, their magnetic fields are better described by the MC model. Although the differences are rather subtle, this implies that the field configuration of GJ 285 is different from the other three: either GJ 285 has a significant zero-field component, while GJ 388, GJ 729, and GJ 406 do not, or the last three stars must be better described by the MC geometry, while the RC geometry is preferred for GJ 285.
In what sense is GJ 285 different from the other three? We discussed above that the status of convection is probably not the determining parameter because at least one of the three other stars is very likely to share the same convection properties as GJ 285. Another possible difference between GJ 285 and the other stars is the rotation rate; GJ 285 shows the highest value of v sini in our sample (see Table 2). Recent measurements of Irwin et al. (2011) provide the rotation period of GJ 285 P = 2.78 d, which agrees well with the P = 2.7758 d derived from Zeeman Doppler imaging by Morin et al. (2008). From this, Reiners et al. (2012) estimate an equatorial rotation velocity of veq = 5.8 km s-1, which is consistent with our determination of v sini and i = 90°. There is no evidence of equally fast rotation of GJ 729 or GJ 406 (see Reiners et al. 2012), but Engle et al. (2009) report a rotation rate of P = 2.23 d for GJ 388 (P = 2.2399 d from (Morin et al. 2008)), meaning that this star may actually be rotating faster than GJ 285. At this point, the situation remains inconclusive, and more information from stars with measured rotation periods and magnetic field distributions is required.
In our sample, the maximum field strength correlates with the (projected) rotation rate. While the average field strength saturates at Rossby numbers, Ro ~ 0.1 and B ≈ 4 kG (Reiners et al. 2009), the local field strength found in the present work in individual components does not saturate. From our small sample, we cannot conclusively answer the question of whether local field strength scales with rotation rate, but we can conclude that it grows beyond the typical field strengths we find in sunspots and that there is a clear trend that Bmax scales with rotation. Again, a larger sample is required to fully address this question.
The detection of localized field components with the strength of up to 7.5 kG (GJ 285) provides important information about the surface field geometry of active M dwarfs. If these structures are stable over long time intervals, they must be in equipartition with the surrounding plasma – a situation similar to sunspots. As can be computed using the available model atmospheres, the equipartition field at the level of the non-magnetized photosphere of a mid-M dwarf is of the order of only 4−5 kG. As in sunspots, the equipartion field strength is higher deeper in the atmosphere. The high localized field strength can, therefore, be in equipartition with the surrounding plasma if we observe these magentic structures at deeper atmospheric levels. This is possible if the regions of strong magnetic fields have cooler temperatures than the rest of the atmosphere. This effect is known as the Wilson depression: the suppression of convection by the magnetic field in the sunspot leads to a temperature drop to ≈4000 K and to lower gas pressure, and allows one to observe deeper layers when looking through the spot. Alternatively, if one assumes that the localized regions of strong fields are not in equipartition with the surrounding plasma, then they must be transient events. Consequently, the distribution and/or amplitude of filling factors are expected to change in time. Unfortunately, no accurate estimate of the temperature contrast is available for M dwarfs because their surfaces remain unresolved, and high-quality time series of spectroscopic observations in Stokes I are not yet available. A line-depth ratio method proposed by Catalano et al. (2002) to measure temperature contrast in cool stars gives uncertain results for stars of type M (see Berdyugina 2005). Photometry seems to be a promising method of testing the spot contrast, but there are two basic effects that may (and do) noticeably modify the amplitude of the light curves: stellar flares and spot distribution. The former can still be, to a certain degree, accounted for, and reasonably accurate light curves have resently been constructed at least for some stars in (Irwin et al. 2011). However, having an accurate flux variability curve does not allow one to reconstruct the temperature contrast uniquely because the spot distribution is not known in the first place. In other words, the light curve amplitude will look similar in case of a single small spot with a high-temperature contrast or a few small spots each having weaker temperature contrast. Accurate phase-resolved observations can at least provide the information required to probe the magnetic and temperature structure of spots in low-mass stars.
Acknowledgments
We wish to thank Prof. Manfred Schuessler for his useful comments on the paper. We acknowledge financial support from CRC 963 – Astrophysical Flow Instabilities and Turbulence (project A16) and Deutsche Forschungsgemeinschaft (DFG) Research Grant RE1664/7-1 to D.S. and funding through a Heisenberg Professorship, RE 1664/9-1 to A.R. We also acknowledge the use of electronic databases (VALD, SIMBAD, NASA’s ADS) and cluster facilities at the computing centre of Georg August University Göttingen (GWDG). This research has made use of the Molecular Zeeman Library (Leroy 2004).
References
- Afram, N., Berdyugina, S. V., Fluri, D. M., Solanki, S. K., & Lagg, A. 2008, A&A, 482, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asensio Ramos, A., & Trujillo Bueno, J. 2006, ApJ, 636, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V. 2005, Liv. Rev. Sol. Phys., 2, 8 [Google Scholar]
- Berdyugina, S. V., & Solanki, S. K. 2002, A&A, 385, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Catalano, S., Biazzo, K., Frasca, A., & Marilli, E. 2002, A&A, 394, 1009 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donati, J.-F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Donati, J.-F., Forveille, T., Collier Cameron, A., et al. 2006, Science, 311, 633 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Donati, J.-F., Morin, J., Petit, P., et al. 2008, MNRAS, 390, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Dulick, M., Bauschlicher, C. W., Jr.,Burrows, A., et al. 2003, ApJ, 594, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Engle, S. G., Guinan, E. F., & Mizusawa, T. 2009, AIP Conf. Ser., 1135, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 1992, The Observation and Analysis of Stellar Photospheres (Cambridge University Press) [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harrison, J. J., & Brown, J. M. 2008, ApJ, 686, 1426 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., Berta, Z. K., Burke, C. J., et al. 2011, ApJ, 727, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Johns-Krull, C. M. 2007, ApJ, 664, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Johns-Krull, C. M., & Valenti, J. A. 2000, Stellar Clusters and Associations: Convection, Rotation, and Dynamos, ASP Conf. Proc., 198, 371 [Google Scholar]
- Johns-Krull, C. M., & Valenti, J. A. 1996, ApJ, 459, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Kaeufl, H.-U., Ballester, P., Biereichel, P., et al. 2004, Proc. SPIE, 5492, 1218 [CrossRef] [Google Scholar]
- Kochukhov, O. P. 2007, in in Proc. Physics of Magnetic Stars, 109 [Google Scholar]
- Kochukhov, O., Heiter, U., Piskunov, N., et al. 2009, Cool Stars, Stellar Systems, and the Sun, AIP Conf. Proc., 1094, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Leroy, B. 2004, Molecular Zeeman Library Reference Manual, avalaible at http://bass2000.obspm.fr/mzl/download/mzl-ref.pdf [Google Scholar]
- Morin, J., Donati, J.-F., Petit, P., et al. 2008, MNRAS, 390, 567 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Morin, J., Donati, J.-F., Petit, P., et al. 2010, MNRAS, 407, 2269 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Piskunov, N. 1999, Polarization, 243, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Reiners, A. 2012, Liv. Rev. Sol. Phys., 9, 1 [Google Scholar]
- Reiners, A., & Basri, G. 2006, ApJ, 644, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., & Basri, G. 2007, ApJ, 656, 1121 (RB07) [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Schmitt, J. H. M. M., & Liefke, C. 2007, A&A, 466, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reiners, A., Basri, G., & Browning, M. 2009, ApJ, 692, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Joshi, N., & Goldman, B. 2012, AJ, 143, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., & Linsky, J. L. 1985, ApJ, 299, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, J. H. M. M., & Liefke, C. 2004, A&A, 417, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shulyak, D., Reiners, A., Wende, S., et al. 2010, A&A, 523, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valenti, J. A., Johns-Krull, C. M., & Piskunov, N. E. 2001, Cool Stars, Stellar Systems and the Sun, AIP Conf. Proc., 223, 1579 [Google Scholar]
- Wallace, L., Livingston, W. C., Bernath, P. F., & Ram, R. S. 1999, NSO Technical Report #99-001 (Tucson: National Solar Observatory) [Google Scholar]
- Wende, S., Reiners, A., & Ludwig, H.-G. 2009, A&A, 508, 1429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wende, S., Reiners, A., Seifahrt, A., & Bernath, P. F. 2010, A&A, 523, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Forward simulation of FeH and Na i lines assuming two different distributions of surface magnetic fields. Thick black symbols: simulated observed spectrum; dashed violet line: computation with zero magnetic field; red line: computation with multi-component magnetic field shown on the bottom plots; blue line : computations with homogeneous magnetic field (i.e. f = 1) of the same average intensity as multi-component magnetic field. Columns 1–4 correspond to the assumed S/N of 100 and 500, respectively. Atmospheric parameters are the same for all simulations. Open blue diamonds in the bottom plots show the true distribution of filling factors used to simulate observations. |
| In the text | |
 |
Fig. 2 Examples of theoretical fits to selected FeH lines and resulting distributions of filling factors for two spectra of GJ 1002 taken in two different observing runs with CRIRES. Top panels: run 385.D-0273, Teff = 3100 K, α(Fe) = −4.37, υsini = 2.43 km s-1. Middle panels: run 079.D-0357, Teff = 3100 K, υsini = 1.85 km s-1, α(Fe) = −4.47. Bottom panels: same as top panels but adopting atmospheric parameters from the middle panels: implementation of these parameters results in a spurious detection of the magnetic field as illustrated on the corresponding plot of filling factors (see text). Dashed violet line: computation with zero magnetic field; red line: computation with multi-component magnetic field shown on the right hand side; blue line: computations with homogeneous magnetic field (i.e. f = 1) of the same average intensity as multi-component magnetic field. Vertical dashed lines mark the edges of the actual fit region. |
| In the text | |
 |
Fig. 3 Same as Fig. 2 but for Ti i in GJ 1002. Top panels: Teff = 3100 K, α(Ti) = −7.24, υsini = 2.43 km s-1. Middle panels: Teff = 3100 K, α(Ti) = −7.24, υsini = 1.85 km s-1. Bottom panels: Teff = 3050 K, α(Ti) = −7.24, υsini = 2.60 km s-1. |
| In the text | |
 |
Fig. 4 Same as Fig. 3 but for Na i lines. Atmospheric parameters are: Teff = 3100 K, α(Na) = −5.87, υsini = 2.43 km s-1. |
| In the text | |
 |
Fig. 5 Examples of theoretical fits to selected FeH lines and resulting distributions of filling factors for GJ 388 assuming RC (first and second rows) and MC (third and fourth rows) magnetic field models. Atmospheric parameters Teff = 3400 K, α(Fe) = −4.64, υsini = 3 km s-1. Dashed violet line: computation with zero magnetic field; red line: computation with multi-component magnetic field shown in the bottom right plot; blue line: computations with homogeneous magnetic field (i.e. f = 1) of the same intensity as in the multi-component magnetic field. |
| In the text | |
 |
Fig. 6 Same as Fig. 5 but for GJ 729. Atmospheric parameters Teff = 3400 K, α(Fe) = −4.40, υsini = 4 km s-1. |
| In the text | |
 |
Fig. 7 Same as Fig. 5 but for GJ 285. Atmospheric parameters Teff = 3300 K, α(Fe) = −4.37, υsini = 6 km s-1. |
| In the text | |
 |
Fig. 8 Same as Fig. 5 but for GJ 406. Atmospheric parameters Teff = 3100 K, α(Fe) = −4.08, υsini = 3 km s-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


