| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A133 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321910 | |
| Published online | 24 March 2014 | |
Neptune’s ring arcs: VLT/NACO near-infrared observations⋆ and a model to explain their stability
1
Institut de Mécanique Céleste et de Calcul de Ephémérides, UMR 8028 du
CNRS,
77 avenue Denfert-Rochereau,
75014
Paris,
France
2
Laboratoire d’Astronomie de Lille, Université Lille
1, 1 impasse de
l’observatoire, 59000
Lille,
France
e-mail:
Stefan.Renner@univ-lille1.fr
3
Observatoire de Paris, LESIA, 5 place Jules Janssen, 92195
Meudon Cedex,
France
4
Université Pierre et Marie Curie, 4 place Jussieu, 75005
Paris,
France
5
Observatoire de Paris, SYRTE, 61 avenue de
l’Observatoire, 75014
Paris,
France
6
NAXYS, Namur Center for Complex Systems, Department of
Mathematics, University of Namur, 5000
Namur,
Belgium
7
European Southern Observatory, Alonso de Cordova 3107, Vitacura, Casilla 19001
Santiago 19,
Chile
Received: 17 May 2013
Accepted: 15 February 2014
Context. Neptune’s incomplete ring arcs have been stable since their discovery in 1984 although these structures should be destroyed in a few months through differential Keplerian motion. Regular imaging data are needed to address the question of the arc stability.
Aims. We present the first NACO observations of Neptune’s ring arcs taken at 2.2 μm (Ks band) with the Very Large Telescope in August 2007, and propose a model for the arc stability based on co-orbital motion.
Methods. The images were aligned using the ephemerides of the satellites Proteus and Triton and were suitably co-added to enhance ring or satellite signals. Resonance theory and N-body simulations were used to model the arcs’ confinement.
Results. We derive accurate mean motion values for the arcs and Galatea and confirm the mismatch between the arcs’ position and the location of the 42:43 corotation inclination resonance. We propose a new confinement mechanism where small co-orbital satellites in equilibrium trap ring arc material. We constrain the masses and locations of these hypothetical co-orbital bodies.
Key words: planets and satellites: individual: Neptune / planets and satellites: rings / celestial mechanics / techniques: photometric
© ESO, 2014
1. Introduction
Four arcs (Courage, Liberté, Egalité, Fraternité) confined in a 40 degrees azimuthal range are embedded in the much fainter continuous Adams ring around Neptune (Smith et al. 1989). These incomplete rings have been stable since their discovery in 1984 (Hubbard et al. 1986), while they should be destroyed in a few months through differential Keplerian motion. The arcs are close to but not within a 42:43 corotation inclination resonance (CIR) forced by Galatea (Dumas et al. 1999; Sicardy et al. 1999), which was thought to be responsible for the azimuthal confinement of the arc system (Goldreich et al. 1986; Porco 1991). Moreover, adaptive-optics images obtained in 2002 and 2003 with the Keck telescope showed that the brightness and longitudes of the arcs changed significantly (de Pater et al. 2005). Different theories were able to solve, at least partly, the question of the arcs’ stability. If the arcs have a sufficient fraction of the mass of Galatea, a 42:43 corotation eccentricity resonance (CER) can match the current arcs’ semi-major axis and stabilize the system (Namouni & Porco 2002). Alternatively, small co-orbital satellites might also be able to confine the dusty arc material. These hypothetical co-orbital bodies would be in a stable stationary configuration equivalent to the Lagrangian points (Renner & Sicardy 2004).
Here we report photometric and astrometric measurements of the arcs obtained with the VLT adaptive-optics fed camera NACO on 2007 August 30 and 31. From the accurate determination of the mean motions, we confirm the mismatch between the position of the arcs and the location of the 42:43 CIR and provide an insight into the mechanisms responsible for the dust confinement.
Data information.
 |
Fig. 1 Top: single 1.5 min exposure of Neptune in the Ks band (2.2 μm), 2007 August 31 (UT start time 01:40:11), revealing the satellites Proteus (P), Galatea (G), Larissa (L) and Despina (D). The frame is 5.5 arcsec wide. North is up and east is left. Bottom: image of Neptune’s ring and moon system obtained by co-adding 70 individual frames of the 2007 August 30 data (2.2 μm, 105 min total exposure time, between UT 01:07:39 and 06:19:28). The figure is 9 × 7.5 arcsec2. North is up and east is left. |
2. Observations
We used the high-angular resolution adaptive-optics fed camera NACO (Lenzen et al. 2003; Rousset et al. 2003) at the European Southern Observatory (ESO) Very Large Telescope (VLT) to image the Neptunian system of moons and ring arcs on 2007 August 30 and 31, see Fig. 1. We used the intermediate plate-scale S27 with a pixel size of about 27 milli-arcsecond (mas) on sky, corresponding to ~570 km at Neptune’s geocentric distance of 29.07 AU (Table 1). For comparison, the smallest arc Courage has a total length of about 3000 km (Porco et al. 1995). Images were acquired in the Ks broad-band filter centred on 2.2 μm, which corresponds to a strong absorption in the methane spectrum, hence reducing the scattered light from Neptune itself. Data in the H band (1.87 μm) had also been taken, but cannot be used here as Neptune’s scattered light is too strong in this colour. The images were processed in the usual manner for near-infrared images: bad pixel correction, sky-substraction, and flat-fielding. Images were aligned using the ephemerides of the satellites Triton and Proteus (Jacobson 2009). An example of the frames is presented in Fig. 1.
To centre the images, we first determined an approximate location of the centre of the planet using a jitter information recorded during the observations. We used the ephemerides of Jacobson (2009) to compare the expected relative positions of Triton and Proteus with their observed relative positions in the NACO images, and estimate the position of Neptune’s centre. Then the images were filtered by subtracting the median image of all the frames. This procedure removes the diffuse scattered light around Neptune, and thus allows one to improve the determination of the satellite photocentres. Two iterations of the last two steps are necessary to achieve a sub-pixel accuracy for the satellite positions. Finally, the pixel size and orientation on sky were determined from a comparison of the expected relative positions of Triton and Proteus with their observed relative positions in pixels in the images. The adjusted parameters are the scale of the images (mas/pixel, cf. Table 1), the position angle Pcor of the celestial north direction with respect to the frame columns (Pcor = 0.40 ± 0.03 deg), and the position of Neptune’s centre. From Table 1, the accuracy on the planet’s centre position is about 0.37 pixels, that is, ~10 mas. Then each image was reprojected onto Neptune’s equatorial plane. Afterwards, single frames were rotated and co-added to increase the signal from the ring arcs or a given satellite, taking into account its orbital motion1.
 |
Fig. 2 Top: projected and co-added images of Neptune’s equatorial plane, 2007 August 30 (60 min total exposure time) on the left, August 31 (109.5 min exposure time) on the right, revealing material at the Fraternité and Egalité locations, the satellites Proteus (P), Larissa (L), Galatea (G), Despina (D), and the Le Verrier ring. Image dimension: 16.4 arcsec2. Bottom: corresponding brightness longitudinal profiles obtained from the images on top (converted into equivalent width). The angular resolution corresponds to 2 deg. The X-axis origin is the longitude LFr of the centre of arc Fraternité, from J2000 ascending node (respectively LFr = 341.62 and 349.01 deg). |
3. Results
3.1. Photometry
Brightness longitudinal profiles of the ring arcs are presented in Fig. 2. On 2007 August 30, 40 frames taken between UT 02:48:06 and 05:37:35 were co-added (after correction for the orbital motion) to produce the left panel (total exposure time 60 min). Similarly, 73 frames taken on 2007 August 31 between UT 00:10:17 and 06:09:39 were co-added to produce the right panel. The profiles were obtained by subtracting the sky background and Neptune’s scattered light from the arcs signal. To perform this operation, we integrated the ring region in the radial direction over 10 pixels. We selected circular annuli on both sides of the ring arcs, summed the pixels in the radial direction, and fitted a two-degree polynomial as a function of the longitude. The radial width of these inner and outer circular rings are ~5 and 30 pixels, respectively, depending on the observing night. The average of the two polynomial fits was subtracted from the arcs’ flux. The brightness longitudinal profiles are given in equivalent width, that is, the width of a perfect Lambert diffuser that would reflect sunlight at the distance of Neptune. Following earlier studies of Neptune’s rings (Smith et al. 1989; Porco et al. 1995), the equivalent width is defined by E(λ) = μ∫I(λ)/F(λ)dr, where I(λ) is the observed flux reflected from the arcs, πF(λ) is the incident solar flux, λ is the wavelength, and μ is the cosine of the emission angle with respect to the ring-plane normal.
Astrometry and Ks magnitudes of Neptune’s inner satellites.
We detected the arcs Fraternité and Egalité, with flux densities and longitudinal extensions similar to those of the previous Keck observations (de Pater et al. 2005). Taking into account the small changes in distance and phase angle, the equivalent width of the arc Fraternité is EFr = 71 ± 10 m compared with ~65 m in October 2003 (de Pater et al. 2005). We note that Egalité is ~20% fainter than Fraternité in our data. According to de Pater et al. (2005), Egalité was 17% brighter than Fraternité in 2002 while its intensity decreased to 7% below that of Fraternité in 2003. Therefore the decrease in intensity might be as high as ~44% between 2002 and 2007. Moreover, the arcs Fraternité and Egalité are poorly separated in our data. New observations with a higher signal-to-noise ratio might reveal whether this lower separation is real or caused by instrumental problems. The satellite Galatea is much brighter than the ring arcs and roughly at the same longitude as Egalité the first night of data, preventing the detection of this arc. For the same reason, the fainter arcs Liberté and Courage are not detectable.
A radial profile of the Le Verrier ring, obtained by combining pixels in azimuth away from the satellites, is presented in Fig. 3. The ring is detected at a radial distance ~53 000 km from Neptune’s centre, as given in Porco et al. (1995). The other bump at ~62 000 km is caused by Galatea and ring arcs, and the long trend arises from the scattered light of Neptune. We note that the Le Verrier ring is only detectable on the first night of data (30 August 2007).
 |
Fig. 3 Radial profile obtained by combining pixels over 80 degrees in azimuth, away from satellites, on 2007 August 30. The total exposure time is 72 min. The Le Verrier ring is detected at a radial distance of 53 000 km. The other bump at ~62 000 km is caused by Galatea and ring arcs, and the long trend arises from the scattered light of Neptune. The Le Verrier ring is not detectable on the second night of data. |
Table 2 lists the Ks magnitudes of Neptune’s inner satellites (Larissa, Galatea, Despina, and Thalassa), also providing details about the photometric calibration. Aperture photometry of ~15 pixels was used to integrate the flux of the satellites Larissa, Galatea, Despina, and 7 pixels for Thalassa. To our knowledge, this is the first ground-based detection of Thalassa, which has a small size (estimated diameter of 40 km from Voyager data; Thomas & Veverka 1991) and is located very close to Neptune (at about only two planetary radii). Therefore the magnitude derived for this moon (23.1 ± 0.6) is probably not very meaningful. The magnitude of Proteus is mK(Proteus) = 18.6 ± 0.2 on the image K2a (Table 1), using an aperture radius of 30 pixels. We note that Proteus, Larissa, and Galatea present a ~+ 0.2 mag difference with the 1.87 μm measurements of Dumas et al. (1999). Finally, we measured on the reference frame K1 (Table 1) a magnitude for Triton mK(Triton) = 12.4 ± 0.1. This is consistent with earlier photometric observations with the IRCAM infrared camera at the 3.8-m UKIRT telescope on Mauna Kea, which led to mK(Triton) = 12.27 ± 0.04 (Kesten et al. 1998), taking into account the effect of distance.
3.2. Astrometry and mean motions
The astrometry of Larissa, Galatea, Despina, Thalassa is summarized in Table 2, which gives for each satellite the orbital radius r and longitude L, measured in the ring plane from the J2000 ascending node of Neptune’s equatorial plane. From the satellite positions and Voyager data (Owen 1991; Porco et al. 1995) we computed the average mean motions. We recall here that Proteus and Triton were used to determine the origin, scale, and orientation of the images (Sect. 2). From the method used, these two satellites are by definition at the positions based on Jacobson’s solution (2009) and are therefore not listed in Table 2. For Thalassa, which is close to Neptune and faint in our images, we note a difference of + 0.00263 ± 0.00015 deg day-1 with respect to the value given in Jacobson (2004).
On the stacked image with respect to the reference frame K2a (see Table 1), we derived a longitude of 349.01 ± 0.60 deg for the arc Fraternité. Using the position of the middle of this arc measured from Voyager data (251.88 deg at epoch JD 2 447 757.0) as given in Porco et al. (1995), this yields the following average mean motion for the arcs: nARCS = 820.11213 ± 0.00008 deg day-1. From Galatea measurements (Table 2) we computed an average mean motion nG = 839.66123 ± 0.00008 deg day-1. We used this measurement to compare nARCS with the mean motion of the 42:43 CIR, initially thought to confine dust within the ring to form stable arcs (Goldreich et al. 1986; Porco 1991). The 42:43 CIR with Galatea creates 86 equally spaced corotation sites around Neptune, with a mean motion given by 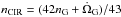 , where
, where  is Galatea’s nodal precession rate. Using
is Galatea’s nodal precession rate. Using 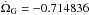 deg day-1 (Owen 1991), nCIR = 820.11760 ± 0.00008 deg day-1 where the uncertainty is caused by that on Galatea’s mean motion. This value is similar to the previous arc mean motion measurements (Nicholson et al. 1995; Sicardy et al. 1999; Dumas et al. 1999, 2002; de Pater et al. 2005), showing that the arcs are not at the location of the 42:43 CIR with Galatea. The drift in mean motion is Δn = nCIR − nARCS = 5.5 ± 0.1 × 10-3 deg day-1, equivalent to a mismatch Δa ≃ 300 ± 5 m in semi-major axis, the half-width of the CIR being 250 ± 100 m (Porco 1991; Owen 1991; Foryta & Sicardy 1996). Note that this mismatch is the same as was reported in Sicardy et al. (1999), but with higher accuracy. This drift translates into a 36 ± 0.7 deg difference for the arcs’ longitude over the 18 years between the Voyager and VLT data. Therefore, the stability of the arcs cannot be explained with the CIR model. The next section details another possible mechanism relying on corotation resonances (more precisely, co-orbital equilibrium configurations), in addition to the existing model of Namouni and Porco (2002).
deg day-1 (Owen 1991), nCIR = 820.11760 ± 0.00008 deg day-1 where the uncertainty is caused by that on Galatea’s mean motion. This value is similar to the previous arc mean motion measurements (Nicholson et al. 1995; Sicardy et al. 1999; Dumas et al. 1999, 2002; de Pater et al. 2005), showing that the arcs are not at the location of the 42:43 CIR with Galatea. The drift in mean motion is Δn = nCIR − nARCS = 5.5 ± 0.1 × 10-3 deg day-1, equivalent to a mismatch Δa ≃ 300 ± 5 m in semi-major axis, the half-width of the CIR being 250 ± 100 m (Porco 1991; Owen 1991; Foryta & Sicardy 1996). Note that this mismatch is the same as was reported in Sicardy et al. (1999), but with higher accuracy. This drift translates into a 36 ± 0.7 deg difference for the arcs’ longitude over the 18 years between the Voyager and VLT data. Therefore, the stability of the arcs cannot be explained with the CIR model. The next section details another possible mechanism relying on corotation resonances (more precisely, co-orbital equilibrium configurations), in addition to the existing model of Namouni and Porco (2002).
4. Confinement models
4.1. Corotation eccentricity resonance
As suggested by Namouni and Porco (2002), the 42:43 CER (resonant argument ΨCER = 43λ − 42λG − ϖG) can match the current arcs’ semi-major axis and stabilize the system, if the arcs have a sufficient fraction of the mass of Galatea. This resonance creates 43 potential maxima, each of length 8.37 deg, which does not completely account for the angular lengths of the arcs. The ring mass determined to shift the CER to the arcs’ position, ≃0.002 Galatea’s mass, assumes an eccentricity of 10-6 for Galatea and would correspond to a small satellite of 10 km in radius (for a density of ≃1 g cm-3). The mass required in this model cannot be contained in a single body since Voyager data excluded undetected satellites of radius larger than 6 km (Smith et al. 1989; Porco et al. 1995). The exact origin of the small residual orbital eccentricity of Galatea, consistent with a forcing by Adams ring’s small mass, has to be determined too.
4.2. Co-orbital moonlets
We propose here an alternative model for Neptune’s arcs stability. It basically assumes that the Adams ring is a collection of a few moonlets (four in our case) that maintain stable co-orbital relative positions akin to the Lagrangian L4/L5 points (Renner & Sicardy 2004). The observed arcs would then be composed of dust trapped between those co-orbital satellites. This generalizes Lissauer’s original shepherding model (Lissauer 1985) and is an adaption of Sicardy & Lissauer (1992). In such a model, Adams ring would be in an intermediate situation between a fully collisional ring with only small particles, and a fully accreted system where only one satellite survives, after swallowing up all the ring material. The possible origin of these moonlets is discussed in more detail in Sect. 5.
4.2.1. Family of stable stationary configurations
There is an infinity of stationary configurations for co-orbital moonlets compatible with the observed azimuthal lengths of Neptune’s arcs. However, we show here how the observed inter-arc regions lead to a limited space of possible mass ratios between the satellites, achieving equilibrium.
New results on the existence of stationary configurations for N co-orbital satellites with small and arbitrary masses (revolving on circular and planar orbits around a planet) were derived in Renner and Sicardy (2004). The existence of solutions depends on the parity of N: if N is odd, then there always exists a set of mass values that achieves stationarity for any arbitrary angular separation between the satellites. However, strictly positive masses restrict this existence to sub-domains of angular separations. If N is even, additional conditions are required to achieve stationarity. The case N = 3 can be completely treated analytically for small arbitrary satellite masses, giving all the possible solutions and their linear stability. For N ≥ 4 a numerical scheme allows us to derive the possible stable stationary configurations for given satellite masses: by adding a non-conservative term in the equations of motion, which brings energy in the rotating frame of the co-orbital satellites (i.e. increases the Jacobi constant), the satellites converge towards the linearly stable equilibria2. Integrating these perturbed equations and exploring random initial coordinates with random masses then provides the domains of stable stationary points. These domains correspond to configurations where the co-orbitals are either positioned near the L4 and L5 points of the most massive satellite, or are grouped near one of these two points.
 |
Fig. 4 Subset of stationary configurations for N = 4 satellites, akin to the Lagrangian L4/L5 points. The satellite S1 is the most massive. We assume that the mass ratios mi/m1 of the satellites Si (i = 2,3,4) with respect to S1 are lower than 0.03, and that the angular separations are compatible with the observed inter-arc regions (Φ32 = 11 ± 3 deg, Φ43 = 12.5 ± 3 deg and Φ42 = 23.5 ± 3 deg). We obtain a continuum of masses (see table) in equilibrium where the co-orbital satellites are close to the L4/L5 point of S1: S2 at a longitude with respect to S1 between 43 and 56.75°, S3 between 51.28 and 70.74° and S4 between 65.66 and 80.1°. |
We applied the method above to N = 4 satellites (where the satellite N = 1 is by convention the most massive) with random initial mass ratios mi/m1 (i = 2,3,4) lower than three percent, and stored the stable solutions with angular separations satisfying Φ32 = 11 ± 3 deg, Φ43 = 12.5 ± 3 deg and Φ42 = 23.5 ± 3 deg (where Φij is the azimuthal separation between the satellites i and j), that is, configurations compatible with the observed inter-arc regions (Porco 1991; Dumas et al. 2002; de Pater et al. 2005). We obtained a continuum of mass values with angular configurations where the co-orbitals are near the L4 (or L5) point of the most massive satellite. Thus, three small co-orbital bodies near the L4/L5 point of a more massive Lagrangian satellite (mass ratios lower than three percent3) are close to a stable stationary configuration and may librate around that equilibrium. The results are summarized in Fig. 4.
4.2.2. Full numerical integrations
To study the arcs’ dynamics, we used the Mercury integrator package (Chambers 1999) with the Burlish-Stoer algorithm and simulated the motion of Galatea, four co-orbital satellites initially in equilibrium (selecting a given stationary configuration from the previous section), and four arc (test) particles of Adams ring. State vectors were converted to geometric orbital elements using the algorithm given by Renner and Sicardy (2006). Unlike osculating elements, the geometric elements are not contaminated by the short-period terms caused by planetary oblateness. Typical results are presented in Figs. 5–9. We used the physical parameters of Neptune (mass, radius, oblateness) given by Owen (1991) from the analysis of Voyager data. Galatea (MG = 1.94 × 1018 kg) is initially on a circular and inclined (iG = 0.0544 deg) orbit with a semi-major axis aG = 61 952.606 km.
 |
Fig. 5 Motion of four co-orbital satellites and four test particles (arcs) around Neptune, without Galatea. The figure shows the orbital radius (km) vs. longitude (deg) in a frame rotating with the most massive Lagrangian satellite S1 (diameter =10.4 km, assuming a density of 1 g cm-3). The other satellites S2, S3, and S4 have diameters of 2.2, 2.8, and 2.3 km, respectively. Integration time is 150 years. The co-orbital bodies are in a stable stationary configuration. The system of co-orbital satellites and arcs is ≃0.25 km outside the CIR, as given by the observations. |
 |
Fig. 6 Same as Fig 5, including Galatea’s perturbations. The top and middle figures correspond to an integration time of 20 and 40 years, respectively. The full radial excursion of about 60 km is the result of the forced eccentricity due to the 42:43 Lindblad resonance (LER) with Galatea. The moonlets have a slow libration motion around their equilibrium configuration. For the arc particles, we note small azimuthal modulations of density caused by the proximity of the CIR. At the bottom, the resulting azimuthal density profiles of the arcs are given. These profiles are obtained from the time cumulated single particle evolutions (0−20 years in solid line, 20−40 years dashed-dotted). |
 |
Fig. 7 Resonant arguments (deg) vs. time (years) for the co-orbital satellite S1 and for the simulation shown in Fig. 6. The system of co-orbital satellites and arcs is inside the 42:43 LER with Galatea (bottom), but outside the CIR (top), with a drift in mean motion compatible with the observations (nCIR − nARCS = 5.5 ± 0.1 × 10-3 deg day-1). |
 |
Fig. 8 Motion of four co-orbital satellites (top) and four arc particles (bottom) over 103 years, including Galatea’s perturbations. The satellites have a libration motion around the linearly stable equilibrium. The test particles remain closely confined between the satellites, as long as no close encounters with the co-orbital moons occur (here after about 200 years, see Fig. 9). |
 |
Fig. 9 Time evolution of the orbital elements of the arc particles for the simulation shown in Fig. 8. Top: semi-major axis (km). For clarity, the semi-major axis of the first particle (resp. the third and fourth) has been shifted by − 10 (resp. by + 10 and + 20) km. The downward points are due to encounters with Galatea. Middle: mean longitudes (deg) with respect to satellite S1. Bottom: eccentricity of the first particle, which exhibits stronger perturbations from close encounters with the co-orbital satellites, though it remains bound to the Adams ring region. |
The four co-orbital satellites have the following masses: m1 = 6 × 1014 kg, m2/m1 = 0.009078, m3/m1 = 0.019537, and m4/m1 = 0.010995. Assuming a density of 1 g cm-3, this corresponds to a radius ~5.2 km for m1 and between 1.1 and 1.4 km for the other co-orbital bodies. This is compatible with the Voyager data that exclude undetected satellites of radius larger than 6 km (Smith et al. 1989; Porco et al. 1995). The initial geometric semi-major axis is a = 62 932.7 km, that is, 0.25 km outside the 42:43 CIR (resonant argument ΨCIR = 2 [43λ − 42λG − ΩG], see Fig. 7). With initial angular separations Φ21 = 48.31 deg, Φ31 = 59.38 deg, Φ41 = 72.19 deg with respect to m1, they are initially in a stable stationary configuration (see previous section). The test particles are at the same semi-major axis. The system of co-orbital satellites and arc particles is located inside the 42:43 Lindblad eccentricity resonance (LER) with Galatea, which corresponds to a librating resonant argument ΨLER = 43λ − 42λG − ϖ, see Fig. 7.
The particle/satellite orbital radii in a frame rotating with the most massive Lagrangian satellite S1 (mass m1) are shown in Figs. 5, 6, and 8, and the time evolution of the orbital elements of the arc particles is given in Fig. 9. The system is numerically stable under the effects of Galatea’s perturbations: the moonlets have a slow libration motion around their equilibrium configuration. In order of increasing longitude, the second and third test particles remain closely confined between the satellites during the total integration time span (one thousand years). The fourth, external particle librates with a significant amplitude of about 20 degrees, while the first exhibits close encounters with the co-orbital moons after about 200 years. However, this particle remains bound to the Adams ring region. The eccentricity amplitude resulting from these close encounters is ~2 × 10-4, that is, about half of the forced eccentricity due to the LER resonance with Galatea. This value is retrieved through the impulse approximation (Julian & Toomre 1966):  , where mS = m1 = 6 × 1014 kg, MP is Neptune’s mass, a is the semi-major axis of the co-orbital system, and x is the minimum particle/satellite distance during a close approach, here assumed to be about twice the Hill radius of the satellite (to avoid chaotic motions or physical collisions).
, where mS = m1 = 6 × 1014 kg, MP is Neptune’s mass, a is the semi-major axis of the co-orbital system, and x is the minimum particle/satellite distance during a close approach, here assumed to be about twice the Hill radius of the satellite (to avoid chaotic motions or physical collisions).
Therefore, considering only gravitational interactions, two arcs can be strongly maintained at least one thousand years with a four co-orbitals’ model (and four arcs on shorter time scales of at least few tens of years). Small dust particles can escape confinement more quickly, taking into account dissipative forces (radiation pressure, Poynting-Robertson drag). We note in Figs. 6 and 8 small azimuthal modulations of density caused by the proximity of the CIR. The total mass of the co-orbital system (~3 × 10-4MG) is too small to shift the 42:43 CER at the arcs’ current position as envisaged in Namouni and Porco (2002).
The model proposed here naturally explains the observed azimuthal lengths of the arcs, as the result of the equilibrium configuration between the small co-orbital moonlets. The method to derive the possible linearly stable stationary configurations for a given set of N masses, as proposed in Renner & Sicardy (2004), is outlined in the previous section.
5. Discussion
5.1. Formation processes
The origin of the arc system could be the breakup of a parent satellite or the accretion of ring material within the Roche zone of the planet. The latter is outside the Adams ring for a density of 1 g cm-3 (Esposito 2002), allowing a mixture of collisional rings and accreted moonlets. The Galatea secular torque (Goldreich et al. 1986) could help to set a few ring moonlets in stable stationary configurations, providing the energy generated by the Lindblad resonance is higher than that dissipated through collisions. The change rate of energy (per unit mass) 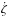 for particles around corotation points, averaged over one libration period TC, is given by (Sicardy 1991)
for particles around corotation points, averaged over one libration period TC, is given by (Sicardy 1991)
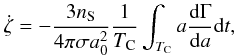 where nS is the satellite’s mean motion, a the semi-major axis, a0 the average orbital radius, σ the arc surface density, and dΓ/da the torque density, that is, the torque exerted by the satellite per unit radius. Because of the presence of the term a in front of dΓ/da, the energy received is proportional to the gradient d2Γ/da2 of the torque density. Therefore the energy is positive, that is, the arc is stable, if the gradient of the torque density across the arc is negative. The torque density peak is positive if the resonance is outside the satellite (outer Lindblad resonance) and negative if it is inside (inner Lindblad resonance), that is, the torque tends to push particles away from the satellite (Meyer-Vernet & Sicardy 1987). As a consequence, the gradient of the torque density tends to be negative (positive) just outside an outer (inner) Lindblad resonance, and positive (negative) just inside. Thus, to be trapped, an arc should remain just outside (inside) the outer (inner) Lindblad resonance radius. This is the case for Neptune’s ring arcs which are located 2 km outside the 42:43 LER with Galatea (Porco 1991). Assuming that the torque Γ obeys the standard formula (Goldreich & Tremaine 1982), Sicardy & Lissauer (1992) have shown that most of the energy given by 42:43 LER with Galatea is actually used to excite the orbital eccentricity of the particles, and not to confine them in a libration region. However, the standard torque formula may not be applicable for Neptune’s arcs since it assumes that Lindblad resonances m + 1:m overlap and that the particle orbital phases are randomized between successive encounters. Furthermore, using the energy equation above to assess the stability of the arcs against collisions depends on physical parameters that are poorly known (self-gravitation, pressure, viscosity, etc.). Thus, the presence of arcs around Neptune would imply that the energy provided by the Lindblad resonance is sufficient to form and maintain a few co-orbital bodies in equilibrium.
where nS is the satellite’s mean motion, a the semi-major axis, a0 the average orbital radius, σ the arc surface density, and dΓ/da the torque density, that is, the torque exerted by the satellite per unit radius. Because of the presence of the term a in front of dΓ/da, the energy received is proportional to the gradient d2Γ/da2 of the torque density. Therefore the energy is positive, that is, the arc is stable, if the gradient of the torque density across the arc is negative. The torque density peak is positive if the resonance is outside the satellite (outer Lindblad resonance) and negative if it is inside (inner Lindblad resonance), that is, the torque tends to push particles away from the satellite (Meyer-Vernet & Sicardy 1987). As a consequence, the gradient of the torque density tends to be negative (positive) just outside an outer (inner) Lindblad resonance, and positive (negative) just inside. Thus, to be trapped, an arc should remain just outside (inside) the outer (inner) Lindblad resonance radius. This is the case for Neptune’s ring arcs which are located 2 km outside the 42:43 LER with Galatea (Porco 1991). Assuming that the torque Γ obeys the standard formula (Goldreich & Tremaine 1982), Sicardy & Lissauer (1992) have shown that most of the energy given by 42:43 LER with Galatea is actually used to excite the orbital eccentricity of the particles, and not to confine them in a libration region. However, the standard torque formula may not be applicable for Neptune’s arcs since it assumes that Lindblad resonances m + 1:m overlap and that the particle orbital phases are randomized between successive encounters. Furthermore, using the energy equation above to assess the stability of the arcs against collisions depends on physical parameters that are poorly known (self-gravitation, pressure, viscosity, etc.). Thus, the presence of arcs around Neptune would imply that the energy provided by the Lindblad resonance is sufficient to form and maintain a few co-orbital bodies in equilibrium.
The exact origin of the proposed configuration of co-orbital bodies is still unknown. If accretion plays a significant role, we propose that such a mechanism is hierarchical: a (previously accreted) satellite could gather some ring material around its L4 or L5 Lagrangian point. Then larger co-orbital particles would form close to L4/L5 until a stationary configuration is reached (see Sect. 4.2). The ring arcs observed would be the residual material confined in between these small satellites. Simulations of self-gravitating and colliding particles (see, e.g., Rein & Liu 2012) need to be performed to study the formation mechanisms of small satellites close to the Roche zone of a planet. Once the system of co-orbital bodies is in a stationary configuration, the secular torque and therefore the ring orbital migration are reduced (Sicardy & Lissauer 1992).
5.2. Model improvements
Close encounters with the co-orbital moonlets make particles escape from the arcs into the diffuse part of the Adams ring; however, this is not sufficient to explain the density contrast between these two ring regions. Subkilometer-sized particles are also necessary to reproduce the dust ratios observed and the clumpy structure of the arc system (Porco et al. 1995; Salo & Hänninen 1998). Part of the arc material could originate from debris knocked off the hypothetical co-orbital moonlets. The observed changes in the relative intensities and locations of the arcs (de Pater et al. 2005) could result, in part, from the libration motion of the co-orbital satellites around the equilibrium configuration. Dissipative effects such as collisions need to be included in the dynamical models. Indeed, with typical relative velocities of ~1 m s-1, the orbital elements of the arc particles can be significantly modified. A coupling with the CER model might also be investigated: the arcs would remain stable during longer time scales, if confined by co-orbital bodies massive enough to displace the CER with Galatea to the arcs’ semi-major axis (Namouni & Porco 2002).
5.3. Dynamical evolution
The dynamical evolution of Neptune’s partial rings is unknown: the existence of a system of small co-orbital satellites might be part of an incomplete process of satellite formation. Alternatively, Neptune’s arcs are transitory, resulting in a new ring if the equilibrium configuration breaks down. A new report on observations of Neptune’s ring arcs obtained by the Hubble Space Telescope during 2004−2009 (Showalter et al. 2013) shows that the leading two arcs (Courage, Liberté) have now vanished, while the trailing two (Egalité, Fraternité) appear to have remained quite stable. Though submitted to confinement mechanisms, the arcs evolve rapidly.
6. Conclusions
We have analyzed high-angular resolution near-infrared images of Neptune’s ring arcs obtained in 2007 at the ESO VLT with the adaptive-optics fed camera NACO. We detected the arcs Fraternité and Egalité, derived more accurate mean motion values for the arcs and Galatea, and confirmed the mismatch between the arcs’ mean motion and the angular velocity associated with the 42:43 CIR with Galatea. Additional data, in particular with Galatea far from the arc system (Showalter et al. 2013), are needed to follow the global time evolution of the system. In return, this will help to build a more comprehensive theory for the arcs’ confinement. In our model, the stability of Neptune’s arcs results from the co-orbital relative equilibria of a few moonlets, making the Adams ring an intermediate structure between a fully collisional disk composed of only small particles and a fully accreted satellite. The main advantage of this model is that it naturally explains the observed arc azimuthal lengths as the result of the relative angular positions of the satellites in equilibrium.
For this last step, three angles B,P,U are tabulated (Table 1).
References
- Borderies, N., & Longaretti, P.-Y. 1987, Icarus, 72, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Borderies-Rappaport, N., & Longaretti, P.-Y. 1994, Icarus, 107, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dumas, C., Terrile, R. J., Smith, B. A., Schneider, G., & Becklin, E. E. 1999, Nature, 400, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Dumas, C., Terrile, R. J., Smith, B. A., & Schneider, G. 2002, AJ, 123, 1776 [NASA ADS] [CrossRef] [Google Scholar]
- Esposito, L. W. 2002, Rep. Prog. Phys., 65, 1741 [Google Scholar]
- Foryta, D. W., & Sicardy, B. 1996, Icarus, 123, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1982, ARA&A, 20, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., Tremaine, S., & Borderies, N. 1986, AJ, 92, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard, W. B., Brahic, A., Sicardy, B., et al. 1986, Nature, 319, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobson, R. A. 2009, AJ, 137, 4322 [NASA ADS] [CrossRef] [Google Scholar]
- Julian, W. H., & Toomre, A. 1966, ApJ, 146, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Kesten, P. R., Davies, J. K., Cruikshank, D. P., & Roush, T. L. 1998, DPS meeting, 30, 44.02 [Google Scholar]
- Lenzen, R., Hartung, M., Brandner, W., et al. 2003, SPIE, 4841, 944 [Google Scholar]
- Lissauer, J. J. 1985, Nature, 318, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer-Vernet, N., & Sicardy, B. 1987, Icarus, 69, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Moeckel, R. 1994, J. Dyn. Diff. Eq., 6, 35 [CrossRef] [Google Scholar]
- Namouni, F., & Porco, C. C. 2002, Nature, 417, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Nicholson, P. D., Mosqueira, I., & Matthews, K. 1995, Icarus, 113, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, W. M., Vaughan, R. M., & Synnot, S. P. 1991, AJ, 101, 1511 [NASA ADS] [CrossRef] [Google Scholar]
- de Pater, I., Gibbard, S. G., Chiang, E., et al. 2005, Icarus, 174, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Porco, C. C. 1991, Science, 253, 995 [NASA ADS] [CrossRef] [Google Scholar]
- Porco, C. C., Nicholson, P. D., Cuzzi, J. N., et al. 1995, Neptune and Triton (University of Arizona Press) [Google Scholar]
- Rein, H., & Liu, S.F. 2012, A&A, 537, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renner, S., & Sicardy, B. 2004, Celest. Mech., 88, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Renner, S., & Sicardy, B. 2006, Celest. Mech., 94, 237 [Google Scholar]
- Rousset, G., Lacombe, F., Puget, P., et al. 2003, SPIE, 4839, 140 [Google Scholar]
- Salo, H., & Hänninen, J. 1998, Science, 282, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Showalter, M. R., de Pater, I., French, R. S., & Lissauer, J. J. 2013, Am. Astron. Soc., DPS meeting, 45, 20601 [Google Scholar]
- Sicardy, B. 1991, Icarus, 89, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Sicardy, B., & Lissauer, J. J. 1992, Adv. Space Res., 12, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Sicardy, B., Roddier, F., Roddier, C., et al. 1999, Nature, 400, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, B. A., Soderblom, L. A., Banfield, D., et al. 1989, Science, 246, 1422 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Thomas, P., & Veverka, J. 1991, J. Geophys. Res., 96, 19261 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Top: single 1.5 min exposure of Neptune in the Ks band (2.2 μm), 2007 August 31 (UT start time 01:40:11), revealing the satellites Proteus (P), Galatea (G), Larissa (L) and Despina (D). The frame is 5.5 arcsec wide. North is up and east is left. Bottom: image of Neptune’s ring and moon system obtained by co-adding 70 individual frames of the 2007 August 30 data (2.2 μm, 105 min total exposure time, between UT 01:07:39 and 06:19:28). The figure is 9 × 7.5 arcsec2. North is up and east is left. |
| In the text | |
 |
Fig. 2 Top: projected and co-added images of Neptune’s equatorial plane, 2007 August 30 (60 min total exposure time) on the left, August 31 (109.5 min exposure time) on the right, revealing material at the Fraternité and Egalité locations, the satellites Proteus (P), Larissa (L), Galatea (G), Despina (D), and the Le Verrier ring. Image dimension: 16.4 arcsec2. Bottom: corresponding brightness longitudinal profiles obtained from the images on top (converted into equivalent width). The angular resolution corresponds to 2 deg. The X-axis origin is the longitude LFr of the centre of arc Fraternité, from J2000 ascending node (respectively LFr = 341.62 and 349.01 deg). |
| In the text | |
 |
Fig. 3 Radial profile obtained by combining pixels over 80 degrees in azimuth, away from satellites, on 2007 August 30. The total exposure time is 72 min. The Le Verrier ring is detected at a radial distance of 53 000 km. The other bump at ~62 000 km is caused by Galatea and ring arcs, and the long trend arises from the scattered light of Neptune. The Le Verrier ring is not detectable on the second night of data. |
| In the text | |
 |
Fig. 4 Subset of stationary configurations for N = 4 satellites, akin to the Lagrangian L4/L5 points. The satellite S1 is the most massive. We assume that the mass ratios mi/m1 of the satellites Si (i = 2,3,4) with respect to S1 are lower than 0.03, and that the angular separations are compatible with the observed inter-arc regions (Φ32 = 11 ± 3 deg, Φ43 = 12.5 ± 3 deg and Φ42 = 23.5 ± 3 deg). We obtain a continuum of masses (see table) in equilibrium where the co-orbital satellites are close to the L4/L5 point of S1: S2 at a longitude with respect to S1 between 43 and 56.75°, S3 between 51.28 and 70.74° and S4 between 65.66 and 80.1°. |
| In the text | |
 |
Fig. 5 Motion of four co-orbital satellites and four test particles (arcs) around Neptune, without Galatea. The figure shows the orbital radius (km) vs. longitude (deg) in a frame rotating with the most massive Lagrangian satellite S1 (diameter =10.4 km, assuming a density of 1 g cm-3). The other satellites S2, S3, and S4 have diameters of 2.2, 2.8, and 2.3 km, respectively. Integration time is 150 years. The co-orbital bodies are in a stable stationary configuration. The system of co-orbital satellites and arcs is ≃0.25 km outside the CIR, as given by the observations. |
| In the text | |
 |
Fig. 6 Same as Fig 5, including Galatea’s perturbations. The top and middle figures correspond to an integration time of 20 and 40 years, respectively. The full radial excursion of about 60 km is the result of the forced eccentricity due to the 42:43 Lindblad resonance (LER) with Galatea. The moonlets have a slow libration motion around their equilibrium configuration. For the arc particles, we note small azimuthal modulations of density caused by the proximity of the CIR. At the bottom, the resulting azimuthal density profiles of the arcs are given. These profiles are obtained from the time cumulated single particle evolutions (0−20 years in solid line, 20−40 years dashed-dotted). |
| In the text | |
 |
Fig. 7 Resonant arguments (deg) vs. time (years) for the co-orbital satellite S1 and for the simulation shown in Fig. 6. The system of co-orbital satellites and arcs is inside the 42:43 LER with Galatea (bottom), but outside the CIR (top), with a drift in mean motion compatible with the observations (nCIR − nARCS = 5.5 ± 0.1 × 10-3 deg day-1). |
| In the text | |
 |
Fig. 8 Motion of four co-orbital satellites (top) and four arc particles (bottom) over 103 years, including Galatea’s perturbations. The satellites have a libration motion around the linearly stable equilibrium. The test particles remain closely confined between the satellites, as long as no close encounters with the co-orbital moons occur (here after about 200 years, see Fig. 9). |
| In the text | |
 |
Fig. 9 Time evolution of the orbital elements of the arc particles for the simulation shown in Fig. 8. Top: semi-major axis (km). For clarity, the semi-major axis of the first particle (resp. the third and fourth) has been shifted by − 10 (resp. by + 10 and + 20) km. The downward points are due to encounters with Galatea. Middle: mean longitudes (deg) with respect to satellite S1. Bottom: eccentricity of the first particle, which exhibits stronger perturbations from close encounters with the co-orbital satellites, though it remains bound to the Adams ring region. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


