| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A140 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201323049 | |
| Published online | 21 February 2014 | |
Transiting exoplanets from the CoRoT space mission
XXV. CoRoT-27b: a massive and dense planet on a short-period orbit⋆
1
Instituto de Astrofísica de Canarias (IAC),
38200
La Laguna, Tenerife
Spain
e-mail:
hannu.parviainen@astro.ox.ac.uk
2
Dept. Astrofísica, Universidad de La Laguna (ULL),
38206,
La Laguna Tenerife,
Spain
3
Department of Physics, Denys Wilkinson Building, Keble Road,
Oxford
OX1 3RH,
UK
4
INAF-Catania Astrophysical Observatory,
via S. Sofia 78,
95123
Catania,
Italy
5
Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique
de Marseille) UMR 7326, 13388
Marseille,
France
6
IAG, Universidade de São Paulo, 05508-090
Säo Paulo,
Brazil
7
LESIA, UMR 8109 CNRS, Observatoire de Paris, UVSQ, Université
Paris-Diderot, 5 place J.
Janssen, 92195
Meudon Cedex,
France
8
Institute of Planetary Research, German Aerospace Center, Rutherfordstrasse 2,
12489
Berlin,
Germany
9
Thüringer Landessternwarte, CoRoT (DLR),
Sternwarte 5, Tautenburg,
07778
Tautenburg,
Germany
10
NASA Ames Research Center, MS 244-30, PO Box 1, 94035-0001 Moffett Field, USA
11
Research and Scientific Support Department, ESTEC/ESA,
PO Box
299, 2200 AG
Noordwijk, The
Netherlands
12
Department of Physics and Astronomy, Aarhus
University, Ny Munkegade
120, 8000
Aarhus C,
Denmark
13
Rheinisches Institut für Umweltforschung an der Universität zu
Köln, Aachener Strasse
209, 50931
Kölen,
Germany
14
Institut d’Astrophysique Spatiale, Université Paris XI,
91405
Orsay,
France
15
Observatoire de Haute-Provence, Saint-Michel-l’Observatoire
04670,
France
16
Institut d’Astrophysique de Paris, 98bis boulevard Arago, 75014
Paris,
France
17
University of Vienna, Institute of Astronomy,
Türkenschanzstr.
17, 1180
Vienna,
Austria
18
Observatoire de la Côte d’Azur, Laboratoire Cassiopée,
BP 4229,
06304
Nice Cedex 4,
France
19
School of Physics and Astronomy, Raymond and Beverly Sackler
Faculty of Exact Sciences, Tel Aviv University, 69978
Tel Aviv,
Israel
20
Institut für Astrophysik, Georg-August-Universität,
Friedrich-Hund-Platz
1, 37077
Göttingen,
Germany
21
Centro de Astrofísica, Universidade do Porto,
rua das Estrelas,
4150-762
Porto,
Portugal
22
LUTH, Observatoire de Paris, CNRS, Université Paris Diderot; 5
place Jules Janssen, 92195
Meudon,
France
Received:
14
November
2013
Accepted:
31
December
2013
Aims. We report the discovery of a massive and dense transiting planet CoRoT-27b on a 3.58-day orbit around a 4.2 Gyr-old G2 star. The planet candidate was identified from the CoRoT photometry, and was confirmed as a planet with ground-based spectroscopy.
Methods. The confirmation of the planet candidate is based on radial velocity observations combined with imaging to rule out blends. The characterisation of the planet and its host star was carried out using a Bayesian approach where all the data (CoRoT photometry, radial velocities, and spectroscopic characterisation of the star) are used jointly. The Bayesian analysis included a study whether the assumption of white normally distributed noise holds for the CoRoT photometry and whether the use of a non-normal noise distribution offers advantages in parameter estimation and model selection.
Results. CoRoT-27b has a mass of 10.39 ± 0.55MJup, a radius
of 1.01 ± 0.04RJup, a mean
density of 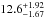 g cm-3, and an effective
temperature of 1500 ± 130 K.
The planet orbits around its host star, a 4.2 Gyr-old G2-star with a mass M⋆ = 1.06M⊙ and a radius
R⋆ = 1.05R⊙, on a
0.048 ± 0.007 AU orbit of
3.58 days. The radial velocity observations allow us to exclude highly eccentric orbits,
namely, e < 0.065 with 99%
confidence. Given its high mass and density, theoretical modelling of CoRoT-27b is
demanding. We identify two solutions with heavy element mass fractions of 0.11 ± 0.08M⊕ and 0.07 ± 0.06M⊕, but even
solutions void of heavy elements cannot be excluded. We carry out a secondary eclipse
search from the CoRoT photometry using a method based on Bayesian model selection, but
conclude that the noise level is too high to detect eclipses shallower than 9% of the
transit depth. Using a non-normal noise model was shown not to affect the parameter
estimation results, but led to significant improvement in the sensitivity of the model
selection process.
g cm-3, and an effective
temperature of 1500 ± 130 K.
The planet orbits around its host star, a 4.2 Gyr-old G2-star with a mass M⋆ = 1.06M⊙ and a radius
R⋆ = 1.05R⊙, on a
0.048 ± 0.007 AU orbit of
3.58 days. The radial velocity observations allow us to exclude highly eccentric orbits,
namely, e < 0.065 with 99%
confidence. Given its high mass and density, theoretical modelling of CoRoT-27b is
demanding. We identify two solutions with heavy element mass fractions of 0.11 ± 0.08M⊕ and 0.07 ± 0.06M⊕, but even
solutions void of heavy elements cannot be excluded. We carry out a secondary eclipse
search from the CoRoT photometry using a method based on Bayesian model selection, but
conclude that the noise level is too high to detect eclipses shallower than 9% of the
transit depth. Using a non-normal noise model was shown not to affect the parameter
estimation results, but led to significant improvement in the sensitivity of the model
selection process.
Key words: planets and satellites: detection / stars: individual: CoRoT-27 / techniques: photometric / techniques: radial velocities / techniques: spectroscopic / methods: statistical
© ESO, 2014
1. Introduction
We report the discovery of a new massive high-density transiting planet on a short-period orbit, CoRoT-27b. The planet falls within the scarcely populated overlapping mass regime between planets and brown dwarfs (Leconte et al. 2009; Baraffe et al. 2010), and contributes to our understanding of the high-mass tail of the planet population.
Distinguishing between high-mass planets and low-mass brown dwarfs is an ambiguous task that depends on the definition of a planet (Schneider et al. 2011). If we decide to use the formation history as the discriminating factor – naming objects formed by core accretion as planets, and objects formed by gravitational collapse as brown dwarfs – we may be able to identify sets of observables characteristic to the two populations. Thus, while a mass estimate is not enough to distinguish between the formation histories, the differences in the observable distributions (orbital eccentricity, host rotation rate, host metallicity, etc.) may allow us to infer the likely formation history for a given object based on a probabilistic model.
The currently known population of massive short-period planets has shown some tentative trends towards higher orbital eccentricities and host star rotation rates and lower host star metallicities than observed for the lower-mass planets (Southworth et al. 2009; Bakos et al. 2011).
Furthermore, the massive close-in planets are predominantly found around F-type stars (Bouchy et al. 2011), Kepler-75b (Hébrard et al. 2013) being the only massive short-period star found around a G-type star before CoRoT-27b. Bouchy et al. (2011) propose that this trend is real instead of an observation bias and that it is due to differences in tidal braking by G- and F-dwarfs. The massive close-in companions around G-dwarfs would rapidly migrate inwards and be engulfed by the host star owing to the star’s strong tidal braking, while the companions around F-dwarfs with weaker tidal braking would be spared this fate (Barker & Ogilvie 2009).
While the trends in eccentricity and host star properties are based on small number statistics, already the large variability in these properties may be a sign of mixing objects of different nature. While the detection of possible distinguishable populations will require a proper cluster analysis with significantly more objects, each new planet discovery in this mass and period regime will get us a bit closer to understanding the fringe regions of the planet and brown dwarf distributions.
2. Data
2.1. CoRoT light curve
The CoRoT satellite offers two time cadences. The survey mode delivers data with a cadence of 512 s (long cadence, cl, from here on), created by stacking 16 exposures of 32 s. For the planet candidates identified during an observing run, a fast time sampling of 32 s (short cadence, cs) is also available (Surace et al. 2008). Furthermore, data of bright (≲R = 13.5 mag) targets have been acquired with three-colour photometry, while the fainter ones are only observed in a single passband.
CoRoT-27 was observed continuously for 83.5 days (from 8 July 2011 to 30 September 2011) in the monochromatic mode during the LRc08 run towards the galactic centre. We present the catalogue IDs, coordinates, and magnitudes in Table 1. The star was first observed in the cl mode, and the mode was changed to cs after a promising transit candidate with a depth of ~1% was discovered.
CoRoT-27 IDs, coordinates, and magnitudes.
The light curve consists of 6920 cl and 114368 cs points in total, of which 788 and 5897 are marked as extreme outliers by the CoRoT pipeline. Further 1022 and 9869 points are marked as exposures obtained during the crossing of South Atlantic Anomaly (SAA), a region of the satellite’s orbit where it is exposed to high doses of radiation (Pinheiro da Silva et al. 2008). We exclude the points marked as extreme outliers from the analysis, but keep the inside-SAA points. The rationale behind keeping the inside-SAA points is that while the number of high-energy particle hits increases during the SAA crossings, the true number of points affected by the particle-hit events does not justify the removal of 10% of the data. Including inside-SAA sections increases the number of outliers somewhat, but this can be accounted for by using a non-normal noise model in the analysis (see Sect. 4.4).
We find one contaminating star within the CoRoT aperture mask (see Fig. 1) and estimate that it contributes 2.42% ± 0.95% of the measured flux using a code developed by Bordé and Pasternacki (Pasternacki et al. 2012). We did not remove the contamination from the light curve before the combined light curve and RV analysis, but instead included contamination to the model with a normal prior based on the given estimate.
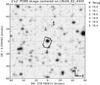 |
Fig. 1 POSS image showing the surroundings of CoRoT-27 and the photometric aperture mask (solid line). One contaminating star (marked as 1) falls partially within the aperture mask, with an estimated contamination factor of 2.4% ± 0.95%. |
The final light curve used in the analysis is shown in Fig. 2. The light curve consists of 6132 cl and 108471 cs points (89% and 95% of all the data), features one large jump near the end of the cl data and several smaller jumps. The light curve contains 12 cl and 11 cs transits. We did not attempt to carry out a global detrending to correct for the jumps and other systematics, but decided to use a local approach to estimate the systematic trends around each individual transit.
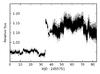 |
Fig. 2 CoRoT-observed white light curve showing the long and short time cadence photometric data with extreme outliers (as marked by the CoRoT photometric pipeline) removed. The individual transits are visible by eye in the cl data. |
We estimate photometric point-to-point scatter of 4.3 and 12.5 ppt (parts per thousand) for cl and cs, respectively, assuming independent and identically distributed (i.i.d.) noise following a normal distribution, and 2.9 and 8.9 ppt assuming logistically distributed i.i.d. noise (see the discussion about noise models in Sect. 4.4). The cl noise estimates are higher than expected for i.i.d. noise, which can be explained by correlated (red) noise from instrumental and physical sources (stellar granulation, etc., see Aigrain et al. 2009 for an overview of the CoRoT-specific error sources and Pont et al. 2006 for an introduction to red noise in the context of photometric time series).
2.2. Ground-based observations
2.2.1. Photometric follow-up
Ground-based photometric follow-up of CoRoT candidates is verifying whether a transit that is detected in CoRoT’s large apertures is on a target star instead of being caused by some nearby binary system (Deeg et al. 2009). An 18-min-long time series was acquired with the 1.2 m Euler Telescope during a transit on 29 September 2011 with excellent 0.5′′ seeing. The seeing was poor, however, when the corresponding off-transit data were taken a day later. This strong difference in seeing meant that the 1% deep transit signal could not observed. However, none of the nearby fainter stars showed any relevant brightness variation. The good on-transit images also did not show any very close contaminating stars with a brightness that is sufficient (R < 20.5) to cause the transit signal. Contaminants causing a false alarm could therefore be excluded for any distances greater than ~1′′ from the target, giving a very high probability that the transit does indeed arise on the target star.
2.2.2. Spectroscopic follow-up
 |
Fig. 3 HARPS-observed radial velocities shown with a best-fit circular orbit (top) and residuals (bottom). |
High-precision radial-velocity observations were performed using HARPS at the 3.6 m telescope in La Silla Observatory, ESO, Chile (programme ID 188.C-0779). The thirteen measurements, shown in Fig. 3, were carried out from 14 June to 21 August 2012, over 69 days. The HARPS mode with a spectral resolution of 110 000 was used. The signal-to-noise ratio of the observations varies from 1 to 5 at 550 nm during exposures of 1800 s, except the first two exposures of 3600 s. The radial velocities (RV) were computed using cross-correlation with a G2 mask (Baranne et al. 1996; Pepe et al. 2002) after spectrum extraction with the HARPS pipeline. The cross-correlation function of CoRoT-27 shows a single peak with FWHM of 8.5 km s-1. From measured B − V = 0.96 and HARPS calibration of the cross-correlation function, the estimated projected rotational velocity is 4.3 ± 0.5 km s-1, in agreement with the spectroscopic analysis. A simultaneous observation of the sky background allowed monitoring its evolution and impact on the stellar cross-correlation function, but all the observations performed on this faint star were unaffected by the sky background.
The HARPS data show a highly dispersed RV sequence, with a standard deviation of 1 km s-1 and peak-to-peak variation of 2.77 km s-1. The mean error on individual measurements is 140 m/s due to the faintness of the star. The bisector spans, displayed in Fig. 4, show a standard deviation of 230 m/s without correlation with the RV. This is a good indication that the detected RV signal is due neither to photospheric activity nor to the blending effect of a background star.
3. Spectral analysis
As is now standard practice in the analysis of CoRoT stars, we used the co-added HARPS spectrum to derive the fundamental photospheric quantities of the planet hosting star CoRoT-27, employing two different methods. The derived parameters include the effective temperature (Teff), surface gravity (log g), metallicity ([M/H]), micro- and macro-turbulence velocities (vmicro and vmacro, respectively), and sky-projected stellar rotation velocity (vsini ).
A first method relies on the spectral analysis package Spectroscopy Made Easy (SME, version 305), which calculates synthetic spectra of stars and fits them to observed high-resolution spectrum (Valenti & Piskunov 1996). It uses a non-linear least squares algorithm to solve the model atmosphere parameters (Teff, log g, [M/H]), as well as the vsini , vmicro and vmacro velocities. A set of LTE plane-parallel stellar model atmosphere grids (Kurucz 1993; Hauschildt et al. 1999; Gustafsson et al. 2008) are included with the SME distribution.
 |
Fig. 4 Bisector span as a function of radial velocity. The bisector spans show no correlation with the RV. |
HARPS-observed RVs, their errors and bisector spans.
We also used a customised IDL software suite to derive the fundamental photospheric parameters. We compared the co-added HARPS spectrum with a grid of theoretical model spectra from Castelli & Kurucz (2004), Coelho et al. (2005), and Gustafsson et al. (2008), using spectral features that are sensitive to the different photospheric parameters.
Briefly, we used the wings of the Hα line to estimate the effective temperature of the star, and the Mg i 5167, 5173, 5184 Å lines, from the Ca i 6162 and 6439 Å lines, and from the Na i D lines to determine its surface gravity. The metal abundance and vmicro were derived applying the method described in Blackwell & Shallis (1979). We adopted the calibration from Bruntt et al. (2010) to estimate vmicro. The projected rotational velocity v sin i was measured by fitting the profiles of several clean and unblended metal lines.
Consistent results were obtained with the two methods. The final adopted values for CoRoT-27 are Teff = 5900 ± 120 K, log g = 4.4 ± 0.1 dex, [M/H] = −0.1 ± 0.1 dex, vsini = 4.0 ± 1.0 km s-1, vmicro = 1.3 ± 0.5 km s-1, and vmacro = 1.9 ± 0.5 km s-1.
4. Planet characterisation
4.1. Overview
We use a Bayesian parameter estimation approach to characterise the planet and its orbit. The CoRoT-observed light curve and the HARPS-observed radial velocities are modelled jointly, and the information from stellar characterisation is used to set a prior on the stellar density. The posterior probability density estimates for the parameters are obtained using Markov chain Monte Carlo (MCMC) sampling, and the final physical quantities are obtained by combining the parameter posteriors with the results form the stellar characterisation. In addition to the basic characterisation of the planet, our analysis includes the search for a secondary eclipse. The search is carried out using a method based on Bayesian model selection between two competing models (with and without an eclipse), and is described in detail in Parviainen et al. (2013). The Bayesian approach facilitates the use of non-normal noise models in the analysis, and we investigate how the assumptions about the noise properties affect the outcomes of the parameter estimation and secondary eclipse search.
The analysis code is written in Python and Fortran and uses the common scientific Python libraries: NumPy, SciPy, Matplotlib (Hunter 2007), and PyFITS. We model the transit shape using a version of the Giménez transit model (Giménez 2006) optimised for efficient computation of large light curves1. The MCMC sampling of the posterior density is carried out using emcee (Foreman-Mackey et al. 2012), a Python implementation of the affine invariant Markov chain sampler (Goodman & Weare 2010). The sampler was chosen for its ability to efficiently sample correlated parameter spaces and for its self-adaptive nature, which reduces the need to tweak the MCMC proposal distribution parameters by hand.
The light curve analysis is carried out for a subset of the data. We include a time span of 15.3 h centred on each individual transit into the analysis. Instead of detrending the light curve using a static polynomial fit to the out-of-transit data (as often done) or using the light curve filtered with running median or Savitzky-Golay filter, we model the background continuum using a separate Legendre series expansion for each transit. The Legendre polynomials are chosen for their orthogonality over the interval [−1,1], and the times around each transit are mapped to this interval. The coefficients of the Legendre series are free parameters in the MCMC analysis, which allows us to propagate the uncertainties in the background estimation to the physical parameter estimates.
This approach is feasible since we have multiple transit observations that allow us to reduce the degeneracy between the transit shape and background variations. The shape of the transit signal is constant over different transits, but the background variations are not. We carry out the analysis separately up to Legendre series expansion orders of 3, 4, and 5 to assess the effects from increasingly complex background modelling on the physical parameter estimates.
We carry out the MCMC runs using 800 parallel Monte Carlo chains (walkers in emcee terms). We run the MCMC iteratively in batches of 400 steps, each batch iteration starting from the end state of the previous batch, until the parallel chains have converged to sample the true posterior distribution, and the median of each parameter is stable thorough an MCMC run. We use a thinning factor of 10 (a value chosen based on the average chain autocorrelation length), finally ending up with 800 × 40 = 32 000 independent posterior samples. Thanks to our optimised transit-model code, the computation for a single MCMC batch iteration takes several tens of minutes on a single eight-core desktop computer, and the chains are found to converge after five to seven batch iterations.
The simulations are computed for three background models and four noise models in total, described below, ending up with a final set of 12 separate posterior estimates for each parameter.
4.2. Bayesian parameter estimation
The unnormalised posterior probability for a model parametrised by a parameter vector
θ, given the light curve DLC
and radial velocities DRV, can be calculated as
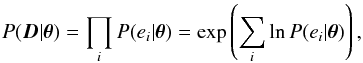 (1)where the first factor
is the prior probability for θ, the second is the likelihood for
the light curve data, given θ, and the last the likelihood for
the RV data, also given θ. The likelihoods are defined as
(1)where the first factor
is the prior probability for θ, the second is the likelihood for
the light curve data, given θ, and the last the likelihood for
the RV data, also given θ. The likelihoods are defined as
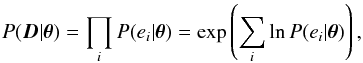 (2)where
e are the
differences between the observed and modelled values (errors). The latter form is
preferred for numerical stability, since the product over a large number of individual
probabilities can easily lead to under- or overflows.
(2)where
e are the
differences between the observed and modelled values (errors). The latter form is
preferred for numerical stability, since the product over a large number of individual
probabilities can easily lead to under- or overflows.
The exact form of P(e | θ) depends on the assumptions made about the underlying noise distribution. We assume normally distributed i.i.d. errors for the RV observations, but consider four noise distributions for the light curve data, described in more detail below.
4.3. Parametrisation and priors
The basic parametrisation of the combined light curve and RV model includes the 14 parameters listed in Table 3. The mixture light curve noise models (discussed in Sect. 4.4) add four parameters, and the model used in the eclipse search adds one parameter. Finally, the coefficients of the Legendre series add from four to six parameters per transit, yielding from 96 to 144 additional parameters, in total, for 24 transits.
Since the affine invariant sampler is effective in sampling correlated parameter spaces, we parametrise the limb darkening using the two coefficients of the quadratic limb darkening law directly, instead of using their linear combinations. The quality of the light curve is not high enough to constrain the two degenerate limb darkening coefficients, and we use the theoretical models by Claret & Bloemen (2011) to construct a normal prior N(μ = 0.27, σ = 0.06) on the quadratic (v) coefficient (see Csizmadia et al. 2013 for a detailed overview of the effects of limb darkening on parameter estimates from transit light curves). The prior constrains the values of v, but is wide enough to account for the uncertainties in the stellar characterisation and theoretical stellar atmosphere modelling.
We let the eccentricity vary freely even when the RV data does not implicitly support significantly non-zero eccentricity. This is done in order to obtain robust estimates of the maximum eccentricity and the physical parameters derived from the analysis. Both the stellar density and semi-major axis estimates have been shown to be sensitive to the orbital eccentricity (Kipping 2010), and fixing the eccentricity to zero would lead to underestimated uncertainties for these parameters.
The flux contamination from a nearby star is also included in the model, and has a normal prior N(μ = 2.42%,σ = 0.95%) based on the estimate from the contamination analysis. Other parameters have uninformative uniform priors during the system characterisation and informative priors based on the posterior densities from the system characterisation during the eclipse search.
Parametrisations used by the transit light curve (LC), radial velocity (RV), and eclipse (EC) models.
4.4. Noise models
We consider four different zero-centred noise models, all without correlated noise.
First, we have the normal distribution
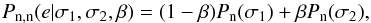 (3)and the more heavily
tailed logistic distribution
(3)and the more heavily
tailed logistic distribution 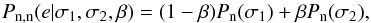 (4)The normal
distribution works as a standard against which we compare the other models. The logistic
distribution was chosen as the second two-parameter model since its shape is close to the
normal distribution, but it includes heavier tails that make the analysis less sensitive
to outliers. Student’s distribution would be the next step from logistic distribution,
allowing for enhanced flexibility in the distribution shape (and introducing one
additional parameter). However, logistic distribution is significantly faster to evaluate,
and Student’s distribution was not included in the analysis.
(4)The normal
distribution works as a standard against which we compare the other models. The logistic
distribution was chosen as the second two-parameter model since its shape is close to the
normal distribution, but it includes heavier tails that make the analysis less sensitive
to outliers. Student’s distribution would be the next step from logistic distribution,
allowing for enhanced flexibility in the distribution shape (and introducing one
additional parameter). However, logistic distribution is significantly faster to evaluate,
and Student’s distribution was not included in the analysis.
Next, we consider two mixture models. The mixture models are linear combinations of two
distributions, where the first distribution models the body of the distribution and the
other one the tails. The mixture normal-normal distribution models the noise with two
normal distributions with a common mean but different σ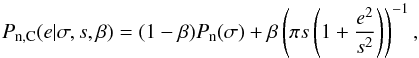 (5)where β is the mixing factor
weighting the two distributions. The mixture normal-Cauchy distribution models the noise
with a mixture of normal and Cauchy distributions as
(5)where β is the mixing factor
weighting the two distributions. The mixture normal-Cauchy distribution models the noise
with a mixture of normal and Cauchy distributions as
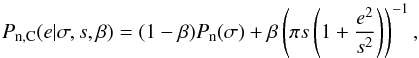 (6)where s is the Cauchy
distribution’s half width at half maximum. The normal distribution is again used to model
the main body of the distribution, while the Cauchy distribution adds long tails.
(6)where s is the Cauchy
distribution’s half width at half maximum. The normal distribution is again used to model
the main body of the distribution, while the Cauchy distribution adds long tails.
 |
Fig. 5 Parameter estimates for different noise and background models. The Legendre series depth tells the maximum order of Legendre polynomials used in the continuum fitting. N corresponds to normal error model, L to logistic, NN to combined normal-normal model, and NC to combined normal-Cauchy model. |
4.5. Parameter estimation results
We show the parameter estimates from the MCMC runs that employ all combinations of noise and background models for transit duration, radius ratio, scaled semi-major axis, and impact parameter in Fig. 5. The runs are labelled as LDE, where D is depth of the Legendre expansion (D ∈ { 3,4,5 }), and E the noise model (E ∈ { N,L,NN,NC }). The estimates show very little sensitivity to the chosen noise or background model, and we adopt the values from the simplest background model and the simplest non-normal noise model; that is, from the L3L MCMC run. The final parameter estimates, corresponding to the posterior median values and the 68% confidence limits, are listed in Table 4, and the posterior distributions and correlations are shown in Fig. 10. We omit the limb darkening coefficients from Fig. 10, since the normal prior on the v coefficient reduces the correlations to inconsequential.
We show the median and the 95% limits of the predictive distribution for the RV model in Fig. 6 and for the light curve model in Fig. 7. The radial velocities in Fig. 6 have the systemic velocity removed, and the light curve data shown in Fig. 7 are normalised using the best-fit background model, phase folded, and binned for visualisation purposes. Finally, we show the individual transits from the L3L run (and the 95% predictive distribution limits) in Fig. 8.
Based on Fig. 5, the noise model only plays a minor role in the parameter estimation. However, this may not be the case in a model comparison problem, such as the search for secondary eclipses described in Sect. 5.1. We show the light curve residual distributions and the estimated noise distributions for the normal and logistic noise models in Fig. 9. The logistic model reproduces the true error distribution with much higher accuracy than the normal model. The two mixture models yield close-to equal fits from the logistic model, but at the price of adding four parameters.
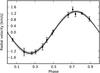 |
Fig. 6 Phase-folded radial velocity points with the median (black line) and the 95% limits (shaded area) of the predictive distribution. |
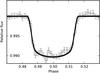 |
Fig. 7 Phase-folded and binned light curve with the median (black line) and the 95% limits (shaded area) of the predictive distribution. |
5. Discussion
5.1. Secondary eclipse search
5.1.1. Overview
We search for secondary eclipses using the method based on Bayesian model selection described in Parviainen et al. (2013). In summary, we integrate the posterior density over the whole parameter space for the models with (M1) and without (M0) eclipse signals. The models use the same parametrisation as the combined transit and RV analysis, but the eclipse model also includes a planet-star flux ratio (defined as the ratio between the fluxes per projected surface area element, so that eclipse depth ΔF = fk2) as a new parameter. The parameter priors are derived from the posterior densities of the L3 normal and logistic MCMC runs, and for the flux ratio we assign a Jeffreys’ prior (Jeffreys 1946) from 10-3 to 5 × 10-2.
Since the planet characterisation MCMC runs have shown that the heavy-tailed noise distributions model the point-to-point scatter better than the normal distribution, we improve upon the approach by Parviainen et al. (2013) by calculating the model posteriors also for the logistic noise distribution. We do not consider the two mixture models since the improvement in the modelling of the distribution was not substantial enough to justify the introduction of four additional parameters.
5.1.2. Results
We find very low Bayes factors, B10, of 0.0069 and 0.013 in favour of the eclipse model for the normal and logistic noise models, respectively. We also carried out Bayes factor mapping as described in Parviainen et al. (2013), and find maximum Bayes factors below two for both noise models. Thus, we can rule out a detectable secondary eclipse in the light curve data.
5.1.3. Sensitivity tests
 |
Fig. 8 Individual transits with the median (black line) and the 95% limits (shaded area) of the predictive distribution. The upper panel shows the cl data and the lower panel the cs data. |
 |
Fig. 9 Residual distributions for the normal and logistic noise models. The shaded area shows the residual distribution and the thick line the fitted noise model. The long cadence data features a long positive tail missing from the short cadence data. |
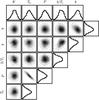 |
Fig. 10 Marginal distributions for the fitting parameter set and the parameter–parameter correlations. The estimates are found in Table 4. |
Planet and star parameters.
We tested the sensitivity of the eclipse search method by injecting eclipse signals of various depths to the data. We find that the cut-off between a detectable and undetectable signal is sharp for both noise models, but that the use of the logistic noise model increases our sensitivity to the signal. Our tests show detection thresholds for flux ratio of 10% and 9% for the normal and logistic models, respectively. This is significantly higher than the flux ratios that can be expected for the system. While the threshold is on a similar scale for both noise models, the models show a difference in the detection sensitivity when going above the threshold. For f = 0.12, for example, we obtain a maximum B10 of 5.4 for the normal and 44.7 for the logistic model, respectively.
The differences in sensitivity between the two models can be explained by Fig. 9. While the difference between the models is minor in the parameter estimation, the maximum likelihood obtained for the logistic model is 102080 higher than the one for the normal model. The normal model assumes larger scatter to the data than the logistic, and yields a lower significance for small signals close to the noise limit.
5.2. Search for additional planets
We carried out a search for additional planets from the photometry and radial velocities after removing the best-fitting transit and RV models of CoRoT-27b from the data. No new significant planet signals were detected.
5.3. Structure and composition of CoRoT-27b
CoRoT-27b is a massive hot Jupiter with a mass of 10.39 MJup, a radius of 1.007 RJup, and an inferred density of 12.60 g cm-3. Only a few other giant planets share the same parameter space: HAT-P-20b (Bakos et al. 2011), CoRoT-20b (Deleuil et al. 2012), WASP-18b (Hellier et al. 2009), XO-3b (Johns-Krull et al. 2008), and the most similar Kepler-75b (KOI-889b, Hébrard et al. 2013) with a density of 11 g cm-3 for a mass of 9.9 MJup and a radius of 1.03 RJup. Among these, HAT-P-20b and CoRoT-20b have been modelled and are believed to contain large amounts of heavy elements in their interior.
Combined stellar (PARSEC, Bressan et al. 2012) and planetary (CEPAM, Guillot & Morel 1995; Guillot 2010) evolution models of the CoRoT-27b system were calculated with SET (Guillot & Havel 2011; Havel et al. 2011). Posterior probabilities of the planet’s bulk composition were computed with an MCMC algorithm using a likelihood based on stellar (resp. planetary) observables [Fe/H], Teff, ρ⋆, log g⋆ (resp. transit depth Δf and radial velocity K), and grids of models for the star and the planet. The results are presented in terms of planetary radii as a function of age in Fig. 11. Solutions within 68.3%, 95.5%, and 99.7% confidence regions are shown with different colours.
Planetary evolution models are calculated in two cases: the “standard” case (which assumes that the thermal evolution of the planet is only a consequence of the loss of its primordial entropy through the irradiated planetary atmosphere, Fig. 11), and one in which a fraction of the incoming stellar flux is converted into kinetic energy and then dissipated at the centre of the planet (see Guillot & Showman 2002; Guillot et al. 2006, for a discussion). In addition, for each of these cases, two classes of models are considered: one in which the planet is made of a central rocky core and a solar-composition envelope; and at the other extreme (not shown), the second class considers that the heavy elements are only present in the envelope (using an equivalent helium mass fraction Yequiv for the SCVH EOS). We clearly do not know which one of these assumptions is closer to reality, but they represent the two extremes for the planetary radii as a function of the heavy element content (see Guillot et al. 2006; Baraffe et al. 2008; Ikoma et al. 2006).
Both the “standard” and “dissipated-energy” models provide solutions for the planetary
radius that match the available constraints. In fact, for a given age, the difference in
planetary radius between the two models is small compared to the uncertainty reported in
Table 4 (about half, or 0.02 RJup, for the 1σ confidence region shown
in Fig. 11). We therefore consider global solutions
that mix both cases2. For the first class of models,
we infer a core mass of 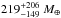 , which
translates into a heavy element mass fraction of
, which
translates into a heavy element mass fraction of 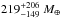 .
For the second class of models, we infer a heavy element mass fraction of
.
For the second class of models, we infer a heavy element mass fraction of
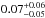 ,
which translates into a heavy elements mass of
,
which translates into a heavy elements mass of 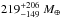 . As expected
(Baraffe et al. 2008), mixing the heavy elements
in the envelope significantly reduces the amount needed to match the observed radius:
about a 40% reduction, or 147 M⊕. Interestingly, models with no
heavy elements at all cannot be excluded, and they match the 1σ confidence region in Fig.
11 well. Also, putting all heavy elements in a
massive rocky core allows for a much higher 1σ limit of about 2 MJup (against
1.35 MJup for the Yequiv class of
models). While qualitatively in line with what has been found for irradiated transiting
giant planets (Miller & Fortney 2011),
CoRoT-27b may require a surprisingly high amount of heavy elements. In fact, the core
class of models has demanded using the Zapolsky &
Salpeter (1969) zero-temperature EOS to properly span the possible core masses
matching the constraints. This EOS should be accurate enough within 1–20% range for rocky
materials (e.g. Fortney et al. 2007; Mordasini et al. 2012). Formation of such a planet with
a very high amount of heavy elements remain uncertain (Mordasini et al. 2012; Mordasini 2013)
and would favour solutions with higher planetary radii in the case of CoRoT-27b.
. As expected
(Baraffe et al. 2008), mixing the heavy elements
in the envelope significantly reduces the amount needed to match the observed radius:
about a 40% reduction, or 147 M⊕. Interestingly, models with no
heavy elements at all cannot be excluded, and they match the 1σ confidence region in Fig.
11 well. Also, putting all heavy elements in a
massive rocky core allows for a much higher 1σ limit of about 2 MJup (against
1.35 MJup for the Yequiv class of
models). While qualitatively in line with what has been found for irradiated transiting
giant planets (Miller & Fortney 2011),
CoRoT-27b may require a surprisingly high amount of heavy elements. In fact, the core
class of models has demanded using the Zapolsky &
Salpeter (1969) zero-temperature EOS to properly span the possible core masses
matching the constraints. This EOS should be accurate enough within 1–20% range for rocky
materials (e.g. Fortney et al. 2007; Mordasini et al. 2012). Formation of such a planet with
a very high amount of heavy elements remain uncertain (Mordasini et al. 2012; Mordasini 2013)
and would favour solutions with higher planetary radii in the case of CoRoT-27b.
 |
Fig. 11 Transit radius of CoRoT-27b as a function of age, as computed by SET. The 68.3%, 95.5%, and 99.7% confidence regions are denoted by black, dark grey, and light grey areas, respectively. The curves represent the thermal evolution of a 10.39 MJup planet with an equilibrium temperature of 1500 K. Text labels indicate the amount of heavy elements in the planet (its core mass, in Earth masses). Dashed lines represent planetary evolution models for which 0.25% of the incoming stellar flux is dissipated into the core of the planet, whereas plain lines do not account for this dissipation (standard models). |
5.4. Blending
While the photometric follow-up excludes contaminants located >1′′ from the main target, we cannot rule out the possibility of a closer contaminant, which would have the effect of diluting the transit and thus lead to an under-estimated planet radius (as with Kepler-14b, Buchhave et al. 2011). The true planet-to-star area ratio A depends on the contamination factor c (the fraction of the flux in the aperture contributed by other stars than the one being occulted) and the observed (blended) planet-to-star area ratio Ab as: A = Ab(1 − c)-1. Consequently, the planet-to-star radius ratio k (hence the planet radius) scales as Rp ∝ k ∝ A0.5 ∝ (1 − c)-0.5, and the planet density as ρ ∝ A-1.5 ∝ (1 − c)1.5. Figure 12 illustrates the dependence of Rp and ρ on contamination factors ranging from 0 to 0.99.
A coarse estimate for the maximum contamination can be obtained based on the properties of the current massive planet population. The radii of the known transiting exoplanets with MP > 5 MJup vary from 0.86 to 1.28 RJup. Thus, assuming that the true CoRoT-27b radius lies roughly within this range, we would obtain a maximum contamination factor of ~0.4, which would correspond to a minimum density of ~6 g cm-3.
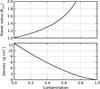 |
Fig. 12 Effects of possible blending on the planet radius and density. |
5.5. Age of the system
Theoretical modelling yields two age estimates for the star: a young star of
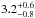 Myr, or an older star of 4.2 ± 2.7 Gyr. The young solution can be ruled out based on planetary
contraction models, while the older solution can explain the measured mass density and
radius for a range of planetary core masses.
Myr, or an older star of 4.2 ± 2.7 Gyr. The young solution can be ruled out based on planetary
contraction models, while the older solution can explain the measured mass density and
radius for a range of planetary core masses.
5.6. Stellar rotation period
An attempt was made to measure the stellar rotation period using the method by McQuillan et al. (2013) based on the autocorrelation function (ACF). The analysis was carried out using a jump-corrected version of the light curve, but no periods could be detected reliably. The result is not surprising given the amount of systematics in the light curve (see Fig. 2).
5.7. Tidal evolution
The system of CoRoT-27 – where a massive planet is moving close to the star and for which high-quality parameters can be determined from both the transits and the spectroscopic observations – is particularly well suited to the study of tidal evolution. The starting point in any tidal evolution study is the choice of the dissipation parameters. We used the results of the analysis done by (Hansen 2010) on the distribution of extrasolar planetary systems with a hot Jupiter, in terms of period, eccentricity, and mass. His results correspond to quality factors in the ranges 2 × 106 < Qp < 2 × 107 and 4 × 106 < Qs < 108 for the planet and the star, respectively.
One immediate consequence is that the planet rotation is almost synchronous; depending on the value adopted for Qp, the synchronisation is reached in less than 100 Myr. This upper limit corresponds to a planet in the less dissipative boundary of the interval given by Hansen and to the case in which the planet is assumed to be initially spinning very fast. In the more favourable cases the synchronisation is reached in 10 Myr.
The other consequence is the almost unchanged eccentricity and semimajor axis of CoRoT-27b during the system’s lifetime. Even if parameters lead to a dissipation greater than allowed by the values determined by Hansen, the variation in the eccentricity during the lifetime of the system is less than half its current value. Tidal dissipation is not strong enough to force the circularisation of the orbit (the currently low eccentricity may be primordial). For the semi-major axis, the variation is almost negligible: only a few thousandths of AU in the considered time span.
However, difficulties appear when the stellar rotation is considered. Presently, the star has a slow rotation, and the transfer of the angular momentum of the orbit to the star via the tides raised on the star should make it faster. If so, the star should be even slower in the past. Simulations with the adopted dissipation factors lead to period values that are abnormally high, on time scales shorter than the system’s lifetime. This result contradicts with the fast rotations observed in young star clusters, where the periods are always shorter than a few days (see Gallet & Bouvier 2013). The only way to explain the present star period is to admit that the star rotation is not being accelerated, but is being braked.
 |
Fig. 13 Rotation evolution of the star CoRoT-27 obtained with composite models including magnetic braking, with reduction factors f = 0.15 (blue), 0.25 (black) and 0.35 (brown), and the acceleration of the star rotation due to the tidal interaction with the super Jupiter CoRoT 27b, with dissipation values Qs = 7 × 106,10 × 106, and 13.5 × 106. |
We have studied this possibility with the simple model given by Bouvier et al. (1997) for the angular momentum evolution of low-mass stars due to magnetic braking. However, the calibration constant given by Bouvier et al. is too large and leads to having P = 0 in times smaller than the system lifetime. It has been conjectured that the given calibration constant needs a correction for stars more massive than the Sun, and Pätzold et al. (2012) have corrected it using a factor f = 0.1 in the study of the tidal evolution of CoRoT-21b around a F-star. A composite model with an undetermined factor f < 1 and tidal dissipation values consistent with Hansen determinations allows us to find solutions where the initial rotation period is nearly as long as the periods of stars in young clusters and evolves to the presently observed rotation period in ca. 4 Gyr. They are shown in Fig. 13. The solutions in this figure correspond to f = 0.15, 0.25 and 0.35. We may see that in the worst case (f = 0.35), typical dissipation values are not able to avoid a premature reaching of P = 0 by the solutions. In each case, three solutions are shown that correspond to dissipation values Qs = 7 × 106,10 × 106 and 13.5 × 106 respectively (from top to bottom on the left side of the figure). These values of Qs refer to the present time. In the two tidal theories used in the modelling (Mignard 1979; Ferraz-Mello 2013), the tidal response is fixed by physical properties of the body, and the values of Qs are not constant but vary with the frequency of the main tide components, that is, with the orbital and rotational periods.
 |
Fig. 14 CoRoT-27b mass, period, and density compared with the population of confirmed transiting exoplanets. Planets with masses higher than 20 MJup and densities higher than 15 g cm-3 have been excluded. |
5.8. CoRoT-27b in context
CoRoT-27b’s mass places it inside the overlapping mass regime between low-mass brown dwarfs and massive planets (Leconte et al. 2009; Baraffe et al. 2010). The exact nature of objects in this mass range is not straightforward to establish, and, indeed, depends on the definition of a planet (see Schneider et al. 2011, for an overview). Definition by mass – whether the object is massive enough to have sustained deuterium fusion at some point of its history – has ambiguities, since the deuterium-burning mass limit can vary from 11 to 16 MJup depending on the object’s metal and helium content (Spiegel et al. 2011). Also, systems exist with multiple companions likely to be on both sides of the deuterium burning limit (Marcy et al. 2001). The definition by formation history – whether the object formed by accretion or gravitational collapse – is not without problems either, since we have no reliable means of probing the formation history of an individual object. However, the planet and brown dwarf populations may show some systematic differences on measurable properties, but if such differences exist, more objects are required for any groupings to become discernible.
Considering deuterium burning, CoRoT-27b’s 2σ upper mass limit exceeds the minimum deuterium burning mass limit of 11 MJup (Spiegel et al. 2011), but is well below the conventional 13 MJup limit. Thus, it is unlikely, but not completely excluded, that CoRoT-27b would have ever sustained deuterium fusion.
Given the dearth of known massive short-period planets, any statistical analyses are fated to be dominated by small number statistics. Keeping this in mind, massive short-period planets show a tentative preference to be found orbiting relatively rapidly rotating stars on eccentric orbits (Bakos et al. 2011; Southworth et al. 2009, also Fig. 16), without significant correlation between planetary mass and host-star metallicity (Bakos et al. 2011). They are also more common around binary systems than single stars (Udry et al. 2002). We show the CoRoT-27b mass, density, and period compared with the population of transiting exoplanets in Fig. 14; planetary masses and eccentricities for massive close-in planets in Fig. 15; and the average vsini , eccentricity, and metallicity as a function of the planetary mass in Fig. 163. CoRoT-27b can be seen to stand out slightly from the population averages in all cases. While the deviations from the vsiniand metallicity trends are not that significant (inside 2σ in both cases), the lack of detectable orbital eccentricity is more significant, but not exceptional. All in all, including CoRoT-27b in the population averages of Fig. 16 weakens the known trends.
What comes to finding systematic groupings of properties hinting at possible differences in formation and evolution history of objects in the transition region, the currently available set of objects is still too small for any meaningful inferences. Figure 15 shows two tentative clusters in mass-eccentricity space, with a group of relatively low-eccentricity planets with masses below 11MJup, and another loose group of higher-eccentricity planets. However, no other common factors were identified between the members of two clusters, and many more massive objects are required to confirm (or discard) the significance of these groups.
6. Conclusions
 |
Fig. 15 CoRoT-27b mass and eccentricity compared with the population of confirmed transiting exoplanets with periods <10 d and masses 5 < Mp < 20MJup. |
 |
Fig. 16 Mean vsini , orbital eccentricity and host-star metallicity as a function of planet mass for transiting planets with period <10 d. The error bars correspond to the standard error of the mean, the grey dots show the minima and maxima inside a mass bin, the numbers mark the number of planets in each bin, and the grey shaded area with a black contour line shows the parameter estimates with their uncertainty (or the 99% confidence upper limit at 0.064 for eccentricity). The dotted horizontal line with a grey error bar shows the average for planets with masses <5 MJup. |
We have reported a new massive short-period transiting exoplanet CoRoT-27b, described the properties of the star and the planet, and detailed the analysis methods used to derive them.
CoRoT-27b was found by the CoRoT-satellite and confirmed by using radial velocities. The stellar properties were determined based on spectral characterisation and further refined with theoretical modelling and transit fitting. We carried out searches for secondary eclipses and additional planets, but found no significant evidence of either from the data. We described our approach to modelling the planet’s structure and composition in Sect. 5.3 and concluded that even given its high density, the planet properties can be explained by models with a wide range of heavy element mass fractions. However, the inferred high planetary density may also be a product of underestimated planetary radius due to an unresolved contaminating third light source. Since close-in contaminating sources could not be entirely ruled out, we presented the effects from possible contamination on the planetary radius and density in Sect. 5.4. We studied the tidal evolution of the system in Sect. 5.7, showing that the planet rotation is likely almost synchronous and that the tidal dissipation is not strong enough to strongly affect the orbital eccentricity during the lifetime of the system. Finally, we investigated how CoRoT-27b fits the bigger picture of massive short-period objects within the overlapping mass regime between planets and brown dwarfs. Its properties stand out slightly from the average properties of massive planets, and adding it to the population weakens the tentative trends that have been proposed to separate the massive planets from less massive ones.
All in all, CoRoT-27b is an important addition to a scarcely populated class of massive close-in planets. It is the second object of this type to be found around a G-dwarf, while the rest are predominantly found orbiting hotter F-type stars. More massive short-period planets (and low-mass short-period brown dwarfs) are still required for inferences of any statistical significance, but each new object of this type will help us paint a picture of the differences and similarities between the two populations.
The code is freely available from https://github.com/hpparvi/PyTransit
From http://www.exoplanets.org, accessed 10.8.2013.
Acknowledgments
First and foremost we would like to thank the anonymous referee for her/his prompt review. H.P. has received support from RoPACS during this research, a Marie Curie Initial Training Network funded by the European Commission’s Seventh Framework Programme. H.P. has received funding from the Väisälä Foundation through the Finnish Academy of Science and Letters during this research. The team at the IAC acknowledges funding by grant AYA2012-39346-C02 of the Spanish Ministry of Economy and Competitiveness (MINECO). This research was supported by an appointment to the NASA Postdoctoral Program at the Ames Research Center, administered by Oak Ridge Associated Universities through a contract with NASA. A.S. acknowledges support from the European Research Council/European Community under the FP7 through Starting Grant agreement number 239953. The research leading to these results has received funding from the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement no. 267251.
References
- Aigrain, S., Pont, F., Fressin, F., et al. 2009, A&A, 506, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bakos, G. A., Hartman, J., Torres, G., et al. 2011, ApJ, 742, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., & Barman, T. 2008, A&A, 482, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., & Barman, T. S. 2010, Reports Prog. Phys., 73, 016901 [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 373 [Google Scholar]
- Barker, A. J., & Ogilvie, G. I. 2009, MNRAS, 395, 2268 [NASA ADS] [CrossRef] [Google Scholar]
- Blackwell, D., & Shallis, M. 1979, MNRAS, 186, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Bouchy, F., Bonomo, A. S., Santerne, A., et al. 2011, A&A, 533, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvier, J., Forestini, M., & Allain, S. 1997, A&A, 326, 1023 [NASA ADS] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Buchhave, L. A., Latham, D. W., Carter, J. A., et al. 2011, ApJSS, 197, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004 [arXiv:astro-ph/0405087] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coelho, P., Barbuy, B., Meléndez, J., Schiavon, R. P., & Castilho, B. V. 2005, A&A, 443, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csizmadia, S., Pasternacki, T., Dreyer, C., et al. 2013, A&A, 549, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deeg, H. J., Gillon, M., Shporer, A., et al. 2009, A&A, 506, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deleuil, M., Meunier, J. C., Moutou, C., et al. 2009, AJ, 138, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Deleuil, M., Bonomo, A. S., Ferraz-Mello, S., et al. 2012, A&A, 538, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferraz-Mello, S. 2013, Celest. Mech. Dyn. Astron., 116, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2012 [arXiv:1202.3665] [Google Scholar]
- Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Gallet, F., & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giménez, A. 2006, A&A, 450, 1231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
- Guillot, T. 2010, A&A, 520, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T., & Havel, M. 2011, A&A, 527, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T., & Morel, P. 1995, A&AS, 109, 109 [NASA ADS] [Google Scholar]
- Guillot, T., & Showman, A. P. 2002, 165, 156 [Google Scholar]
- Guillot, T., Santos, N. C., Pont, F., et al. 2006, A&A, 453, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, B. M. S. 2010, ApJ, 723, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Havel, M., Guillot, T., Valencia, D., & Crida, A. 2011, A&A, 531, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hébrard, G., Almenara, J.-M., Santerne, A., et al. 2013, A&A, 554, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hellier, C., Anderson, D. R., Cameron, A. C., et al. 2009, Nature, 460, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
- Ikoma, M., Guillot, T., Genda, H., Tanigawa, T., & Ida, S. 2006, ApJ, 650, 1150 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jeffreys, H. 1946, Proc. R. Soc. A Math. Phys. Eng. Sci., 186, 453 [Google Scholar]
- Johns-Krull, C. M., McCullough, P. R., Burke, C. J., et al. 2008, ApJ, 677, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2010, MNRAS, 407, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. 1993, ATLAS9 Stellar Atmos. Programs 2 km s grid. Kurucz CD-ROM No. 13 (Cambridge MA: Smithson. Astrophys. Obs) [Google Scholar]
- Leconte, J., Baraffe, I., Chabrier, G., Barman, T., & Levrard, B. 2009, A&A, 506, 385 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marcy, G. W., Butler, R. P., Vogt, S. S., et al. 2001, ApJ, 555, 418 [NASA ADS] [CrossRef] [Google Scholar]
- McQuillan, A. Aigrain, S., & Mazeh, T. 2013, MNRAS, 432, 1203 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mignard, F. 1979, Moon Planets, 20, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, N., & Fortney, J. J. 2011, ApJ, 736, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Mordasini, C. 2013, A&A, 558, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., Georgy, C., et al. 2012, A&A, 547, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parviainen, H., Deeg, H. J., & Belmonte, J. A. 2013, A&A, 550, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasternacki, T., Bordé, P., & Csizmadia, S. 2012, in Proc. 2nd CoRoT Symp., 117 [Google Scholar]
- Pätzold, M., Endl, M., Csizmadia, S., et al. 2012, A&A, 545, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Mayor, M., & Rupprecht, G. 2002, The Messenger, 9 [Google Scholar]
- Pinheiro da Silva, L., Rolland, G., Lapeyrere, V., & Auvergne, M. 2008, MNRAS, 384, 1337 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., Zucker, S., & Queloz, D. 2006, MNRAS, 373, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, J. Dedieu, C. Le Sidaner, P., Savalle, R., & Zolotukhin, I. 2011, A&A, 532, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Southworth, J., Hinse, T. C., Dominik, M., et al. 2009, ApJ, 707, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Spiegel, D. S., Burrows, A., & Milsom, J. A. 2011, ApJ, 727, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Surace, C., Alonso, R., Barge, P., et al. 2008, in Adv. Softw. Control Astron. II, eds. A. Bridger, & N. M. Radziwill, Proc. SPIE 7019, 70193B [Google Scholar]
- Udry, S., Mayor, M., Naef, D., et al. 2002, A&A, 390, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zapolsky, H. S., & Salpeter, E. E. 1969, ApJ, 158, 809 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Parametrisations used by the transit light curve (LC), radial velocity (RV), and eclipse (EC) models.
All Figures
 |
Fig. 1 POSS image showing the surroundings of CoRoT-27 and the photometric aperture mask (solid line). One contaminating star (marked as 1) falls partially within the aperture mask, with an estimated contamination factor of 2.4% ± 0.95%. |
| In the text | |
 |
Fig. 2 CoRoT-observed white light curve showing the long and short time cadence photometric data with extreme outliers (as marked by the CoRoT photometric pipeline) removed. The individual transits are visible by eye in the cl data. |
| In the text | |
 |
Fig. 3 HARPS-observed radial velocities shown with a best-fit circular orbit (top) and residuals (bottom). |
| In the text | |
 |
Fig. 4 Bisector span as a function of radial velocity. The bisector spans show no correlation with the RV. |
| In the text | |
 |
Fig. 5 Parameter estimates for different noise and background models. The Legendre series depth tells the maximum order of Legendre polynomials used in the continuum fitting. N corresponds to normal error model, L to logistic, NN to combined normal-normal model, and NC to combined normal-Cauchy model. |
| In the text | |
 |
Fig. 6 Phase-folded radial velocity points with the median (black line) and the 95% limits (shaded area) of the predictive distribution. |
| In the text | |
 |
Fig. 7 Phase-folded and binned light curve with the median (black line) and the 95% limits (shaded area) of the predictive distribution. |
| In the text | |
 |
Fig. 8 Individual transits with the median (black line) and the 95% limits (shaded area) of the predictive distribution. The upper panel shows the cl data and the lower panel the cs data. |
| In the text | |
 |
Fig. 9 Residual distributions for the normal and logistic noise models. The shaded area shows the residual distribution and the thick line the fitted noise model. The long cadence data features a long positive tail missing from the short cadence data. |
| In the text | |
 |
Fig. 10 Marginal distributions for the fitting parameter set and the parameter–parameter correlations. The estimates are found in Table 4. |
| In the text | |
 |
Fig. 11 Transit radius of CoRoT-27b as a function of age, as computed by SET. The 68.3%, 95.5%, and 99.7% confidence regions are denoted by black, dark grey, and light grey areas, respectively. The curves represent the thermal evolution of a 10.39 MJup planet with an equilibrium temperature of 1500 K. Text labels indicate the amount of heavy elements in the planet (its core mass, in Earth masses). Dashed lines represent planetary evolution models for which 0.25% of the incoming stellar flux is dissipated into the core of the planet, whereas plain lines do not account for this dissipation (standard models). |
| In the text | |
 |
Fig. 12 Effects of possible blending on the planet radius and density. |
| In the text | |
 |
Fig. 13 Rotation evolution of the star CoRoT-27 obtained with composite models including magnetic braking, with reduction factors f = 0.15 (blue), 0.25 (black) and 0.35 (brown), and the acceleration of the star rotation due to the tidal interaction with the super Jupiter CoRoT 27b, with dissipation values Qs = 7 × 106,10 × 106, and 13.5 × 106. |
| In the text | |
 |
Fig. 14 CoRoT-27b mass, period, and density compared with the population of confirmed transiting exoplanets. Planets with masses higher than 20 MJup and densities higher than 15 g cm-3 have been excluded. |
| In the text | |
 |
Fig. 15 CoRoT-27b mass and eccentricity compared with the population of confirmed transiting exoplanets with periods <10 d and masses 5 < Mp < 20MJup. |
| In the text | |
 |
Fig. 16 Mean vsini , orbital eccentricity and host-star metallicity as a function of planet mass for transiting planets with period <10 d. The error bars correspond to the standard error of the mean, the grey dots show the minima and maxima inside a mass bin, the numbers mark the number of planets in each bin, and the grey shaded area with a black contour line shows the parameter estimates with their uncertainty (or the 99% confidence upper limit at 0.064 for eccentricity). The dotted horizontal line with a grey error bar shows the average for planets with masses <5 MJup. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


