| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201322817 | |
| Published online | 03 February 2014 | |
Elliptical instability of compressible flow in ellipsoids
Institute of Geophysics, University of Göttingen,
Friedrich-Hund-Platz 1,
37077
Göttingen,
Germany
e-mail: niels.clausen@geo.physik.uni-goettingen.de; andreas.tilgner@geo.physik.uni-goettingen.de
Received:
8
October
2013
Accepted:
10
December
2013
Context. Elliptical instability is due to a parametric resonance of two inertial modes in a fluid velocity field with elliptical streamlines. This flow is a simple model of the motion in a tidally deformed, rotating body. Elliptical instability typically leads to three-dimensional turbulence. The associated turbulent dissipation together with the dissipation of the large scale mode may be important for the synchronization process in stellar and planetary binary systems.
Aims. In order to determine the influence of the compressibility on the stability limits of tidal flows in stars or planets, we calculate the growth rates of perturbations in flows with elliptical streamlines within ellipsoidal boundaries of small ellipticity. In addition, the influence of the orbiting frequency of the tidal perturber ΩP and the viscosity of the fluid are taken into account.
Methods. We studied the linear stability of the flow to determine the growth rates. We solved the Euler equation and the continuity equation. The viscosity was introduced heuristically in our calculations. We assumed a power law for the radial dependence of the background density. Together with the use of the anelastic approximation, this enabled us to use semi-analytical methods to solve the equations.
Results. It is found that the growth rate of a certain mode combination depends on the compressibility. However, the influence of the compressibility is negligible for the growth rate maximized over all possible modes if viscous bulk damping effects can be neglected. The growth rate maximized over all possible modes determines the stability of the flow. The stability limit for the compressible fluid confined to an ellipsoid is the same as for incompressible fluid in an unbounded domain. Depending on the ratio ΩP/ΩF, with ΩF the spin rate of the central object in the frame of the rotating tidal perturber, certain pairs of modes resonate with each other. The size of the bulk damping term depends on the modes that resonate with each other. Therefore the growth rate of the viscous flow depends on the compressibility. Estimates for the stability limit in viscous fluids are given.
Key words: hydrodynamics / instabilities / waves
© ESO, 2014
1. Introduction
The study of tidal friction has a long history in geo- and astrophysics (e.g., Darwin 1879). The basic picture of a tidally deformed fluid body is that of an ellipsoid with the long axis pointing towards the tidal companion, and in which the fluid rotates with respect to the major axes of the ellipsoid, so that each fluid particle follows an elliptical streamline. It was discovered in the mid 1970s that flows of constant vorticity with elliptical streamlines are prone to a hydrodynamic instability, the so-called elliptical instability (for a review, see Kerswell 2002). One expects to find vastly different dissipation rates in laminar and in unstable turbulent flows. A determination of the stability limit of the basic tidal flow is thus an indispensable prerequisite to any computation of tidal friction. In this paper, we compute the stability limit within a simple model of tidal flow taking into account the compressibility of a stellar or planetary envelope.
Fluids in solid body rotation (i.e., flows with circular streamlines) support a type of waves known as inertial waves in which the Coriolis force acts as a restoring force. In elliptical instability, the finite ellipticity couples inertial modes in pairs and can lead to instability if certain resonance conditions are met. The same phenomenon is often called a triad resonance, the triad being formed by the two inertial waves and the basic, elliptically deformed flow which is itself counted as third wave.
In this paper, we calculate the growth rate of the elliptical instability in a slightly deformed sphere. Incompressible flows have already been investigated in this geometry (Lacaze et al. 2004; Le Bars et al. 2010). Elliptical instability can be studied in its simplest form in an unbounded domain (Bayly 1986; Landman & Saffman 1987; Waleffe 1990; Miyazaki & Fukumoto 1992; Miyazaki 1993; Miyazaki et al. 1995). Another convenient geometry is an elliptically deformed cylinder (Gledzer et al. 1975; Malkus 1989; Eloy et al. 2003), and other studies exist for deformed spheroids (Gledzer & Ponomarev 1977; Kerswell 1994; Cébron et al. 2010a) and spherical shells (Aldridge et al. 1997; Seyed-Mahmoud et al. 2000; Cébron et al. 2012b).
Several additional ingredients have been added to the problem, such as stratification (Miyazaki & Fukumoto 1992; Miyazaki 1993; Guimbard et al. 2010), magnetic fields (Kerswell 1994; Lacaze et al. 2006; Herreman et al. 2009; Cébron et al. 2012a), rotation of the elliptical perturbation (Craik 1989; Gledzer & Ponomarev 1992; Miyazaki 1993; Miyazaki et al. 1995; Seyed-Mahmoud et al. 2000; Le Bars et al. 2010), and viscosity (Landman & Saffman 1987; Kerswell 1994; Lacaze et al. 2004; Le Bars et al. 2010). The importance of the elliptical instability for tidal dissipation is examined in a recent paper by Barker & Lithwick (2013). They studied the non-linear evolution of the elliptical instability. They performed three-dimensional hydrodynamical simulations of a box with periodic boundary conditions with a base flow such that this box can be considered as a small patch of a tidally deformed fluid in a planet or a star. They found that for the astrophysically relevant values of the ellipticity the wave driving mechanism is not sustained permanently because of the presence of strong columnar vortices whose presence effectively suppresses the driving mechanism. This leads to less dissipation compared to the case with a sustained wave driving mechanism, but it is certainly higher compared to case with a stable flow. A strong stratification can prevent the process of re-laminarization as found in an experiment with a stratified fluid in a rotating cylinder by Guimbard et al. (2010). The same holds for the instability in the presence of a weak magnetic field (see Barker & Lithwick 2014, a companion paper to Barker & Lithwick 2013). Barker & Lithwick (2014) found that this field prevents the vortices from forming. They calculated the dissipation and conclude that the inferred tidal dissipation is potentially important at short orbital periods. In this companion paper they also neglect the effects of a realistic geometry and the additional presence of turbulent convection, both of which possibly enhance the dissipation such that the instability becomes important more generally.
The influence of a temperature-gradient on the elliptical instability in a triaxial ellipsoid was examined by Cébron et al. (2010b) with numerical methods. They found that the growth rate of the elliptical instability is significantly enhanced by a thermal stratification and that in a convective flow the elliptical instability can still grow, but with a reduced growth rate. They were not able to reach the regime of very large Reynolds numbers, where the results of Fabijonas & Holm (2003) predict an increased tidal destabilization. For stars the case of a bi-layer flow with a stable stratified and a convective region is interesting. In the paper by Cébron et al. (2010b) it was shown that even in such a flow the instability can grow over the whole fluid.
In this paper, we will include the rotation of the perturbation, viscous dissipation, and most importantly, compressibility. The last has been neglected in nearly all other publications on the subject with the exception of the work by Cébron et al. (2013) who numerically simulated one particular set of parameters. In contrast, we use a semi-analytical method to obtain a broad overview. The most important issue this study will address is how the compressibility of the flow influences growth rates of the elliptical instability. Surprisingly, we will find that the structure of the most unstable modes in ideal fluids depend on the compressibility, but the maximum growth rate is independent of compressibility. Section 2 collects all the formulas describing the model and Sect. 3 explains their numerical implementation. The results are presented in Sect. 4.
2. Mathematical formulation of the model
We consider the equatorial tide raised on a central body by a tidal perturber or perturbing
body. We choose a frame of reference in which the perturbing body is at rest and use a
Cartesian coordinate system x,y,z with its origin at the center of the
central body, its z-axis directed along the rotation axis of the reference
system, and the x-axis is pointing towards the perturbing body. This
reference frame rotates at rate
ΩP = ΩPẑ (hats denote
unit vectors) relative to inertial space. In this frame, the central body rotates about the
z-axis with angular velocity 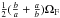 within an ellipsoid
with semi-major axes a,b,c and the surface
within an ellipsoid
with semi-major axes a,b,c and the surface 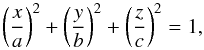 (1)so that the motion of
the central body within the chosen frame of reference is given by the velocity field
u0:
(1)so that the motion of
the central body within the chosen frame of reference is given by the velocity field
u0:
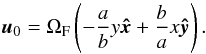 (2)In order to
determine the stability of this flow, we start from the full Euler equation
(2)In order to
determine the stability of this flow, we start from the full Euler equation
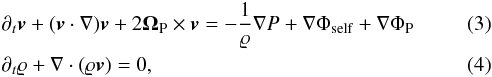 where
v stands for the velocity, ϱ the density,
P the pressure, and Φself for the potential terms created by
the central body itself (gravitational and centrifugal), whereas ΦP is the
perturbing tidal potential. We will assume u0 to be
a stationary solution of the above equations for suitable density profiles and potentials
ρ0 and Φ0:
where
v stands for the velocity, ϱ the density,
P the pressure, and Φself for the potential terms created by
the central body itself (gravitational and centrifugal), whereas ΦP is the
perturbing tidal potential. We will assume u0 to be
a stationary solution of the above equations for suitable density profiles and potentials
ρ0 and Φ0: 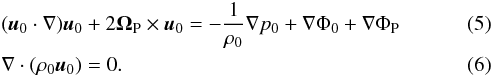
In order to end with a tractable problem, we will have to choose a density profile such
that the eigenmode calculation below leads to a separable equation. This is achieved by
setting 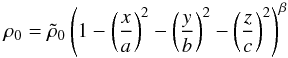 (7)for arbitrary
prefactors
(7)for arbitrary
prefactors  and exponents β (Wu 2005a).
and exponents β (Wu 2005a).
The question arises which beta one should use for the calculations. We must first determine
which polytropic index n in the polytropic relation 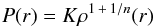 (8)is appropriate for the
central body. We choose n = 3, n = 3/2,
and n = 0 for our calculations; n = 3 is suitable for
stars which are well modeled by a relativistic completely degenerate electron gas, like
relativistic white dwarfs. The same polytropic index also describes main sequence stars with
M ≳ M⊙, (Kippenhahn & Weigert 1990). n = 3/2 is
appropriate for objects which are well modeled by a non relativistic completely degenerate
electron gas, like non-relativistic white dwarfs and brown dwarfs. And
n = 3/2 is also relevant for main sequence stars with
a mass below M ~ 0.4 M⊙, these are fully
convective stars (Kippenhahn & Weigert 1990;
Chabrier et al. 2009). For planets, the range of
n is 0 ≤ n ≲ 1.5, depending on how massive they are
(Horedt 2004). For Jupiter mass objects,
n = 1 is a good value (Chabrier et al.
2009). ρ(r) in the polytropic case can be
obtained by solving the Lane-Emden equation. This equation can be derived through the usage
of (8), the equation for hydrostatic
equilibrium and the Poisson equation (Kippenhahn &
Weigert 1990). The values for ρ(r) in the
polytropic case are taken from Horedt (1986). We
determine the appropriate β by simply fitting the power law (7) to the ρ(r)
for the polytropic profiles.
(8)is appropriate for the
central body. We choose n = 3, n = 3/2,
and n = 0 for our calculations; n = 3 is suitable for
stars which are well modeled by a relativistic completely degenerate electron gas, like
relativistic white dwarfs. The same polytropic index also describes main sequence stars with
M ≳ M⊙, (Kippenhahn & Weigert 1990). n = 3/2 is
appropriate for objects which are well modeled by a non relativistic completely degenerate
electron gas, like non-relativistic white dwarfs and brown dwarfs. And
n = 3/2 is also relevant for main sequence stars with
a mass below M ~ 0.4 M⊙, these are fully
convective stars (Kippenhahn & Weigert 1990;
Chabrier et al. 2009). For planets, the range of
n is 0 ≤ n ≲ 1.5, depending on how massive they are
(Horedt 2004). For Jupiter mass objects,
n = 1 is a good value (Chabrier et al.
2009). ρ(r) in the polytropic case can be
obtained by solving the Lane-Emden equation. This equation can be derived through the usage
of (8), the equation for hydrostatic
equilibrium and the Poisson equation (Kippenhahn &
Weigert 1990). The values for ρ(r) in the
polytropic case are taken from Horedt (1986). We
determine the appropriate β by simply fitting the power law (7) to the ρ(r)
for the polytropic profiles.
It is easily verified that
∇·(ρ0u0) = 0 and
∇ × { (u0·∇)u0 + 2ΩP × u0 } = 0.
The curl of the gradient terms in Eq. (5) is
trivially zero, and 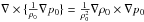 which is zero in a
polytropic atmosphere in hydrostatic equilibrium.
u0 and ρ0 as given
above are therefore solutions of the Euler equation for some perturbing potential, albeit
not necessarily for the perturbing potential of a point mass at a finite distance. One may
view ρ0 either as an approximation to the density profile of the
state excited by a tidal perturber idealized as a point mass, or as the exact profile for a
perturbing potential which approximates a real tidal potential.
which is zero in a
polytropic atmosphere in hydrostatic equilibrium.
u0 and ρ0 as given
above are therefore solutions of the Euler equation for some perturbing potential, albeit
not necessarily for the perturbing potential of a point mass at a finite distance. One may
view ρ0 either as an approximation to the density profile of the
state excited by a tidal perturber idealized as a point mass, or as the exact profile for a
perturbing potential which approximates a real tidal potential.
We will now consider the linear stability of the ground state. All quantities are
decomposed into their value in the basic state indicated by an index zero and a perturbation
which is considered to be small:
ϱ = ρ0 + ρ,
v = u0 + u,
P = p0 + p, and
Φself = Φ0 + Φ. The linearized equations are:
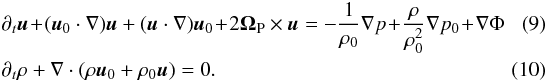 We
will restrict ourselves to well mixed ground states
ρ0,p0 of constant
entropy in atmospheres characterized by an adiabatic exponent γ, and only
allow perturbations of the ground state which obey the adiabatic equation of state, so that
We
will restrict ourselves to well mixed ground states
ρ0,p0 of constant
entropy in atmospheres characterized by an adiabatic exponent γ, and only
allow perturbations of the ground state which obey the adiabatic equation of state, so that
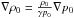 and
p/p0 = γρ/ρ0
for small deviations ρ,p from the ground state. The right hand side of the
linearized Euler equation then simplifies according to
and
p/p0 = γρ/ρ0
for small deviations ρ,p from the ground state. The right hand side of the
linearized Euler equation then simplifies according to
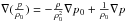 .
.
The equation of continuity is next simplified by invoking the anelastic approximation. This approximation is valid if the density deviations from ρ0 are small and if velocities are small compared with the speed of sound. The latter condition is violated at the surface of a star or a planet where the speed of sound tends to zero. The validity of the anelastic approximation has already been discussed in detail in the more restricted scope of eigenmode calculations as they will be done below. It appears that the region where the anelastic approximation fails is too small to modify global results such as inertial mode frequencies (Ivanov & Papaloizou 2010), so that we shall adopt the anelastic approximation from here on.
The linear stability problem is now reduced to 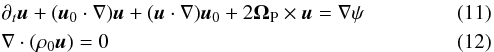 with
with
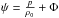 . We will solve these equations
subject to the boundary condition
. We will solve these equations
subject to the boundary condition 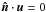 on the ellipsoidal surface (1). These
boundary conditions describe a solid wall in a laboratory experiment more directly than the
surface of an atmosphere, but the results below suggest that the detailed choice of boundary
conditions does not matter for the main findings of this paper.
on the ellipsoidal surface (1). These
boundary conditions describe a solid wall in a laboratory experiment more directly than the
surface of an atmosphere, but the results below suggest that the detailed choice of boundary
conditions does not matter for the main findings of this paper.
We now follow a procedure similar to that used by Gledzer
& Ponomarev (1992). We first remove dimensions by rescaling the Cartesian
coordinates with their respective semi-major axes (which maps the ellipsoidal surface on a
sphere of radius 1) and we rescale time with ΩF, 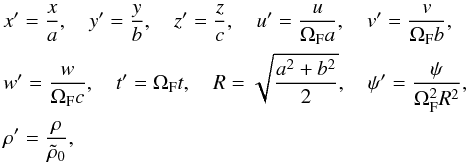 (13)where
u, v, and w are the x,
y, and z components of u,
respectively. For simplification we consider only the case
(13)where
u, v, and w are the x,
y, and z components of u,
respectively. For simplification we consider only the case
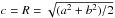 .
It will become plausible below that a change in c will not cause
substantial changes. This restriction to certain ellipsoidal shapes will simplify the
calculations below. In these new variables, Eq. (11) becomes after omitting primes
.
It will become plausible below that a change in c will not cause
substantial changes. This restriction to certain ellipsoidal shapes will simplify the
calculations below. In these new variables, Eq. (11) becomes after omitting primes 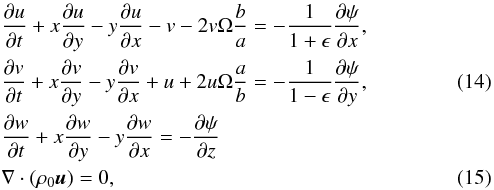
with ϵ = (a2 − b2)/(a2 + b2) being the ellipticity of the boundaries in the x,y-plane and Ω = ΩP/ΩF.
We now switch from Cartesian coordinates (x,y,z) to cylindrical
coordinates (s,φ,z). In cylindrical coordinates, the above system of
equations can be expressed as 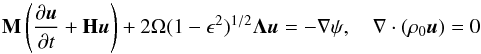 (16)with
(16)with
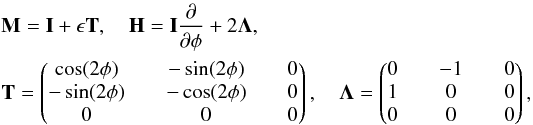 where
I is the identity matrix. It matters at this stage that we restricted
c to c = R because otherwise, the
equation M = I + ϵT would contain
additional terms.
where
I is the identity matrix. It matters at this stage that we restricted
c to c = R because otherwise, the
equation M = I + ϵT would contain
additional terms.
We now use a Galerkin method. We seek solutions to Eq. (16) in the form 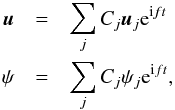 (17)where
the uj are solutions of the
unperturbed eigenvalue problem (ϵ = 0)
(17)where
the uj are solutions of the
unperturbed eigenvalue problem (ϵ = 0)
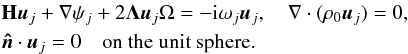 (18)This
is the equation for inertial modes in a sphere. j is a proxy for the
indices
(nj,mj,kj)
which characterize an inertial mode in a sphere (Greenspan
1968). The variables n, m, and k
will be indexed by j if it is necessary to distinguish different modes and
will appear without an index otherwise. k is the azimuthal wavenumber, and
n is the spatial degree or latitudinal wavenumber (on the surface of the
sphere, the pressure distribution is given by the spherical harmonic
(18)This
is the equation for inertial modes in a sphere. j is a proxy for the
indices
(nj,mj,kj)
which characterize an inertial mode in a sphere (Greenspan
1968). The variables n, m, and k
will be indexed by j if it is necessary to distinguish different modes and
will appear without an index otherwise. k is the azimuthal wavenumber, and
n is the spatial degree or latitudinal wavenumber (on the surface of the
sphere, the pressure distribution is given by the spherical harmonic
 ). The index
m numbers the eigenvalues for any fixed n and
k and varies over a finite range. These equations can be solved
analytically in the incompressible case (Zhang et al.
2001). They are still separable within the anelastic approximation provided that
the density is of the form
). The index
m numbers the eigenvalues for any fixed n and
k and varies over a finite range. These equations can be solved
analytically in the incompressible case (Zhang et al.
2001). They are still separable within the anelastic approximation provided that
the density is of the form 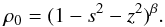 (19)Repeating the steps of
Wu (2005a), one arrives at an eigenvalue problem
for ψ which is written as a product in the form
ψ(x1,x2,φ,t) = ψ1(x1)ψ2(x2)ζ(φ,t).
(x1,x2,φ)
are the ellipsoidal coordinates used in Wu (2005a)
and introduced by Bryan (1889). One must be careful to
distinguish the index which characterizes the different inertial modes from the index used
in Eqs. (20) and (21) which stands for the two coordinates
x1 and x2. In this paragraph we
omit the index which characterizes the different inertial modes. The range of the three
coordinates is x1 ∈ [μ,1],
x2 ∈ [−μ,μ], with
μ = −(ω + k)/(2(1 + Ω))
and φ is the azimuthal angle so that
φ ∈ [0,2π]. μ is
half the frequency of the inertial mode with respect to the frame rotating with
ΩP + ΩF and ω is the frequency with respect to the
inertial frame. All variables X (pressure and velocity components) depend
on time t and on the azimuthal angle φ through the
relation
X ∝ ζ(φ,t) = exp [i(kφ − 2μ(ΩP + ΩF)t)].
We adopt the convention that μ ≥ 0 with
k > 0 representing a prograde mode and
k < 0 a retrograde mode. Modes with denotation
(k,μ) and (−k, −μ) are physically the
same modes so that one can restrict either μ or k to
positive numbers and avoid redundancy. It is numerically more accurate to solve for the
gi defined by
(19)Repeating the steps of
Wu (2005a), one arrives at an eigenvalue problem
for ψ which is written as a product in the form
ψ(x1,x2,φ,t) = ψ1(x1)ψ2(x2)ζ(φ,t).
(x1,x2,φ)
are the ellipsoidal coordinates used in Wu (2005a)
and introduced by Bryan (1889). One must be careful to
distinguish the index which characterizes the different inertial modes from the index used
in Eqs. (20) and (21) which stands for the two coordinates
x1 and x2. In this paragraph we
omit the index which characterizes the different inertial modes. The range of the three
coordinates is x1 ∈ [μ,1],
x2 ∈ [−μ,μ], with
μ = −(ω + k)/(2(1 + Ω))
and φ is the azimuthal angle so that
φ ∈ [0,2π]. μ is
half the frequency of the inertial mode with respect to the frame rotating with
ΩP + ΩF and ω is the frequency with respect to the
inertial frame. All variables X (pressure and velocity components) depend
on time t and on the azimuthal angle φ through the
relation
X ∝ ζ(φ,t) = exp [i(kφ − 2μ(ΩP + ΩF)t)].
We adopt the convention that μ ≥ 0 with
k > 0 representing a prograde mode and
k < 0 a retrograde mode. Modes with denotation
(k,μ) and (−k, −μ) are physically the
same modes so that one can restrict either μ or k to
positive numbers and avoid redundancy. It is numerically more accurate to solve for the
gi defined by
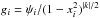 ,
i = 1,2. The eigenvalue problem for the eigenvalue
l and the eigenfrequency μ reads
,
i = 1,2. The eigenvalue problem for the eigenvalue
l and the eigenfrequency μ reads ![\begin{eqnarray} \label{gleichung} (1-x_i^2)\frac{{\rm d}^2g_i}{x_i^2}-2x_i(|k|&+&1)\frac{{\rm d}g_i}{{\rm d}x_i}+ \frac{2\beta x_i(1-x_i^2)}{x_i^2-\mu^2}\frac{{\rm d}g_i}{{\rm d}x_i} \nonumber \\ &+&\left[ \lambda^2-\frac{2\beta|k|x_i^2}{x_i^2-\mu^2}+\frac{2\beta k\mu}{x_i^2-\mu^2}\right]g_i=0, \end{eqnarray}](/articles/aa/full_html/2014/02/aa22817-13/aa22817-13-eq106.png) (20)with
the boundary conditions
(20)with
the boundary conditions
![\begin{eqnarray} \label{randbedingungen} && \frac{{\rm d}g_1}{{\rm d}x_1}\bigg\vert_{x_1\,=\,1}=\frac{\lambda^2+2\beta[(k\mu-|k|)/(1-\mu^2)]}{2(|k|+1)}g_1\vert_{x_1\,=\,1}\nonumber \\ && \frac{{\rm d}g_1}{{\rm d}x_1}\bigg\vert_{x_1\,=\,\mu}=-\frac{(k-|k|\mu)}{1-\mu^2}g_1\vert_{x_1\,=\,\mu}\\ && \frac{{\rm d}g_2}{{\rm d}x_2}\bigg\vert_{|x_2|\,=\,\mu}=-\textrm{sgn}(x_2)\frac{(k-|k|\mu)}{1-\mu^2}g_2|_{|x_2|\,=\,\mu} \nonumber \end{eqnarray}](/articles/aa/full_html/2014/02/aa22817-13/aa22817-13-eq107.png) (21)and
λ2 = l(l + 1) − |k|(| k| + 1).
In general, both μ and l have to be determined
numerically, but for β = 0, l is simply given by
l = n.
(21)and
λ2 = l(l + 1) − |k|(| k| + 1).
In general, both μ and l have to be determined
numerically, but for β = 0, l is simply given by
l = n.
Once the eigenfunctions are found, we define the scalar product
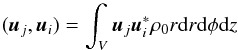 (22)which differs from the
usual scalar product by the factor ρ0. The eigenvalues
calculated in the anelastic approximation are orthogonal with this scalar product. This can
be proven along the same lines as the proof for the orthogonality of inertial modes in the
incompressible case (Greenspan 1968).
(22)which differs from the
usual scalar product by the factor ρ0. The eigenvalues
calculated in the anelastic approximation are orthogonal with this scalar product. This can
be proven along the same lines as the proof for the orthogonality of inertial modes in the
incompressible case (Greenspan 1968).
We substitute (17) in (16) and multiply this equation by ρ0uj. We obtain the system
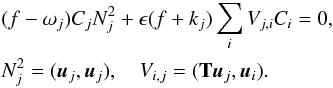 (23)We
assume the uj to be normalized so
that
(23)We
assume the uj to be normalized so
that 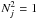 . We
proceed on the assumption that Vj,i ≠ 0 only
for
nj = ni
and
kj = ki ± 2.
The latter condition can be proven in general by noting that the dependence of the variables
on the azimuthal angle is given by exp(ikφ). The first condition is less
obvious. It was proven analytically by Kerswell
(1993) for incompressible fluids. This proof can not simply be adapted to the
compressible case because no analytical expressions exist for the modes in this case.
However, we calculated the Vj,i numerically for
all mode combinations with indices up to n = 20 and
| k| = 10. In all cases, the results appeared to converge to zero as the
spatial resolution used in the integration was improved.
. We
proceed on the assumption that Vj,i ≠ 0 only
for
nj = ni
and
kj = ki ± 2.
The latter condition can be proven in general by noting that the dependence of the variables
on the azimuthal angle is given by exp(ikφ). The first condition is less
obvious. It was proven analytically by Kerswell
(1993) for incompressible fluids. This proof can not simply be adapted to the
compressible case because no analytical expressions exist for the modes in this case.
However, we calculated the Vj,i numerically for
all mode combinations with indices up to n = 20 and
| k| = 10. In all cases, the results appeared to converge to zero as the
spatial resolution used in the integration was improved.
Based on the above, we can infer that the elliptical instability comes from an interaction of the modes with azimuthal wavenumber k and k + 2, whereas the spatial degree n must be the same for the interacting modes. Modes in resonance will be written as (k,k + 2) and the spatial degree n will be stated separately.
Application of perturbation theory to (23)
with the small parameter ϵ leads to the inviscid growth rate
σinv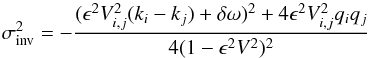 (24)with
δω = ωi − ωj,
(24)with
δω = ωi − ωj,
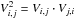 , and
qj = −2μj.
Eq. (24) is the same as Eq. (3.5) of Gledzer & Ponomarev (1992). It follows from this
equation that instability is possible only if
| δω| ≤ O(ϵ).
, and
qj = −2μj.
Eq. (24) is the same as Eq. (3.5) of Gledzer & Ponomarev (1992). It follows from this
equation that instability is possible only if
| δω| ≤ O(ϵ).
Viscosity is included heuristically in our calculations by adding a damping rate to
σinv. Two different expressions are used, one for the growth
rate with free slip boundaries, σfs, and one for no slip
boundaries, σns. The two approximations are 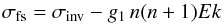 (25)and
(25)and 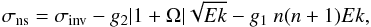 (26)where
g1 and g2 are constants on the
order of 1 which in this paper are always chosen as
g1 = g2 = 1, n is
the spatial degree of the two interacting modes and Ek is the Ekman number.
Equation (26) contains two dissipative
terms. The second one corresponds to dissipation in the bulk, whereas the first one is due
to friction inside Ekman layers at the boundaries. The first term is usually computed in the
frame of reference in which the boundaries are at rest and expressed in multiples of the
rotation rate of that frame, yielding decay rates of inertial modes of the form
(26)where
g1 and g2 are constants on the
order of 1 which in this paper are always chosen as
g1 = g2 = 1, n is
the spatial degree of the two interacting modes and Ek is the Ekman number.
Equation (26) contains two dissipative
terms. The second one corresponds to dissipation in the bulk, whereas the first one is due
to friction inside Ekman layers at the boundaries. The first term is usually computed in the
frame of reference in which the boundaries are at rest and expressed in multiples of the
rotation rate of that frame, yielding decay rates of inertial modes of the form
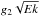 with g2 typically between 0.1 and 1 (Greenspan 1968). Transformed to the frame of reference and the unit of
time used in Eq. (14), the decay rate is
with g2 typically between 0.1 and 1 (Greenspan 1968). Transformed to the frame of reference and the unit of
time used in Eq. (14), the decay rate is
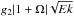 with
Ek = ν/(| ΩF + ΩP|R2)
and ν the viscosity. In many standard applications of rotating fluid
mechanics, n and Ek are both small enough for the term in
with
Ek = ν/(| ΩF + ΩP|R2)
and ν the viscosity. In many standard applications of rotating fluid
mechanics, n and Ek are both small enough for the term in
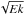 to dominate. For free-slip boundary conditions on the other hand, only the bulk dissipation
must be considered. We use n(n + 1) in the bulk damping
term, because the velocity field of an inertial mode contains on the surface only the
spherical harmonic
to dominate. For free-slip boundary conditions on the other hand, only the bulk dissipation
must be considered. We use n(n + 1) in the bulk damping
term, because the velocity field of an inertial mode contains on the surface only the
spherical harmonic 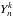 . Assuming this
is a reasonable approximation to the inertial mode at any radius r, and
using
. Assuming this
is a reasonable approximation to the inertial mode at any radius r, and
using 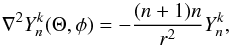 (27)one justifies the
formula for σfs (Lorenzani
2001).
(27)one justifies the
formula for σfs (Lorenzani
2001).
3. Numerical implementation
We used numerical methods to calculate the growth rates according to Eq. (24). We first calculate the frequencies for
β = 0 of inertial modes in a sphere by solving Eq. (29) from Wu (2005a)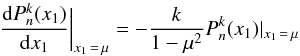 (28)by
bisection. We use these eigenfrequencies, together with the corresponding eigenvalues
l as starting values for a shooting method to solve Eq. (20). As noted in Wu (2005a), “the number of eigenmodes remains conserved when β
varies, with a close one-to-one correspondence between modes in different density profiles”.
So we increment β in steps of 0.1 and use the eigenvalues of the foregoing
β as an initial point for the shooting method. The integration of the ODE
was done by use of a Runge Kutta Cash-Karp method of fifth order with an adaptive stepsize
control. Because the endpoints of the ODE for one variable are both singular points, we used
the method of shooting to a fitting point (Press et al.
1992).
(28)by
bisection. We use these eigenfrequencies, together with the corresponding eigenvalues
l as starting values for a shooting method to solve Eq. (20). As noted in Wu (2005a), “the number of eigenmodes remains conserved when β
varies, with a close one-to-one correspondence between modes in different density profiles”.
So we increment β in steps of 0.1 and use the eigenvalues of the foregoing
β as an initial point for the shooting method. The integration of the ODE
was done by use of a Runge Kutta Cash-Karp method of fifth order with an adaptive stepsize
control. Because the endpoints of the ODE for one variable are both singular points, we used
the method of shooting to a fitting point (Press et al.
1992).
The next step is to calculate the integrals for Eq. (24). We only have to consider the modes which satisfy the resonance condition. Through a simple calculation the condition for the frequency detuning δω can be made more precise: Instability is possible only if | δω| < 4ϵ + 2ϵ2.
Finally we want to solve the integrals Vi,j by Gaussian quadrature. It is not feasible to calculate these integrals in the ellipsoidal coordinate space (x1,x2,φ) because in these coordinates the limits of integration depend on the eigenfrequencies, and for the integration of Vi,j we consider two wave functions with in general two different eigenfrequencies. Therefore we perform the integration in (s,z,φ) space. The scalars ψ1 and ψ2 were obtained at several points x1 and x2 by the numerical integration of the ODE (20). The final integrations were performed using Gaussian quadrature with Gauss-Legendre abscissas and weights with a resolution of 50 points in both s and z directions. The integration in φ direction can be performed analytically. We know x1(s,z) and x2(s,z) and obtain ψ1(x1(s,z),x2(s,z))ψ2(x1(s,z),x2(s,z)). The scalars ψ1 and ψ2 were obtained at some points x1 and x2 which in general do not coincide with the points we need for the Gaussian quadrature. Therefore we need the scalars ψ1,ψ2 at arbitrary points x1,x2. This was accomplished by a cubic-spline interpolation.
4. Results
We start by investigating the effect of compressibility on individual inertial modes and the growth rate of triad resonances. We will first consider inviscid flows and include viscous effects at the end of this section.
Figure 3 shows the dispersion relation for k = −1 and k = 1 for incompressible fluids and for β = 18. As expected, compressibility modifies the inertial mode frequencies. There is a noteworthy distinction between the cases kq > 0 and kq < 0 in that the modes with the frequency q with the smallest absolute value at any given n always occurs for kq < 0. These low frequency modes will become relevant later on.
The mode frequencies change continuously with β so that individual modes can be tracked as a function of β. Figures 1 and 2 shows a few examples of triads with (ki,kj) = (−1,1). It can be seen that a chosen triad may lead to instability or not depending on β. A variation of β modifies both the structure and frequency of the inertial modes and hence the integrals in Vi,j and δω in Eq. (24). As expected from this equation, the positive growth rates in Figs. 1a and 2a are found around the β for which δω = 0. Figures 1b and 2b give the variation of δω with β and demonstrate the effect of compressibility on mode frequencies.
 |
Fig. 1 a) Growth rates of modes (−1,1) for various n as a function of the compressibility parameter β for ϵ = 0.04, Ωp = 0 and Ek = 0. b) Corresponding δω. |
 |
Fig. 3 Frequencies of inertial modes in the co-rotating frame, q, for β = 0 (circles and squares) and β = 18 (x and plus) as a function of the spatial degree n. Only the modes with k = −1 (green, respectively plus and circles) and k = 1 (blue, respectively x and squares) are shown. |
The case | k| = 1, n = 2 is exceptional because it corresponds to the purely toroidal motion in the spin-over mode. All toroidal modes have no radial velocity component, which implies for a radially dependent background density profile ρ0 that ρ0 drops from the continuity equation ∇·(ρ0u) = 0. The density profile ρ0 then disappears completely from the eigenvalue and stability problems, so that β does not affect the growth rate or the δω in the triad (−1,1) with n = 2. In addition, these two modes are the only ones in exact resonance with δω = 0 at β = 0.
 |
Fig. 4 Maximum growth rates as a function of Ω for Ek = 0. For this figure we take into account all modes with | k| ≤ 10 and n ≤ 40. The (solid) black line in this figure is the growth rate given by Eq. (29). |
It will now be argued that while the properties of inertial modes depend on
compressibility, the stability of the flow as a whole does not. For an inviscid fluid, the
two control parameters apart from β determining stability are the
ellipticity of the deformation, ϵ, and the ratio of the rotation rates Ω
defined below Eq. (24). The tidal flow is
unstable if any two inertial modes form a triad with positive growth rate. Since there is an
infinity of modes, a computational search for instability is necessarily restricted to a
finite subset. Figure 4a and b is the result of a scan of
all modes with | k| ≤ 10 and n ≤ 40. These two panels
display the maximum growth rate found in this subset for the chosen ϵ as a
function of Ω for different β. Inertial modes appear only within a limited
band of frequencies, so that resonances are impossible in the interval
−3/2 < Ω < −1/2
(Craik 1989). Figure 4 shows a part of the complementary interval by way of example. The various curves
appear to have a common envelope σud given by
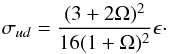 (29)This expression stems
from the calculation of the inviscid growth rate in an incompressible, infinitely extended
fluid (Miyazaki et al. 1995). Some deviations remain
between Eq. (29) and the computed maximum
growth rates in Fig. 4. However, these deviations become
smaller and smaller if larger numbers of eigenmodes are included in the search for unstable
triads. This can already be seen by comparing panels a and b of Fig. 4: Fig. 4b is for the smaller
ϵ. For a given subset of allowed eigenmodes, fewer pairs of modes will
meet the criterion | δω| ≤ O(ϵ)
required by Eq. (24) for the smaller
ϵ, so that larger deviations remain between the envelope and the computed
maximum growth rates. It is plausible to assume that the deviations will entirely disappear
if all inertial modes are taken into consideration.
(29)This expression stems
from the calculation of the inviscid growth rate in an incompressible, infinitely extended
fluid (Miyazaki et al. 1995). Some deviations remain
between Eq. (29) and the computed maximum
growth rates in Fig. 4. However, these deviations become
smaller and smaller if larger numbers of eigenmodes are included in the search for unstable
triads. This can already be seen by comparing panels a and b of Fig. 4: Fig. 4b is for the smaller
ϵ. For a given subset of allowed eigenmodes, fewer pairs of modes will
meet the criterion | δω| ≤ O(ϵ)
required by Eq. (24) for the smaller
ϵ, so that larger deviations remain between the envelope and the computed
maximum growth rates. It is plausible to assume that the deviations will entirely disappear
if all inertial modes are taken into consideration.
We thus arrive at the picture that the stability limit does not depend on
β, but β determines which modes are unstable. We will
now compute the spatial degree n of the most unstable modes. A resonance
can only occur if two modes i and j have frequencies such
that
ωi − ωj < O(ϵ).
For a smaller ϵ, we expect for purely statistical reasons that a larger
pool of eigenmodes is necessary to find any resonance and that the unstable modes have a
higher n for smaller ϵ. Because
ωi = (1 + Ω)qi − ki
for all i, the frequencies qi
and qj have to obey 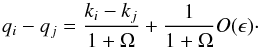 (30)In other words, if
there is a mode at frequency qj, it can only
form an unstable triad if there is another mode with a frequency in an interval of size
O(ϵ)/(1 + Ω) centered around
qj + (ki − kj)/(1 + Ω).
Let us first consider the case of small | Ω |, so that
qi − qj ≈ ki − kj + O(ϵ).
All eigenmode frequencies obey | qi| ≤ 2.
Assuming that these frequencies are statistically uniformly distributed over the interval
available for inertial modes, and that the matrix elements appearing in Eq. (24) do not systematically vary with frequency,
one will find on average one resonance with positive growth rate among a number
N of modes proportional to 1/ϵ. Only
a finite number of modes exist with an n smaller than some limit
L: for every n and k, there are
n − |k | modes if k ≠ 0 and
n − 1 modes if k = 0. For every n, the
index k has to obey | k| ≤ n so that
there are n2 − 1 modes of spatial degree n and
N(L) modes exist with
n ≤ L, with N(L) given
by:
(30)In other words, if
there is a mode at frequency qj, it can only
form an unstable triad if there is another mode with a frequency in an interval of size
O(ϵ)/(1 + Ω) centered around
qj + (ki − kj)/(1 + Ω).
Let us first consider the case of small | Ω |, so that
qi − qj ≈ ki − kj + O(ϵ).
All eigenmode frequencies obey | qi| ≤ 2.
Assuming that these frequencies are statistically uniformly distributed over the interval
available for inertial modes, and that the matrix elements appearing in Eq. (24) do not systematically vary with frequency,
one will find on average one resonance with positive growth rate among a number
N of modes proportional to 1/ϵ. Only
a finite number of modes exist with an n smaller than some limit
L: for every n and k, there are
n − |k | modes if k ≠ 0 and
n − 1 modes if k = 0. For every n, the
index k has to obey | k| ≤ n so that
there are n2 − 1 modes of spatial degree n and
N(L) modes exist with
n ≤ L, with N(L) given
by: 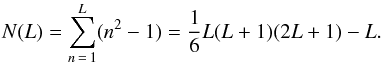 (31)For large
L, one has N ∝ L3, and in
order for these modes to contain a resonance, one needs
L ∝ ϵ−1/3, independently
of Ω or β. The smaller the deformation ϵ, the higher the
typical spatial complexity of the modes involved in resonances.
(31)For large
L, one has N ∝ L3, and in
order for these modes to contain a resonance, one needs
L ∝ ϵ−1/3, independently
of Ω or β. The smaller the deformation ϵ, the higher the
typical spatial complexity of the modes involved in resonances.
 |
Fig. 5 Mean value of the spatial degree < n >, for the modes with a growth rate of at least 0.1σud (dashed lines) or 0.8σud (solid lines) as a function of ϵ for β = 0 (green x), β = 2.8 (red circles), and β = 18 (blue squares), together with fits according to Eq. (31). |
Figure 5 verifies this scaling. This figure has been obtained as follows: At fixed ϵ, 20 equidistant points have been chosen in the interval of Ω ranging from −0.45 to 0.5. For every point, we determined the triad with the mode with the smallest n for which the growth rate is at least 0.1σud and 0.8σud. This minimal n, averaged over all points, is ⟨ n ⟩ and is shown in Fig. 5 as a function of ϵ. The averaging procedure is intended to remove the occasional outlier which occurs if a mode with a very low n happens to be part of a growing triad. The average ⟨ n ⟩ is rather a measure of the minimum n that is typically necessary to obtain a resonance with a given ϵ. As expected from the argument above, ⟨ n ⟩ ∝ ϵ−1/3 for small ϵ.
We now turn to the case of large | Ω | in Eq. (30). For | Ω | tending to infinity, qi − qj tends to zero. At the same time, we see from Eq. (24) that positive growth rates are only possible for qiqj < 0, so that qi and qj both have to go to zero as 1/|Ω | if | Ω | goes to infinity. Figure 3 shows that n must be large enough to find any eigenvalue with an absolute value below some prescribed bound. This yields a minimal spatial degree nmin necessary to find a resonance at a given Ω. The corresponding mode frequency needs to lie in the appropriate interval of size O(ϵ)/(1 + Ω) for a positive growth rate. This additional condition is possibly met only for n larger than nmin.
We therefore need a relationship between the smallest frequencies and the spatial degrees of the modes. As already stated the frequencies of inertial modes in a uniform density sphere can be calculated according to Eq. (29) from Wu (2005a) , see Eq. (28).
For large n the asymptotic expansion (Abramowitz & Stegun 1972)
![\begin{eqnarray} P_n^k(\cos\theta)&=&\frac{\Gamma(n+k+1)}{\Gamma(n+3/2)}\left(\frac 1 2 \pi \sin \theta \right)^{-1/2}\nonumber \\ &&\times \cos\left[\left(n+\frac 1 2\right)\theta-\frac \pi 4 +\frac{k\pi}{2}\right]+O\left(n^{-1}\right) \end{eqnarray}](/articles/aa/full_html/2014/02/aa22817-13/aa22817-13-eq229.png) (32)holds.
We set μ = cos(θ) and
θ = π/2 + ϵw
with ϵw small for μ small. A
short calculation shows that for small μ and large n, Eq.
(28) is equivalent to
(32)holds.
We set μ = cos(θ) and
θ = π/2 + ϵw
with ϵw small for μ small. A
short calculation shows that for small μ and large n, Eq.
(28) is equivalent to ![\begin{eqnarray} \label{frerel} -k\cos\left[\left(n+\frac 1 2\right)\epsilon_w\right.&+&\left.\frac{(n+k)\pi}{2}\right] \nonumber\\ &=&\left(n+\frac 1 2\right)\sin\left[\left(n+\frac 1 2\right)\epsilon_w+\frac{\left(n+k\right)\pi}{2}\right]. \end{eqnarray}](/articles/aa/full_html/2014/02/aa22817-13/aa22817-13-eq233.png) (33)For
n + k even this gives
(33)For
n + k even this gives
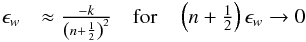 (34a)
(34a)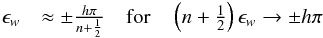 (34b)and
for n + k odd
(34b)and
for n + k odd
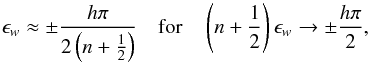 (35)where
h is an integer. For large n and small k the
μ with the smallest absolute value tends towards zero as
k/(n + 1/2)2.
We can classify these modes as “slow modes”, because if the frequency of modes on any other
branch of the dispersion relation in Fig. 3 tends to zero,
it does so only in 1/(n + 1/2). We
thus have to distinguish two cases when computing nmin: the
growing resonance is either between two slow modes, or at least one of the two inertial
modes involved is not a slow mode. In the latter case,
nmin ∝ |Ω |, whereas in the former case,
(35)where
h is an integer. For large n and small k the
μ with the smallest absolute value tends towards zero as
k/(n + 1/2)2.
We can classify these modes as “slow modes”, because if the frequency of modes on any other
branch of the dispersion relation in Fig. 3 tends to zero,
it does so only in 1/(n + 1/2). We
thus have to distinguish two cases when computing nmin: the
growing resonance is either between two slow modes, or at least one of the two inertial
modes involved is not a slow mode. In the latter case,
nmin ∝ |Ω |, whereas in the former case,
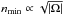 .
However, since | k1 − k2| = 2, and
choosing the indices such that
k2 > k1, a
resonance between slow modes can only occur if k1 = −1 and
k2 = 1, and from (30) we can deduce that Ω must be negative. In summary, we expect
nmin ∝ Ω for positive Ω, and for negative Ω, too, except when
modes with frequencies of approximately
k/(n + 1/2)2
can resonate with each other.
.
However, since | k1 − k2| = 2, and
choosing the indices such that
k2 > k1, a
resonance between slow modes can only occur if k1 = −1 and
k2 = 1, and from (30) we can deduce that Ω must be negative. In summary, we expect
nmin ∝ Ω for positive Ω, and for negative Ω, too, except when
modes with frequencies of approximately
k/(n + 1/2)2
can resonate with each other.
 |
Fig. 6 Minimum value of n, nmin as a function of Ω for various ϵ and positive Ω. a) β = 2.8 and β = 18 and b) β = 0. |
 |
Fig. 8 Maximum growth rates as a function of Ω for Ek ≠ 0. For this figure we take into account all modes with a maximum | k| ≤ 10 and n ≤ 40. a) Calculated for free slip boundary conditions according to Eq. (25). b) Calculated for no slip boundary conditions according to Eq. (26). The (solid) black line in this figure is the growth rate given by Eq. (29). The (dashed without marker) cyan line in a) is the growth rate given by Eq. (36) with d2 = 3.35. |
Figure 6 proves this scaling to be correct for positive Ω. We find nmin = d1Ω, with a prefactor d1 which depends on β. We can deduce from that figure that d1 = 3, 5, and 10 for β = 0, 2.8, and 18, respectively. Some points lie above the line nmin = d1Ω because some modes with spatial degree nmin, even though their frequency is small enough, do not find another mode to resonate with. For negative Ω (Fig. 7), one also finds points below nmin = d1|Ω |. These correspond to resonances between two slow modes and always involve the azimuthal wavenumbers k1 = −1 and k2 = 1. Since Ω > 0 in most applications, we will use nmin = d1Ω in the estimation of dissipation effects below.
We have up to here considered ideal fluids only. The remainder of this section will deal
with viscous effects. Figure 8 shows the maximum growth rate
if dissipation is heuristically taken into account according to Eqs. (25) and (26). The dissipation for no slip boundaries formally depends on
n. However, at the Ek and n under
consideration, the first term corresponding to friction at boundaries dominates and it is
independent of mode structure. Therefore, the maximum growth rates in Fig. 4 are the same as before except for a downward shift, and are given by
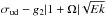 .
Instability is expected if
.
Instability is expected if 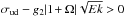 , independently of
β. Values of c depend on the inertial modes and may vary
by an order of magnitude, but since the uncertainties on Ek are in practice
much larger, there is little incentive to determine the prefactor c more
accurately.
, independently of
β. Values of c depend on the inertial modes and may vary
by an order of magnitude, but since the uncertainties on Ek are in practice
much larger, there is little incentive to determine the prefactor c more
accurately.
Free slip boundary conditions allow only bulk dissipation and are more complicated because dissipation now increases with n. This puts a natural limit to the spatial degrees n it is useful to consider, which restricts altogether the number of modes suitable for instabilities because | k| ≤ n and there is only a finite number of modes for a given k and n. If one includes more and more eigenvalues in the stability analysis, the curve of the maximum growth rate approaches a smooth curve of the same type as σud up to some approximation, until additional modes suffer from such a high damping rate that they can not improve the maximum growth rate any more.
The precise stability limit now depends on the structure of the unstable modes and hence on
β and Ω, but as an estimate, we can take the growth rate for free slip
boundaries to be the inviscid growth rate reduced by the decay rate of modes with the
expected spatial degree, for which we may reasonably take ⟨ n ⟩ for small
| Ω | and nmin for large | Ω |, or as a formula interpolating
between these two limits,
n = d1|Ω| + d2ϵ−1/3.
For the parameters of Fig. 8, only the term in
d2ϵ−1/3 is
important and one arrives at 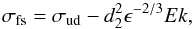 (36)which is again
independent of β. From Fig. 8a, we
deduce that d2 is roughly 3.35.
(36)which is again
independent of β. From Fig. 8a, we
deduce that d2 is roughly 3.35.
5. Examples: Io’s tides on Jupiter, the binary system V636 Centauri and the Earth
The results from the previous section are used for three examples. We consider the 0.85 M⊙ secondary as the perturbing object within the binary system V636 Centauri, the terrestrial core in the Earth Moon system, and the tides on Jupiter raised by Io.
The choice of the correct boundary conditions is generally ambiguous. For the Earth’s core it is clear that no-slip boundary conditions apply. The choice for the two remaining examples is not so clear. One finds in the literature arguments both in favor of no slip (Tassoul 1987, 1995; see also Tassoul & Tassoul 1997) as well as free slip boundary conditions (Rieutord 1992, 2008; see also Rieutord & Zahn 1997).
An even bigger problem is how to deal with additional fluid motion, such as convection, on
which the tides are superimposed. The simplest approach is to ignore such motions, which is
certainly justified if their amplitudes is much smaller than the amplitude of the tidal
flow. Another approach consists in introducing a turbulent viscosity. However, turbulence
modeling is always uncertain, and according to at least one well established turbulence
model, elliptical instability is enhanced and not suppressed under some circumstances (Fabijonas & Holm 2003). When using a turbulent
viscosity for the present problem, one has to deal with the unusual situation that one needs
to compute the damping of a motion with a period which is typically shorter than the turn
over time of the turbulent eddies. Several authors (Wu
2005b and in a similar form Ogilvie & Lin
2007) have used the following expression for the turbulent viscosity
νt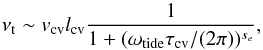 (37)where
vcv, lcv, and
τcv are the characteristic convection velocity, mixing length,
and turnover time and ωtide = 2|ΩF | is the
frequency of the tidal forcing. se is a constant, generally
se = 1 or se = 2 is used. Goldreich & Nicholson (1977) and Goodman & Oh (1997) suggested that
se = 2, while Zahn
(1977) argues for se = 1. For tides faster than
τcv, one expects a turbulent viscosity proportional to
vcv and a mixing length given by the distance traveled by
particles during one tidal period,
lcvTf/τcv,
with
Tf = 2π/ωtide,
which corresponds to se = 1 in Eq. (37). Numerical simulations by Penev et al. (2009) confirm this expectation, but because
of limited spatial resolution they were not able to simulate reliably the case of
Tf ≪ τcv, the regime for which
se = 2 has been proposed.
(37)where
vcv, lcv, and
τcv are the characteristic convection velocity, mixing length,
and turnover time and ωtide = 2|ΩF | is the
frequency of the tidal forcing. se is a constant, generally
se = 1 or se = 2 is used. Goldreich & Nicholson (1977) and Goodman & Oh (1997) suggested that
se = 2, while Zahn
(1977) argues for se = 1. For tides faster than
τcv, one expects a turbulent viscosity proportional to
vcv and a mixing length given by the distance traveled by
particles during one tidal period,
lcvTf/τcv,
with
Tf = 2π/ωtide,
which corresponds to se = 1 in Eq. (37). Numerical simulations by Penev et al. (2009) confirm this expectation, but because
of limited spatial resolution they were not able to simulate reliably the case of
Tf ≪ τcv, the regime for which
se = 2 has been proposed.
That se = 2 should be used at small tidal periods is in
accordance with results from Ogilvie & Lesur
(2012). Therfore we use se = 2 for the case
Tf ≪ τcv and
se = 1 for
Tf ≳ τcv. In order to apply Eq.
(37), one needs numbers for
vcv, lcv, and
τcv. The mixing length is estimated by
lcv ≈ H, with
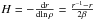 the density scale height. Therefore an order of magnitude estimation gives
the density scale height. Therefore an order of magnitude estimation gives
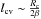 .
The convective velocity is approximated by
vcv ≈ (F/ρ)1/3,
with the energy flux
.
The convective velocity is approximated by
vcv ≈ (F/ρ)1/3,
with the energy flux 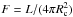 and
Rc the radius of the central body. An order of magnitude for
vcv is therefore obtained by using
and
Rc the radius of the central body. An order of magnitude for
vcv is therefore obtained by using
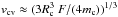 , with
mc the mass of the central body. Finally,
τcv = lcv/vcv.
, with
mc the mass of the central body. Finally,
τcv = lcv/vcv.
Parameters for the example objects.
Table 1 lists for the three examples the growth rate
for an inviscid fluid, and the damping rates computed for molecular and turbulent
viscosities. In the no slip case the damping rate D is given by
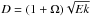 according to Eq. (26). We neglect the volume
damping term because Ω and Ek are small enough in both cases. In the free
slip case,
according to Eq. (26). We neglect the volume
damping term because Ω and Ek are small enough in both cases. In the free
slip case, 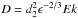 according to Eq. (36). For
d2 we choose 3.35, the value extracted from Fig. 8a. We neglect the terms which are relevant if Ω is large
(see the last paragraph in Sect. 4) because Ω is small enough in both cases. The ellipticity
is calculated according to
according to Eq. (36). For
d2 we choose 3.35, the value extracted from Fig. 8a. We neglect the terms which are relevant if Ω is large
(see the last paragraph in Sect. 4) because Ω is small enough in both cases. The ellipticity
is calculated according to 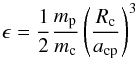 (38)with
mp the mass of the perturbing body and
acp the distance between the central and the perturbing body.
The Ekman number is calculated according to
(38)with
mp the mass of the perturbing body and
acp the distance between the central and the perturbing body.
The Ekman number is calculated according to
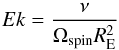 (39)with
RE = Rco the radius at the edge of
the outer conducting region in the case of the Earth and the Jupiter-Io system and
RE = Rc in the case V636 Centauri
and Ωspin = ΩF + ΩP.
(39)with
RE = Rco the radius at the edge of
the outer conducting region in the case of the Earth and the Jupiter-Io system and
RE = Rc in the case V636 Centauri
and Ωspin = ΩF + ΩP.
Instability is expected if the inviscid growth rate exceeds the viscous damping in Table 1. Table 2 summarizes the result of different modeling assumptions. In practice, the turbulence model decides on whether instability is predicted or not. Unfortunately, we have no turbulence model we can safely rely upon.
Summary of the stability characteristics of the flow for the examples Jupiter-Io (J-I) and V636 Centauri (VC).
6. Conclusion and discussion
We computed the linear stability limit of tidal flow within the anelastic approximation through a perturbation calculation in which the small parameter is the deformation of the central body from spherical shape. The instabilities are described as superpositions of two inertial modes of the rotating sphere. The perturbation calculation is tractable if the initially three dimensional problem of the computation of the inertial modes is separable and reduces to the solution of an ordinary differential equation. This is the case if the density profile obeys a power law. For an inviscid fluid, the growth rate of the combination of two chosen modes depends on the density profile, but the growth rate maximized over all possible combinations does not. Furthermore, the maximum growth rate is the same as the one known for elliptical instability in infinitely extended, incompressible fluids. The fact that one finds the same maximum growth rates in so widely different situations justifies some tolerance towards modeling assumptions. For example, we restricted our analysis to density profiles obeying power laws and to the boundary condition that the velocity normal to the boundary be zero at the surface. After the calculations presented here, we expect that different modes will be found to be the most unstable for more realistic assumptions, but that the stability limit of the flow will stay the same. In the same fashion, we do not expect the particular choice of the major axis parallel to the rotation axis in Eq. (14) to affect the stability limit.
We added viscous effects empirically. If friction at a solid boundary dominates dissipation, the stability is easily determined as a function of the rotation rates of the central body and the tidal companion, the tidal deformation, and the Ekman number. If on the other hand bulk dissipation dominates, the dissipation depends on the flow structure of the unstable modes and therefore on all details of the model, in particular the density profile. However, dissipation depends mostly on the spatial degree which on average obeys a simple scaling law as a function of tidal deformation, so that an estimate of the stability limit is still possible.
Viscous damping also depends on boundary conditions, and models of an object’s interior help to decide on which approximation to the viscous damping is most accurate. For instance, the dissipation in Ekman layers usually dominates if a solid core is present. However, if one wants to predict the stability limit of a particular astrophysical object, the biggest uncertainty comes from a possible turbulent viscosity. Progress in the calculation of tidal dissipation thus mostly hinges on advances in the treatment of turbulence.
Acknowledgments
The authors acknowledges research funding by Deutsche Forschungsgemeinschaft (DFG) under grant SFB 963/1, project A5.
References
- Abramowitz, M., & Stegun, I. A. 1972, Handbook of Mathematical Functions (New York: Dover Publications) [Google Scholar]
- Aldridge, K., Seyed-Mahmoud, B., Henderson, G., & van Wijngaarden, W. 1997, Phys. Earth Planet. Int., 103, 365 [Google Scholar]
- Archinal, B. A., A’Hearn, M. F., Bowell, E., et al. 2011, Celest. Mech. Dyn. Astron., 109, 101 [Google Scholar]
- Barker, A. J., & Lithwick, Y. 2013, MNRAS, 435, 3614 [NASA ADS] [CrossRef] [Google Scholar]
- Barker, A. J., & Lithwick, Y. 2014, MNRAS, 437, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Bayly, B. J. 1986, Phys. Rev. Lett., 57, 2160 [NASA ADS] [CrossRef] [Google Scholar]
- Bryan, G. H. 1889, Phil. Trans. R. Soc. London Ser. A, 180, 187 [Google Scholar]
- Cébron, D., Le Bars, M., Leontini, J., Maubert, P., & Le Gal, P. 2010a, Phys. Earth Planet. Inter., 182, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Cébron, D., Maubert, P., & Le Bars, M. 2010b, Geophys. J. Int., 182, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Cébron, D., Le Bars, M., Maubert, P., & Le Gal, P. 2012a, Geophys. Astrophys. Fluid Dyn., 106, 524 [NASA ADS] [CrossRef] [Google Scholar]
- Cébron, D., Le Bars, M., Moutou, C., & Le Gal, P. 2012b, A&A, 539, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cébron, D., Le Bars, M., Le Gal, P., et al. 2013, Icarus, 226, 1642 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., Baraffe, I., Leconte, J., Gallardo, J., & Barman, T. 2009, AIP Conf. Proc., 1094, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Clausen, J. V., Bruntt, H., Claret, A., et al. 2009, A&A, 502, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Craik, A. D. D. 1989, J. Fluid Mech., 198, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Darwin, G. H. 1879, Phil. Trans. R. Soc. London, 170, 1 [Google Scholar]
- DeWijs, G. A., Kresse, G., Vocadlo, L., et al. 1998, Nature, 392, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Eloy, C., Le Gal, P., & Le Dizès, S. 2003, J. Fluid Mech., 476, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Fabijonas, B. R., & Holm, D. D. 2003, Phys. Rev. Lett., 90, 124501(1) [NASA ADS] [CrossRef] [Google Scholar]
- Gledzer, E. B., & Ponomarev, V. M. 1977, Izvestiya Atmospheric and Oceanic Physics, 13, 565 [Google Scholar]
- Gledzer, E. B., & Ponomarev, V. M. 1992, Izvestiya Atmospheric and Oceanic Physics, 240, 1 [Google Scholar]
- Gledzer, E. B., Dolzhansky, F. V., Obhukov, A. M., & Ponomarev, V. M. 1975, Izvestiya Atmospheric and Oceanic Physics, 11, 617 [Google Scholar]
- Goldreich, P., & Nicholson, P. 1977, Icarus, 30, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J., & Oh, S. P. 1997, ApJ, 486, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Greenspan, H. P. 1968, The Theory of rotating Fluids (Cambridge: Cambridge University Press) [Google Scholar]
- Guillot, T., Stevenson, D. J., Hubbard, W. B., & Saumon, D. 2004, in Jupiter: The Planet, Satellites and Magnetosphere, F. Bagenal, D. Dowling, & W. McKinnon (Cambridge: Cambridge University press), 35 [Google Scholar]
- Guimbard, D., Le Dizès, S., Le Bars, M., Le Gal, P., & Leblanc, S. 2010, J. Fluid Mech., 660, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Herreman, W., Le Bars, M., & Le Gal, P. 2009, Phys. Fluids, 21, 046602 [NASA ADS] [CrossRef] [Google Scholar]
- Horedt, G. P. 1986, Ap&SS, 126, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Horedt, G. P. 2004, Polytropes (Dordrecht, Boston, London: Kluwer Academic Publisher) [Google Scholar]
- Ivanov, P. B., & Papaloizou, J. C. B. 2010, MNRAS, 407, 1609 [NASA ADS] [CrossRef] [Google Scholar]
- Kerswell, R. R. 1993, Geophys. Astrophys. Fluid Dyn., 72, 107 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kerswell, R. R. 1994, J. Fluid Mech., 274, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Kerswell, R. R. 2002, Ann. Rev. Fluid Mech., 34, 83 [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution (Berlin, Heidelberg: Springer Verlag) [Google Scholar]
- Lacaze, L., Le Gal, P., & Le Dizès, S. 2004, J. Fluid Mech., 505, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lacaze, L., Herreman, W., Le Bars, M.,Le Dizès, S., & Le Gal, P. 2006, Geophys. Astrophys. Fluid Dyn., 100, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Landman, M. J., & Saffman, P. G. 1987, Phys. Fluids, 30, 2339 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bars, M., Lacaze, L., Le Dizès, S., Le Gal, P., & Rieutord, M. 2010, Phys. Earth Planet. Inter., 178, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Lorenzani, S. 2001, Ph.D. Thesis, University of Göttingen, Germany [Google Scholar]
- Malkus, W. V. R. 1989, Geophys. Astrophys. Fluid Dyn., 48, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Miesch, M. S. 2005, Liv. Rev. Sol. Phys., 2, 1 [Google Scholar]
- Miyazaki, T. 1993, Phys. Fluids A: Fluid Dyn., 5, 2702 [NASA ADS] [CrossRef] [Google Scholar]
- Miyazaki, T., & Fukumoto, Y. 1992, Phys. Fluids A: Fluid Dyn., 4, 2515 [NASA ADS] [CrossRef] [Google Scholar]
- Miyazaki, T., Imai, T., & Fukumoto, Y. 1995, Phys. Fluids, 7, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I., & Lesur, G. 2012, MNRAS, 422, 1975 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I., & Lin, D. N. C. 2007, ApJ, 661, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Penev, K., Baranco, J., & Sasselov, D. 2009, ApJ, 705, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in Fortran 77 (Cambridge: Cambridge University Press) [Google Scholar]
- Rieutord, M. 1992, A&A, 259, 581 [Google Scholar]
- Rieutord, M. 2008, EAS Pub. Ser., 29, 127 [CrossRef] [EDP Sciences] [Google Scholar]
- Rieutord, M., & Zahn, J.-P. 1997, ApJ, 474, 760 [NASA ADS] [CrossRef] [Google Scholar]
- Seyed-Mahmoud, B., Henderson, G., & Aldridge, K. 2000, Phys. Earth Planet. Inter., 117, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Tassoul, J.-L. 1987, ApJ, 322, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Tassoul, J.-L. 1995, ApJ, 444, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Tassoul, M., & Tassoul, J.-L. 1997, ApJ, 481, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Waleffe, F. 1990, Phys. Fluids A, 2, 76 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Wicht, J., & Tilgner, A. 2010, Space Sci. Rev., 152, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y. 2005a, ApJ, 635, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y. 2005b, ApJ, 635, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
- Zhang, K., Earnshaw, P., Liao, X., & Busse, F. H. 2001, J. Fluid Mech., 437, 103 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Summary of the stability characteristics of the flow for the examples Jupiter-Io (J-I) and V636 Centauri (VC).
All Figures
 |
Fig. 1 a) Growth rates of modes (−1,1) for various n as a function of the compressibility parameter β for ϵ = 0.04, Ωp = 0 and Ek = 0. b) Corresponding δω. |
| In the text | |
 |
Fig. 2 Same as Fig. 1 but for ϵ = 0.16. |
| In the text | |
 |
Fig. 3 Frequencies of inertial modes in the co-rotating frame, q, for β = 0 (circles and squares) and β = 18 (x and plus) as a function of the spatial degree n. Only the modes with k = −1 (green, respectively plus and circles) and k = 1 (blue, respectively x and squares) are shown. |
| In the text | |
 |
Fig. 4 Maximum growth rates as a function of Ω for Ek = 0. For this figure we take into account all modes with | k| ≤ 10 and n ≤ 40. The (solid) black line in this figure is the growth rate given by Eq. (29). |
| In the text | |
 |
Fig. 5 Mean value of the spatial degree < n >, for the modes with a growth rate of at least 0.1σud (dashed lines) or 0.8σud (solid lines) as a function of ϵ for β = 0 (green x), β = 2.8 (red circles), and β = 18 (blue squares), together with fits according to Eq. (31). |
| In the text | |
 |
Fig. 6 Minimum value of n, nmin as a function of Ω for various ϵ and positive Ω. a) β = 2.8 and β = 18 and b) β = 0. |
| In the text | |
 |
Fig. 7 Same as in Fig. 6 but for negative Ω. |
| In the text | |
 |
Fig. 8 Maximum growth rates as a function of Ω for Ek ≠ 0. For this figure we take into account all modes with a maximum | k| ≤ 10 and n ≤ 40. a) Calculated for free slip boundary conditions according to Eq. (25). b) Calculated for no slip boundary conditions according to Eq. (26). The (solid) black line in this figure is the growth rate given by Eq. (29). The (dashed without marker) cyan line in a) is the growth rate given by Eq. (36) with d2 = 3.35. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


