| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322712 | |
| Published online | 13 February 2014 | |
Hydrogen lines as a diagnostic tool for studying multicomponent emitting regions in hot young stars: magnetosphere, X-wind, and disk wind
1
Pulkovo Astronomical Observatory of the Russian Academy of
Sciences,
Pulkovskoe shosse 65,
196140
St. Petersburg,
Russia
e-mail:
lvtamb@mail.ru, grinin@gao.spb.ru
2
The V.V. Sobolev Astronomical Institute of the St. Petersburg
University, Petrodvorets, 198904
St. Petersburg,
Russia
3
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
e-mail:
weigelt@mpifr-bonn.mpg.de
Received:
19
September
2013
Accepted:
3
January
2014
Infrared interferometric observations with high spatial and spectral resolution and their quantitative modeling provide us with a unique opportunity to improve our understanding of the circumstellar environment of young stars and the accretion-ejection process. The goal of this paper is to investigate various models of the emitting regions in young Herbig Ae/Be stars that consist of (i) a compact rotating magnetosphere; (ii) an X-wind; and (iii) a disk wind. These models can be used, for example, to quantitatively interpret line profile measurements and infrared interferometric observations with the AMBER instrument of the Very Large Telescope Interferometer (VLTI) in the high spectral resolution mode (R = 12 000). VLTI/AMBER observations allow us to resolve the disk wind region and study the flux contribution of the unresolved magnetosphere and X-wind region to the total line flux. Analyzing the results of our non-LTE calculations, we conclude that the mechanisms of the different broadening of emission lines of different series include (1) the kinematic expansion due to the motion of the outflowing, accelerating gas in the magneto-centrifugal disk wind; (2) the Stark effect; and (3) the rotation of the magnetosphere. We also investigated extinction effects that can influence the shape of the line profiles. We considered the obscuration of the outer disk wind by an opaque dust and gas disk, the obscuration of the disk wind by a flared disk or by dust in the disk wind itself, and absorption of the star and disk continuum radiation in the disk wind along the line of sight. We show that due to extinction effects, the line profiles can change from double-peaked to single-peaked and P Cygni profiles. We studied the contribution of the different components of the stellar environment to different hydrogen emission lines and investigated how this contribution is dependent on the model parameters. The results of this study can be used for the detailed modeling of the emitting regions of individual young stars.
Key words: line: profiles / techniques: spectroscopic / techniques: interferometric / stars: pre-main sequence / stars: winds, outflows
© ESO, 2014
1. Introduction
Hydrogen emission lines are present in the spectra of many astrophysical objects and are often used to model the emitting regions. High atomic series lines, in particular, the Brackett series, can be used for these studies (e.g., Garcia Lopez et al. 2006; Weigelt et al. 2007; Kraus et al. 2008; Donehew & Brittain 2010; Caratti o Garatti 2013; Lumsden et al. 2012). A comparison of these lines with the Hα lines shows that the latter are often substantially wider than the infrared lines (see, e.g., Hamann & Person 1992; Reipurth et al. 1996; Drew et al. 1997).
Several teams have modeled the hydrogen line profiles or interferometric observables of T Tauri stars (TTSs) or Herbig Ae/Be stars (HAEBEs) (e.g., Muzerolle et al. 2001; Kurosawa et al. 2006, 2011; Lima et al. 2010; Proga et al. 1998; Tambovtseva et al. 2001; Muzerolle et al. 2004; Rousselet-Perraut et al. 2010; Weigelt et al. 2011; Lumsden et al. 2012). It is difficult to investigate the structure of the emitting region in hot young stars because this region usually consists of several components. It generally includes an accreting zone (e.g., a magnetosphere) and an ejecting zone (e.g., a magneto-centrifugal disk wind or a jet). The role that these components play in the emission process probably varies between different stars. Therefore it is necessary to model many different stars to improve our understanding of these regions.
In this paper, we investigate the hydrogen line profiles of the Balmer, Paschen, and Brackett series and, in particular, their broadening under conditions that are typical in hot young Herbig Ae/Be stars, and we study the dependence of the line profiles on the model parameters. For this purpose we use the non-LTE solution for hydrogen atoms derived on the basis of the Sobolev approximation (Sobolev 1960) with exact integration over the whole emitting volume (Grinin & Tambovtseva 2011; Weigelt et al. 2011 and references therein). In Sect. 2, we briefly describe the model of the disk wind we used for HAEBEs and present the model parameters. The results of the line profile modeling are shown, including the influence from kinematic expansion and the Stark effect. Section 3 presents the results of the line profile modeling in the presence of a magnetosphere. Section 4 presents a comparison of the emitting regions of X-wind and disk wind models at Brγ frequencies, and Sect. 5 presents the results of the line profile modeling in the presence of extinction. The appendix contains additional material concerning line profile properties.
2. Disk wind model
Our modeling is based on the magneto-centrifugal disk wind (Blandford & Payne 1982). The model has successfully been applied to low-mass T Tauri stars and explains the formation of jets and their properties well (e.g., Königl 1991; Wardle & Königl 1993; Königl & Pudritz 2000; Ferreira et al. 2006; Ferreira 2007 and Lima et al. 2010).
The model we developed for the more luminous and massive Herbig Ae/Be stars was described in detail in Grinin & Tambovtseva (2011) and Weigelt et al. (2011). In the present paper, we briefly summarize the main properties of the model and the calculation method. We used an approach similar to that proposed by Shlosman & Vitello (1993) for cataclysmic variables and Kurosawa et al. (2006) for T Tauri stars. The method permits a simple parametrization of the disk wind and has geometric and kinematic properties similar to those used in MHD computations. The geometry of the disk wind assumed in this paper is presented in Fig. 1.
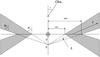 |
Fig. 1 Geometry of the disk wind model assumed in this paper. |
The center of the coordinates is located at point S. The tangential velocity component u(ω) and poloidal1 velocity component v(l) change along the trajectories of motion, or streamlines, as given by
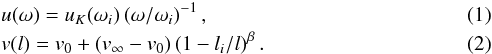 Here,
ω =
l sinθ is the distance from the axis
of symmetry for the point with coordinates (l,θ); ωi = li sinθ,
uK (ωi)
= (G M∗/ωi)1/2
at the starting point (ωi), v0 and
v∞
are the initial and terminal velocities, G is the gravitation constant, M∗ is the stellar
mass, and β is
a parameter.
Here,
ω =
l sinθ is the distance from the axis
of symmetry for the point with coordinates (l,θ); ωi = li sinθ,
uK (ωi)
= (G M∗/ωi)1/2
at the starting point (ωi), v0 and
v∞
are the initial and terminal velocities, G is the gravitation constant, M∗ is the stellar
mass, and β is
a parameter.
We assumed the initial velocity v0 to be the sound velocity in the disk wind, v∞ =fuK(ωi), where uK(ωi) is the Keplerian velocity at distance ωi from the star, and f is a scale factor.
The total mass-loss rate Ṁw is the integral over
the entire disk surface from which the matter outflow occurs,
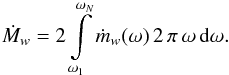 (3)Here, ṁw is the local mass-loss
rate through a unit area on the disk surface with ṁw(ω) ~ ω−γ,
and γ is a
model parameter. The factor of two in front of the integral takes mass loss from both disk
surfaces into account. The density of the matter along the streamlines is obtained from
v(l) and Ṁw through the mass
continuity equation, while the gas temperature along the streamlines is assumed to be
constant. This is a good approximation because according to Safier (1993) and Garcia et al. (2001), the disk wind is rapidly heated by
ambipolar diffusion to to a temperature of up to 10 000 K.
(3)Here, ṁw is the local mass-loss
rate through a unit area on the disk surface with ṁw(ω) ~ ω−γ,
and γ is a
model parameter. The factor of two in front of the integral takes mass loss from both disk
surfaces into account. The density of the matter along the streamlines is obtained from
v(l) and Ṁw through the mass
continuity equation, while the gas temperature along the streamlines is assumed to be
constant. This is a good approximation because according to Safier (1993) and Garcia et al. (2001), the disk wind is rapidly heated by
ambipolar diffusion to to a temperature of up to 10 000 K.
For simplicity, we considered a disk wind consisting solely of hydrogen atoms. We calculated the excitation and ionization states of the atoms using our codes developed by Grinin & Katysheva (1980), Grinin & Mitskevich (1990), and Tambovtseva et al. (2001) for media with steep velocity gradients. The radiation terms in the stationarity equations corresponding to transitions between discrete levels were taken into account in the Sobolev approximation (SA) (Sobolev 1960). After calculating the source function with the SA, we performed an exact integration over the whole volume of the emitting region.
The algorithm for our computations is as follows:
-
1.
We fix the parameters describing the wind geometry(θi,ωi) and its kinematics and matter ejection rate (Ṁw(θi),f,β) and compute the velocity and density distribution along the ith streamline.
-
2.
After subdividing the integration region into a grid with cells at the coordinates l,θ,ϕ, and after specifying the temperature regime in the wind, we solve the set of stationarity equations for the hydrogen atom for each cell and find the atomic level populations and gas-ionization state along each streamline. We considered a 15-level hydrogen atom plus continuum (see Grinin & Tambovtseva 2011; Weigelt et al. 2011 for more details).
-
3.
We compute the intensities of the selected hydrogen lines at the given frequencies. To compute the required variables for each point of the integration region, we use a double interpolation in l and ω.
To model B-type HAEBEs (HBEs), we used the parameters and emission spectra of the star MWC 297 (spectral type B1.5, L∗ = 10 600L⊙, Teff = 23 700 K, R∗ = 6.1 R⊙, M∗ = 10 M⊙; Kraus et al. 2008) as a typical representation of Herbig Be stars and the parameters of the Herbig Ae star RR Tau (spectral type A0, L∗ = 50 L⊙, Teff = 10 000 K, R∗ = 2.1 R⊙, M∗ = 2.5 M⊙; Rostopchina 1999) to model HAEs. The models B1 to B6 refer to the HBEs; models A1 to A7 refer to HAEs. The gas electron temperature Te is assumed to be constant and equal to 10 000 K in all models except B5 and B6; in the latter models Te = 8000 K.
The choice of the disk wind parameters is conditioned by the results of the magneto-centrifugal disk wind model for TTSs with some changes in the launching region because of the difference in the inner accretion disk structure (e.g., Natta et al. 2001; Dullemond et al. 2001). The range of the mass-loss values is based on the estimates of mass loss and accretion rates from the literature (e.g., Hillenbrand et al. 1992; Lada & Adams 1992; Hartmann et al. 1993; Tambovtseva et al. 2001; Muzerolle et al. 2004; Garcia Lopez et al. 2006; Donehew & Brittain 2011; Klaassen et al. 2013; Mendigutía et al. 2013).
All our models assumed the accretion disk to be transparent for radiation up to a distance equal to the dust sublimation radius, which is about 3 AU for HBEs and 0.4 AU for HAEs. Beyond the sublimation radius, we considered the disk to be an opaque screen shielding the disk wind moving away from the observer, that is, the observer does not see the entire emission from the backside of the disk (see Sect. 5 for more details). In all cases, except when otherwise mentioned (Sect. 5), the intensity of the lines are shown in units of the stellar continuum.
 |
Fig. 2 Top: sketch of disk wind models with different mass loading. The length of the streamlines is proportional to the local mass-loss rate. Top left: the bulk of the disk wind is ejected along streamlines near the star (γ = 4, model B1). Top right: the bulk of the disk wind is ejected along the outer streamlines (γ = 1, model B2). Middle: kinematics for models B1 (left) and B2 (right). The poloidal velocity at the first streamline (solid) and the sixth outermost streamline (dashed) are presented. The dotted lines represent the rotational velocity component. Bottom: the computed Hα (blue), Paα (green), and Brγ (red) line profiles (normalized to one) of models B1 (left) and B2 (right) for a disk inclination angle (the angle between the system axis and the viewing direction) of 20°. |
2.1. Kinematic expansion effect
We considered two variants of the disk wind model with different geometries and a mass loading parameter γ. The disk wind structure, including an inclination of streamlines and mass loading (the so-called ejection efficiency), depend on the strength and configuration of the magnetic field in the disk (see, e.g., Ferreira 2007, and references therein). Two configurations were chosen to demonstrate the role of the radial expansion in the rotating and accelerating gas (Fig. 2).
One type of model implies that the moving gas is restricted within two cones with the angles θ1 = 30° and θN = 60° for the first and last streamlines, respectively (Fig. 2 left). The optically thin and optically thick lines originate in different regions of the disk wind due to opacity effects. With this type of geometry, the zone of the optically thin line formation is located near to the base of the disk wind, where the poloidal velocities are still low (because the wind is not very accelerated yet) and therefore do not broaden the line much. Thus, the optically thin lines are narrower than the optically thick lines, such as Hα, which originates in a more extended, high-velocity region of the disk wind.
The second type of disk wind model (Fig. 2 right) implies that the disk wind has a flat configuration (θ1 = 45°,θN = 60°), and the bulk of the matter is loaded on the outer streamlines (the parameter γ is small). With this type of geometry, the zone of the optically thin line formation “shifts” farther away from the star. Thus, one can expect that a different broadening of the lines of different series can be caused by opacity effects.
Disk-wind model parameters.
Figure 2 shows the schemes of the two geometries mentioned above together with the behavior of the poloidal and rotational velocity components and the resulting computed line profiles of Hα (6562.8 Å), Paα (1.876 μm) and Brγ (2.166 μm) for the two types of models calculated for a luminous Herbig Be star. The velocities are shown for the innermost streamline 1 and the outermost streamline 6. The line profiles are given for the inclination i = 20°, which is close to that obtained from the modeling and observation of the star MWC 297 (Weigelt et al. 2011). In spite of the different geometries, we obtained a similar opacity dependence. The line profiles show that in all cases the optically thin Brγ line is narrow and the optically thick Hα line is wide. To demonstrate how the line widths change with inclination, we calculated the Hα and Brγ line profiles for the additional model B3 (Table 1), which is the same as B2 (Fig. 2), but with a lower acceleration of matter (β = 2). The results are presented in Fig. 3. For a small inclination (Fig. 3a, b), the Hα line profile is much wider than that of the Brγ line. When the system is observed under large inclinations (Fig. 3c, d), the difference between line profiles becomes very small because the projection of the poloidal velocity on the line of sight decreases.
 |
Fig. 3 Top: emission profiles of the Hα (solid) and Brγ (dashed) lines of model B3. Bottom: the same for model A1. Inclinations are 0 a); 20 b); 45 c); and 75°d). |
In Fig. 3 we present the Hα and Brγ line profiles for a Herbig Ae star (model A1 in Table 1) for comparison. HAEs apparently do not show the differential broadening HBEs do. The shapes of the calculated HAEs line profiles differ from those of HBEs. However, the general trend is the same: The width of the optical and infrared lines are most different when observed nearly pole-on. However, in the case of the HAE stars, the Hα line profiles are highly asymmetric due to self-absorption. In contrast, the optically thinner Brγ line does not show this asymmetry.
Figure 4 shows the changes in the Hα and Brγ line profiles in model B3 for different parameters β indicating different accelerations: β = 0.7 (rapid acceleration), β = 2 (moderate acceleration), and β = 5 (very low acceleration). In all cases, the other kinematic parameters remain the same. The inclination 0° (pole-on) is chosen to obtain the strongest acceleration effect. One can see that a faster acceleration leads to a wider line profile. This is easy to understand because in this case, the highest (terminal) velocities are reached faster. In the same figure, we also show the analog line profiles for the case when the disk is transparent for the radiation of the disk wind up to the distance of only rtr = 0.5 AU from the star (i.e., instead of up to the sublimation radius of 3 AU as for the other HBE models). One can see that the Hα line profile changes dramatically. In contrast, the Brγ line practically does not change except for rapid acceleration. Below, we discuss screening effects in more detail.
 |
Fig. 4 Top: comparison of the normalized emission profiles of the Hα (solid) and Brγ (dashed) lines of model B3 with different values of the parameter β of the velocity law. Inclination i is 0° and β = 0.7a); 2 b); and 5 c). Bottom: the same for a disk wind with the screen discussed in the text (rtr = 0.5 AU). |
Figure 5 presents the brightness maps of the disk wind of a Herbig Ae star (model A2 in Table 1) at various observed radial velocities within the Hα and Brγ line frequencies. The radial velocities are marked in the plots in km s-1. These maps are useful for showing the actual observable emitting region of the disk wind across the two lines. The brightness scale is arbitrary and different for the Hα and Brγ lines to emphasize the distinctness of the images.
Figure 6 presents the Hα and Brγ brightness maps for velocity 0 km s-1 with identical brightness scales. For the chosen mass-loss rate (10-7 M⊙ yr-1), the Brγ intensity distribution at zero radial velocity is slightly asymmetric because the gas in the emitting region is partly nontransparent. The image is symmetric for optically thin gas, and our calculations confirm this for models with lower mass-loss rates (<10-7 M⊙ yr-1).
 |
Fig. 5 Images of the disk wind in the Hα and Brγ lines for model A2 for a mass-loss rate of 10-7M⊙ yr-1 and inclination i = 90°. The brightness maps are presented for several radial velocities shown in the panels in km s-1 (see details in the text). The colors represent the intensity in erg ster-1 s-1 Å-1 cm-2. |
 |
Fig. 6 Same intensity distribution as in Fig. 5 for the radial velocity 0 km s-1, but here both images are shown with the same intensity scale. |
2.2. Stark effect
Observations of Herbig Ae/Be stars (e.g., Finkenzeller & Mundt 1984; Reipurth et al. 1996; Drew et al. 1997; Grinin et al. 2001) reveal very wide Balmer lines in the spectra of some stars. For optically thick lines such as Hα, Stark broadening can cause the observed line widths. It should be noted that the Stark wings in the profile of the absorption coefficient do not play an important role in the formation of the spectral line when a medium is optically thin in the line frequencies because in this case the main part of the radiation is concentrated on the Doppler part of the profile. The Stark wings (as all Lorentz wings in the absorption coefficient profile) are only important in optically thick media.
The effect of this mechanism on the Balmer line profiles for T Tauri stars has been
investigated by Muzerolle et al. (2001) (in the
context of magnetospheric accretion) and Kurosawa et al. (2006) (magnetospheric accretion and disk wind). As a result, the
Hα line
profiles computed with and without damping are significantly different: the equivalent
width and line wings strongly increased in the former case. To determine the effect of the
Stark broadening for the Herbig Ae/Be stars, we used a Voigt profile of the absorption
coefficient instead of a Doppler profile. We used the Voigt function H(a,y) of
the form (Mihalas 1978) 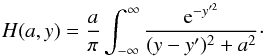 (4)Here, a = Γ/(4πΔλD),
y = (λ − λ0)/ΔλD,
y′ = (λ′ − λ0)/ΔλD,λ0
is the line center wavelength, the Doppler line width is
(4)Here, a = Γ/(4πΔλD),
y = (λ − λ0)/ΔλD,
y′ = (λ′ − λ0)/ΔλD,λ0
is the line center wavelength, the Doppler line width is
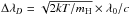 , where T is the temperature of the
gas, mH is the mass of the hydrogen atom, and
k is the
Boltzmann constant. The damping Γ is taken from Vernazza et al. (1973):
, where T is the temperature of the
gas, mH is the mass of the hydrogen atom, and
k is the
Boltzmann constant. The damping Γ is taken from Vernazza et al. (1973): 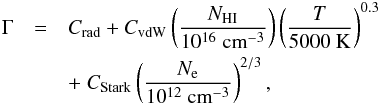 (5)where
nHI and ne are the
number density of neutral hydrogen atoms and the electron density, respectively,
Crad,CvdW,
and CStark are natural, van der Waals, and
linear Stark broadening constants, respectively. The values of the broadening constants
for Hα are
taken from Luttermoser & Johnson (1992).
(5)where
nHI and ne are the
number density of neutral hydrogen atoms and the electron density, respectively,
Crad,CvdW,
and CStark are natural, van der Waals, and
linear Stark broadening constants, respectively. The values of the broadening constants
for Hα are
taken from Luttermoser & Johnson (1992).
Figure 7 presents the Hα line profiles calculated with the Voigt and Doppler profiles of the absorption coefficient (model B5). One can see that the Stark effect significantly broadens the Hα line. At the same time, this effect does not noticeably influence the Brγ line because the gas emitting at the frequencies of this line is optically thin.
 |
Fig. 7 Left: the Hα line profile calculated with Voigt (solid) and Doppler (dashed) profiles of the absorption coefficient (model B5; inclination i = 20°). Right: the Hα (solid) and Brγ (dashed) line profiles computed in model B5 for a Herbig Be star (inclination i = 20°). |
3. Hybrid model: disk wind, X-wind, and magnetosphere
The most prominent optical line in the spectra of the Herbig Ae/Be stars, the Hα line, can have various profile shapes (e.g., Reipurth et al. 1996). All kinds of shapes from the classification by Reipurth et al. are observed: P Cygni, single- and double-peaked (see, e.g., Böhm & Catala 1995; Grinin et al. 2001; Mora et al. 2001; Feigelson et al. 2003; Beskrovnaya & Pogodin 2004; Movsessian et al. 2008; Grady et al. 2011; Montesinos 2009; Mendigutía 2012). Such a vast sample of profile shapes suggests that this line originates in a very complex environment possibly including the accretion disk, disk wind, jet, and magnetosphere. Therefore, the question arises, which components of the complex, multicomponent environment of intermediate-mass young stars are responsible for the line profiles and have to be modeled? To answer this question, we considered three components of a typical Herbig Ae star’s environment with parameters of the star RR Tau discussed in Sect. 2. All three model components are sketched in Fig. 8: magnetosphere (MS), X-wind, and disk wind.
 |
Fig. 8 Three components of the hybrid model (Sect. 3): magnetosphere, X-wind, and disk wind (not to scale.) |
The disk-wind model is described in Sect. 2. To model the X-wind (whose physical mechanism has been proposed by Shu et al. 1988), we used a similar approach as for the disk wind, but with the following required modification: the X-wind starts only near the truncation radius; therefore, the wind-launching region is very narrow compared with the disk wind.
Magnetospheric accretion models are well developed for T Tauri stars (Königl 1991; Hartmann et al. 1994; Ostriker & Shu 1995; Muzerolle et al. 1998, 2001; Kurosawa et al. 2006). The structure and parameters of the magnetosphere in HAEBEs are still not fully understood. Natta et al. (2000) presented direct evidence of the gas infall in HAEs. Using a non-LTE analysis of the line optical depths, they showed that the infalling gas cannot be heavily hydrogen depleted, which suggests a similarity between HAEs and classical T Tauri stars, where gas infall occurs in an analogous fashion. Estimates of the accretion rates for HAEs obtained by modeling the line profiles have been made, for example, by Tambovtseva et al. (2001), Muzerolle et al. (2004), and Mendigutia et al. (2011).
Unlike for T Tauri stars, it is not well known whether Herbig Ae stars possess a well-developed magnetosphere. HAEs differ from TTSs for the following reasons:
-
HAEs are rapid rotators;
-
they are much more luminous;
-
their own magnetic fields are probably very weak2;
-
veiling in the spectra is absent.
When modeling the magnetosphere in HAEs, the following has to be taken into account: (i) The inner accretion disk cannot be treated as cool; (ii) the rotation of the magnetosphere cannot be neglected; and (iii) the rotation of the star has to be included. In the papers cited above, each team chose different approaches to study magnetospheric accretion onto Herbig Ae/Be stars. In our paper (Tambovtseva et al. 2001), we considered a compact, rapidly rotating magnetosphere through which a free-fall gas motion occurs. The rotation of the star as well as the inner warm accretion disk were also taken into consideration. This modeling successfully reproduced the line profiles of the first three lines of the Balmer series for the UX Ori-type stars (UXORs). Muzerolle et al. (2004) applied a magnetospheric accretion model developed for TTSs to Herbig Ae stars and also to UXORs and reproduced NaD and Hα line profiles, decreasing the rotation velocity of the star in order to increase the size of the magnetospheric zone. Mendigutía et al. (2011), using the same scheme, reproduced the Hα and NaD line profiles of the UX Ori-type star BF Ori, one of the most slowly rotating UXORs.
Our approach is as follows: (i) we include the rotation of the star and the rotation of the magnetosphere; (ii) we simulate a situation where rotating, free-falling gas reaches the star at a latitude of about 60° rather than at the equator.
According to Elsner & Lamb (1977), the
accretion disk is truncated at radius rT in magnetospheric accretion. Measured
in stellar radii of a Herbig Ae star (e.g., 2 R⊙ for a star like RR Tau), 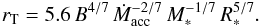 (6)Here,
B is the
average surface magnetic field strength in units of kG, the mass accretion rate
Ṁacc is in units of 10-8 M⊙ yr-1, the stellar mass
M∗
is in units of 2.5 M⊙, and the stellar radius R∗ is in units of
2 R⊙.
(6)Here,
B is the
average surface magnetic field strength in units of kG, the mass accretion rate
Ṁacc is in units of 10-8 M⊙ yr-1, the stellar mass
M∗
is in units of 2.5 M⊙, and the stellar radius R∗ is in units of
2 R⊙.
The measured longitudinal field strengths of Herbig Ae stars are weak: typically a few hundred Gauss (Wade et al. 2007, 2009; Alecian et al. 2008; Hubrig et al. 2007). Using the value 100 G in Eq. (6), we obtain rT = 1.5 R∗ for Ṁacc = 10-8 M⊙ yr-1 and 2.1 R∗ for Ṁacc = 10-7 M⊙ yr-1 (for B = 500 G, the corresponding rT are 3.8 and 7 R∗). By definition the truncation radius is shorter than the co-rotation radius, which is typically 2 R∗. We assumed in the following that the truncation radius is equal to the corotation radius rc. This suggests that the accretion disk of HAEs, in contrast to TTSs, can approach very close to the star and can be more heated by the stellar radiation.
Compared with our previous magnetospheric model (Tambovtseva et al. 2001), our new model employs more realistic temperature and velocity
laws. In the following, we briefly summarize the model assumptions and parameters. We
calculated the corotation radius rc and determined the rotation velocity of
the gas, U(rc), at radius
rc
for a rapidly rotating young star. Then, we assumed the value of the rotational velocity of
the star, U∗, at the point where the rotating,
infalling gas reaches the star. With the weak magnetic fields found in Herbig Ae stars, one
cannot expect with confidence that the magnetic field will control the gas motion and
transport the gas up to the poles through the channels corresponding to the dipole magnetic
lines3. Therefore, we assumed that the magnetosphere
region has a disk-like structure with a height hm, and the accreting gas strikes the
stellar surface at some altitude between the equator and pole. To avoid solid-body rotation,
we assumed that the gas rotational velocity component u(r) changes
as 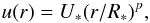 (7)where U∗ is the
rotational velocity of the star at a latitude of about 60°, r is the distance of the
star, and p is
a parameter. The poloidal velocity of the gas, v(r), is assumed to be equal to the
thermal velocity at rc, v0, and its final
value at the stellar surface is derived from the equation of motion for the rotating medium
in the gravity field:
(7)where U∗ is the
rotational velocity of the star at a latitude of about 60°, r is the distance of the
star, and p is
a parameter. The poloidal velocity of the gas, v(r), is assumed to be equal to the
thermal velocity at rc, v0, and its final
value at the stellar surface is derived from the equation of motion for the rotating medium
in the gravity field: 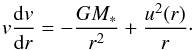 (8)The electron temperature
Te
is assumed to change as
(8)The electron temperature
Te
is assumed to change as 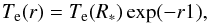 (9)where r1 = ((r − R∗)/R∗)q,
Te(R∗) is the
temperature of the gas near the star surface, and q is a parameter. It should be noted that the best
validity range of inclinations for this approach is 40–90°.
(9)where r1 = ((r − R∗)/R∗)q,
Te(R∗) is the
temperature of the gas near the star surface, and q is a parameter. It should be noted that the best
validity range of inclinations for this approach is 40–90°.
In this section, we consider a hybrid model consisting of a compact rotating magnetosphere from which the matter accretes onto the star and an outflow caused by a wind originating on the disk surface. We considered two wind models: an X-wind with a very narrow launch region starting just from the corotation radius, and an extended disk wind starting farther away from the star. Assumed combinations of the emitting regions in the hybrid models are as follows: MS + X-wind (model A), and MS + disk wind (model B). When calculating the population of the hydrogen atomic levels, we took the stellar radiation and the gas dynamics into account. The parameters of the X-wind and disk wind models used in the hybrid model are listed in Table 2. The kinematics and temperature law in the magnetosphere are described with Eqs. (7)–(9). The parameters of the magnetospheric model are as follows: Te(R∗) = 10 000 K, q = 1.5, U(r∗) = 70 km s-1, half-thickness hm is 0.75 R∗ and rC = 2 R∗. The calculations were carried out for a typical Herbig Ae star with an effective temperature of 10 000 K, M∗ = 2.5 M⊙ and R∗ = 2.1 R⊙, which are the parameters of the star RR Tau (Rostopchina 1999). The stellar radiation was calculated using the Kurucz model (Kurucz 1979). The accretion rates range from 10-8 to 10-7 M⊙ yr-1. The corresponding mass-loss rate was chosen as (0.1−0.3)Ṁacc.
Parameters of the X-wind and the disk-wind models discussed in Sect. 3 (hybrid model).
 |
Fig. 9 Behavior of the gas electron temperature in the accreting zone for different power indices q marked at the curves (left) and velocity components (right). |
Figure 9 shows the behavior of the electron temperature in the accreting zone for different power indices q (left) and the velocity field (right). With the help of non-LTE calculations, we investigated the influence of the excitation and ionization conditions in the accreting gas on the Hα (Fig. 10) and Brγ (Fig. 11) line profiles. These figures show how the line profiles change between the magnetosphere models MS1 (the populations of the atomic levels are controlled by the star radiation and the gas kinematics) and MS2 (the population atomic levels are controlled by the gas kinematics). The line profiles are given for rotating and nonrotating magnetospheres. The case when the star is “switched off” (MS2) is quite realistic. This means that the matter accreting onto the star is so dense that the radiation of the star has little influence on the excitation and de-excitation of the atomic levels. Both the Hα and Brγ line profiles little change their shape with inclination from moderate to large ones. The rotation of the gas in the magnetosphere leads to noticeable changes in the shapes and widths of the line profiles, especially in the Hα line. When the star radiation is not taken into account when calculating the ionization state and the populations of the atomic levels (MS1 model), a broadened double-peaked profile is obtained because of the rotation effect, and a more narrow triangle-like in the case without rotation. In MS2 model, the rotation only broadens the profile. The same is valid for the Brγ line but not as strongly.
 |
Fig. 10 Top: Hα line profiles of the magnetospheric accretion model MS1 with (left) and without (right) rotation and Ṁacc = 1 × 10-7 M⊙ yr-1. The numbers in the panel indicate the inclination angles i. Bottom: the same for model MS2. |
 |
Fig. 11 Top: Brγ line profiles in the magnetospheric accretion model MS1: with (left) and without (right) rotation and Ṁacc = 1 × 10-7 M⊙ yr-1. The numbers in the panels describe the inclination angle i. Bottom: the same for model MS2. |
 |
Fig. 12 Hα and Brγ line profiles for scenario A (i.e., hybrid model MS + X-wind, top) and B (i.e., hybrid model MS + disk wind, bottom): the emission line formed in the MS is shown by the blue line, in the X-wind (A) or disk wind (B) by the red line. The black line represents the line profile forming in both regions. Inclinations are marked in each panel. |
In Fig. 12, we present the Hα and Brγ hybrid model line profiles forming according to scenario A (i.e., MS1 + X-wind) and B (i.e., MS1 + disk wind). The blue line represents the profile caused only by the emission from the magnetosphere, the red line represents the profile caused only by the emission from the X-wind region (A) or disk wind (B) with the parameters of the models from Table 2, and the black line is the line profile caused by both model components. It is taken into account that emission forming in the magnetosphere may be absorbed by the matter in the wind. In all scenarios, the accretion rate is Ṁacc = 1 × 10-7 M⊙ yr-1 and Ṁw/Ṁacc = 0.1. In the appendix, we show a case where Ṁacc = 1 × 10-8 M⊙ yr-1 with the ratios Ṁw/Ṁacc = 0.1 and 0.3 (Fig. A.3).
From our calculations, we conclude that with the accretion and mass loss rates assumed, the presence of a magnetosphere can broaden the line profiles mainly in the wings. The effect of the line profile broadening decreases with increasing inclination. The influence of the magnetosphere also depends on the Ṁacc/Ṁw ratio: the influence decreases when this ratio increases.
4. Comparison of X-wind and disk-wind-emitting regions at different wavelengths across the Brγ line
The wavelength-dependent size of the Brγ emitting region has been investigated by several teams in the context of the interpretation of interferometric observations (e.g., Malbet et al. 2007; Kraus et al. 2008, 2012; Eisner et al. 2007, 2010; Weigelt et al. 2007, 2011). Because only a few Herbig stars have been investigated, it is difficult to make a final conclusion on the emitting region, except to state that the Brγ line emission probably traces the compact magnetospheric accretion region, the X-wind region, or the more extended disk-wind region in these stars.
 |
Fig. 13 Model images of the disk wind (model A2, top) and model images of the X-wind (Table 2, bottom) in the Brγ line at the radial velocity 0 km s-1. The mass-loss rate used in both models is 10-7 M⊙ yr-1. Edge-on (left) and pole-on (right) orientations are presented. The brightness scale is arbitrary and given in logarithmic units. |
In Figs. 13 and 14, we present the brightness maps of the disk wind model A2 and the X-wind model with parameters from Table 2 at three different wavelengths within the Brγ line expressed in radial velocities (0 and ±50 km s-1). To compare the emitting regions correctly, we calculated the X-wind model with the same mass loss rate, 10-7 M⊙ yr-1, as in A2. Images are shown edge-on and pole-on. One can see from the figures that the X-wind pole-on images are much smaller than the disk wind images at all presented velocities. The edge-on images of the disk wind at nonzero radial velocities are asymmetric, while those of the X-wind are practically unchanged.
The wavelength-dependent model images of the X-wind and disk wind intensity distributions discussed above (e.g., Figs. 5, 6, 13, and 14) are very useful for quantitative interpretation of infrared interferometric observations of Herbig stars. Infrared interferometry can provide us with unique insights into the inner wind region of young stellar objects (YSOs) because this observing technique allows us to study YSOs with unprecedented angular resolution. Studies of accretion and ejection processes in the wind region of YSOs are of fundamental importance for our understanding of star formation. To study these processes, we have to resolve the innermost wind-launching regions in the continuum and in lines. Infrared interferometry is able to study both the gas and dust distribution in the innermost AU or even sub-AU environments of YSOs and constrain their physical properties (e.g., Dullemond & Monnier 2010). Furthermore, the unique combination of high spatial resolution and additionally high spectral resolution (R = 12 000) offered by AMBER VLTI instrument allows us to derive kinematic properties (e.g., Dullemond & Monnier 2010). The spatial resolution of AMBER is high enough to resolve the disk wind region of Herbig stars, whose size is approximately 0.1 to 10 AU (see Table 1). For example, the disk wind size of the Herbig star MWC 297 was determined to be ~6.3 mas (HWHM) or ~1.6 AU (Weigelt et al. 2011). The much more compact magnetosphere of Herbig stars (e.g., size ~a few stellar radii as in the examples calculated in Sect. 3) and inner dominant X-wind region (see Figs. 13 and 14) are essentially unresolvable for current infrared interferometers. Therefore, infrared interferometry can only determine whether a point-like magnetosphere or X-wind emission region is present and measure its flux contribution to the total emission line flux.
For the quantitative interpretation of interferometric observations, the model images (e.g., Figs. 5, 6, 13, and 14) were compared with the available interferometric observations of the astronomical target in the following way. From the model images, we derived the visibilities, wavelength-differential phases and closure phases of the model images. In the next step, we compared these model visibilities and phases with the corresponding interferometrically observed visibilities and phases of the astronomical target. Furthermore, we compared the line profile of the model and the target. This comparison of the target with model predictions allowed us to constrain physical parameters of the disk wind, as described in more detail in our MWC 297 project (Weigelt et al. 2011).
5. Screening and extinction effects
In this section, we consider the dependence of the line profiles on extinction effects. Two effects are illustrated in Fig. 15. In a complex environment, one can expect screening caused by an opaque gas and dust disk, meaning that the observer does not see the entire emission from the backside of the disk (Fig. 15, left). The disk becomes nontransparent starting at the sublimation radius or even closer to the star because of an optically thick gas disk or refractive dust grains in the inner region. In this case, the part of the wind that moves away from the observer (i.e., behind the disk; see Fig. 15) may be partially obscured. Therefore, the red part of the line profile will be changed. Changes in the Hα, Paβ, and Brγ lines due to this screening effect (scenario in Fig. 15 left) are shown in Fig. 16. The line profiles depend on the radius rtr at which the disk becomes opaque for the disk wind radiation. The derived line profiles are shown for two different inclinations: close to pole-on (20°) and close to edge-on (70°).
 |
Fig. 15 Illustration of screening effects. Left: obscuration by an opaque disk that becomes opaque at radii larger than rtr. Right: obscuration by a flared dusty disk or dusty disk wind. |
 |
Fig. 16 Screening effects (scenario in Fig. 15left). The Hα (top), Paβ (middle), and Brγ (bottom) line profiles in model A7 for the different rtr: 200 R∗ (solid), 30 R∗ (dashed), and 20 R∗ (dotted-dashed). |
Note that the Paβ and Brγ lines vary in a different way. A similar effect was reported by Kraus et al. (2008), who presented VLT/ISAAC observations of the blueshifted Brγ and Paβ lines for two stars: HD 163296 (=MWC275, spectral type A3, i ~ 46−60°) and V921 Sco (spectral type B0, i ≤ 70°). This blueshift effect can in principle be explained by screening of the red part of the disk wind by a dusty opaque disk.
Figure 16 shows that the inclination angle plays an important role. One can see that the Hα line profile dramatically changes if an opaque disk obscures the outer part of the disk wind. However, the Brγ line remains almost unchanged except for very rapid acceleration. This suggests that the Brγ line forms in a region close to the star (≤rtr).
 |
Fig. 17 Influence of screening by an optically thick, dusty disk wind or a flared dusty disk (scenario in Fig. 15 right) on the Brγ line profile (model B6; inclination angle i = 70°; see Table 1). The solid line represents the unscreened line profile, while the long-dashed (hs = 100 R∗; θ = 20°), short-dashed (hs = 120 R∗; θ = 20°), and dotted-dashed (hs = 130 R∗; θ = 25°) lines show models with screening. |
 |
Fig. 18 Brγ line
profile (model A1) normalized to the continuum of the accretion disk plus continuum of
the star with absorption of the disk and star continuum radiation by the opaque disk
wind taken into account. Top: i = 50°,
middle: i = 70° and bottom:
i = 80°. The ratio of the disk
continuum |
The second reason for changes in the line profiles due to screening effects is the obscuration of the disk wind by optically thick layers of a flared disk or dust in the disk wind itself (Fig. 15, right). In this case, mainly the blue part of the line profile is influenced; that is, the line profile becomes redshifted (Fig. 17). To demonstrate this effect more clearly, we chose a model containing an extended disk wind with a small θ1 (model B6). We simulated this screening effect by introducing a screen with a sharp upper boundary at a given distance from the center (input parameters are the angle θ under which a screen is seen from the star center and the height hs of the screen counted from the disk midplane to the disk surface). If hs is increased, the line profile will change from double-peaked to a strongly asymmetric single peak. This effect can be significant for large inclinations.
A third type of the line profile modification in the context of extinction effects may be
caused by changes in the disk continuum due to the absorption of the disk radiation in the
disk wind itself. Together with the absorption of the stellar radiation in the disk wind,
this effect leads to a very interesting result: single- or double-peaked line profiles
transform into P Cygni-type profiles analog to that originating in expanding spherical
stellar winds. This phenomenon can explain P Cygni profiles observed in young
intermediate-mass stars that do not have stellar winds. Figure 18 shows the transformation of the Brγ line profile for the cases
with different ratios Rcon of the disk continuum
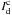 to the stellar
continuum
to the stellar
continuum 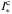 (
(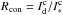 ). This effect can be
obtained if (i) the disk wind is powerful enough to absorb the continuum radiation (e.g., if
the mass-loss rate is higher than or on the order of 10-7 M⊙ yr-1); and (ii) the disk continuum
contributes noticeably to the total continuum compared to the star. In Table 3, we give the
values of Rcon calculated in the far outer wing of the
line for inclinations 50, 70 and 80°. Figures 18 and 19 present the Brγ line profiles for all these
values (model A1). The profiles marked with “a” in the panels are calculated with negligible
contribution of the disk continuum.
). This effect can be
obtained if (i) the disk wind is powerful enough to absorb the continuum radiation (e.g., if
the mass-loss rate is higher than or on the order of 10-7 M⊙ yr-1); and (ii) the disk continuum
contributes noticeably to the total continuum compared to the star. In Table 3, we give the
values of Rcon calculated in the far outer wing of the
line for inclinations 50, 70 and 80°. Figures 18 and 19 present the Brγ line profiles for all these
values (model A1). The profiles marked with “a” in the panels are calculated with negligible
contribution of the disk continuum.
Disk-to-star continuum ratio Rcon.
 |
Fig. 19 Same as in Fig. 18 for the case of Rcon = R5 from Table 3. Inclinations are marked in the panels. |
The line profiles become strongly asymmetric and redshifted except for nearly edge-on orientation (80°). Because the absorption in the disk wind and the ratio Rcon are different for optically thick and thin hydrogen lines, the lines of different series can have different shapes or shifts. For example, in the star PV Cep (A5), the ratio Rcon for Brγ is higher than that for Paβ by about a factor of 7 (Caratti o Garatti et al. 2013). Figure 20 illustrates a case when Rcon for the Brγ line is equal to R5 (Table 3), and for the Paβ line it is seven times lower. For the reasons mentioned above, the Brγ and Paβ lines differ significantly in their shapes and intensities.
 |
Fig. 20 Comparison of the Brγ and Paβ line profiles (model A1; Rcon for the Brγ line is equal to the R5 values and for the Paβ line the values are seven times lower; inclination 50°). See text for details. |
It should be noted that in the case of strong extinction, such objects are mainly observed due to radiation scattered by the circumstellar dust. This can significantly change the line profile and transform the double-peaked profile to the single-peaked lines (see, e.g., Grinin et al. 2012).
6. Summary and conclusion
 |
Fig. A.1 Hα line profiles in models A1, A2, A3, and A4 (from bottom to top). The inclination i is marked in the panels. |
The aim of the present paper was to investigate the properties of the hydrogen lines of different series in Herbig Ae/Be stars to study the following questions: (i) which physical mechanism is responsible for the different broadening of different hydrogen emission lines? (ii) why are the profiles of the emission lines of many stars seen at large inclinations double- or single-peaked? (iii) which emitting regions contribute to the formation of different emission lines? for this purpose, we developed hybrid models that consist of a magnetosphere and an X-wind or disk wind component and calculated the influence of these components on the emission line profiles. Using these models, we aim to predict the line profiles and spatial intensity distributions of the modeled emitting regions because both are needed to interpret infrared interferometric observations performed with high spectral resolution. We obtained the following results:
-
(1)
The kinematic expansion effect, that is, the formation ofemission lines in the outflowing, accelerating gas in themagneto-centrifugal disk winds, is a mechanism that is probablyresponsible for the line broadening. The main reason for thedifference in the line widths of different lines (e.g., Hα and Brγ) is the strong stratification of the emitting disk wind regions by kinematic conditions in combination with the large differences in the optical depths for different transitions. Under such conditions, noticeable differences in the widths of the profiles of the different lines are inevitable. The optically thin lines, such as the Brγ line, can be observed at the base of the wind, where the poloidal velocities are still low and the velocities are still dominated by Keplerian motion. However, the optically thick lines, such as Hα, are emitted in the extended region of the disk wind because of the lower escape probability.
-
(2)
The Stark effect can broaden the line width if the electron density is high enough. This can be achieved by either a high electron temperature or a high mass-loss rate of the disk wind. Depending on the conditions in the gas, the Stark effect can broaden the whole line or form large wings.
-
(3)
Under certain conditions, the line emission from the rotating magnetosphere can broaden the line profiles.
We studied the contribution of the different components of the circumstellar environment to the different hydrogen emission lines and investigated how this contribution is dependent on the model parameters. We studied the dependence of the line profiles on the velocity laws, the mass accretion rate, the mass ejection efficiency, and various other physical parameters of the disk wind, X-wind, and magnetosphere. The results of this study can be used to model the emitting regions of individual young stars. Extinction effects can play an important role in line profile shapes. Different extinction effects are able to shift profiles to blue or red velocities or change them dramatically from double-peaked to single or P Cygni profiles. We also studied a new effect: The shape of the line profile can be significantly changed by absorption of the disk continuum radiation by the disk wind.
 |
Fig. A.3 Hα and Brγ line profiles in the hybrid model MS + disk wind (model A4). Profiles are given for the Ṁw/Ṁacc ratio 0.1 and 0.3 (marked on the right). The profiles formed by the magnetosphere (blue line), the disk wind (red line), and by both regions (hybrid model; black line) are shown. The inclination angles are shown in the panel. Ṁacc = 1 × 10-8 M⊙ yr-1. |
Grady et al. (2010) claimed that in HAEs, the gas accretes to the pole regions of the star. Their arguments are that hot regions that produce OVI lines exist. However, both in our model and in the magnetospheric accretion models for classical TTSs, these hot regions also exist, but in the HAEs, they may be seen pole-on and under moderate inclinations. Under large inclinations (greater than 40°–50°), they may not be seen due to strong absorption in the disk and disk wind.
Acknowledgments
We thank the referee for his or her comments that helped to improve the manuscript. This research has been supported in part by the program of the Presidium of RAS N 21 and grant N. Sh.- 1625.2012.2.
References
- Alecian, E., Wade, G. A., Catala, C., et al. 2008, Contrib. Astron. Obs. Skalnaté Pleso, 38, 235 [Google Scholar]
- Beskrovnaya, N. G., & Pogodin, M. A. 2004, A&A, 414, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm, T., & Catala, C. 1995, A&A, 301, 155 [NASA ADS] [Google Scholar]
- Caratti o Garatti, A., Garcia Lopez, R., Weigelt, G., et al. 2013, A&A, 554, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donehew, B., & Brittain, S. 2011, ApJ, 141, 46 [Google Scholar]
- Drew, J. E., Busfield, G., Hoare, M. G., et al. 1997, MNRAS, 286, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., & Monnier, J. D. 2010, ARA&A, 48, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Elsner, R. F., & Lamb, F. K. 1977, ApJ, 215, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Eisner, R. F., Chiang, E. I., Lane, B. F., & Akeson, R. I. 2007, ApJ, 657, 447 [Google Scholar]
- Eisner, R. F., Monnier, J. D., Woillez, J., et al. 2010, ApJ, 718, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, J. 2007, in Jets from Young Stars (Berlin, Heidelberg: Springer-Verlag), Lect. Not. Phys., 723, 181 [Google Scholar]
- Ferreira, J., Dougados, C., & Cabrit, S. 2006, A&A, 453, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia Lopez, R., Natta, A., Testi, L., & Habart, E. 2006, A&A, 459, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grady, C. A., Pérez, M. R., Thé, P. S., et al. 1995, A&A, 302, 472 [NASA ADS] [Google Scholar]
- Grady, C. A., Pérez, M. R., Talavera, A., et al. 1996, A&ASS, 120, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grady, C. A., Sitko, M. L., Russell, R. W., et al. 2000, in Protostars and Planets IV, eds. V. Mannings, A. P. Boss, & S. R. Russell (Tucson: Univ. Arizona Press), 513 [Google Scholar]
- Grady, C. A., Hamaguchi, K., Schneider, G., et al. 2010, ApJ, 719, 1565 [NASA ADS] [CrossRef] [Google Scholar]
- Grinin, V. P., & Katysheva, N. A. 1980, Izv. Krymsk. Astrofiz. Obs. (Bulletin of the Crimean Astrophys. Observatory), 62, 59 [NASA ADS] [Google Scholar]
- Grinin, V. P., & Mitskevich, A. S. 1990, Astrophys., 32, 216 [Google Scholar]
- Grinin, V. P., & Tambovtseva, L. V. 2011, Astron. Rep., 55, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Grinin, V. P., Thé, P. S., de Winter, D., et al. 1994, A&A, 392, 165 [NASA ADS] [Google Scholar]
- Grinin, V. P., Kozlova, O. V., Natta, A., et al. 2001, A&A, 379, 482 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grinin, V. P., Tambovtseva, L. V., & Weigelt, G. 2012, A&A, 544, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamann, F., & Persson, S. E. 1992, ApJSS, 82, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Hewett, R., & Calvet, N. 1994, ApJ, 426, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L., Strom, S. E., Vrba, F. J., & Keene, J. 1992, ApJ, 397, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Hubrig, S., Pogodin, M. A., Yudin, R. V., et al. 2007, A&A, 463, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klaassen, P. D., Juhssz, A., Mathews, G. S., et al. 2013, A&A, 555, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, S., Hofmann, K.-H., Benisty, M., et al. 2008, A&A, 489, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, S., Calvet, N., Hartmann, L., et al. 2012, ApJ, 752, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Königl, A. 1991, ApJ, 370, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Königl, A., & Pudritz, R. E. 2000, in Protostars and Planets IV, eds. V. Mannings, A. P. Boss, & S. S. Russell (Tucson: University of Arizona Press),759 [Google Scholar]
- Königl, A., & Salmeron, R. 2011, in Physical Processes in Circumstellar Disks around Young Stars, eds. P. J. V. Garcia (Chicago, IL: University of Chicago Press), 283 [Google Scholar]
- Kurosawa, R., Harries, T. J., & Symington, N. H. 2006, MNRAS, 370, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1979, ApJSS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Adams, F. C. 1992, ApJ, 393, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Lima, G. H. R. A., Alencar, S. H. P., Calvet, N., et al. 2010, A&A, 522, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lumsden, S. L., Wheelwright, H. E., Hoare, M. G., et al. 2013, MNRAS, 424, 1088 [Google Scholar]
- Luttermoser, D. G., & Johnson, H. R. 1992, ApJ, 388, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Malbet, F., Benisty, M., de Wit, W.-J., et al. 2007, A&A, 464, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mendigutía, I., Eiroa, C., Montesinos, B., et al. 2012, A&A, 529, A34 [Google Scholar]
- Mihalas D. 1978, Stellar Atmospheres, 2nd edn. (San Francisco: W. H. Freeman and Co.) [Google Scholar]
- Montesinos, B., Eiroa, C., Mora, A., & Merín, B. 2009, A&A, 495, 901 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mora, A., Merin, B., Solano, E., et al. 2001, A&A, 378, 116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Movsessian, T. A., Magakian, T., Yu., Sargsyan, D. M., & Nikogossian, E. H. 2008, Astrophys., 51, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., Calvet, N., & Hartmann, L. 1998, ApJ, 492, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., Calvet, N., & Hartmann, L. 2001, ApJ, 550, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., DAlessio, P., Calvet, N., & Hartmann, L. 2004, ApJ, 617, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Natta, A., Grinin, V. P., & Tambovtseva, L. V. 2000, ApJ, 542, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Natta, A., Prusti, T., Neri, R., et al. 2001, A&A, 371, 186 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ostriker, E., & Shu, F. H. 1995, ApJ, 447, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Proga, D., Stone, J. M., & Drew, J. E. 1998, MNRAS, 295, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Reipurth, B., Pedrosa, A., & Lago, M. T. V. T. 1996, A&AS, 120, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rostopchina, A. N. 1999, Astron. Rep., 43, 113 [NASA ADS] [Google Scholar]
- Safier, P. 1993, ApJ, 408, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Safier, P. 1999, ApJ, 510, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Shlosman, I., & Vitello, P. 1993, ApJ, 409, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Lizano, S., Ruden, S. P., & Najita, J. 1988, ApJ, 328, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Sobolev, V. V. 1960, Moving Envelopes of Stars (Harvard Univ., Cambridge, Leningr. Gos. Univ., Leningrad, 1947) [Google Scholar]
- Stecklum, B., Caratti o Garatti, A., & Linz, H. 2012, ASP Conf. Proc., 464, 369 [Google Scholar]
- Tambovtseva, L. V., Grinin, V. P., & Kozlova, O. V. 1999, Astrophys., 42, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Tambovtseva, L. V., Grinin, V. P., Rodgers, B., & Kozlova, O. V. 2001, Astron. Rep., 45, 442 [NASA ADS] [CrossRef] [Google Scholar]
- Tatulli, E., Isella, A., Natta, A., et al. 2007, A&A, 464, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1973, ApJ, 184, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Wade, G. A., Bagnulo, S., Drouin, D., et al. 2007, MNRAS, 376, 1145 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Wade, G. A., Alecian, E., Grunhut, J., et al. 2009, in Proc. Conf. Astronomical Polarimetry 2008: Science from Small to Large Telescopes, Quebec, Canada, July 2008, eds. P. Bastien, & N. Manset, ASP Conf. Ser. [arXiv:0901.0347] [Google Scholar]
- Wardle, M., & Königl, A. 1993, ApJ, 410, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Weigelt, G., Kraus, S., Driebe, T., et al. 2007, A&A, 464, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weigelt, G., Grinin, V. P., Groh, J. H., et al. 2011, A&A, 527, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Supplementary material
In this appendix, we show additional theoretical material that can be useful for interpreting the emission spectra of young intermediate-mass stars. In Figs. A.1, A.2, we present variations in the profiles of the Hα, Paβ, and Brγ lines in the framework of the disk wind models A1, A2, A3, and A4. The mass-loss rates in these models range from 1 × 10-9 to 1 × 10-6 M⊙ yr-1 (from bottom to top in models A1, A2, A3, and A4) and the inclination angles are 20, 40, 60, and 80° (from left to right). The line profiles are normalized to the stellar continuum.
Figure A.3 illustrates the variation of the line profiles in the scenario MS + disk wind with parameters of model A4, accretion rate Ṁacc = 1 × 10-8 M⊙ yr-1, and Ṁw/Ṁacc ratio 0.1 or 0.3. One can see that for both ratios, the Hα line does not change noticeably with inclination, while the Brγ line changes significantly at a ratio equal to 0.1.
All Tables
Parameters of the X-wind and the disk-wind models discussed in Sect. 3 (hybrid model).
All Figures
 |
Fig. 1 Geometry of the disk wind model assumed in this paper. |
| In the text | |
 |
Fig. 2 Top: sketch of disk wind models with different mass loading. The length of the streamlines is proportional to the local mass-loss rate. Top left: the bulk of the disk wind is ejected along streamlines near the star (γ = 4, model B1). Top right: the bulk of the disk wind is ejected along the outer streamlines (γ = 1, model B2). Middle: kinematics for models B1 (left) and B2 (right). The poloidal velocity at the first streamline (solid) and the sixth outermost streamline (dashed) are presented. The dotted lines represent the rotational velocity component. Bottom: the computed Hα (blue), Paα (green), and Brγ (red) line profiles (normalized to one) of models B1 (left) and B2 (right) for a disk inclination angle (the angle between the system axis and the viewing direction) of 20°. |
| In the text | |
 |
Fig. 3 Top: emission profiles of the Hα (solid) and Brγ (dashed) lines of model B3. Bottom: the same for model A1. Inclinations are 0 a); 20 b); 45 c); and 75°d). |
| In the text | |
 |
Fig. 4 Top: comparison of the normalized emission profiles of the Hα (solid) and Brγ (dashed) lines of model B3 with different values of the parameter β of the velocity law. Inclination i is 0° and β = 0.7a); 2 b); and 5 c). Bottom: the same for a disk wind with the screen discussed in the text (rtr = 0.5 AU). |
| In the text | |
 |
Fig. 5 Images of the disk wind in the Hα and Brγ lines for model A2 for a mass-loss rate of 10-7M⊙ yr-1 and inclination i = 90°. The brightness maps are presented for several radial velocities shown in the panels in km s-1 (see details in the text). The colors represent the intensity in erg ster-1 s-1 Å-1 cm-2. |
| In the text | |
 |
Fig. 6 Same intensity distribution as in Fig. 5 for the radial velocity 0 km s-1, but here both images are shown with the same intensity scale. |
| In the text | |
 |
Fig. 7 Left: the Hα line profile calculated with Voigt (solid) and Doppler (dashed) profiles of the absorption coefficient (model B5; inclination i = 20°). Right: the Hα (solid) and Brγ (dashed) line profiles computed in model B5 for a Herbig Be star (inclination i = 20°). |
| In the text | |
 |
Fig. 8 Three components of the hybrid model (Sect. 3): magnetosphere, X-wind, and disk wind (not to scale.) |
| In the text | |
 |
Fig. 9 Behavior of the gas electron temperature in the accreting zone for different power indices q marked at the curves (left) and velocity components (right). |
| In the text | |
 |
Fig. 10 Top: Hα line profiles of the magnetospheric accretion model MS1 with (left) and without (right) rotation and Ṁacc = 1 × 10-7 M⊙ yr-1. The numbers in the panel indicate the inclination angles i. Bottom: the same for model MS2. |
| In the text | |
 |
Fig. 11 Top: Brγ line profiles in the magnetospheric accretion model MS1: with (left) and without (right) rotation and Ṁacc = 1 × 10-7 M⊙ yr-1. The numbers in the panels describe the inclination angle i. Bottom: the same for model MS2. |
| In the text | |
 |
Fig. 12 Hα and Brγ line profiles for scenario A (i.e., hybrid model MS + X-wind, top) and B (i.e., hybrid model MS + disk wind, bottom): the emission line formed in the MS is shown by the blue line, in the X-wind (A) or disk wind (B) by the red line. The black line represents the line profile forming in both regions. Inclinations are marked in each panel. |
| In the text | |
 |
Fig. 13 Model images of the disk wind (model A2, top) and model images of the X-wind (Table 2, bottom) in the Brγ line at the radial velocity 0 km s-1. The mass-loss rate used in both models is 10-7 M⊙ yr-1. Edge-on (left) and pole-on (right) orientations are presented. The brightness scale is arbitrary and given in logarithmic units. |
| In the text | |
 |
Fig. 14 Same as in Fig. 13 at the radial velocities −50 km s-1 (top) and + 50 km s-1 (bottom). |
| In the text | |
 |
Fig. 15 Illustration of screening effects. Left: obscuration by an opaque disk that becomes opaque at radii larger than rtr. Right: obscuration by a flared dusty disk or dusty disk wind. |
| In the text | |
 |
Fig. 16 Screening effects (scenario in Fig. 15left). The Hα (top), Paβ (middle), and Brγ (bottom) line profiles in model A7 for the different rtr: 200 R∗ (solid), 30 R∗ (dashed), and 20 R∗ (dotted-dashed). |
| In the text | |
 |
Fig. 17 Influence of screening by an optically thick, dusty disk wind or a flared dusty disk (scenario in Fig. 15 right) on the Brγ line profile (model B6; inclination angle i = 70°; see Table 1). The solid line represents the unscreened line profile, while the long-dashed (hs = 100 R∗; θ = 20°), short-dashed (hs = 120 R∗; θ = 20°), and dotted-dashed (hs = 130 R∗; θ = 25°) lines show models with screening. |
| In the text | |
 |
Fig. 18 Brγ line
profile (model A1) normalized to the continuum of the accretion disk plus continuum of
the star with absorption of the disk and star continuum radiation by the opaque disk
wind taken into account. Top: i = 50°,
middle: i = 70° and bottom:
i = 80°. The ratio of the disk
continuum |
| In the text | |
 |
Fig. 19 Same as in Fig. 18 for the case of Rcon = R5 from Table 3. Inclinations are marked in the panels. |
| In the text | |
 |
Fig. 20 Comparison of the Brγ and Paβ line profiles (model A1; Rcon for the Brγ line is equal to the R5 values and for the Paβ line the values are seven times lower; inclination 50°). See text for details. |
| In the text | |
 |
Fig. A.1 Hα line profiles in models A1, A2, A3, and A4 (from bottom to top). The inclination i is marked in the panels. |
| In the text | |
 |
Fig. A.2 Same as in Fig. A.1 for Paβ (solid) and Brγ (dashed) line profiles. |
| In the text | |
 |
Fig. A.3 Hα and Brγ line profiles in the hybrid model MS + disk wind (model A4). Profiles are given for the Ṁw/Ṁacc ratio 0.1 and 0.3 (marked on the right). The profiles formed by the magnetosphere (blue line), the disk wind (red line), and by both regions (hybrid model; black line) are shown. The inclination angles are shown in the panel. Ṁacc = 1 × 10-8 M⊙ yr-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


