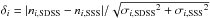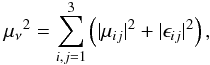| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A123 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201322641 | |
| Published online | 19 February 2014 | |
Limits on the neutrino magnetic dipole moment from the luminosity function of hot white dwarfs
1
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Str. 1,
8574
Garching,
Germany
e-mail:
marcelo@MPA-Garching.MPG.DE
2
Instituto de Astrofísica de La Plata, UNLP-CONICET, Paseo del Bosque s/n,
1900
La Plata,
Argentina
e-mail:
mmiller@fcaglp.unlp.edu.ar
Received:
10
September
2013
Accepted:
26
November
2013
Context. Recent determinations of the white dwarf luminosity function (WDLF) from very large surveys have extended our knowledge of the WDLF to very high luminosities. This, together with the availability of new full evolutionary white dwarf models that are reliable at high luminosities, have opened the possibility of testing particle emission in the core of very hot white dwarfs, where neutrino processes are dominant.
Aims. We use the available WDLFs from the Sloan Digital Sky Survey and the SuperCOSMOS Sky Survey to constrain the value of the neutrino magnetic dipole moment (μν).
Methods. We used a state-of-the-art stellar evolution code to compute a grid of white dwarf cooling sequences under the assumptions of different values of μν. Then we constructed theoretical WDLFs for different values of μν and performed a χ2-test to derive constraints on the value of μν.
Results. We find that the WDLFs derived from the Sloan Digital Sky Survey and the SuperCOSMOS Sky Survey do not yield consistent results. The discrepancy between the two WDLFs suggests that the uncertainties are significantly underestimated. Consequently, we constructed a unified WDLF by averaging the SDSS and SSS and estimated the uncertainties by taking into account the differences between the WDLF at each magnitude bin. Then we compared all WDLFs with theoretical WDLFs. Comparison between theoretical WDLFs and both the SDSS and the averaged WDLF indicates that μν should be μν < 5 × 10-12 eħ/(2mec). In particular, a χ2-test on the averaged WDLF suggests that observations of the disk WDLF exclude values of μν > 5 × 10-12eħ/(2mec) at more than a 95% confidence level, even when conservative estimates of the uncertainties are adopted. This is close to the best available constraints on μν from the physics of globular clusters.
Conclusions. Our study shows that modern WDLFs, which extend to the high-luminosity regime, are an excellent tool for constraining the emission of particles in the core of hot white dwarfs. However, discrepancies between different WDLFs suggest there might be some relevant unaccounted systematic errors. A larger set of completely independent WDLFs, as well as more detailed studies of the theoretical WDLFs and their own uncertainties, is desirable to explore the systematic uncertainties behind this constraint. Once this is done, we believe the Galactic disk WDLF will offer constraints on the magnetic dipole moment of the neutrino similar to the best available constraints obtainable from globular clusters.
Key words: white dwarfs / stars: luminosity function, mass function / elementary particles
© ESO, 2014
1. Introduction
In the Standard Model of particle physics, neutrinos are massless and only have weak force interactions. However, the confirmation of neutrino oscillations by many experiments (Giunti & Chung 2007) implies that they must be massive and mixed. In fact, the neutrino is the only particle, up to now, that really exhibits properties beyond the Standard Model. Consequently, the Standard Model must be extended to cope with neutrino masses.
In many extensions of the Standard Model neutrinos acquire electromagnetic properties (see Broggini et al. 2012 for a review), which makes studying the electromagnetic properties of neutrinos a basic tool for investigating the physics beyond the Standard Model. The idea that neutrinos could have a magnetic dipole moment (μν) is as old as the idea of the neutrinos themselves. Pauli discussed the possibility that the neutrino might have an intrinsic magnetic dipole moment in the same letter in which he proposed the very existence of the particle (Pauli 1930).
Even the very feeble weak interaction between the neutrino and the electron has a huge
impact on the hot dense plasmas found in astrophysical environments (Fowler & Hoyle 1964). Indeed, the dominant energy-loss mechanism
in hot white dwarfs occurs through neutrino emission (Lamb
& van Horn 1975). Effective coupling in a plasma occurs between the
neutrino and the electromagnetic field (photons) by means of the ambient electrons of the
medium. The most interesting process is the plasma process
(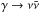 )
in which a photon decays into a neutrino/anti-neutrino pair. This process becomes
kinematically possible because in a plasma the electromagnetic field acquires a dispersion
relation, (ω2 − c2k2)ħ2 = Π2 > 0,
which roughly amounts to an effective photon mass. Then, plasmons1 with Π > 2mνc2
can decay into a neutrino/anti-neutrino pair. As mentioned above, this is only possible
within the Standard Model, because of the indirect coupling of the neutrino and the photon
that is mediated by the ambient electrons.
)
in which a photon decays into a neutrino/anti-neutrino pair. This process becomes
kinematically possible because in a plasma the electromagnetic field acquires a dispersion
relation, (ω2 − c2k2)ħ2 = Π2 > 0,
which roughly amounts to an effective photon mass. Then, plasmons1 with Π > 2mνc2
can decay into a neutrino/anti-neutrino pair. As mentioned above, this is only possible
within the Standard Model, because of the indirect coupling of the neutrino and the photon
that is mediated by the ambient electrons.
If a direct interaction between neutrinos and photons is allowed, for example, by a neutrino magnetic dipole moment or a neutrino millicharge, then the neutrino emission through plasmon decays will be enhanced. This will lead to significant observable consequences for the stellar evolution theory (see Raffelt 1996, 2000, 2012, for very detailed reviews and Heger et al. 2009, for a discussion of the impact on massive stars). Raffelt (1990) and then Raffelt & Weiss (1992) showed that the properties of red giants from the color-magnitude diagram (CMD) of Galactic globular clusters implied μν ≲ 3 × 10-12μB, where μB = eħ/(2mec) is the Bohr magneton. More recently, Viaux et al. (2013a,b) analyzed the CMD of the Galactic globular cluster M5 and concluded that μν < 4.5 × 10-12 μB at the 95% confidence level.
In particular a neutrino magnetic dipole moment will influence the cooling of hot white dwarfs and lead to observable consequences in the white dwarf luminosity function (WLDF, Blinnikov & Dunina-Barkovskaya 1994) and the rate of period change of hydrogen-deficient pulsating white dwarfs (DOVs and DBVs, O’Brien & Kawaler 2000; Winget et al. 2004). Unfortunately, up to now it has been impossible to determine the rate of period change generated by secular cooling in DOVs or DBVs (Vauclair et al. 2011; Chote et al. 2013; Dalessio et al. 2013), although some hints have recently been found by Redaelli et al. (2011). Blinnikov & Dunina-Barkovskaya (1994) showed that the early WDLF of Fleming et al. (1986) implied that the magnetic dipole moment is μν ≲ 10-11μB.
Isern et al. (2008) have shown, in the context of the strong CP problem, that modern WDLFs offer a new possibility to learn about elementary particle physics. In this work we show that, with the recent determinations of the hot end of the WLDF (Krzesinski et al. 2009; Rowell & Hambly 2011) and with the aid of state-of-the-art white dwarf models, it is possible to obtain constraints on the value of μν that can compete with those derived from red giants and globular clusters. Because astrophysical determinations are often prone to unknown systematic uncertainties, the determination of similar constraints by different and independent methods is desirable. To take into account possible systematic errors in the determination of the WDLF, we relied on two completely independent sets of WDLFs derived from the Sloan Digital Sky Survey (SDSS) and the SuperCosmos Sky Survey (SSS). These helped us to estimate the real uncertainties behind the observed WDLFs and derive constraints on the value of μν. Finally, we suggest work that can be carried out to improve the use of the WDLF as a tool to constrain the electromagnetic properties of the neutrino.
2. Input physics and white dwarf models
The calculations reported here were done using the LPCODE stellar evolutionary code (Althaus et al. 2012). This code has been used to study different problems related to the formation and evolution of white dwarfs (García-Berro et al. 2010; Renedo et al. 2010; Miller Bertolami et al. 2013). A description of the input physics and numerical procedures employed in LPCODE can be found in these works. Here we only summarize some points of specific interest for the present work.
For the white dwarf regime, LPCODE takes into account the effects of element diffusion caused by gravitational settling, and chemical and thermal diffusion, see Althaus et al. (2003) for details. Both latent heat release and the release of gravitational energy resulting from carbon-oxygen phase separation (Isern et al. 2000, 1997) were included following the phase diagram of Horowitz et al. (2010), see Althaus et al. (2012) for details of the numerical implementation. The radiative opacities are those of OPAL (Iglesias & Rogers 1996). The conductive opacities were taken from Cassisi et al. (2007). Finally, we emphasize that recently, LPCODE has been tested against other white dwarf evolutionary code, and the uncertainties in the cooling ages arising from different numerical implementations of stellar evolution equations were found to be lower than 2% (Salaris et al. 2013).
Including the anomalous energy loss due to the existence of a neutrino magnetic dipole
moment (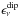 ) is
relatively simple because it is possible to relate the anomalous neutrino emission to the
plasmon neutrino emission predicted by the Standard Model
(
) is
relatively simple because it is possible to relate the anomalous neutrino emission to the
plasmon neutrino emission predicted by the Standard Model
(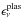 ). This
scaling relation has been computed by Haft et al.
(1994), who found
). This
scaling relation has been computed by Haft et al.
(1994), who found 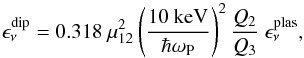 (1)where2μ12 = μν/(10-12μB),
ωP
is the plasma frequency and the ratio Q2/Q3
has a complex expression, but is very close to unity. For simplicity, we approximated
Q2/Q3 ~ 1
because this approximation introduces errors lower than 10% (Haft et al. 1994). It leads to a slight underestimation of the anomalous energy
loss and, thus, to more conservative conclusions. In addition, following Raffelt (1996), we approximated the plasma frequency by
its zero temperature value
(1)where2μ12 = μν/(10-12μB),
ωP
is the plasma frequency and the ratio Q2/Q3
has a complex expression, but is very close to unity. For simplicity, we approximated
Q2/Q3 ~ 1
because this approximation introduces errors lower than 10% (Haft et al. 1994). It leads to a slight underestimation of the anomalous energy
loss and, thus, to more conservative conclusions. In addition, following Raffelt (1996), we approximated the plasma frequency by
its zero temperature value ![\begin{equation} \hbar^2 {\omega_{\rm P}}^2\simeq \frac{4\pi n_{\rm e} {\rm e}^2 \hbar^2}{m_{\rm e}}\left[1+\left(\frac{\hbar}{m_{\rm e} c}\right)^2 \left(3\pi^2n_{\rm e}\right)^{2/3}\right]^{-1/2}, \end{equation}](/articles/aa/full_html/2014/02/aa22641-13/aa22641-13-eq20.png) (2)where ne is the electron
density by number and me is the mass of the electron.
(2)where ne is the electron
density by number and me is the mass of the electron.
To compute the impact of the magnetic dipole moment on the WDLF we computed a small grid of white dwarf cooling sequences that covers the relevant mass range under the assumption of different values of the neutrino magnetic dipole moment. For a correct assessment of the white dwarf cooling times at the high-luminosity end of modern WDLFs, accurate initial models are required. This can not be achieved using artificial initial white dwarf structures because at these luminosities white dwarf structures are still dependent on the previous evolution. For this reason the initial white dwarf models adopted here were taken from Renedo et al. (2010), who computed the full evolutionary calculation of the stages that lead to the formation of DA white dwarfs – from the zero-age main-sequence to the asymptotic giant branch. Even with these full evolutionary models, some initial relaxation of the models is required because the initial structures correspond to models computed under the assumption of standard neutrino losses. Fortunately, we do not expect large changes in the pre-white dwarf evolution (Viaux et al. 2013a,b) because the value of μν is relatively low. The masses of the initial white dwarf models selected for our grid were 0.52490 M⊙, 0.57015 M⊙, 0.60959 M⊙, 0.70511 M⊙, and 0.87790 M⊙. For each of the five initial white dwarf models, five cooling sequences were computed under different assumed magnetic dipole moments; μ12 = 0 (standard sequences), 1, 2, 5 and 10.
In Fig. 1, we show the total neutrino energy losses for a 0.60959 M⊙ model under standard assumptions and under the assumption of a neutrino magnetic dipole moment. An inspection of the emission rates in Fig. 1 shows that for MBol ≲ 2 the models are still relaxing to the new value of the neutrino emission. Consequently, our WDLFs will not be reliable at these bolometric magnitudes. Figure 1 also shows that as the anomalous neutrino emission (due to the value of μ12) is increased by increasing μ12, the feedback on the thermal structure of the white dwarf leads to lower neutrino emission through the standard channels. In Fig. 2 we show the overall impact of the neutrino magnetic dipole moment on the cooling speed of the white dwarf. As expected, after the relaxation phase at MBol ≲ 2, higher values of μν lead to higher cooling speeds of the white dwarf. Finally, it is worth noting (see Figs. 1 and 2) that for all the adopted values of μ12 the neutrino emission becomes negligible at MBol > 10, and thus the shape of the WDLF will not be affected at MBol > 10. This sets the region where normalizations of the WDLF can be performed to study the anomalous neutrino emission.
 |
Fig. 1 Total neutrino energy losses (Lν) for the 0.60959 M⊙ sequences under different assumed values of the neutrino magnetic dipole moment. The thick black line shows the value of the total neutrino emission without a magnetic dipole moment, while the thin red lines show the neutrino emission due to the standard model processes under the assumption of μ12 = 1,2,5, and 10 (from top to bottom). Dashed blue lines show the anomalous neutrino emission under the assumption of μ12 = 1,2,5, and 10 (from bottom to top). |
 |
Fig. 2 Cooling speeds of the 0.60959 M⊙ sequences computed under different assumed values of the neutrino magnetic dipole moment (μ12 = 0,1,2,5 and 10). |
 |
Fig. 3 WDLFs computed under the assumption of different stellar formation rates and ages compared with the WDLF derived from the SDSS (Harris et al. 2006; Krzesinski et al. 2009). See text for discussion. |
3. Theoretical white dwarf luminosity functions
The numerical code used to construct the theoretical WDLFs is a rewritten version of the
code used in Melendez et al. (2012), which is based on the method described by Iben & Laughlin (1989). A detailed explanation of
the method can be found in Iben & Laughlin
(1989), and here we only describe the main points of interest for the present
study. In this approach, the number of white dwarfs per logarithmic luminosity and volume is
computed as 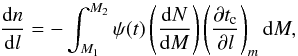 (3)where ψ(t) is the
Galactic stellar formation rate at time t, N(M) is the initial mass function
and tc(l,m) is the time since
the formation of a white dwarf, of mass m, for the star to reach a luminosity log (L/L⊙) = l.
To compute the integral in Eq. (3) we also
need the initial-final mass relation m(M), and the pre-white dwarf
stellar lifetime tev(M). It is worth
noting that for a given white dwarf luminosity (l) and mass of the progenitor (M), the formation time of the
star, t, is
obtained by solving
(3)where ψ(t) is the
Galactic stellar formation rate at time t, N(M) is the initial mass function
and tc(l,m) is the time since
the formation of a white dwarf, of mass m, for the star to reach a luminosity log (L/L⊙) = l.
To compute the integral in Eq. (3) we also
need the initial-final mass relation m(M), and the pre-white dwarf
stellar lifetime tev(M). It is worth
noting that for a given white dwarf luminosity (l) and mass of the progenitor (M), the formation time of the
star, t, is
obtained by solving 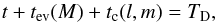 (4)where TD is the age of
the oldest computed stars. The lowest initial mass that produces a white dwarf with
luminosity l at
the present time (M1) is obtained from Eq. (4) when t = 0. The value of
M2
corresponds to the largest stellar mass progenitor that produces a white dwarf. In addition,
to compute Eq. (3) we adopted a Salpeter
initial mass function, the initial-final mass relation from Salaris et al. (2009), and the stellar lifetimes from the BaSTI database (Pietrinferni et al. 2004). A constant stellar formation
rate (SFR) was assumed for the reasons explained below, unless otherwise stated.
(4)where TD is the age of
the oldest computed stars. The lowest initial mass that produces a white dwarf with
luminosity l at
the present time (M1) is obtained from Eq. (4) when t = 0. The value of
M2
corresponds to the largest stellar mass progenitor that produces a white dwarf. In addition,
to compute Eq. (3) we adopted a Salpeter
initial mass function, the initial-final mass relation from Salaris et al. (2009), and the stellar lifetimes from the BaSTI database (Pietrinferni et al. 2004). A constant stellar formation
rate (SFR) was assumed for the reasons explained below, unless otherwise stated.
Owing to the uncertainties in the absolute value of ψ(t) in Eq.
(3) it is necessary to rescale the
theoretical WDLFs to fit the observed WDLF in some luminosity range to compare the
theoretical WDLFs with those derived from observations of the Galactic disk (Harris et al. 2006; De
Gennaro et al. 2008; Krzesinski et al. 2009;
Rowell & Hambly 2011; Kepler 2013). As shown in Fig. 3,
anomalous neutrino emission only affects the bright end of the WDLF. In particular, the WDLF
remains unchanged at MBol > 10 under
the assumptions of different values for the neutrino magnetic dipole moment. In addition, as
noted by Isern et al. (2008), observational errors as
well as theoretical uncertainties, such as the SFR, are lowest around MBol ~ 12. For
this reason, we chose to normalize the theoretical WDLFs so that they give the same number
of stars per volume in the range 10 ≤ MBol ≤ 13. This is, we set
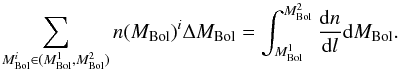 (5)When dealing with the data
of Harris et al. (2006), Rowell & Hambly (2011), and Krzesinski et al. (2009), we took
(5)When dealing with the data
of Harris et al. (2006), Rowell & Hambly (2011), and Krzesinski et al. (2009), we took 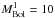 and
and
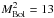 . We
emphasize that the theoretical WDLFs need to be normalized to fit each
observed WDLF. To take advantage of the fact that modern WDLFs extend to very high
luminosities, where the neutrino emissivities are most important, and taking into account
that the theoretical white dwarf models adopted in this work are are still not relaxed at
MBol ≲ 2.5, we compared the theoretical and
observationally derived WDLF within the range33 ≤ MBol ≤ 9.
. We
emphasize that the theoretical WDLFs need to be normalized to fit each
observed WDLF. To take advantage of the fact that modern WDLFs extend to very high
luminosities, where the neutrino emissivities are most important, and taking into account
that the theoretical white dwarf models adopted in this work are are still not relaxed at
MBol ≲ 2.5, we compared the theoretical and
observationally derived WDLF within the range33 ≤ MBol ≤ 9.
In addition, in Fig. 3 we show that the bright end of the WDLF is almost independent of the SFR or the age of the disk, because their main effects are absorbed in the normalization procedure, in agreement with the results of Isern et al. (2008). In particular, note that doubling the SFR in the last few Gyr does not introduce significant departures in the WDLF. In addition, changes in the SFR at earlier times will be absorbed in the normalization procedure of the theoretical WDLFs. Moreover, because we restricted the normalization of the theoretical WDLFs and the comparison with observations at MBol ≲ 13, our comparison is restricted to white dwarfs born in the last ~1 Gyr, which means that it is only sensitive to fluctuations in the SFR in that period. In particular, it is worth noting that hypothetical bursts in the SFR at very late times, that is, shorter than 1 Gyr ago, as those suggested in Rowell (2013), would produce an upward shift of the WDLF at high luminosities (relative to the normalization luminosity range) and cannot be confused with an additional cooling mechanism. However, a burst in the SFR in the last ~1 Gyr might help to hide the impact of extra cooling mechanisms in the WDLF. In view of the previous discussion, a disk age of 11 Gyr was assumed throughout under the assumption of a constant SFR (i.e., TD = 11 Gyr).
 |
Fig. 4 Top panel: comparison between the SDSS- and SSS-WDLFs. Absolute
values of the SSS-WDLF have been corrected for incompleteness by normalization to the
SDSS-WDLF total number of stars in the range 10 < MBol < 13
(small shaded area). Open squares show the averaged WDLF constructed by merging the
WDLFs derived by Harris et al. (2006), Krzesinski et al. (2009), and Rowell & Hambly (2011), see text for details. The gray area
within 3 < MBol < 9
corresponds to the region used for the χ2-like test. Bottom
panel: differences between the SDSS- and SSS-WDLF relative to their own
quoted error bars at each magnitude bin ( |
4. The WDLF of the Galactic disk
The SDSS has increased the number of known white dwarfs by more than one order of magnitude in the past decade. Taking advantage of these large amounts of data, several works have derived WDLFs in different magnitude ranges by means of different techniques. Harris et al. (2006) derived a WDLF from the SDSS DR3 using the reduced proper motions technique for all white dwarfs (without separating them into H-rich, DA, or H-deficient DB4). Because intrinsically bright WD stars can be seen at much greater distances, on average they do not show large proper motions and are not suited to the reduced proper-motion technique. Thus, their WDLF has to be limited to relatively low luminosities (7 < MBol < 16). Using the same technique, but based on the SDSS DR4 and constraining it solely to spectroscopically derived DA-WDs, De Gennaro et al. (2008) derived a DA-only WDLF in the range 5.2 < MBol < 12.4. Also from the SDSS-DR4, but based on the color-selection technique, which works well at high luminosities, Krzesinski et al. (2009) derived high-luminosity WDLFs (both a H-rich-only WDLF and a H-deficient WDLF) for the range 0 < MBol < 7. Using the WDLFs of Harris et al. (2006) and Krzesinski et al. (2009), we constructed a WDLF for DA+DB white dwarfs (from now on SDSS-WDLF).
All the WDLFs mentioned in the previous paragraph have been derived from the SDSS catalog
and might be prone to the same unknown systematic errors or biases. In particular, because a
proper assessment of the uncertainties is crucial for the objective of the present work, we
also included in our analysis the WDLF derived from the SuperCosmos Sky Survey (SSS, Rowell & Hambly 2011). Rowell & Hambly (2011) measured the WDLF from a sample of around
10 000 WDs using the proper-motion technique to derive a very deep WDLF, in the range
1 < MBol < 18.
While the WDLF derived from SSS is admittedly incomplete at around a 50% level, it covers a
larger area of the sky and might be prone to different unknown systematic errors than the
SDSS data (see Rowell & Hambly 2011; Rowell 2013, for details). In particular, it is claimed
that the SSS incompleteness is uniform and does not bias the WDLF (Rowell 2013). While Rowell &
Hambly (2011) developed a new method to derive their WDLF, we here relied on their
WDLF derived with the standard  technique for more direct comparison with the SDSS data. This allowed us to perform a
comparison of different, completely independent WDLFs, and make a better assessment of the
uncertainties behind the WDLF of the Galactic disk.
technique for more direct comparison with the SDSS data. This allowed us to perform a
comparison of different, completely independent WDLFs, and make a better assessment of the
uncertainties behind the WDLF of the Galactic disk.
4.1. Comparison between the SDSS and SSS WDLFs
A preliminary comparison between our theoretical WDLFs and the SDSS and the SSS WDLFs suggested that the two WDLFs were discrepant beyond their quoted error bars. To obtain a quantitative measure of the differences between the two WDLFs we performed a χ2-like statistical test. Because the WDLF derived from the SSS is incomplete at around a 50% level, absolute numbers of both WDLFs will differ. Therefore, the WDLF from the SSS survey must first be rescaled before one can compare it with the SDSS-WDLF. Consequently, we rescaled the WDLF of Rowell & Hambly (2011) so that the total number of stars per unit volume in the range 10 ≤ MBol ≤ 13 is similar to the one in the SDSS-WDLF (Harris et al. 2006), as we did with the theoretical WDLFs. The derived correction factor is c = 1.862, which is consistent with the claimed incompleteness of around 50%.
Then we redefined the values of the Rowell &
Hambly (2011) WDLF (RH11) in each magnitude bin as ni,SSS = c ni,RH11
and σi,SSS = c σi,RH11.
To define both WDLFs at the same magnitude bins in the range MBol < 7, where
the WDLF of Krzesinski et al. (2009) is given at
half magnitude bins, we added the two values of the corresponding two bins of the Rowell & Hambly (2011) as
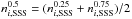 and
and
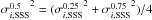 (from now the SSS-WDLF). This
left two WDLFs given at the same magnitude points and with the same number of stars per
volume in the magnitude range 10 < MBol < 13.
Figure 4 shows the absolute and relative differences
between the number densities of the SDSS-WDLF and the SSS-WDLF relative to a measure of
their quoted error bars.
(from now the SSS-WDLF). This
left two WDLFs given at the same magnitude points and with the same number of stars per
volume in the magnitude range 10 < MBol < 13.
Figure 4 shows the absolute and relative differences
between the number densities of the SDSS-WDLF and the SSS-WDLF relative to a measure of
their quoted error bars.
A more quantitative indication of the differences between the two WDLFs can be obtained
as follows: if both WDLFs were realizations of distributions with the same mean value
μi in each magnitude
bin and with the quoted variances5, then at each
magnitude bin the quantity 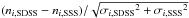 would be a random variable with a normal distribution of unit variance and zero mean.
Then,
would be a random variable with a normal distribution of unit variance and zero mean.
Then, 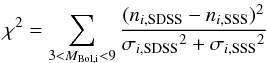 (6)should
follow a χ2 square distribution with eight degrees
of freedom. The probability that the actual value of χ2 = 51.16
occurs under the previous assumptions is lower than P = 10-7.
(6)should
follow a χ2 square distribution with eight degrees
of freedom. The probability that the actual value of χ2 = 51.16
occurs under the previous assumptions is lower than P = 10-7.
Clearly, the SDSS and SSS are not consistent within their quoted error bars. Either some mean values are inaccurate beyond the quoted error bars, or error bars in the WDLFs have been significantly underestimated6. It is worth noting that differences between SSS and SDSS WDLFs are not restricted to high luminosities, where the proper-motion technique adopted by Rowell & Hambly (2011) might not be best suited. In particular, differences between Harris et al. (2006) and Rowell & Hambly (2011) WDLFs are very significant (in terms of their quoted error bars) in the range 7.5 < MBol < 9.5 (see Fig. 4). From this comparison we are forced to conclude that at least one of the WDLFs is more uncertain than quoted by its own error bars. Owing to the incompleteness of the SSS-WDLF, and the lack of reddening correction, one possible cause for the observed inconsistency is that incompleteness is not uniform at all magnitude bins, which biases the final SSS-WDLF (Rowell, priv. comm.). In addition, the lack of reddening corrections in the SSS-WDLF would tend to affect bright magnitudes more, which would also bias the SSS-WDLF. The other possible cause for this discrepancy is just that uncertainties are larger than quoted in both WDLFs. In view of this discrepancy and in the absence of a third independent WDLF we decided on a two-way approach. On the one hand, we assumed the two WDLFs to be equally valid and derived from them an averaged WDLF (Sect. 4.2). This averaged WDLF was then compared with theoretical models to obtain constraints for μν (Sect. 5). On the other hand, we assumed that the inconsistency is due to some unexplained bias in the SSS-WDLF and compared the theoretical models directly with the SDSS-WDLF (Sect. 5).
In the next section we estimate a WDLF taking into account the systematic differences between the two WDLFs.
 |
Fig. 5 Comparison of our theoretical WDLFs constructed under the assumption of different values of μ12 with the unified WDLF constructed merging the WDLFs derived by Harris et al. (2006), Krzesinski et al. (2009), and Rowell & Hambly (2011). Red error bars correspond to those derived as σi = Max [σi,Uni,σi,SSS,σi,SDSS]. See Sect. 4 for details. The inset shows the value of the χ2 per degree of freedom ν of the χ2-test for the two different sets of error bars. Gray areas indicate the magnitude ranges used for the χ2-test (3 < MBol < 9) and for the normalization procedure (10 < MBol < 13). |
4.2. Averaged WDLF of the Galactic disk
The comparison between the SDSS- and SSS- WDLFs suggests that the uncertainties in the
WDLFs have been significantly underestimated. This led us to use both the SDSS and SSS to
obtain a unified WDLFs with error bars that take into account the differences between the
two derived WDLFs. If the values ni,SSS and
ni,SDSS were consistent
in each magnitude bin, then it is clear that the best estimation of the WDLF would be a
weighted average of the values and the new uncertainties would be given by
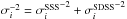 .
However, the uncertainty estimated in this way would not reflect the differences in the
values of
.
However, the uncertainty estimated in this way would not reflect the differences in the
values of 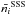 and
and
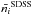 , as it should. In
fact, dealing with discrepant data is difficult (see for example Hanson 2005). A detailed systematic treatment of the discrepant SSS and
SDSS data is beyond the scope of the present work. However, an intuitively reasonable
estimation of the unified WDLFs and its uncertainties is given by
, as it should. In
fact, dealing with discrepant data is difficult (see for example Hanson 2005). A detailed systematic treatment of the discrepant SSS and
SDSS data is beyond the scope of the present work. However, an intuitively reasonable
estimation of the unified WDLFs and its uncertainties is given by 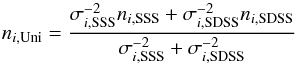 (7)and
(7)and
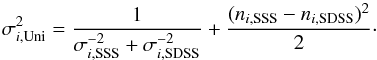 (8)Note that this
expression for
(8)Note that this
expression for 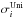 is
restricted to the standard variance summation rule when
is
restricted to the standard variance summation rule when
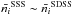 , and for
significantly discrepant data it approaches the value of the unbiased sample variance
estimator (for a two-point sample). Thus, this estimation of the uncertainties in the
WDLFs has the advantage that it reduces the uncertainty in those bins where the SDSS and
SSS WDLFs are consistent and increases the uncertainty when the SDSS and SSS WDLFs are
discrepant.
, and for
significantly discrepant data it approaches the value of the unbiased sample variance
estimator (for a two-point sample). Thus, this estimation of the uncertainties in the
WDLFs has the advantage that it reduces the uncertainty in those bins where the SDSS and
SSS WDLFs are consistent and increases the uncertainty when the SDSS and SSS WDLFs are
discrepant.
Averaged WDLF of the Galactic disk.
The unified disk WDLFs derived in this way (Table 1) can now be compared with the theoretical WDLFs. For the objective of the present work, the most significant difference between this new WDLF and the SDSS and SSS WDLFs is that the error bars now reflect the discrepancies between different estimations of the WDLFs.
5. Constraints on μν and discussion
In Fig. 5 we compare the WDLF derived in the previous section by averaging both the SDSS- and SSS-WDLFs with the theoretically computed ones under the assumption of different values of the magnetic dipole moment of the neutrino. In addition, in Fig. 6 we show the result of the χ2-test performed on the averaged disk-WDLF derived in Eqs. (7) and (8). As can be directly appreciated from Figs. 5 and 6, the χ2-test shows that values of μ12 ≳ 5 are significantly at variance with the observations. In fact, when adopting the error bars derived in Eq. (8) (black line in Figs. 5 and 6), Fig. 6 shows that WDLFs constructed with μ12 ≥ 5 can be rejected at more that a 99.9% confidence level (i.e. ≳3σ-like). Even when a more conservative error estimation is adopted (Max [σSDSS, σSSS, σUni], red lines in Figs. 5 and 6), values of μ12 ≥ 5 can be rejected at more that a 95% confidence level (i.e. ~2σ-like).
 |
Fig. 6 Significance level of the χ2-test for the WDLFs shown in Fig. 5. It is clear that, under the error estimation presented in Eq. (8), magnetic dipole moments larger than μ12 = 5 can be discarded at the 99.9% confidence level. Black (red) line shows the result when the value of σUni (Max [σSDSS, σSSS, σUni]) is adopted as the uncertainty – see Table 1. |
As noted in Sect. 4.1, the discrepancy between the SDSS- and SSS-WDLFs might also be related to some unexplained bias (e.g. incompleteness) in the SSS-WDLF. If this is the case, the SDSS-WDLF should be preferred. In Fig. 7 we compare the theoretical WDLFs with the SDSS-WDLF, also by means of a χ2-test. It is clear from this comparison that values of μ12 ≥ 5 are at variance with observations. However, in this case, the χ2-values are still too high for μ12 = 0, 1 and 5 and the models do not fit the observations because the error bars are significantly smaller than in the averaged WDLF. The failure of the models to fulfill a χ2-test can be because either the quoted error bars are too low (as suggested by the comparison with the SSS-WDLF) or because the uncertainties in the theoretical models become more relevant. In the latter case the impact of the possible existence of short-term fluctuations in the SFR should be explored.
It is worth noting that our theoretical WDLFs are derived only taking into account DA-WD models. This would naively suggest that our theoretical WDLF should be compared with observational WDLFs only for DAs (De Gennaro et al. 2008). While this might in principle be true, it might also be misleading because of our current lack of a complete understanding of the spectral evolution of white dwarfs – see Fontaine & Wesemael (1987) for an early description of the problem. In particular, white dwarfs with an extremely thin H-envelope such as those studied by Shibahashi (2013), and references therein, will cool as DB white dwarfs, but will still be classified as DA. Even worse, the fraction of such DA white dwarfs with extremely thin H-envelopes probably depends on the magnitude bin. In view of this situation, we chose to compare our theoretical WDLF with DA-only and DA+DB WDLFs. Fortunately, differences between DA-only and DA+DB WDLFs are most likely on the order of 10 to 20% (De Gennaro et al. 2008), values which are within the error bars of our averaged WDLF (Table 1). Indeed, when a χ2-test was performed on the individual WDLFs derived from the SDSS, they all yielded similar conclusions, regardless of whether they were DA-only WDLFs (De Gennaro et al. 2008)7 or DA+DB WDLFs (Harris et al. 2006; Krzesinski et al. 2009). In short, the comparison of our theoretical WDLFs with all the WDLFs derived from the SDSS suggest that models with μ12 < 5 agree better with the observed disk WDLFs. However, because of the significantly lower error bars, a χ2-test indicates that all theoretical models fail to fit the observations within the quoted error bars. The same is true for a χ2-test performed on the WDLF derived from the SSS, because the low error bars the test rejects all theoretical models – although in this case theoretical models with μ12 = 5 and 10 are closer to the observations. We consider this to be another indication that the quoted error bars in those works might be underestimated, although this result can also be related to the absence of an estimation of the systematic errors in theoretical models. Certainly, this result calls for a larger set of completely independent WDLFs as well as for the derivation of WDLFs by means of different WDLF estimators (Geijo et al. 2006).
 |
Fig. 7 Comparison of our theoretical WDLFs constructed under the assumption of different values of μ12 with the SDSS-WDLF (for all WDs) derived by Harris et al. (2006) and Krzesinski et al. (2009). The inset shows the value of the χ2 per degree of freedom ν of the χ2-test. Gray areas indicate the magnitude ranges used for the χ2-test (3 < MBol < 9) and for the normalization procedure 10 < MBol < 13. |
6. Summary and conclusions
We have compared the observed WDLFs derived from two different surveys (SDSS and SSS) and showed that these WDLFs are not consistent within their quoted error bars. Consequently, we constructed a unified disk-WDLF (Table 1) by averaging the SSS and SDSS WDLFs and estimating the uncertainty in the derived values by taking into account the discrepancy between the two sets of data as well as their own quoted error bars. Then we used this averaged disk-WDLF to constrain neutrino physics. To this aim we computed 25 white dwarf evolutionary sequences under the assumption of different values of the neutrino magnetic dipole moment (μ12 = 0, 1, 2, 5, and 10). With these sequences, theoretical WDLFs for the Galactic disk were computed for the different values of μ12 and compared with the observations. A χ2-test on the unified disk-WDLF (SDSS+SSS) yielded that values of μ12 ≥ 5 can be rejected at more than a 95% confidence level, even when a conservative estimation of the error bars is adopted. Moreover, a direct comparison with the SDSS-WDLFs suggested that values of μ12 > 5 can be rejected. This result is not far from the best available constraints on μ12 from the CMD of globular clusters and is based on independent astronomical determinations. This results shows the power of the new WDLFs to constrain the value of the magnetic dipole moment of the neutrino. However, the discrepancy between the SDSS and SSS WDLFs needs to be addressed, probably by means of a larger set of completely independent WDLFs.
Future determinations of the WDLF of the Galactic disk based on independent surveys and different WDLF estimators will allow a better determination of the actual disk-WDLF. In addition to a better statistical treatment of all available WDLFs, other improvements should be performed in the computation of the theoretical WDLFs. First, to improve the constraints derived in this work it would be desirable to construct WDLFs that include the contribution of H-rich and H-deficient white dwarfs. A systematic exploration of the impact of the uncertainties in the SFR of the disk in the past Gyr needs to be made to estimate systematic errors in the comparison of theoretical and inferred WDLFs. Finally, it would be interesting to test the impact of a magnetic dipole moment on the pre-white dwarf stages and how they affect the derived white dwarf models. We believe that, once this is done, the WDLF will offer constraints on the magnetic dipole moment of the neutrino similar to the best available constraints obtained from the CMD of globular clusters.
When comparing the WDLF of De Gennaro et al. (2008) with theoretical models, we restricted the normalization region and the range of the χ2-test to the regions were it is valid (10 < MBol < 12.4 and 5.2 < MBol < 9.2, respectively).
Acknowledgments
M3B is supported by a fellowship for postdoctoral researchers from the Alexander von Humboldt Foundation. M3B thanks H. Harris, N. Rowell, N. Hambly, S. De Gennaro and J. Krzesinski for the data and instructive comments about their respectively WDLFs, J. Isern, G. Raffelt and N. Rowell for reading and commenting on a preliminary version of the article, and J. Beacom for comments and suggestions that have strongly improved the final version of the manuscript. L. Althaus is warmly thanked for extensive and instructive discussions about the physics of white dwarfs throughout the years. This research was partially supported by PIP 112-200801-00940 from CONICET and by ANPCyT through PMT III (BID 1728/OCAR). This work is dedicated to the memory of my uncle, Miguel Bertolami, who introduced me to science.
References
- Althaus, L. G., García-Berro, E., Isern, J., Córsico, A. H., & Miller Bertolami, M. M. 2012, A&A, 537, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Córsico, A. H., & Montgomery, M. H. 2003, A&A, 404, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blinnikov, S. I., & Dunina-Barkovskaya, N. V. 1994, MNRAS, 266, 289 [NASA ADS] [Google Scholar]
- Broggini, C., Giunti, C., & Studenikin, A. 2012 [arXiv:1207.3980] [Google Scholar]
- Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Chote, P., Sullivan, D. J., Montgomery, M. H., & Provencal, J. L. 2013, MNRAS, 431, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Dalessio, J., Sullivan, D. J., Provencal, J. L., et al. 2013, ApJ, 765, 5 [NASA ADS] [CrossRef] [Google Scholar]
- De Gennaro, S., von Hippel, T., Winget, D. E., et al. 2008, AJ, 135, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Fleming, T. A., Liebert, J., & Green, R. F. 1986, ApJ, 308, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., & Wesemael, F. 1987, in Second Conference on Faint Blue Stars, eds. A. G. D. Philip, D. S. Hayes, & J. W. Liebert, IAU Colloq., 95, 319 [Google Scholar]
- Fowler, W. A., & Hoyle, F. 1964, ApJS, 9, 201 [Google Scholar]
- García-Berro, E., Torres, S., Althaus, L. G., et al. 2010, Nature, 465, 194 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Geijo, E. M., Torres, S., Isern, J., & García-Berro, E. 2006, MNRAS, 369, 1654 [NASA ADS] [CrossRef] [Google Scholar]
- Giunti, C., & Chung, W. K. 2007, Fundamentals of Neutrino Physics and Astrophysics (Oxford University Press) [Google Scholar]
- Haft, M., Raffelt, G., & Weiss, A. 1994, ApJ, 425, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Hanson, K. M. 2005, in Bayesian Inference and Maximum Entropy Methods in Science and Engineering, eds. K. H. Knuth, A. E. Abbas, R. D. Morris, & J. P. Castle, AIP Conf. Ser., 803, 431 [Google Scholar]
- Harris, H. C., Munn, J. A., Kilic, M., et al. 2006, AJ, 131, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Friedland, A., Giannotti, M., & Cirigliano, V. 2009, ApJ, 696, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Horowitz, C. J., Schneider, A. S., & Berry, D. K. 2010, Phys. Rev. Lett., 104, 231101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Iben, Jr., I., & Laughlin, G. 1989, ApJ, 341, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., Mochkovitch, R., Garcia-Berro, E., & Hernanz, M. 1997, ApJ, 485, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., García-Berro, E., Hernanz, M., & Chabrier, G. 2000, ApJ, 528, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., García-Berro, E., Torres, S., & Catalán, S. 2008, ApJ, 682, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Kepler, S. O. 2013, in 18th European White Dwarf Workshop., eds. J. ski Krzesiń, G. Stachowski, P. Moskalik, & K. Bajan, ASP Conf. Ser., 469, 83 [Google Scholar]
- Krzesinski, J., Kleinman, S. J., Nitta, A., et al. 2009, A&A, 508, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamb, D. Q., & van Horn, H. M. 1975, ApJ, 200, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M., Althaus, L. G., & García-Berro, E. 2013, ApJ, 775, L22 [NASA ADS] [CrossRef] [Google Scholar]
- O’Brien, M. S., & Kawaler, S. D. 2000, ApJ, 539, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Pauli, W. 1930, Open Letter, 4 December [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Raffelt, G. 2012 [arXiv:1201.1637] [Google Scholar]
- Raffelt, G., & Weiss, A. 1992, A&A, 264, 536 [NASA ADS] [Google Scholar]
- Raffelt, G. G. 1990, ApJ, 365, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Raffelt, G. G. 1996, Stars as laboratories for fundamental physics (University of Chicago Press) [Google Scholar]
- Raffelt, G. G. 2000, Phys. Rep., 333, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Redaelli, M., Kepler, S. O., Costa, J. E. S., et al. 2011, MNRAS, 415, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Renedo, I., Althaus, L. G., Miller Bertolami, M. M., et al. 2010, ApJ, 717, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Rowell, N. 2013, MNRAS, 434, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Rowell, N., & Hambly, N. C. 2011, MNRAS, 417, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Serenelli, A., Weiss, A., & Miller Bertolami, M. 2009, ApJ, 692, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Althaus, L. G., & García-Berro, E. 2013, A&A, 555, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shibahashi, H. 2013, in EPJ Web Conf., 43, 5006 [Google Scholar]
- Vauclair, G., Fu, J.-N., Solheim, J.-E., et al. 2011, A&A, 528, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viaux, N., Catelan, M., Raffelt, G. G., Redondo, J., & Valcarce, A. A. R. 2013a, in Eur. Phys. J. Web Conf., 43, 2004 [Google Scholar]
- Viaux, N., Catelan, M., Stetson, P. B., et al. 2013b, A&A, 558, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winget, D. E., Sullivan, D. J., Metcalfe, T. S., Kawaler, S. D., & Montgomery, M. H. 2004, ApJ, 602, L109 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Total neutrino energy losses (Lν) for the 0.60959 M⊙ sequences under different assumed values of the neutrino magnetic dipole moment. The thick black line shows the value of the total neutrino emission without a magnetic dipole moment, while the thin red lines show the neutrino emission due to the standard model processes under the assumption of μ12 = 1,2,5, and 10 (from top to bottom). Dashed blue lines show the anomalous neutrino emission under the assumption of μ12 = 1,2,5, and 10 (from bottom to top). |
| In the text | |
 |
Fig. 2 Cooling speeds of the 0.60959 M⊙ sequences computed under different assumed values of the neutrino magnetic dipole moment (μ12 = 0,1,2,5 and 10). |
| In the text | |
 |
Fig. 3 WDLFs computed under the assumption of different stellar formation rates and ages compared with the WDLF derived from the SDSS (Harris et al. 2006; Krzesinski et al. 2009). See text for discussion. |
| In the text | |
 |
Fig. 4 Top panel: comparison between the SDSS- and SSS-WDLFs. Absolute
values of the SSS-WDLF have been corrected for incompleteness by normalization to the
SDSS-WDLF total number of stars in the range 10 < MBol < 13
(small shaded area). Open squares show the averaged WDLF constructed by merging the
WDLFs derived by Harris et al. (2006), Krzesinski et al. (2009), and Rowell & Hambly (2011), see text for details. The gray area
within 3 < MBol < 9
corresponds to the region used for the χ2-like test. Bottom
panel: differences between the SDSS- and SSS-WDLF relative to their own
quoted error bars at each magnitude bin ( |
| In the text | |
 |
Fig. 5 Comparison of our theoretical WDLFs constructed under the assumption of different values of μ12 with the unified WDLF constructed merging the WDLFs derived by Harris et al. (2006), Krzesinski et al. (2009), and Rowell & Hambly (2011). Red error bars correspond to those derived as σi = Max [σi,Uni,σi,SSS,σi,SDSS]. See Sect. 4 for details. The inset shows the value of the χ2 per degree of freedom ν of the χ2-test for the two different sets of error bars. Gray areas indicate the magnitude ranges used for the χ2-test (3 < MBol < 9) and for the normalization procedure (10 < MBol < 13). |
| In the text | |
 |
Fig. 6 Significance level of the χ2-test for the WDLFs shown in Fig. 5. It is clear that, under the error estimation presented in Eq. (8), magnetic dipole moments larger than μ12 = 5 can be discarded at the 99.9% confidence level. Black (red) line shows the result when the value of σUni (Max [σSDSS, σSSS, σUni]) is adopted as the uncertainty – see Table 1. |
| In the text | |
 |
Fig. 7 Comparison of our theoretical WDLFs constructed under the assumption of different values of μ12 with the SDSS-WDLF (for all WDs) derived by Harris et al. (2006) and Krzesinski et al. (2009). The inset shows the value of the χ2 per degree of freedom ν of the χ2-test. Gray areas indicate the magnitude ranges used for the χ2-test (3 < MBol < 9) and for the normalization procedure 10 < MBol < 13. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.