| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 7 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322512 | |
| Published online | 06 February 2014 | |
Pumping of the 4.8 GHz H2CO masers and its implications for the periodic masers in G37.55+0.20
Center for Space Research, Potchefstroom Campus, North-West University, 2520 Potchefstroom, South Africa
e-mail: johan.vanderwalt@nwu.ac.za
Received: 20 August 2013
Accepted: 7 January 2014
Context. Periodic or regular flaring of class II CH3OH masers in nine high mass star forming regions is now a well established phenomenon. Amongst the nine star forming regions, G37.55+0.20 is the only case at present where apart from the presence of a periodic class II CH3OH maser, correlated flaring of another masing species, H2CO in this case, has been detected.
Aims. We perform numerical calculations to investigate under which conditions the 110−111 transition (4.8 GHz) of ortho-H2CO is inverted in order to address the question of the correlated flaring of the 6.7 GHz CH3OH and 4.8 GHz H2CO masers in G37.55+0.20.
Methods. We developed a numerical code to study the population inversion of o-H2CO. Equilibrium solutions for the level populations are found by integrating the rate equations using Heun’s method.
Results. It is found that collisional excitation with H2 as well as radiative excitation by the free-free radio continuum radiation from a nearby ultra- or hyper-compact H ii region can invert the 110−111 transition. It is also found that radiative excitation by the dust infrared radiation field does not lead to an inversion of the 110−111 transition. The 211−212 (14.5 GHz) and 312−313 (28.9 GHz) transitions are inverted only in the presence of the free-free continuum radiation field of a very compact H ii region.
Conclusions. Due to the different pumping mechanisms of the H2CO and CH3OH masers it is unlikely that the near simultaneous flaring of the CH3OH and H2CO masers in G37.55+0.20 is due to changes in the pumping of the masers.
Key words: masers / stars: formation / ISM: molecules / radio lines: ISM
© ESO, 2014
1. Introduction
The phenomenon of periodic or regular flaring of class II CH3OH masers associated with a small number of high mass star forming regions is now well established and is considered as one of the most peculiar phenomena in maser science (Menten 2012). Periodic or regular flaring behaviour of 6.7, 12.2, and 107 GHz CH3OH masers have been reported and discussed by Goedhart et al. (2003, 2007, 2009), van der Walt et al. (2009), Araya et al. (2010) and Szymczak et al. (2011). Currently nine confirmed periodic maser sources are known.
Since the original discovery of periodic flaring of the 6.7 GHz CH3OH masers in G9.62+0.20E by Goedhart et al. (2003), numerous suggestions/hypotheses have been proposed about the underlying mechanisms responsible for the periodic behaviour of the masers. The underlying mechanisms can be divided into two groups, i.e. radiative mechanisms that affect the pumping of the masers and, background source effects which affect the flux of seed photons amplified by the maser.
Amongst the nine known periodic CH3OH maser sources, G37.55+0.20 (IRAS 18566+0408) is at present the only where another masing species, H2CO in this case, shows flaring behaviour which occurs almost coincident in time with the CH3OH maser flares (Araya et al. 2010). Based on the fact that both species flare and that CH3OH is radiatively pumped (Sobolev & Deguchi 1994; Sobolev et al. 1997), Araya et al. (2010) concluded that the H2CO maser in G37.55+0.20 must also be radiatively pumped. These authors therefore proposed an underlying mechanism which raises the dust temperature and which in turn affects the infrared pumping radiation field, resulting in an increase in the amplification of the masers.
Level population calculations for H2CO have been done in the past by, e.g. Thaddeus (1972), Boland & de Jong (1981), and Baan et al. (1986). Boland & de Jong (1981) presented a model in which the H2CO masers in NGC 7538-IRS1 are radiatively pumped by the free-free radio continuum radiation of a nearby compact H ii region. A number of authors, e.g. Mehringer et al. (1994) and Hoffman et al. (2003), however, argued that the Galactic 4.8 GHz H2CO maser emission is due to collisional rather than radiative excitation from dust emission. On the other hand, numerical calculations strongly suggest that the class II CH3OH masers are pumped by infrared radiation (Sobolev & Deguchi 1994; Sobolev et al. 1997) which obviously raises the question of the underlying mechanism that apparently drives both the CH3OH and H2CO maser flares in G37.55+0.20.
Thus, although the pumping of the Galactic 4.8 GHz H2CO masers is an interesting problem as such, the near simultaneous flaring of the 6.7 GHz CH3OH and 4.8 GHz H2CO masers in G37.55+0.20 puts the question of the pumping of the H2CO masers in a new context. In fact, careful comparison of the 6.7 GHz CH3OH and 4.8 GHz H2CO flare profiles as presented by Araya et al. (2010) reveals a remarkable similarity between the two. This also again raises the question of the pumping of the 4.8 GHz H2CO masers and what the implication thereof is for identifying the underlying mechanism responsible for the CH3OH and H2CO maser flares in G37.55+0.20 especially when considering that the two types of masers are 2000 AU apart (Araya et al. 2010). The aim of this paper is to present the results of an investigation into the pumping of the 4.8 GHz H2CO masers and to use the results as a step to understand the underlying mechanism for the flaring of the masers in G37.55+0.20 and hopefully also of the other periodic maser sources.
2. Theory and calculational procedure
Within the framework of the escape probability method the rate equations for the level populations can be written as ![\begin{eqnarray} \nonumber \frac{{\rm d}N_i}{{\rm d}t} & = & \sum_{j < i}\left[\left(-N_i + \left(\frac{g_i}{g_j}N_j - N_i\right)W\mathcal{N}_{ij}\right)\beta_{ij}A_{ij}\right. \\ \nonumber & & +~\left. C_{ij}\left(N_j\frac{g_i}{g_j}{\rm e}^{-E_{ij}/{kT}} - N_i\right)\right]\\ \nonumber & & +~ \sum_{j > i}\left[N_j + \left(N_j - \frac{g_j}{g_i}N_i\right)W\mathcal{N}_{ji}\right)\beta_{ji}A_{ji} \\ & & +~\left. C_{ji}\left(N_j - N_i\frac{g_j}{g_i}{\rm e}^{-E_{ji}/{kT}}\right)\right] \label{eq:rate} \end{eqnarray}](/articles/aa/full_html/2014/02/aa22512-13/aa22512-13-eq8.png) (1)where Ni is the number density in level i, gi the statistical weight of level i, Aij the Einstein-A coefficient for spontaneous emission between levels i and j, W the dilution factor for an external radiation field and
(1)where Ni is the number density in level i, gi the statistical weight of level i, Aij the Einstein-A coefficient for spontaneous emission between levels i and j, W the dilution factor for an external radiation field and 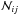 the photon occupation number for this field at frequency νij. Cij = nH2Kij is the collision rate with nH2 the H2 number density and Kij the collision rate coefficient. βij is the escape probability. The rate equations were supplemented with the particle number conservation requirement
the photon occupation number for this field at frequency νij. Cij = nH2Kij is the collision rate with nH2 the H2 number density and Kij the collision rate coefficient. βij is the escape probability. The rate equations were supplemented with the particle number conservation requirement 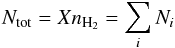 (2)with X the abundance of the molecule under consideration relative to that of H2.
(2)with X the abundance of the molecule under consideration relative to that of H2.
We assume that the maser region is embedded in or surrounded by a layer of warm dust at temperature Td. For the dust radiation field we assume the isotropic optically thin case and therefore that the dust radiation field is given by 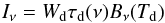 (3)with Bν(Td) the Planck function and τd(ν) = τd(ν0)(ν/ν0)− p the dust optical depth where we have set τd(ν0 = 1013 Hz) = 1 and p = 2 (see e.g. Pavlakis & Kylafis 1996; Sobolev et al. 1997; Cragg et al. 2002). Wd ≤ 1 is a geometric dilution factor.
(3)with Bν(Td) the Planck function and τd(ν) = τd(ν0)(ν/ν0)− p the dust optical depth where we have set τd(ν0 = 1013 Hz) = 1 and p = 2 (see e.g. Pavlakis & Kylafis 1996; Sobolev et al. 1997; Cragg et al. 2002). Wd ≤ 1 is a geometric dilution factor.
The photon occupation number, 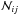 , enters in the derivation of Eq. (1) through the product of c2/hν3 with the mean intensity of the continuum radiation field averaged over the line profile. For dust emission it is given by
, enters in the derivation of Eq. (1) through the product of c2/hν3 with the mean intensity of the continuum radiation field averaged over the line profile. For dust emission it is given by 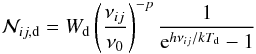 (4)while for the radiation field of a nearby H ii region it is given by
(4)while for the radiation field of a nearby H ii region it is given by 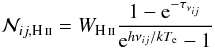 (5)where Te is the electron temperature, τνij the optical depth of the H ii region at frequency νij, and WH ii the corresponding geometric dilution factor. In the case where the continuum radiation field consists of both that of dust and an H ii region the product
(5)where Te is the electron temperature, τνij the optical depth of the H ii region at frequency νij, and WH ii the corresponding geometric dilution factor. In the case where the continuum radiation field consists of both that of dust and an H ii region the product 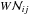 in Eq. (1) is to be replaced by
in Eq. (1) is to be replaced by 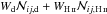 .
.
The optical depth between levels i and j is given by 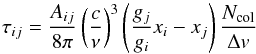 (6)where xi and xj are the fractional number of molecules in levels i and j respectively, Ncol = XnH2d the column density of the masing molecule under consideration with d the source dimension that determines the photon escape, and Δv the FWHM of the local velocity field. Following Cragg et al. (2002, 2005) we will refer to the quantity Ncol/Δv as the specific column density. For the escape probability we used the expression for the large velocity gradient approximation, i.e.
(6)where xi and xj are the fractional number of molecules in levels i and j respectively, Ncol = XnH2d the column density of the masing molecule under consideration with d the source dimension that determines the photon escape, and Δv the FWHM of the local velocity field. Following Cragg et al. (2002, 2005) we will refer to the quantity Ncol/Δv as the specific column density. For the escape probability we used the expression for the large velocity gradient approximation, i.e. 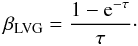 (7)The set of rate equations was solved using Heun’s method (Kreyszig 1979) with a time step of one second. Using Heun’s method requires an initial distribution for the level populations which we took as a Boltzmann distribution with a temperature equal to the gas kinetic temperature (henceforth indicated by Tk). For a given nH2 the calculation always started with a small H2CO specific column density such that the system is completely optically thin in all radiative transitions. An equilibrium solution for this initial specific column density was then found by letting the system evolve over a long enough time. The specific column density is then increased by a small amount and the equilibrium solution for the previous value of the specific column density is then used as the initial distribution. The process is repeated until the required specific column density is reached. Experimentation with this procedure has shown that starting with the optically thin case and progressively calculating solutions for increasing optical depth is very stable and repeatable.
(7)The set of rate equations was solved using Heun’s method (Kreyszig 1979) with a time step of one second. Using Heun’s method requires an initial distribution for the level populations which we took as a Boltzmann distribution with a temperature equal to the gas kinetic temperature (henceforth indicated by Tk). For a given nH2 the calculation always started with a small H2CO specific column density such that the system is completely optically thin in all radiative transitions. An equilibrium solution for this initial specific column density was then found by letting the system evolve over a long enough time. The specific column density is then increased by a small amount and the equilibrium solution for the previous value of the specific column density is then used as the initial distribution. The process is repeated until the required specific column density is reached. Experimentation with this procedure has shown that starting with the optically thin case and progressively calculating solutions for increasing optical depth is very stable and repeatable.
In applying the above method in more extensive calculations it is not practical to find the equilibrium level populations by letting the system evolve over, e.g. ≥106 s. Instead we used a convergence criterium to determine when to stop the calculation. For the present calculations it was required that the maximum value of the relative change in one time step over all levels be less than 10-7, i.e. | Ni(tj + 1) − Ni(tj) | /Ni(tj) < 10-7 for all i. From a number of trial runs it was found that when using this convergence criterium, the level populations differ by less than 1% from the equilibrium solutions found when allowing the system to evolve over a sufficiently long time (>106 s).
The Einstein-A and collision rate coefficients of the first 40 levels of o-H2CO were taken from the Leiden Atomic and Molecular Database (Schöier et al. 2005). The H2-H2CO collision rate coefficients used are from the recent calculations of Wiesenfeld & Faure (2013).
The calculational procedure was tested by considering the two limiting cases where (a) collisions dominate and; (b) where the radiation field dominates and is an undiluted black body radiation field. In the first case it is expected that in equilibrium the level populations be described by a Boltzmann distribution with temperature equal to the gas kinetic temperature and in the second case by a Boltzmann distribution with temperature equal to that of the black body. In both these cases it was found that the equilibrium level populations calculated with the above method produced the correct temperatures with an accuracy of less than one per cent.
3. Results
There are basically three processes in the physical environment that can play a role in the pumping of the masers, i.e. collisional excitation, radiative excitation via the dust continuum emission, and radiative excitation through the free-free continuum emission from an ultra- or hypercompact H ii region. We consider each of these separately. The focus will be on the 110 − 111 transition but we will also later present results for other possible masing transitions.
3.1. Collisional excitation
In the absence of radiation fields the effect of collisions on the level populations is determined by Tk, nH2, and the relative abundance of H2CO, XH2CO. We do not consider explicitly the dependence on the relative abundance of H2CO but implicitly through the H2CO specific column density, XH2COnH2ℓ/Δv (Eq. (6)). For illustrative purposes we considered gas kinetic temperatures in steps of 40 K between 140 K and 300 K and H2 densities between 104 cm-3 and 3 × 107 cm-3.
In Fig. 1 we show the optical depth, τ4.8, of the 110 − 111 transition as a function of the H2CO specific column density for five values of Tk. The calculation was done for a specific value of nH2 for each value of Tk. The choices for the densities will be explained below. It is seen that for the combinations of lower temperatures and H2 densities there is no inversion below specific column densities of about 3 × 1011 cm-3 s. For the higher temperatures, i.e. 260 K and 300 K, an inversion occurs already from the lowest considered specific column densities with the resulting optical depth being very small (τ4.8 ≪ 1) for specific column densities less than about 3 × 1011 cm-3 s. Significant amplification for all five combinations of Tk and nH2 occurs only for specific column densities greater than about 1012 cm-3 s.
 |
Fig. 1 Comparison of the dependence of τ4.8 on the H2CO specific column density for five combinations of Tk and nH2. No radiative excitation was considered. |
To investigate and illustrate the behaviour of τ4.8 for more general combinations of Tk and nH2 in terms of the dependence of τ4.8 on the specific column density would require a large number of graphs such as in Fig. 1 which is unpractical. Instead we will characterize the dependence of τ4.8 on the specific column density for a single combination of Tk and nH2 with τ4.8(max), the maximum negative value of τ4.8 over the considered range of specific column densities. The detailed information of the dependence of τ4.8 on specific column density for a given combination of Tk and nH2 is therefore lost. However, τ4.8(max) is still a usefull quantity to investigate under which conditions a population inversion occurs.
In Fig. 2 we therefore show the dependence of τ4.8(max) on nH2 for 104 cm-3 ≤ nH2 ≤ 3 × 107 cm-3 for the five values of Tk used in Fig. 1. For each temperature the population inversion occurs only above a “threshold” value of nH2 which increases with increasing Tk. It is also seen that the density where τ4.8(max) is a maximum ranges from about 7 × 104 cm-3 at Tk = 140 K to about 4 × 105 cm3 at 300 K and that τ4.8(max) is a maximum for Tk ~ 180 K. The respective H2 densities used in Fig. 1 are those where τ4.8(max) has a maximum for the five values of Tk. It is also interesting to note that the H2 densities where τ4.8(max) is a maximum are significantly smaller for what is found, for example, for OH masers (Pavlakis & Kylafis 1996).
 |
Fig. 2 Comparison of the dependence of τ4.8(max) on nH2 for five values of Tk. |
3.2. Radiative excitation: Dust infrared radiation
We examined the effect of the dust radiation field for different dust temperatures, and values of p and Wd (Eq. (4)) when collisions are absent. It can be stated that no instance could be found where the dust emission on its own results in a population inversion, not for the 110 − 111 transition nor between any other levels.
 |
Fig. 3 Comparison of the dependence of τ4.8 on the H2CO specific column density when excitation through collisions and the dust radiation field are included with the case when only collisional excitation is considered. All results are for nH2 = 1.3 × 105 cm-3. |
Although the dust radiation field in itself does not lead to a population inversion, it nevertheless affects the level populations and therefore the population inversion of the 110 − 111 transition. The effect of the dust radiation field is small as is shown in Fig. 3 where we compare τ4.8 for the case of Tk = 180 K for Td equal to 100 K and 180 K with pure collisional excitation when Tk = 180 K. In Fig. 4 we show the dependence τ4.8(max) on nH2 for Tk = 180 K, Td = 100 K and for Wd equal 0.5 and 1.0. The dust infrared radiation field is seen to mostly affect τ4.8(max) for nH2 less than 105 cm-3.
 |
Fig. 4 Comparison of the dependence of τ4.8(max) on nH2 when excitation through collisions and the dust radiation field is included with the case of pure collisional excitation is considered. In all three cases Tk = 180 K and Td = 100 K where the dust emission is included. |
3.3. Radiative excitation: Free-free continuum emission
In Fig. 5 we show the dependence of τ4.8(max) on the emission measure for an H ii region with an electron temperature of 104 K and a dilution factor, WH ii = 1 and where collisions were ignored. The range in emission measures from 5 × 107 to 4 × 1011 pc cm-6 corresponds to turnover frequencies in the radio continuum spectral energy distribution from about 4 GHz to 274 GHz. It is seen that the free-free emission from the H ii region can cause a population inversion for the 110 − 111 transition. For emission measures greater than about 4 × 1011 pc cm-6τ4.8 increases very rapidly to a value of 500 and remains constant at that value. The maximum negative optical depth is found at an emission measure of about 8 × 1010 pc cm-6 which translates to a turnover frequency of about 80 GHz.
 |
Fig. 5 Dependence of τ4.8(max) on the emission measure for the case when collisions and the dust radiation field are ignored. The H2 density used in this case was 105 cm-3. |
The effect of including collisional excitation is shown in Fig. 6. The same combinations of Tk and nH2 as used in Fig. 2 have been used. The underlying dependence of τ4.8 on the specific column density as seen in Fig. 2 can also be seen in this case. However, comparison with Fig. 2 shows that the free-free emission has a significant effect in that an inversion of the 110 − 111 transition now occurs for all five combinations of Tk and nH2 already at a specific column density of 108 cm-3 s whereas this is not the case when collisions are the only excitation mechanism. In fact, the effect on τ4.8 is seen to be greatest for the lower temperatures. The maximum negative values which τ4.8 can have are, however, less than in the case of pure collisional excitation. It should also be noted that the specific column densities where τ4.8 has a maximum negative value has shifted to larger values in the presence of the free-free continuum radiation field than without it.
 |
Fig. 6 Graph showing the dependence of τ4.8 on the H2CO specific column density for five values of Tk in the presence of a free-free continuum radiation field. The emission measure used was 109 pc cm-6 with WH ii = 1. |
With regard to the influence of the free-free continuum radiation field we lastly compare in Fig. 7 the dependence of τ4.8(max) on nH2 for emission measures of 108 pc cm-6, 109 pc cm-6, and 1010 pc cm-6. Also shown is the case for collisional excitation. In all four cases we used Tk = 180 K. The free-free continuum radiation field is seen to significantly affect the optical depth over most of the range of nH2 with the effect being greatest toward lower densities where the inversion is exclusively due to that of the free-free continuum radiation.
 |
Fig. 7 Comparison of τ4.8(max) as a function of nH2 for different emission measures. The gas kinetic temperature was taken as 180 K. |
3.4. Inversion of other transitions
In Fig. 8 we compare the dependence of the optical depth on the H2CO specific colum density for a number of transitions in order to investigate the possibility of a population inversion for other transitions. We are in particular interested in the 211 − 212 transition since Boland & de Jong (1981) predicted a detectable maser line for this transition. In the upper panel we show the results for the case of collisional excitation for the 110 − 111 transition as well as for the 211 − 212 (14.5 GHz), 312 − 313 (28.9 GHz) and 413 − 414 (48.3 GHz) transitions. Our choice for the last three transitions is based on the slower spontaneous decay rates from the upper to the lower levels for these transitions compared to other transitions. The gas kinetic temperature was taken as 180 K and nH2 = 1.3 × 105 cm-3. In this case only the 110 − 111 transition shows a population inversion.
 |
Fig. 8 Comparison of optical depths for a number of transitions. The calculations were done for Td = 100 K, Wd = 1.0, and WH ii = 1.0. The solid lines are for Tk = 180 K with nH2 = 1.3 × 105 cm-3 and the dashed lines for Tk = 300 K with nH2 = 4 × 105 cm-3. The emission measure is indicated in each of the panels. |
The middle and bottom panels show the results for more general cases where collisions and the dust- and free-free continuum radiation fields were included. The middle panel is for the case when the associated H ii region has an emission measure of 109 pc cm-6 and the bottom panel for an emission measure of 1010 pc cm-6. The 211 − 212 transition is seen to show only a very weak inversion while there are no inversions for the 312 − 313 and 413 − 414 transitions for an emission measure of 109 pc cm-6. For an emission measure of 1010 pc cm-6 the 211 − 212 transition shows a larger negative optical depth while the 312 − 313 transition shows only a very weak inversion. These results suggests that apart from the 110 − 111 transition, the 211 − 212 and 312 − 313 transitions are inverted only in the presence of the free-free continuum radiation field and then only for fairly large values of the emission measure. The optical depth for the 28.9 GHz maser is, however, so small that it is unlikely that it will be detected while the 14.5 GHz maser is expected to be detectable but significantly fainter than the 4.8 GHz maser.
4. Discussion
The results presented above show that the 4.8 GHz H2CO masers can be pumped via collisions with H2 as well as radiatively by the free-free continuum emission from a nearby ultra- or hypercompact H ii region but not by the dust infrared radiation field. Before discussing the implication of this result for the interpretation of the CH3OH and H2CO flares in G37.55+0.20E is it necessary to consider a few aspects of the results presented above.
Inspection of Figs. 1, 2, and 5 shows that the maximum value for the optical depth for the 110 − 111 transition lies between −2.5 and −3.0. This means that our calculations predict an amplification factor (e−τ4.8) of at most 20. Even if the brightness temperature of the background source is 104 K it will therefore not be possible to explain maser brightness temperatures greater than 2 × 105 K. On the other hand, the model by Boland & de Jong (1981) could produce optical depths of −5 with which it is possible to explain brightness temperatures of the order of 106 K. The reason for this difference between the present calculations and that of Boland & de Jong (1981) is not clear. Within the framework of the present calculations is it therefore possible to explain the fainter but not the brightest Galactic 4.8 GHz H2CO masers.
A second point to be noted is that in the case of purely collisional excitation the H2CO specific column density where τ4.8 is a maximum lies between about 5 × 1012 cm-3 s and 1013 cm-3 s. Although the aim of the present calculations is not to discuss any particular source, the values of the H2CO specific column density where τ4.8 reaches a maximum should be taken note of as it might imply very large maser path lengths. For example, for Tk = 180 K and nH2 = 1.3 × 105 cm-3 (see Fig. 1), τ4.8 is a maximum at an H2CO specific column density of 5 × 1012 cm-3 s. With the specific column density given by XH2COnH2ℓ/Δv, the maser path length, ℓ, is found to be 7.5 pc with Δv = 3 km s-1 and XH2CO = 5 × 10-7. Such long path lengths are certainly not realistic for masers associated with Galactic star forming regions. It is interesting to note that Araya et al. (2007) refer to having found a similar result, i.e. that very long, parsec scale, path lengths are required to explain the observed brightness temperatures of the 4.8 GHz H2CO masers.
To try to address this problem we note the following. First, in a recent study McCauley et al. (2011) used the 312−313 and 413−414 transitions of o-H2CO to estimate densities in 23 well studied molecular cores. The H2CO specific column densities found by these authors lie between 1.4 × 108 cm-3 s and 5.1 × 1010 cm-3 s with an average of 2.9 × 109 cm-3 s. If the pumping is purely collisional then, refering to Fig. 1, it is seen that these specific column densities are well below of what is required for a reasonable amplification factor for the 110−111 transition. In the presence of a very compact H ii region some inversion of the 110−111 and 211−212 transitions would have been possible (bottom panel of Fig. 8) at these specific column densities. But even in this case the masers would have been very weak. It would therefore appear as if masing of at least the 110−111 transition requires larger specific column densities than what seems to be typically found for H2CO. The need for larger specific column than what is normally found for H2CO in star forming regions might be a reason for the rarity of the 110−111 H2CO masers.
As already noted, the relatively large H2CO specific column densities where the amplification is significant implies unrealistically long maser path lengths. For a given H2 density, Δv, and specific column density, the only way to significantly reduce the maser path length is to increase the relative abundance of H2CO. In the above example we assumed a relative abundance of 5 × 10-7. However, Maret et al. (2004) found relative abundances for H2CO of up to 6 × 10-6 in the inner warm regions of low mass protostellar envelopes. Applying this abundance to the above example would reduce the maser path length to 0.63 pc, which still might be too large. Cragg et al. (2005) found that the 6.7 and 12.2 GHz CH3OH masers have their maximum brightness temperatures for a CH3OH specific column density of about 1013 cm-3 s which is comparable to what is required for the 4.8 GHz H2CO maser. However, this result was found for nH2 = 107 cm-3 which is almost two orders of magnitude larger than the H2 densities where τ4.8(max) for the 4.8 GHz H2CO masers is a maximum. Using an average relative abundance for CH3OH of 10-6 (Maciel 2013) and Δv = 3 × 105 cm s-1, a CH3OH maser path length of 3 × 1017 cm ~ 0.1 pc is found. If the path length of the 4.8 GHz H2CO maser is assumed to have this value, the H2CO relative abundance is required be approximately 4 × 10-5.
Such a large relative abundance for H2CO might seem unreasonable and it is beyond the scope of the present work to make any statements in this regard. However, given the rarity of H2CO masers it might not be unreasonable to postulate rare physical and chemical conditions in localized regions that can give rise to higher relative abundances. To explain the rarity of H2CO masers Hoffman et al. (2003) suggested that the 4.8 GHz maser inversion might be due to a rare collisional excitation. Our calculations have shown that inversion of the 110 − 111 transition can be achieved through collisional excitation with H2 and that it is not necessary to invoke a rare collisional mechanism. However, it seems as if it is still necessary to invoke some rare conditions to explain the 4.8 GHz H2CO masers. Gray (2012) proposes that the rarity of the 4.8 GHz H2CO masers might be due to a short lifetime of these masers. A short lifetime alone, however, might not be sufficient to explain the rarity of the masers. In addition to a short lifetime, larger than average H2CO abundances also seems to be required for the masers to operate.
We now turn to the implications of the above results for the masers in G37.55+0.20. The results presented above that the 110−111 transition can be inverted collisionally via H2 and radiatively via the free-free continuum radiation but not through the dust radiation field is contrary to the conclusion of Araya et al. (2010) that the correlated variability of the CH3OH and H2CO masers in G37.55+0.20 implies the same excitation (pumping) mechanism for the two molecules. If the pumping mechanisms of CH3OH and H2CO are in fact different then any proposed mechanism should be such that it can affect not only the dust temperature but also the gas kinetic temperature and/or the free-free emission from an associated H ii region. As already pointed out the CH3OH and H2CO maser flare profiles presented by Araya et al. (2010) are very similar. Thus, a further constraint is that whatever mechanism is proposed to simultaneously affect the pumping of the CH3OH and H2CO masers, it should be such that the dust and gas temperatures and/or the properties of the H ii region vary correctly in order to produce similar flare profiles. It is very difficult to envisage a single mechanism or even a number of coupled processes that can be responsible for such fine tuning, especially if the two masers are 2000 AU apart.
If the near simultaneous flaring of the H2CO and CH3OH masers cannot be due to pumping effects, the only other possibility left is that it is due to changes in the background seed photon flux. It has been postulated that the periodic CH3OH maser flares in G9.62+0.20E and G22.357+0.066 are due to changes in the free-free emission from parts of the background H ii region against which they are projected (van der Walt 2011; Szymczak et al. 2011). Given that the flare profiles for the two masers in G37.55+0.20 are very similar and also resemble that of the periodic masers in G9.62+0.20E and G22.357+0.066, it is possible that the same underlying mechanism might be responsible for the maser flaring in these three sources.
5. Conclusions
We presented the results of a numerical calculation to determine the physical conditions under which a population inversion for the 110 − 111 transition of H2CO can occur. The underlying aim of these calculations was to interpret the near simultaneous flaring of the 6.7 GHz CH3OH and 4.8 GHz H2CO masers in G37.55+0.20. Considering the results presented above we conclude the following:
-
The 110−111 transition can be inverted via collisional excitation with H2as well as by the free-free continuum of H iiregions with emission measures greater than about5 × 107 pc cm-6.
-
The dust infrared emission does affect the level populations but does not result in a population inversion of the 110 − 111 transition nor of any other possible masing transitions.
-
The maximum amplification found within the framework of our calculations is only about 20 which cannot explain the brightest 4.8 GHz H2CO masers.
-
If collisions are the only excitation mechanism a noteable amplification for the 4.8 GHz masers exists only for H2CO specific column densities above about 5 × 1011 cm-3 s. These specific column densities are significantly larger than what is derived from thermal line emission of H2CO.
-
To avoid unrealistically large maser path lengths it is necessary to postulate higher than average relative abundances for H2CO in the regions where the 4.8 GHz masers operate.
-
The 211−212 and 312−313 transitions are inverted only in the presence of the free-free continuum radiation field of very compact H ii regions.
-
Due to the different pumping mechanisms of the H2CO and CH3OH masers it is unlikely that the near simultaneous flaring of the CH3OH and H2CO masers in G37.55+0.20 is due to changes in the pumping of the masers. Instead, as an alternative it is suggested that the flaring is due to a single process that affects the flux of the background seed photon flux for both of the masers even though they are 2000 AU apart.
Acknowledgments
I would like to thank Melvin Hoare and Sharmila Goedhart for valuable comments on an earlier version of the manuscript as well as an anonymous referee and Malcolm Walmsley for useful comments. This work was supported by the National Research Foundation under grant number 2053475.
References
- Araya, E., Hofner, P., Kurtz, S., et al. 2007, in IAU Symp. 242, eds. J. M. Chapman, & W. A. Baan, 140 [Google Scholar]
- Araya, E. D., Hofner, P., Goss, W. M., et al. 2010, ApJ, 717, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Baan, W. A., Guesten, R., & Haschick, A. D. 1986, ApJ, 305, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Boland, W., & de Jong, T. 1981, A&A, 98, 149 [NASA ADS] [Google Scholar]
- Cragg, D. M., Sobolev, A. M., & Godfrey, P. D. 2002, MNRAS, 331, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Cragg, D. M., Sobolev, A. M., & Godfrey, P. D. 2005, MNRAS, 360, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Goedhart, S., Gaylard, M. J., & van der Walt, D. J. 2003, MNRAS, 339, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Goedhart, S., Gaylard, M. J., & van der Walt, D. J. 2007, in IAU Symp. 242, eds. J. M. Chapman, & W. A. Baan, 97 [Google Scholar]
- Goedhart, S., Langa, M. C., Gaylard, M. J., & van der Walt, D. J. 2009, MNRAS, 398, 995 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, M. 2012, Maser Sources in Astrophysics (Cambridge University Press) [Google Scholar]
- Hoffman, I. M., Goss, W. M., Palmer, P., & Richards, A. M. S. 2003, ApJ, 598, 1061 [NASA ADS] [CrossRef] [Google Scholar]
- Kreyszig, E. 1979, Advanced Engineering Mathematics (Wiley) [Google Scholar]
- Maciel, W. J. 2013, Astrophysics of the Interstellar Medium (Springer) [Google Scholar]
- Maret, S., Ceccarelli, C., Caux, E., et al. 2004, A&A, 416, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCauley, P. I., Mangum, J. G., & Wootten, A. 2011, ApJ, 742, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Mehringer, D. M., Goss, W. M., & Palmer, P. 1994, ApJ, 434, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Menten, K. M. 2012, in IAU Symp. 287, eds. R. S. Booth, W. H. T. Vlemmings, & E. M. L. Humphreys, 506 [Google Scholar]
- Pavlakis, K. G., & Kylafis, N. D. 1996, ApJ, 467, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sobolev, A. M., & Deguchi, S. 1994, A&A, 291, 569 [NASA ADS] [Google Scholar]
- Sobolev, A. M., Cragg, D. M., & Godfrey, P. D. 1997, A&A, 324, 211 [NASA ADS] [Google Scholar]
- Szymczak, M., Wolak, P., Bartkiewicz, A., & van Langevelde, H. J. 2011, A&A, 531, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thaddeus, P. 1972, ApJ, 173, 317 [NASA ADS] [CrossRef] [Google Scholar]
- van der Walt, D. J. 2011, AJ, 141, 152 [NASA ADS] [CrossRef] [Google Scholar]
- van der Walt, D. J., Goedhart, S., & Gaylard, M. J. 2009, MNRAS, 398, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Wiesenfeld, L., & Faure, A. 2013, MNRAS, 432, 2573 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Comparison of the dependence of τ4.8 on the H2CO specific column density for five combinations of Tk and nH2. No radiative excitation was considered. |
| In the text | |
 |
Fig. 2 Comparison of the dependence of τ4.8(max) on nH2 for five values of Tk. |
| In the text | |
 |
Fig. 3 Comparison of the dependence of τ4.8 on the H2CO specific column density when excitation through collisions and the dust radiation field are included with the case when only collisional excitation is considered. All results are for nH2 = 1.3 × 105 cm-3. |
| In the text | |
 |
Fig. 4 Comparison of the dependence of τ4.8(max) on nH2 when excitation through collisions and the dust radiation field is included with the case of pure collisional excitation is considered. In all three cases Tk = 180 K and Td = 100 K where the dust emission is included. |
| In the text | |
 |
Fig. 5 Dependence of τ4.8(max) on the emission measure for the case when collisions and the dust radiation field are ignored. The H2 density used in this case was 105 cm-3. |
| In the text | |
 |
Fig. 6 Graph showing the dependence of τ4.8 on the H2CO specific column density for five values of Tk in the presence of a free-free continuum radiation field. The emission measure used was 109 pc cm-6 with WH ii = 1. |
| In the text | |
 |
Fig. 7 Comparison of τ4.8(max) as a function of nH2 for different emission measures. The gas kinetic temperature was taken as 180 K. |
| In the text | |
 |
Fig. 8 Comparison of optical depths for a number of transitions. The calculations were done for Td = 100 K, Wd = 1.0, and WH ii = 1.0. The solid lines are for Tk = 180 K with nH2 = 1.3 × 105 cm-3 and the dashed lines for Tk = 300 K with nH2 = 4 × 105 cm-3. The emission measure is indicated in each of the panels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


