| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 13 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201322496 | |
| Published online | 18 February 2014 | |
The impact of rotation on the line profiles of Wolf-Rayet stars
Institut für Physik und Astronomie, Universität Potsdam,
Karl-Liebknecht-Str. 24/25,
14476
Potsdam,
Germany
e-mail:
shtomer@astro.physik.uni-potsdam.de
Received:
16
August
2013
Accepted:
8
January
2014
Context. Massive Wolf-Rayet stars are recognized today to be in a very common, but short, evolutionary phase of massive stars. While our understanding of Wolf-Rayet stars has increased dramatically over the past decades, it remains unclear whether rapid rotators are among them. There are various indications that rapidly rotating Wolf-Rayet stars should exist. Unfortunately, due to their expanding atmospheres, rotational velocities of Wolf-Rayet stars are very difficult to measure. However, recently observed spectra of several Wolf-Rayet stars reveal peculiarly broad and round emission lines. Could these spectra imply rapid rotation?
Aims. In this work, we model the effects of rotation on the atmospheres of Wolf-Rayet stars. We further investigate whether the peculiar spectra of five Wolf-Rayet stars may be explained with the help of stellar rotation, infer appropriate rotation parameters, and discuss the implications of our results.
Methods. We make use of the Potsdam Wolf-Rayet (PoWR) non-LTE model atmosphere code. Since the observed spectra of Wolf-Rayet stars are mainly formed in their expanding atmospheres, rotation must be accounted for with a 3D integration scheme of the formal integral. For this purpose, we assume a rotational velocity field consisting of an inner co-rotating domain and an outer domain, where the angular momentum is conserved.
Results. We find that rotation can reproduce the unique spectra analyzed here. However, the inferred rotational velocities at the stellar surface are large (~200 km s-1), and the inferred co-rotation radii (~10R∗) suggest the existence of very strong photospheric magnetic fields (~20 kG).
Key words: stars: Wolf-Rayet / Magellanic Clouds / stars: magnetic field / stars: massive / gamma-ray burst: general / stars: rotation
© ESO, 2014
1. Introduction
All massive stars at solar metallicity with initial masses larger than ~20 M⊙ eventually become Wolf-Rayet (WR) stars (Sander et al. 2012). WR stars have a tremendous influence on their host galaxies, owing to their ionizing radiation and the immense transfer of kinetic energy and momentum to the surrounding interstellar matter, carried with their powerful stellar winds. Their study is thus fundamental to our understanding of the evolution of massive stars, and as a consequence, of galaxies (cf. Crowther 2007, for a thorough review on the properties of WR stars).
Knowing whether WR stars might exhibit rapid rotation is crucial in this context. Rotation dramatically affects the chemical stratification of the star due to rotationally induced mixing (e.g. Heger & Langer 2000), may cause surface deformations such as gravity darkening (von Zeipel 1924) or disk formation (Bjorkman & Cassinelli 1993), and may also contribute to the driving of the wind (Friend & Abbott 1986).
Various theoretical considerations and models suggest that rapidly rotating WR stars may exist. It is observed that many O stars, which are the direct progenitors of WR stars, exhibit rotational velocities of several hundred km s-1 (cf. Penny 1996; Vanbeveren et al. 1998). It has been recently suggested (e.g. de Mink et al. 2013) that the highest rotational velocities observed in O stars might be the result of binary interaction or even merging processes. Indeed, the stellar wind severely dampens the rapid rotation of the star shortly before the WR phase initiates. On the other hand, the continuous contraction of the star leads to faster rotation, so that the stellar rotation of a WR star is determined by these two counteracting mechanisms. Evolutionary models calculated by Meynet & Maeder (2005) with initial rotational velocities of 300 km s-1 predict, especially at low metalliticies, a considerable increase of the rotational velocity as the WR star evolves from a late subtype (WNL) to an early subtype (WNE), reaching values of up to 200 km s-1. WR stars with rapidly rotating cores have been proposed as progenitors of long-duration gamma-ray bursts (LGRBs) by various authors (e.g. Vink & de Koter 2005; Hirschi et al. 2005; Woosley & Heger 2006; Gräfener et al. 2012), relying on the collapsar model of Woosley (1993).
Usually, rotational velocities of stars are determined from the rotational broadening of their absorption lines. However, this method can hardly be applied to WR stars. The spectra of WR stars, especially of early subtypes, are predominantly formed in their dense, extended winds, and thus rarely exhibit such absorption lines in their observed spectra.
Various methods to probe the rotation of WR stars have been proposed throughout the years. A few WR stars have been observed to show periodic photometric variations (e.g. Marchenko & Moffat 1998) which may be attributated to so called co-rotating interaction regions (CIRs) in the wind (Cranmer & Owocki 1996; Chené & St-Louis 2005). Rapid rotation may also lead to an axisymmetric density structure (e.g. Coyne & McLean 1982; Ignace et al. 1996). If layers in which electron scattering occurs become axisymmetric, the departure from spherical symmetry may be detected with linear polarimetry via the so-called line effect (e.g. Harries et al. 1998), i.e. an enhanced polarization of the continuum radiation relative to that of emission lines. While a positive detection of the line effect may be associated with rapid rotation, other scenarios such as close binaries (Brown & McLean 1977) or strong magnetic fields (Poe et al. 1989) were shown to also cause it. Moreover, rotational velocities are very hard to quantify on the basis of polarimetric measurements alone.
Recent spectroscopic studies performed with the non-LTE Potsdam Wolf-Rayet (PoWR) model atmosphere code potentially imply the existence of rapidly rotating WR stars. Hamann et al. (2006) performed a flux-convolution with a rotation profile (e.g. Unsöld 1955) in order to reproduce the broad and round emission lines of the Galactic WN2 star WR 2. Hainich et al. (2014), who extensively analyzed 102 WN stars residing in the Large Magellanic Cloud (LMC), also made use of flux-convolution with rotation profiles of very large rotational velocities for a few of them. Sander et al. (2012) used the same technique for two WO stars. So far, at least ten WR stars have been identified to exhibit round and broad line profiles, and as many as half of them show no signs for binarity.
Alas, the method of flux-convolution with rotation profiles is not valid in the case of expanding atmospheres. The emergent radiation is not simply emitted from one single rotating layer, but rather formed in the expanding stellar wind, a region that extends over tens of stellar radii. To account for rotation in the case of expanding atmospheres, a model of the rotational velocity field is prerequisite. The evaluation of the formal integral must include the effects of the modified velocity field, which is comprised of radial and rotational components. Nevertheless, the fact that rotation profiles help to reproduce the observed spectra of several WR stars is potentially a beacon for rapid rotation in these stars.
To emphasize the striking uniqueness of the spectra analyzed here, we show a comparison (Fig. 1) between the observed spectra of two WN4b stars residing in the LMC: BAT99 7 (solid blue line), analyzed in this work for rapid rotation, and BAT99 134 (dashed brown line). Note the distinct qualitative difference between the two spectra – and this despite their identical spectral class! As opposed to the sharp, triangular-like emission lines of BAT99 134, which are very typical for WNE stars, the spectrum of BAT99 7 exhibits extremely round and broad spectral lines. Note also how the C iv λ5800 multiplet appears stretched and flat-topped in the spectrum of BAT99 7. Out of hundreds of WR stars previously analyzed, only a handful exhibit such exceptional features.
 |
Fig. 1 Comparison between the observed optical spectra of two WN4b stars in the LMC: BAT99 134 (dashed brown line), and BAT99 7 (solid blue line). While the spectrum of BAT99 134 is typical for a WNE subtype, the spectrum of BAT99 7 distinctly shows qualitative differences. |
Ignace (2009) managed to obtain round and broad line profiles as an analytical solution of the transfer equation in the case of optically thick lines and for a specific parameter selection. However, his assumptions (e.g. constant wind velocity, LTE population numbers) do not hold in the case of WR stars. Most importantly, such line profiles are not obtained using non-LTE spectral modeling, independently of the parameter choice. One might further argue that round emission lines could be reproduced by assuming much larger terminal velocities. While a larger terminal velocity indeed yields broader lines, it does not help reproduce their round profiles, as we later show. We therefore currently see no alternatives which can explain the unique spectra analyzed here other than rotation. The prediction that rapidly rotating WR stars may exist, along with the existence of such peculiar spectra, provide the motivation for a proper treatment of rotation in expanding atmospheres of WR stars.
Our paper is structured as follows: Sect. 2 consists of a short description of our sample and of the corresponding observational data. In Sect. 3, we briefly describe the model atmosphere code and the rotational velocity field. In Sect. 4, we explain our methods in detail and present our results. Finally, in Sect. 5, we thoroughly discuss the plausibility and implications of our results.
2. Sample and observational data
We analyze five stars in this work, comprising four LMC stars (BAT99 7, 51, 88, and 94), and one Galactic star (WR 2). These are the only stars, out of the ~180 WN stars analyzed by Hamann et al. (2006) and Hainich et al. (2014), which exhibit peculiarly broad and round spectral emission lines and are not classified as binaries. Stars which were classified as binaries in previous studies (e.g. Schnurr 2008; Foellmi et al. 2003), or whose spectrum appears to be a composite of two spectra, are omitted from this analysis; their study is postponed to future work. No WC stars out of those analyzed by Sander et al. (2012) show round lines in their observed spectra. To restrict the discussion to WN stars, the analysis of WO stars is not included in this work.
The observation used for WR 2 were taken at the “Deutsch-Spanisches Astronomisches Zentrum (DSAZ)”, Calar Alto, Spain with the Boller & Chivens Cassegrain spectrograph at the 2.2 m-telescope. The spectrum covers a spectral range of 3320 to 7400 Å with a spectral resolution of ≈3600 (cf. Hamann et al. 1995, for more details). The optical spectrum of the LMC star BAT99 7 in the domain 4000−6000 Å was taken on 2010 December 23 with FORS2 at the VLT (PI: W.-R. Hamann) with a spectral resolution of ≈1600. For the spectral domain 6000−6800 Å of the star BAT99 7 and for the remaining LMC stars analyzed here, we use co-added, rectified spectra, kindly provided by C. Foellmi. The individual spectra were taken with various instruments, as described by Foellmi et al. (2003)1, with a spectral resolution of about 1000.
3. Model
3.1. PoWR model atmospheres
The PoWR model atmosphere code solves the radiative transfer and rate equations in the co-moving frame, calculates the non-LTE population numbers, and delivers a synthetic spectrum by evaluating the formal integral in the observer’s frame. A closer description of the assumptions (spherical symmetry, stationary mass-loss) and methods used in the code is given by Gräfener et al. (2002) and Hamann & Gräfener (2004). Clumping in the wind is accounted for by the use of a constant clumping factor D which describes the density ratio of a clumped wind to an identical homogenous one (cf. Hamann & Koesterke 1998). Line blanketing is treated using the superlevel approach (Gräfener et al. 2002), as originally implemented by Hillier & Miller (1998).
The inner boundary of a model is denoted with R∗. It is defined at the Rosseland optical depth τRoss = 20 (cf. Hamann et al. 2006). For a given luminosity L∗, the stellar temperature T∗ is defined via the Stefan-Boltzmann relation.
We do not calculate hydrodynamically consistent model atmospheres in this work, but
rather use a pre-specified wind velocity law. In the subsonic region, the velocity field
is defined such that a hydrostatic density stratification is approached. In the supersonic
region, the radial wind velocity at a distance r from the center takes the form of the so-called
β-law:
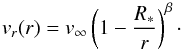 (1)The exponent
β is fixed
to the standard value β = 1 for all models calculated here. The influence
of different values of β is discussed in Sect. 4.4. The terminal velocity v∞ is determined individually for each
star analyzed here. For the Doppler velocity vD corresponding to microturbulent and
thermal motion, we adopt the constant value vD = 100 km s-1 (cf. Hamann & Koesterke 2000).
(1)The exponent
β is fixed
to the standard value β = 1 for all models calculated here. The influence
of different values of β is discussed in Sect. 4.4. The terminal velocity v∞ is determined individually for each
star analyzed here. For the Doppler velocity vD corresponding to microturbulent and
thermal motion, we adopt the constant value vD = 100 km s-1 (cf. Hamann & Koesterke 2000).
Once the population numbers in the wind have been established, the emergent intensities are calculated by solving the transfer equation along rays parallel to the line-of-sight (the formal integral). Without rotation, it is sufficient to evaluate the emergent intensities at distinct impact parameter values only, and finally to integrate over all impact parameters. The azimuthal integration is in this case redundant.
If spectral lines are formed in a non-extended stellar photosphere, the azimuthal
integration can be avoided even in the presence of rotation. In this case, the effect of
rotation may be accounted for very accurately by performing a flux-convolution with
rotation profiles (e.g. Unsöld 1955). However,
since the spectra of WR stars are formed in their dense and extended winds, the use of
rotation profiles is not justified. Rather, for the calculation of the flux
fν at a distance
d from the
star, the emergent intensities 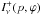 are to be integrated over all
impact parameters p and all azimuthal angles ϕ:
are to be integrated over all
impact parameters p and all azimuthal angles ϕ: 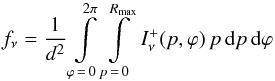 (2)where Rmax is the
upper integration boundary which includes the entire wind (see Fig. 2).
(2)where Rmax is the
upper integration boundary which includes the entire wind (see Fig. 2).
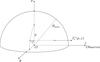 |
Fig. 2 The coordinate system used for the 3D integration scheme. The integration of the
emergent intensities |
The emergent intensity 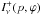 is obtained by integrating
the transfer equation over the optical depth τ along the ray specified by p and ϕ. This evaluation of the
formal integral over τ, together with the integration of
is obtained by integrating
the transfer equation over the optical depth τ along the ray specified by p and ϕ. This evaluation of the
formal integral over τ, together with the integration of
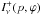 over p and ϕ, covers the wind in all
three dimensions, and hence we name this calculation the “3D integration scheme”.
over p and ϕ, covers the wind in all
three dimensions, and hence we name this calculation the “3D integration scheme”.
3.2. The rotational velocity field
The rotational velocity field adopted here relies on a few assumptions. The stellar atmosphere (including the wind) is divided into two radial domains:
-
1.
the co-rotating domain r ≤ Rcor, where we postulate the existence of a radius Rcor ≥ R∗ up to which the wind co-rotates with the star with the angular velocity ω;
-
2.
the outer domain r > Rcor, where the only forces present are all radial, and where the angular momentum is therefore conserved.
We thoroughly discuss the motivation behind these assumptions in Sect. 5. As a first order approximation, we account for rotation only in the formal integral. Petrenz & Puls (2000) discuss possible effects of rotation on the population numbers in early-type stars. For simplicity, we ignore effects caused by deformations of the stellar surface such as gravity darkening and disk formation. The angular velocity ω of the co-rotating domain (r ≤ Rcor) is assumed to be independent of the latitude θ. Based on hydrodynamical studies by Owocki et al. (1994), we neglect the polar components of the velocity field, which are much smaller than the rotational and radial components.
These assumptions allow one to deduce the form of the rotational velocity field on the
basis of simple physical arguments. Denoting with r the distance between a
wind element and the center of the star, with
the azimuthal unit vector relative to the rotation axis ω, and with
θ the
latitude (measured from the positive direction of the rotation axis), one finds the
rotational velocity field vφ to be:
![\begin{equation} v_\phi(r,\theta) = v_\text{eq} \left(R_\text{cor}\right) \sin \theta \left\{ \begin{array}{cl}\displaystyle \frac{r}{R_\text{cor}} & r \leq R_\text{cor} \\[1em] \displaystyle \frac{R_\text{cor}}{r} & r > R_\text{cor} \end{array} \right. \label{eq:phiform2} \end{equation}](/articles/aa/full_html/2014/02/aa22496-13/aa22496-13-eq40.png) (3)where
(3)where
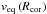 is the
equatorial rotational velocity at the co-rotation radius.
is the
equatorial rotational velocity at the co-rotation radius.
Since we observe the star at an unknown inclination angle i (the angle between the
line-of-sight and the rotation axis ω), the only parameter having a
direct observable influence on the spectrum is 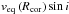 , denoted as of now simply
with vcorsini.
Rcor and vcorsini fully define the
rotational velocity field, and are regarded as free parameters in this analysis.
, denoted as of now simply
with vcorsini.
Rcor and vcorsini fully define the
rotational velocity field, and are regarded as free parameters in this analysis.
Parameters of the suspected rapid rotators.
vcorsini is not to be
confused with the stellar rotational velocity v∗sini, defined as the
rotational velocity at r = R∗. Since the
velocity increases linearly in the rigid-body regime, the rotational velocity at
r = R∗ is given by
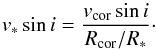 (4)It is thus important to
keep in mind that v∗sini values could
easily be an order of magnitude smaller than corresponding vcorsini values.
v∗sini is the velocity
one usually refers to when discussing the stellar rotational velocity.
(4)It is thus important to
keep in mind that v∗sini values could
easily be an order of magnitude smaller than corresponding vcorsini values.
v∗sini is the velocity
one usually refers to when discussing the stellar rotational velocity.
The extended version of PoWR was tested on several stars which are known to rotate. For stars with photospheric lines, the new version was shown to yield almost identical synthetic spectra to those obtained by means of flux-convolution with a suitable rotation profile. Furthermore, the code was tested on the O supergiant ζ Pup. Similarly to Hillier et al. (2012), we find that rotation, accounted for with the 3D integration scheme, reproduces the observed emission lines much better than a simple flux-convolution.
4. Analysis
4.1. Stellar parameters
The stellar parameters used for the calculation of the synthetic spectra are summarized in Table 1. The basic stellar parameters are listed at the upper part of the table. The values are based on previous studies performed by Hainich et al. (2014) and Hamann et al. (2006), though slight modifications were performed due to the inclusion of rotation in the present studies. The velocity parameters inferred in this work are listed at the bottom part of Table 1. The method of their determination is discussed in Sect. 4.3.
Rt, given in Table 1, is the so called “transformed radius”, originally introduced by Schmutz et al. (1989), and later generalized to include the effect of clumping by Hamann & Koesterke (1998). Schmutz et al. (1989) noticed that emission lines belonging to models calculated with identical temperatures T∗, chemical abundances, and Rt values, have similar equivalent widths, independent of the mass-loss rate Ṁ, radius R∗, and terminal velocity v∞.
The wind efficiency ηmom, given in Table 1, is defined as the ratio of the wind momentum to the
radiation momentum 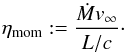 (5)If the wind is
driven only by radiation, ηmom corresponds to the average number
of scatterings in the wind per photon.
(5)If the wind is
driven only by radiation, ηmom corresponds to the average number
of scatterings in the wind per photon.
4.2. Parameter study
To demonstrate how the synthetic spectra of WR stars respond to the rotation parameters vcorsini and Rcor, we focus on the WN4 star BAT99 7 residing in the LMC. The model parameters are summarized in Table 1. Figure 3 depicts several synthetic He ii lines calculated with a constant Rcor value and different vcorsini values (upper panels), and the same lines calculated with a constant vcorsini value and different Rcor values (bottom panels). For the exact values, see caption and legend of Fig. 3.
 |
Fig. 3 Effect of the parameters vcorsini and Rcor on prominent synthetic emission lines of BAT99 7. Each of the upper panels depicts, for a constant value Rcor = R∗, the synthetic profile of an emission line calculated with different vcorsini values. The bottom panels show the synthetic profile of the same spectral lines calculated with different Rcor values and with a constant rotational velocity of vcorsini = 2000 km s-1. |
As is evident from Fig. 3, it is only with large co-rotation radii that rotation significantly affect the spectrum. It is especially striking how the He ii λ4686 line hardly responds to the huge rotational velocities applied when Rcor = R∗. The reason that large Rcor values are needed to significantly affect the spectra is that the line forming regions (LFRs) are situated very far above the stellar surface.
To discuss the radial stratification of the emission strength for the individual emission
lines, we make use of the quantity ξ(r), originally introduced by
Hillier (1987). ξ(r)
serves as a measure for the energy emitted due to a line transition as a function of the
distance r
from the stellar center. An expression for ξ is obtained by means of the Sobolev approximation
(Castor 1970). The energy E emitted in the considered
line satisfies: 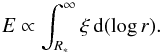 (6)Figure 4 depicts normalized ξ(log r)-plots for several prominent
He ii emission lines belonging to the model of BAT99 7, while Fig. 5 schematically illustrates the rotational velocity as a
function of r
for two cases: Rcor = R∗
(dashed red line) and Rcor = 16 R∗
(solid blue line). We also indicate in Fig. 5 the LFR
of the line He ii λ4686, determined by its corresponding
ξ-plot.
(6)Figure 4 depicts normalized ξ(log r)-plots for several prominent
He ii emission lines belonging to the model of BAT99 7, while Fig. 5 schematically illustrates the rotational velocity as a
function of r
for two cases: Rcor = R∗
(dashed red line) and Rcor = 16 R∗
(solid blue line). We also indicate in Fig. 5 the LFR
of the line He ii λ4686, determined by its corresponding
ξ-plot.
As discussed in Sect. 3.2, the rotational velocity field consists of two domains: the rigid rotation domain r < Rcor, where the φ-component increases linearly with r, and the outer domain r > Rcor, where the φ-component decreases with 1/r. As can be readily seen, without large co-rotation radii, the rotational velocity (dashed red line) falls off rapidly and does not reach significant values in the LFR. The same reasoning holds for all prominent lines of the WR stars analyzed here. One cannot expect a change of the line profile to occur if the rotational velocity field does not reach significant values in the corresponding LFR.
The same analysis was performed with all relevant WNE models, and the result remained identical: rotation without co-rotation hardly affects the synthetic spectra, independently of the WNE model used. It is thus clear that, if stellar rotation is to explain the observed spectra, large co-rotation radii have to be assumed.
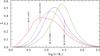 |
Fig. 4 Normalized ξ(log r)-plots for several He ii emission lines belonging to the model of the star BAT99 7. The model parameters are listed in Table 1. The individual lines are formed many stellar radii above the surface. |
 |
Fig. 5 Equatorial rotational velocity as a function of r. Both curves correspond to vcor = 2500 km s-1. However, the dashed red curve is plotted with Rcor = R∗, while the solid blue curve is plotted with Rcor = 16 R∗. We also denote an estimate of the LFR of the line He ii λ4686, determined by its corresponding ξ plot. Note that the LFR remains unaffected by rotation unless large co-rotation radii are assumed. |
4.3. Determination of the rotation parameters
The determination of the most suitable vcorsini and Rcor values is a very difficult task. Firstly, different combinations of vcorsini and Rcor may yield similar line profiles if they imply a similar rotational velocity in the LFR. Secondly, since the inclusion of rotation could affect the equivalent width, previously determined stellar parameters may require readjustment when including rotation. Lastly, the radial wind velocity vr(r), characterized by the terminal velocity v∞, has a large influence on the width and shape of the lines. The value of v∞ thus becomes coupled to the rotation parameters.
Values of v∞, derived using different methods, are given by e.g. Niedzielski et al. (2004), Niedzielski & Skorzynski (2002), Hamann & Koesterke (2000), and Prinja et al. (1990). Unfortunately, corresponding v∞ values often differ by ~1000 km s-1 between these studies, depending on the spectral line considered. We thus cannot blindly adopt values from previous studies for our rotation analysis, which is sensitive to the value of v∞. Instead, the terminal wind velocity v∞ becomes an additional free parameter of our analysis. Determining the three free parameters (vcorsini, Rcor, v∞) without some guiding strategy can be very tricky, especially due to the computational cost.
If we assume that the line width is determined only by Doppler shifts, an analytical
expression for the maximum line width can be derived. The velocities responsible for the
Doppler shift are the expansion velocity given by the β-law (Eq. (1)), the rotational velocity (Eq. (3)), and the Doppler velocity vD. Let us
assume for a moment that a spectral line l with the wavelength λl is formed in a
relatively well-defined region determined by r ≈ rl.
Because the rotational and expansion velocity vectors depend solely on r and are always
perpendicular to each other, the maximum line width due to rotation and
expansion is determined at the latitude θ = i and is given by
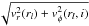 .
This width is slightly increased due to the much smaller intrinsic thermal and
microturbulent motion described by vD, so that the maximum line width is
approximately:
.
This width is slightly increased due to the much smaller intrinsic thermal and
microturbulent motion described by vD, so that the maximum line width is
approximately: 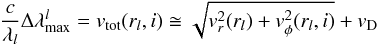 (7)rl may be very roughly
defined as the radius where ξl(r)
reaches its maximum (cf. Fig. 4). The observed
maximum width of the line
(7)rl may be very roughly
defined as the radius where ξl(r)
reaches its maximum (cf. Fig. 4). The observed
maximum width of the line 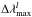 may be
measured from a careful inspection of the observed spectrum. Having obtained a set of data
points
may be
measured from a careful inspection of the observed spectrum. Having obtained a set of data
points 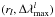 for a specific star, we can
approximately compare a function of the form of Eq. () to the data points in the r − v
space. Of course, the assumption that the lines are formed in a specific radius is an
artificial one, so that exact parameter values cannot be derived with this method.
However, this method does help us to find a suitable parameter domain of vcorsini, Rcor, and
v∞.
for a specific star, we can
approximately compare a function of the form of Eq. () to the data points in the r − v
space. Of course, the assumption that the lines are formed in a specific radius is an
artificial one, so that exact parameter values cannot be derived with this method.
However, this method does help us to find a suitable parameter domain of vcorsini, Rcor, and
v∞.
 |
Fig. 6 Comparison between synthetic spectra calculated with rotation (dotted red line), without rotation (dashed black line), and observations (solid blue line) for the five stars analyzed. The synthetic spectra are convolved with a Gaussian of FWHM = 3 Å to account for instrumental broadening. |
 |
Fig. 7 Zoomed-in sections of Fig. 6 with prominent emission lines of the stars BAT99 94 (upper panels) and BAT99 88 (bottom panels). The observed spectrum (solid blue line) is compared to the synthetic spectrum calculated with rotation (dotted red line), and without rotation (dashed black line). |
Once a suitable parameter domain has been found, we examine the agreement between observations and synthetic spectra calculated with different parameter values in the domain. The final values inferred in this work are determined by identifying the synthetic spectra showing the best agreement with the observations. Any uncertainties here (i.e. the choice of rl) therefore do not bear an effect on the final values presented in Table 1.
4.4. Results
Table 1 compiles the stellar parameters used for the models of the five stars analyzed here. Figure 6 compares the synthetic spectra calculated with rotation (dotted red lines) and without rotation (dashed black lines) to the observations (solid blue lines) for the five stars analyzed. For the synthetic spectrum without rotation, we use the same parameters from Table 1. Figure 7 zooms on several prominent emission lines of BAT99 94 (upper panels) and BAT99 88 (bottom panels) as two illustrative examples which emphasize how rotation helps to reproduce the observations. As can be seen from Figs. 6 and 7, by taking rotation into account, we manage to obtain a good overall agreement along the spectrum for all five stars analyzed. Rotation manages to account for both the broad and round emission profiles as well as the flat-topped ones. Figure 7 illustrates the qualitative difference between the line profiles calculated with and without rotation.
The observed line widths are not always reached for the individual lines. Furthermore, some synthetic lines exhibit asymmetrical features of self-absorption which do not appear in the observation. This is especially notable in the case of WR 2, though almost all stars exhibit them at certain lines (Note, for example, the He ii λ6568 Å line of BAT99 88 in Fig. 7). While the models calculated without rotation exhibit such asymmetric features as well, rotation can either dampen these features or enhance them. This could partially be due to the discontinuity of the rotational velocity field, to which some lines react strongly because their corresponding LFRs intersect the discontinuous domain. These discrepancies could be avoided if the lines were to be treated individually, because distinct sets of parameters can reproduce both their shapes as well as their widths. However, since we aim to treat many lines simultaneously, a compromise has to be found.
We mentioned in Sect. 1 that the round line profiles cannot be reproduced solely by increasing the terminal velocity v∞. As an example, we focus again on the star BAT99 94. Figure 8 compares the observation (solid blue line) and the calculated synthetic spectrum without rotation (dashed black line) for two prominent emission lines of BAT99 94.
For the synthetic spectrum, we use the same stellar parameters as listed in Table 1, but choose a larger terminal velocity, so that the line widths of BAT99 94 are approximately reproduced by the model, and calculate it without rotation. The suitable value is found to be v∞ ≈ 2500 km s-1. Note that while the line widths are approximately matched, the shape of the observed spectral lines appears strikingly different from the synthetic one. We therefore see that larger terminal velocities alone do not help to reproduce the unique spectra analyzed here.
As mentioned in Sect. 3.1, we adopted the value β = 1 for all models in this work, despite the fact that different values of β of the order of 10 were inferred in the case of a few WR stars (cf. Lépine & Moffat 1999). The value β = 1 was shown by e.g. hydrodynamically consistent models performed by Gräfener & Hamann (2005) to yield an appropriate approximation of the wind velocity field for WR stars. Moreover, β = 1 enables us to compare our current results with previous ones. Still, one could wonder whether a special form of the velocity law could explain the round shape of the line profiles. We have tested the effect of varying β, as well as two-β velocity laws, on the synthetic spectra. These tests showed that the effect of β on most emission line profiles is marginal. The obvious reason is that almost all emission lines seen in the optical spectrum are formed in regions where vr ≈ v∞, regardless of the detailed form of the velocity law (see Fig. 4).
4.5. Error estimation
The uncertainties of the stellar parameters are hard to quantify, since they originate in a multitude of sources, e.g. deficient atomic data. On the basis of past studies, we estimate the error in log T∗ to be 0.05 dex, and the error in log Rt to be 0.1 dex. The corresponding uncertainty in Ṁ is 0.15 dex. For WR 2, which resides in the Galaxy, we estimate an uncertainty in log L of 0.3 dex. For the LMC stars, whose distances are known with much better certainty, we estimate an uncertainty in log L of 0.1 dex. The uncertainty in v∞ is 20%. As a consequence, ηmom values are given with a factor 2 uncertainty.
The errors of the velocity parameters given in Table 1 are estimated on the basis of sensitivity tests. An impression of the sensitivity of the models to the rotation parameters may be gained from Fig. 3. We conclude a relative uncertainty in Rcor of 30%. As for vcorsini, we estimate the relative uncertainty to be 20%. Combining these two estimations, we obtain an uncertainty of 50% in v∗sini.
 |
Fig. 8 Two He ii lines belonging to BAT99 94. We compare the observed spectrum (solid blue line) with a synthetic spectrum calculated with the same stellar parameters as in Table 1, but with an increased terminal velocity of v∞ = 2500 km s-1 and without rotation (dashed black line). Note that the line widths match, but the shape of the synthetic lines is qualitatively very different from the observed ones. |
5. Discussion
The results obtained in this work indicate that rotation, even with the simplified model now implemented in PoWR, is capable of explaining almost all peculiarities of the spectra analyzed here: the models reproduce the round emission line profiles and flat-topped lines simultaneously. A good agreement between model and observation is achieved along a large segment of the optical spectrum. But are the inferred parameters plausible? We discuss this in the following section.
5.1. A closer inspection of the stars in the sample
A glance at the spectral types of the few stars which exhibit round emission lines reveals an interesting fact: all round-lined stars are of subtype WNE. Furthermore, all but WR 2 are classified as broad-lined WN stars (suffix b). While emission lines of such broad-lined WN stars indeed tend to be somewhat “roundish” compared to the majority of WN stars, the stars in our sample show a striking difference, as already illustrated in Fig. 1. Most importantly, the spectra of all other broad-lined WN stars in the Galaxy and the LMC can be reproduced without assuming rotation (Hainich et al. 2014; Hamann et al. 2006).
The fact that WR 2 is classified as weak-lined (suffix w) could be the result of dilution of its intrinsic spectrum due to a luminous OB companion. It was recently brought to our attention (A. Moffat, priv. comm.) that WR 2 has a faint B-star companion. However, it contributes only 5−10% to the visual continuum, and thus cannot explain the weak-lined appearance of the spectrum of WR 2.
Since WNE stars are more compact than their WNL counterparts, faster rotation in the WNE phase is plausible. Moreover, the stars in this sample are very compact even compared to typical WNE subtypes, which implies that these stars approach the end of their life cycle. Indeed, a WR star gradually loses its angular momentum due to the stellar wind, so it is not obvious that an evolved WR star should rotate more rapidly than a young one. However, as will be discussed below, contraction can win over the loss of angular momentum, especially at lower metallicities, thus leading to an enhancement of the rotational velocity as the WR star evolves.
It is interesting to note that all stars in our sample have a low metallicity. WR 2 is located in the metal-poor outskirts of our Galaxy, while the average metallicity in the LMC is about 35% solar (e.g. Grocholski et al. 2009). A lower metallicity leads to a smaller opacity of the lines which drive the wind, which in turn implies a smaller mass-loss rate, a fact which was verified by consistent hydrodynamical models calculated by Gräfener & Hamann (2008). One may therefore conclude that lower metallicities reduce the loss of angular momentum. Since the outer layers of the original progenitor star, which rotates approximately as a rigid body, possess more specific angular momentum than the inner layers, and since it is these outer layers which are ejected from the star, a lower mass-loss rate means faster rotation. A lower metallicity should therefore spur a more rapid rotation of the continuously contracting star.
One could argue that the WR phase initiates when the hydrogen has been almost fully removed from the stellar surface, so that, independently of the mass-loss rate, a certain mass already had to be ejected prior to the WR phase. However, rotationally induced mixing can also lead to a hydrogen-poor stellar atmosphere, meaning that rapidly rotating stars at low metallicities could enter the WR phase with a larger angular momentum (e.g. Yoon & Langer 2005). More critical, however, is the effect of low metallicities during the WR phase. Recall that two counteracting mechanisms dictate the rotational velocity of a WR star: the stellar wind, depleting the star of its angular momentum, and the contraction, making it rotate faster. Meynet & Maeder (2005) calculated evolutionary tracks of massive stars with initial masses Mi larger than 20 M⊙ and with initial rotation velocities of 300 km s-1. Their models clearly predict, at LMC metallicities, and in the mass range 20 M⊙ < Mi < 60 M⊙, a significant increase of the rotational velocity as the WR star evolves from a late WN subtype to an early WN subtype. According to these models, while the star enters the WR phase with ~50 km s-1 as a WNL, its equatorial rotational velocity can increase to a value of up to ~200 km s-1 in the evolved WNE phase. In other words, at LMC metallicities, the contraction of the star seems to dominate over the loss of angular momentum due to the stellar wind, causing it to rotate more rapidly. This is in agreement with our finding that only WNE subtypes exhibit round emission line profiles, and that most stars in our sample are observed at lower metallicity.
Note that all stars in our sample have wind efficiencies ηmom larger than
unity. For winds which are driven solely by radiation, this implies that “multiple
scattering” occurs. While it is not unusual for ηmom to exceed unity in the case of WNE
subtypes, a comparison with the wind efficiencies of ~70 WNE subtypes in the LMC
(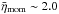 ),
analyzed by Hainich et al. (2014), reveals that the
LMC stars in our sample have slightly higher than average wind efficiencies. BAT99 7 and
BAT99 94, with ηmom > 5, are
especially striking in this sense, while WR 2 has a more or less average wind efficiency.
Gräfener & Hamann (2008) calculated
hydrodynamically consistent models for WN stars and obtained, at LMC metallicities, a
maximum wind efficiency of ηmom ~ 1.2. For a WC model with solar
metallicity, wind efficiencies of up to ~2.5 were reproduced (cf. Gräfener
& Hamann 2005). Monte Carlo simulations performed by Vink et al. (2011) do not yield higher values. While
such studies verify that multiple scattering occurs in stars approaching the Eddington
limit, it is still not clear whether multiple scattering alone can explain the very large
values of ηmom which are inferred from spectral
analyses, a discrepancy known as the “momentum problem”. To solve it, additional wind
driving mechanisms were suggested throughout the years (cf. Maeder 1985; Underhill & Fahey
1987; Poe et al. 1989). Specifically,
Poe et al. (1989) showed that rapid rotation and
magnetic fields can contribute to the driving of the wind, a fact we shall return to in
Sect. 5.4.
),
analyzed by Hainich et al. (2014), reveals that the
LMC stars in our sample have slightly higher than average wind efficiencies. BAT99 7 and
BAT99 94, with ηmom > 5, are
especially striking in this sense, while WR 2 has a more or less average wind efficiency.
Gräfener & Hamann (2008) calculated
hydrodynamically consistent models for WN stars and obtained, at LMC metallicities, a
maximum wind efficiency of ηmom ~ 1.2. For a WC model with solar
metallicity, wind efficiencies of up to ~2.5 were reproduced (cf. Gräfener
& Hamann 2005). Monte Carlo simulations performed by Vink et al. (2011) do not yield higher values. While
such studies verify that multiple scattering occurs in stars approaching the Eddington
limit, it is still not clear whether multiple scattering alone can explain the very large
values of ηmom which are inferred from spectral
analyses, a discrepancy known as the “momentum problem”. To solve it, additional wind
driving mechanisms were suggested throughout the years (cf. Maeder 1985; Underhill & Fahey
1987; Poe et al. 1989). Specifically,
Poe et al. (1989) showed that rapid rotation and
magnetic fields can contribute to the driving of the wind, a fact we shall return to in
Sect. 5.4.
After first submission of this paper, our attention has been drawn to a recent study of line profile variations (LPV) in WR 2 performed by Chené et al. (in prep.). They detect LPVs of the order of 0.5% rms, which is smaller than found in other WR stars (cf. Lépine & Moffat 1999), and which they attribute to stochastic clump activity. A periodicity of the LPVs could not be established. Such periodic variations should occur if co-rotating structures exist which dominate over the stochastic clump activity.
5.2. Are the inferred rotational velocities plausible?
All stars analyzed in this work require rapid rotational velocities in order to significantly influence their corresponding synthetic spectra. But are such velocities conceivable?
The critical rotation velocity at a distance r ≥ R∗ from the center
of a star with an effective mass Meff is given by
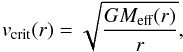 (8)where Meff = M∗(1 − Γe)
is the stellar mass corrected due to the radiative force on the electrons.
(8)where Meff = M∗(1 − Γe)
is the stellar mass corrected due to the radiative force on the electrons.
If we take BAT99 51 as an example, using the parameters from Table 1 and an Eddington factor 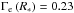 as obtained from our
model, we find the critical velocity at the stellar surface to be
as obtained from our
model, we find the critical velocity at the stellar surface to be
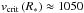 km s-1. The rotational velocity at
the stellar surface (cf. Table 1) is therefore far
below the critical velocity: v∗sini ≈ 0.2 vcrit(R∗).
This implies that the star approximately maintains spherical symmetry even for the
rotation parameters found in this analysis. The same holds for all stars in our sample,
with WR 2 having the largest value of v∗sini = 0.27 vcrit
at the stellar surface. However, due to the co-rotation, the rotational velocity of BAT99
51 grows linearly with r until it reaches the maximum value of
vcorsini = 2000 km s-1 at Rcor. The
critical velocity of BAT99 51 at Rcor is
km s-1. The rotational velocity at
the stellar surface (cf. Table 1) is therefore far
below the critical velocity: v∗sini ≈ 0.2 vcrit(R∗).
This implies that the star approximately maintains spherical symmetry even for the
rotation parameters found in this analysis. The same holds for all stars in our sample,
with WR 2 having the largest value of v∗sini = 0.27 vcrit
at the stellar surface. However, due to the co-rotation, the rotational velocity of BAT99
51 grows linearly with r until it reaches the maximum value of
vcorsini = 2000 km s-1 at Rcor. The
critical velocity of BAT99 51 at Rcor is
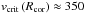 km s-1. We see that the rotational
velocity at the co-rotation radius exceeds the critical velocity by far. This means that
the wind should be partially driven by centrifugal forces.
km s-1. We see that the rotational
velocity at the co-rotation radius exceeds the critical velocity by far. This means that
the wind should be partially driven by centrifugal forces.
Centrifugal forces can, in principle, have two effects on the wind. Firstly, they can affect the mass-loss rate, causing it to no longer be isotropic, but rather enhanced at the equator and reduced towards the poles. Secondly, they can affect the hydrodynamics of the wind, altering the wind velocity field.
The first effect is not expected to occur with the parameters inferred here. According to the theory of radiation driven winds, the mass-loss is not affected by forces which act beyond the so-called “critical point” (Castor et al. 1975, CAK hereafter). Since the centrifugal forces become significant only much further away than the critical point, they do not affect the mass-loss rate. The mass flux can thus be assumed to be isotropic.
However, the centrifugal forces implied from our analysis should bear an effect on the wind velocity, perhaps even to the extent that the β-law (Eq. (1)) no longer holds. The centrifugal force vanishes towards the poles, and reaches its maximum at the equator. The result is a latitude-dependent wind velocity field, which also induces a latitude-dependent density structure. While this potentially has important consequences, a proper treatment of this problem would require a consistent hydrodynamical modeling of the wind, which is beyond the scope of the current work.
However, the departure from spherical symmetry in the wind may be observable with linear polarimetry, as described in Sect. 5.3.
5.3. The line effect
Natural light scattered off free electrons (Thomson scattering) is partially linearly polarized. If the scattering layers of a star are spherically symmetric, the net linear polarization of the continuum radiation due to scattering vanishes. However, if the scattering layers of the star depart from spherical symmetry, the linear polarization of the continuum no longer cancels out. To cope with the contamination of polarimetric data due to interstellar polarization, it is essential to compare the observed continuum polarization to that observed in emission lines. Emission lines formed far from the stellar surface are not expected to show significant polarization because such emission mainly follows recombination processes and is thus unpolarized. A subsequent scattering of these line photons is rare compared to the scattering of continuum photons, as can be also deduced from the general weakness of the electron scattering wings (Hillier 1991; Hamann & Koesterke 1998). Thus, line radiation is less polarized compared to the continuum, an effect termed the “line effect”. The line effect was observed in various WR stars (e.g. Schulte-Ladbeck et al. 1991; Harries et al. 1998), and attempts for a numerical calculation of the continuum polarization due to scattering were performed by e.g. Chandrasekhar (1960), Brown & McLean (1977), Hillier (1991), and Hillier (1994).
Vink (2007) analyzed 13 WR stars in the LMC for the line effect, out of which two were positively detected. Alas, none of the LMC stars analyzed here for rotation are among this sample. Scholz et al. (in prep.) analyzed polarimetric observations of BAT99 7, but did not detect line depolarizations larger than ~2%. The remaining LMC stars analyzed here were so far not studied for linear polarization. Harries et al. (1998) analyzed 16 Galactic WR stars for the line effect, out of which four were positively detected. WR 2 was not among the sampled stars. However, Akras et al. (2013) very recently reported a linear polarization of 3% in optical broadbands of WR 2. In contrast, Chené et al. (in prep.) extensively analyzed polarimetric data of WR 2 and do not find any linear line depolarization down to the 0.05% noise level, and attribute the 3% linear polarization detected by Akras et al. (2013) to scattering off grains in the interstellar matter.
The non-detection of the line effect in WR 2 challenges its rapid rotation suggested in this work. To allow for a quantitative interpretation of the polarimetric data with respect to our rotation model, polarized radiative transfer on top of hydrodynamic wind models would be needed, which is far beyond the scope of this work. In a preliminary fashion, we can qualitatively discuss whether one should expect an observable net continuum polarization from co-rotating winds, as considered here.
Any net polarization will be determined mainly by the following three factors: the amount of scatterings occurring in each layer, the degree of pole-to-equator density contrast in each layer, and the proximity of the scattering layers to the stellar surface.
The relevant physical quantity for assessing the relative amount of scatterings in each layer is the Thomson optical depth, τth. In our model of WR 2, τth is smaller than 0.1 for radii r > 4 R∗, 0.3 in the vicinity of r ~ 2 R∗, 2/3 at r ~ 1.3 R∗, and larger than 1 for radii r < 1.1 R∗. At radii r > 1.1 R∗, the continuum optical depth τRoss is almost completely dominated by τth, meaning that the atmosphere becomes optically thin to continuum at r ~ 1.3 R∗. As the number of scatterings is roughly proportional to τth, we see that most observed photons have been scattered for the last time in the vicinity of r ~ 1.3 R∗. Only few photons are scattered at radii r > 2 R∗.
The pole-to-equator density contrast C = ρ(r,π/2)/ρ(r,0) can be expressed in terms of the mass flux per solid angle ṁ(θ) and the radial wind velocity vr(r,θ) at pole and equator via the mass-continuity equation. For this purpose, we adopt the standard line-driving formalism by Castor et al. (1975), albeit the CAK theory fails to explain the high mass-loss rates of WR stars and also does not account for rotation.
We now follow the arguments by Owocki et al.
(1998): ṁ(θ), determined at the critical
point rc very close to the stellar surface, can
be expressed in terms of the radiative flux F(θ), the effective gravity
geff(θ), and the
force-multiplier parameter α. The Von Zeipel effect (von Zeipel 1924) states that F(θ) ∝ geff(θ),
so that one eventually obtains (cf. Owocki et al.
1998, Eq. (4)) ṁ ∝ geff(θ),
independently of α. Meanwhile, geff(θ) ∝ 1−Ωsinθ,
where 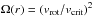 denotes the
squared ratio between the rotational and critical velocities at the stellar surface.
Approximating rc ≅ R∗,
Owocki et al. (1994) obtain ṁ(π/2)/ṁ(0) = 1−Ω.
For WR 2, which has the largest inferred rotation velocity, v∗sini ~ 500 km s-1 (cf. Table 1), and so (ignoring projection effects)
Ω(R∗) = 0.11, and ṁ(π/2)/ṁ(0) = 0.89.
denotes the
squared ratio between the rotational and critical velocities at the stellar surface.
Approximating rc ≅ R∗,
Owocki et al. (1994) obtain ṁ(π/2)/ṁ(0) = 1−Ω.
For WR 2, which has the largest inferred rotation velocity, v∗sini ~ 500 km s-1 (cf. Table 1), and so (ignoring projection effects)
Ω(R∗) = 0.11, and ṁ(π/2)/ṁ(0) = 0.89.
The radial component of the wind velocity at the pole, vr(r,0),
is not affected by the rotation and therefore follows the β-law. At the equator, the
centrifugal force in the co-rotating regime Fcent ∝ r enhances the
radial component of the equatorial velocity vr(r,π/2).
Estimating the expansion velocity ratio between pole and equator, we obtain
vr(r,0)/vr(r,π/2) ~ 0.57,0.5,
and 0.37 at r ~ 1.3 R∗, 2 R∗,
and 4 R∗, respectively. C then follows from the
continuity equation 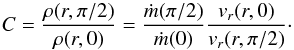 (9)Using Eq. (9), we find C ~ 0.5,0.44, and
0.33 at r ~ 1.3 R∗, 2 R∗,
and 4 R∗, respectively. Although relatively
little scattering occurs in the outermost wind layers, their asymmetry is likely to cause
a net continuum polarization to a certain extent. However, the net polarization is very
hard to estimate without consistent modeling. For example, Hillier (1994, Fig. 2) presented modeling results of the net polarization for a
constant density pole-to-equator contrast of C = 11 throughout the scattering atmosphere for
various total optical depths and inclination angles. Even in the relatively simplified
atmosphere structure he assumed (e.g. constant contrast, point source approximation), the
net polarization is a complicated function of the total optical depth and inclination, and
may cancel out even with the extreme density contrast adopted by him, depending on these
parameters. We therefore stress the need for modeling polarized radiative transfer in
co-rotating atmospheres. Whether an obvious contradiction between the polarimetric data
and the rotation hypothesized here arises remains to be seen.
(9)Using Eq. (9), we find C ~ 0.5,0.44, and
0.33 at r ~ 1.3 R∗, 2 R∗,
and 4 R∗, respectively. Although relatively
little scattering occurs in the outermost wind layers, their asymmetry is likely to cause
a net continuum polarization to a certain extent. However, the net polarization is very
hard to estimate without consistent modeling. For example, Hillier (1994, Fig. 2) presented modeling results of the net polarization for a
constant density pole-to-equator contrast of C = 11 throughout the scattering atmosphere for
various total optical depths and inclination angles. Even in the relatively simplified
atmosphere structure he assumed (e.g. constant contrast, point source approximation), the
net polarization is a complicated function of the total optical depth and inclination, and
may cancel out even with the extreme density contrast adopted by him, depending on these
parameters. We therefore stress the need for modeling polarized radiative transfer in
co-rotating atmospheres. Whether an obvious contradiction between the polarimetric data
and the rotation hypothesized here arises remains to be seen.
5.4. Are the inferred co-rotation radii plausible?
The postulated co-rotation of the wind is motivated by the possible existence of strong magnetic fields in WR stars. In this section, we estimate the required magnetic field strengths that would force the wind plasma to co-rotate with the star up to the inferred co-rotation radii.
Many mechanisms were considered throughout the years which could induce magnetic fields in massive stars. One possibility is that the magnetic fields are “fossil”, i.e. remnants from the time of the star formation (e.g. Donati & Landstreet 2009). Another possibility is that some dynamo mechanism induces the magnetic field, generated by e.g. Tayler-Spruit instabilities (cf. Spruit 2002), or by the convective core of the star (Moss 1989; MacGregor & Cassinelli 2003). A third possibility would be a dynamo generated by sub-surface convection zones that are caused due to iron opacity peaks (Cantiello et al. 2009), leading to the formation of so-called star spots. Magnetic spots have also been invoked as the likely cause of CIRs in hot-star winds. Such spiral patterns that function as footings of magnetic structures may give rise to the discrete absorption components (DACs) that are regularly observed in O-stars, and also to X-ray emitting shocks in WR winds (cf. Ignace et al. 2013). The latter mechanism probably does not generate a magnetic field which has a global structure. The other mechanisms mentioned should generate a global magnetic field.
To obtain an estimation for the magnetic field strengths, we follow the work of Weber & Davis (1967) and Belcher & MacGregor (1976). Constraining our discussion to the
equator (θ = π/2), we
assume a global magnetic field of the form .
Assuming that the magnetic field lines are frozen in the plasma at the stellar surface,
the magnetic field leaves the stellar surface radially. The φ-component of the magnetic
field is negligible up to the co-rotation radius, i.e. Bφ ≈ 0 for
r ≲ Rcor (cf. Belcher & MacGregor 1976). The
Alfv nic
Mach number MA(r) in Gaussian units
is defined by
nic
Mach number MA(r) in Gaussian units
is defined by 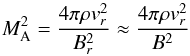 (10)where
ρ(r) is the mass density, and
vr(r)
is the radial expansion velocity of the wind. The last equality holds for r ≲ Rcor.
(10)where
ρ(r) is the mass density, and
vr(r)
is the radial expansion velocity of the wind. The last equality holds for r ≲ Rcor.
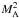 gives the
ratio of the kinetic expansion energy of the plasma ρv2/2
to the magnetic energy density B2/8π.
The Alfv
gives the
ratio of the kinetic expansion energy of the plasma ρv2/2
to the magnetic energy density B2/8π.
The Alfv n
radius rA is set by the condition
n
radius rA is set by the condition
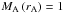 . The wind co-rotates
approximately up to the Alfv
. The wind co-rotates
approximately up to the Alfv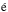 n
radius, i.e. Rcor ≈ rA.
n
radius, i.e. Rcor ≈ rA.
As a consequence of Maxwell’s equation ∇·B = 0, the total magnetic flux Brr2
is a conserved quantity. Since Bφ ≈ 0 up to the
Alfv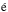 n
radius, this means that B ∝ (r/R∗)-2
for r ≤ rA. Eliminating
ρ(r) from Eq. (10) with the mass continuity equation
Ṁ = 4πρvr2,
we can express the magnetic field in terms of the co-rotation radius:
n
radius, this means that B ∝ (r/R∗)-2
for r ≤ rA. Eliminating
ρ(r) from Eq. (10) with the mass continuity equation
Ṁ = 4πρvr2,
we can express the magnetic field in terms of the co-rotation radius: 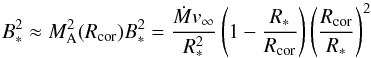 (11)where we
used the beta-law (1) with β = 1 for vr(r)
, and the fact that MA(Rcor) ≈ MA(rA) = 1
(11)where we
used the beta-law (1) with β = 1 for vr(r)
, and the fact that MA(Rcor) ≈ MA(rA) = 1
Using Eq. (11), it is possible to estimate the stellar magnetic field B∗ necessary to confine the matter up to a given co-rotation radius. A more exact estimate should, however, include the effect of the centrifugal forces due to rotation. Table 2 compiles the inferred stellar magnetic fields B∗, derived with Eq. (11). We also give the magnetic fields Bτ = 2/3 at the radius where the Rosseland mean optical depth τRoss reaches 2/3, i.e. at the photosphere. The corresponding radii, denoted with rτ = 2/3, are also indicated in Table 2. The uncertainty in log B∗ is determined by the uncertainties of the parameters in Eq. (11) and is estimated to be 0.45 dex.
Magnetic fields needed to enforce the co-rotation.
Admittedly, the inferred magnetic fields are very strong. To date, attempts to detect magnetic fields in WR stars failed to detect any such fields down to several 100 G (e.g. Kholtygin et al. 2011; de la Chevrotière et al. 2013). These studies, however, do not include any stars that show round profiles like the stars in our sample. If these magnetic fields are globally structured, they should be detectable with circular polarimetry.
Nevertheless, a couple of OB stars were observed to exhibit strong magnetic fields of several kG (see Nazé 2013, for a review on the topic), with one star even reaching a value of ~20 kG (cf. Wade et al. 2012). Since these stars are recognized as progenitors of WR stars, it is plausible that some WR stars can have photospheric magnetic fields of at least this order of magnitude. Due to the contraction of the WR star relative to its progenitor O star, the stellar magnetic field B∗ becomes accordingly stronger at the hydrostatic core if the magnetic flux was conserved during the contraction.
Taking this reasoning one step further, magnetic fields of neutron stars, and specifically those of magnetars, often reach values of 1014−1015 G (e.g. Esposito et al. 2009). WR stars were suggested as direct progenitors of magnetars (cf. Gaensler et al. 2005). A popular explanation for the remarkably strong magnetic fields of magnetars is the contraction of their progenitor stars along with the conservation of the magnetic flux, though this explanation alone might be overly simplistic (cf. Spruit 2008). Indeed, comparing a typical magnetar radius of ~10 km (e.g. Deibel et al. 2013) with a typical radius ~R⊙ of an early WN star (cf. Table 1), flux conservation would imply a 10 orders of magnitude difference between the magnetic field strengths at the surface of a magnetar and an early WR star, which roughly agrees with the values given in Table 2. All in all, the magnetic field strengths inferred here are conveniently situated in a plausible intermediate domain between the progenitor and descendent stars.
This is not the first time such strong magnetic fields are invoked for WR stars. Poe et al. (1989) argued that the winds of some WR stars are partially driven by magnetic and centrifugal forces. Recall that all stars analyzed here have a wind efficiency ηmom larger than average, which potentially indicates that additional mechanisms are driving the wind (cf. Sect. 4.1). Poe et al. (1989) take into account the effects of radiation, rotation, and magnetic fields, to conclude that global photospheric fields of several kG are required to obtain mass-loss rates and terminal velocities observed in some WR stars. On the other hand, Mullan & MacDonald (2005) show that magnetic fields arising from Tayler-Spruit instabilities (cf. Spruit 2002) could also reach several kG.
There is, however, another fact we ought to consider. A star with a large mass-loss rate
and a strong magnetic field cannot maintain rapid rotation over a long time. This is
because the existence of magnetic torques efficiently transfer angular momentum from the
star to its wind (e.g. Hartmann & MacGregor
1982). Friend & MacGregor (1984)
estimated the “spin-down time”, i.e. the time scale over which the angular momentum
J is lost,
as 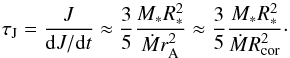 (12)We now ask ourselves
whether we can expect to actually observe rapidly rotating WR stars. To answer this
question, we need to compare the spin-down times with a typical lifetime of a WR star. In
order to discuss this important question properly, we restrict the following discussion to
the LMC stars, since they form the majority in our sample and since they share a common
environment.
(12)We now ask ourselves
whether we can expect to actually observe rapidly rotating WR stars. To answer this
question, we need to compare the spin-down times with a typical lifetime of a WR star. In
order to discuss this important question properly, we restrict the following discussion to
the LMC stars, since they form the majority in our sample and since they share a common
environment.
As is readily seen from Eq. (12), the
spin-down times strongly depend on the co-rotation radius
(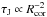 ).
At the beginning of its evolution, a WR star has hardly contracted relative to its O star
progenitor, and therefore has a co-rotation radius of the order of the stellar radius,
i.e. Rcor ≈ R∗.
The mass-loss rate of a young WR star is smaller than that of an evolved one (Nugis & Lamers 2000; Hamann et al. 2006), and its mass is larger. Using the parameters from
Table 1, we can find a lower limit for the
“initial” spin-down times of the stars analyzed here. These lower limits are found to be
of the order of 106
years, somewhat longer than the lifetime of a rotating WR star at LMC metallicities, i.e.
~400 000 years (cf. Meynet & Maeder 2005). However, as the WR star
contracts, the quantity Rcor/R∗
becomes larger. The “current” spin-down times of the evolved WNE subtypes in our sample
are of the order of ~5000−10 000 years. As soon as the magnetic field enforces a large
co-rotation radius, the spin-down times become much smaller.
).
At the beginning of its evolution, a WR star has hardly contracted relative to its O star
progenitor, and therefore has a co-rotation radius of the order of the stellar radius,
i.e. Rcor ≈ R∗.
The mass-loss rate of a young WR star is smaller than that of an evolved one (Nugis & Lamers 2000; Hamann et al. 2006), and its mass is larger. Using the parameters from
Table 1, we can find a lower limit for the
“initial” spin-down times of the stars analyzed here. These lower limits are found to be
of the order of 106
years, somewhat longer than the lifetime of a rotating WR star at LMC metallicities, i.e.
~400 000 years (cf. Meynet & Maeder 2005). However, as the WR star
contracts, the quantity Rcor/R∗
becomes larger. The “current” spin-down times of the evolved WNE subtypes in our sample
are of the order of ~5000−10 000 years. As soon as the magnetic field enforces a large
co-rotation radius, the spin-down times become much smaller.
It is in the WNE phase that WR stars become relatively compact. According to observations, there are approximately as many WNE stars as there are WNL stars, in the Galaxy (see e.g. Hamann et al. 2006) as well as in the LMC (Hainich et al. 2014). This means that the lifetime of WNE subtypes is about half of a full WR lifetime, i.e. ~200 000 years. Assuming that the spin-down times at the WNE phase is ~10 000 years, and assuming that most WR stars at LMC metallicities reach this rapid rotation phase at a certain point, we have, statistically, a 10 000/200 000 = 0.05 chance of observing them. That is, ~5% of the WNE subtypes in the LMC sample should exhibit round emission lines, if rapid rotation and magnetically enforced co-rotation are the causes for it, and as long as the rotation is not concealed due to an unlucky inclination of the star. And indeed, the four stars analyzed here, out of the ~70 WNE subtypes analyzed by Hainich et al. (2014), make about 5% of the sample.
If a massive WR star is to form a GRB according to the collapsar model of Woosley (1993), the inner core of the star (up to ~3 M⊙) should possess a sufficiently large angular momentum when collapsing. Are the sampled stars in this analysis potential progenitors of GRBs? All stars analyzed here are compact WNE subtypes which exhibit broad and round emission lines, i.e. potentially rapidly rotating stars approaching the end of their life cycle, thus fulfilling the main requirement of the collapsar model. On the other hand, it is also clear that not all low-metallicity WR stars end their lives as LGRBs (cf. Woosley & Heger 2006). GRB progenitors need to be rarer than rapidly rotating WR stars are. To become a GRB, the spin-down time should be smaller than the remaining lifetime of the stars. If the stars in our sample were to explode in the next 5000−10 000 years, they might indeed end their lives as GRBs. We currently see no good way of determining with certainty whether this is the case, however.
6. Summary
Among the ~180 WN stars analyzed in the Galaxy and in the LMC, we identified five stars (one galactic, four LMC) whose spectra exhibit exceptionally broad and round emission line profiles. It has been suggested that these profiles might indicate rapid rotation (Hamann et al. 2006). Motivated by this and by the lack of alternative explanations, we extended our code to properly handle rotation in expanding atmospheres of hot stars. For this purpose, we assumed a rotational velocity field which is specified by two parameters: the co-rotation radius Rcor and the projected equatorial velocity at the co-rotation radius vcorsini. These parameters, together with v∞, were regarded as free parameters throughout the analysis. We conclude:
-
Rotation helps to reproduce the unique features observed.
-
If rotation is to explain the peculiar features of these spectra, large co-rotation radii have to be assumed (Rcor ≳ 10 R∗).
-
The rotational velocities are large (v∗sini ~ 200 km s-1) but remain significantly smaller than the critical velocity at the stellar surface. In the stellar wind, the rotational velocities exceed the critical velocities by far.
-
The asymmetry arising in the outer wind layers is likely to induce a net polarization of the continuum, which is not observed in the case of WR 2. However, a conclusive interpretation of the polarimetric data requires a full modeling of polarized radiative transfer in co-rotating atmospheres.
-
Very large magnetic fields (Bτ = 2/3 ~ 20 kG) are necessary to enforce co-rotation up to the inferred radii. If the fields are global, they should be detectable with circular polarimetry.
It might well be that the rotation model we applied here is too simplified. Even if the assumptions adopted in this work hold fully, the actual rotational velocity field, of course, would not consist of two artificially distinct domains, but would rather continuously switch from one domain to the other, as the magnetic field gradually loses control over the wind dynamics. Regardless, stellar rotation, as implemented here, was shown to help produce spectra which show a good agreement with observations along a large segment of the optical spectrum for all stars we analyzed.
And yet rotation is not only conjured up to help reproduce the unique spectra analyzed here. There are various arguments supporting the existence of rapidly rotating WR stars. The progenitors of WR stars are known to exhibit very rapid rotational velocities on average. Evolutionary models predict the existence of WR stars with significant rotational velocities. Moreover, rapid internal rotation is a prerequisite for single-star GRB models. Effects such as induced mixing and gravitational darkening, which were shown to play a role in the evolution of massive stars, originate in stellar rotation. Knowing whether WR stars exhibit rapid rotation is thus, in many aspects, important.
So far, no other consistent spectral models were able to reproduce the unique spectra discussed in this work. If not for rotation, the origin of these spectra remains a mystery.
The single spectra are available at http://wikimbad.obs.ujf-grenoble.fr/Category_Wolf-Rayet_Star.html
Acknowledgments
We thank C. Foellmi for providing spectroscopic data. We further thank U. Rühling for her inspiring work, and R. Hainich for his extensive spectral analyses of the LMC WN stars. We sincerely thank A. Moffat, whose insights significantly deepened the scope of this work. T. Shenar would like to thank the Richard-Winter-Stiftung for their support during the writing of this paper.
References
- Akras, S., Ramirez Velez, J., Hiriart, D., & Lopez, J. M. 2013, in Proc. Conf. Massive Stars: From alpha to Omega, 53 available at http://a2omega-conference.net [Google Scholar]
- Belcher, J. W., & MacGregor, K. B. 1976, ApJ, 210, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Bjorkman, J. E., & Cassinelli, J. P. 1993, ApJ, 409, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., & McLean, I. S. 1977, A&A, 57, 141 [NASA ADS] [Google Scholar]
- Cantiello, M., Langer, N., Brott, I., et al. 2009, A&A, 499, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castor, J. I. 1970, MNRAS, 149, 111 [NASA ADS] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1960, Radiative transfer (Dover Publications) [Google Scholar]
- Chené, A.-N., & St-Louis, N. 2005, J. R. Astron. Soc. Can., 99, 132 [NASA ADS] [Google Scholar]
- Coyne, G. V., & McLean, I. S. 1982, in Be Stars, eds. M. Jaschek, & H.-G. Groth, IAU Symp., 98, 77 [Google Scholar]
- Cranmer, S. R., & Owocki, S. P. 1996, ApJ, 462, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A. 2007, ARA&A, 45, 177 [NASA ADS] [CrossRef] [Google Scholar]
- de la Chevrotière, A., St-Louis, N., Moffat, A. F. J., & the MiMeS Collaboration. 2013, ApJ, 764, 171 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., & de Koter, A. 2013, ApJ, 764, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Deibel, A. T., Steiner, A. W., & Brown, E. F. 2013, ApJ, submitted [arXiv:1303.3270] [Google Scholar]
- Donati, J.-F., & Landstreet, J. D. 2009, ARA&A, 47, 333 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Esposito, P., Burgay, M., Possenti, A., et al. 2009, MNRAS, 399, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Foellmi, C., Moffat, A. F. J., & Guerrero, M. A. 2003, MNRAS, 338, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Friend, D. B., & Abbott, D. C. 1986, ApJ, 311, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Friend, D. B., & MacGregor, K. B. 1984, ApJ, 282, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Gaensler, B. M., McClure-Griffiths, N. M., Oey, M. S., et al. 2005, ApJ, 620, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Gräfener, G., & Hamann, W.-R. 2005, A&A, 432, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfener, G., & Hamann, W.-R. 2008, A&A, 482, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfener, G., Koesterke, L., & Hamann, W.-R. 2002, A&A, 387, 244 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfener, G., Vink, J. S., Harries, T. J., & Langer, N. 2012, A&A, 547, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grocholski, A. J., Parisi, M. C., Geisler, D., et al. 2009, in IAU Symp. 256, eds. J. T. Van Loon, & J. M. Oliveira, 287 [Google Scholar]
- Hainich, R., Rühling, U., Hamann, W. R., et al. 2014, A&A, accepted [arXiv:1401.5474] [Google Scholar]
- Hamann, W.-R., & Gräfener, G. 2004, A&A, 427, 697 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamann, W.-R., & Koesterke, L. 1998, A&A, 335, 1003 [NASA ADS] [Google Scholar]
- Hamann, W.-R., & Koesterke, L. 2000, A&A, 360, 647 [NASA ADS] [Google Scholar]
- Hamann, W.-R., Koesterke, L., & Wessolowski, U. 1995, A&AS, 113, 459 [NASA ADS] [Google Scholar]
- Hamann, W.-R., Gräfener, G., & Liermann, A. 2006, A&A, 457, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harries, T. J., Hillier, D. J., & Howarth, I. D. 1998, MNRAS, 296, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., & MacGregor, K. B. 1982, ApJ, 259, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., & Langer, N. 2000, ApJ, 544, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Hillier, D. J. 1987, ApJS, 63, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Hillier, D. J. 1991, A&A, 247, 455 [NASA ADS] [Google Scholar]
- Hillier, D. J. 1994, A&A, 289, 492 [NASA ADS] [Google Scholar]
- Hillier, D. J., & Miller, D. L. 1998, ApJ, 496, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Hillier, D. J., Bouret, J.-C., Lanz, T., & Busche, J. R. 2012, MNRAS, 426, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschi, R., Meynet, G., & Maeder, A. 2005, A&A, 443, 581 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ignace, R. 2009, Astron. Nachr., 330, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Ignace, R., Cassinelli, J. P., & Bjorkman, J. E. 1996, ApJ, 459, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Ignace, R., Gayley, K. G., Hamann, W.-R., et al. 2013, ApJ, 775, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Kholtygin, A. F., Fabrika, S. N., Rusomarov, N., et al. 2011, Astron. Nachr., 332, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Lépine, S., & Moffat, A. F. J. 1999, ApJ, 514, 909 [NASA ADS] [CrossRef] [Google Scholar]
- MacGregor, K. B., & Cassinelli, J. P. 2003, ApJ, 586, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 1985, A&A, 147, 300 [NASA ADS] [Google Scholar]
- Marchenko, S. V., & Moffat, A. F. J. 1998, ApJ, 499, L195 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 2005, A&A, 429, 581 [Google Scholar]
- Moss, D. 1989, MNRAS, 236, 629 [NASA ADS] [Google Scholar]
- Mullan, D. J., & MacDonald, J. 2005, MNRAS, 356, 1139 [NASA ADS] [CrossRef] [Google Scholar]
- Nazé, Y. 2013 [arXiv:1306.6753] [Google Scholar]
- Niedzielski, A., & Skorzynski, W. 2002, Acta Astron., 52, 81 [Google Scholar]
- Niedzielski, A., Nugis, T., & Skorzynski, W. 2004, Acta Astron., 54, 405 [NASA ADS] [Google Scholar]
- Nugis, T., & Lamers, H. J. G. L. M. 2000, A&A, 360, 227 [NASA ADS] [Google Scholar]
- Owocki, S. P., Cranmer, S. R., & Blondin, J. M. 1994, ApJ, 424, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., Cranmer, S. R., & Gayley, K. G. 1998, in B[e] stars, eds. A. M. Hubert, & C. Jaschek, Astrophys. Space Sci. Lib., 233, 205 [Google Scholar]
- Penny, L. R. 1996, ApJ, 463, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Petrenz, P., & Puls, J. 2000, A&A, 358, 956 [NASA ADS] [Google Scholar]
- Poe, C. H., Friend, D. B., & Cassinelli, J. P. 1989, ApJ, 337, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Prinja, R. K., Barlow, M. J., & Howarth, I. D. 1990, ApJ, 361, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Sander, A., Hamann, W.-R., & Todt, H. 2012, A&A, 540, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmutz, W., Hamann, W.-R., & Wessolowski, U. 1989, A&A, 210, 236 [NASA ADS] [Google Scholar]
- Schnurr, O. 2008, Ph.D. Thesis, Université de Montréal, Canada [Google Scholar]
- Schulte-Ladbeck, R. E., Nordsieck, K. H., Taylor, M., et al. 1991, ApJ, 382, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spruit, H. C. 2008, in AIP Conf. Ser., 983, 391 [Google Scholar]
- Underhill, A. B., & Fahey, R. P. 1987, ApJ, 313, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Unsöld, A. 1955, Physik der Sternatmosphären mit besonderer Berücksichtigung der Sonne (Springer) [Google Scholar]
- Vanbeveren, D., De Loore, C., & Van Rensbergen, W. 1998, A&ARv, 9, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S. 2007, A&A, 469, 707 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., & de Koter, A. 2005, A&A, 442, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., Muijres, L. E., Anthonisse, B., et al. 2011, A&A, 531, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Wade, G. A., Maíz Apellániz, J., Martins, F., et al. 2012, MNRAS, 425, 1278 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, E. J., & Davis, Jr., L. 1967, ApJ, 148, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E. 1993, ApJ, 405, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Heger, A. 2006, ApJ, 637, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2005, A&A, 443, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Comparison between the observed optical spectra of two WN4b stars in the LMC: BAT99 134 (dashed brown line), and BAT99 7 (solid blue line). While the spectrum of BAT99 134 is typical for a WNE subtype, the spectrum of BAT99 7 distinctly shows qualitative differences. |
| In the text | |
 |
Fig. 2 The coordinate system used for the 3D integration scheme. The integration of the
emergent intensities |
| In the text | |
 |
Fig. 3 Effect of the parameters vcorsini and Rcor on prominent synthetic emission lines of BAT99 7. Each of the upper panels depicts, for a constant value Rcor = R∗, the synthetic profile of an emission line calculated with different vcorsini values. The bottom panels show the synthetic profile of the same spectral lines calculated with different Rcor values and with a constant rotational velocity of vcorsini = 2000 km s-1. |
| In the text | |
 |
Fig. 4 Normalized ξ(log r)-plots for several He ii emission lines belonging to the model of the star BAT99 7. The model parameters are listed in Table 1. The individual lines are formed many stellar radii above the surface. |
| In the text | |
 |
Fig. 5 Equatorial rotational velocity as a function of r. Both curves correspond to vcor = 2500 km s-1. However, the dashed red curve is plotted with Rcor = R∗, while the solid blue curve is plotted with Rcor = 16 R∗. We also denote an estimate of the LFR of the line He ii λ4686, determined by its corresponding ξ plot. Note that the LFR remains unaffected by rotation unless large co-rotation radii are assumed. |
| In the text | |
 |
Fig. 6 Comparison between synthetic spectra calculated with rotation (dotted red line), without rotation (dashed black line), and observations (solid blue line) for the five stars analyzed. The synthetic spectra are convolved with a Gaussian of FWHM = 3 Å to account for instrumental broadening. |
| In the text | |
 |
Fig. 7 Zoomed-in sections of Fig. 6 with prominent emission lines of the stars BAT99 94 (upper panels) and BAT99 88 (bottom panels). The observed spectrum (solid blue line) is compared to the synthetic spectrum calculated with rotation (dotted red line), and without rotation (dashed black line). |
| In the text | |
 |
Fig. 8 Two He ii lines belonging to BAT99 94. We compare the observed spectrum (solid blue line) with a synthetic spectrum calculated with the same stellar parameters as in Table 1, but with an increased terminal velocity of v∞ = 2500 km s-1 and without rotation (dashed black line). Note that the line widths match, but the shape of the synthetic lines is qualitatively very different from the observed ones. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


