| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201322418 | |
| Published online | 13 February 2014 | |
First use of synoptic vector magnetograms for global nonlinear, force-free coronal magnetic field models
1
Space Weather Laboratory, NASA Goddard Space Flight Center,
Greenbelt,
MD,
USA
e-mail: tilaye.tadesse.asfaw@nasa.gov; peter.j.macneice@nasa.gov
2
Max-Planck-Institut für Sonnensystemforschung,
Max-Planck-Strasse
2, 37191
Katlenburg-Lindau,
Germany
e-mail:
wiegelmann@mps.mpg.de
3
National Solar Observatory, Sunspot
NM
88349,
USA
e-mail: sgosain@nso.edu; apevtsov@nso.edu
Received:
31
July
2013
Accepted:
19
December
2013
Context. The magnetic field permeating the solar atmosphere is generally thought to provide the energy for much of the activity seen in the solar corona, such as flares, coronal mass ejections (CMEs), etc. To overcome the unavailability of coronal magnetic field measurements, photospheric magnetic field vector data can be used to reconstruct the coronal field. Currently, there are several modelling techniques being used to calculate three-dimensional field lines into the solar atmosphere.
Aims. For the first time, synoptic maps of a photospheric-vector magnetic field synthesized from the vector spectromagnetograph (VSM) on Synoptic Optical Long-term Investigations of the Sun (SOLIS) are used to model the coronal magnetic field and estimate free magnetic energy in the global scale. The free energy (i.e., the energy in excess of the potential field energy) is one of the main indicators used in space weather forecasts to predict the eruptivity of active regions.
Methods. We solve the nonlinear force-free field equations using an optimization principle in spherical geometry. The resulting three-dimensional magnetic fields are used to estimate the magnetic free energy content Efree = Enlfff − Epot, which is the difference of the magnetic energies between the nonpotential field and the potential field in the global solar corona. For comparison, we overlay the extrapolated magnetic field lines with the extreme ultraviolet (EUV) observations by the atmospheric imaging assembly (AIA) on board the Solar Dynamics Observatory (SDO).
Results. For a single Carrington rotation 2121, we find that the global nonlinear force-free field (NLFFF) magnetic energy density is 10.3% higher than the potential one. Most of this free energy is located in active regions.
Key words: magnetic fields / Sun: corona / Sun: photosphere
© ESO, 2014
1. Introduction
In the solar coronal plasma, magnetic energy is the prime energy reservoir that fuels the dynamical evolution of eruptive events, but it remains an open question to how the magnetic energy is released. The amount of energy associated with the magnetic field is much larger than other energy sources, and the dynamics of the coronal configuration is determined by the evolution of its magnetic field (Forbes 2000; Low 2001).
Free energy is defined as excess of energy as compared with potential field. One can, in principle, release more energy than free energy by, for example, annihilating magnetic field. Numerically, one can also get pre-post flare difference in energy larger than free magnetic energy if the magnetic field at the photosphere changes (e.g., some flux elements disappear). It quantifies the energy deviation of the coronal magnetic field from its potential state (Metcalf et al. 2005; Régnier 2007; Aschwanden 2012). The magnetic free energy is stored in the form of electric currents flowing along the magnetic field. Free magnetic energy of solar magnetic fields can be affected by several processes such as photospheric shearing flows, magnetic flux emergence and magnetic reconnection (e.g., Welsch 2006; Fang et al. 2012).
To understand the role that the magnetic field plays in energizing the solar corona, it is
important to calculate the amount of free energy needed to quantify the energy budget in a
catastrophic energy release event, as well as for estimating upper limits in forecasting
individual events in real-time. Using various extrapolation techniques for the coronal
magnetic field under the assumption of force-free fields, the spatial and temporal evolution
of the coronal magnetic free energy during solar flares has been extensively studied (Régnier & Canfield 2006; Guo et al. 2008; Jing et al. 2010;
Tadesse et al. 2012a; Meyer et al. 2013). From the 3D coronal magnetic configurations, we can
derive the magnetic energy in the corona as 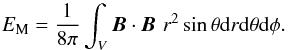 (1)The free magnetic
energy in spherical geometry is calculated by computing the nonpotential field
Bnlfff(r,θ,φ) with a
numerical nonlinear force-free field (NLFFF) code and a potential field Bpot(r,θ,φ) for the same
photospheric boundary data, so that the difference of the magnetic field energy density in
the coronal volume V encompassing the active regions of interest can be quantified as
EMfree = EMnlfff − EMpot.
(1)The free magnetic
energy in spherical geometry is calculated by computing the nonpotential field
Bnlfff(r,θ,φ) with a
numerical nonlinear force-free field (NLFFF) code and a potential field Bpot(r,θ,φ) for the same
photospheric boundary data, so that the difference of the magnetic field energy density in
the coronal volume V encompassing the active regions of interest can be quantified as
EMfree = EMnlfff − EMpot.
Since the corona is optically thin, direct measurements of the 3D magnetic field are very difficult to implement and interpret. Therefore, the present observations for the magnetic fields based on the spectropolarimetric method (the Zeeman and the Hanle effects) are limited to low layers of solar atmosphere (photosphere and chromosphere). Even if direct measurement techniques for the 3D magnetic fields in the chromosphere and the corona have considerably improved in recent decades (Lin et al. 2000, 2004; Liu & Lin 2000), further developments are needed before accurate data are routinely available. Thus, the problem of measuring the coronal field and its embedded electrical currents leads us to use numerical modelling to infer the field strength in the higher layers of the solar atmosphere from the measured photospheric field.
Force-free extrapolation of photospheric magnetic fields is currently used as the primary tool for the modelling of coronal magnetic fields. In this model assumption, the corona magnetic forces are dominant so that all nonmagnetic forces, such as the plasma pressure gradient and gravity, can be neglected in the lowest order (Gary 2001). This implies that, if appreciable currents are present, these must be aligned with the magnetic field, since the resulting Lorentz forces could otherwise not be balanced by the nonmagnetic forces. The equilibrium structure of the static coronal magnetic field can be described using the force-free assumption as
![\begin{eqnarray} &&(\nabla \times\boldsymbol{B})=\alpha\boldsymbol{B}\Rightarrow(\nabla \times\boldsymbol{B})\times\boldsymbol{B}=0 \label{two}\\[3mm] && \nabla \cdot\boldsymbol{B}=0, \label{three} \end{eqnarray}](/articles/aa/full_html/2014/02/aa22418-13/aa22418-13-eq7.png) where
B is the magnetic field. The force-free
parameter α of
Eq. (2) can be a function of position, but
the combination of Eqs. (2) and (3) (B·∇α = 0) requires
that α be
constant along a given field line. Potential (α = 0) and linear force-free fields (whenever
α is constant
everywhere in the volume under consideration) can be used as a first step to model the
general structure of magnetic fields in the solar corona. Practically, the pre-eruptive
magnetic fields are nonlinear force-free fields (α being a function of position) as supported by both
observational and theoretical reasons. For details of those models, we direct the readers to
Wiegelmann & Sakurai (2012).
where
B is the magnetic field. The force-free
parameter α of
Eq. (2) can be a function of position, but
the combination of Eqs. (2) and (3) (B·∇α = 0) requires
that α be
constant along a given field line. Potential (α = 0) and linear force-free fields (whenever
α is constant
everywhere in the volume under consideration) can be used as a first step to model the
general structure of magnetic fields in the solar corona. Practically, the pre-eruptive
magnetic fields are nonlinear force-free fields (α being a function of position) as supported by both
observational and theoretical reasons. For details of those models, we direct the readers to
Wiegelmann & Sakurai (2012).
Nonlinear force-free field codes have been routinely applied to the reconstruction of the coronal field of a single active region using the Cartesian geometry. In that case, the curvature of the solar surface does not play an important role. The Solar Dynamics Observatory (SDO) mission has made repeated observations of large scale events in which connections between widely separated active regions may play fundamental role (Martens et al. 2012). Even before SDO, it was known that large-scale connectivity is important for solar eruptive and non-eruptive activity (e.g., studies of sympathetic flares, transequatorial loops (Pevtsov 2000), effects of distant active regions on large-scale coronal brightness (Pevtsov & Acton 2001), eruption of filaments triggered by remote flux emergence, and evolution (e.g., Balasubramaniam et al. 2011). Therefore, these needs motivate us to implement a NLFFF procedure in spherical geometry (Wiegelmann 2007; Tadesse et al. 2009, 2011, 2012a,b, 2013b, 2014; Guo et al. 2012; Amari et al. 2013)
Nonlinear force-free reconstruction of the global solar magnetic field from line-of-sight component of synoptic magnetograms has been developed by Contopoulos et al. (2011). In this study, we estimate the free magnetic energy for global corona using the synoptic vector magnetograms from SOLIS/VSM. We compare the extrapolated potential and NLFFF magnetic loops with extreme ultraviolet (EUV) observations by the atmospheric imaging assembly (AIA) on board SDO. This comparison helps to identify whether the NLFFF model reconstructs the magnetic configuration better than the potential field model in the global scale. In this paper, we present some descriptions of the dataset used for analysis in Sect. 2. The spherical optimization procedure used for modeling 3D magnetic field in global corona is presented in Sect. 3. Then, we present results of our studies in Sect. 4. A summary and discussions are finally presented in Sect. 5.
2. Instrumentation and data set
In this paper, we use the first ever synoptic vector magnetograms, which include Carrington maps of the three components of the magnetic field vector, the radial Br, the poloidal Bθ, and the toroidal Bφ, to first perform a global nonlinear force free field extrapolation based on optimization algorithm (Wiegelmann 2007; Tadesse et al. 2009). The synoptic vector field maps are derived using daily full disk photospheric vector magnetograms from vector spectromagnetograph (VSM) instrument on the synoptic optical long-term investigations of the Sun (SOLIS), a synoptic observing facility (Keller et al. 2003; Balasubramaniam & Pevtsov 2011). More detail about these synoptic maps and their properties can be found in Gosain et al. (2013). Here, we briefly describe the instrument characteristics and the full disk vector field observations.
The vector spectromagnetograph routinely obtains full disk magnetograms in photospheric and chromospheric lines as a part of the synoptic program of National Solar Observatory, known as the NSO Integrated Synoptic Program (NISP). To obtain full disk photospheric vector magnetograms, SOLIS/VSM measures Stokes (S = I, Q, U, V) profiles in photospheric Fe I 630.15−630.25 nm line pair. A single full disk scan (2048 scan lines) takes only about 20 minutes, thanks to the long slit of the spectrograph, which intersects the solar disk from one limb to another in one shot. The spatial sampling is 1 arcsec per pixel with square pixels. The spectral sampling is 2.4 pm per pixel. A single Stokes set (I,Q,U,V) per slit position is obtained typically in about 0.6 s. The telescope itself is designed to be free of instrumental polarization by employing symmetric optical configuration and performing polarization modulation just after the prime focus after the slit. Dual beam analysis of polarization using a polarizing beam splitter avoids seeing that is induced cross talks in the signal. The polarimeter calibration is done routinely to calibrate the Stokes vector for cross-talks. The signal-to-noise ratio in the continuum of the Stokes profiles is typically >1000. The magnetic field vector is inferred from the calibrated Stokes profiles by performing inversion in the framework of the Milne-Eddington model for stellar atmosphere, which follows Unno-Rachkovsky formalism (Skumanich & Lites 1987).
Only pixels with a polarization signal above the threshold of 0.1% of continuum intensity, Ic, are inverted to obtain the magnetic (field strength, inclination angle, and azimuth angle) and thermodynamic (e.g., Doppler width, Doppler velocity, source function, temperature) parameters. The threshold of 0.1% of Ic corresponds to typical noise level in the continuum. Using this threshold avoids fitting profiles buried in the noise.
Further details about instrument and pipeline reduction steps can be found elsewhere (e.g., Jones et al. 2002; Henney et al. 2006; Balasubramaniam & Pevtsov 2011). The noise in SOLIS magnetograms is estimated to be a few gauss in longitudinal and 70 G in the transverse field measurements (Tadesse et al. 2013a). The 180 degree azimuth ambiguity is resolved using a different (faster) ambiguity resolution method developed by Rudenko & Anfinogentov (2011).
3. Magnetic field modelling
For modelling the coronal magnetic field in a global scale, we use the variation principle originally proposed by Wheatland et al. (2000). Wiegelmann (2007) has developed an optimization method to reconstruct the NLFFF for global solar corona by minimizing an objective functional L that combines Lorentz forces and the divergence of the magnetic field in spherical geometry. The code has been tested with semi-analytic force-free solutions (Low & Lou 1990). If the functional is minimized to zero, Eqs. (2) and (3) are satisfied simultaneously. The optimization procedure in the spherical geometry has been implemented by Tadesse et al. (2009) for a restricted area with large field of views. Later, Tadesse et al. (2011) modified the objective function of the optimization method (Wiegelmann & Inhester 2010) for spherical geometry as
![\begin{eqnarray} &&L=L_{\rm f}+L_{\rm d}+\nu L_\mathrm{photo} \label{4} \\[1.5mm] && L_\mathrm{f}=\int_{V}B^{-2}\big|(\nabla\times {\boldsymbol{B}})\times {\boldsymbol{B}}\big|^2 r^2\sin\theta {\rm d}r {\rm d}\theta {\rm d}\phi \nonumber \\[1.5mm] &&L_\mathrm{d}=\int_{V}\big|\nabla\cdot {\boldsymbol{B}}\big|^2 r^2\sin\theta {\rm d}r {\rm d}\theta {\rm d}\phi \nonumber \\[1.5mm] && L_\mathrm{photo}=\int_{S}\big(\boldsymbol{B}-\boldsymbol{B}_\mathrm{obs}\big)\cdot\textbf{W}(\theta,\phi)\cdot\big( \boldsymbol{B}-\boldsymbol{B}_\mathrm{obs}\big) r^{2}\sin\theta {\rm d}\theta {\rm d}\phi,\nonumber \end{eqnarray}](/articles/aa/full_html/2014/02/aa22418-13/aa22418-13-eq25.png) (4)where
Lf
and Ld measure how well the force-free Eqs.
(2) and divergence-free (3) conditions are fulfilled, respectively. The
main reason for modification of the code was that we need to deal with boundary data of
different noise levels and qualities, or even miss some data points completely. Hence, the
third integral, Lphoto, is the surface integral over the
photosphere, which allows us to relax the field on the photosphere towards a force-free
solution without too much deviation from the original surface field data.
(4)where
Lf
and Ld measure how well the force-free Eqs.
(2) and divergence-free (3) conditions are fulfilled, respectively. The
main reason for modification of the code was that we need to deal with boundary data of
different noise levels and qualities, or even miss some data points completely. Hence, the
third integral, Lphoto, is the surface integral over the
photosphere, which allows us to relax the field on the photosphere towards a force-free
solution without too much deviation from the original surface field data.
 |
Fig. 1 Synoptic Carrington maps of the vector magnetic field components are shown for CR-2121. The panels from top to bottom show the distribution of the Br, Bφ and Bθ components, respectively. The Br map is scaled between ±100 G, and the Bφ and Bθ maps are scaled to ±20 G. The positive values of Br, Bφ and Bθ point, respectively, upward, westward and southward. |
 |
Fig. 2 Global field lines of the potential field model and the NLFFF model overlaid on the AIA 171 Å and composite AIA (171, 193, and 211 Å) images. Green and red lines represent open and closed magnetic field lines, respectively. |
The SOLIS/VSM provides full disk vector magnetograms from which synoptic Carrington maps of the vector magnetic field components are synthesized. However, for pixels below the polarization threshold the inversion was not performed and field data will be missing for these pixels (see Fig. 1). Typically, the field is missing where its magnitude is small; thus, these pixels would have a small impact on the model even if they were measured correctly. Within the error margin of a measured field value, any value is just as good as any other, and from this range of values, we take the value that fits the force-free field best. To treat those pixels with missing data, we used the diagonal matrix, W(θ,φ), which gives different weights to the observed surface field components depending on the relative accuracy in measurement. We choose W = (BT/max(BT))2. This seems to be a reasonable choice, as the measurement error in the transverse field is higher in weak field regions (Wiegelmann & Inhester 2010). In this sense, the missing data is considered the most inaccurate and is taken into account by setting W(θ,φ) to zero in all elements of the matrix.
The photospheric magnetic field has a plasma-β of order unity, which does not satisfy the force-free condition (Gary 2001). Therefore, the vector magnetogram data are inconsistent with the force-free assumption, which is absolutely essential condition for NLFFF extrapolation. To find suitable boundary conditions for the NLFFF field modelling, we have to preprocess the measured synoptic vector magnetograms by using a preprocessing scheme developed by Tadesse et al. (2009) in spherical geometry. This preprocessing scheme removes forces and torques from the boundary and approximates the photospheric magnetic field to the low plasma-β force-free chromosphere. For a detailed description of the current code implementation, we refer to Wiegelmann (2007) and Tadesse et al. (2011). Tadesse et al. (2012a) has compared the difference between the boundary data before and after the preprocessing and found that the maximum change in the transverse field is 30 G for SOLIS/VSM data. The final preprocessed field values on the boundary are consistent with the observed data within noise levels (noise due to fluctuations in intensity), which are about 1 G and 70 G for longitudinal and transverse components, respectively.
4. Results
This study requires extrapolating the three-dimensional potential and NLFFF coronal fields from the photospheric boundary on global scale. We use synoptic maps of photospheric vector magnetic field observed during 4–31 March 2012. During this observation, there were about 25 active regions all over the solar globe. To use our spherical optimization code for global corona, we adopt a uniform spherical grid using r, θ, and φ with nr = 300, nθ = 450, and nφ = 900 grid points in the direction of radius, latitude, and longitude, respectively, with the field of view of [rmin = 1 R⊙:rmax = 2.5 R⊙] × [θmin = −90°:θmax = 90°] × [φmin = 0°:φmax = 360°]. To avoid the mathematical singularities at the poles, we do not use grid points exactly at the south and north pole but set them half a grid point apart at θmin = −90° + dθ/2 and θmax = 90°−dθ/2 (see, Wiegelmann 2007). We set W(θ,φ) = 0 for those pixels where there are no measurements on the polar regions. The code solves the NLFFF equations in the bounded domain between 1 R⊙ and the source surface at 2.5 R⊙. The outer boundary is kept fixed using the initial potential field values. All current-carrying field lines have to be confined the volume. The domain outside 2.5 R⊙ is not included in the model, because the force-free approach is no longer justified here. The magnetic field extrapolation has been carried out by excluding the polar regions for almost global corona where the magnetic field measurements are highly being influenced by noise. Before performing NLFFF extrapolations, we use the preprocessed radial magnetic field component Br to compute the corresponding potential field using a spherical harmonic expansion for initializing our spherical NLFFF code during relaxation towards a force-free state in the computational volume.
 |
Fig. 3 Field lines of a) the potential field model and b) the NLFFF model around ARs 11429 and 11 430 overlaid on the AIA 171 Å image. Green and red lines represent open and closed magnetic field lines, respectively. |
 |
Fig. 4 Magnetic field line skeletons a) of the entire solar globe from the NLFFF model and b) image of the sun observed by SOHO/LASCO C2 coronagraph at 16:33UT. |
The main purpose of this work is to study the structures of the global potential and NLFFF magnetic fields and to estimate free magnetic energy available to power solar eruptions during Carrington rotation 2121. In addition, we compare which of those two models best agrees with observation in global environment. To do this, we plot the selected fieldlines of the potential and NLFFF models in Fig. 2. We overlay the field lines with an AIA 171 Å and a composite (171 Å, 193 Å, and 211 Å) image. The field lines of the potential and NLFFF models are reconstructed from the same footpoints. Some of potential field lines in Fig. 3a have an obvious deviation from the observed EUV loops. There are more field lines open to the upper boundary in NLFFF than potential fields. Most of AIA coronal loops are best overlaid by NLFFF lines than potential ones (see Fig. 3b). Therefore, the qualitative comparison between the model magnetic field lines and the observed EUV loops indicates that the NLFFF model provides a more consistent field for global corona magnetic field reconstruction. Figure 4 shows that there is over all similarity between the corresponding NLFFF model field lines and image of the sun observed by the SOHO/LASCO C2 coronagraph. However, one can see that NLFFF does not well represent a linear structure above a coronal helmet in the low-left corner in Fig. 4b. This could be due to the missing data from the polar region.
In addition to the above, to compare the degree of disagreement between the two model
vector field solutions in the global corona volume that are specified on the identical sets
of grid points, we use the vector correlation metric (Cvec), which is
also used to the standard correlation coefficient for scalar functions. The correlation was
calculated (Schrijver et al. 2006) from 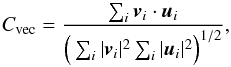 (5)where vi and
ui are the
vectors at each grid point i. If the vector fields are identical, then
Cvec = 1; if vi ⊥ ui
, then Cvec = 0. The degree of convergence towards
a force-free and divergence-free model solution can be quantified by the integral measures
of the Lorentz force and the divergence terms in the minimization functional in Eq. (4), which are computed over the entire solar
globe. The Lf and Ld of Eq. (4) measure how well the force-free and
divergence-free conditions are fulfilled, respectively. In Table 1, we provide some quantitative measures to rate the quality of our
reconstruction. Column 1 names
the corresponding models. Columns 2–3 show how well the force-balance and solenoidal
conditions are fulfilled for both models. Figure 5
shows how well the functional L converge to zero during iteration process. In the
last column, the vector correlation shows that there is disagreement between the two model
field solutions.
(5)where vi and
ui are the
vectors at each grid point i. If the vector fields are identical, then
Cvec = 1; if vi ⊥ ui
, then Cvec = 0. The degree of convergence towards
a force-free and divergence-free model solution can be quantified by the integral measures
of the Lorentz force and the divergence terms in the minimization functional in Eq. (4), which are computed over the entire solar
globe. The Lf and Ld of Eq. (4) measure how well the force-free and
divergence-free conditions are fulfilled, respectively. In Table 1, we provide some quantitative measures to rate the quality of our
reconstruction. Column 1 names
the corresponding models. Columns 2–3 show how well the force-balance and solenoidal
conditions are fulfilled for both models. Figure 5
shows how well the functional L converge to zero during iteration process. In the
last column, the vector correlation shows that there is disagreement between the two model
field solutions.
Evaluation of the reconstruction quality for the potential field and NLFFF models.
 |
Fig. 5 Evolution of the entire functional L (blue line) and its three terms in Eq. (4) during the optimization process. The black line corresponds to Lphoto, the red line to Lf, and the green line to Ld. |
The energy stored in the magnetic field as a result of a field line stressing into a
nonpotential configuration has been identified as the source of flare energy. Therefore, to
understand the physics of solar flares, including the local reorganisation of the magnetic
field and the acceleration of energetic particles, we have to first estimate the free
magnetic energy available for such phenomena. This free magnetic energy can be converted
into kinetic and thermal energy. We estimate the free magnetic energy, which is the
difference between the extrapolated NLFFF and the potential field with the same normal
boundary conditions in the photosphere. We therefore estimate the upper limit to the free
magnetic energy associated with the coronal currents of the form 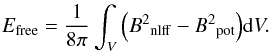 (6)The
parameters Bpot and Bnlff represent
the potential and NLFFF magnetic field, respectively. Our result for the estimation of
free-magnetic energy in Table 2 shows that the NLFFF
model has 10.3% more energy than
the corresponding potential field model. Figure 6a
shows a synoptic map of the global free magnetic energy relative to the potential energy on
the photosphere. In Fig. 6b, we plot the free magnetic
energy density on the latitudinal plane θ = 20° relative to potential field in the
coronal height. There are strong free energy concentrations above each active region over
the solar globe.
(6)The
parameters Bpot and Bnlff represent
the potential and NLFFF magnetic field, respectively. Our result for the estimation of
free-magnetic energy in Table 2 shows that the NLFFF
model has 10.3% more energy than
the corresponding potential field model. Figure 6a
shows a synoptic map of the global free magnetic energy relative to the potential energy on
the photosphere. In Fig. 6b, we plot the free magnetic
energy density on the latitudinal plane θ = 20° relative to potential field in the
coronal height. There are strong free energy concentrations above each active region over
the solar globe.
Magnetic energy associated with the 3D potential and NLFFF field configurations calculated from synoptic vector magnetogram.
The use of preprocessed boundary data and measurement error due to noise may influence the estimation of free magnetic energy (Tadesse et al. 2012a). As the preprocessing procedure filters out, small-scale surface field fluctuations, the magnetic energy of the NLFFF obtained from the preprocessed boundary data is smaller than the corresponding energy without preprocessing. The magnetic energy computed from the original data without preprocessing is 5 × 1033 erg, which is about 4.2% higher than that obtained from the preprocessed boundary data. However, this energy does not correspond to the NLFF magnetic field solution, since the original boundary data without preprocessing is not a consistent boundary condition for NLFFF modelling.
 |
Fig. 6 a) Synoptic map of the global free magnetic energy relative to the potential energy and b) free magnetic energy map on the latitudinal plane θ = 20° relative to potential field (increasing density from black to white). |
5. Conclusion and outlook
Most of the NLFFF procedures are implemented in a Cartesian coordinates. Therefore, both potential and nonlinear force-free field (NLFFF) codes in Cartesian geometry are not well suited for larger domains, since the spherical nature of the solar surface cannot be neglected when the field of view is large. Therefore, it is necessary to implement a NLFFF procedure in spherical geometry for use when large-scale boundary data are in use.
In this study, we have investigated the coronal magnetic field and free magnetic energy associated with the global corona by analyzing Carrington synoptic maps of the photospheric vector magnetic field, which are synthesized from the vector spectromagnetograph (VSM) on Synoptic Optical Long-term Investigations of the Sun (SOLIS). This has been observed during 4–31 March, 2012. The Carrington rotation number for this observation is 2121. During this particular observation, there were about ten active regions distributed across the globe. We have used our spherical NLFFF and potential codes to compute the magnetic field solutions over global corona. This is the first NLFFF magnetic field extrapolation for the global corona using real data.
We have compared the magnetic field solutions from both potential and NLFFF models. The qualitative comparison between the model magnetic field lines and the observed EUV loops indicates that the NLFFF model provides a more consistent field for global corona magnetic field reconstruction. For this particular Carrington rotation, we find that the global NLFFF magnetic energy density is 10.3% higher than the potential one. For the future, we plan to study the evolution of global free magnetic energy. In this study, most of this free energy is located in active regions.
Acknowledgments
The authors would like to thank the referee for his/ her constructive and helpful comments. This work utilizes SOLIS data obtained by the NSO Integrated Synoptic Program (NISP), managed by the National Solar Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA), Inc. under a cooperative agreement with the National Science Foundation. This research was supported by an appointment to the NASA Postdoctoral Program at the Goddard Space Flight Center (GSFC), administered by Oak Ridge Associated Universities through a contract with NASA. The work of T. Wiegelmann was supported by DLR-grant 50 OC 4530501.
References
- Amari, T., Aly, J. J., Canou, A., et al. 2013, A&A, 553, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aschwanden, M. J. 2012, Sol. Phys., 287, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Balasubramaniam, K. S., & Pevtsov, A. 2011, in Proc. SPIE, 8148, 09 [Google Scholar]
- Balasubramaniam, K. S., Pevtsov, A. A., Cliver, E. W., et al. 2011, ApJ, 743, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Contopoulos, I., Kalapotharakos, C., & Georgoulis, M. K. 2011, Sol. Phys., 269, 351 [NASA ADS] [CrossRef] [Google Scholar]
- De Rosa, M. L., Schrijver, C. J., Barnes, G., et al. 2009, ApJ, 696, 1780 [Google Scholar]
- Fang, F., Manchester, IV, W., Abbett, W. P., et al. 2012, ApJ, 754, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, T. G. 2000, J. Geophys. Res., 105, 23153 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, G. A. 2001, Sol. Phys., 203, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Gosain, S., Pevtsov, A. A., Rudenko, G. V., et al. 2013, ApJ, 772, 52 [Google Scholar]
- Guo, Y., Ding, M. D., Wiegelmann, T., et al. 2008, ApJ, 679, 1629 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y., Ding, M. D., Liu, Y., et al. 2012, ApJ, 760, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Henney, C. J., Keller, C. U., & Harvey, J. W. 2006, in ASP Conf. Ser., 358, 92 [Google Scholar]
- Jing, J., Tan, C., Yuan, Y., et al. 2010, ApJ, 713, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, H. P., Harvey, J. W., Henney, C. J., et al. 2002, in SOLMAG 2002, Proceedings of the Magnetic Coupling of the Solar Atmosphere Euroconference, ESA SP, 505, 15 [Google Scholar]
- Keller, C. U., Harvey, J. W., & Giampapa, M. S. 2003, in Proc. SPIE, 4853, 194 [Google Scholar]
- Lin, H., Penn, M. J., & Tomczyk, S. 2000, ApJ, 541, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, H., Kuhn, J. R., & Coulter, R. 2004, ApJ, 613, L177 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., & Lin, H. 2008, ApJ, 680, 1496 [NASA ADS] [CrossRef] [Google Scholar]
- Low, B. C. 2001, J. Geophys. Res., 106, 25141 [NASA ADS] [CrossRef] [Google Scholar]
- Low, B. C., & Lou, Y. Q. 1990, ApJ, 352, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Malanushenko, A., Schrijver, C. J., DeRosa, M. L., et al. 2012, ApJ, 756, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Martens, P. C., Attrill, G. D. R., Davey, A. R., et al. 2012, Sol. Phys., 275, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalf, T. R., Leka, K. D., & Mickey, D. L. 2005, ApJ, 623, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, K. A., Sabol, J., Mackay, D. H., et al. 2013, ApJ, 770, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Pevtsov, A. A. 2000, ApJ, 531, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Pevtsov, A. A., & Acton, L. W. 2001, ApJ, 554, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Régnier, S. 2007, ApJ, 669, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Régnier, S., & Canfield, R. C. 2006, A&A, 451, 319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rudenko, G. V., & Anfinogentov, S. A. 2011 [arXiv:1104.1228] [Google Scholar]
- Schatten, K. H., Wilcox, J. M., & Ness, N. F. 1969, Sol. Phys., 6, 442 [Google Scholar]
- Schrijver, C. J., & De Rosa, M. L. 2003, Sol. Phys., 212, 165 [Google Scholar]
- Schrijver, C. J., De rosa, M. L., Metcalf, T. R., et al. 2006, Sol. Phys., 235, 161 [Google Scholar]
- Schrijver, C. J., De Rosa, M. L., Metcalf, T., et al. 2008, ApJ, 675, 1637 [Google Scholar]
- Skumanich, A., & Lites, B. W. 1987, ApJ, 322, 473 [Google Scholar]
- Tadesse, T., Wiegelmann, T., & Inhester, B. 2009, A&A, 508, 421 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tadesse, T., Wiegelmann, T., Inhester, B., et al. 2011, A&A, 527, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tadesse, T., Wiegelmann, T., Inhester, B., et al. 2012a, Sol. Phys., 281, 53 [NASA ADS] [Google Scholar]
- Tadesse, T., Wiegelmann, T., Inhester, B., et al. 2012b, Sol. Phys., 277, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Tadesse, T., Wiegelmann, T., Inhester, B., et al. 2013a, A&A, 550, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tadesse, T., Wiegelmann, T., MacNeice, P. J., et al. 2013b, Astrophys. Space Sci., 347, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Tadesse, T., Wiegelmann, T., MacNeice, P. J., et al. 2014, Sol. Phys., 289, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Welsch, B. T. 2006, ApJ, 638, 1101 [Google Scholar]
- Wheatland, M. S., & Leka, K. D. 2011, ApJ, 728, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Wheatland, M. S., & Régnier, S. 2009, ApJ, 700, 88 [Google Scholar]
- Wheatland, M. S., Sturrock, P. A., & Roumeliotis, G. 2000, ApJ, 540, 1150 [Google Scholar]
- Wiegelmann, T. 2004, Sol. Phys., 219, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T. 2007, Sol. Phys., 240, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T., & Inhester, B. 2010, A&A, 516, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiegelmann, T., & Sakurai, T. 2012, Liv. Rev. Sol. Phys., 9, 5 [Google Scholar]
- Wiegelmann, T., Thalmann, J. K., Inhester, B., et al. 2012, Sol. Phys., 281, 37 [NASA ADS] [Google Scholar]
All Tables
Evaluation of the reconstruction quality for the potential field and NLFFF models.
Magnetic energy associated with the 3D potential and NLFFF field configurations calculated from synoptic vector magnetogram.
All Figures
 |
Fig. 1 Synoptic Carrington maps of the vector magnetic field components are shown for CR-2121. The panels from top to bottom show the distribution of the Br, Bφ and Bθ components, respectively. The Br map is scaled between ±100 G, and the Bφ and Bθ maps are scaled to ±20 G. The positive values of Br, Bφ and Bθ point, respectively, upward, westward and southward. |
| In the text | |
 |
Fig. 2 Global field lines of the potential field model and the NLFFF model overlaid on the AIA 171 Å and composite AIA (171, 193, and 211 Å) images. Green and red lines represent open and closed magnetic field lines, respectively. |
| In the text | |
 |
Fig. 3 Field lines of a) the potential field model and b) the NLFFF model around ARs 11429 and 11 430 overlaid on the AIA 171 Å image. Green and red lines represent open and closed magnetic field lines, respectively. |
| In the text | |
 |
Fig. 4 Magnetic field line skeletons a) of the entire solar globe from the NLFFF model and b) image of the sun observed by SOHO/LASCO C2 coronagraph at 16:33UT. |
| In the text | |
 |
Fig. 5 Evolution of the entire functional L (blue line) and its three terms in Eq. (4) during the optimization process. The black line corresponds to Lphoto, the red line to Lf, and the green line to Ld. |
| In the text | |
 |
Fig. 6 a) Synoptic map of the global free magnetic energy relative to the potential energy and b) free magnetic energy map on the latitudinal plane θ = 20° relative to potential field (increasing density from black to white). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


