| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 9 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201322180 | |
| Published online | 21 February 2014 | |
Non-LTE spectral analysis of the AM CVn system PTF 09hpk during quiescence
Institute for Astronomy and Astrophysics, Kepler Center for Astro and
Particle Physics, Eberhard Karls University,
Sand 1,
72076
Tübingen,
Germany
e-mail:
gehron@astro.uni-tuebingen.de
Received:
1
July
2013
Accepted:
3
December
2013
Context. AM Canum Venaticorum stars are close, interacting binary systems with a white dwarf primary surrounded by a helium-dominated accretion disk. Because of the short orbital periods, the unseen secondary must be compact, too. Different evolutionary scenarios for the formation of these systems resulting in different kinds of secondaries are possible.
Aims. Quantitative spectral analyses of accretion-disk spectra can reveal the nature of the secondary. We investigate a particular AM CVn system, discovered recently by the Palomar Transient Factory, PTF 09hpk. It is the only known AM CVn star exhibiting unambiguously both outbursts and superoutbursts. We characterize the accretion disk in quiescence and determine abundances of trace elements.
Methods. We calculated line-blanketed nonlocal thermodynamic equilibrium (non-LTE) models and computed accretion-disk spectra by self-consistent solution of radiative transfer and vertical structure equations. These are compared to optical spectra taken during quiescence.
Results. In quiescence, the disk has a uniform effective temperature of 6000 K. An optically thin boundary layer causes the observed He ii λ 4686 Å emission feature. The disk around the massive white dwarf primary (1.2 M⊙) is dominated by helium and is strongly hydrogen-deficient (<−5 dex relative to the solar value). For heavy elements (C, N, O, Mg, Si, Fe), we find moderate to strong subsolar abundances, with depletions down to −2.5 dex for iron. The N/O ratio is >10.
Conclusions. According to the high N/O ratio, the secondary of PTF 09hpk is either a helium white dwarf or a helium star. The low metallicity points to a halo origin of the system or it might be the consequence of heavy-metal sedimentation if the secondary is an old, low-mass helium white dwarf.
Key words: accretion, accretion disks / stars: dwarf novae / novae, cataclysmic variables / stars: individual: PTF1 J0719+4858
© ESO, 2014
1. Introduction
AM Canum Venaticorum (AM CVn) systems are close, interacting binary systems with very short orbital periods below the 78 min period minimum of cataclysmic variables (CVs). AM CVn systems consist of a white dwarf (WD) and a helium-rich, Roche-lobe filling donor. The short separation between the two stars causes a mass transfer from the donor to the more massive WD via an accretion disk. Spectra of AM CVn systems are dominated by double-peaked spectral lines of helium in emission or absorption according to the helium-rich donor.
Known AM CVn systems with their orbital period and type.
AM CVn systems are supposed to contribute to the Type Ia supernova production rate (Solheim & Yungelson 2005; Wang & Han 2012). Additionally, they are strong sources of low-frequency gravitational-wave radiation, which will be detectable with the future evolved Laser Interferometer Space Antenna eLISA (e.g., Amaro-Seoane et al. 2013).
Presently, 34 (45 including sub-period-minimum CVs and candidates) AM CVn systems are known (Table 1 and references therein), and can be divided into subgroups according to their orbital periods. The first group includes HM Cnc, V407 Vul, and ES Cet with ultra-short periods. There is reason to believe that these systems are direct-impact accretors without an accretion disk (Roelofs et al. 2010). AM CVn binaries from the short-period group (Porb < 20 min) are characterized by absorption-line spectra according to high mass-accretion rates of about 10-8 M⊙ yr-1. In contrast, AM CVn systems with orbital periods above 40 min (long-period group) are characterized by emission-line spectra according to low mass-accretion rates of about 10-11 M⊙ yr-1. Located between these two extremes (20 min < Porb < 40 min) are the outbursting systems, which undergo helium-dwarf-nova (HDN) cycles. These are dwarf-nova (DN) cycles known from hydrogen-rich CVs in a helium-rich equivalent. Depending on the state in the HDN cycle they show emission-line spectra during quiescence and absorption-line spectra during outburst.
Dwarf nova outbursts are the result of a thermal instability, when the gas within the accretion disk reaches a critical temperature according to the accumulation of matter during quiescence (for a detailed description, see Osaki 2005). This causes a change in viscosity and a heating front propagates into the low-temperature regions resulting in a collapse of material onto the primary that releases large amounts of gravitational potential energy. Once the heating front reaches the disk’s edge the whole disk becomes ionized and the mass-transfer rate from the disk onto the WD is higher than the rate from the secondary into the disk. The outburst is at its maximum and the ongoing accretion onto the primary results in a decrease in accumulated matter.
Based on observational evidence, one can conclude that most outbursting AM CVn systems show only superoutbursts, analogous to the superoutbursts in hydrogen-rich DNe such as SU Ursae Majoris (SU UMa) stars (e.g. Osaki & Kato 2013). The outburst’s amplitude of HDNe range from 3.5 mag to 6.0 mag with recurrence times between 45 days and 450 days.
One exception is PTF1 J071912.13+485834.0 (hereafter PTF 09hpk), which was detected in outburst by the Palomar Transient Factory (PTF) on 2009 December 01. It is an AM CVn system with an orbital period of Porb = 1606 s (Levitan et al. 2011). This object is characterized by the existence of superoutbursts corresponding to the SU UMa subclass of DN in CVs as well as normal outbursts conforming to the U Geminorum (U Gem) subclass of DN in CVs. Therefore PTF 09hpk is the only known AM CVn system with unambiguous normal outbursts (Kotko et al. 2012; Levitan et al. 2013); KL Dra shows short duration bursts, that can also be identified as normal outbursts (Ramsay et al. 2012). The superoutbursts in PTF 09hpk show a rise time from the last measurement in quiescence to the peak magnitude in outburst of 3.2 d with Δ mv = 3.6 mag. One observes a short duration decrease in the optical flux around a few days after the start of the outburst (so-called dips); these are also seen in other AM CVn systems such as KL Dra (Ramsay et al. 2012). Between superoutbursts, PTF 09hpk shows normal outbursts with an amplitude around Δ mv = 2.0 mag for a recurrence time of 10 d. In addition to the photometric observations, PTF provides outburst spectra taken with WHT/ACAM and quiescence spectra taken by Keck-I/LRIS (Levitan et al. 2011).
To characterize the properties of AM CVn systems in general, we model nonlocal thermodynamic equilibrium (non-LTE) accretion-disk spectra for PTF 09hpk during quiescence. In the following section we briefly describe our modeling of accretion disks and their spectra. In Sect. 3, we describe the vertical structures and the spectra of accretion-disk models representing PTF 09hpk and show the comparison of our models with observations. We close with a short recap of our main results and a discussion in Sect. 4.
2. Accretion-disk modeling
We use our accretion-disk code AcDc to calculate the vertical structure and the spectrum of accretion disks (Nagel et al. 2004); AcDc is based on the assumption of a geometrically thin disk (thickness is much smaller than the diameter), which allows us to decouple vertical and radial structures. In connection with the assumption of axial symmetry we can divide the disk into concentric annuli of plane-parallel geometry. In that way the radiative transfer becomes a one-dimensional equation. Additionally, the mass of the accretion disk is far smaller than the mass of the central object, so we neglect self-gravitation.
The radial distribution of effective temperature Teff for a stationary accretion disk can
then be calculated by ![\begin{equation} T_{\rm eff}(r) = \left[\frac{3 G M_1 \dot{M}}{8 \pi \sigma \, r^3} \left( 1 - \sqrt{\frac{R_\mathrm{1}}{r}} ~ \right) \right]^{\frac{1}{4}} \label{eq:effective-temperature} \end{equation}](/articles/aa/full_html/2014/02/aa22180-13/aa22180-13-eq26.png) (1)(e.g.,
Marsh 1999), where M1 and
R1
denote the mass and the radius of the central object, Ṁ is the mass-accretion rate,
G the
gravitational constant, and σ the Stefan-Boltzmann constant.
(1)(e.g.,
Marsh 1999), where M1 and
R1
denote the mass and the radius of the central object, Ṁ is the mass-accretion rate,
G the
gravitational constant, and σ the Stefan-Boltzmann constant.
The following set of coupled equations were solved simultaneously for each disk ring under
the constraint of particle number and charge conservation. We need the equation of the
radiation transfer for the specific intensity I at frequency
ν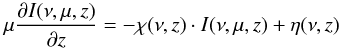 (2)with the emission and
absorption coefficients η and χ, respectively. Additionally, z describes the geometrical
disk height above the midplane and μ = cosϑ, where ϑ is the angle between ray
and z
directions.
(2)with the emission and
absorption coefficients η and χ, respectively. Additionally, z describes the geometrical
disk height above the midplane and μ = cosϑ, where ϑ is the angle between ray
and z
directions.
The hydrostatic equation represents the equilibrium between gravitation,
gas pressure, and radiation pressure 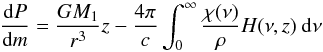 (3)with ρ denoting the mass density,
m the column
mass, and
(3)with ρ denoting the mass density,
m the column
mass, and 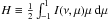 the
Eddington flux.
the
Eddington flux.
Additionally, we need to consider the energy balance between the viscously
generated energy Emech and the radiative energy loss
Erad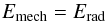 (4)with
(4)with
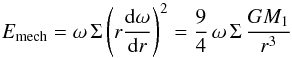 (5)and
(5)and
![\begin{equation} E_\mathrm{rad} = 4 \pi \int_0^\infty \left[ \eta(\nu , z) - \chi(\nu , z) \cdot J(\nu , z)\right] \mathrm{d}\nu \end{equation}](/articles/aa/full_html/2014/02/aa22180-13/aa22180-13-eq48.png) (6)with the mean intensity
(6)with the mean intensity
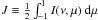 , the surface mass density
Σ, and the angular velocity
ω. Our model
code neglects energy transport through convection. Evaluating the Schwarzschild criterion
and assuming that the adiabatic temperature gradient is ∇ad = 0.4, we find that the
vertical structure of the cool (quiescence) disk models is stable against convection. We do
not expect that ∇ad
is reduced below 0.4 due to a
shifting ionization balance, because helium is almost completely neutral everywhere. These
models are utilized for the chemical abundance determinations.
, the surface mass density
Σ, and the angular velocity
ω. Our model
code neglects energy transport through convection. Evaluating the Schwarzschild criterion
and assuming that the adiabatic temperature gradient is ∇ad = 0.4, we find that the
vertical structure of the cool (quiescence) disk models is stable against convection. We do
not expect that ∇ad
is reduced below 0.4 due to a
shifting ionization balance, because helium is almost completely neutral everywhere. These
models are utilized for the chemical abundance determinations.
Furthermore, we require the non-LTE rate equations for the population
numbers ni of atomic levels
i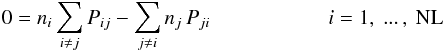 (7)with the rate
coefficients Pij = Rij + Cij,
consisting of radiative and electron collisional components, and the total number of non-LTE
levels (NL). The full spectrum of the complete disk is then obtained by integrating the
individual spectra of the disk rings. The spectra are Doppler shifted according to the
radial component of the Keplerian rotational velocity in the disk.
(7)with the rate
coefficients Pij = Rij + Cij,
consisting of radiative and electron collisional components, and the total number of non-LTE
levels (NL). The full spectrum of the complete disk is then obtained by integrating the
individual spectra of the disk rings. The spectra are Doppler shifted according to the
radial component of the Keplerian rotational velocity in the disk.
There are several input parameters that we have to provide for the calculation of individual disk rings: the mass M1 and radius R1 of the primary, the chemical abundances, the Reynolds number Re specifying the viscosity, the mass-accretion rate Ṁ, and the disk’s extension determined by the radius of the inner edge ri and the outer edge ro. An important prerequisite for the calculation of synthetic spectra is the model atom. It is compiled from the Tübingen Model-Atom Database (TMAD1). Our disk models are based on the model atom summarized in Table 2. We indicate the chemical abundance of an element X with [X] = log (abundance/solar abundance).For the He-dominated models presented in the following section we set metal abundances to a subsolar value and, later on, vary them in order to match observations. We will also constrain the Fe-abundance. For this, we computed additional models including iron.
Statistics of the model atoms used in our cold accretion-disk models corresponding to the quiescence state.
The numerical capabilities of stellar model-atmosphere and disk codes are exceeded by using classical model atoms for the iron group elements. Therefore, reducing the quantity of levels and lines is inevitable. The Tübingen Iron-Group Opacity (TIRO) service creates atomic data files and cross-section data for radiative bound-bound and bound-free transitions of iron group elements. The TIRO service is based on the program IrOnIc (Iron Opacity and Interface) (Rauch & Deetjen 2003) that combines all atomic levels of an ion to a few so-called superlevels. All levels within one superlevel are in LTE, but the superlevels themselves are treated in non-LTE. Transitions between superlevels as well as transitions within one superlevel are considered. For model-atmosphere calculations, the LIN lists (including theoretically calculated wavelengths) from Kurucz (2009) were used to consider the total opacity properly. In total, we consider Fe i-iv with 22 superlevels (116 469 individual levels) and 75 superlines (23 411 882 individual lines).
3. Synthetic spectra for PTF 09hpk
In the following, we present our models for the cold accretion disk in PTF 09hpk representing the quiescence state. The WD’s influence on the quiescence spectrum seems relatively small because spectral depressions from the WD photosphere are not visible in contrast to other systems such as SBSS 1108+574 (Carter et al. 2014). Therefore, we neglect irradiation by the primary and its influence on the optical spectral range. Assuming the extinction law by Fitzpatrick (1999), we fix E(B − V) = 0.15. We model one cold disk representing the quiescence state. We divide the disk into 30 concentric annuli with the properties of each ring presented in Fig. 1. Additionally, Fig. 2 shows representative spectra without rotational broadening for one disk ring during quiescence and for the boundary layer (Sect. 3.5).
We utilize optical spectra of PTF 09hpk that were presented by Levitan et al. (2011). When comparing models with the observations, we normalize the models to the observed continuum flux at a particular, arbitrarily chosen wavelength. In addition, the computed spectra are convolved with a Gaussian (FWHM = 3 Å) to match the spectral resolution.
 |
Fig. 1 Properties of the disk rings corresponding to the accretion-disk model. We show the radial run of vertical extension of the disk from midplane h, effective temperature Teff, viscosity α, total Rosseland optical depth τtot, and surface density Σ. |
 |
Fig. 2 Disk-ring spectra at r = 9.33 × 108 cm for the disk (blue) and at r = 4.47 × 108 cm for the boundary layer (red) with prominent lines identified (no rotational broadening). |
3.1. Central object
To constrain the mass of the primary WD, we use the model grid by Nagel et al. (2009) consisting of different masses for the central star (M1 = 0.6 M⊙ −1.4 M⊙) with a wide range of mass-accretion rates (Ṁ = 10-8 M⊙ yr-1−10-11 M⊙ yr-1) and with various chemical compositions. The comparison between the model grid spectra and the observations of PTF 09hpk during quiescence yields the mass of the central star of about M1 = (1.2 ± 0.2) M⊙. Although such massive WDs are rather infrequent, they can be part of an AM CVn system, for instance in CR Boo and V803 Cen (Roelofs et al. 2007). It should be noted that the grid of Nagel et al. (2009) is not only informative on central-object parameters, but also on other parameters such as the inclination angle and the mass-accretion rate, thereby reducing the risk of possible degeneracies with following parameters.
With the mass of the central star fixed to 1.2 M⊙, its radius follows from a WD mass-radius relation (e.g., Wood et al. 1987). Accordingly, a carbon-oxygen WD with 1.2 M⊙ and Teff = 20 000 K has a radius of R1 = RWD = 4.06 × 108 cm.
3.2. Mass accretion
In addition to the mass of the WD, the mass-accretion rate strongly influences the
strength of spectral lines. We choose a nonstationary model representing an optically thin
disk with strong emission lines as expected during quiescence (Wood et al. 1986). We assume that Teff is constant
over the radial extent of the disk, which can be obtained by decreasing the mass-accretion
rate towards the radial inside 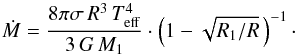 (8)We calculate three models
with Teff = 5000 K, 6000 K, and 7500 K for a 1.2 M⊙
primary. Simultaneously, we aim to set the Reynolds number in such a way that the
viscosity is rather low (
(8)We calculate three models
with Teff = 5000 K, 6000 K, and 7500 K for a 1.2 M⊙
primary. Simultaneously, we aim to set the Reynolds number in such a way that the
viscosity is rather low (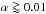 ,
see Fig. 1) representing a cold disk with a low
mass-accretion rate within the disk (Kotko et al.
2012).
,
see Fig. 1) representing a cold disk with a low
mass-accretion rate within the disk (Kotko et al.
2012).
The vertical runs of Rosseland optical depth, density, and temperature are presented in Fig. 3 for one disk ring in the radial interior (left panels) and one ring in the radial exterior (right panels). The effect of a higher mass-accretion rate ascribed to a higher effective temperature can be best seen in the density which increases with rising Teff. In the model with Teff = 7500 K, the Rosseland optical depth becomes large enough so that an absorption-line spectrum is formed (top panel). In contrast, the two other models are optically thin and produce emission-line spectra.
The behavior deduced from the vertical structure is reflected in the synthetic spectra in Fig. 4. They demonstrate quite clearly that a higher mass-accretion rate according to a higher effective temperature results in a change from an emission-line to an absorption-line spectrum. The models with Teff = 5000 K and 6000 K are characterized by broad and strong emission lines. We get the closest matching to the observation with Teff = (6000 ± 500) K and Re = 300 000 according to a nonstationary accretion rate of (0.074−41.5) × 10-12 M⊙ yr-1.
 |
Fig. 3 Vertical structure of an inner disk ring (left panels) at radius r = 13.38 × 108 cm and an outer disk ring (right) at r = 40.56 × 108 cm during quiescence at different effective temperatures for the accretion disk. Shown are the temperature T (bottom panel), the density ρ (middle), and the Rosseland optical depth τross (top). |
3.3. Geometry
The variation of the inclination angle leads to differences in the spectra according to the changing radial projection of the Kepler rotation velocity and the limb darkening of the accretion disk. First of all, the width and strength of the spectral lines are altered (Fig. 5). The comparison between model and observation of PTF 09hpk leads to i = (40 ± 20)°.
Unlike the inclination angle, it is more difficult to constrain the disk extension. On
the one hand, theories describing DNe and HDNe suggest that the extension changes during
an outburst cycle (Smak 1984; Osaki 2005). On the other hand, the location of the disk’s inner and
outer edges slightly affect the profile of spectral lines in different ways. A constraint
for the disk’s outer edge is provided by the tidal and circularization radius. The tidal
radius rtidal is the biggest possible outer edge
resulting from interaction with the secondary and can be calculated approximately
following Warner (2003)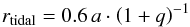 (9)with
a the
separation and q ≡ M2/M1
the mass ratio of the secondary and the primary. By using Kepler’s laws, a can be eliminated, so
that
(9)with
a the
separation and q ≡ M2/M1
the mass ratio of the secondary and the primary. By using Kepler’s laws, a can be eliminated, so
that 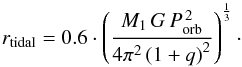 (10)Representatives
of the AM CVn systems have a small mass ratio (q < 0.1, Arbutina 2011). The mass of the primary (M1 = 1.2 M⊙)
and the orbital period (Porb = 1 606 s) in connection with
an assumed mass ratio of q = 0.1 result in rtidal = 1.23 × 1010 cm ≈ 30.3 RWD.
In a similar way it is possible to estimate the circularization radius rcirc, which is
the smallest possible outer edge corresponding to the radius where the transferred matter
has lost all its energy, but has left all its angular momentum (Warner 2003):
(10)Representatives
of the AM CVn systems have a small mass ratio (q < 0.1, Arbutina 2011). The mass of the primary (M1 = 1.2 M⊙)
and the orbital period (Porb = 1 606 s) in connection with
an assumed mass ratio of q = 0.1 result in rtidal = 1.23 × 1010 cm ≈ 30.3 RWD.
In a similar way it is possible to estimate the circularization radius rcirc, which is
the smallest possible outer edge corresponding to the radius where the transferred matter
has lost all its energy, but has left all its angular momentum (Warner 2003): 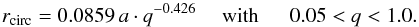 (11)With the previous
values we find rcirc = 5.17 × 109 cm ≈ 12.7 RWD.
For a stable configuration, the accretion disk’s outer edge ro is considered
to be rtidal ≥ ro ≥ rcirc.
(11)With the previous
values we find rcirc = 5.17 × 109 cm ≈ 12.7 RWD.
For a stable configuration, the accretion disk’s outer edge ro is considered
to be rtidal ≥ ro ≥ rcirc.
 |
Fig. 4 Accretion-disk spectra for a 1.2 M⊙ primary representing the disk under an inclination angle of i = 40 ° compared to the observation (black line). For clarification, the computed spectra are shifted vertically (from top to bottom: + 0.3, 0.0, −0.1). |
In the case of PTF 09hpk, it is possible to constrain the disk’s outer and inner edges from the observed spectra. The influence on line profiles and spectral slope is pictured in Fig. 6 during quiescence. We conclude ri = (9.33 ± 2.03) × 108 cm ≈ (2.3 ± 0.5) RWD and ro = (6.08 ± 0.81) × 109 cm ≈ (15.0 ± 2.0) RWD.
3.4. Element abundances
Our disk models can be used to constrain the abundances of trace elements.
Hydrogen: from the absence of Balmer lines, we can obtain an upper limit of the H abundance. Figure 7 shows that Hα and Hβ become visible in our model near [H] = −6. The upper limit is estimated to be [H] < −5.
Carbon: the strongest C lines predicted by our models are C ii λ 4267 Å (Fig. 8) and λ 6580 Å. These lines are not seen in the observation and we conclude [C] < −2.
Nitrogen: Levitan et al. (2011) identified an emission feature at 8200 Å as due to N i λ 8212 Å. It is a multiplet in the quartet system with seven components in the range 8185−8242 Å that explains why no pure double-peaked profile is seen (Fig. 8). According to our models, a significant contribution from Mg ii λ 8228 Å can be excluded. Another N emission line in the quiescence model is near 7452 Å, namely the N i λλ 7424−7468 Å multiplet (Fig. 8). It can barely be seen in the observation. We finally infer [N] = −1.
Oxygen: the strongest O line in the model is the multiplet O i λλ 7772−7775 Å. The lack of the line in the observed spectrum leads to [O] < −2 (Fig. 8).
Magnesium: from the absence of the Mg i λλ 5167−5184 Å multiplet we conclude [Mg] < −1 (Fig. 8). We note that the emission feature observed around 5180 Å was attributed to Fe ii λλ 5169/5192 Å by Levitan et al. (2011, see below).
Silicon: an emission feature near 6360 Å was identified by Levitan et al. (2011) as the Si ii λλ 6347/6371 Å doublet (Fig. 8). It is the strongest Si line predicted by our models. We infer [Si] < −2.
 |
Fig. 5 Accretion-disk spectra with Teff = 6000 K at different inclination angles compared to the observation (black line). For clarification, the computed spectra are shifted vertically (from top to bottom: 0.000, −0.015, −0.030). |
 |
Fig. 6 Model spectra for accretion disks with different extensions, compared to the observation (black line). Shown are the changes of the inner edge (top left panel), the outer edge (right), and simultaneous changes (bottom) under i = 40 °. The given numbers correspond to the disk rings in Fig. 1. For clarification, the computed spectra are shifted vertically (from top to bottom; top panels: −0.03, −0.06, −0.09; bottom panel: + 0.05, 0.00, −0.05). |
Iron: Levitan et al. (2011) claimed the presence of Fe ii lines. The most significant is an emission feature near 5180 Å which was attributed to Fe ii λλ 5169/5192 Å. Our models exhibit a dense emission line curtain of Fe ii in the region 4500−5500 Å when [Fe] > −3, hampering the identification of individual lines (Fig. 9). However, it appears probable that the identification of the 5180 Å emission with Fe ii λ 5169 Å is correct while no Fe ii line at 5192 Å is in the model. To calculate the emerging spectrum, the Kurucz line lists (2009; POS lists, including lines with laboratory measured good wavelengths) were used to identify iron-group lines. And lines near that position have much lower gf-values (g is the statistical weight of the lower atomic level and f is the oscillator strength of the line transition) or much higher excitation energies. We also note the above mentioned possible blend with Mg ii λ 5180 Å. A more secure handle on the Fe abundance is offered by a strong and isolated Fe ii multiplet (λλ 6148−6248 Å) consisting of five lines with the two strongest components near 6148 Å and 6248 Å. There are two emission features at these positions in the observation, and their strengths are curtailed by the models with [Fe] = −2 and −3. Hence we adopt [Fe] = −2.5 (Fig. 9).
In summary, the investigated metals exhibit significantly subsolar abundances (Table 3). The abundances of N and Fe could be measured, while upper limits for C, O, Mg, and Si were determined. We estimate the errors to be on the order of 0.5 dex
Trace element abundances in PTF1 J0719+4858.
 |
Fig. 7 Accretion-disk spectra with increasing hydrogen abundance from bottom to top. For clarification, the computed spectra are shifted vertically (from top to bottom + 0.2, + 0.1, 0.0). |
 |
Fig. 8 Accretion-disk spectra with different chemical abundances. Shown are the changes for carbon (top left panel), magnesium (top right panel), silicon (middle left panel), oxygen (middle right panel), and nitrogen (bottom panels). |
 |
Fig. 9 Accretion-disk spectra with increasing iron abundance from bottom to top. |
3.5. Boundary layer
The boundary layer (BL) constitutes the link between the accretion disk and the WD. The material at the inner disk edge moves with Keplerian velocity around 3000 km s-1 and in contrast the surface of the WD moves at several 100 km s-1 (e.g., Sion et al. 2007). Within the BL, viscosity causes a decreasing velocity from the accreting material converting large amounts of kinetic energy into heat and radiation. With a considerably high mass-accretion rate (Ṁ > 10-10 M⊙ yr-1) during the outburst state, the BL becomes optically thick and reaches temperatures around several 100 000 K (Pringle 1977; Pringle & Savonije 1979). In contrast, with a low mass-accretion rate or during the transition from outburst to quiescence the BL becomes optically thin with temperatures around several 10 000 K (Regev & Hougerat 1988; Fisker & Balsara 2005).
We model the optically thin and relatively cold BL with one additional disk ring close to the surface of the WD (r = 1.1 RWD). We take the same mass and radius of the WD into account and assume the same chemical abundances (excluding Fe) for the BL. Thereby the intention is to generate a He ii λ 4686 Å emission line (without destroying the current results of the remaining He i emission lines) by determining suitable values for the effective temperature and the Reynolds number, respectively. This approach is presented in Fig. 11 which indicates that the generation of the He ii emission line can only be achieved with a high effective temperature (left panel) and a simultaneously low Reynolds number around 1000 (middle panel). The only possibility of influencing the width of the He ii emission line significantly is to change the orbital speed of the BL. Figure 11 (right panel) suggests that the BL rotates with (40 ± 20) % Kepler velocity (v = (0.4 ± 0.2) vkep).
We obtain the best fit to the He ii emission line with Teff = (20 000 ± 5000) K and Re = 4000 ± 2 000 for the additional disk ring representing the BL. The effects of the BL on other spectral lines and the general spectral behavior are presented in Fig. 10 and demonstrate that the BL provides a better match between observation and the accretion-disk model in general. In this regard, it should be remembered that irradiation by WD and BL are not considered. Using the BL we are able to confirm the existence of He ii λ 4200 Å and He ii λ 5412 Å (cf. Figs. 2 and 10). The He ii λ 4200 Å line identified by Levitan et al. (2011) has not been previously seen in an AM CVn system.
 |
Fig. 10 Accretion-disk spectra during quiescence. Shown are the differences between the model with BL (blue) and without BL (red). The red model spectrum is scaled to fit the observed continuum flux near 7000 Å. The same scaling factor is applied to the blue model. Spectra in zoom panels are scaled to the local observed continuum. |
4. Summary and discussion
We analyzed optical spectra of the AM CVn system PTF 09hpk with NLTE line-blanketed accretion-disk models. The main results can be summarized as follows.
-
The disk spectra are best reproduced assuming a massive (1.2 M⊙) WD primary and a mass-accretion rate during outburst of 10-9 M⊙ yr-1.
-
The quiescence spectrum can be matched with a disk model assuming a radially constant effective temperature of Teff = 6000 K, according to a nonstationary accretion rate in the disk varying radially between 0.074 × 10-12 M⊙ yr-1 and 41.5 × 10-12 M⊙ yr-1.
-
Simple modeling of the boundary layer as an additional, hot inner disk ring with Teff = 20 000 K can explain the appearance of the He ii λ 4686 Å emission feature during quiescence.
-
The disk is strongly hydrogen deficient (mass fraction <10-5 times solar).
-
The quantitative analysis of emission lines from N, Mg, and Fe in the quiescent disk spectrum reveals moderate to strong subsolar abundances ([N] = −1, [Mg] = −2, [Fe] = −2.5).
-
A similar conclusion is drawn from the absence of lines from C, O, and Si, resulting in upper abundance limits of [C] < −2, [O] < −2, [Si] < −2.
 |
Fig. 11 Accretion-disk spectra for different BL properties. Shown are the changes of Teff (left panel) and Reynolds number (middle) for the BL. The right panel illustrates the results with a different velocity deviating from the Keplerian velocity. |
4.1. Nature of the secondary
Three formation channels have been proposed for the formation of the ultracompact AM CVn binaries (e.g., Nelemans et al. 2010). They all result in secondaries with stripped H-envelopes, exhibiting He-rich material produced by CNO cycling, but with characteristic differences for the abundances of H as well as C, N, and O (see Nelemans et al. 2010, for details).
-
(i)
White dwarf channel. The donor is a very low-mass helium WD(M < 0.3 M⊙). The resulting abundance ratios among C, N, and O depend in detail on mass and metallicity of the progenitor.
-
(ii)
Helium star channel. The progenitor of the secondary was a He-core burning star. The abundance pattern depends on the duration of the initial post-common envelope phase, because subsequent Roche-lobe overflow starts when He-core burning is less or more advanced. Initial N enhancement by CNO cycling as well as later C and O enhancement by He burning occurs.
-
(iii)
Evolved main-sequence star channel. The progenitor was a H-core burning main sequence star. A rather narrow range of CNO abundance ratios is predicted; however, a wide range (2 dex) of possible residual H mass fractions (up to about 25%) is predicted.
Can we decide, through which channel PTF 09hpk evolved? Clearly, the tight upper limit that we were able to determine for the H abundance indicates that the secondary is either a helium WD or a former helium star. The lower limits for the N/C (>10) and N/O ratio (>10) indicate a donor star that has burned hydrogen via the CNO cycle and has not developed a subsequent helium-burning phase. This favors the WD channel, but the helium-star channel with an unevolved progenitor cannot be excluded.
A rather striking result is the general subsolar abundance of all examined metals, most notably of iron (−2.5 dex) but also of magnesium and silicon (−2 dex and < −2 dex, respectively). A similar result was found for the AM CVn star GP Com (Marsh et al. 1991). From the absence of lines of Si, Ca, and Fe, a depletion of at least 3 dex was derived. It has been argued that GP Com is a halo object with low primordial abundances. That would mean, however, that other investigated elements (N, O, and Ne) would be strongly overabundant. As a solution to this problem, it was suggested by Marsh et al. (1991) that these species were produced in the primary of GP Com and later transferred to and mixed with the secondary star during a common envelope stage. We may add that an extreme Si depletion (3 dex) was found in another AM CVn system (CE 315; Nagel et al. 2009), but instead, as in the case of GP Com, an oversolar N abundance was found (Ramsay et al. 2006)
Accordingly, PTF 09hpk could be a halo object. We speculate, however, that there might be another explanation for the low metallicity. In a recent investigation of the role of extremely low-mass (ELM, M < 0.2 M⊙) helium WDs for the orbital evolution of compact WD binaries, the effects of gravitational settling of metals were emphasized (Kaplan et al. 2012). It is argued that the long (~Gyr) life of the ELM WDs prior to Roche-lobe overflow may allow for complete sedimentation of heavier metals from the outermost layers. Therefore, the mass transferred will vary from nearly pure H to nearly pure He. Kaplan et al. (2012) suggest that the pronounced absence of heavy metals in the X-ray spectra of HM Cnc (Strohmayer 2008) points to an ELM origin that lived a long time before mass-transfer initiation.
Acknowledgments
We thank David Levitan for providing us with the observed spectrum of PTF 09hpk. Kim Gehron is supported by the German Astrophysical Virtual Observatory (GAVO) project of the German Federal Ministry of Education and Research (BMBF) under grant 05A11VTB, Thomas Rauch by the German Aerospace Center (DLR) under grant 050R1301. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France and of NASA’s Astrophysics Data System. The TIRO service (http://astro.uni-tuebingen.de/~TIRO) used to calculate opacities for this paper was constructed as part of the activities of GAVO.
References
- Amaro-Seoane, P., Aoudia, S., Babak, S., et al. 2013, GW Notes, 6, 4 [Google Scholar]
- Anderson, S. F., Becker, A. C., Haggard, D., et al. 2008, AJ, 135, 2108 [NASA ADS] [CrossRef] [Google Scholar]
- Arbutina, B. 2011, Serb. Astron. J., 183, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Augusteijn, T., van der Hooft, F., de Jong, J. A., & van Paradijs, J. 1996, A&A, 311, 889 [NASA ADS] [Google Scholar]
- Breedt, E., Gänsicke, B. T., Marsh, T. R., et al. 2012, MNRAS, 425, 2548 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, P. J., Marsh, T. R., Steeghs, D., et al. 2013, MNRAS, 429, 2143 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, P. J., Steeghs, D., Marsh, T. R., et al. 2014, MNRAS, 437, 2894 [NASA ADS] [CrossRef] [Google Scholar]
- Copperwheat, C. M., Marsh, T. R., Littlefair, S. P., et al. 2011, MNRAS, 410, 1113 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, A. J., Djorgovski, S. G., Mahabal, A. A., et al. 2012, ATel, 4678, 1 [NASA ADS] [Google Scholar]
- Fisker, J. L., & Balsara, D. S. 2005, ApJ, 635, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., Brassard, P., Green, E. M., et al. 2011, ApJ, 726, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Kaplan, D. L., Bildsten, L., & Steinfadt, J. D. R. 2012, ApJ, 758, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Kotko, I., Lasota, J.-P., Dubus, G., & Hameury, J.-M. 2012, A&A, 544, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. L. 2009, in AIP Conf. Ser. 1171, eds. I. Hubeny, J. M. Stone, K. MacGregor, & K. Werner, 43 [Google Scholar]
- Levitan, D., Fulton, B. J., Groot, P. J., et al. 2011, ApJ, 739, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Levitan, D., Kupfer, T., Groot, P. J., et al. 2013, MNRAS, 430, 996 [NASA ADS] [CrossRef] [Google Scholar]
- Littlefair, S. P., Dhillon, V. S., Marsh, T. R., et al. 2007, MNRAS, 381, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Littlefield, C., Garnavich, P., Applegate, A., et al. 2013, AJ, 145, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Marsh, R. T. 1999, in Astrophysical Discs an EC Summer School, eds. J. A. Sellwood, & J. Goodman, ASP Conf. Ser., 160, 3 [Google Scholar]
- Marsh, T. R., Horne, K., & Rosen, S. 1991, ApJ, 366, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Nagel, T., Dreizler, S., Rauch, T., & Werner, K. 2004, A&A, 428, 109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagel, T., Rauch, T., & Werner, K. 2009, A&A, 499, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelemans, G., Yungelson, L. R., van der Sluys, M. V., & Tout, C. A. 2010, MNRAS, 401, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Osaki, Y. 2005, Proc. Japan Academy, Ser. B, Phys. Biol. Sci., 81, 291 [Google Scholar]
- Osaki, Y., & Kato, T. 2013, PASJ, 65, 50 [NASA ADS] [Google Scholar]
- Pringle, J. E. 1977, MNRAS, 178, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E., & Savonije, G. J. 1979, MNRAS, 187, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsay, G., Groot, P. J., Marsh, T., et al. 2006, A&A, 457, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramsay, G., Barclay, T., Steeghs, D., et al. 2012, MNRAS, 419, 2836 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsay, G., Howell, S. B., Wood, M. A., et al. 2014, MNRAS, in press [arXiv:1311.4339] [Google Scholar]
- Rau, A., Roelofs, G. H. A., Groot, P. J., et al. 2010, ApJ, 708, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Rauch, T., & Deetjen, J. L. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 103 [Google Scholar]
- Regev, O., & Hougerat, A. A. 1988, MNRAS, 232, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Roelofs, G. H. A., Groot, P. J., Benedict, G. F., et al. 2007, ApJ, 666, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Roelofs, G. H. A., Rau, A., Marsh, T. R., et al. 2010, ApJ, 711, L138 [NASA ADS] [CrossRef] [Google Scholar]
- Sion, E. M., Godon, P., & Szkody, P. 2007, in The Seventh Pacific Rim Conference on Stellar Astrophysics, eds. Y. W. Kang, H.-W. Lee, K.-C. Leung, & K.-S. Cheng, ASP Conf. Ser., 362, 175 [Google Scholar]
- Smak, J. 1984, Acta Astron., 34, 161 [NASA ADS] [Google Scholar]
- Solheim, J.-E. 2010, PASP, 122, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Solheim, J.-E., & Yungelson, L. R. 2005, in 14th European Workshop on White Dwarfs, eds. D. Koester & S. Moehler, ASP Conf. Ser., 334, 387 [Google Scholar]
- Strohmayer, T. E. 2008, ApJ, 679, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Thorstensen, J. R., Fenton, W. H., Patterson, J. O., et al. 2002, ApJ, 567, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., & Han, Z. 2012, New A Rev., 56, 122 [Google Scholar]
- Warner, B. 2003, Cataclysmic Variable Stars, Cambridge Astrophysics (Cambridge University Press) [Google Scholar]
- Wood, J., Horne, K., Berriman, G., et al. 1986, MNRAS, 219, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, M. A., Winet, D. E., & van Horn, H. M. 1987, in Second Conference on Faint Blue Stars, eds. A. G. D. Philip, D. S. Hayes, & J. W. Liebert, IAU Colloq., 95, 639 [Google Scholar]
- Woudt, P. A., & Warner, B. 2011, ATel, 3705, 1 [NASA ADS] [Google Scholar]
- Woudt, P. A., Warner, B., de Budé, D., et al. 2012, MNRAS, 421, 2414 [NASA ADS] [CrossRef] [Google Scholar]
- Woudt, P. A., Warner, B., & Motsoaledi, M. 2013, ATel, 4726, 1 [NASA ADS] [Google Scholar]
All Tables
Statistics of the model atoms used in our cold accretion-disk models corresponding to the quiescence state.
All Figures
 |
Fig. 1 Properties of the disk rings corresponding to the accretion-disk model. We show the radial run of vertical extension of the disk from midplane h, effective temperature Teff, viscosity α, total Rosseland optical depth τtot, and surface density Σ. |
| In the text | |
 |
Fig. 2 Disk-ring spectra at r = 9.33 × 108 cm for the disk (blue) and at r = 4.47 × 108 cm for the boundary layer (red) with prominent lines identified (no rotational broadening). |
| In the text | |
 |
Fig. 3 Vertical structure of an inner disk ring (left panels) at radius r = 13.38 × 108 cm and an outer disk ring (right) at r = 40.56 × 108 cm during quiescence at different effective temperatures for the accretion disk. Shown are the temperature T (bottom panel), the density ρ (middle), and the Rosseland optical depth τross (top). |
| In the text | |
 |
Fig. 4 Accretion-disk spectra for a 1.2 M⊙ primary representing the disk under an inclination angle of i = 40 ° compared to the observation (black line). For clarification, the computed spectra are shifted vertically (from top to bottom: + 0.3, 0.0, −0.1). |
| In the text | |
 |
Fig. 5 Accretion-disk spectra with Teff = 6000 K at different inclination angles compared to the observation (black line). For clarification, the computed spectra are shifted vertically (from top to bottom: 0.000, −0.015, −0.030). |
| In the text | |
 |
Fig. 6 Model spectra for accretion disks with different extensions, compared to the observation (black line). Shown are the changes of the inner edge (top left panel), the outer edge (right), and simultaneous changes (bottom) under i = 40 °. The given numbers correspond to the disk rings in Fig. 1. For clarification, the computed spectra are shifted vertically (from top to bottom; top panels: −0.03, −0.06, −0.09; bottom panel: + 0.05, 0.00, −0.05). |
| In the text | |
 |
Fig. 7 Accretion-disk spectra with increasing hydrogen abundance from bottom to top. For clarification, the computed spectra are shifted vertically (from top to bottom + 0.2, + 0.1, 0.0). |
| In the text | |
 |
Fig. 8 Accretion-disk spectra with different chemical abundances. Shown are the changes for carbon (top left panel), magnesium (top right panel), silicon (middle left panel), oxygen (middle right panel), and nitrogen (bottom panels). |
| In the text | |
 |
Fig. 9 Accretion-disk spectra with increasing iron abundance from bottom to top. |
| In the text | |
 |
Fig. 10 Accretion-disk spectra during quiescence. Shown are the differences between the model with BL (blue) and without BL (red). The red model spectrum is scaled to fit the observed continuum flux near 7000 Å. The same scaling factor is applied to the blue model. Spectra in zoom panels are scaled to the local observed continuum. |
| In the text | |
 |
Fig. 11 Accretion-disk spectra for different BL properties. Shown are the changes of Teff (left panel) and Reynolds number (middle) for the BL. The right panel illustrates the results with a different velocity deviating from the Keplerian velocity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


