| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A139 | |
| Number of page(s) | 8 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201322569 | |
| Published online | 27 January 2014 | |
Modelling of the radio emission from the Vela supernova remnant
1 Centre for Space Research, North-West University, Potchefstroom Campus, 2531 Potchefstroom, South Africa
e-mail: iurii.sushch@nwu.ac.za
2 Astronomical Observatory of Ivan Franko National University of Lviv, 79005 Lviv, Ukraine
3 Humboldt Universität zu Berlin, Institut für Physik, 12489 Berlin, Germany
4 Astronomical Observatory of Taras Shevchenko National University of Kyiv, 04053 Kyiv, Ukraine
Received: 30 August 2013
Accepted: 28 November 2013
Supernova remnants (SNRs) are widely considered to be sites of Galactic cosmic ray (CR) acceleration. Vela is one of the Galactic composite SNRs closest to Earth accompanied by the Vela pulsar and its pulsar wind nebula (PWN) Vela X. The Vela SNR is one of the most studied remnants and it benefits from precise estimates of various physical parameters such as distance and age. Therefore, it is a perfect object for a detailed study of physical processes in SNRs. The Vela SNR expands into the highly inhomogeneous cloudy interstellar medium (ISM) and its dynamics are determined by the heating and evaporation of ISM clouds. It features an asymmetrical X-ray morphology, which is explained by the expansion into two media with different densities. This could occur if the progenitor of the Vela SNR exploded close to the edge of the stellar wind bubble of the nearby Wolf-Rayet star γ2 Velorum causing one part of the remnant to expand into the bubble. The interaction of the ejecta and the main shock of the remnant with ISM clouds causes formation of secondary shocks at which additional particle acceleration takes place. This may lead to the almost uniform distribution of relativistic particles inside the remnant. We calculate the synchrotron radio emission within the framework of the new hydrodynamical model that assumes the supernova explosion at the edge of the stellar wind bubble. The simulated radio emission agrees well with both the total radio flux from the remnant and the complicated radio morphology of the source.
Key words: ISM: supernova remnants / ISM: clouds / ISM: individual objects: Vela SNR
© ESO, 2014
1. Introduction
The Vela supernova remnant (SNR) is one of the most studied and closest SNRs to the Earth. The distance and the age of the Vela SNR have been determined accurately enough to make it a perfect object for the investigation of physical processes. Several estimates of the distance to the remnant exist (see Sushch et al. 2011, and references therein), the most reliable of which was determined from the VLBI parallax measurements of the Vela pulsar and is 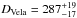 pc (Dodson et al. 2003). Equatorial coordinates (J2000 epoch) of the Vela pulsar, which is assumed to be situated in the geometrical centre of the remnant, are αVela = 08h35m20.66s and δVela = −45°10′35.2′′. The age of the Vela SNR is usually considered to be the characteristic age of the Vela pulsar (PSR B0833-45) which is about 1.1 × 104 years (Reichley et al. 1970). However, the characteristic age of the pulsar is estimated assuming that the pulsar spin-down braking index is equal to 3 (spin-down due to the magnetic dipole radiation) and that the initial rotational period is negligible in comparison to the current one (see e.g. Gaensler & Slane 2006). Lyne et al. (1996) estimated the braking index for the Vela pulsar to be very low, 1.4 ± 0.2, which may increase the estimate of the real age of the pulsar up to a factor of 5 compared to the characteristic age. Meanwhile, an age estimate can be also obtained from the Vela SNR dynamics. A shock velocity Vsh of the middle-aged adiabatic SNR depends on the shock radius Rsh and the age tage as Vsh = 0.4Rsh/tage. In the case of the Vela SNR, we know both Rsh ~ 20 pc (from the angular size and the distance to the Vela SNR) and Vsh ~ 660−1020 km s-1 (from the post-shock temperature of 0.5–1.2 keV of the X-ray emitting gas) (Aschenbach et al. 1995; Sushch et al. 2011), which results in the hydrodynamical age of tage = (0.7−1.2) × 104 yr, which is close to the characteristic age.
pc (Dodson et al. 2003). Equatorial coordinates (J2000 epoch) of the Vela pulsar, which is assumed to be situated in the geometrical centre of the remnant, are αVela = 08h35m20.66s and δVela = −45°10′35.2′′. The age of the Vela SNR is usually considered to be the characteristic age of the Vela pulsar (PSR B0833-45) which is about 1.1 × 104 years (Reichley et al. 1970). However, the characteristic age of the pulsar is estimated assuming that the pulsar spin-down braking index is equal to 3 (spin-down due to the magnetic dipole radiation) and that the initial rotational period is negligible in comparison to the current one (see e.g. Gaensler & Slane 2006). Lyne et al. (1996) estimated the braking index for the Vela pulsar to be very low, 1.4 ± 0.2, which may increase the estimate of the real age of the pulsar up to a factor of 5 compared to the characteristic age. Meanwhile, an age estimate can be also obtained from the Vela SNR dynamics. A shock velocity Vsh of the middle-aged adiabatic SNR depends on the shock radius Rsh and the age tage as Vsh = 0.4Rsh/tage. In the case of the Vela SNR, we know both Rsh ~ 20 pc (from the angular size and the distance to the Vela SNR) and Vsh ~ 660−1020 km s-1 (from the post-shock temperature of 0.5–1.2 keV of the X-ray emitting gas) (Aschenbach et al. 1995; Sushch et al. 2011), which results in the hydrodynamical age of tage = (0.7−1.2) × 104 yr, which is close to the characteristic age.
Early radio observations of the Vela constellation (Rishbeth 1958) revealed three localised regions of enhanced brightness temperature: Vela X, Vela Y, and Vela Z. Vela X is the most intense emission region which is believed to be a pulsar wind nebula (PWN) of the Vela pulsar (see e.g. Abramowski et al. 2012, and references therein). It was first interpreted as a PWN associated with the Vela pulsar by Weiler & Panagia (1980). Subsequent observations at 29.9, 34.5, and 408 MHz revealed one more region of intensified emission Vela W, which features two peaks and is weaker than Vela Y and Vela Z (Alvarez et al. 2001). The spectral shape of the Vela W radio emission is similar to the spectral shape of the radio emission from Vela Y and Vela Z which suggests the same nature of these localised emission regions (Alvarez et al. 2001).
The Vela SNR is one of the brightest sources on the X-ray sky. The X-ray emission appears to be dimmer, but more extended in the south-west (SW) part in comparison to the north-east (NE) part of the remnant (Aschenbach et al. 1995; Lu & Aschenbach 2000). The bulk of the X-ray emission is distributed all over the SNR without evidence of the main shock. Both features were recently explained in Sushch et al. (2011) within the assumption that the Vela SNR progenitor supernova exploded on the border of the stellar wind bubble (SWB) of the nearby Wolf-Rayet (WR) star in the binary system γ2 Velorum and that the remnant expands in a highly inhomogeneous, cloudy, interstellar medium (ISM). Indeed, exploding at the border of the SWB, the remnant would expand into two media with different densities, which in turn would cause a change of the X-ray luminosity and size from the NE part to the SW part of the remnant. If the remnant expands into the cloudy ISM with a high ratio of the clouds’ volume averaged number density to the intercloud number density, its dynamics and X-ray emission would be determined mostly by the matter initially concentrated in the clouds (White & Long 1991). Because of a two-component core-corona structure of clouds in the Vela SNR (Miceli et al. 2006), the heating and evaporation of clouds results in the two-component structure of the remnant’s interior. The hot evaporated gas component with the volume filling factor close to unity dominates the shock dynamics, while the cooler and denser component with the filling factor close to zero dominates the X-ray radiation from the remnant. The role of the initial intercloud ISM gas is negligible (Sushch et al. 2011).
The nearby WC8+O8-8.5III binary system γ2 Velorum contains the closest WR star to the Earth. There are several recent estimates of the distance to γ2 Velorum which are based on different measurements, but give similar results. Millour et al. (2007) provide an interferometric estimate of the distance of 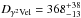 pc. Based on the orbital solution for the γ2 Velorum binary obtained from the interferometric data, North et al. (2007) calculated the distance at
pc. Based on the orbital solution for the γ2 Velorum binary obtained from the interferometric data, North et al. (2007) calculated the distance at 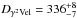 pc. Finally, the estimate of the distance based on Hipparcos parallax measurements is
pc. Finally, the estimate of the distance based on Hipparcos parallax measurements is 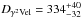 pc (van Leeuwen 2007), which has been used for calculations in this paper. Equatorial coordinates (J2000 epoch) of γ2 Velorum are αγ2Vel = 08h09m31.95s and δγ2Vel = −45°20′11.7′′ (van Leeuwen 2007).
pc (van Leeuwen 2007), which has been used for calculations in this paper. Equatorial coordinates (J2000 epoch) of γ2 Velorum are αγ2Vel = 08h09m31.95s and δγ2Vel = −45°20′11.7′′ (van Leeuwen 2007).
In this paper, we present a simulation of the radio synchrotron emission from the Vela SNR. The simulation was performed in the framework of the Sushch et al. (2011) model using estimates of physical parameters of the Vela SNR and its interior derived in that work (see Table 1). The nucleon number densities n, corresponding filling factors f, and the kinetic gas temperatures T are presented for both hot and cool components of the remnant’s interior. The simulated radio emission from the remnant is compared to the observational data presented in Alvarez et al. (2001).
The paper is structured as follows: in Sect. 2, the geometrical model of the Vela SNR−γ2 Velorum system is presented. In Sect. 3, the synchrotron radio emission from the spherical SNR with the uniform distribution of electrons is investigated, which is then applied to the Vela SNR in Sect. 4 assuming the Vela SNR to be a combination of two hemispheres with different radii. The morphology and the overall flux of the radio emission are discussed and compared to observational data. Finally, results are discussed in Sect. 5 and summarised in Sect. 6.
Physical parameters of the Vela SNR derived in Sushch et al. (2011).
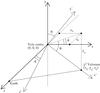 |
Fig. 1 Definition of coordinate systems K and K′. See text for explanation. |
 |
Fig. 2 Schematic illustration of the xy-projection of the Vela SNR in K′ (left) and K (right) coordinate systems. The direction towards the position of γ2 Velorum is shown with an arrow. |
2. Geometrical model
As shown in Sushch et al. (2011), if the radius of the stellar wind bubble (SWB) around γ2 Velorum is about 30–70 pc it should physically intersect with the Vela SNR which would cause the change of physical properties of the remnant in the part which expands into the SWB. It has been suggested that the progenitor supernova exploded on the border of the SWB which naturally explained the step-like change in properties from the NE to the SW part of the remnant. Expanding into media with different densities, the Vela SNR can be aproximated as a combination of two hemispheres, south-western (SW) and north-eastern (NE), with radii RSW = 23 pc and RNE = 18 pc, respectively (Sushch et al. 2011). However, in order to explain the complicated morphology of the source a detailed geometrical model of the system is required.
We define a coordinate frame K by its origin at the centre of the Vela SNR, the z-axis coinciding with the direction towards Earth, the y-axis tangent to a line of declination, and the x-axis tangent to a circle of right ascension of the celestial sphere with the radius r = DVela (Fig. 1). The xy-projection of the Vela SNR can be then easily converted into equatorial coordinates using coordinate transformations 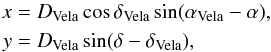 (1)assuming that (α − αVela) and (δ − δVela) are small.
(1)assuming that (α − αVela) and (δ − δVela) are small.
A K′ frame is defined, in turn, by its origin in the centre of the Vela SNR, with the x′-axis coinciding with the direction towards γ2 Velorum and the y′- and z′-axes defined in a way that the y′z′-plane separates NE and SW hemispheres of the Vela SNR (Fig. 2, left panel). The K′ frame can be transformed to the K frame by the rotation as 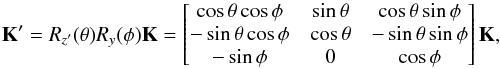 (2)where Rz′(θ) and Ry(φ) are rotation matrices for the rotation around the z′-axis through angle θ and around the y-axis through angle φ respectively. In Fig. 2, projections of the Vela SNR on the xy-plane in K′ and K coordinate systems are shown schematically. The xy-projection in the K coordinate system reflects how the remnant is seen on the sky by the observer. It can be transformed into the equatorial coordinate system using coordinate transformation equations (Eq. (1)).
(2)where Rz′(θ) and Ry(φ) are rotation matrices for the rotation around the z′-axis through angle θ and around the y-axis through angle φ respectively. In Fig. 2, projections of the Vela SNR on the xy-plane in K′ and K coordinate systems are shown schematically. The xy-projection in the K coordinate system reflects how the remnant is seen on the sky by the observer. It can be transformed into the equatorial coordinate system using coordinate transformation equations (Eq. (1)).
 |
Fig. 3 Distributions of rotation angles φ (left panel) and θ (central panel) obtained for the known estimates of distances to the Vela SNR and γ2 Velorum (see text for explanation). The mutual dependence of rotation angles is shown in the right panel. |
For given coordinates (x0,y0,z0) of γ2 Velorum in the K-frame, the rotation angles φ and θ can be estimated as 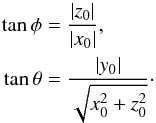 (3)In turn, x0, y0, and z0 can be calculated using the known distances and equatorial coordinates of the sources by transformation equations
(3)In turn, x0, y0, and z0 can be calculated using the known distances and equatorial coordinates of the sources by transformation equations 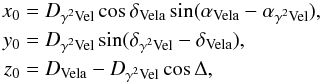 (4)where Δ is the angular distance between Vela and γ2 Velorum, which is given by
(4)where Δ is the angular distance between Vela and γ2 Velorum, which is given by 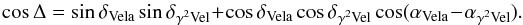 (5)Assuming that estimates of distances to the Vela SNR (
(5)Assuming that estimates of distances to the Vela SNR (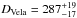 pc) and γ2 Velorum (
pc) and γ2 Velorum (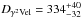 pc) follow asymmetric Gaussian distributions and that asymmetric errors correspond to standard deviations of the distribution, one can obtain distributions of the rotation angles φ and θ from Eqs. (3) and (4) by varying distance estimates. Angle distributions presented in Fig. 3 (left and middle panels) show the probability of the true angle φtrue/θtrue being in the range of angles (φ + δφ)/(θ + δθ). Each histogram contains 50 bins, i.e. δφ = 1.8° and δθ = 0.6°. By calculating the mode for each distribution the most probable values of rotation angles φ and θ can be estimated:
pc) follow asymmetric Gaussian distributions and that asymmetric errors correspond to standard deviations of the distribution, one can obtain distributions of the rotation angles φ and θ from Eqs. (3) and (4) by varying distance estimates. Angle distributions presented in Fig. 3 (left and middle panels) show the probability of the true angle φtrue/θtrue being in the range of angles (φ + δφ)/(θ + δθ). Each histogram contains 50 bins, i.e. δφ = 1.8° and δθ = 0.6°. By calculating the mode for each distribution the most probable values of rotation angles φ and θ can be estimated:  (6)The angles φ and θ are correlated and their mutual dependence is shown in the right panel in Fig. 3.
(6)The angles φ and θ are correlated and their mutual dependence is shown in the right panel in Fig. 3.
3. Radio emission from the spherical SNR with uniform electron distribution
The radio emission from the Vela SNR shows an indication of the brightening towards the centre which is not usually expected in shell-like SNRs, where electrons emitting synchrotron radiation are accelerated at the main shock and are concentrated close to the edge of the remnant. In the case of the Vela SNR, the radio luminosity grows towards the centre of the remnant featuring several localised maxima within the SNR. This morphology suggests a nearly uniform distribution of relativistic electrons inside the remnant. Possible reasons for such a distribution of electrons are discussed in Sect. 5. In this section and the following one we investigate the radio emission from the SNR with a uniform distribution of relativistic electrons and apply this model to the case of the Vela SNR, considering it to be a composition of two hemispheres with uniform distribution of relativistic electrons and magnetic fields in each of them.
We assume that the distribution of the relativistic electron density Ne(γ) with energies follows a power law 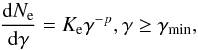 (7)where γ is the electron Lorentz factor, γmin is the minimal electron Lorentz factor, Ke is the normalization constant and p is the electron spectral index. Then the overall synchrotron flux density at frequency ν from the spherical SNR located at distance D can be calculated as (Rybicki & Lightman 1985)
(7)where γ is the electron Lorentz factor, γmin is the minimal electron Lorentz factor, Ke is the normalization constant and p is the electron spectral index. Then the overall synchrotron flux density at frequency ν from the spherical SNR located at distance D can be calculated as (Rybicki & Lightman 1985) 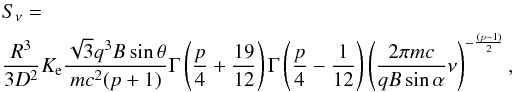 (8)where B is the magnetic field, R is the radius of the SNR, q is the electron charge, m is the electron mass, c is the speed of light, and α is the angle between the magnetic field and electron velocity. It is assumed that electron velocities are isotropically distributed and a root mean square value
(8)where B is the magnetic field, R is the radius of the SNR, q is the electron charge, m is the electron mass, c is the speed of light, and α is the angle between the magnetic field and electron velocity. It is assumed that electron velocities are isotropically distributed and a root mean square value 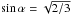 can be used.
can be used.
The flux density depends on three parameters, namely radius of the SNR R, magnetic field inside the SNR B, and constant Ke. If the distance to the remnant is known, the radius can be calculated directly from the angular size of the SNR.
The interior magnetic field is assumed to be determined mainly by shock-cloud interactions which result in vorticity and turbulence generation (see numerical calculations of shock-cloud interactions in Inoue et al. 2012, and references therein). It was shown in Inoue et al. (2012) that magnetic field amplification is determined by saturation at β = 8πPgas/B2 ~ 1 (the equilibrium condition of the magnetic pressure and the thermal pressure of particles Pgas). In the case of the Vela SNR, the evaporated cloud material with spatially nearly uniform thermal pressure fills up practically all the volume of the remnant, therefore the magnetic field will be uniform within the remnant and can be estimated as 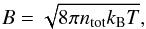 (9)where ntot = n/μ is the total number density of electrons and nuclei, n is the nucleon number density, μ = 16/27 is the molar mass, and T is the kinetic gas temperature inside the remnant.
(9)where ntot = n/μ is the total number density of electrons and nuclei, n is the nucleon number density, μ = 16/27 is the molar mass, and T is the kinetic gas temperature inside the remnant.
Finally, to calculate Ke one should know the total energy in relativistic electrons Ee and the size of the remnant. The total energy in electrons is given by the integration of the electron energy spectrum over all electron energies and over the volume of the remnant 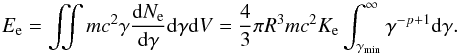 (10)Then parameter Ke can be expressed as
(10)Then parameter Ke can be expressed as 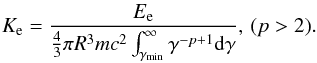 (11)
(11)
Physical parameters of the relativistic electron population inside the Vela SNR.
4. Radio emission from the Vela SNR
We assume that the explosion of the supernova was spherically symmetrical. In this scenario the energy transferred to relativistic electrons in the SW and NE parts of the remnant would be the same and equal to a half of the total energy in electrons Ee. Since the SW and NE parts of the remnant have different sizes, relativistic electron densities in these parts would be also different 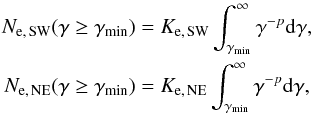 (12)where parameter Ke, SW/NE is dependent on the size of the hemisphere and can be estimated from Eq. (11) for RSW/NE. We assume that the minimal energy of electrons is γminmc2 = 100 MeV. The total energy in electrons Ee and the electron spectral index can be derived from the observational data as discussed below. Magnetic fields inside the remnant BNE/SW can be calculated using Eq. (9) and estimates of nucleon number density
(12)where parameter Ke, SW/NE is dependent on the size of the hemisphere and can be estimated from Eq. (11) for RSW/NE. We assume that the minimal energy of electrons is γminmc2 = 100 MeV. The total energy in electrons Ee and the electron spectral index can be derived from the observational data as discussed below. Magnetic fields inside the remnant BNE/SW can be calculated using Eq. (9) and estimates of nucleon number density  and kinetic temperature
and kinetic temperature 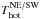 of the hot component (dominant across the remnant) listed in Table 1. In the NE part of the remnant the magnetic field is BNE = 46 μG, while in the SW part it is BSW = 30 μG.
of the hot component (dominant across the remnant) listed in Table 1. In the NE part of the remnant the magnetic field is BNE = 46 μG, while in the SW part it is BSW = 30 μG.
4.1. Integrated flux density
By fitting the model flux density (Eq. (8)) to the observational data one can calculate the total energy in electrons Ee and the electron spectral index p for the assumed minimal electron Lorentz factor γmin. Alvarez et al. (2001) provide the flux density from the whole remnant SXYZ and flux densities from localised emission regions SX, SY, and SZ from Vela X, Vela Y, and Vela Z, respectively (see Table 2 therein). The ratio of the integrated flux density SXYZ to the sum of components SX + SY + SZ shows appropriate self-consistency. Vela X is the PWN associated with the Vela pulsar and should not be taken into account for the study of the emission from the Vela SNR itself. Therefore, the flux density from the whole remnant SXYZ which includes the emission from the PWN Vela X cannot be used here. The emission from Vela Y and Vela Z comes mainly from the NE part of the remnant. Flux densities of Vela Y and Vela Z were summed up and the resulting cumulative flux density (Fig. 4) is assumed to be the flux density of the NE part of the Vela SNR. The model fit of the data (solid line in Fig. 4) results in the following values for the fitting parameters1 which corresponds to a fraction of the total explosion energy transferred to electrons of
which corresponds to a fraction of the total explosion energy transferred to electrons of 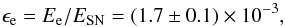 (15)which is close to the typical value expected for SNRs (see e.g. Katz & Waxman 2008; Gabici 2008). Flux densities at 29.9 MHz and 34.5 MHz were not fit since they show some indication of absorption (Alvarez et al. 2001). For the known p and Ee, the relativistic electron densities and parameters Ke for both NE and SW parts of the remnant can be calculated. They are presented in Table 2.
(15)which is close to the typical value expected for SNRs (see e.g. Katz & Waxman 2008; Gabici 2008). Flux densities at 29.9 MHz and 34.5 MHz were not fit since they show some indication of absorption (Alvarez et al. 2001). For the known p and Ee, the relativistic electron densities and parameters Ke for both NE and SW parts of the remnant can be calculated. They are presented in Table 2.
 |
Fig. 4 Sum of the integrated flux density spectra from Vela Y and Vela Z, presented in Alvarez et al. (2001). The straight line represents a model fit to the data. |
 |
Fig. 5 Simulated brightness temperature maps at 408 MHz in equatorial coordinates overlaid with galactic coordinates. Maps are calculated for ϵe = 1.7 × 10-3 (upper panels) and ϵe = 2.6 × 10-3 (lower panels). Two sets of rotation angles are considered: most probable values φ = 71.1°, θ = 9.3° (left panels) and values that best describe observational data φ = 35°, θ = 21° (right panels). The colour reflects the brightness temperature in K. The angular resolution of the modelled brightness temperature distributions is 4′. In each map white down- and up-pointing triangles denote peak locations of Vela Y an Vela Z, respectively; two white circles show locations of two peaks of Vela W; a white square denotes the position of the Vela X peak (Alvarez et al. 2001); and a cross reflects the location of γ2 Velorum. The bottom right map represents “the best-fit” scenario; it is overlaid with observed 408 MHz radio contours with 51′ angular resolution from Haslam et al. (1982). The contours represent the brightness temperature in K and the steps are 4 K from 40 K to 100 K, 10 K from 100 K to 150 K, and 25 K farther on; the contours of 60 and 100 K are shown with the bold lines. Unlike the map presented in Alvarez et al. (2001), here the galactic background is not removed, which explains the difference in values of the brightness temperature. Alvarez et al. (2001) adopted two background temperatures of 50 K and 60 K at 408 MHz. Besides Vela X in the centre, additional prominent sources (RCW 38 (α = 08h59m,δ = −47°32′) and Puppis A (α = 08h23m,δ = −42°42′)) and weaker compact sources (RCW 36, RCW 33, and RCW 27, clockwise along the NE-north surface) are visible. |
4.2. Morphology
The brightness temperature map of the Vela SNR at 408 MHz in equatorial coordinates was simulated using the geometrical model presented in Sect. 2. The emission was modelled in 3D in the K′ coordinate system, treating every unit volume as a separate emitter. Then the 3D-model of the remnant was converted to the K coordinate system and projected onto the xy-plane. Finally, the xy-plane was converted to the equatorial coordinates as described in Sect. 2.
Primarily, the simulation was performed using estimates of the physical parameters of the electron population obtained from the fit of the observed radio spectrum (see the subsection above) and the mode values φ0 and θ0 of rotation angles φ and θ. In the top left panel in Fig. 5 the simulated temperature brightness map for these values is shown. The colour corresponds to the brightness temperature in K. The brightness temperature distribution is determined by the integration of the radio emission along the line of sight. The radio emission is stronger in the NE hemisphere of the remnant because of the higher density of relativistic electrons and stronger magnetic field. The emission would peak in the centre of the remnant in the two limiting cases, namely, when the centre of the Vela SNR and γ2 Velorum are located on the same line of sight, i.e. φ = 90° and θ = 0°, and in the case when the Vela SNR centre−γ2 Velorum symmetry axis is perpendicular to the line of sight, i.e. the Vela SNR and γ2 Velorum are located at the same distance and φ = 0°. In the intermediate case 0 < φ < 90°, the peak of the brightness temperature is shifted to the NE part of the remnant, as shown in Fig. 5 (top left panel) for the case of the most probable values of φ = 71.1° and θ = 9.3°.
For φ ≤ 40°, a second, considerably fainter peak appears in the SW part of the remnant. It is not seen for φ > 40° because of the overlapping effect, which causes the contamination of the SW part of the remnant by the radio emission from the NE hemisphere. Remarkably, these two theoretically predicted peaks correspond to the observed morphology of the brightness temperature distribution in the Vela SNR; i.e. they correspond to the existence of “hot spots” in both parts of the remnant: two close localised regions of Vela Y and Vela Z in the NE, and two peaks of Vela W in the SW. The peaks of the emission regions Vela Y and Vela Z are shown as down- and up-pointing triangles, respectively, and the peaks of the Vela W region are shown as filled circles in each map in Fig. 5. For another combination of angles φ = 35° and θ = 21°, which is also compatible with estimates for the distances to the Vela SNR and γ2 Velorum, the positions of the simulated brightness temperature peaks coincide with the observed localised regions (Fig. 5, top right), suggesting that the complicated morphology of the Vela SNR might be a result of superimposed emission in the system with a specific spatial orientation.
Modelled peak brightness temperatures on the top right panel in Fig. 5 are slightly lower than the observed brightness temperatures of the Vela Y, Vela Z, and Vela W peaks. As reported by Alvarez et al. (2001), the brightness temperature of the Vela Y and Vela Z peaks is about 90 K and the brightness temperature of Vela W peaks is 35−40 K, while on the simulated map peak temperatures are ~50 K and ~15 K, respectively. This difference is expected given that the observed cumulative Vela Y and Vela Z flux density at 408 MHz is 1.5 times higher than the model fit to the data at this frequency (Fig. 4). Therefore, in order to be able to accurately compare the simulated and observed brightness temperature distributions one has to derive the total energy in electrons directly from the observed flux density at 408 MHz. The spectral index is assumed to be p = 2.47 as obtained in a fit. The derived physical parameters of the electron population are presented in Table 2. Using these new estimates, we simulate the brightness temperature distribution for the two sets of φ and θ discussed above (Fig. 5, bottom left and bottom right panels). In this case, the simulated peak brightness temperatures for the combination of angles φ = 35° and θ = 21° (Fig. 5, bottom right) are in a good agreement with the observational results. The brightness temperature of the NE peak is about 80 K and the brightness temperature of the SW peak is about 25 K. This consistency with the observational data is another confirmation of the validity of our model.
5. Discussion
5.1. Uniform distribution of relativistic electrons
A typical middle-aged SNR in the adiabatic stage of evolution is a powerful source of both thermal X-ray and nonthermal synchrotron radio emission. A strong shock wave compresses and heats the interstellar gas up to keV temperatures creating a shell-like X-ray morphology due to the concentration of the shocked plasma downstream of the shock front. At the same time the shock wave accelerates charged particles, electrons, protons, and nuclei, to ultrarelativistic energies via the diffusive shock acceleration mechanism. Since both the magnetic field and relativistic electrons are also concentrated downstream of the shock front, the radio-brightness distribution of the SNR would also feature a shell-like morphology.
Although the Vela SNR is in the adiabatic stage of evolution it does not show the usual behaviour of so-called Sedov SNRs2 as described above. Its dynamics are mainly determined by the interaction of the SN ejecta with numerous clouds with a volume averaged density considerably higher than the density of the intercloud ISM (Sushch et al. 2011, and references therein). While in the adiabatic Sedov SNR, the hot postshock plasma is the swept-up and heated ISM gas; in the Vela SNR the hot postshock plasma is predominantly the heated and evaporated cloud gas. This difference has a prominent role in the postshock distribution of relativistic electrons. Because of the low ISM density the transfer of the SN explosion energy into the ISM (and, in turn, into the cosmic ray acceleration) is small while the main channel of the ejecta kinetic energy dissipation is the interaction with clouds through the heating and evaporation of the cloud gas.
Primarily, the dominant process that takes place in the Vela SNR is the interaction between the ejecta and clouds with the generation of the transmitted shock in the cloud and the reflected shock in the ejecta. Because of the large cloud/intercloud ISM density contrast for the expected Vela SN ejecta mass of Mej ~ 10 M⊙ (Limongi & Chieffi 2006) and velocity of 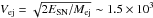 km s-1, the main dissipation of the kinetic energy of the ejecta takes place at reverse shocks generated in the ejecta–clouds interaction. Because of the low temperature of the ejecta plasma (zero pressure in the analytical treatment of Truelove & McKee 1999 and Tej ~ 104 K in numerical simulations of Moriya et al. 2013), the sonic Mach number should be high (up to 100–150 for Tej ~ 104 K) and, thus, the reverse shock will be a region of effective CR (including relativistic electrons) acceleration. It is more complicated to estimate parameters of the transmitted shocks, where the transmitted shock velocity depends on the ejecta and cloud densities
km s-1, the main dissipation of the kinetic energy of the ejecta takes place at reverse shocks generated in the ejecta–clouds interaction. Because of the low temperature of the ejecta plasma (zero pressure in the analytical treatment of Truelove & McKee 1999 and Tej ~ 104 K in numerical simulations of Moriya et al. 2013), the sonic Mach number should be high (up to 100–150 for Tej ~ 104 K) and, thus, the reverse shock will be a region of effective CR (including relativistic electrons) acceleration. It is more complicated to estimate parameters of the transmitted shocks, where the transmitted shock velocity depends on the ejecta and cloud densities 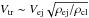 . For the expected cloud radius rcl ~ 0.05 pc and the number densities
. For the expected cloud radius rcl ~ 0.05 pc and the number densities 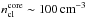 and
and 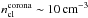 in the two-component approximation in which the cloud consists of a dense core and a corona around the core (Miceli et al. 2006), at the initial phase of the ejecta-cloud interaction the velocity of the transmitted shock should be high enough for the effective particle acceleration, but it will decrease with the distance from the point of the SN explosion because of the decrease in the ejecta density.
in the two-component approximation in which the cloud consists of a dense core and a corona around the core (Miceli et al. 2006), at the initial phase of the ejecta-cloud interaction the velocity of the transmitted shock should be high enough for the effective particle acceleration, but it will decrease with the distance from the point of the SN explosion because of the decrease in the ejecta density.
With time, the main shock will form. The downstream gas will be dominated by the evaporated plasma with a contribution of the ejecta plasma reheated by the reverse shock. The contribution of the shocked intercloud plasma is negliglible. Hot postshock plasma will additionally heat and destroy clouds by thermal conductivity and will generate transmitting shocks.
The total mass of the ejecta and evaporated clouds inside the Vela SNR is about 30 M⊙ (see Table 1), i.e. the mass of evaporated clouds is only about twice the ejecta mass Mej ~ 10 M⊙, suggesting that the direct ejecta-cloud interaction was effective and, in turn, that effective acceleration of relativistic electrons at strong reverse shocks took place. The almost uniform distribution of clouds in the ISM leads to a uniform system of strong reverse shocks and, thus, to a nearly uniform distribution of relativistic electrons inside the Vela SNR. The almost uniform distribution of the relativistic electrons inside the Vela SNR remains with time because of the strong turbulent magnetic field (see Sect. 3) that restrains the diffusion from the acceleration region. At the same time, the large magnetic field of the Vela SNR (about 50 μG) does not modify the energy spectrum of relativistic electrons radiated in the range of 30–2700 MHz. The characteristic frequency of a photon emitted by an electron with energy ϵe is given by (Rybicki & Lightman 1985) ![\begin{equation} \nu_{\mathrm{ch}} = 0.29 \frac{3q\sin{\alpha}}{4\pi m^{3}c^{5}} \epsilon_{\mathrm{e}}^{2} B \simeq 190 \left[\frac{\epsilon_{\mathrm{e}}}{1\,\mathrm{GeV}}\right]^2 \left[\frac{B}{50~\mu\mathrm{G}}\right] \mathrm{[MHz]}; \end{equation}](/articles/aa/full_html/2014/01/aa22569-13/aa22569-13-eq168.png) (16)in other words, to emit a 2700 MHz photon an electron with energy ϵe,2700 ~ 3.8 GeV is needed. The cooling time for synchrotron radiation of such an electron is (Blumenthal & Gould 1970)
(16)in other words, to emit a 2700 MHz photon an electron with energy ϵe,2700 ~ 3.8 GeV is needed. The cooling time for synchrotron radiation of such an electron is (Blumenthal & Gould 1970) ![\begin{equation} t_{\mathrm{syn}} = 1.3\times10^{6} \left[\frac{\epsilon_{\mathrm{e}}}{4\,\mathrm{GeV}}\right]^{-1} \left[\frac{B}{50~\mu\mathrm{G}}\right]^{-2} \mathrm{[y]}. \end{equation}](/articles/aa/full_html/2014/01/aa22569-13/aa22569-13-eq170.png) (17)This time is much longer than the estimate of the age of the Vela SNR (regardless of the uncertainty that occurs due to the low braking index of the pulsar), suggesting that electrons can indeed survive over the time inside the remnant emitting synchrotron radiation.
(17)This time is much longer than the estimate of the age of the Vela SNR (regardless of the uncertainty that occurs due to the low braking index of the pulsar), suggesting that electrons can indeed survive over the time inside the remnant emitting synchrotron radiation.
5.2. Local discrepancies of the modelled and observed morphology
The modelled brightness temperature map of the Vela SNR predicts two local elongated peaks, one in the NE part of the remnant and one in the SW part of the remnant. Observations show that there are two localised peaks in each part of the remnant, but the identical brightness temperatures of the two NE peaks, Vela Y and Vela Z, and the two SW peaks, Vela W, suggest that physically the two observed peaks in each part of the remnant have the same nature and are two parts of the same peak which could be split because of some deviations from our idealised symmetric model. Another small discrepancy between the modelled and observed morphologies is that the peaks of Vela W are slightly offset from the modelled peak in the SW part of the remnant. One of the most natural reasons for these discrepancies is that the initial distribution of clouds and, thus, relativistic electrons does not necessarily have to be uniform.
Both discrepancies can also be naturally explained by the existence of the PWN Vela X inside the remnant. The peak of the radio emission from Vela X, as reported by Alvarez et al. (2001), is indicated with a filled square in all maps in Fig. 5. The expansion of the PWN can change the distribution of the internal gas and the cloud matter inside the Vela SNR “pushing” them to the outer regions of the remnant. This, in turn, would change the distribution of relativistic electrons responsible for the synchrotron radiation if they are accelerated at local shocks generated in clouds. However, the evolution and expansion of Vela X is not yet well understood. The PWN features different morphologies at different wavebands. At radio and GeV energies an extended (2° × 3°) “halo” emission is observed featuring a “two-wing” structure (Grondin et al. 2013), which is located mostly to the south of the Vela pulsar (as seen in the equatorial coordinates). While the X-ray observations by ROSAT revealed a much smaller (45′ × 12′) emission region (“cocoon”) (Markwardt & Ögelman 1995). Subsequent high-resolution X-ray observations with Chandra revealed a structure of the X-ray emission to be a composition of two toroidal arcs (17′′ and 30′′ away from the pulsar) and a 4′-long collimated jet (Helfand et al. 2001). Finally, in the TeV range, emission spatially coincident with both halo and cocoon is detected (Aharonian et al. 2006; Abramowski et al. 2012). According to the morphology of the halo emission from Vela X, the interaction of the PWN with the internal medium of the remnant is expected to provide a more important effect on the SW hemisphere of the remnant since the main part of the PWN is located there. Expanding towards the position of the Vela W peaks, the PWN may cause an increase in the electron density and, thus, the enhancement of the synchrotron emission in that region.
Another effect, which may be responsible for the distribution of electrons inside the remnant is the propagation of the reverse shock inside the remnant. It is argued in the literature that the reverse shock of the SNR may be the reason of the asymmetrical structure of Vela X with respect to the pulsar position (Blondin et al. 2001). Because of the difference in the properties of the ambient medium on the NE and SW sides of the remnant, it is possible that the reversed shock was formed earlier in the NE part of the SNR and reached the PWN Vela X suppressing it, while in the SW part of the remnant, interaction of the PWN with the reverse shock has not yet been established (Blondin et al. 2001). If this is the case, then the reverse shock should also influence the distribution of electrons and the intensity of the emission.
6. Summary
The radio emission from the Vela SNR was simulated in the framework of the hydrodynamical model presented in Sushch et al. (2011). This model is based on two hypotheses:
-
the progenitor of the Vela SNR exploded at theborder of the stellar wind bubble of the nearby binary systemγ2 Velorum which causes theremnant to expand into two media with different densities,
-
the remnant expands into the inhomogeneous medium in which the main bulk of mass is concentrated in small clouds.
Originally the model was elaborated to explain a peculiar X-ray emission from the source. In this paper, we have shown that the observed radio flux from the remnant can also be well explained within this model giving it further observational support.
It was shown that the complicated radio morphology that features several localised emission regions can be explained by the relative positioning of the Vela SNR and γ2 Velorum, assuming that relativistic electrons responsible for the synchrotron radio emission are distributed uniformly inside the remnant. The expected observed image of the Vela SNR depends on how these two objects are positioned relative to each other. We show that for rotation angles φ = 35° and θ = 21° the expected brightness temperature map of the remnant would feature two peaks in
the NE and SW parts of the remnant, which are coincident with the observed localised emission regions Vela Y, Vela Z, and Vela W. The simulated brightness temperatures of the peaks are in good agreement with the observed brightness temperatures in local emission regions.
We also argue that the PWN Vela X located inside the remnant, which was not taken into account in this study, may play a notable role in the distribution of relativistic electrons within the remnant and, thus, in the morphology of the radio emission of the Vela Y, Vela Z, and Vela W regions. The detailed model of the Vela X contribution to the radio emission of Vela SNR will be considered elsewhere.
The evolution of the typical SNR at the adiabatic stage in the homogeneous ISM can be described by the Sedov solution (Sedov 1959) for a point explosion.
Acknowledgments
We would like to thank the referee, Richard Strom, for many useful comments and suggestions, which appreciably improved the paper.
References
- Abramowski, A., Acero, F., Aharonian, F., et al. 2012, A&A, 548, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, A&A, 448, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alvarez, H., Aparici, J., May, J., & Reich, P. 2001, A&A, 372, 636 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aschenbach, B., Egger, R., & Trümper, J. 1995, Nature, 373, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, J. M., Chevalier, R. A., & Frierson, D. M. 2001, ApJ, 563, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Dodson, R., Legge, D., Reynolds, J. E., & McCulloch, P. M. 2003, ApJ, 596, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Gabici, S. 2008 [arXiv:0811.0836] [Google Scholar]
- Gaensler, B. M., & Slane, P. O. 2006, ARA&A, 44, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Grondin, M.-H., Romani, R. W., Lemoine-Goumard, M., et al. 2013, ApJ, 774, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Haslam, C. G. T., Salter, C. J., Stoffel, H., & Wilson, W. E. 1982, A&AS, 47, 1 [NASA ADS] [Google Scholar]
- Helfand, D. J., Gotthelf, E. V., & Halpern, J. P. 2001, ApJ, 556, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, T., Yamazaki, R., Inutsuka, S.-i., & Fukui, Y. 2012, ApJ, 744, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, B., & Waxman, E. 2008, JCAP, 1, 18 [Google Scholar]
- Limongi, M., & Chieffi, A. 2006, ApJ, 647, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, F. J., & Aschenbach, B. 2000, A&A, 362, 1083 [NASA ADS] [Google Scholar]
- Lyne, A. G., Pritchard, R. S., Graham-Smith, F., & Camilo, F. 1996, Nature, 381, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B., & Ögelman, H. 1995, Nature, 375, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Miceli, M., Reale, F., Orlando, S., & Bocchino, F. 2006, A&A, 458, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Millour, F., Petrov, R. G., Chesneau, O., et al. 2007, A&A, 464, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moriya, T. J., Blinnikov, S. I., Tominaga, N., et al. 2013, MNRAS, 428, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- North, J. R., Tuthill, P. G., Tango, W. J., & Davis, J. 2007, MNRAS, 377, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Reichley, P. E., Downs, G. S., & Morris, G. A. 1970, ApJ, 159, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Rishbeth, H. 1958, Aust. J. Phys., 11, 550 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1985, Radiative processes in astrophysics (John Wiley & Sons) [Google Scholar]
- Sedov, L. I. 1959, Similarity and Dimensional Methods in Mechanics (New York: Academic Press) [Google Scholar]
- Sushch, I., Hnatyk, B., & Neronov, A. 2011, A&A, 525, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Truelove, J. K., & McKee, C. F. 1999, ApJS, 120, 299 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, Hipparcos, the New Reduction of the Raw Data, Astrophys. Space Sci. Lib., 350, [Google Scholar]
- Weiler, K. W., & Panagia, N. 1980, A&A, 90, 269 [NASA ADS] [Google Scholar]
- White, R. L., & Long, K. S. 1991, ApJ, 373, 543 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Definition of coordinate systems K and K′. See text for explanation. |
| In the text | |
 |
Fig. 2 Schematic illustration of the xy-projection of the Vela SNR in K′ (left) and K (right) coordinate systems. The direction towards the position of γ2 Velorum is shown with an arrow. |
| In the text | |
 |
Fig. 3 Distributions of rotation angles φ (left panel) and θ (central panel) obtained for the known estimates of distances to the Vela SNR and γ2 Velorum (see text for explanation). The mutual dependence of rotation angles is shown in the right panel. |
| In the text | |
 |
Fig. 4 Sum of the integrated flux density spectra from Vela Y and Vela Z, presented in Alvarez et al. (2001). The straight line represents a model fit to the data. |
| In the text | |
 |
Fig. 5 Simulated brightness temperature maps at 408 MHz in equatorial coordinates overlaid with galactic coordinates. Maps are calculated for ϵe = 1.7 × 10-3 (upper panels) and ϵe = 2.6 × 10-3 (lower panels). Two sets of rotation angles are considered: most probable values φ = 71.1°, θ = 9.3° (left panels) and values that best describe observational data φ = 35°, θ = 21° (right panels). The colour reflects the brightness temperature in K. The angular resolution of the modelled brightness temperature distributions is 4′. In each map white down- and up-pointing triangles denote peak locations of Vela Y an Vela Z, respectively; two white circles show locations of two peaks of Vela W; a white square denotes the position of the Vela X peak (Alvarez et al. 2001); and a cross reflects the location of γ2 Velorum. The bottom right map represents “the best-fit” scenario; it is overlaid with observed 408 MHz radio contours with 51′ angular resolution from Haslam et al. (1982). The contours represent the brightness temperature in K and the steps are 4 K from 40 K to 100 K, 10 K from 100 K to 150 K, and 25 K farther on; the contours of 60 and 100 K are shown with the bold lines. Unlike the map presented in Alvarez et al. (2001), here the galactic background is not removed, which explains the difference in values of the brightness temperature. Alvarez et al. (2001) adopted two background temperatures of 50 K and 60 K at 408 MHz. Besides Vela X in the centre, additional prominent sources (RCW 38 (α = 08h59m,δ = −47°32′) and Puppis A (α = 08h23m,δ = −42°42′)) and weaker compact sources (RCW 36, RCW 33, and RCW 27, clockwise along the NE-north surface) are visible. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


