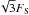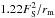| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A144 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321836 | |
| Published online | 27 January 2014 | |
An exploration of Pluto’s environment through stellar occultations
1 LESIA-Observatoire de Paris, CNRS, Univ. Pierre et Marie Curie, Univ. Paris-Diderot, 92190 Meudon, France
e-mail: francoise.roques@obspm.fr
2 Department of Astronomy, New Mexico State University, PO Box 30001, MSC 4500, Las Cruces NM 88003-8001, USA
3 European Southern Observatory, Alonso de Córdova 3107, Vitacura, 19001 Casilla, Santiago 19, Chile
4 Max-Planck-Institut für extraterrestrische Physik, Postfach 1312, 85741 Garching, Germany
5 Université de Franche-Comté, Institut UTINAM, CNRS/INSU, UMR 6213, 25030 Besançon Cedex, France
6 Department of Physics and Astronomy, University of Sheffield, Sheffield S3 7RH, UK
7 Department of Physics, University of Warwick, Coventry CV4 7AL, UK
8 Observatório do Valongo/UFRJ, Ladeira Pedro Antonio 43, CEP 20. 080-090 Rio de Janeiro RJ, Brazil
9 Observatório Nacional/MCTI, R. General José Cristino 77, CEP 20921-400 Rio de Janeiro RJ, Brazil
10 Centro Universitário Estadual da Zona Oeste, Av. Manual Caldeira de Alvarenga 1203, CEP 23. 070-200 Rio de Janeiro RJ, Brazil
11 Observatoire de Genève, 1290 Sauverny, Switzerland
12 International Occultation Timing Association, European Section, 30459 Hannover, Germany
Received: 5 May 2013
Accepted: 3 December 2013
Context. Pluto has five known satellites with diameters ranging from ~1200 km down to ~40 km, a possible outcome of a collisional origin. Smaller objects probably exist and may maintain tenuous rings, thus representing hazards during the New Horizons flyby of July 2015.
Aims. The goal is to provide an upper limit for the numbers of unseen small bodies and/or equivalent widths of putative Pluto rings.
Methods. We use a Pluto stellar appulse on April 10, 2006, and a stellar occultation by the dwarf planet on June 14, 2007, to scan Pluto’s surroundings.
Results. Our best data set places a 3σ upper limit of 0.3 km for the radius of isolated moonlets that we can detect. In the absence of detection, we derive an upper limit of 15 000 for the number of such bodies at distances smaller than ~70 000 km from Pluto’s system barycenter. We place a 3σ upper limit of typically 30−100 m for the equivalent width of ring material at barycentric distances ranging from 13 000 to 70 000 km. This limit applies for narrow rings only, i.e. less than about 10 km in width.
Key words: Kuiper belt: general / occultations
© ESO, 2014
1. Introduction
The dwarf planet Pluto is surrounded by a large satellite about half its size, Charon, discovered from the ground in 1978 (Christy & Harrington 1978). Two smaller satellites, Nix and Hydra, were discovered with the Hubble Space Telescope (HST) in 2005 (Weaver et al. 2006; Buie et al. 2006), with diameters roughly estimated to be 100 km or less (Tholen et al. 2008). HST observations revealed a fourth satellite, S/2011 (134340) 1 (P4 for short), orbiting between Nix and Hydra (Showalter et al. 2011). A fifth satellite was detected inside Nix’ orbit, S/g12 (134340) 1 (P5 for short), see Showalter et al. (2012). Both P4 and P5 have diameters of less than 40 km. Subsequent studies provided orbital elements and mass estimates for Charon, Nix and Hydra (Tholen et al. 2008; Buie et al. 2013). Occultation observations have provided Charon’s radius at kilometric accuracy (Gulbis et al. 2006; Sicardy et al. 2006b; Person et al. 2006), as well as constraints on Charon’s orbital elements (Sicardy et al. 2011).
Observations circumstances.
Dynamical studies showed that stable additional satellites may exist around Pluto at specific regions of the phase space (Nagy et al. 2006; Giuliatti Winter et al. 2010; Pires Dos Santos et al. 2011; Giuliatti Winter et al. 2013), in particular between Nix and Hydra’s orbits, as confirmed by the detection of P4, and inside Nix’ orbit as confirmed by the detection of P5. It has also been suggested that collisions between Pluto’s small satellites may have led to the formation of debris rings around the planet (Durda & Stern 2000; Steffl et al. 2006). Observationally, searches for additional satellites of Pluto were conducted with deep HST exposures (Steffl et al. 2006). This led to a negative detection at a 90% confidence level up to magnitudes ranging from mV = 24 to 26.8, depending on Plutocentric distances. Moreover, search for rings in HST images by Steffl & Stern (2007) did not reveal material with I/F (standard measurement of reflectance for planetary rings, with I the observed intensity and πF, the incident solar flux) larger than ~5 × 10-7 (3σ limit) at more than 42 000 km from the Pluto-Charon barycenter, i.e. outside the minimum distance where dynamically stable rings are expected, see Nagy et al. (2006) and details below.
Here we report results obtained with a different method, which is based on the use of high signal-to-noise stellar appulses or occultations from the ground. During such observations, the observed star provides a high resolution (km-level) scan of Pluto’s surroundings, as shown by preliminary results and analysis by Boissel (2010).
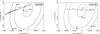 |
Fig. 1 Left: geometry of the April 10, 2006 Pluto stellar appulse. The stellar tracks as seen from VLT (Paranal) and NTT, 2p2 telescopes (La Silla) are shown relative to the Pluto-Charon barycenter (the cross at origin). The quantity f (resp. g) on the horizontal (resp. vertical) axis is the offset relative to the Pluto-Charon barycenter in the plane of the sky, counted positively toward the local celestial J2000 east (resp. north). The arrow indicates the direction of stellar motion. Note the interruptions in the observations (Table 1). Pluto’s body is shown as a circle next to the cross, and the satellites positions are shown at 6:00 UT, the approximate mid-time of observations. A close-up view of the stellar tracks as seen from VLT, NTT and 2p2 are shown in Fig. 2. Right: geometry of the June 14, 2007 Pluto occultation, as seen from the LNA160 telescope. Symbols are the same as for the left panel. The satellites are shown at 01:30 UT, the approximate mid-time of observations. All the satellite positions are derived from the orbital solution of Tholen et al. (2008). |
 |
Fig. 2 Close-up view of left panel of Fig. 1, showing the stellar tracks observed from VLT (black), NTT (red) and 2p2 (blue) telescopes. Note the interruptions in the observations (Table 1). |
2. Observations
2.1. Circumstances
We used two events involving Pluto to search for rings and/or small satellites around the dwarf planet. The first event was a stellar approach, or appulse, with no occultation involved. It was observed on April 10, 2006 from the European Southern Observatory (ESO) facilities in Chile. The second event, on June 14, 2007, was a stellar occultation that was detected from Chile, Brazil and Namibia. The choice of these two particular events, among those we have observed since 2002, stems from the high signal-to-noise ratio (S/N) of the data, and from the fact that a significant region around Pluto was scanned during those events (see Figs. 1 and 2). For the 2006 appulse, we used three telescopes in Chile: one at Paranal, the ESO Very Large Telescope (VLT) Yepun equipped with the NACO adaptive optics camera (Lenzen et al. 2003; Rousset et al. 2003), and two at La Silla, the New Technology Telescope (NTT) equipped with the SOFI infrared camera (Moorwood et al. 1998), and the 2.2 m (2p2) telescope equipped with its guiding camera. Concerning the 2007 occultation, three observing sites were used: Paranal (VLT) in Chile, Pico dos Dias Observatory (Laboratório Nacional de Astrofísica, LNA) in Brazil, and the Hakos Internationale Amateursternwarte (IAS) observatory in Namibia. However, for this event, only the light curve obtained with the largest telescope of LNA has sufficient S/N to search for ring or satellite, the other instruments being hampered by cloud passages or too small telescope diameters. Table 1 provides further details on the circumstances of the observations used in his paper.
2.2. Data reductions
The data were first processed by dark current subtraction and flat field division. The light curves were then obtained through classical aperture photometry method. For each data set, various aperture sizes were tested to optimize S/N by minimizing contamination by the sky and faint background stars.
For all the observations but one (VLT/NACO), Pluto, Charon and the star were not optically resolved on the images near the occultation time. Consequently, the measured flux includes the contributions of all three objects. Pluto’s system contributions was measured later, when it was separated from the target star. For all these observations, the ratio Pluto’s system/star was measured within 4 hours of the main event (appulse or occultation). The sub-Earth east longitudes of Pluto during the April 4, 2006 and June 14, 2007 events were close to 321 and 348 degrees, respectively. For those values of longitudes, Pluto’s magnitude varies by less than 1% in 4 hours (Buie et al. 2010a), which remains negligible for our purposes.
The LNA observation (June 14, 2007) was made in broadband with a CCD response ranging from 0.3 to 0.9 μm (Table 1). In order to minimize chromatic effects (i.e. differential extinctions), special care was paid to measure the flux from the various objects at the same airmass as during the occultation. For all light curves, a third order polynomial fit was performed to eliminate low frequency sky transparency variations. This finally provides the normalized stellar light curves φ(t), where unity corresponds to the full stellar flux, and zero, to the complete disappearance of the star.
In the case of the 2006 VLT/NACO observations, which made use of adaptive optics, the images of the star, Pluto and Charon could be separated, implying that aperture photometry could be performed on the star only. However, due to the nearby location of Pluto and Charon in the sky plane, contaminating flux from the dwarf planet and its satellite was present in the aperture. Because this contamination varies slowly and smoothly with time, we eliminated it by normalizing the flux of a running average of 500 points and obtain the light curve φ(t). At a rate of two images per second, this running average corresponds to 250 s, or about about 1600 km in the plane of the sky at an average star velocity of 6.41 km s-1, see Table 1 (note that two blocks among the eleven acquired at VLT have actually acquisition rates of one image per second, so the above numbers must be multiplied by two). This approach is valid as long as we search for rings with radial extensions significantly smaller than 1600 km. As discussed later, this is justified by the fact that direct HST images do not reveal rings with such extensions, at levels that are more sensitive than those that are obtained with stellar occultations.
2.3. Geometric reconstruction of the events
Due to the uncertainties on the star position and on Pluto’s ephemeris, the motion of the star relative to the dwarf planet may contain errors of more than 0.15 arcsec. This corresponds to more than 3000 km when projected in the plane of the sky. Observations made during the events themselves must be used in order to reconstruct a posteriori the geometry of the appulse or the occultation with a greater accuracy.
Occulted stars and Pluto’s system geometry.
2.3.1. The April 10, 2006 Pluto appulse
During this event, no occultation was observed (Fig. 1), so the geometry of the appulse can only be retrieved by using images where Pluto, Charon and the star are optically resolved.
Such resolution was achieved only in the VLT/NACO adaptive optics images, where the star minimum angular separations to Pluto and Charon were about 0.5 and 0.3 arcsec, respectively, while the angular separation between Pluto and Charon was about 0.6 arcsec. The NACO images were used to measure the relative motion of the star’s photocenter, or center-of-light (COL), with respect to Pluto’s COL during the 2.2 h of observations. During that interval, 11 data blocks were recorded (Table 1), for a total of 10 407 images, while Pluto moved by about 2.3 arcsec with respect to the star. We fitted the 10 407 positions of Pluto’s COL relative to the star to the positions expected from the DE413/PLU017 Pluto ephemeris, see Giorgini et al. (1996) and the Jet Propulsion Laboratory “Horizons” webpage1.
In this fit, the adjusted parameters are (1) the NACO pixel scale, (2) the NACO orientation, and a constant offset (3) in right ascension and (4) in declination for Pluto ephemeris. The fit provides a NACO plate scale of 27.2516 ± 0.0021 milli-arcsec (mas) per pixel, and a position angle P = 0.26069° ± 0.0033° for the local celestial J2000 north direction with respect to the (vertical) columns of the array. The standard deviation of the fit is about 4 mas, corresponding to roughly 100 km projected in the sky plane at Pluto’s distance. The formal error on the position of Pluto relatively to the star in the sky plane is then of the order of 100 km/ , i.e about one kilometer. However, systematic errors caused by a possible offset between Pluto’s center-of-body (COB) and COL largely dominate the final error on the geometry of the appulse, see below.
, i.e about one kilometer. However, systematic errors caused by a possible offset between Pluto’s center-of-body (COB) and COL largely dominate the final error on the geometry of the appulse, see below.
Using the HST images, Buie et al. (2010b) showed that the displacement between Pluto’s COB and COL may reach more than 100 km. As Charon’s diameter is about the half of Pluto’s, and as its albedo map is more homogeneous than that of Pluto, COL displacements are significantly smaller for Charon than for Pluto, with typical values of 20−40 km (Buie et al. 2010b). Those results apply to visible bands, while VTL/NACO images were taken in the near infrared (broadband 1−2.5 μm, see Table 1), but the same arguments can be used to prefer Charon over Pluto to provide an astrometric reference point in the NACO images.
To measure Charon COL, we used the last two blocks among the 11 listed in Table 1. This choice stems from the fact that light contamination from the star on Charon’s COL was at its minimum value. Moreover, the airmass was the smallest from our data set, so that the image quality was better in those last two blocks. Consequently, this method allows us in principle to pin down the geometry of the event to typical accuracies of 20−40 km. In particular, we find that the whole Pluto-Charon system presented at that time an offset of −74 mas in right ascension and +16 mas in declination with respect to the DE413 Pluto-Charon barycentric ephemeris. Furthermore, when comparing the relative positions of the COLs of Charon and Pluto with the Plutocentric Charon’s PLU017 ephemeris, we find a discrepancy of 32 mas (or 71 km) projected in the plane of the sky, which is likely attributable to a displacement of Pluto’s COL relative to its COB. More precisely, we find that Pluto’s COL must be displaced by 23 mas (52 km) to the west and 22 mas (48 km) to the south in order to agree with the PLU017 ephemeris. However, note that part of this discrepancy may also be due in part to an error in the PLU017 ephemeris. For instance, the latter disagrees by up to 18 mas (or about 40 km) in the plane of the sky with the ephemeris derived by Tholen et al. (2008), Sicardy et al. (2011) and Buie et al. (2013), so that errors of ~40 km may also affect Charon’s Plutocentric ephemeris. In summary, it appears that both Pluto’s COL and COB misalignements and a possible Plutocentric Charon’s ephemeris uncertainties limit the final accuracy of our astrometric reconstruction to about 50 km, in the plane of the sky.
2.3.2. The June 14, 2007 occultation
This event was observed from three sites: ESO Paranal (Chile), IAS (Hakos site, Namibia), and LNA at Pico dos Dias (Brazil), see Table 1. In practice, only the LNA light curve has sufficient S/N to permit search for material around Pluto. However, a simultaneous fit to the three data sets was used to provide the offset to be applied to Pluto’s right ascension and declination, see details in Sicardy et al. (2011). More precisely, using a template for Pluto atmospheric profile, a fit is simultaneously performed to all of the light curves, using as free parameters Pluto’s offset, and a boundary condition (the pressure at a given level) for the planet atmosphere. From this fit, we derive a Pluto’s barycentric offset of −98 mas in right ascension and +79 mas in declination for that date (in the sense observed minus DE413 ephemeris position). The formal error bar on the retrieved geometry is ±5 km (1σ level). However, systematic biases associated with possible errors in Pluto’s atmospheric models can reach ≈± 25 km in the plane of the sky, roughly 40% of the scale height at half-light levels (Sicardy et al. 2011). Note that this is about twice as accurate as the method used for the April 10, 2006 appulse described above.
For both the April 2006 and June 2007 events, once the star position relative to Pluto’s center was determined in the sky plane, it was projected in Charon’s orbital plane, because we assume that the material we are searching for is confined in the satellite orbital plane. This projection is performed using the Charon orbital pole position given in Table 2. Finally, the distance to the Pluto-Charon barycenter is calculated using the parameters of the PLU017 solution.
To summarize this section, we estimate that the astrometric reconstructions of the two events have typical accuracies − in the plane of the sky − of 50 km for the 2006 appulse, and of 25 km for the 2007 occultation. Once projected into Charon’s orbital plane, we find that those accuracies become 80 and 40 km, respectively. Thus, all the radial scales used in this paper and shown in the plots will carry those respective uncertainties.
3. Formation and evolution of putative rings around Pluto
Steffl et al. (2006) discuss the possibility that Nix, Hydra and Charon may have been formed during a collisional event involving Pluto and an incoming body. Thus, several moons, including yet to be discovered debris, may orbit the system. Moreover, it is thought that small Kuiper Belt bodies regularly collide with those satellites (Durda & Stern 2000), and might be a potential source of rings around Pluto. The small escape velocities at Nix and Hydra’s surfaces, between 30 and 90 m s-1, allow the collisionally produced particles to escape through the satellite Lagrange points L1 and L2, and form tenuous rings gravitationally bound to the Pluto-Charon system (Stern et al. 2006). In contrast, the larger escape velocity at Charon, ~500 m s-1, prevents the particles from evading the satellite’s gravitational well. Steffl & Stern (2007) have used the HST images to search for sunlight sent back by putative rings around Pluto. Assuming that all of the background light in the images is induced by hypothetical rings, they provide an upper limit of their normal optical depth τ⊥ at different barycentric distances, with value in the range τ⊥ ~ 10-7−10-5 depending on the barycentric distance and particle albedos, see Sect. 5.
Nagy et al. (2006) studied the stability of putative rings on S orbits, i.e around Pluto alone, and on P orbits, i.e. around the barycenter of the Pluto-Charon system. They find that stable S orbits exist up to a Plutocentric distance of 0.5A ≈ 9800 km, where A = 19 570 km is the Pluto-Charon distance (Tholen et al. 2008), while stable P orbits can be found beyond a barycentric distance of 2.15A ≈ 42 100 km. As expected, the average semi-major axes of Nix and Hydra, aNix = 49 242 km and aHydra = 65 082 km (Tholen et al. 2008), fall inside the stability zone for P orbits. More extensive studies by Giuliatti Winter et al. (2010) and Giuliatti Winter et al. (2013) have confirmed and refined those conclusions, while Pires Dos Santos et al. (2011) have shown that stable regions exist between Nix and Hydra, and just inside Nix’ orbit.
4. Search for individual moonlets
4.1. Method
We use the normalized lightcurves φ(t) displayed in Fig. 3 to place upper limits on the amount of material orbiting Pluto. We assume that it may exist only into two extreme forms: isolated, opaque spherical moonlets, or semi-transparent complete rings. Moreover, we assume that this material resides in the common orbital plane of the satellites. The scope is to simplify our analysis and avoid exploring many different configurations, even though the authors quoted in the previous section have explored the possibility of inclined orbits for moonlets orbiting Pluto.
To constrain the number of putative moonlets or the amount of dust in rings, we make use of a quantity called equivalent width E, which is a function of the total amount of material that blocks the stellar flux. This quantity is defined as E = ∫Δl[1 − φ(t)]·dl, where Δl is the interval of distance travelled by the star relatively to Pluto, in the plane of the sky or in Pluto’s equatorial plane, depending on whether we search for moonlets or equatorial rings, respectively. For more details, the reader is referred to Sicardy et al. (1991).
 |
Fig. 3 Normalized flux-versus-distance light curves, where unity corresponds to the unocculted stellar flux, and the zero level corresponds to the complete star disappearance. The successive positions of the occulted stars on the sky have been projected into Pluto’s equatorial plane, relative either to Pluto’s center (lower scale) or to the system barycenter (upper scale). From top to bottom: NACO (note the interruptions in the observation); La Silla/NTT; La Silla/2.2 m; Pico dos Dias (LNA) before the occultation by Pluto; Pico dos Dias (LNA) after the occultation by Pluto (the arrows indicate the direction of time). The satellites’ distances are taken from Tholen et al. (2008) for Charon, Nix and Hydra, and from Showalter et al. (2011, 2012) for P4 and P5, and are indicated by the vertical dotted lines. The radii Runst,S (in Plutocentric distance, dashed line) is the boundary inside which stable S-orbits can exist around Pluto (Nagy et al. 2006). Grey zones are regions of stability allowed by Nix and Hydra (Pires Dos Santos et al. 2011). |
The shadow of a moonlet in the plane of the observer is parametrized by the Fresnel scale 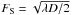 , where D ~ 4.6 × 109 km is Pluto’s geocentric distance (Table 2) and λ is the wavelength of observation. In visible and near-infrared bands (Table 1), FS typically varies from 1 to 2 km, respectively. Our best data set (NACO, April 10, 2006) will allow us to detect sub-kilometer moonlets, whose radii are denoted rm, see below. Thus, for this data set, we have rm ≪ FS ~ 2 km, a case known as the Fraunhofer regime. Moreover, the projected star radius r∗ ~ 0.15 km, estimated from star’s magnitude (Boissel 2010), has a negligible effect on the shadow structure because it is small compared to FS.
, where D ~ 4.6 × 109 km is Pluto’s geocentric distance (Table 2) and λ is the wavelength of observation. In visible and near-infrared bands (Table 1), FS typically varies from 1 to 2 km, respectively. Our best data set (NACO, April 10, 2006) will allow us to detect sub-kilometer moonlets, whose radii are denoted rm, see below. Thus, for this data set, we have rm ≪ FS ~ 2 km, a case known as the Fraunhofer regime. Moreover, the projected star radius r∗ ~ 0.15 km, estimated from star’s magnitude (Boissel 2010), has a negligible effect on the shadow structure because it is small compared to FS.
In the Fraunhofer regime, a moonlet shadow exhibits two scales of variations: a central region of radius 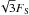 where the signal slowly varies around unity (Nihei et al. 2007), see the vertical solid lines in Fig. 4. This region is surrounded by “ripples" that rapidly oscillate around unity, and whose amplitudes decrease over a larger radial distance. In fact, the envelope of those ripples is the classical Airy function caused by an aperture of radius rm. More precisely, it can be shown from Roques et al 1987 that the first zero for the ripple amplitude is reached at a distance from the shadow center that we call the Airy scale,
where the signal slowly varies around unity (Nihei et al. 2007), see the vertical solid lines in Fig. 4. This region is surrounded by “ripples" that rapidly oscillate around unity, and whose amplitudes decrease over a larger radial distance. In fact, the envelope of those ripples is the classical Airy function caused by an aperture of radius rm. More precisely, it can be shown from Roques et al 1987 that the first zero for the ripple amplitude is reached at a distance from the shadow center that we call the Airy scale, 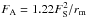 (see the vertical dotted lines in Fig. 4).
(see the vertical dotted lines in Fig. 4).
Thus, a sub-km moonlet causes significant fluctuations within a radius ~FA from its center. For the NACO data, we have FS ~ 2 km, so that FA ~ 5/rm km, where rm is expressed in km.
Following the definition of E given above, the equivalent width measured during the acquisition of the ith data point, and caused by a putative moonlet, is: ![\begin{equation} E_{\rm m}(i) = [1-\phi(i)] \cdot \Delta s(i), \label{eq:E_m} \end{equation}](/articles/aa/full_html/2014/01/aa21836-13/aa21836-13-eq62.png) (1)where Δs(i) is the distance travelled by the star in the plane of the sky relative to Pluto during the acquisition of the ith data point. This distance is obtained by multiplying the integration time by the star velocity relative to Pluto (Table 1), neglecting the moonlet velocity around Pluto.
(1)where Δs(i) is the distance travelled by the star in the plane of the sky relative to Pluto during the acquisition of the ith data point. This distance is obtained by multiplying the integration time by the star velocity relative to Pluto (Table 1), neglecting the moonlet velocity around Pluto.
4.2. Results
Figure 5 displays Em as a function of the distance s travelled in the plane of the sky from the first point of each data set. In the best data set (NACO), the S/N varied during the observation, but overall we obtain a 3σ standard deviation of 0.15 km for Em.
For interpreting Em in term of moonlet size, we generated synthetic occultation lightcurves using the numerical schemes provided in Roques et al. (1987). The signal fluctuations caused by a moonlet depend in a complicated way on its size, but also on its miss distance relative to the star. We generated synthetic occultation lightcurves caused by sub-km spherical moonlets, by changing their sizes and miss distances relative to the star.
For each synthetic event, we calculated the quantity Em (Eq. (1)), by using relevant values of Δs(i), i.e. 3.2 or 6.4 km, corresponding to the integration times of 0.5 or 1 sec used for NACO (Table 1). Note that because the ripples surrounding the shadow center oscillate around unity, Em can be positive or negative, as seen in Fig. 4d. We then define Emax as the maximum possible value of | Em | for a given miss distance. Our results are summarized in Fig. 6, which shows Emax as a function miss distance for various body radii rm. As expected from the discussion above and from Fig. 4, for a given value of rm, the values of Emax are significant for miss distances smaller than the Airy scale 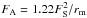 corresponding to that particular radius. As rm increases, FA decreases, but the value of Emax increases. As a result, Fig. 6 shows that bodies with radii rm larger than ~0.3 km would be detected above the NACO 3sigma limit (0.15 km) for a miss distance of ~7 km, i.e. within a band of width W ~ 14 km surrounding the body in the plane of the sky.
corresponding to that particular radius. As rm increases, FA decreases, but the value of Emax increases. As a result, Fig. 6 shows that bodies with radii rm larger than ~0.3 km would be detected above the NACO 3sigma limit (0.15 km) for a miss distance of ~7 km, i.e. within a band of width W ~ 14 km surrounding the body in the plane of the sky.
In summary, at the 3σ level, the NACO data set permits to detect opaque bodies with radii larger than ~0.3 km in a band of area stot·W projected in the plane of the sky.
Here stot is the total length scanned by the star in the sky plane, which amounts to stot ~ 38 200 km. This corresponds to an area (stot·W)/ | sin(B) | ~ 9.105 km2 when projected into Pluto’s equatorial plane, where B is the sub-observer Pluto latitude (see values in Table 2). From those numbers, we derive a 3σ upper limit of Σ(rm > 0.3 km) ~ 1.210-6 km-2 for the surface density of moonlets with radii larger than ~0.3 km, in Pluto’s equatorial plane. The region probed by NACO has a typical barycentric radius RNACO ~ 70 000 km (Fig. 3), in which we can place a maximum number of 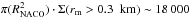 moonlets with radii larger than 0.3 km.
moonlets with radii larger than 0.3 km.
Hitherto, six bodies have been detected in Pluto’s system (the dwarf planet itself and its five satellites) with radii larger than ~14 km. If we suppose that this population has a power law of the type 1/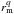 , this would imply a value of q < 2.1. However, in an accreting system that is thought to have led to Pluto’s satellites after a giant impact (Stern et al. 2006), a power law does not apply. Moreover, most of the regions that we probed are dynamically unstable, due to the gravitational effects of the satellites, see Fig. 3 and Nagy et al. (2006); Pires Dos Santos et al. (2011). Thus, our lack of detection of sub-km moonlets is most probably the consequence of the larger satellites perturbations that ejected the smaller bodies, rather than the effect of a peculiar shallow cumulative size distribution with index q = 2.1. Note that the other lightcurves increase the total length stot scanned around Pluto by a factor of about 3. This is at the expense of lower S/N, however (Fig. 5). Hence, the absence of any detection in those data sets brings little further information on the index q of power law that describes the size distribution of the putative debris.
, this would imply a value of q < 2.1. However, in an accreting system that is thought to have led to Pluto’s satellites after a giant impact (Stern et al. 2006), a power law does not apply. Moreover, most of the regions that we probed are dynamically unstable, due to the gravitational effects of the satellites, see Fig. 3 and Nagy et al. (2006); Pires Dos Santos et al. (2011). Thus, our lack of detection of sub-km moonlets is most probably the consequence of the larger satellites perturbations that ejected the smaller bodies, rather than the effect of a peculiar shallow cumulative size distribution with index q = 2.1. Note that the other lightcurves increase the total length stot scanned around Pluto by a factor of about 3. This is at the expense of lower S/N, however (Fig. 5). Hence, the absence of any detection in those data sets brings little further information on the index q of power law that describes the size distribution of the putative debris.
 |
Fig. 4 a) Normalized diffracted stellar flux Φ (see scale on the left) caused by a moonlet of radius rm = 0.3 km, as a function of the distance l travelled in the plane of the sky, at a resolution of 0.02 km. We assume here a zero miss-distance (diametric occultation) and a Fresnel scale of FS = 2 km, relevant to NACO observations. The vertical solid lines define the central Fresnel region of radius |
 |
Fig. 5 Search for individual opaque moonlets using the scans shown in Figs. 1 and 2. The equivalent width Em is defined in Eq. (1). The distance s is counted along the path of the star in the plane of the sky, starting from the first point of observation at the respective sites. The grey bands have heights of ± 1 km and are centered on Em = 0 km (solid horizontal lines), so that to provide the scale for Em. |
The visible mV of an object of radius rm and geometric albedo pV at distance DAU (in astronomical units) from Earth and Sun is ![\hbox{$m_V = 5\cdot \log_{10}\left[1.496\times10^8 D_{\rm AU}^{2}/\left(r_{\rm m}\sqrt{p_V}\right)\right] + m_{V_{\odot}}$}](/articles/aa/full_html/2014/01/aa21836-13/aa21836-13-eq97.png) , where mV⊙ = −26.7 is the Sun apparent at 1 AU. Taking rm = 0.3 km, we obtain mV in the range 33−35.5, assuming a range 0.38–0.04 for the moonlet albedo, corresponding respectively to Charon’s albedo (Buie et al. 1997) and Uranus’ rings (Karkoschka 2001). Such objects are impossible to detect individually from Earth, the limiting magnitude for moonlets being mV ≈ 27.5, based on HST observations (Steffl et al. 2006). Even by considering the total flux of 15 000 objects of radius rm = 0.3 km distributed within a distance 70 000 km from Pluto as discussed above, the magnitude per arcsec2 we obtain ranges from 26.3 to 28.8, which is beyond the performance of current photometric techniques.
, where mV⊙ = −26.7 is the Sun apparent at 1 AU. Taking rm = 0.3 km, we obtain mV in the range 33−35.5, assuming a range 0.38–0.04 for the moonlet albedo, corresponding respectively to Charon’s albedo (Buie et al. 1997) and Uranus’ rings (Karkoschka 2001). Such objects are impossible to detect individually from Earth, the limiting magnitude for moonlets being mV ≈ 27.5, based on HST observations (Steffl et al. 2006). Even by considering the total flux of 15 000 objects of radius rm = 0.3 km distributed within a distance 70 000 km from Pluto as discussed above, the magnitude per arcsec2 we obtain ranges from 26.3 to 28.8, which is beyond the performance of current photometric techniques.
5. Search for ring material
5.1. Method
To constrain the amount of dust in a putative ring, we use the equivalent width, which makes no hypothesis on its width nor its transparency. We define the equivalent width Er of a ring by 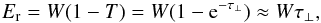 (2)where W is its physical width, T its normal transmission and τ⊥ its normal optical depth. The approximation stems from the assumption τ⊥ ≪ 1. As defined here, Er is the width of the opaque ring that would block the same amount of stellar light as the actual ring over the distance W, see more details in Sicardy et al. (1991).
(2)where W is its physical width, T its normal transmission and τ⊥ its normal optical depth. The approximation stems from the assumption τ⊥ ≪ 1. As defined here, Er is the width of the opaque ring that would block the same amount of stellar light as the actual ring over the distance W, see more details in Sicardy et al. (1991).
If B is the inclination of the ring plane to the line-of-sight (coincident with the sub-observer Pluto latitude B given in Table 2, since we assume here that the rings are equatorial), then a multi-layer ring has an apparent optical depth τ = τ⊥/ | sinB |. Further complications arise because diffraction by small, distant rings particles increase the ring apparent optical depth by a factor of two (Cuzzi 1985), so the apparent optical depth is actually τ = 2τ⊥/ | sinB |. From these considerations, and for a multi-layer ring with τ⊥ ≪ 1 we obtain the expression ![\begin{equation} E_{\rm r}= \frac{|\sin(B)|}{2} \int_{\Delta r} [1-\phi(r)]{\rm d}r \end{equation}](/articles/aa/full_html/2014/01/aa21836-13/aa21836-13-eq108.png) (3)for the equivalent width of a putative ring contained in the radial interval of width Δr. Note that the normalized flux-versus-time light curve φ(t) has been converted into φ(r), the flux-versus-radial distance r in the dwarf planet equatorial plane, see Fig. 3. Depending on whether we look for P orbits or S orbits, and if r is counted from Pluto’s barycenter, or from the Pluto-Charon barycenter.
(3)for the equivalent width of a putative ring contained in the radial interval of width Δr. Note that the normalized flux-versus-time light curve φ(t) has been converted into φ(r), the flux-versus-radial distance r in the dwarf planet equatorial plane, see Fig. 3. Depending on whether we look for P orbits or S orbits, and if r is counted from Pluto’s barycenter, or from the Pluto-Charon barycenter.
 |
Fig. 6 Maximum possible value of | Em | (see Fig. 4) Emax caused by a body of radius rm vs. the miss distance to shadow center. Here we give examples with rm = 0.2, 03, 0.4 and 0.5 km, assuming a Fresnel scale of FS = 2 km. Due to the ripples surrounding the moonlet shadow (Fig. 4), the maximum value of | Em | exhibits rapid fluctuations that have been averaged out for clarity by binning the results over intervals of 1.2 km. See text for discussion. |
The maximum spatial resolution is reached by using windows containing only one data point. The physical width Δr(i) of such window is the radial distance travelled by the star in Pluto’s equatorial plane during the acquisition of the ith data point, and the corresponding equivalent width of putative ring material in this interval is: ![\begin{equation} E_{\rm r}(i)=\frac{|\sin{B}|}{2}[1-\phi(i)]\Delta r(i). \label{eq:Er} \end{equation}](/articles/aa/full_html/2014/01/aa21836-13/aa21836-13-eq115.png) (4)Note that the radial velocity of the star is largest at maximum distance and decreases to zero at closest approach (Table 3). It is unnecessary to look for objects as large as Nix and Hydra, with diameters of ~100 km, as they would have be found in the HST images. Thus, before calculating Er(i), we divide the lightcurves by a running average estimated over 100 km-wide windows, in order to smooth out low-frequency flux variations.
(4)Note that the radial velocity of the star is largest at maximum distance and decreases to zero at closest approach (Table 3). It is unnecessary to look for objects as large as Nix and Hydra, with diameters of ~100 km, as they would have be found in the HST images. Thus, before calculating Er(i), we divide the lightcurves by a running average estimated over 100 km-wide windows, in order to smooth out low-frequency flux variations.
Minimum and maximum spatial resolutions, and maximum radial velocities of the stellar image in Charon’s orbital plane, relative to the system barycenter.
5.2. Results
The equivalent widths Er(i) versus r are shown in Fig. 7. Using boxes of width 100 km we performed a statistical analysis of Er(i) and derived in each box the 3σ deviation of Er(i), denoted E3σ. The value of E3σ for the best data set (NACO) is plotted in Fig. 8. It scans regions ranging from ~13 000 to ~70 000 km in barycenter distances. Note that for smaller distances, the radial velocity, and hence Δr(i) in Eq. (4) is smaller (Fig. 1), providing smaller values of E3σ of about 30 m. Around the plutocentric radius of 30 000 km, E3σ reaches a maximum of about 100 m, due to the contamination of the stellar flux by the nearby Charon image (Fig. 1). For larger radii, the S/N increases again because the contaminating effect of Charon decreases and because the star was observed at higher elevation. This improves the photometric quality of the data and provides values of E3σ back to about 30 m.
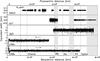 |
Fig. 7 Same as Fig. 3, but now plotting the equivalent widths Er of possible ring material (from Eq. (4)) vs. distance in Pluto’s equatorial plane. Note that the vertical scale for NACO is different from that of the other plots. |
 |
Fig. 8 Our results (black line) compared with the 3σ upper limits for rings equivalent widths based on HST images, assuming extremes geometric albedos of pV = 0.04 (stars) and pV = 0.38 (crosses). The radial resolution of the HST data points is 1000 km (instead of 1500 km in Steffl & Stern 2007) and was provided by A. J. Steffl (priv. comm.). Grey zones and vertical lines have the same meaning as in Fig. 3. |
5.3. Comparison with HST results
Upper limits for the normal optical depth τ⊥ of Pluto’s putative rings have been derived by Steffl & Stern (2007), see their Fig. 3. These authors first derived the I/F ratio in HST images, where I is the observed intensity and πF is the incident solar flux. The normal optical depth is then derived from τ⊥ = (I/F)⊥/pV, where pV is the visible geometric albedo of the ring particles.
Steffl & Stern (2007) consider a minimum value of pV = 0.04, corresponding to Uranus’ dark rings (Karkoschka 2001), and a maximum value pV = 0.38, corresponding to Charon’s albedo (Buie et al. 1997). A revised version of those results has been provided to us by A. Steffl (priv. comm., 2011), where the optical depth is given with a radial resolution of 1000 km (or 2 pixels of the HST images), instead of the 1500 km used in Steffl & Stern (2007), and between radial distances of 1000 and 100 000 km, instead of 40 000 and 100 000 km. Multiplying the values of τ⊥ by W = 1000 km finally provides the upper limit for the equivalent width Er of rings in each radial bin resolved by HST images.
The resulting upper limits for Er are plotted in Fig. 8, together with our own limits derived from the NACO data. We first note that the NACO and HST have comparable sensitivity for ring detection (especially in the dark case pV = 0.04) at radial distances smaller than about 25 000 km, while HST is more sensitive than NACO at larger radii. Second, we note that the NACO profile has a better radial resolution than the HST profiles, which has a resolution of 1000 km. We might degrade our radial resolution to 1000 km by binning our profile over 200 points, for direct comparison with the HST results. However, this procedure, would degrade our sensitivity by a factor of  , by assuming the noise is normally distributed. Thus, NACO provides a comparable, or a few times less sensitive threshold for ring detection when compared to HST, but on a smaller radial scale (5−10 km). In other words, NACO is better suited for revealing narrow (a few kilometers) rings, while HST has a better sensitivity for detecting broad (1000 km or more) diffuse rings.
, by assuming the noise is normally distributed. Thus, NACO provides a comparable, or a few times less sensitive threshold for ring detection when compared to HST, but on a smaller radial scale (5−10 km). In other words, NACO is better suited for revealing narrow (a few kilometers) rings, while HST has a better sensitivity for detecting broad (1000 km or more) diffuse rings.
We finally note that the ring-detection sensitivity of HST decreases close to the dwarf planet, due to the scattered light from the latter. In the cases of good S/N stellar occultations in general (and even without using adaptive optics), the sensitivity is largely independent of the distance to the planet.
5.4. Confined rings around Pluto
Here, we briefly comment on the possibility of rings caused by meteoroidal collisions on small Pluto’s satellites. As shown by Stern et al. (2006), Nix and Hydra are small enough so that ejecta scooped by collisions can escape the satellite Hill’s sphere. They can create tenous rings of width W ~ 2rH, where rH is the radius of the satellite Hill’s sphere. This radius is given by rH = a(ms/3MP)1/3, where ms (resp. MP) is the satellite’s (resp. Pluto’s) radius and a is the orbital radius. For a satellite of density ρs and radius Rs this yields: 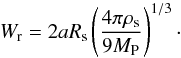 (5)Using MP = 1.3 × 1022 kg for Pluto’s mass, and assuming that ρs = 1650 kg m-3 (i.e. Charon’s density), we obtain:
(5)Using MP = 1.3 × 1022 kg for Pluto’s mass, and assuming that ρs = 1650 kg m-3 (i.e. Charon’s density), we obtain:  (6)Considering Nix and Hydra, whose typical radii are estimated to 50 km, and with typical orbital radii of 50 000 km, we obtain Wr ~ 2500 km. This is much larger than the scales over which we are sensitive to ring detection (i.e. a few kilometers), so we bring little constraints on diffuse material associate with Nix or Hydra. Concerning P4, with a typical radius of 15 km and a ~ 59 000 km (Showalter et al. 2011), we obtain Wr ~ 900 km, quite larger again than our spatial resolution.
(6)Considering Nix and Hydra, whose typical radii are estimated to 50 km, and with typical orbital radii of 50 000 km, we obtain Wr ~ 2500 km. This is much larger than the scales over which we are sensitive to ring detection (i.e. a few kilometers), so we bring little constraints on diffuse material associate with Nix or Hydra. Concerning P4, with a typical radius of 15 km and a ~ 59 000 km (Showalter et al. 2011), we obtain Wr ~ 900 km, quite larger again than our spatial resolution.
Conversely, inverting Eq. (6), imposing Wr = 5 km and adopting a ~ 50 000 km, we obtain the typical radius of a satellite that could maintain a ring of width 5 km: Rs,km ~ 5000/a km ~ 0.1 km. Many such objects may exist around Pluto, even if we account for the destabilizing effect of the satellites. Our limit for the equivalent widths of narrow rings being typically 50 m (Fig. 8), this would imply optical depths of τ ~ 50/5000 = 0.01. This is much larger than the optical depths encountered in faint rings associated with moonlets around giant planets, e.g. Jupiter’s main ring with τ ~ 10-6 (Showalter et al. 1987), or Saturn’s G ring, τ ~ 10-5 (Hedman et al. 2007). However, our limit on τ is comparable to the optical depths of Neptune’s main rings (Le Verrier and Adams), which have both τ ~ 0.01 (Horn et al. 1990).
Thus, our observations place limit on Pluto narrow rings that are comparable in width and optical depth to the continuous component (i.e. excluding the arcs) of Neptune’s Adams rings.
6. Conclusions
We used light curves derived from a Pluto stellar appulse and an occultation to search for material around the dwarf planet. This allows us to place a maximum number of ~15 000 moonlets with radii larger than 0.3 km inside a region of radius ~70 000 km around Pluto’s system barycenter. We derive upper limits of 30−100 m for the equivalent width of putative narrow (less than 10 km) rings at barycentric distances between 13 000 and 70 000 km, see the summary in Fig. 8. We note that the NACO data and HST results have comparable sensitivity at radial distances smaller than about 25 000 km, and that HST is more sensitive than NACO at larger radii. While NACO is better suited for revealing narrow kilometer-sized rings, HST has a better sensitivity for detecting broad diffuse rings.
See also http://ssd.jpl.nasa.gov/horizons.cgi
Acknowledgments
This work is based on observations performed at the European Southern Observatory (ESO), proposals 077.C-028 and 079.C-0345, and on observations made at Laboratório Nacional de Astrofísica (LNA), Itajubá-MG, Brazil. We aknowledge ANR-11-IS56-002 grant “Beyond Neptune II”. We also thank L. Young for valuable comments.
References
- Boissel, Y. 2010, Ph.D. Thesis, Observatoire de Paris, France [Google Scholar]
- Boissel, Y., Sicardy, B., Roques, F., et al. 2008, BAAS, 40, 483 [NASA ADS] [Google Scholar]
- Buie, M. W., Tholen, D. J., & Wasserman, L. H. 1997, Icarus, 125, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Buie, M. W., Grundy, W. M., Young, E. F., et al. 2006, AJ, 132, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Buie, M. W., Grundy, W. M., Young, E. F., et al. 2010a, AJ, 139, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Buie, M. W., Grundy, W. M., Young, E. F., et al. 2010b, AJ, 139, 1128 [NASA ADS] [CrossRef] [Google Scholar]
- Buie, M. W., Tholen, D. J., & Grundy, W. M. 2013, AJ, 144, 15 [Google Scholar]
- Christy, J. W., & Harrington, R. S. 1978, AJ, 83, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Cuzzi, J. N. 1985, Icarus, 63, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Dohnanyi, J. S. 1969, J. Geophys. Res., 74, 2431 [NASA ADS] [Google Scholar]
- Durda, D. D., & Stern, S. A. 2000, Icarus, 145, 220 [Google Scholar]
- Elliot, J. L., Dunham, E. W., Bosh, A. S., et al. 1989, Icarus, 77, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Giorgini, J. D., Yeomans, D. K., Chamberlin, A. B., et al. 1996, BAAS, 28, 1158 [NASA ADS] [Google Scholar]
- Giuliatti Winter, S. M., Winter, O. C., Guimarães, A. H. F., & Silva, M. R. 2010, MNRAS, 404, 442 [NASA ADS] [Google Scholar]
- Giuliatti Winter, S. M., Winter, O. C., Vieira Neto, E., & Sfair, R. 2013, MNRAS, 430, 1892 [NASA ADS] [CrossRef] [Google Scholar]
- Gulbis, A. A. S., Elliot, J. L., Person, M. J., et al. 2006, Nature, 439, 48 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hedman, M. M., Burns, J. A., Tiscareno, M. S., et al. 2007, Sciences, 317, 653 [CrossRef] [Google Scholar]
- Horn, L. J., Hui, J., Lane, A. L., & Colwell, J. E. 1990, Geophys. Res. Lett., 17, 1745 [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard, W. B., Hunten, D. M., Dieters, et al. 1988, Nature, 336, 452 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karkoschka, E. 2001, Icarus, 151, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Lenzen, R., Hartung, M., Brandner, et al. 2003, Proc. SPIE, 4841, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Moorwood, A., Cuby, J.-G., & Lidman, C. 1998, The Messenger, 91, 9 [NASA ADS] [Google Scholar]
- Nagy, I., Süli, Á., & Érdi, B. 2006, MNRAS, 370, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Nihei, T. C., Lehner, M. J., Bianco, F. B., et al. 2007, AJ, 134, 1596 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, M., & Sari, R. 2005, Icarus, 173, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Pasachoff, J. M., Babcock, B. A., Souza, S. P., et al. 2006, BAAS, 38, 523 [NASA ADS] [Google Scholar]
- Person, M. J., Elliot, J. L., Gulbis, A. A. S., et al. 2006, AJ, 132, 1575 [NASA ADS] [CrossRef] [Google Scholar]
- Pires Dos Santos, P. M., Giuliatti Winter, S. M., & Sfair, R. 2011, MNRAS, 410, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Roques, F., Moncuquet, M., & Sicardy, B. 1987, AJ, 93, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Rousset, G., Lacombe, F., Puget, P., et al. 2003, Proc. SPIE, 4839, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Showalter, M. R., Burns, J. A., Cuzzi, J. N., & Pollack, J. B. 1987, Icarus, 69, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Showalter, M. R., Hamilton, D. P., Stern, S. A., et al. 2011, Central Bureau Electronic Telegrams, 2769, 1 [Google Scholar]
- Showalter, M. R., Weaver, H. A., Stern, S. A., et al. 2012, Central Bureau Electronic Telegrams, 9253, 1 [Google Scholar]
- Sicardy, B., Roques, F., & Brahic, A. 1991, Icarus, 89, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Sicardy, B., Widemann, T., Lellouch, E., et al. 2006a, Nature, 424, 168 [Google Scholar]
- Sicardy, B., Bellucci, A., Gendron, E., et al. 2006b, Nature, 439, 52 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sicardy, B., Bolt, G., Broughton, J., et al. 2011, AJ, 141, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Steffl, A. J., & Stern, S. A. 2007, AJ, 133, 1485 [NASA ADS] [CrossRef] [Google Scholar]
- Steffl, A. J., Mutchler, M. J., Weaver, H. A., et al. 2006, AJ, 132, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, S. A., Weaver, H. A., Steffl, A. J., et al. 2006, Nature, 439, 946 [NASA ADS] [CrossRef] [Google Scholar]
- Tholen, D. J., Buie, M. W., Grundy, W. M., & Elliott, G. T. 2008, AJ, 135, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, H. A., Stern, S. A., Mutchler, M. J., et al. 2006, Nature, 439, 943 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Minimum and maximum spatial resolutions, and maximum radial velocities of the stellar image in Charon’s orbital plane, relative to the system barycenter.
All Figures
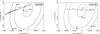 |
Fig. 1 Left: geometry of the April 10, 2006 Pluto stellar appulse. The stellar tracks as seen from VLT (Paranal) and NTT, 2p2 telescopes (La Silla) are shown relative to the Pluto-Charon barycenter (the cross at origin). The quantity f (resp. g) on the horizontal (resp. vertical) axis is the offset relative to the Pluto-Charon barycenter in the plane of the sky, counted positively toward the local celestial J2000 east (resp. north). The arrow indicates the direction of stellar motion. Note the interruptions in the observations (Table 1). Pluto’s body is shown as a circle next to the cross, and the satellites positions are shown at 6:00 UT, the approximate mid-time of observations. A close-up view of the stellar tracks as seen from VLT, NTT and 2p2 are shown in Fig. 2. Right: geometry of the June 14, 2007 Pluto occultation, as seen from the LNA160 telescope. Symbols are the same as for the left panel. The satellites are shown at 01:30 UT, the approximate mid-time of observations. All the satellite positions are derived from the orbital solution of Tholen et al. (2008). |
| In the text | |
 |
Fig. 2 Close-up view of left panel of Fig. 1, showing the stellar tracks observed from VLT (black), NTT (red) and 2p2 (blue) telescopes. Note the interruptions in the observations (Table 1). |
| In the text | |
 |
Fig. 3 Normalized flux-versus-distance light curves, where unity corresponds to the unocculted stellar flux, and the zero level corresponds to the complete star disappearance. The successive positions of the occulted stars on the sky have been projected into Pluto’s equatorial plane, relative either to Pluto’s center (lower scale) or to the system barycenter (upper scale). From top to bottom: NACO (note the interruptions in the observation); La Silla/NTT; La Silla/2.2 m; Pico dos Dias (LNA) before the occultation by Pluto; Pico dos Dias (LNA) after the occultation by Pluto (the arrows indicate the direction of time). The satellites’ distances are taken from Tholen et al. (2008) for Charon, Nix and Hydra, and from Showalter et al. (2011, 2012) for P4 and P5, and are indicated by the vertical dotted lines. The radii Runst,S (in Plutocentric distance, dashed line) is the boundary inside which stable S-orbits can exist around Pluto (Nagy et al. 2006). Grey zones are regions of stability allowed by Nix and Hydra (Pires Dos Santos et al. 2011). |
| In the text | |
 |
Fig. 4 a) Normalized diffracted stellar flux Φ (see scale on the left) caused by a moonlet of radius rm = 0.3 km, as a function of the distance l travelled in the plane of the sky, at a resolution of 0.02 km. We assume here a zero miss-distance (diametric occultation) and a Fresnel scale of FS = 2 km, relevant to NACO observations. The vertical solid lines define the central Fresnel region of radius |
| In the text | |
 |
Fig. 5 Search for individual opaque moonlets using the scans shown in Figs. 1 and 2. The equivalent width Em is defined in Eq. (1). The distance s is counted along the path of the star in the plane of the sky, starting from the first point of observation at the respective sites. The grey bands have heights of ± 1 km and are centered on Em = 0 km (solid horizontal lines), so that to provide the scale for Em. |
| In the text | |
 |
Fig. 6 Maximum possible value of | Em | (see Fig. 4) Emax caused by a body of radius rm vs. the miss distance to shadow center. Here we give examples with rm = 0.2, 03, 0.4 and 0.5 km, assuming a Fresnel scale of FS = 2 km. Due to the ripples surrounding the moonlet shadow (Fig. 4), the maximum value of | Em | exhibits rapid fluctuations that have been averaged out for clarity by binning the results over intervals of 1.2 km. See text for discussion. |
| In the text | |
 |
Fig. 7 Same as Fig. 3, but now plotting the equivalent widths Er of possible ring material (from Eq. (4)) vs. distance in Pluto’s equatorial plane. Note that the vertical scale for NACO is different from that of the other plots. |
| In the text | |
 |
Fig. 8 Our results (black line) compared with the 3σ upper limits for rings equivalent widths based on HST images, assuming extremes geometric albedos of pV = 0.04 (stars) and pV = 0.38 (crosses). The radial resolution of the HST data points is 1000 km (instead of 1500 km in Steffl & Stern 2007) and was provided by A. J. Steffl (priv. comm.). Grey zones and vertical lines have the same meaning as in Fig. 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.