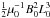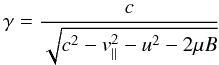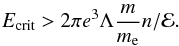| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 15 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201321715 | |
| Published online | 03 January 2014 | |
Particle acceleration and transport in reconnecting twisted loops in a stratified atmosphere
1 Jodrell Bank Centre for Astrophysics, University of Manchester, Manchester M13 9PL, UK
e-mail: mykola.gordovskyy@manchester.ac.uk
2 School of Physics and Astronomy, Univesity of Glasgow, Glasgow G12 8QQ, UK
Received: 16 April 2013
Accepted: 20 August 2013
Context. Twisted coronal loops should be ubiquitous in the solar corona. Twisted magnetic fields contain excess magnetic energy, which can be released during magnetic reconnection, causing solar flares.
Aims. The aim of this work is to investigate magnetic reconnection, and particle acceleration and transport in kink-unstable twisted coronal loops, with a focus on the effects of resistivity, loop geometry and atmospheric stratification. Another aim is to perform forward-modelling of bremsstrahlung emission and determine the structure of hard X-ray sources.
Methods. We use a combination of magnetohydrodynamic (MHD) and test-particle methods. First, the evolution of the kinking coronal loop is considered using resistive MHD model, incorporating atmospheric stratification and loop curvature. Then, the obtained electric and magnetic fields and density distributions are used to calculate electron and proton trajectories using a guiding-centre approximation, taking into account Coulomb collisions.
Results. It is shown that electric fields in twisted coronal loops can effectively accelerate protons and electrons to energies up to 10 MeV. High-energy particles have hard, nearly power-law energy spectra. The volume occupied by high-energy particles demonstrates radial expansion, which results in the expansion of the visible hard X-ray loop and a gradual increase in hard X-ray footpoint area. Synthesised hard X-ray emission reveals strong footpoint sources and the extended coronal source, whose intensity strongly depends on the coronal loop density.
Key words: Sun: flares / acceleration of particles / Sun: X-rays, gamma rays
© ESO, 2014
1. Introduction
Twisted magnetic fields should be ubiquitous in the solar corona. Various types of photospheric motions, such as shear and rotation (often observed in sunspots, see for example Brown et al. 2003) add helicity to the coronal field structure. At the same time, the new emerging magnetic flux requires a non-zero helicity in order to form a loop, instead of a diffuse magnetic field arcade (see simulations by Archontis et al. 2010, and discussion therein). Twisted coronal loops are often directly observed in extreme ultra-violet (EUV; see e.g. Raouafi 2009; Srivastava et al. 2010) and found in reconstructed coronal magnetic fields (e.g. Regnier & Amari 2004; Malanushenko et al. 2011).
The twisted magnetic field contains excess magnetic energy which can be released with the field relaxing towards a potential configuration. For this reason twisted fluxtubes in the corona are often associated with solar flares and other active events. A number of observational works reveal the presence of a twisted magnetic field in pre-flare active regions; some of them directly associate the twisted magnetic ropes with the energy release (see e.g. Srivastava et al. 2010). Furthermore, there seems to be a strong link between kink and torus instabilities in the twisted coronal ropes, and the ejection of plasmoid and a subsequent coronal mass ejection (CME), which is confirmed by observational evidence and simulations (see Amari et al. 2000; Toeroek & Kliem 2005; Gibson & Fan 2006; Fan 2010). However, reconnection in twisted magnetic loops in the corona could also explain events with no plasmoid ejection or CME. Aschwanden et al. (2009) showed that a substantial number of small flares occur in a simple single loop configuration, also known as self-contained flares. It is suggested that magnetic reconnection in twisted coronal loops in an active region with no open field could explain these phenomena.
There are several studies concerning magnetohydrodynamic (MHD) properties of twisted coronal loops. Kliem, Toeroek, and colleagues investigated kink and torus instabilities in twisted loops in zero-beta plasma (Toeroek & Kliem 2005; Kliem et al. 2000, 2010). The model was later applied to study the ejective eruptions and CME. Browning & Van der Linden (2003) and Browning et al. (2008) considered stability of twisted magnetic loops using a semi-analytical approach, determining criteria for ideal kink instability and subsequent relaxation during a nonlinear phase of the instability. These results have been recently generalised by Bareford et al. (2013). These criteria has been used by Browning et al. (2008), Hood et al. (2009), and later by Gordovskyy & Browning (2011) to perform numerical simulations of magnetic reconnection in a kink unstable magnetic fluxtube. All these studies consider instability and magnetic reconnection in a fluxtube, which is cylindrically symmetric.
Gordovskyy & Browning (2011, 2012) show that the energy release during reconnection in a twisted loop could provide a more convenient model of particle acceleration when compared to the standard model. The main benefit is that particle energization is distributed within the loop, rather than localized in the upper corona and hence, the energy losses due to various transport effects (collisions, return current) are reduced. Indeed, it is easier to accelerate a larger number of particles in a large-scale distributed region rather than in a compact volume, and hence, this scenario may have important consequences for the particle number problem (see e.g. Brown 1976). Gordovskyy et al. (2012) also demonstrated that reconnection in twisted loops with magnetic field convergence near footpoints could provide a configuration for particle re-acceleration in the lower corona and chromosphere (Brown et al. 2009). They also show that the developed model can explain some features of the variation in hard X-ray sources recently observed with RHESSI (Kontar et al. 2011).
Gordovskyy & Browning (2012) used the model developed in Hood et al. (2009) and Gordovskyy & Browning (2011) to study particle acceleration in twisted loops using the test-particle approach. This study recently has been extended by Gordovskyy et al. (2012) to incorporate collisions and magnetic field convergence. The obtained time-dependent particle distributions are used to predict the structure of hard X-ray sources.
In the present paper we develop a model of energy release in an unstable twisted coronal loop, focusing both on thermal and non-thermal components. The model combines 3D MHD simulations and test-particle calculations of electron and proton trajectories in presence of Coulomb collisions. The key new feature of this model are the large-scale curvature of the twisted magnetic fluxtube, and stratification of the ambient atmosphere. The latter affects the MHD part of the simulations through density-dependent anomalous resistivity, as well as particle acceleration due to Coulomb scattering of high-energy electrons and, to a lesser extent, protons. In the present paper we also calculate hard X-ray bremsstrahlung emission, enabling direct comparison of our model with observations.
2. Evolution of kinking twisted coronal loops
In this section, we consider the evolution of a curved twisted coronal loop using a MHD approach. The method and model set-up are described in Sect. 2.1. The derivation of the configuration with twisted fluxtube using ideal MHD is described in Sect. 2.2, and the evolution of twisted loop after kink instability is described in the Sect. 2.3.
2.1. Model and main equations
Consider a three-dimensional domain with the dimensions x = [−xmax; + xmax], y = [−ymax; + ymax] and z = [0;zmax]. The evolution of magnetic field B, electric field E, current density j, plasma velocity v, density ρ and specific thermal energy w with time t can be described by the standard set of resistive MHD equations: ![\begin{eqnarray} \frac{\partial \rho}{\partial t} &=& - {\boldsymbol \nabla} \cdot (\rho {\boldsymbol v}) \label{mhd-rho} \\ \frac{\partial {\boldsymbol v}}{\partial t} &=& - ({\boldsymbol v} \cdot {\boldsymbol \nabla}) {\boldsymbol v} - \frac 1{\rho} {\boldsymbol j} \times {\boldsymbol B} - \frac 1{\rho}{\boldsymbol \nabla}p + \rho {\boldsymbol g} \label{mhd-velo} \\ \frac{\partial w}{\partial t} &=& - ({\boldsymbol v} \cdot {\boldsymbol \nabla})w - (\Gamma-1)w\; {\boldsymbol \nabla} \cdot {\boldsymbol v} + \frac{\eta}{\rho}j^2 +S_{\rm other} \label{mhd-nrg} \\ \frac{\partial {\boldsymbol B}}{\partial t} &=& - {\boldsymbol \nabla} \times {\boldsymbol E} \label{mhd-magn} \\ {\boldsymbol E} &=& - {\boldsymbol v} \times {\boldsymbol B} + \eta {\boldsymbol j} \label{mhd-ele} \\ {\boldsymbol j} &=& \frac 1{\mu_0} [{\boldsymbol \nabla} \times {\boldsymbol B}]\label{mhd-curr} \\ p &=& (\Gamma -1 ) \rho w. \label{mhd-gas} \end{eqnarray}](/articles/aa/full_html/2014/01/aa21715-13/aa21715-13-eq11.png) Here, μ0 is the magnetic permeability of the vacuum and η is resistivity. The source term Sother accounts for all other sources of heating, mostly due to numerical dissipation and shock viscosity used in the MHD simulations (see Arber et al. 2001). The specific heat ratio is Γ = 5/3. The temperature can be derived from the specific energy as T = ℳ(Γ − 1)/ℛw. Here, ℛ is the universal gas constant, and ℳ is the average molar mass equal to ℳ = 0.5mpNA, corresponding to fully ionised hydrogen. The gravitational acceleration, g = −gz, is assumed to be constant in the whole domain. The last term in Eq. (3) accounts for all other possible sources of heating. In the present simulations, it is an artificial viscous dissipation used to stabilise the solution.
Here, μ0 is the magnetic permeability of the vacuum and η is resistivity. The source term Sother accounts for all other sources of heating, mostly due to numerical dissipation and shock viscosity used in the MHD simulations (see Arber et al. 2001). The specific heat ratio is Γ = 5/3. The temperature can be derived from the specific energy as T = ℳ(Γ − 1)/ℛw. Here, ℛ is the universal gas constant, and ℳ is the average molar mass equal to ℳ = 0.5mpNA, corresponding to fully ionised hydrogen. The gravitational acceleration, g = −gz, is assumed to be constant in the whole domain. The last term in Eq. (3) accounts for all other possible sources of heating. In the present simulations, it is an artificial viscous dissipation used to stabilise the solution.
The set of Eqs. (1)–(7) is solved numerically using Lagrangian remap MHD code LARE3D by Arber et al. (2001). The numerical grid of 256 × 256 × 512 elements (along the X-, Y-, and Z-axis, respectively) is uniform in each direction. (The resolution is higher in the vertical direction to reduce the error due to density stratification.)
 |
Fig. 1 Initial density (panel a)), temperature (panel b)), and column density (panel c)) distributions. Solid lines correspond to the low-density case (Model A); dotted lines correspond to the high-density case (Model B). |
The lower boundary of the domain is used as a driver to create a configuration with a twisted rope, as discussed in the Sect. 2.2. Conditions for the four side boundaries are based upon the assumption that the plasma is stationary (v = 0), and all the remaining parameters are constant across a boundary (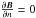 ,
, 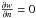 ,
, 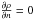 , where
, where 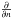 denotes a gradient across a boundary). All the parameters (v and B, w and ρ) are constant through the upper boundary. In addition, gravitational acceleration is set to zero at the upper boundary to maintain its stability (see e.g. Archontis et al. 2010).
denotes a gradient across a boundary). All the parameters (v and B, w and ρ) are constant through the upper boundary. In addition, gravitational acceleration is set to zero at the upper boundary to maintain its stability (see e.g. Archontis et al. 2010).
Initially, there is a plain-parallel gravitationally stratified atmosphere. The initial density distribution is constructed so that it is similar to that in empirical models (e.g., Vernazza et al. 1981). At the photospheric level, the density is expected to be around 1.67 × 10-4 kg m-3, and the temperature is ~ 6000 K. In the model chromosphere, the density decreases exponentially by a factor of 100 for every 1 Mm. At z ≈ 2–3 Mm, the temperature drastically increases to ~ 1 MK. In the model corona, the scale height becomes substantially larger, so that the density decreases by a small factor, while the temperature is nearly constant. The initial density is defined using the following formula: 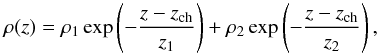 (8)and the corresponding initial pressure can be calculated from
(8)and the corresponding initial pressure can be calculated from 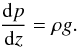 (9)The temperature is then derived from the gas law. Parameters ρ1, z1, ρ2, and z2 are chosen so that the initial density and temperature profiles satisfy the criteria described above, while zch is used to shift the profile in a vertical direction. In the present simulations, we use two initial atmospheres: low-density with the coronal density corresponding to quiet corona (~ 109 cm-3) (Model A thereafter), and high-density with the coronal density corresponding to cases of extremely high density above active regions (~ 1010 cm-3) (Model B thereafter; see e.g. Tripathi et al. 2008). The parameters for Eq. (8) are given in Table 2.1, and the density and temperature for Models A and B are shown in Fig. 1. In addition, Fig. 1 shows the column density defined as
(9)The temperature is then derived from the gas law. Parameters ρ1, z1, ρ2, and z2 are chosen so that the initial density and temperature profiles satisfy the criteria described above, while zch is used to shift the profile in a vertical direction. In the present simulations, we use two initial atmospheres: low-density with the coronal density corresponding to quiet corona (~ 109 cm-3) (Model A thereafter), and high-density with the coronal density corresponding to cases of extremely high density above active regions (~ 1010 cm-3) (Model B thereafter; see e.g. Tripathi et al. 2008). The parameters for Eq. (8) are given in Table 2.1, and the density and temperature for Models A and B are shown in Fig. 1. In addition, Fig. 1 shows the column density defined as 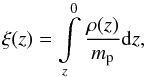 (10)where mp is the proton mass.
(10)where mp is the proton mass.
By introducing the scale length L0, characteristic magnetic field B0 and characteristic plasma density ρ0 one can derive the dimensionless variables for all used physical parameters. Thus, 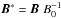 ,
, 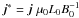 ,
, 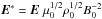 , ρ∗ = ρρ0,
, ρ∗ = ρρ0, 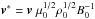 ,
, 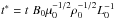 ,
, 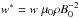 , and
, and 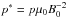 , and
, and 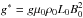 , where starred variables denote dimensionless physical parameters. The position vector and all the length variables are scaled as
, where starred variables denote dimensionless physical parameters. The position vector and all the length variables are scaled as 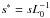 . The dimensionless resistivity can be derived as
. The dimensionless resistivity can be derived as 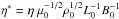 . Later in the paper we refer to the dimensionless parameters (dropping the star symbol) everywhere, except for the cases where units are given explicitly. In the present simulations, we use the following scaling parameters: L0 = 106 m, B0 = 4 × 10-3 T, and ρ0 = 3.3 × 10-12 kg m-3, yielding the characteristic velocity v0 = 1.95 × 106 m s-1 and time t0 = 0.53 s.
. Later in the paper we refer to the dimensionless parameters (dropping the star symbol) everywhere, except for the cases where units are given explicitly. In the present simulations, we use the following scaling parameters: L0 = 106 m, B0 = 4 × 10-3 T, and ρ0 = 3.3 × 10-12 kg m-3, yielding the characteristic velocity v0 = 1.95 × 106 m s-1 and time t0 = 0.53 s.
2.2. Derivation of configuration with twisted fluxtube
A magnetic field configuration with a twisted, bended fluxtube is constructed by adding a twist to an initially potential magnetic field.
The initial configuration is the potential field of two magnetic monopoles located outside the numerical domain: 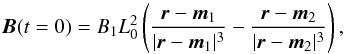 (11)where r is the position vector, and m1 and m2 are the positions of the monopoles: m1 = [0;a; − h] and m2 = [0; − a; − h]. The depth of the “monopoles”, h, determines the convergence of the magnetic field towards footpoints. In our simulations, a = 6.4L0 and h = 0.2L0, providing the convergence ratio (the magnitude of magnetic field at the footpoint to that at the loop-top) of ~ 10.
(11)where r is the position vector, and m1 and m2 are the positions of the monopoles: m1 = [0;a; − h] and m2 = [0; − a; − h]. The depth of the “monopoles”, h, determines the convergence of the magnetic field towards footpoints. In our simulations, a = 6.4L0 and h = 0.2L0, providing the convergence ratio (the magnitude of magnetic field at the footpoint to that at the loop-top) of ~ 10.
 |
Fig. 2 Maximum rotational velocity (solid line) and final twist angle (dashed line) as functions of the distance from the centre of rotation. |
The helicity is injected into the system by applying rotation at the footpoints. Then we follow the evolution of the magnetic field using ideal MHD. The centres of rotation are the points with the maximum magnetic field at the lower boundary: x = 0 and y ≈ ± 6.4L0. Rotational velocity corresponds to the solid rotation case (see Fig. 2), where vrot ~ r inside the footpoint radius R = 0.5L0: ![\begin{eqnarray} v_{\rm rot}(r)= \omega_{\rm twist}r \times \left[1-\tanh \left(\frac{r-R}{0.05 L_0}\right)\right]\frac t{t_{\rm twist}}\exp \left(-\frac t{t_{\rm twist}}\right), \end{eqnarray}](/articles/aa/full_html/2014/01/aa21715-13/aa21715-13-eq88.png) (12)where ωtwist and ttwist are the characteristic angular velocity and time, respectively.
(12)where ωtwist and ttwist are the characteristic angular velocity and time, respectively.
The rotation is applied through vx and vy components at the lower boundary, while the vertical velocity is zero. The magnetic field components are kept constant across the lower boundary (∂B/∂z = 0), along with the specific internal energy (∂w/∂z = 0). The density at the lower boundary is kept constant, ρ(z = 0,t) = ρ(z = 0,t = 0), and similar to the upper boundary, the gravitational acceleration is set to zero here to maintain boundary stability. In all the experiments, we have used ωtwist = 0.1 rad/s and ttwist = 250t0. Hence, the rotational velocity is low, vtwist ~ 10-2v0, and the field structure, effectively, goes through a sequence of quasi-equilibrium states. After ttwist ~ 103t0, the total twist is about 8π, and the magnetic configuration is nearly force-free but apparently kink-unstable. The obtained field geometry is similar to that in Gordovskyy et al. (2012), except we now have a more realistic bended loop and gravitationally stratified atmosphere.
 |
Fig. 3 Magnetic field lines during kink instability development: view from the top at t ≈ 800t0. The blue colour denotes the field lines connecting the footpoint centres; green colour denotes an ambient field. |
The evolution of the models during and after the onset of kink instability is considered using resistive MHD, as described in the Sect. 2.3.
2.3. Magnetic reconnection in twisted coronal loops
The kink instability occurs approximately at t = 920t0 and t = 950t0 in the Model A and Model B, respectively. In both cases, the m = 1 kink mode dominates, resulting in the sigmoid structure (Fig. 3).
The simulations are switched from an ideal to resistive MHD regime at t = 896t0. The resistivity consists of two components: uniform and constant background resistivity ηback and non-uniform current-driven anomalous resistivity ηcr. The need to specify some functional form for anomalous electric resistivity (or magnetic diffusion coefficient) is an intrinsic flaw in MHD simulations of magnetic reconnection; the resistivity in most numerical models is arbitrary to some extent. Many studies, however, attempt to use some physically motivated form of anomalous resistivity, most often assuming that it is caused by the development of ion-acoustic turbulence (see Ugai 1992; Uzdensky 2003; Barta et al. 2011). In the present simulations, we adopt similar approach and use current-driven anomalous resistivity. The total resistivity is defined as 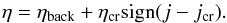 (13)The critical current jcr can be derived from the criteria vdrift > vcr, which is normally used in such simulations (e.g. Kliem et al. 2000). Here, vdrift = j/(en) is the electron drift velocity and the critical velocity equal to the sound speed
(13)The critical current jcr can be derived from the criteria vdrift > vcr, which is normally used in such simulations (e.g. Kliem et al. 2000). Here, vdrift = j/(en) is the electron drift velocity and the critical velocity equal to the sound speed 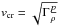 . Hence, the expression for a critical current can be written as
. Hence, the expression for a critical current can be written as 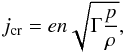 (14)and by using the scaling parameters introduced above, this formula can be reduced to a more convenient form
(14)and by using the scaling parameters introduced above, this formula can be reduced to a more convenient form 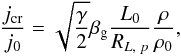 (15)where
(15)where 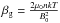 is the gas to magnetic pressure ratio and
is the gas to magnetic pressure ratio and 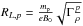 is the Larmor radius of a thermal proton. The problem, however, is that in global MHD models the current density is limited by the numerical grid resolution. In our simulations the grid resolution is δL = L0/256 ≈ 4 × 10-3L0 or ~4 km in real terms, while it is widely accepted that a realistic thickness of a RCS is about the Larmor radius of the proton RL,p, which is ~1 m in the corona. Hence, the grid resolution is by a factor ~103−104 larger than realistic RCS thickness, which means that the real current densities should be ~103 − 104 higher. To overcome this problem, we introduce a correcting factor of δL/RL,p = 4 × 103 for jcr resulting in the following form:
is the Larmor radius of a thermal proton. The problem, however, is that in global MHD models the current density is limited by the numerical grid resolution. In our simulations the grid resolution is δL = L0/256 ≈ 4 × 10-3L0 or ~4 km in real terms, while it is widely accepted that a realistic thickness of a RCS is about the Larmor radius of the proton RL,p, which is ~1 m in the corona. Hence, the grid resolution is by a factor ~103−104 larger than realistic RCS thickness, which means that the real current densities should be ~103 − 104 higher. To overcome this problem, we introduce a correcting factor of δL/RL,p = 4 × 103 for jcr resulting in the following form: 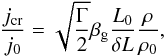 (16)which brings the critical current just above the current densities before the kink instability.
(16)which brings the critical current just above the current densities before the kink instability.
 |
Fig. 4 Total magnetic energy and total kinetic energies as functions of time for the low-density (solid lines) and the high-density models (dashed lines). Time is measured in t0 units, while the energies are measured in |
 |
Fig. 5 Selected magnetic field lines (left panels) and current density iso-surfaces (j = 0.5) (right panels) during magnetic reconnection in the Model A (low-density case). Different colours are used for magnetic field lines to demonstrate the change of connectivity. Blue lines originate almost at the centre of the footpoint at y ≈ 6.4; red lines originate almost at the centre of the footpoint (y ≈ − 6.4); other lines belonging to the twisted fluxtube are shown in green. The corresponding times are shown at the lower left corners. |
The background resistivity is ηback = 10-6. This value is substantially higher than real classical resistivity in the corona (which would be about 10-9, if we consider our scaling parameters), but it is not expected to affect the model, as the corresponding diffusion time is tdiff ≈ (δL)2/ηback ≈ ~ 102 − 103t0, where δL is the grid step. As far as the value for the anomalous resistivity is concerned, it is more difficult to determine a physically-justified ηcr. Therefore, the experiment with low-density atmosphere (Model A) has been repeated with several values of η1: 10-4, 4 × 10-4, 10-3 and 4 × 10-3. As in earlier MHD experiments with Lare code, we did not find any noticeable difference in the equilibrium formed after the reconnection (Gordovskyy et al. 2011). The main difference is the speed of relaxation: it is nearly proportional to 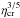 . Additionally, it was found that dissipation due to numerical viscosity increases for higher ηcr values. This can be explained by faster plasma flows in models with faster energy release. This effect was found to be especially significant in the experiment with ηcr = 4 × 10-3: the energy lost due to (artificial) viscous dissipation was comparable to Ohmic heating. Therefore, for particle trajectory calculations in Sect. 3 we use experiments with ηcr = 10-3.
. Additionally, it was found that dissipation due to numerical viscosity increases for higher ηcr values. This can be explained by faster plasma flows in models with faster energy release. This effect was found to be especially significant in the experiment with ηcr = 4 × 10-3: the energy lost due to (artificial) viscous dissipation was comparable to Ohmic heating. Therefore, for particle trajectory calculations in Sect. 3 we use experiments with ηcr = 10-3.
Once the field goes unstable, the current density drastically increases near loop-top and footpoints. The current density is high in these two regions due to different reasons: near footpoints strong currents appear due to magnetic field convergence, while the current density near the loop-top becomes high because of the kink resulting in formation of magnetic rope. These regions, however, are not compact: they are extended along the loop legs and from time to time the footpoint regions get merged with the loop-top one. The increase in the current density above critical threshold switches on the anomalous resistivity, which, in turn, results in magnetic reconnection and dissipation of magnetic energy. This is qualitatively similar to the reconnection scenario in previous studies (Browning et al. 2008; Hood et al. 2009; Gordovskyy & Browning 2012).
Just after the kink, the current is concentrated in a cylindrical structure following the loop legs. At the top of the loop, there is a current ring corresponding to the magnetic plasmoid. The current density is particularly high near the footpoints (due to magnetic field convergence) and in the ring at the top of the loop. As in previous experiments (e.g., Hood et al. 2009; Gordovskyy & Browning 2011; Bareford et al. 2013), the current gradually becomes filamentary and weakens. It almost disappears after t ≈ 1900t0, apart from the footpoints, where it remains below jcr level.
Total magnetic and kinetic energies for the MHD models are plotted versus time in Fig. 4. The magnetic energy variations are similar in both models. The difference in the maximum energy and the energy of the relaxed state is due to the density-dependent anomalous resistivity current threshold. The latter is higher in the high-density case, and this is why the current density and magnetic energy can reach a higher value before the reconnection starts. Similarly, as the reconnection proceeds, the maximum current density in this case gets below the critical current threshold earlier, while the magnetic energy is still relatively high. As far as the kinetic energy is concerned, the low- and high-density cases are different during the helicity injection phase. Both model loops demonstrate weak kink oscillations; however the frequency of oscillations and their amplitude are substantially smaller in the high-density case (Model B) than those in the low-density case (Model A). After the kink occurs (at approximately t > 900 t0), the kinetic energy variations are similar: they peak at ~0.002 of initial model energy and then gradually decay. The kinetic energy at this stage is associated largely with reconnection outflows.
In contrast with previous simulations of kink instability in coronal loops (Kliem et al. 2010), we do not observe separation and emergence of the plasmoid. The difference apparently appears because magnetic reconnection in our simulations occurs in a completely closed magnetic configuration, and the overlying ambient magnetic field lines are tied either to lower (photospheric) or side boundaries. The reconnection happens mostly at the very top of the kinking loop near the upper part of the plasmoid ring between the twisted field lines and the overlying ambient field lines. This results in the reduction of a twist and radial expansion of the loop, which is similar to the previous simulations of the initially cylindrical loop (Gordovskyy & Browning 2011, 2012). The main two differences with these previous simulations are: (a) the process now, obviously, is not cylindrically symmetric and the current density varies strongly both along the loop and within its cross-section; (b) the absence of magnetic diffusion very close to the footpoints mean the two footpoints remain connected in the final equilibrium, and all the field lines remain connected to both footpoints (unlike in Gordovskyy & Browning 2011). The latter is explained by the sketch in Fig. 6.
3. Electrons and protons in a twisted coronal loop
In this section, we consider particle motion in reconnecting a twisted coronal loop based on the electric and magnetic fields, and plasma density obtained in the MHD simulations (see Sect. 2.3). The methodology is explained in Sect. 3.1, which followed by a description of the trajectories (Sect. 3.2), energy spectra (Sect. 3.3), and spatial distribution (Sect. 3.5).
3.1. Test-particle motion in presence of Coulomb collisions
Let us consider the motion of charged test-particles using the guiding-centre approximation with the particle trajectory described by the velocity parallel to magnetic field v||(t), drift velocity perpendicular to the magnetic field u(t), and Larmor gyration velocity vg(t). This approach is valid in this model, since the magnetic field is non-zero throughout the domain, and the proton and electron gyro-radii are much smaller than the characteristic scale L0.
The trajectories of changed particles in the presence of collisions can be described by the following set of equations: ![\begin{eqnarray} \frac {{\rm d} {\boldsymbol r}}{{\rm d}t} &=& {{\boldsymbol u}} + \frac{(\gamma v_{||})}\gamma {\boldsymbol b} \label{gca-pos}\\ {\boldsymbol u} &=& {\boldsymbol u}_E + \frac mq \frac {(\gamma v_{||})^2}{\gamma \kappa^2 B} [{\boldsymbol b} \times ({\boldsymbol b}\cdot {\boldsymbol \nabla}){\boldsymbol b}] \nonumber \\ &&+ \frac mq \frac \mu {\gamma \kappa^2 B} [{\boldsymbol b} \times {\boldsymbol \nabla} (\kappa B)]\label{gca-drift}\\ \frac{{\rm d} (\gamma v_{||})}{{\rm d}t} &=& \frac qm {\boldsymbol E}\cdot {\boldsymbol b} - \frac \mu \gamma ({\boldsymbol b} \cdot {\boldsymbol \nabla}(\kappa B))\nonumber \\ && \left[ v \frac{\delta \alpha}{\delta t}\right]_{\rm coll} + \left[\alpha \frac {\delta v}{\delta t} \right]_{\rm coll}\label{gca-vpara}\\ \frac{{\rm d}\mu }{{\rm d}t} &=& \left[\frac{v(1-\alpha^2)}B \frac{\delta v}{\delta t}\right]_{\rm coll} -\left[\frac{\alpha v^2}B \frac{\delta \alpha}{\delta t}\right]_{\rm coll}\cdot\label{gca-mgm} \end{eqnarray}](/articles/aa/full_html/2014/01/aa21715-13/aa21715-13-eq146.png) Here, r is particle position, μ is specific magnetic moment
Here, r is particle position, μ is specific magnetic moment 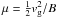 , uE is the E × B-drift velocity uE = E × B/B2, and b is the magnetic field direction b = B/B. Apart from the last two terms in Eqs. (19) and (20), this is the standard set of relativistic guding-centre equations (Northrop 1963). The relativistic factors are defined as
, uE is the E × B-drift velocity uE = E × B/B2, and b is the magnetic field direction b = B/B. Apart from the last two terms in Eqs. (19) and (20), this is the standard set of relativistic guding-centre equations (Northrop 1963). The relativistic factors are defined as
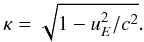 The collisional terms in the equations above are defined below by Eqs. (22) and (25). Let us discuss them and their numerical implementation in more details. In collisional terms, we ignore the relativistic factor γ, since particles with a value of γ noticeably greater than 1 are not significantly affected by Coulomb collisions. The average collisional energy loss of a particle with mass m moving with speed
The collisional terms in the equations above are defined below by Eqs. (22) and (25). Let us discuss them and their numerical implementation in more details. In collisional terms, we ignore the relativistic factor γ, since particles with a value of γ noticeably greater than 1 are not significantly affected by Coulomb collisions. The average collisional energy loss of a particle with mass m moving with speed 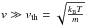 in fully ionised thermal plasma with temperature T can be expressed as (see e.g. Emslie 1978):
in fully ionised thermal plasma with temperature T can be expressed as (see e.g. Emslie 1978): 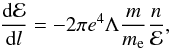 (21)where Λ is the Coulomb logarythm. For non-relativistic particles, the kinetic energy ℰ = mv2/2 and Eq. (21) can be rewritten as
(21)where Λ is the Coulomb logarythm. For non-relativistic particles, the kinetic energy ℰ = mv2/2 and Eq. (21) can be rewritten as 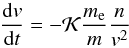 (22)where
(22)where 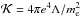 and Λ ≈ 20. The Eq. (22) yields variations in the full velocity δv/δt for Eqs. (19) and (20). The full velocity in the right-hand side of Eq. (22) is calculated as
and Λ ≈ 20. The Eq. (22) yields variations in the full velocity δv/δt for Eqs. (19) and (20). The full velocity in the right-hand side of Eq. (22) is calculated as 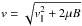 . Here the drift velocity is disregarded, since (a) it is normally comparable to or lower than the thermal velocity vth, and (b) the main component of the drift, uE, is caused predominantly by bulk plasma motion.
. Here the drift velocity is disregarded, since (a) it is normally comparable to or lower than the thermal velocity vth, and (b) the main component of the drift, uE, is caused predominantly by bulk plasma motion.
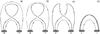 |
Fig. 6 Schematic sketch showing change of connectivity during magnetic reconnection in the twisted loop. |
 |
Fig. 7 Typical electron trajectories, their energies and pitch-angles. Particles are injected with thermal energies at the locations denoted by squares on the lower panel. Blue, green, and red lines denote particles, which are non-thermal at some point, while grey lines denote particles, which remain thermal throughout simulations. See text for more details. |
 |
Fig. 8 Typical proton trajectories, their energies and pitch-angles. Particles are injected with thermal energies at the locations denoted by squares on the lower panel. Blue, green, and red lines denote particles, which are non-thermal at some point, while grey lines denote particles, which remain thermal throughout simulations. See text for more details. |
The pitch-angle distribution of high-energy particles in thermal plasma changes with time due to Coulomb collisions as 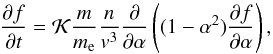 (23)where the pitch-angle is defined as α = v| |/v. In terms of individual particles, the pitch-angle diffusion represents random deflections with respect to a chosen direction. Let us evaluate the probability of a test-particle to be deflected. Equation (23) means that the fraction of particles changing its pitch-angle from α to α + δα within the time interval δt is
(23)where the pitch-angle is defined as α = v| |/v. In terms of individual particles, the pitch-angle diffusion represents random deflections with respect to a chosen direction. Let us evaluate the probability of a test-particle to be deflected. Equation (23) means that the fraction of particles changing its pitch-angle from α to α + δα within the time interval δt is 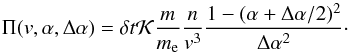 (24)This, in turn, means the following: if individual particles are deflected by Δα with probability Π(v,α,Δα) as per Eq. (24), then the pitch-angle distribution of the whole particle population should satisfy Eq. (23).
(24)This, in turn, means the following: if individual particles are deflected by Δα with probability Π(v,α,Δα) as per Eq. (24), then the pitch-angle distribution of the whole particle population should satisfy Eq. (23).
In the numerical scheme used here, the pitch-angle diffusion is implemented through stochastic jumps of a particle pitch-angle by a fixed value of either Δα = 0.05 or Δα = −0.05 after every timestep δt with the probability of Π(v,α,Δα) or Π(v,α, − Δα), respectively (which means the pitch-angle remains the same with the probability 1 − Π(v,α,Δα) − Π(v,α, − Δα)). Hence, the variation in pitch-angle with time can be written as: 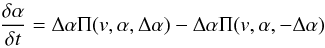 (25)with probabilities Π as per Eq. (24).
(25)with probabilities Π as per Eq. (24).
In each numerical experiment, we calculate trajectories for ~ 106 test electrons and protons. Initially, particles are uniformly distributed within the simulation domain, have Maxwellian velocity distributions corresponding to the temperature of 1 MK, and are uniformly distributed with respect of the pitch-angle α from − 1 to 1.
The calculations have been performed using the GCA code based on the second order Runge-Kutta scheme (Gordovskyy et al. 2010, 2011). In addition to the usual limitations on the integration timestep (δt ≪ δr/v and δt ≪ v/a, where δr is the grid step and a is the acceleration), the collisional terms add another requirement: 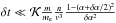 , which is necessary for Π(v,α,δα) ≪ 1. (When Π(v,α,δα) ~ 1, the scheme used for pitch-angle scattering calculations becomes unstable, and, obviously, the probability cannot be Π(v,α,δα) > 1.)
, which is necessary for Π(v,α,δα) ≪ 1. (When Π(v,α,δα) ~ 1, the scheme used for pitch-angle scattering calculations becomes unstable, and, obviously, the probability cannot be Π(v,α,δα) > 1.)
The time-dependent electric and magnetic fields and their spatial derivatives for the right-hand side of Eqs. (17)–(20) are taken from the resistive MHD simulations described in Sect. 2.3. The data for each particle position is derived by linear interpolation of the data within four-dimensional (x,y,z,t) cells from the ajacent grid points (see Gordovskyy et al. 2011, 2012; Gordovskyy & Browning 2011). The domain boundaries are closed for thermal test-particles with ℰ < 1 keV and open for higher energy particles. Each particle is followed until the end of simulations at t = 1800t0 or until it leaves the domain through one of the boundaries.
3.2. Particle trajectories
Typical electron and proton trajectories are shown in the Figs. 7 and 8, respectively. In general, both species are very adiabatic and hence, behave very similarly, The main difference, of course, is that protons are much (by factor of ~43) slower. As a result, their trajectories are smoother, since the effect of small-scale fluctuations (in the parallel electric field value, magnetic field curvature etc) is negligible due to time averaging.
The majority of particles remain in the thermal distribution; only a few particles (~5%) are accelerated beyond 1 keV. This is comparable to typical acceleration efficiencies derived from observed hard X-ray emission. This validates the use of a test-particle approach, as the effect of high-energy particles on the magnetic and electric field should be considerably low.
Particles move predominantly along the magnetic field lines. Despite the connectivity changes, all the field lines of the twisted loop remain connected to both footpoints, and there is no open field. As a result, during the reconnection most of high-energy particles remain in or around the twisted loop and precipitate towards one of the footpoints.
Particles accelerated by a parallel electric field in an almost collisionless corona have a very narrow pitch-angle distribution around α = ± 1, which means they are strongly collimated along the magnetic field (Gordovskyy et al. 2011; Gordovskyy & Browning 2012). However, they get scattered due to collisions in the denser chromosphere, getting a wider pitch-angle distribution. As a result, there is a small but noticeable fraction of high-energy particles reflected by the converging field back to the corona. Electrons with energies up to ~100 keV and nearly all the protons are thermalised before reaching the lower boundary. Hence, only a small fraction of energetic electrons (with ℰ > 100 keV) and some particles accelerated near the footpoints (which did not have enough time to thermalise) can get to the photosphere (i.e., the lower boundary of the simulation domain).
3.3. Particle energy spectra
There are two main factors affecting particle energies: parallel electric field and Coulomb scattering. The appearance of a strong electric field is a transient and local effect, while collisional deceleration of high-energy particles is always present. Hence, unlike in the collisionless models by Gordovskyy et al. (2011) and Gordovskyy & Browning (2012), it is not possible to characterise the acceleration process by the final spectra in this type of model, as these spectra are inevitably thermal. We consider the energy spectra at three different stages of the reconnection process: just after the kink instability occurs, during the fastest energy release (i.e., when dℰm/dt is highest), and during the decay stage. The energy spectra for protons and electrons for low- and high-density cases are shown in Figs. 9–12.
The electron energy distributions at the beginning of reconnection are similar to those obtained in simulations with no collisions (Gordovskyy & Browning 2011): the spectra are combinations of a Maxwellian thermal distribution and nearly power-law high-energy tail. However, in the low-density case the high-energy tail, surprisingly, appears to be softer than in previous studies; its power-law index is about 2.0–3.5, which is observed in many flares. In the high-density case, the “high-energy” tail is harder, the spectral index is about 1.5–2.0. At the later stages (t = 1100−1500t0), the electric fields gradually decay and the collisions become dominant. This results in the hardening of the spectra around a few keV, and at some point, a gap appears between the thermal part and high-energy part. This spectral hardening at lower energies (of few deka-keV) is similar to that, which appears in thick-target models.
Comparing electron and proton energy spectra demonstrates the contrast in acceleration times: electron non-thermal spectra are formed within ~1−10t0 after a kink, while it takes around 10−100 t0 to form a smooth high-energy tail for protons. At the same time, protons lose their energies due to collisions faster than electrons with the same energy (since 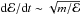 ). As a result, it is more difficult in a collisional plasma to accelerate protons than electrons. The difference in proton and electron acceleration efficiencies can also be explained in terms of the electric field required to accelerate particles with energy ℰ in presence of collisions in plasma with density n. Indeed, particles are accelerated if
). As a result, it is more difficult in a collisional plasma to accelerate protons than electrons. The difference in proton and electron acceleration efficiencies can also be explained in terms of the electric field required to accelerate particles with energy ℰ in presence of collisions in plasma with density n. Indeed, particles are accelerated if 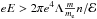 , or if the minimum field required to accelerate particles is
, or if the minimum field required to accelerate particles is
 |
Fig. 9 Electron energy spectra in the Model A. Times are shown above corresponding panels. |
 |
Fig. 10 Electron energy spectra in the Model B. Times are shown above corresponding panels. |
(For thermal electrons (ℰ = kBT, m = me), this becomes the standard expresion for Dreicer field.) Obviously, this Ecrit value for protons is higher by a factor of mp/me than Ecrit for electrons. Therefore, when the typical electric field in the system is higher than both Ecrit(protons) and Ecrit(electrons), the proton acceleration efficiency should be similar to that for electrons. However, when the typical electric field is lower than Ecrit(protons) but higher than Ecrit(electrons), the number of high-energy protons should be lower than that of electrons, which is the case in the Model B.
 |
Fig. 11 Proton energy spectra in the Model A. Times are shown above corresponding panels. |
 |
Fig. 12 Proton energy spectra in the Model B. Times are shown above corresponding panels. |
This difference between the low-density and high-density cases can also be seen in total energetics. Thus, the total energy carried by high-energy protons and electrons in the Model A (low-density case) is nearly equal and is about 6–8% of the energy released during the reconnection, (although the maximum total non-thermal proton energy is reached slightly later then maximum total non-thermal electron energy). At the same time, the total energy carried by non-thermal electrons in the high-density case (Model B) reaches ~4% of the energy released during reconnection, while protons carry less than 1%. These values, however, show the energies contained in non-thermal particles at a given moment and do not necessarily reflect the total energies deposited by non-thermal particles (or, in other words, the electromagnetic energy converted into thermal energy through non-thermal particles). This would depend on the value of the electric field compared to the local Ecrit value. Thus, particles accelerated by electric field E ~ Ecrit are almost instantly thermalised, which means that the number of non-thermal particles in the system at any time remain low, although a substantial amount of energy is converted from electric to thermal in this process.
 |
Fig. 13 Normalised pitch-angle distributions of high-energy particles (ℰ > 5 keV) during fast reconnection stage (t = 1120t0). Left panels (a) and c)) are for electrons; right panels (b) and d)) are for protons. Upper panels (a) and b)) correspond to the low-density case (Model A), while lower panels correspond to the high-density case (Model B). |
Here, we define non-thermal as particles with energies >1 keV (the temperature of the initial distribution corresponds to around 100 eV). The energy spectrum below this energy is not correct in the present model, since Eq. (21) is only valid for non-thermal electrons with an energy that is much higher than kBT for the ambient plasma.
3.4. Particle pitch-angle distributions
In collisionless models of particle acceleration by parallel electric fields, the pitch-angle distribution is trivial: since perpendicular velocities remain ~ vth and parallel velocitites increase drastically, all non-thermal particles are strongly collimated along magnetic field lines (i.e., vg/v| | ≪ 1), apart from particles being reflected by converging magnetic field. Collisions, however, result in effective scattering of supra-thermal particles with moderate energies at ~ 1–10 keV. Pitch-angle distributions are shown in Fig. 13.
It can be seen that particles in the low-density case (Fig. 13a, b) are also well-collimated along the field lines, although the collimation is not as strong as in collisionless models. The majority of particles (~ 80%) have pitch-angles | α | > 0.75. In the high-density case, however, pitch-angle distributions are more isotropic: ~ 40–50% of particles have pitch-angles of | α | < 0.75.
The pitch-angle distributions also reveal the preferred directions of acceleration for diferent species. Thus, protons tend to have positive pitch-angles indicating that they move predominantly towards y = + 6.4L0 footpoint, while electrons tend to have negative pitch-angles and, hence, move towards the opposite footpoint. This effect can also be seen in spatial distribution (see next section). Coulomb collisions strongly affect particles in Model B, and, as the result, the proton-electron footpoint asymmetry almost disappears in the high-density case.
3.5. Particle spatial distribution and synthetic hard X-ray intensities
The helicity does not change its sign in the initial configuration, which means the current has preferential direction. This results in charge separation at the early stages of reconnection: electrons and protons are accelerated towards different footpoints, producing the electron-proton asymmetry of footpoints that can be seen in Fig. 14. As the current structure becomes filamentary with time, the acceleration process becomes more chaotic and footpoint asymmetry decreases. At the end of reconnection, only a slight assymetry can be seen. This is consistent with observations showing time delay in appearance of a second footpoint source.
 |
Fig. 14 High-energy (ℰ > 5 keV) electron and proton distribution in X − Y plane. Most of the particles are concentrated at low heights close to the footpoints. |
 |
Fig. 15 Synthetic hard X-ray emission at 10 keV from the simulated flaring loop in low-density atmosphere. |
Figure 14 also shows that the footpoint area (which represents the cross-section of the volume occupied by high-energy particles just above the photosphere) increases with time. During the reconnection, the radius of footpoints increases from ~0.5 Mm to nearly 1.2 Mm. This effect is mainly due to the reconnection between the field lines of the twisted fluxtube and ambient field lines (see discussion in Gordovskyy & Browning 2011).
Based on the electron distributions derived in Models A and B, we calculate intensities of the bremsstrahlung hard X-ray emission from the flaring loop. We use the simplified form of the bremsstrahlung cross-section (see e.g. Kontar et al. 2002): 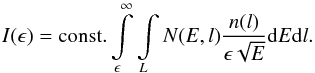 (26)The synthetic intensity maps are shown in Figs. 15 and 16 for four different moments. In order to compare them with observational data, they are smoothed by a Gaussian profile with the half-width of ~1.5 Mm (comparable to the RHESSI spatial resolution). The main difference between the low-density case (Model A) and high-density case (Model B) is that the latter shows noticeable extended emission from the loop, while the low-density case has noticeable emission only from the footpoints. This can be easily explained by comparing the electron mean-free-path in these two models: in the low-density model, the mean free path for the energies ~10 keV is substantially longer than the loop length (~20 Mm), while it is only ~1 Mm in the high-density case.
(26)The synthetic intensity maps are shown in Figs. 15 and 16 for four different moments. In order to compare them with observational data, they are smoothed by a Gaussian profile with the half-width of ~1.5 Mm (comparable to the RHESSI spatial resolution). The main difference between the low-density case (Model A) and high-density case (Model B) is that the latter shows noticeable extended emission from the loop, while the low-density case has noticeable emission only from the footpoints. This can be easily explained by comparing the electron mean-free-path in these two models: in the low-density model, the mean free path for the energies ~10 keV is substantially longer than the loop length (~20 Mm), while it is only ~1 Mm in the high-density case.
 |
Fig. 16 Synthetic hard X-ray emission at 10 keV from the simulated flaring loop in high-density atmosphere. |
4. Summary
In the present work, we use a combination of MHD and test-particle methods to study energy release and high-energy particle motion in a reconnecting twisted coronal loop. The approach is generally similar to that previously used in 2D (Gordovskyy et al. 2011) and 3D models (Gordovskyy & Browning 2011, 2012): time-dependent electric and magnetic fields and density distributions are used as an input for guiding-centre test-particle calculations of proton and electron trajectories. The main benefits from the present model are that
-
we use a realistic loop-like structure (similarlyto Kliemet al. 2010), and the twist is createdby slow footpoint rotation;
-
we take into account strong stratification in the lower atmosphere and consider different densities in the corona;
-
we take into account the effect of Coulomb collisions on test-particle motion.
Therefore, this study attempts to combine energy release during reconnection with particle acceleration and transport within a single model. Obviously, the main problem is that the feedback of energetic particle motion on the electric and magnetic field evolution is ignored. However, this should not significantly affect evolution of the system in the cases studied here, since the acceleration efficiency is low: high energy particles carry less than ~10% and hence, the plasma is almost “thermal” (see also Gordovskyy et al. 2012).
Magnetic reconnection in the present models is similar to that observed in cylindrical fluxtubes with analytical magnetic field twist profiles (e.g. Hood et al. 2009; Gordovskyy & Browning 2011). Thus, a strong, helically shaped current is formed after the kink occurs; the current stucture gradually becomes filamentary as the reconnection proceeds. The connectivity changes in two different ways: first, the magnetic twist is reduced and second, as shown by Gordovskyy & Browning (2011), the twisted loop field lines reconnect with ambient field lines, resulting in an effective increase in the loop cross-section. However, there are several features in the present model, which are not observed in models with cylindrical fluxtubes. First, a current torus, almost perpendicular to the loop, is formed near the loop-top just after the kink. Second, although the magnetic energy dissipates in three extended regions (near the footpoints and the loop-top), the field connectivity changes mainly due to magnetic reconnection just below the magnetic torus, which is formed near the loop-top after the kink. Finally, dissipation of the azimutal field leads to a substantial shortening of the loop field lines. The density of the plasma in the corona does not seem to have a noticeable effect on reconnection, as expected, since the plasma beta is low (around 10-1) in both cases.
Particles can be accelerated almost anywhere within the reconnecting loop, although they are predominantly energised close to the loop-top, where the ratio of electric field to Dreicer field is the highest. The energy spectra are combinations of Maxwellian thermal distributions at low energies (below keV) and are nearly power-low high-energy tails. The spectral indices for electrons in the 10–100 keV range are between 1.5 and 3.0, which means the spectra are slightly softer than in similar collisionless models. The electron spectra are harder in the case with dense coronal plasma (1011 cm-3) than in the case with normal coronal density (109 cm-3). The acceleration efficiency strongly depends on the ambient plasma density. This is not surprising, since the particle acceleration generally depends on the ratio of electric field to the so-called critical electric field Ecrit ~ mn/ℰ (i.e. the minimum electric field required to produce runaway particles; it is equal to the Dreicer field in case of thermal electrons) (see Sect. 3.3). In both cases (low- and high-density corona), the electric field is higher than the corresponding Ecrit value for electrons. However, in the high-density case the electric field in the system is comparable to the corresponding Ecrit value for protons, and there is almost no proton acceleration. This results in an interesting picture: in the low-density medium, the non-thermal particle energy is nearly equally split between protons and electrons, while in the high-density medium, protons remain nearly thermal amid a substantial number of non-thermal electrons. This can potentially explain why some flares effectively accelerate both electrons and ions, and other flares produce substantial number of electrons, while not showing any noticeable ion emission. Many phenomenological models suggest that this happens because, even though there are plenty of ions, their energy is insufficient to produce nuclear de-excitation lines needed for detection. However, it might be the case that ions in electron-only flares do not get accelerated due to high plasma density in the acceleration region.
High-energy particles are rather uniformly distributed along the flaring loop. There is a noticeable increase in the particle number towards footpoints, which can be easily explained by lower average parallel velocities due to magnetic field convergence. There is a visible proton-electron asymmetry between footpoints at the early stages of acceleration, because the initial configuration has a non-zero net current and hence, the electric field has a preferential direction along the fluxtube before it gets filamentary. Although this proton-electron asymmetry would result in the development of an oppositely-directed large-scale electric field along the reconnecting loop (the so-called return current electric field), this effect can still exist, as the non-thermal proton-electron current can be compensated by an ambient thermal electron current, provided the plasma is highly ionised and the number of high-energy particles is low (which is the case here; see Zharkova & Gordovskyy 2004, 2005). In the high-density case, this effect is less noticeable owing to pitch-angle scattering due to Coulomb collisions.
In general, the structure of the synthetic hard X-ray sources is similar to that observed with RHESSI (e.g. Lin 2011). There are high-intensity footpoint sources, which are flat (their height is only about 0.5–1.0 Mm), and weaker extended emission from the whole loop. The ratio of the footpoint and extended source intensities depends on the plasma density in the loop. In the case of normal coronal density, the emission comes mostly from the foopoints, while the intensity of the extended source in the high-density case is comparable to the footpoint intensities. The size of the footpoint sources increases with time (due to expansion of the twisted loop as discussed in Sect. 3.5; however, this effect is less prominent in hard X-ray due to the assumed temporal and spatial resolution of the instrument.
Similar to Gordovskyy & Browning (2012), we assume that the appearance of a strong parallel electric field due to anomalous resistivity in fragmented current structures is the main mechanism that accelerates particles. Other mechanisms, such as acceleration due to magnetic field contraction and large scale MHD waves, are included within our model and can have an effect, although they are found to be negligible compared to the parallel electric field (for the assumed value of anomalous resistivity and the adopted length scale).
Our work suggests that large-scale MHD turbulence develops during magnetic reconnection and results in fragmentation of initially solid current (see also Browning et al. 2008; Hood et al. 2009). This phenomenon affects particle behaviour: proton and electron trajectories become more stochastic, as they are accelerated through repeated encounters with current fragments (see Sect. 3.2 and Gordovskyy & Browning 2011, 2012; see also Cargill et al. 2012, for review). Another important factor, which can affect particle acceleration and transport is MHD turbulence at smaller spatial scales (e.g. Miller et al. 1996; Larosa et al. 1996; Cho & Lazarian 2006; Cargill & Vlahos 2009; Bian & Kontar 2010; Bian et al. 2010). Turbulence results in field line stochasticity and fast reconnection in multiple small-scale current sheets (Lazarian & Vishniak 1999; Eyink et al. 2011). Hence, the presence of small-scale turbulence, in principle, could drastically change characteristics of the electric field in the model and lead to a different picture of particle acceleration. The implications of turbulence for particle acceleration are summarized in Lazarian et al. (2012).
Furthermore, turbulence can make substantial contribution to particle scattering during their transport. Scattering due to Coulomb collisions considered in the present model is expected to be dominant in the dense chromosphere and transition region. At the same time, small-scale MHD turbulence can be important for particle scattering in the low-density corona, along with various types of self-induced kinetic waves. Thus, high-energy ions have been shown to generate kinetic Alfven waves (e.g. Voitenko 1998), which, in turn, result in noticeable heating in the corona (Gordovskyy et al. 2005) (while collisional scattering results only in effective heating of dense transition region and chromosphere).
However, it is impossible to include these microscopic effects in our large-scale model. The macroscopic description of these microscopic effects is required for them to be included in large-scale transport models, which necessitates more studies into this issue.
The scenario developed in the present paper is a good candidate for interepreting small non-eruptive explosive events occuring in single loop configurations. A benefit of this model is reduced energy losses during particle transport due to more uniform (rather than localized at the loop-top) acceleration (see discussion in Gordovskyy et al. 2012). The model, however, needs to be further improved; in particular, one needs to consider the possibility of continuous helicity injection (or footpoint twisting).
Acknowledgments
This work is funded by Science and Technology Facilities Council (UK).
References
- Amari, T., Luciani, J. F., Mikic, Z., & Linker, J. 2000, ApJ, 529, L49 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Arber, T. G., Longbottom, A. W., Gerrard, C. L., & Milne, A. M. 2001, J. Comput. Phys., 171, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Archontis, V., Tsinganos, K., & Gontikakis, C. 2010, A&A, 512, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aschwanden, M. J., Wuelser, J. P., Nitta, N. V., & Lemen, J. R. 2009, Sol. Phys., 256, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Bareford, M. R., Hood, A. W., & Browning, P. K. 2013, A&A, 550, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barta, M., Buechner, J., Karlicky, M., & Skala, J. 2011, ApJ, 737, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Bian, N. H., & Browning, P. K. 2008, ApJ, 687, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Bian, N. H., & Kontar, E. P. 2010, Phys. Plasmas, 17, 062308 [NASA ADS] [CrossRef] [Google Scholar]
- Bian, N. H., Kontar, E. P., & Brown, J. C. 2010, A&A, 519, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, D. S., Nightingale, R. W., Alexander, D., et al. 2003, Sol. Phys., 216, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C. 1976, Phil. Trans. R. Soc. London, Ser. A, 281, 473 [Google Scholar]
- Brown, J. C., Turkmani, R., Kontar, E. P., MacKinnon, A. L., & Vlahos, L. 2009, A&A, 508, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Browning, P. K., & van der Linden, R. A. M. 2003, A&A, 400, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Browning, P. K., Gerrard, C., Hood, A. W., Kevis, R., & van der Linden, R. A. M. 2008, A&A, 485, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cargill, P. J., & Vlahos, L. 2009, Turbulence in Space Plasmas (Springer), Lect. Notes Phys., 778 [Google Scholar]
- Cargill, P. J., Vlahos, L., Baumann, G., Drake, J. F., & Nordlund, A. 2012, Space Sci. Rev., 173, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Cho, J., & Lazarian, A. 2006, ApJ, 638, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Emslie, A. G. 1978, ApJ, 224, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Eyink, G., Lazarian, A., & Vishniak, E. T. 2011, ApJ, 743, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y. 2010, ApJ, 719, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, S. E., & Fan, Y. 2006, ApJ, 637, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Gordovskyy, M., & Browning, P. K. 2011, ApJ, 729, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Gordovskyy, M., & Browning, P. K. 2012, Sol. Phys., 277, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Gordovskyy, M., Zharkova, V. V., Voitenko, Yu. M., & Goossens, M. 2005, Adv. Space Res., 35, 1743 [NASA ADS] [CrossRef] [Google Scholar]
- Gordovskyy, M., Browning, P. K., & Vekstein, G. E. 2010, A&A, 519, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gordovskyy, M., Browning, P. K., & Vekstein, G. E. 2011, ApJ, 720, 1603 [Google Scholar]
- Gordovskyy, M., Browning, P. K., Kontar, E. P., & Bian, N. H. 2012, Sol. Phys., accepted [Google Scholar]
- Hood, A. W., Browning, P. K., & van der Linden, R. A. M. 2009, A&A, 506, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kliem, B., Karlicky, M., & Benz, A. O. 2000, A&A, 360, 715 [NASA ADS] [Google Scholar]
- Kliem, B., Linton, M. G., Toeroek, T., & Karlicky, M. 2010, Sol. Phys., 266, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P., Brown, J. C., & McArthur, G. K. 2002, Sol. Phys., 210, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P., Hannah, I. G., & Bian, N. H. 2011, ApJ, 730, L22 [Google Scholar]
- Kowal, G., de Gouveia Del Pino, E. M., & Lazarian, A. 2012, Phys. Rev. Lett., 19, 297 [Google Scholar]
- Larosa, T. N., Moore, R. L., & Miller, J. A. 1996, ApJ, 467, L454 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A., & Vishniak, E. T. 1999, ApJ, 517, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A., Vlahos, L., Kowal, G., et al. 2012, Space Sci. Rev., 173, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, R. P. 2011, Space Sci. Rev., 159, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Malanushenko, A., Yusuf, M. H., & Longcope, D. W. 2011, ApJ, 736, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. A., Larosa, T. N., & Moore, R. L. 1996, ApJ, 461, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Northrop, T. 1963, The Adiabatic Motion of Charged Particles (New York: Interscience) [Google Scholar]
- Raouafi, N. E. 2009, ApJ, 691, L128 [NASA ADS] [CrossRef] [Google Scholar]
- Regnier, S., & Amari, T. 2004, A&A, 425, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Srivastava, A. K., Zaqarashvili, T. V., Kumar, P., & Khodachenko, M. L. 2010, ApJ, 715, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Toeroek, B., & Kliem, T., ApJ, 630, L97 [Google Scholar]
- Tripathi, D., Mason, H. E., Young, P. R., & Del Zanna, G. 2008, A&A, 481, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ugai, M. 1992, Phys. Plasmas B, 4, 2953 [Google Scholar]
- Uzdensky, D. 2003, ApJ, 587, 450 [NASA ADS] [CrossRef] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Voitenko, Yu. M. 1998, Sol. Phys., 182, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., & Gordovskyy, M. 2004, ApJ, 604, 884 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., & Gordovskyy, M. 2005, A&A, 432, 1033 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Initial density (panel a)), temperature (panel b)), and column density (panel c)) distributions. Solid lines correspond to the low-density case (Model A); dotted lines correspond to the high-density case (Model B). |
| In the text | |
 |
Fig. 2 Maximum rotational velocity (solid line) and final twist angle (dashed line) as functions of the distance from the centre of rotation. |
| In the text | |
 |
Fig. 3 Magnetic field lines during kink instability development: view from the top at t ≈ 800t0. The blue colour denotes the field lines connecting the footpoint centres; green colour denotes an ambient field. |
| In the text | |
 |
Fig. 4 Total magnetic energy and total kinetic energies as functions of time for the low-density (solid lines) and the high-density models (dashed lines). Time is measured in t0 units, while the energies are measured in |
| In the text | |
 |
Fig. 5 Selected magnetic field lines (left panels) and current density iso-surfaces (j = 0.5) (right panels) during magnetic reconnection in the Model A (low-density case). Different colours are used for magnetic field lines to demonstrate the change of connectivity. Blue lines originate almost at the centre of the footpoint at y ≈ 6.4; red lines originate almost at the centre of the footpoint (y ≈ − 6.4); other lines belonging to the twisted fluxtube are shown in green. The corresponding times are shown at the lower left corners. |
| In the text | |
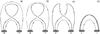 |
Fig. 6 Schematic sketch showing change of connectivity during magnetic reconnection in the twisted loop. |
| In the text | |
 |
Fig. 7 Typical electron trajectories, their energies and pitch-angles. Particles are injected with thermal energies at the locations denoted by squares on the lower panel. Blue, green, and red lines denote particles, which are non-thermal at some point, while grey lines denote particles, which remain thermal throughout simulations. See text for more details. |
| In the text | |
 |
Fig. 8 Typical proton trajectories, their energies and pitch-angles. Particles are injected with thermal energies at the locations denoted by squares on the lower panel. Blue, green, and red lines denote particles, which are non-thermal at some point, while grey lines denote particles, which remain thermal throughout simulations. See text for more details. |
| In the text | |
 |
Fig. 9 Electron energy spectra in the Model A. Times are shown above corresponding panels. |
| In the text | |
 |
Fig. 10 Electron energy spectra in the Model B. Times are shown above corresponding panels. |
| In the text | |
 |
Fig. 11 Proton energy spectra in the Model A. Times are shown above corresponding panels. |
| In the text | |
 |
Fig. 12 Proton energy spectra in the Model B. Times are shown above corresponding panels. |
| In the text | |
 |
Fig. 13 Normalised pitch-angle distributions of high-energy particles (ℰ > 5 keV) during fast reconnection stage (t = 1120t0). Left panels (a) and c)) are for electrons; right panels (b) and d)) are for protons. Upper panels (a) and b)) correspond to the low-density case (Model A), while lower panels correspond to the high-density case (Model B). |
| In the text | |
 |
Fig. 14 High-energy (ℰ > 5 keV) electron and proton distribution in X − Y plane. Most of the particles are concentrated at low heights close to the footpoints. |
| In the text | |
 |
Fig. 15 Synthetic hard X-ray emission at 10 keV from the simulated flaring loop in low-density atmosphere. |
| In the text | |
 |
Fig. 16 Synthetic hard X-ray emission at 10 keV from the simulated flaring loop in high-density atmosphere. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.