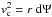| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A131 | |
| Number of page(s) | 22 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201321061 | |
| Published online | 22 January 2014 | |
Unifying static analysis of gravitational structures with a scale-dependent scalar field gravity as an alternative to dark matter
1 Fisika Teorikoaren eta Zientziaren Historia Saila, Zientzia eta Teknologia Fakultatea, Euskal Herriko Unibertsitatea, 644 Posta Kutxatila, 48080 Bilbao, Spain
e-mail: vincenzo.salzano@ehu.es
2 Institute of Theoretical Astrophysics, University of Oslo, 0315 Oslo, Norway
e-mail: D.F.Mota@astro.uio.no
3 Dipartimento di Fisica, Universita’ degli Studi di Napoli “Federico II” and INFN, Sezione di Napoli, Complesso Universitario di Monte S. Angelo, Via Cinthia, Edificio N, 80126 Napoli, Italy
e-mail: capozzie@na.infn.it
4 INAF − Osservatorio Astronomico di Capodimonte, Salita Moiariello 16, 80131 Napoli, Italy
e-mail: napolita@na.astro.it
Received: 8 January 2013
Accepted: 7 November 2013
Aims. We investigated the gravitational effects of a scalar field within scalar-tensor gravity as an alternative to dark matter. Motivated by chameleon, symmetron, and f(R)-gravity models, we studied a phenomenological scenario where the scalar field has both a mass (i.e. interaction length) and a coupling constant to the ordinary matter that scale with the local properties of the considered astrophysical system.
Methods. We analysed the feasibility of this scenario using the modified gravitational potential obtained in its context and applied it to the galactic and hot gas/stellar dynamics in galaxy clusters and elliptical/spiral galaxies respectively. This is intended to be a first step in assessing the viability of this new approach in the context of “alternative gravity” models.
Results. The main results are 1. the velocity dispersion of elliptical galaxies can be fitted remarkably well by the suggested scalar field, with model significance similar to a classical Navarro-Frenk-White dark halo profile; 2. the analysis of the stellar dynamics and the gas equilibrium in elliptical galaxies has shown that the scalar field can couple with ordinary matter with different strengths (different coupling constants), producing and/or depending on the different clustering state of matter components; 3. elliptical and spiral galaxies, combined with clusters of galaxies, show evident correlations among theory parameters, which suggest both the general validity of our results on all scales and a way toward a possible unification of the theory for all types of the gravitational systems we considered. All these results demonstrate that the proposed scalar field scenario can work fairly well as an alternative to dark matter.
Key words: dark matter / galaxies: elliptical and lenticular, cD / galaxies: clusters: intracluster medium / galaxies: spiral / gravitation
© ESO, 2014
1. Introduction
Dark matter and dark energy are nowadays widely accepted as the main components of our Universe, although reliable clues about their origin, nature, and properties are still missing. There is a long list of possible dark matter candidates, ranging from standard to sterile neutrinos, from axions to super-symmetric candidates, from light to super-heavy scalar fields (see, e.g. Bertone et al. 2005; Krauss 2006, and references therein), while dark baryons seem to have a minor contribution. Concerning the nature of dark energy, which is the largest component in the mass-energy balance of the Universe with ≈69% from latest Planck results (Planck Collaboration 2014), a coherent cosmological model explaining all the open issues and the related observed phenomena still needs to be found.
These two dark ingredients are the pillars of the current cosmological concordance model, the Λ-cold dark matter (ΛCDM), where Λ stands for the cosmological constant (Carroll et al. 1992; Sahni & Starobinski 2000), which is assumed to drive the Universe expansion. This model provides a suitable fit to most of the cosmological data (Planck Collaboration 2014; Sanchez et al. 2006; Seljak et al. 2005; Tegmark et al. 2004), but it is also well known that it is affected by many serious theoretical problems that motivate the search for alternatives.
On a phenomenological ground, alternative models to dark matter have proposed a modification of the gravitational acceleration (Milgrom 1983) within the context of MOND, which only later after his initial formulation was related to the context of the relativistic gravitation theory (Bekenstein 2004, 2005; Sanders 2005). On a more theoretical basis, more general candidates for the acceleration-driver counterpart have been proposed. Such models range from scalar fields rolling down self-interaction potentials to phantom fields, from phenomenological unified models of dark energy and dark matter to alternative theories of gravity (Capozziello 2002; Koivisto & Mota 2006; Li et al. 2007; Capozziello & Francaviglia 2008; Copeland et al. 2006; Manera & Mota 2006; Mota 2008; Padmanabhan 2003; Peebles & Rathra 2003; Koivisto et al. 2009; Capozziello & De Laurentis 2011).
Among all these approaches, in Mota et al. (2011, Paper I, hereafter) we focussed on a particular scenario where a scalar field might be used to unify the cosmological scale acceleration of the Universe with the formation and dynamics of gravitational structures by mimicking dark matter on astrophysical scales.
Scalar fields play an important role in connecting cosmology and particle physics (Binetruy 2006; Linde 2008). In particular, theories such as the chameleon fields (Khoury & Weltman 2004; Mota & Shaw 2006; Brax et al. 2004), f(R) gravity (Hu & Sawicki 2007; Starobinsky 2007; Capozziello et al. 2003), and symmetron models (Hinterbichler & Khoury 2010; Olive & Pospelov 2008; Davis et al. 2012), all share the fundamental ingredient of a scalar field, which couples to matter via gravitational interaction, and it is short-ranged in highly dense regions and long-ranged in low-density regions. Such a scalar field would be relatively light on cosmological scales, thus describing cosmological evolution without differentiating much from the ΛCDM model, and at the same time, it would also be able to satisfy local gravity constraints. Moreover, on different astrophysical scales, the effect of the scalar field would be suppressed or enhanced according to the local astrophysical density.
Starting from these broad properties, we propose a new parameterization for a massive scalar field theory where we introduce a field mass (or an interaction length) and a coupling constant with ordinary matter that may change with scale. Our primary goal is to test whether this parameterization, based on the chameleon or symmetron theories, can account for different observational facts, regardless of the underlying physical mechanism producing such a scalar field. Some recent papers (Oyaizu et al. 2008; Brax et al. 2012) analyse symmetron and f(R) gravity theories (of which chameleon models are an extension) in the context of structure formation, but they still consider the field as a background cosmology ingredient. Here we propose a scaling mechanism for which the field can explain both dark energy (on cosmological scales) and dark matter (on astrophysical scales).
In Paper I we studied the feasibility for this scale-dependent scalar field to work on different gravitational scales by using various cosmological indicators: Type-Ia supernovae and their Hubble diagram, low surface brightness spiral galaxies and their rotation curves, clusters of galaxies and their mass profiles.
Here we want to go beyond Paper I, by extending our analysis to elliptical galaxies and modelling their velocity dispersion profiles. As we show in the following sections, this new test has provided us with new evidence that has motivated a modification of the original approach followed in Paper I and a new analysis of the gravitational objects studied in that same work (namely, spiral galaxies and clusters of galaxies). Finally we unify all the results into a more general scheme.
The article is organized as follows. In Sect. 2 we give a brief but exhaustive summary of all the main properties of the scalar field theory and describe all the main hypothesis underlying our work. In Sect. 3 we accurately describe the used astrophysical data and the way we involved them in our analysis. In Sect. 4 we show results concerning elliptical galaxies, and in Sect. 5 we discussion the implications for a unified picture of all the gravitational structures we have considered. Conclusions are drawn in Sect. 6.
2. The scalar-tensor field theory
The most general action governing the dynamics of a scalar field can be written as (Esposito-Farese & Polarski 2001): 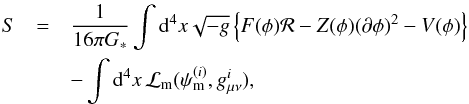 (1)where g is the determinant of the metric gμν, ℛ is the Ricci scalar,
(1)where g is the determinant of the metric gμν, ℛ is the Ricci scalar, 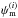 are the various matter fields, ℒm is the Lagrangian density of ordinary matter, φ is the scalar field, F(φ) and Z(φ) are two functions of the field that regulate its dynamics, and V(φ) is the scalar field potential. Depending on the expression of the given functions F(φ) and Z(φ) and of the potential V(φ), one can recover general scalar field theories, such as the chameleon or the symmetron mechanisms. The main consequence of this action is easily seen when linear perturbations of matter are taken into account. A wide class of theories leads to a perturbation equation like this (Davis et al. 2012; Brax et al. 2004; Bertschinger & Zukin 2008):
are the various matter fields, ℒm is the Lagrangian density of ordinary matter, φ is the scalar field, F(φ) and Z(φ) are two functions of the field that regulate its dynamics, and V(φ) is the scalar field potential. Depending on the expression of the given functions F(φ) and Z(φ) and of the potential V(φ), one can recover general scalar field theories, such as the chameleon or the symmetron mechanisms. The main consequence of this action is easily seen when linear perturbations of matter are taken into account. A wide class of theories leads to a perturbation equation like this (Davis et al. 2012; Brax et al. 2004; Bertschinger & Zukin 2008): 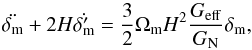 (2)where the dots mean time derivative, k is the wave-number length, a the scale factor, H the Hubble function, δm the matter density contrast, and Ωm the matter density parameter. The quantity Geff can be interpreted as an effective gravitational constant, because in general relativity the gravitational coupling GN is a constant, while in many alternative theories of gravity the strength of gravity can vary with time and place. A time-varying gravitational coupling is a well known property of scalar-tensor theories and a generic feature of all modified gravity theories where the Newtonian potential and the spatial curvature potential are different (Bertschinger & Zukin 2008; Acquaviva et al. 2005; Clifton et al. 2005). Within the context of massive scalar field models, it has the general expression (Gannouji et al. 2009):
(2)where the dots mean time derivative, k is the wave-number length, a the scale factor, H the Hubble function, δm the matter density contrast, and Ωm the matter density parameter. The quantity Geff can be interpreted as an effective gravitational constant, because in general relativity the gravitational coupling GN is a constant, while in many alternative theories of gravity the strength of gravity can vary with time and place. A time-varying gravitational coupling is a well known property of scalar-tensor theories and a generic feature of all modified gravity theories where the Newtonian potential and the spatial curvature potential are different (Bertschinger & Zukin 2008; Acquaviva et al. 2005; Clifton et al. 2005). Within the context of massive scalar field models, it has the general expression (Gannouji et al. 2009): 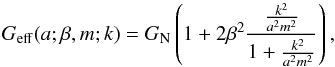 (3)where β is the coupling constant of the scalar field with matter, and if the field is at the minimum, the scalar field mass is m2 = V,φφ. In particular, the term proportional to β2 results from the scalar field-mediated force, which is negligible if the physical length scale of the perturbation is much larger than the range of the scalar field-mediated force, namely, if a/k ≫ m-1. In this case matter fluctuations grow as in general relativity.
(3)where β is the coupling constant of the scalar field with matter, and if the field is at the minimum, the scalar field mass is m2 = V,φφ. In particular, the term proportional to β2 results from the scalar field-mediated force, which is negligible if the physical length scale of the perturbation is much larger than the range of the scalar field-mediated force, namely, if a/k ≫ m-1. In this case matter fluctuations grow as in general relativity.
Taking the inverse Fourier transform of Eq. (3), it is straightforward to obtain the corresponding expression of the gravitational potential for a point mass distribution, ψ(r). Remembering that a potential ∝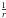 in real space yields a k-2 term in Fourier space, we can recognise in Eq. (3) the point-like gravitational potential per unit mass:
in real space yields a k-2 term in Fourier space, we can recognise in Eq. (3) the point-like gravitational potential per unit mass: 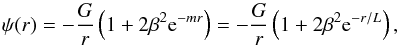 (4)where m is the mass of the scalar field, L ∝ m-1 is the interaction range of the scalar field, and β still is the coupling constant between matter and the scalar field. The gravitational potential given in Eq. (4) has been calculated for a point-like source, and it has to be generalized to extended systems in a numerical way. Depending on the particular gravitational system we consider, we adopt different geometrical hypothesis: for cluster of galaxies and elliptical galaxies we adopt spherical symmetry, while spiral galaxies are assumed to be thin disks.
(4)where m is the mass of the scalar field, L ∝ m-1 is the interaction range of the scalar field, and β still is the coupling constant between matter and the scalar field. The gravitational potential given in Eq. (4) has been calculated for a point-like source, and it has to be generalized to extended systems in a numerical way. Depending on the particular gravitational system we consider, we adopt different geometrical hypothesis: for cluster of galaxies and elliptical galaxies we adopt spherical symmetry, while spiral galaxies are assumed to be thin disks.
The point-like potential can be split into two terms. The Newtonian component for a point-like mass m is 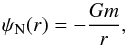 (5)and its extended integral is the well-known expression:
(5)and its extended integral is the well-known expression: 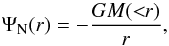 (6)where M( <r) is the mass enclosed in a sphere with radius r. The correction term from the scalar field effect is
(6)where M( <r) is the mass enclosed in a sphere with radius r. The correction term from the scalar field effect is 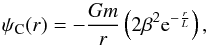 (7)whose extended integral is given by
(7)whose extended integral is given by 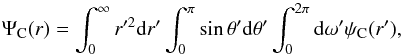 (8)where the angular part is analytically derivable, while the radial integral has to be numerically estimated once the mass density is given. A fundamental difference between the corrected and the Newtonian terms is that in the latter the matter outside the spherical shell of radius r does not contribute to the potential, while in the former the external mass distribution enters into the potential integral, with a possible non-negligible contribution.
(8)where the angular part is analytically derivable, while the radial integral has to be numerically estimated once the mass density is given. A fundamental difference between the corrected and the Newtonian terms is that in the latter the matter outside the spherical shell of radius r does not contribute to the potential, while in the former the external mass distribution enters into the potential integral, with a possible non-negligible contribution.
We also observe that a possible dependence of the coupling constant with scale, i.e. β = β(r), should be considered when evaluating the integral or the physical observable quantities that we will define in subsequent sections. Since we do not know what the possible analytical behaviour of β(r) is, we assume it is a constant or that it depends weakly on the scale, i.e. dβ/dr ≈ 0, as we will verify a posteriori.
2.1. Hypothesis
In this section we want to describe in more detail the main properties and requirements of our parametrization and the motivations behind our approach. In Paper I we assumed only one single scalar field working at each considered gravitational scale and/or object. In particular, we focussed on Type Ia supernovae, clusters of galaxies and spiral galaxies. The scalar field was characterized by interaction length L (or a mass), which should be related to the dimension of the gravitating structure under exam, and a coupling constant β that indicates the strength of the interaction between the field and the kind of matter that constitutes the considered gravitational object. We worked under the hypothesis that matter was only made up of the observed baryons (hot gas and galaxies in clusters of galaxies; gas and stars in spiral galaxies) with the scalar field generating a dynamical effect similar to the classical dark matter. In practice, we replaced the eventual new and exotic dark matter component with an effective mass induced by the modified gravitational interaction from the scalar field with ordinary matter.
First of all, we found that while Type Ia supernovae could be theoretically used to detect an effective gravitational constant Geff, because this can affect their light curves by changing both the thermonuclear energy release and the time scale of stellar explosion, its effects are actually too weak to be clearly detected with current data.
More interestingly, in Paper I we showed that both the rotation curves of low surface brightness spiral galaxies and the matter profiles in clusters of galaxies, obtained using only visible galactic, stellar, and gas mass components while substituting dark matter with the proposed scalar field, can be fitted fairly well within our alternative scenario. The interaction length values of the scalar field are in turn consistent with the characteristic dimensions of the considered gravitational systems. On the other hand, the coupling between the field and ordinary baryonic matter is convincingly well constrained in ranges that scale quite well with the matter content of galaxies and/or clusters of galaxies.
All these results seemed to point towards the possibility of a unifying view of dark matter and dark energy via a scalar field with the properties we have assumed, at least on galactic and cluster scales. But it is important to stress that all these results from Paper I were obtained when assuming the coupling constant β to be unique and fixed for all the intervening mass components.
As we show in Sect. 4, this turns out not to be the case for elliptical galaxies. For them we have to consider the possibility that the scalar field coupling constant will have different values depending on the different mass components of a galaxy. This eventuality might have two implications: 1. we have separate values for the coupling constants, one for each baryonic mass component (i.e. stars and gas); or 2. we have only one coupling constant but its measurement might be affected by the matter’s clustering state.
It is possible to state that these two options do not conflict. Indeed, in the first case, the scalar field theory predicts that the field can couple in different ways with different kinds of matter (Brax et al. 2004). This would mean that the scalar field can couple differently with ordinary matter (baryons, neutrinos, quarks, and so on). In the second case, the different values could depend on the clustered states of the matter and be a consequence of a screening effect that can suppress the field effects and produce an apparent (measured), lower value of the coupling constant β. Such a screening effect is called the thin-shell effect in the chameleon theory, and a similar effect is also present in the symmetron theory. It mainly affects gravitational systems where the inner value of the scalar field is different from the background and also reflects in a difference between the inner and the external matter densities (Brax et al. 2004; Capozziello & Tsujikawa 2008; Davis et al. 2012).
We suggest carrying out a possible mixed scenario in order to make the two options above coexist. We take the case of a cluster of galaxies and consider the galaxies and the gas inside it: if the scalar field scales with the density, we can argue that there are two scalar fields, one driving the formation and the dynamics of the cluster and another one driving the formation and the dynamics of the galaxies inside it. We can think that all the sub-structures inside the cluster experience the cluster-scale scalar field, but as long as the systems evolve, there will be a point where the (over-) densities representing the galaxies are high enough to turn on the screening effect, which from then on washes the cluster-scale scalar field effect out. This process would result in a suppression of the coupling constant of the cluster-scale scalar field with matter in galaxies, as long as the latter ones can be considered as clustered small structures within a larger structure.
In this picture, the diffuse hot gas in the cluster is spread through the cluster scale and can be considered as having only one typical scale, that of the cluster. This assumption is valid provided that the hydrostatic equilibrium is realized. In this case, the scalar field-gas coupling constant should contain information about the cluster-scale scalar field. The same assumption cannot be equally made for galaxy systems, such as spiral and elliptical galaxies, where the gas can be strongly disturbed by local phenomena (stellar winds, supernovae, radio jets by active nuclei, etc.).
Within this framework, the total gravitational potential can be written in two equivalent ways. We can define 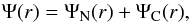 (9)if we want to highlight the separation between the correction that the scalar field provides to the gravitational potential and the classical Newtonian term. Alternatively, we can write
(9)if we want to highlight the separation between the correction that the scalar field provides to the gravitational potential and the classical Newtonian term. Alternatively, we can write 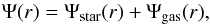 (10)where the suffix star refers to the stellar component in galaxies, but it can be replaced by galaxy when writing the cluster potentials. Each of the two terms is finally given by
(10)where the suffix star refers to the stellar component in galaxies, but it can be replaced by galaxy when writing the cluster potentials. Each of the two terms is finally given by 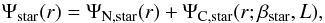 (11)and
(11)and 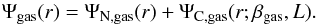 (12)We point out that the same scalar field, with mass ∝L-1, can interact differently with ordinary matter, with two values for the coupling constant, βstar and βgas, depending on their clustering state.
(12)We point out that the same scalar field, with mass ∝L-1, can interact differently with ordinary matter, with two values for the coupling constant, βstar and βgas, depending on their clustering state.
Finally, we have to point out here that our approach is implicitly based on a static assumption for the gravitational structures we are considering. Namely, we are ignoring that 1. the values of the scalar field parameters could be subjected to temporal evolution, so that an analysis of how perturbations and over-density collapse work would be necessary; and 2. a dynamical analysis under the influence of a scalar field should be performed to verify the stability of such gravitational systems.
Elliptical galaxies.
3. Elliptical galaxies: working model
As pointed out in Sect. 1, we want to extend the test of our scalar field hypothesis on galactic scales with elliptical galaxies.
3.1. Preliminaries
While spiral galaxies easily have interpretable flat rotation curves (that were one of the first historical proofs for dark matter), elliptical galaxies are pressure-supported systems dominated by hot random motions. The orbital distribution of stars is very difficult to model, and consequently the mass distribution is highly uncertain because of the well known mass-anisotropy degeneracy.
One way to gain insight into the internal dynamics is to use the information stored in the line-of-sight velocity dispersion as a function of position by solving the Jeans equation. Under spherical symmetry and assuming no rotation, the only effective equation governing the galaxy equilibrium is the radial Jeans equation: 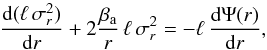 (13)where ℓ(r) is the luminosity density of the galaxy, σr(r) the radial velocity dispersion, and Ψ(r) the total gravitational potential. The anisotropy parameter βa is defined as
(13)where ℓ(r) is the luminosity density of the galaxy, σr(r) the radial velocity dispersion, and Ψ(r) the total gravitational potential. The anisotropy parameter βa is defined as 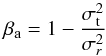 (14)where σt is the one-dimensional tangential velocity dispersion (defined as a combination of the two angular components of the velocity dispersion tensor,
(14)where σt is the one-dimensional tangential velocity dispersion (defined as a combination of the two angular components of the velocity dispersion tensor, 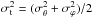 ), and σr is the radial component. When σt = σr, the system is called isotropic and βa = 0; when βa = 1 the system is fully radial anisotropic; for βa → − ∞, it is fully tangential.
), and σr is the radial component. When σt = σr, the system is called isotropic and βa = 0; when βa = 1 the system is fully radial anisotropic; for βa → − ∞, it is fully tangential.
In Eq. (13), the unknown quantities are the anisotropy parameter and the mass that generates the potential, while ℓ(r) is given by the tracer distribution. Thus, different combinations of orbital anisotropy and radial distribution of the mass can produce the same observed dispersion profile. This mass–anisotropy degeneracy can be solved by using independent measurements for the mass. One possibility for that is to use the information from X-ray emission from the hot gas (Mathews & Brighenti 2003), i.e. density and temperature, and to solve the hydrostatic balance within the galaxy potential, provided that the gas is at the hydrostatic equilibrium, but this is not always true in elliptical galaxies (Diehl & Statler 2007; Humphrey et al. 2006).
Despite all these modelling complications, Jeans analysis has been extensively used in elliptical galaxies, taking strong advantage of discrete kinematical tracers probing the gravitational potential out to many effective radii (Reff). Globular clusters (Puzia et al. 2004; Bergond et al. 2006; Romanowsky et al. 2009; Shen & Gebhardt 2010; Schuberth 2010; Woodley et al. 2010) or planetary nebulae (PNe, see, e.g. Napolitano et al. 2001, 2002; Mendez et al. 2001; Peng et al. 2004; Douglas et al. 2007; Coccato et al. 2009; Teodorescu et al. 2010; Napolitano et al. 2011) have made it possible to extend kinematics up to 5 − 7 Reff, from the ≈Reff achievable with only stellar observations. Furthermore, the analysis of satellites orbiting the galaxies could extend up to 50 − 500 kpc (≲10 Reff) (Klypin & Prada 2009). However, globular clusters have classically been used as mass tracers for bright galaxies, but their samples are too small in ordinary elliptical galaxies. On the other hand, PNe have been systematically used to map the mass profile of ellipticals (see e.g. Romanowsky et al. 2003; Napolitano et al. 2009, 2011, N+11 hereafter, and references therein).
The selection of viable objects for our analysis was made within the elliptical galaxy sample observed with the Planetary Nebula Spectrograph (Douglas et al. 2002) and presented in Coccato et al. (2009, C+09 hereafter), where stellar kinematics of the central regions are combined with PNe kinematics of the galaxy regions outside the Reff. PNe data give strong hints about the mass profiles of elliptical galaxies, but also put forward many more questions. Nowadays, many alternative scenarios are equally feasible. Two exemplary cases are Romanowsky et al. (2003) and Dekel et al. (2005). In the former, using the PNe, the galaxies velocity dispersion profiles are found to decline with radius, and dynamical modelling of the data indicates the presence of little if any dark matter in these galaxies’ haloes; in the latter, starting from disk-galaxy merger simulations, the lower-than-expected velocities are in fact compatible with galaxy formation in dark matter haloes, so it depends on inner dynamics (elongated orbits) or on projection effects.
For our analysis, we are interested in galaxies that have both extended (stellar and/or PNe) kinematics and published X-rays observations (Fukazawa et al. 2006). We need both because we want to explore the coupling of the scalar field with all the mass components of the gravitational systems under examination.
Among the 16 galaxies reported in C+09, the only one that had a complete dataset for our purpose is NGC 4374, since other galaxies for which both long-slit and PNe kinematics were available, such as NGC 3377, NGC 3379, and NGC 4494, did not have a reliable deprojected X-ray emitting gas density profile1. All the required photometric properties of NGC 4374 are reported in Table 1.
3.2. Line-of-sight velocity dispersion
The general solution to the Jeans equation, Eq. (13), is 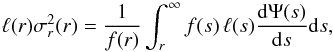 (15)where the function f is the solution to
(15)where the function f is the solution to 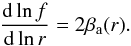 (16)By projecting the velocity ellipsoid along the line of sight, one can obtain the line-of-sight velocity dispersion, which is the kinematical quantity observed and reported in C+09:
(16)By projecting the velocity ellipsoid along the line of sight, one can obtain the line-of-sight velocity dispersion, which is the kinematical quantity observed and reported in C+09: ![\begin{equation} \label{eq:los_dispersion} \sigma_{\rm los}^2(R) = \frac{2}{I(R)} \left[ \int_{R}^{\infty} \frac{\ell \, \sigma_{r}^2 \, r}{\sqrt{r^2-R^{2}}} \mathrm{d}r - R^2 \int_{R}^{\infty} \frac{\beta_{\rm a} \, \ell \, \sigma_{r}^2}{r \sqrt{r^2-R^2}}\mathrm{d}r \right], \end{equation}](/articles/aa/full_html/2014/01/aa21061-13/aa21061-13-eq95.png) (17)where R is the projected distance from the centre of the galaxy, and I(R) the stellar surface brightness profile. To calculate the line-of-sight velocity dispersion σlos, one needs two ingredients: an analytical expression for the anisotropy function and the total gravitational potential (which enters in σr).
(17)where R is the projected distance from the centre of the galaxy, and I(R) the stellar surface brightness profile. To calculate the line-of-sight velocity dispersion σlos, one needs two ingredients: an analytical expression for the anisotropy function and the total gravitational potential (which enters in σr).
Concerning the anisotropy function, the usual way of proceeding is to compare observations with profiles derived from cosmological N-body simulations. Many models can be used: the simplest isotropy (βa = 0); a constant anisotropy profile; the Osipkov-Merritt model, but it provides a poor fit to the simulations. We decided to work with the anisotropy model given in Mamon & Lokas (2005a,b, 2006): 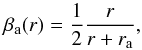 (18)where ra is a typical anisotropy length, assumed to be ra ≃ 14 Reff. This value2 thus provides a good fit to the data from dissipation-less cosmological N-body simulations (for a more exhaustive discussion about reliable anisotropy models, see Fig. 2 and Sect. 3.2 of Mamon & Lokas 2005b).
(18)where ra is a typical anisotropy length, assumed to be ra ≃ 14 Reff. This value2 thus provides a good fit to the data from dissipation-less cosmological N-body simulations (for a more exhaustive discussion about reliable anisotropy models, see Fig. 2 and Sect. 3.2 of Mamon & Lokas 2005b).
3.3. Modelling galaxy components
Finally, to calculate the gravitational potential, we need to model the galaxy components. In this case we have stars, hot gas, and the central black hole.
The stellar luminosity density can be obtained by deprojecting the observed surface brightness profile I(R). Galaxies in our sample are fitted with the mostly used Sersic profile: ![\begin{equation} \label{eq:sersic} I(R) = I_{0} \exp \left[ -\left( \frac{R}{a_{\rm s}}\right)^{1/m}\right], \end{equation}](/articles/aa/full_html/2014/01/aa21061-13/aa21061-13-eq103.png) (19)where I0 is the central surface brightness (in units of L⊙ pc-2), as the Sersic scale parameter (in kpc), and m the Sersic shape parameter. The luminosity density can be obtained by the approximation first proposed in Prugniel & Simien (1994):
(19)where I0 is the central surface brightness (in units of L⊙ pc-2), as the Sersic scale parameter (in kpc), and m the Sersic shape parameter. The luminosity density can be obtained by the approximation first proposed in Prugniel & Simien (1994): 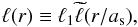 (20)with
(20)with
![\begin{eqnarray} &&\widetilde{\ell}(x) \simeq x^{-p} \, \exp(-x^{1/m}),\\ &&\ell_{1} = \frac{L_{\rm tot}}{4 \pi \, m \, \Gamma[(3-p)m] a_{\rm s}^{3}}, \end{eqnarray}](/articles/aa/full_html/2014/01/aa21061-13/aa21061-13-eq107.png) where function p is defined in Lima et al. (1999) as
where function p is defined in Lima et al. (1999) as 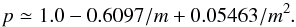 (23)The total galaxy luminosity (in solar units) in the V-band, where observations for NGC4374 were performed, is
(23)The total galaxy luminosity (in solar units) in the V-band, where observations for NGC4374 were performed, is 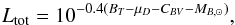 (24)where BT is the galaxy B-band apparent magnitude, MB, ⊙ the Sun absolute magnitude in the B-band, CBV3 galaxy color needed to convert all luminosity parameters from the band B to the band V, and μD the galaxy distance modulus (see Table 1). It is worth stressing that we also need
(24)where BT is the galaxy B-band apparent magnitude, MB, ⊙ the Sun absolute magnitude in the B-band, CBV3 galaxy color needed to convert all luminosity parameters from the band B to the band V, and μD the galaxy distance modulus (see Table 1). It is worth stressing that we also need ![\begin{equation} I_{0} = \frac{L_{\rm tot}}{2 \pi \, m \, \Gamma[2m] a_{\rm s}^2} \end{equation}](/articles/aa/full_html/2014/01/aa21061-13/aa21061-13-eq115.png) (25)which appears in Eq. (17) through the surface brightness expression I(R) and the stellar mass-to-light ratio Y∗ in order to convert the luminosity density into the mass density that enters in the gravitational potential.
(25)which appears in Eq. (17) through the surface brightness expression I(R) and the stellar mass-to-light ratio Y∗ in order to convert the luminosity density into the mass density that enters in the gravitational potential.
The central black hole is assumed to have a constant density inside its typical size, the Schwarzschild radius rBH, which is 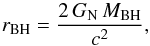 (26)where of course GN is the Newton gravitational constant and c the light velocity. The black hole mass MBH is obtained using the relation that exists between a super massive black hole and the host galaxy luminosity (Gultekin et al. 2009):
(26)where of course GN is the Newton gravitational constant and c the light velocity. The black hole mass MBH is obtained using the relation that exists between a super massive black hole and the host galaxy luminosity (Gultekin et al. 2009): ![\begin{equation} M_{\rm BH} = 10^{8.95+1.11 \cdot \log[10, L_{\rm tot}/10^{11}]}. \end{equation}](/articles/aa/full_html/2014/01/aa21061-13/aa21061-13-eq121.png) (27)Its density is assumed to be nought outside rBH.
(27)Its density is assumed to be nought outside rBH.
The gas profiles are assumed to follow the traditionally used β-model4 (Cavaliere & Fusco-Femiano 1978): 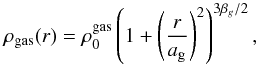 (28)where the central gas density, ρgas,0, the gas core length, ag, and the constant βg are provided by Fukazawa et al. (2006), where fitting mass profiles with hot gas X-ray emissions are derived.
(28)where the central gas density, ρgas,0, the gas core length, ag, and the constant βg are provided by Fukazawa et al. (2006), where fitting mass profiles with hot gas X-ray emissions are derived.
 |
Fig. 1 Mock elliptical galaxy analysis. Left panel: velocity dispersion profile; Right panel: circular velocity profile. Dark lines: solid − scalar field with two coupling constants; dot-dashed − scalar field with one coupling constant; dashed − classical NFW dark matter profile. Light lines: dashed − stellar velocity dispersion (circular velocity) in the classical dark matter approach; dotted − gas velocity dispersion (circular velocity) in the classical dark matter approach; dot-dashed − dark matter velocity dispersion (circular velocity). Vertical lines: dotted − effective radius Reff, limit achievable with only stellar photometry; dashed − 5−6 Reff, limit achievable with PNe reconstructed kinematics; solid: virial radius rvir. |
We recall that in the classical Newtonian approach the total dynamical mass is made of two counterparts, dark matter and baryons (stars, gas, and black hole), so that 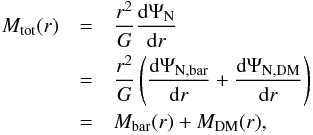 (29)where ΨN is the Newtonian potential and
(29)where ΨN is the Newtonian potential and 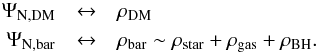 (30)As we pointed out in Sect. 2, in our approach the total gravitational potential is made of a Newtonian term and a corrective one
(30)As we pointed out in Sect. 2, in our approach the total gravitational potential is made of a Newtonian term and a corrective one 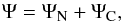 (31)so that the dynamical mass is
(31)so that the dynamical mass is 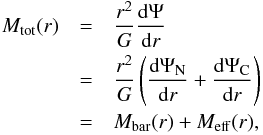 (32)where
(32)where 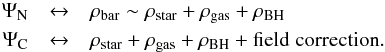 (33)The effective mass Meff is therefore due to the modification of gravity produced by the scalar field, instead of requiring a new kind of matter, such as the dark one. Of course, the term ΨC has contributions only from visible baryonic mass, i.e. stars, gas, and black hole, plus correction induced by the scalar field.
(33)The effective mass Meff is therefore due to the modification of gravity produced by the scalar field, instead of requiring a new kind of matter, such as the dark one. Of course, the term ΨC has contributions only from visible baryonic mass, i.e. stars, gas, and black hole, plus correction induced by the scalar field.
By comparing Eqs. (29) and (32), it is straightforward to observe that if we want that the scalar field fits data as well as dark matter, we need 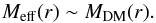 (34)For this reason we also realize a fit of our data in the classical context of dark matter in order to compare the two approaches. We use the classical Navarro-Frenk-White (NFW) model density given by the relation (Navarro et al. 1996):
(34)For this reason we also realize a fit of our data in the classical context of dark matter in order to compare the two approaches. We use the classical Navarro-Frenk-White (NFW) model density given by the relation (Navarro et al. 1996): ![\begin{equation} \label{eq:NFW} \rho_{\rm DM}(r) = \rho_{0}^{\rm DM} \left(\frac{r}{a_{\rm d}}\right)^{-1} \left[1+\frac{r}{a_{\rm d}} \right]^{-2}\cdot \end{equation}](/articles/aa/full_html/2014/01/aa21061-13/aa21061-13-eq138.png) (35)In Mamon & Lokas (2005b) more dark matter models are considered: the generalized NFW model introduced by Jing & Suto (2000), with inner slope − 3/2 instead of − 1, as in the classical NFW profile; the convergent model of Navarro et al. (2004), with an inner slope that is a power-law function of radius. We have verified that using these two models does not give any substantial change in the general mass profiles and in the fitting of velocity dispersion curves; thus, the classical NFW model is sufficient for our requirements. Generally, one is used to convert the quantities appearing in Eq. (35), i.e.
(35)In Mamon & Lokas (2005b) more dark matter models are considered: the generalized NFW model introduced by Jing & Suto (2000), with inner slope − 3/2 instead of − 1, as in the classical NFW profile; the convergent model of Navarro et al. (2004), with an inner slope that is a power-law function of radius. We have verified that using these two models does not give any substantial change in the general mass profiles and in the fitting of velocity dispersion curves; thus, the classical NFW model is sufficient for our requirements. Generally, one is used to convert the quantities appearing in Eq. (35), i.e. 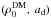 in more useful quantities which include the virial radius, rv, namely the radius enclosing a mass whose mean density is ≈100 times the critical density of the Universe, and the concentration parameter,
in more useful quantities which include the virial radius, rv, namely the radius enclosing a mass whose mean density is ≈100 times the critical density of the Universe, and the concentration parameter, 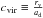 .
.
Finally, with all these ingredients, we are able to derive the observed quantity, i.e. the line-of-sight velocity dispersion, σlos. We underline here that the data we are considering are derived from the sum in quadrature of two terms: the line-of-sight velocity dispersion and the rotation velocity. The final quantity, 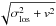 (see N+11), is a more efficient indicator of the total kinetic energy and is essentially ≈σlos, because the rotation velocity in NGC 4374 is not dynamically significant compared to random motion, which is ~50 km s-1 against a velocity dispersion of ~200 − 250 km s-1.
(see N+11), is a more efficient indicator of the total kinetic energy and is essentially ≈σlos, because the rotation velocity in NGC 4374 is not dynamically significant compared to random motion, which is ~50 km s-1 against a velocity dispersion of ~200 − 250 km s-1.
Depending on the approach we consider, σlos will be a function of different sets of parameters. On one hand, in the classical approach with an NFW density profile for the dark matter component, it will be 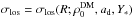 . On the other hand, when the modified gravity approach with a scalar field is considered, it will be σlos = σlos(R;β,L,Y∗). The statistical analysis to search for the parameters values that best fit our working model will be based on the minimization of the chi-square function, defined as
. On the other hand, when the modified gravity approach with a scalar field is considered, it will be σlos = σlos(R;β,L,Y∗). The statistical analysis to search for the parameters values that best fit our working model will be based on the minimization of the chi-square function, defined as 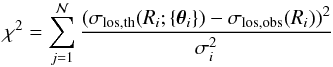 (36)where
(36)where 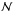 is the number of data points,
is the number of data points, 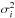 are the observationally-derived measurement variances, and { θi } is the parameters theory vector, i.e.,
are the observationally-derived measurement variances, and { θi } is the parameters theory vector, i.e., 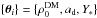 in the dark matter approach and { θi } = { β,L,Y∗ } in the scalar field approach.
in the dark matter approach and { θi } = { β,L,Y∗ } in the scalar field approach.
To minimise the χ2 we use the Markov chain Monte Carlo (MCMC) method and test its convergence with the method described by Dunkley et al. (2005). The MCMC method makes it possible to fix some priors on the fitting parameters. As a conservative choice, we decided to leave them as free as possible: we have β > 0 (given that in all the expressions above we always have β2, we do not really have the possibility of distinguishing between a positive or a negative value; moreover, the scalar field theory predicts it to be positive), and L, 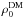 , ad, and Y∗ > 0 are all positive definite quantities.
, ad, and Y∗ > 0 are all positive definite quantities.
4. Elliptical galaxies: analysis and results
4.1. Mock galaxy test
To check the validity of our analysis and the degree to which the observed velocity dispersion is fitted to derive clues about the scalar field properties, we start by performing an ideal-case study, using a mock galaxy with all its intrinsic quantities fixed following the same prescriptions of Mamon & Lokas (2005b).
According to their prescriptions, we considered an elliptical galaxy with a baryonic and a dark matter component characterised by the following parameters:
-
B-band luminosity
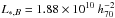 L⊙ (where h70 = 1 if H0 ≡ 100 × h = 70 km s-1 Mpc-1), from which, using all the relations given in Sect. 2 of Mamon & Lokas (2005b), we obtained a Sersic shape parameter m = 3.12 and a Sersic length as = 11.6
L⊙ (where h70 = 1 if H0 ≡ 100 × h = 70 km s-1 Mpc-1), from which, using all the relations given in Sect. 2 of Mamon & Lokas (2005b), we obtained a Sersic shape parameter m = 3.12 and a Sersic length as = 11.6 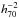 kpc;
kpc; -
a typical stellar mass-to-light ratio Y∗ = 6.5;
-
a total mass-to-light ratio Y = 100 corresponding to a virial radius, rvir = 79 Reff and to a concentration parameter c = 9.70;
-
a black hole to stellar mass ratio MBH/M∗ = 0.0015;
-
a β-model for the gas component with index βg = −1.5 and core radius rc = Reff/10.
Using Eq. (17), and assuming the dark matter halo described by quantities in point 3 above, we obtain the total velocity dispersion of this mock galaxy, shown in the left-hand panel of Fig. 1. This has a slightly decreasing trend with the radius, which eventually changes its slope outside 50−60 kpc, well beyond typical radial coverage by PN kinematics.
Elliptical galaxies: NFW dark matter.
Then we tried to recover (only in a qualitative way) the total velocity dispersion profile with a scalar field. As shown in the left-hand panel of Fig. 1, the scalar field prediction with a single coupling constant for all mass components and with theory parameters β = 0.05 and L ≈ 1000 kpc does not match the velocity dispersion profile of the dark matter case. The values for these two parameters are severely limited because the velocity dispersion in the inner region is completely dominated by the stellar component: it works like a sort of normalization factor and strongly constrains the value that β can have. If we give a value for β that is too different and higher than 0.05, we will have a completely wrong velocity dispersion reconstruction. In particular, in the scalar field approach, where no dark matter is considered, the total velocity dispersion is almost equivalent to the only-stellar velocity dispersion well beyond the radial extent of PNe measurements, eventually rising only after this limit. Thus, we can conclude that a scalar field with only one coupling constant cannot simulate a dark matter profile in a consistent and sufficient way.
Things change drastically if one considers the possibility that the scalar field has different coupling constants for each intervening mass component. In this case, we have stars and gas, and if we assume βstar = 0.05,βgas = 5.6, and the common length L ≈ 90 kpc, it is possible to decouple the effects from any of them. In fact, the model that includes two coupling constants nicely reproduces the velocity dispersion profiles of the classical case; i.e., the scalar field can mimic the profile of a NFW dark halo.
In the right-hand panel of Fig. 1 we instead show the circular velocity curve, calculated from the relation 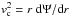 . We can see how it is rather flat out to 100 kpc, clearly showing how dominant is the dark matter in the total galaxy potential. The latter property is what we expect to be able to reproduce with the scalar field. We finally stress that if we had adopted the circular velocity as observational quantity (as done, for example, for spiral galaxies), we would not have any chance of distinguishing between the two approaches, i.e., one or two coupling constants for the scalar field with the baryonic matter. This is clearly shown in the right-hand panel of Fig. 1 where we can see how the two different cases for the scalar field give two equivalent reproductions of the NFW profile, at least in the depicted distance range: the two lines are indistinguishable since they perfectly overlap. This is an important issue to be considered when evaluating results for spiral galaxies in the next sections.
. We can see how it is rather flat out to 100 kpc, clearly showing how dominant is the dark matter in the total galaxy potential. The latter property is what we expect to be able to reproduce with the scalar field. We finally stress that if we had adopted the circular velocity as observational quantity (as done, for example, for spiral galaxies), we would not have any chance of distinguishing between the two approaches, i.e., one or two coupling constants for the scalar field with the baryonic matter. This is clearly shown in the right-hand panel of Fig. 1 where we can see how the two different cases for the scalar field give two equivalent reproductions of the NFW profile, at least in the depicted distance range: the two lines are indistinguishable since they perfectly overlap. This is an important issue to be considered when evaluating results for spiral galaxies in the next sections.
4.2. Real data: NGC 4374
Starting from these preliminary considerations, we can move to the analysis of a real system: NGC 4374 (see Table 1), which is our test case for elliptical galaxy dynamics. This system has been shown to possess a standard NFW halo profile (N+11), so it will be important to see whether its dynamics can be interpreted equally well with the scalar field potential.
We make use of the PNe sample discussed in N+11, which we refer the reader to for more details on the PNe sample properties and on the derivation of the kinematical profiles we use in our analysis. The PNe dispersion profile extends out to ≈5 Reff, which is a large enough distance to explore any deviation in the galaxy dynamics from a pure Newtonian no-dark matter behaviour.
This galaxy has been also analysed in the context of f(R) theories (Napolitano et al. 2012), where a Yukawa-like modification of the gravitational potential is adopted as alternative to dark matter. This approach is different from the one we are adopting here, because the possibility of breaking the contribution of all mass components (stars and gas) in the gravitational budget is a peculiar feature of our theoretical scenario that cannot be included in their physical model.
Before we go on with the dynamical model, we need to pay some attention to the modelling of the stellar component, because in both cases (ΛCDM framework or scalar field), it is the one that dominates the velocity dispersion profile in the inner region, with lower uncertainties with respect to PNe data at larger distances from the centre. This implies a stronger weight on the global fit to the velocity dispersion. For NGC 4374 there are different literature models of its stellar photometry (mainly depending on the extension of the adopted datasets): a typical De Vaucouleurs profile (a Sersic profile with index m = 4), with Reff = 5.97 kpc (Cappellari et al. 2006); a Sersic profile with Reff = 11.69 kpc and m = 7.98 (Kormendy et al. 2009); and a Sersic profile with Reff = 9.34 kpc and m = 6.11 (N+11). The first model has some problems for fitting data both at short and very large distances from the centre, since the De Vaucouleurs profile is not always able to describe all the intrinsic features of an elliptical galaxy. The second model allows a better fit to the stellar profile but fails to recover the behaviour of surface brightness at small radii (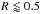 kpc). Finally, the third model gives a very good fit of the stellar profile in a wider range than the previous one, namely, 0.09 ≲ R ≲ 38 kpc, out to the distances covered by PNe observations. For this reason we decided to adopt the model profile from N+11 in the following dynamical analysis. Furthermore, we adopted two different approaches in order to optimize the goodness of the surface brightness reconstruction: we considered, one after the other, all the available data points and only data points with R > 0.09 kpc.
kpc). Finally, the third model gives a very good fit of the stellar profile in a wider range than the previous one, namely, 0.09 ≲ R ≲ 38 kpc, out to the distances covered by PNe observations. For this reason we decided to adopt the model profile from N+11 in the following dynamical analysis. Furthermore, we adopted two different approaches in order to optimize the goodness of the surface brightness reconstruction: we considered, one after the other, all the available data points and only data points with R > 0.09 kpc.
 |
Fig. 2 Left panel: velocity dispersion curve of NGC4374. Dark lines: solid line is the total velocity dispersion in the scalar field approach, i.e. scalar field + baryons; dot-dashed line is the total velocity dispersion in the classical approach, i.e. dark matter + baryons. Light lines: dashed line is the stellar velocity dispersion in the NFW approach; dotted line is the dark matter velocity dispersion. Right panel: the same as before but on a logarithmic scale. |
Elliptical galaxies: Scalar field.
4.3. Dark matter
We started by using our model machinery, by assuming the standard Newton dynamics and a NFW dark halo, and by cross-checking our results with the ones presented in N+11. Our results are in Table 2 and somehow differ with the results discussed in their Sect. 3.5.1. Before we go into the details of this discrepancy, we need to point out that there are some critical differences between the two approaches. Here we use ae parametrized stellar surface density, while in N+11 they use an interpolated function. Furthermore, we assume here an anisotropy profile that is rather different from the one constrained by N+11, where they have also used the kurtosis information. These two main differences can produce some substantial divergence in the modelling of the very central data points, thus affecting the parameters that are more sensitive to the small radii fit. For this reason, we repeated the models, including all the kinematics data points and excluding the data at R > 0.09 kpc and R > 1 kpc, and finally found substantial differences, as shown in Table 2.
In particular, we have obtained a lower value of the central density 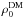 and a higher value for the NFW radius ad with no statistically significant difference between the total and the R > 0.09 cut sample. If, however, we consider the expected relation between these two parameters derivable from a collisionless ΛCDM universe with WMAP5 parameters (Eq. (13) and the blue contours of Fig. 7 in N+11), we have correspondence at 1σ level. The concentration parameter, c ≈ 4, matches the lower limit of most of the cases shown in Table 2 of N+11 and, in particular, with their assumed best reference model (i.e., an adiabatically contracted NFW profile with an anisotropy distribution that is different from the one adopted here, which should result in a more concentrated dark matter density profile).
and a higher value for the NFW radius ad with no statistically significant difference between the total and the R > 0.09 cut sample. If, however, we consider the expected relation between these two parameters derivable from a collisionless ΛCDM universe with WMAP5 parameters (Eq. (13) and the blue contours of Fig. 7 in N+11), we have correspondence at 1σ level. The concentration parameter, c ≈ 4, matches the lower limit of most of the cases shown in Table 2 of N+11 and, in particular, with their assumed best reference model (i.e., an adiabatically contracted NFW profile with an anisotropy distribution that is different from the one adopted here, which should result in a more concentrated dark matter density profile).
 |
Fig. 3 Dark matter profile vs. radii for clusters of galaxies. Dashed line is the observationally derived estimation of dark matter; solid line is the theoretical estimation for the effective dark matter component; dot-dashed lines are the 1σ confidence levels given by errors on fitting parameters plus statistical errors on mass profiles. |
 |
Fig. 3 continued. |
The virial radius is notably larger, while the virial mass is perfectly consistent with their results even if showing a wider confidence level extending primarily to higher values. If we compare these results with Fig. 11 in N+11, we see that our value for the parameters (cvir,log Mvir) fall in the region limited by the results inferred from late-type galaxies dynamics and from weak lensing of all type of galaxies and groups (Napolitano et al. 2009). In particular, the values coming from the r > 0.09 kpc subsample match this last curve perfectly.
Concerning the luminous stellar counterpart, we found values that are slightly higher for the stellar mass-to-light ratio, Y∗ ≈ 6.6, which is, however, perfectly compatible with a Salpeter initial mass function (Fig. 5 in N+11).
Looking at the left-hand panel of Fig. 2 we see how the stellar component dominates the velocity dispersion profile only in the very central regions (R ≲ 1.0 kpc), with the black hole contribution only important for very small scales and with the NFW dark matter becoming dominant in the line-of-sight velocity dispersion profile at ≈10 kpc, which corresponds to ≈1 − 2 Reff.
When using only data with R > 1.0 kpc, we have been able to recover results that are more similar to N+11 for what concerns the NFW profile: a higher central density parameter for the dark matter profile (even if it is again lower than the one measured in N+11) and a lower value for the NFW length (but still higher than N+11). The couple (cvir,log Mvir) is now compatible with both the weak lensing inferred trend and with the relation derived from WMAP5-based simulations. Finally, the virial radius is now only a 30% higher than the value found in N+11.
4.4. Scalar field
If we now move to the scalar field alternative approach, it is clear (right panel of Fig. 2) that this is as successful as the classical dark matter approach for modelling the dispersion profile. The greatest differences with respect to the NFW profile are found at the very small radii, where the scalar field model shows a steeper slope while the NFW one seems to reach a plateau, and in the very outer region, where the scalar field model stays flatter than the NFW profile. However more extended data would allow us to adjust the two models better at the greatest distance and possibly to recover better agreement also on shorter scales. However, as seen by the χ2 results in Table 3, the best fit is also very good in this case: while the NFW and the scalar field approaches are almost equivalent when all the data points are used, if we consider the value of the reduced χ2 (with the NFW χ2 slightly smaller than the scalar field one) for the best fit to the data points with R > 0.09, the scalar field turns out to provide far better significance of the fit with respect to the NFW model. In this case, the stellar mass-to-light ratio is less than the NFW-based one, and it is now more compatible with the Kroupa IMF (Kroupa 2001) values found in N+11.
Even more importantly, the scalar field parameters turned out to be consistent with what we argued for the double coupling-constant hypothesis in Sect. 2.1. First, the stellar mass component shows the lowest coupling constant among all the mass components, even lower than the one related to the black hole. As anticipated, this can be the consequence of the average effect of the screening action made by the scalar field on the stellar component. The same does not happen to the black hole, since this represents a singularity, and it is difficult to explain the change in the field from inside to outside and the comparison with its classical Newtonian force. Second, the coupling constant that refers to the gas seems to be mostly correlated with the galaxy gravitational potential and the scalar field mass.
To conclude, we stress that both the classical dark matter and the scalar field approaches seem to be unable to describe the small shoulder in the dispersion profile that is present at R ≈ 10 kpc, precisely where the PNe data overlap the only stellar kinematics. One may think that this can be a consequence of some orbital anisotropy that is unaccounted for. In fact, this mainly depends on the choice we made to use a parametric form of the star density ℓ(r) instead of a smoothed light profile as in N+11 where it was possible to recover all the details of the dispersion profile (with a low degree of radial anisotropy). This means that the observed kinematics is somehow strongly sensitive to the tracer space density distribution.
5. Unifying the scenario
The results obtained with the elliptical galaxy NGC 4374 are not meant to have enough general application to drive any conclusion on the newly proposed multi-coupling constant scenario. However, it is not surprising that the proper handling of physically more complex, multi-component systems like ellipticals has opened new perspectives on the scalar field approach. If our scenario is correct, this will in fact be made more evident on gravitational systems where the evolutionary status is different (as is the case of spiral galaxies, as we show in next sections) or where matter shows very different phases. But a more detailed analysis in this sense is not the purpose of our work and will be developed in forthcoming papers.
Since we do not expect to extend the elliptical sample soon, owing to the difficulty of finding galaxies both with extended stellar (PNe) kinematics and with no faint gas profiles, in this section we try to re-interpret the results of Paper I in terms of the new evidence found for NGC 4374, i.e. the possibility of disentangling the various mass components with respect to the coupling constant with the scalar field. In this respect we aim to draw a common scenario for all the gravitating systems (galaxies: spirals and ellipticals, and clusters) in a consistent way.
5.1. Clusters of galaxies
By comparing Fig. 3 with the corresponding figures in Paper I (Figs. 3, 4 in that paper), we see that the new approach of using the two mass components has allowed us to improve the model fit in nine cases, especially at small radii. In one case (RXJ1159), the new approach has produced a remarkable fit where the model in Paper I failed completely. Only for three clusters has the mass profile reconstruction not got any benefit by the two-component approach, although the deviation of the best fit from the data is never worse than at the 1σ confidence level.
Looking at Table 4 we can quantify the differences with Paper I better: the interaction length diminishes slightly in most of the objects, still staying compatible with typical cluster scales (≈1 Mpc; see also Eq. (36)), while the coupling constant with gas is generally larger than previous estimates. Two objects in particular have very large coupling constant values, i.e. clusters A262 and MKW4.
 |
Fig. 4 Scalar field length plotted versus mean (gas-density weighted) cluster temperature and the radius r500 defined in the text. |
Clusters of galaxies: Scalar field.
On the other hand, the coupling constant related to galaxies is always much lower than the one related to the gas (as expected from the discussion in Sect. 2.1), except for two cases, i.e. clusters A133 and RXJ1159. It is interesting to note that among all these exceptions, two (MKW4 and RXJ1159) are considered more similar to groups than to real clusters of galaxies or even as extended elliptical galaxies (Vikhlinin et al. 2005), thus for all these systems, the argument adopted for normal clusters of galaxies might not apply straightforwardly.
For the other two objects no particular features were found in literature to explain the anomalies. We can only note that A262 seems to be as small as MKW4 (i.e. they share the same data extension), and unlike the latter it is believed to be a normal cluster of galaxies. A possible relation between the cluster scale and the gas coupling constant is possible: if we think about this last one as a concentration parameter, we can expect that smaller structures exhibit a higher value for it. For A133 nothing peculiar was found in the literature to justify the high value for the galaxy coupling constant we found; we can only verify that the fit with data is really good.
As in Paper I we want to find some relations among the scalar field parameters and the physical properties of the considered gravitational systems to establish whether this alternative scenario can be a valid alternative to general relativity and dark matter. First of all, in the right-hand panel of Fig. 4, we have a relation between the interaction length, L, and the radius r500, the distance from the centre corresponding to an over-density of ≈500 times relative to the critical density at the cluster redshift. We prefer this quantity for the virial radius rvir used in Paper I, because while the latter is derived using a relation coming from cosmological simulations (Bryan & Norman 1998; Evrard et al. 1996) and thus depending on the gas-weighted average temperature of the cluster, the former is derived in (Vikhlinin et al. 2005) directly from observational data by using the hydrostatic equilibrium equation. We have also verified that the two distances are proportional, with 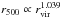 .
.
The relation between the scalar field length L and the radius r500 is derived from an error weighted fit excluding the previously described four peculiar clusters (right panel of Fig. 4): 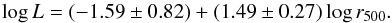 (37)We have also found a relation between L and the average gas-weighted temperature ⟨ T ⟩, left panel of Fig. 4:
(37)We have also found a relation between L and the average gas-weighted temperature ⟨ T ⟩, left panel of Fig. 4: 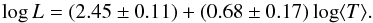 (38)As we pointed out in Paper I, a relation exists between the cluster mass and average temperature, i.e.
(38)As we pointed out in Paper I, a relation exists between the cluster mass and average temperature, i.e. 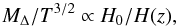 (39)where Δ is the over-density level relative to the critical density at the cluster redshift, so that M180 = Mvir. With the previous phenomenological expressions holding, this mass-temperature relation can be easily converted in
(39)where Δ is the over-density level relative to the critical density at the cluster redshift, so that M180 = Mvir. With the previous phenomenological expressions holding, this mass-temperature relation can be easily converted in 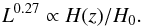 (40)In Fig. 5 we can verify that assuming a fiducial WMAP quintessence model5, with Ωm = 0.259 and w = −1.12, and assuming H0 = 72.4 km s-1 Mpc-1, the previous relation is able to match the chosen fiducial model following the relation H(z)/H0 = (0.169 ± 0.006)L0.27.
(40)In Fig. 5 we can verify that assuming a fiducial WMAP quintessence model5, with Ωm = 0.259 and w = −1.12, and assuming H0 = 72.4 km s-1 Mpc-1, the previous relation is able to match the chosen fiducial model following the relation H(z)/H0 = (0.169 ± 0.006)L0.27.
 |
Fig. 5 Comparison between the Hubble function H(z) calculated from the fiducial model described in the text and the Hubble function obtained by the empirical relation H(z) ∝ L0.27. Error bars are calculated from the errors on the interaction length L. |
Spiral galaxies: scalar field.
In Figs. 6 we also represent the scaled temperature profiles versus the distance from the centre of any cluster scaled with respect to the scalar field length obtained by the fit, showing the same good reproduction of the self-similarity that characterizes the classical dark matter approach. Moreover, as in Paper I, we detected the absence of the subgroups that the clusters are divided into depending on the mean temperature values (Vikhlinin et al. 2005). The only exception with respect to Paper I is A133, whose profile now appears to be shrunk, even if no peculiar elements have been found in the literature and no analysis problems have been encountered.
 |
Fig. 6 Temperature profiles for all clusters plotted as a function of distance from the centre and in units of the scalar field length L. The temperatures are scaled to the mean (gas-density weighted) cluster temperature. Dashed line is for high temperature clusters (⟨ T ⟩ > 5 keV); solid line is for intermediate temperature clusters (2.5 < ⟨ T ⟩ < 5 keV); dotted line is for low temperature clusters (⟨ T ⟩ < 2.5 keV). |
5.2. LSB spiral galaxies
We now consider the case of spiral galaxies. Modelling these systems involves the same number of parameters of elliptical galaxies, i.e. the parameters associated to the scalar field and the stellar mass-to-light ratio, Y∗. As discussed for the elliptical case, the latter parameter cannot vary arbitrarily but has to be consistent with stellar population models. As for the spiral systems sample adopted in this work, one can expect Y∗ to vary in the range ≈0.5 and ≈2. We have decided to be conservative and let the model parameters vary in the interval [0;5] (for any further and detailed description see Paper I).
Before we proceed to illustrate the results, we need to point out that the two-component approach for the spiral galaxies suffer from some additional noise source with respect to the analysis performed in Paper I and can somehow affect the results. As we have exhaustively discussed in Paper I, the gas data are very noisy, and in some cases they can also show particular features that are unavoidable due to intrinsic dynamical properties (i.e. negative velocities due to counter rotating disks, large scatter from non-circular motion, etc.). While these effects have been mitigated in Paper I, where the use of stars and gas together allowed the more circular velocity of stars to dilute the noisy features of the gas, here the coupling of the gas component to the scalar field might result in highly uncertain and irregular profiles. To improve the accuracy of the fit for the gas component, we have tried in this work to obtain a more accurate fit of the gas density. The result of this new analysis is evident in the smoother trend of most of the galaxies.
 |
Fig. 7 Rotation curves of LSB galaxies. Dots are velocities from data; solid line is the theoretical model, |
 |
Fig. 7 continued. |
The new models of the spiral rotation curves seem to give results that are less clear than the one obtained for clusters in the previous section (see Fig. 7). By decoupling the gas and the star components, we do not gain much in the quality of the fits (except slightly better agreement with the data of NGC 4173 and NGC 9211, where the models are closer to the ones obtained in Paper I). This is the consequence of the evidence shown in the previous section when testing the method on elliptical galaxies. We have seen that the effect of the decoupling of the mass components does not show up in the circular velocity but only the velocity dispersion. In the LSB analysis, since we are modelling the circular velocity, we should expect a minimal improvement by adding a further coupling constant, which implies that we are limited to reliably decoupling the different mass components in spiral galaxies because of the unsuitability of the dynamical probe (the rotation curve).
 |
Fig. 8 Correlation among the scalar field coupling constants and the central surface brightness of spiral galaxies. |
 |
Fig. 9 Correlation among scalar field coupling constants and the maximum stellar velocity. |
We recall that this induced idea has to be considered with caution, since elliptical and spiral galaxies are completely different gravitational structures from a dynamical point of view: elliptical galaxies are dominated by random motions while spiral galaxies are dominated by ordered (rotational) motions. Moreover we can add another element that makes our global results more homogeneous and consistent with each other: the decoupling (with an effective improvement in fits) is given for elliptical galaxies and clusters of galaxies, which are both hot systems (i.e. dominated by random motions) and are supposed to be virialized, whereas this does not happen for spiral galaxies. Thus it is possible that the possibility of decoupling the different mass components is related to the equilibrium reached in those two kinds of gravitational structures, while in spiral galaxies stars and gas are again more strictly correlated. In that case, we would also have a correlation of our scalar field analysis with the evolutionary state of the gravitational objects; but to verify this is beyond the scope of this paper.
For all these reasons we have proceeded with the star and gas component decoupling approach also for LSB systems and we have found we have a clear distinct behaviour for the coupling constants. First of all, unsurprisingly the gas coupling constant seems to be very similar to the only one coupling constant of Paper I, and it is very well constrained in the range [1.1;2.1] with only four exceptions: UGC 3851, which has the lowest value (as in Paper I); UGC 4173, which has a value below one, but still being compatible with the previous range at the highest 1σ confidence limit; UGC 4325 and UGC 5721, which have higher values. This means that the dominant coupling constant for LSBs is the one from the gas component.
On the other hand, the stellar coupling constant shows double behaviour: there are galaxies with βstar ≫ 1 (UGC 1230, UGC 3137, UGC 3371, UGC 3851, UGC 4173, UGC 4278, UGC 8286, UGC 9211) and galaxies with βstar < 1 (UGC 5721, UGC 7524, UGC 7603, UGC 8837, UGC 10310). Two systems (UGC 1281 and UGC 4325) have βstar < 1, but their 1σ confidence level is compatible with values ≫1.
The systems with the larger βstar are noticeably also the ones with the lower stellar mass-to-light ratio. This is a warning for a possible degeneracy working among these two parameters. Such a degeneracy has already been discussed in Paper I where we also noticed an anti-correlation between the Y∗ and the only one β adopted. The choice to break down β into two coupling constants ensures us that βgas is unaffected by any degeneracy, while βstar is not. This is a major benefit we have gained by adopting of the mass component decoupling approach, and we could add that the main coupling constant one should rely on is βgas. Interestingly, the gas status is really what makes the big difference between cold and hot dynamical systems that correspondingly possess cold and hot gas.
Concerning the best fit stellar mass-to-light ratios, we have 11 of 15 galaxies compatible at 1σ level with the previously prescribed range; one (UGC 7524) has a higher value; and three (UGC 7603, UGC 8286, UGC 8837) have values below 0.5. Among these three, the first two were peculiar in Paper I too, even if they can be considered acceptable, and UGC 7603 in particular still has the lowest value, Y∗ = 0.052. Only in two cases (UGC 4325 and UGC 5721) do we have more compatible values mainly due to their large errors. In general, in Paper I we did obtain a better match of Y∗ with the prescribed range in 10 of 15 cases.
Finally, the interaction length shows a wider range than the cluster galaxy case, and it is not as well constrained as in that case. One particular case is UGC 3137: even in Paper I it was one of the galaxies with the greatest interaction length, but now it has a too high value, L ≈ 500 kpc, which is difficult to understand. Either way, by taking a look at its rotational profile, we can see how it satisfies two main requirements: 1. it is the second largest object in the sample (or, better, the second object for which observations of the gas component were done up to a larger distance from the centre); 2. it is the clearest case in which it seems to have reached the expected plateau in the rotation curve. Lacking more detailed, extended, and less disturbed data for the galaxies in our sample we cannot conclude anything but can only argue that in spiral galaxies, more than in clusters and the elliptical galaxies, the degeneracy among parameters due to limited extension of the data could be more important.
 |
Fig. 10 Correlation among scalar field coupling constants and the gas mass. |
 |
Fig. 11 Correlation among scalar field coupling constants and the total baryonic mass. |
 |
Fig. 12 Baryonic Tully-Fisher relation for our galaxy sample: contributions from different velocity components. |
As in Paper I, we searched for possible scaling relations, including for comparing our alternative approach with more popular theories, like MOND (Swaters 2010). A correlation among the gas coupling constant (probably more related to the global gravitational structure properties than the star related parameter) and the extrapolated central disk surface brightness μ0,R (reported in Table 3 of Paper I) is possible, see left-hand panel of Fig. 8: 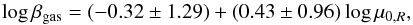 (41)between the same quantity and the maximum rotational velocity, see left-hand panel of Fig. 9:
(41)between the same quantity and the maximum rotational velocity, see left-hand panel of Fig. 9: 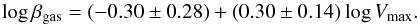 (42)Excluding only peculiar cases with respect to βgas (UGC 3851, UGC 4173, UGC 4325, UGC 5721), we can see that the dispersion around such relations is quite low. We also show in the left-hand panel of Fig. 10 the relation between βgas and the total gas mass of each galaxy:
(42)Excluding only peculiar cases with respect to βgas (UGC 3851, UGC 4173, UGC 4325, UGC 5721), we can see that the dispersion around such relations is quite low. We also show in the left-hand panel of Fig. 10 the relation between βgas and the total gas mass of each galaxy: 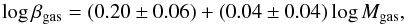 (43)clearly, the parameter is quite independent of such quantity, giving a further confirmation of our preliminary hypothesis dβ/dr ≈ 0 (see Sect. 2). In the left-hand panel of Fig. 11, we show the relation with the total baryonic (stars and gas) mass:
(43)clearly, the parameter is quite independent of such quantity, giving a further confirmation of our preliminary hypothesis dβ/dr ≈ 0 (see Sect. 2). In the left-hand panel of Fig. 11, we show the relation with the total baryonic (stars and gas) mass: 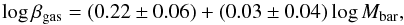 (44)in this case, in the estimation of the stellar counterpart, we have to take the stellar mass-to-light ration, Y∗, into account which is actually one of the fit parameters. No change is detected when moving from the gas to the total baryonic.
(44)in this case, in the estimation of the stellar counterpart, we have to take the stellar mass-to-light ration, Y∗, into account which is actually one of the fit parameters. No change is detected when moving from the gas to the total baryonic.
This does not happen when considering the coupling constant with stars. Since it is possible that a degeneracy between the coupling constant and the stellar mass-to-light ratio is at work, we more properly consider the quantity 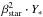 that appears in the stellar rotational contribution, finally having (right panel of Fig. 8):
that appears in the stellar rotational contribution, finally having (right panel of Fig. 8): 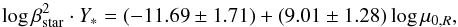 (45)and (right panel of Fig. 9)
(45)and (right panel of Fig. 9) 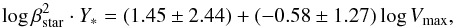 (46)which holds only for the galaxies with βstar ≫ 1, while the others show a more scattered distribution.
(46)which holds only for the galaxies with βstar ≫ 1, while the others show a more scattered distribution.
The relation between 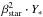 and Mgas or Mbar is less evident than the previous case. Taking a look at the right-hand panels of Figs. 10, 11, we can only detect (more clearly in the Mbar case) three subgroups: two galaxies in the bottom left-hand corner (UGC 7603 and UGC 8837), corresponding to very low values for both βstar and Y∗; four galaxies in the middle (UGC 1281, UGC 4325, UGC 5721 and UGC 10310), corresponding to low values of βstar; and an almost constant
and Mgas or Mbar is less evident than the previous case. Taking a look at the right-hand panels of Figs. 10, 11, we can only detect (more clearly in the Mbar case) three subgroups: two galaxies in the bottom left-hand corner (UGC 7603 and UGC 8837), corresponding to very low values for both βstar and Y∗; four galaxies in the middle (UGC 1281, UGC 4325, UGC 5721 and UGC 10310), corresponding to low values of βstar; and an almost constant 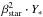 group made of the remaining objects. On the other hand, the length parameter, L, does not show a clear ordered pattern when compared with the same quantities as before.
group made of the remaining objects. On the other hand, the length parameter, L, does not show a clear ordered pattern when compared with the same quantities as before.
An even more interesting relation to be tested here is the well-known baryonic Tully-Fisher (BTF) relation (McGaugh 2012), which relates the total baryonic mass of spiral galaxies, Mbar, to the maximum observed velocity, Vmax, which becomes approximately flat in the outer regions, Vf, and is actually quantified to be 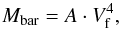 (47)with A = 47 ± 6 M⊙ km-4 s4. To make the comparison with our results clearer, we can rewrite the previous in the equivalent expression:
(47)with A = 47 ± 6 M⊙ km-4 s4. To make the comparison with our results clearer, we can rewrite the previous in the equivalent expression: 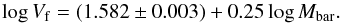 (48)Since it is possible to verify from previously plotted rotational curves, not all the galaxies in our sample seem to have reached the flatness regime in the rotational curve, so that the Vf appearing in the previous formulas will be more exactly Vmax for us, i.e., the maximum velocity evaluated at the maximum distance from the centre and available from the data.
(48)Since it is possible to verify from previously plotted rotational curves, not all the galaxies in our sample seem to have reached the flatness regime in the rotational curve, so that the Vf appearing in the previous formulas will be more exactly Vmax for us, i.e., the maximum velocity evaluated at the maximum distance from the centre and available from the data.
In our alternative scenario, the total velocity can be written as the sum of different terms: 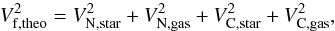 (49)where the suffixes N and C, as explained in previous sections, are related to the (extended) Newtonian and corrective terms in our gravitational potential model.
(49)where the suffixes N and C, as explained in previous sections, are related to the (extended) Newtonian and corrective terms in our gravitational potential model.
If we first consider the quantity Vf,theo made up of VN,gas, which is derived entirely from direct velocity observations; VN,star, which mixes direct velocity observations and a fit parameter, Y∗ (which also enters in the calculation of Mbar); and 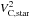 and
and 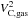 , which completely depend on our theoretical model, we obtain
, which completely depend on our theoretical model, we obtain 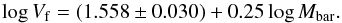 (50)They agree very well with the expected BTF relation. We can also check that the BTF relation is verified for any of the components of the total velocity (of course, we consider the maximum velocity for any of these). For the velocity term derived from the stellar pseudo-Newtonian contribution to the gravitational potential, we can identify two groups: galaxies with Y∗ > 2 give
(50)They agree very well with the expected BTF relation. We can also check that the BTF relation is verified for any of the components of the total velocity (of course, we consider the maximum velocity for any of these). For the velocity term derived from the stellar pseudo-Newtonian contribution to the gravitational potential, we can identify two groups: galaxies with Y∗ > 2 give 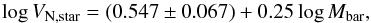 (51)and galaxies with Y∗ < 2 give
(51)and galaxies with Y∗ < 2 give 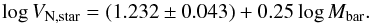 (52)The velocity term from the gas pseudo-Newtonian contribution (excluding UGC 4325) gives
(52)The velocity term from the gas pseudo-Newtonian contribution (excluding UGC 4325) gives 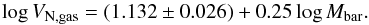 (53)The velocity term from the corrective gas contribution (excluding UGC 5721, UGC 7603, UGC 8837, and UGC 10310) gives
(53)The velocity term from the corrective gas contribution (excluding UGC 5721, UGC 7603, UGC 8837, and UGC 10310) gives 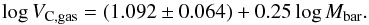 (54)The velocity term from the corrective stellar contribution (excluding UGC 3851) gives
(54)The velocity term from the corrective stellar contribution (excluding UGC 3851) gives 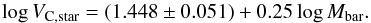 (55)All the previous relations are shown in Figs. 12, 13. It is interesting to note that, for these last two quantities, if we relax the condition for which the coefficient of Mbar has to be equal to 0.25, and we leave it free, we obtain the values 0.037 and 0.033 respectively, which are quite consistent with a scenario where the contribution to the rotation curve coming from the effective mass produced by the modified gravity of the chosen scalar field is practically independent of the baryon mass (at least for the family of spiral galaxies considered), so arguing in favour of a more universal task for our mechanism.
(55)All the previous relations are shown in Figs. 12, 13. It is interesting to note that, for these last two quantities, if we relax the condition for which the coefficient of Mbar has to be equal to 0.25, and we leave it free, we obtain the values 0.037 and 0.033 respectively, which are quite consistent with a scenario where the contribution to the rotation curve coming from the effective mass produced by the modified gravity of the chosen scalar field is practically independent of the baryon mass (at least for the family of spiral galaxies considered), so arguing in favour of a more universal task for our mechanism.
 |
Fig. 13 Baryonic Tully-Fisher relation for our galaxy sample: total rotational velocity. |
 |
Fig. 14 Correlation among the scalar field parameters Spirals are LSB spiral galaxies; filled squares are clusters of galaxies; filled circle is the elliptical galaxy NGC 4374. The dashed line is the best fit for clusters only; dotted line is the best fit for spiral galaxies only; dot-dashed line is the best fit for the total sample. Objects in brackets are the peculiar cases described in the text and not considered in the fits. |
5.3. Unified picture
In this section we qualitatively draw some conclusions from the results that we have derived from the different gravitational structures discussed above. In particular we refer to the new evidence that a scalar field can mimic dark matter on different scales by changing its properties depending on either the local physical conditions, namely the matter density, or the matter status.
As in Paper I, we consider the relation among the scalar field parameters and the gas density/mass of any structure in order to check for a universal correlation among parameters on all scales, from galaxies to galaxy clusters.
For galaxy clusters it is natural to check this because the gas is the main contribution to the mass (under the assumption that there is no dark matter, as in the current work). The same argument is not intuitive for galaxies, since gas is not the main component on a galactic scale; however, because we have found that the coupling constant of the gas with the scalar field can be larger than the one of stars, this component turns out to have a significant impact on the observational quantities too, sometimes even greater than the stellar one.
 |
Fig. 15 Correlation among the scalar field parameters and the gas density. Spirals are LSB spiral galaxies; the filled squares are clusters of galaxies; filled circle is the elliptical galaxy NGC 4374. Dashed line is the best fit only for clusters; the dotted line is the best fit for spiral galaxies only; the dot-dashed line is the best fit for the total sample. Objects in brackets are the peculiar cases described in the text and not considered in the fits. |
We start by verifying how the scalar field parameters are correlated with each other. One of our main hypotheses is that the coupling constants β are independent of the scale or, more precisely, that dβ/dr ~ 0. We can verify a posteriori that this hypothesis is satisfied quite well by taking a look at the top pane of Fig. 14. Here a linear regression of the spiral galaxy parameters gives 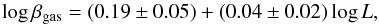 (56)for clusters of galaxies, we obtain
(56)for clusters of galaxies, we obtain 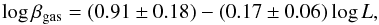 (57)and using all data together, we finally get
(57)and using all data together, we finally get 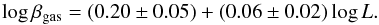 (58)We can verify how coherently each gravitational structure family is located in parameter space: the clusters of galaxies lie in a very well constrained region on the right-hand side of the left-hand panel in Fig. 14. Spiral galaxies are on the opposite side with a larger dispersion mainly due to the uncertainties on the interaction length. The only elliptical galaxy that we have analysed is interestingly located right in between the spirals and the galaxy cluster regions very close to the area where the smallest clusters and/or group of galaxies are located. This evidence suggests that the properties of the scalar field are related to the dynamical properties of the gravitational systems, because cold dynamical systems like spirals are clearly separated by hot dynamical systems (elliptical galaxies and galaxy clusters). This result is interesting since the connection between dynamics (especially anisotropy of the orbits) and scalar field parameters has also been found in other f(r) formulations (Napolitano et al. 2012).
(58)We can verify how coherently each gravitational structure family is located in parameter space: the clusters of galaxies lie in a very well constrained region on the right-hand side of the left-hand panel in Fig. 14. Spiral galaxies are on the opposite side with a larger dispersion mainly due to the uncertainties on the interaction length. The only elliptical galaxy that we have analysed is interestingly located right in between the spirals and the galaxy cluster regions very close to the area where the smallest clusters and/or group of galaxies are located. This evidence suggests that the properties of the scalar field are related to the dynamical properties of the gravitational systems, because cold dynamical systems like spirals are clearly separated by hot dynamical systems (elliptical galaxies and galaxy clusters). This result is interesting since the connection between dynamics (especially anisotropy of the orbits) and scalar field parameters has also been found in other f(r) formulations (Napolitano et al. 2012).
For the coupling constant related to stars (in galaxies) and galaxies (in clusters), in the right-hand panel of Fig. 14 we can see a larger dispersion in the parameter space, but also a clear segregation: the left half of the diagram is dominated by spiral galaxies, the right half by clusters of galaxies, and the central region populated by elliptical galaxies (although a larger sample is required) and smaller clusters and/or group of galaxies.
We can eventually reach the same conclusion by looking at the correlation between scalar field parameters and the gas density as in Fig. 15. When considering the top left and right panels of this figure, we can see that the parameters do not distribute randomly, but seem to follow a trend. For the interaction length, the top left-hand corner is populated by clusters of galaxies, the bottom right-hand one by spiral galaxies, and the centre possibly by elliptical galaxies and group of galaxies, with a clear linear trend and a dispersion that is larger for spiral galaxies than for clusters. A linear regression in the log-log space where the interaction length L is the dependent variable gives, for spiral galaxies: 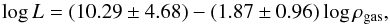 (59)for clusters of galaxies,
(59)for clusters of galaxies, 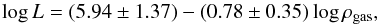 (60)and for all systems together,
(60)and for all systems together, 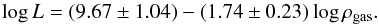 (61)For the gas coupling constant, on the other hand, we have a linear trend that is almost compatible with a constant βgas, thus confirming our previous hypothesis (dβ/dr ≈ 0). In particular, for spiral galaxies we have
(61)For the gas coupling constant, on the other hand, we have a linear trend that is almost compatible with a constant βgas, thus confirming our previous hypothesis (dβ/dr ≈ 0). In particular, for spiral galaxies we have 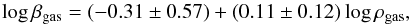 (62)for clusters of galaxies we have
(62)for clusters of galaxies we have 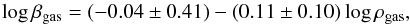 (63)and for the total sample
(63)and for the total sample 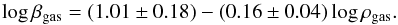 (64)When considering the combination of βstar and Y∗ or βgal, the large spread does not allow us to define a clear trend, and no data regression is produced.
(64)When considering the combination of βstar and Y∗ or βgal, the large spread does not allow us to define a clear trend, and no data regression is produced.
6. Conclusions and discussion
In this work we have investigated the dynamical properties of several astrophysical systems from galaxies to clusters of galaxies, within the theoretical framework of scalar-tensor theories as an alternative to the dark matter paradigm, and looked for observational signatures in galaxy kinematics and X-ray equilibrium.
The crucial ingredients of our work are some novel properties of the scalar field with respect to previous analyses (Paper I): (i) a new parametrization of the theory where we introduced the coupling of the scalar field with the different baryonic components of the gravitational systems (stars and gas) and (ii) its mass (or interaction length) that varies with scale.
This new parametrization with basically two coupling constants allowed the scalar field to mimic dark matter, i.e. reproduces observations remarkably well without introducing a new kind of matter but by modifying gravity.
Going into more detail on the results in the different astrophysical tests that we performed here, results have shown that (i) the velocity dispersion of elliptical galaxies can be fit by a scalar field very well, even better than assuming a classical NFW profile for the dark matter component; (ii) a scalar field can reproduce the matter profile in clusters of galaxies fairly well, as estimated by X-ray observations and without the need for any additional dark matter; (iii) good fits to the rotation curves of low surface brightness galaxies are obtained.
All these results show that the scalar field gravity theories with the peculiar properties we assumed can be compatible with a wide range of astrophysical tests and can be considered as a viable alternative to dark matter. In particular, our results show the possibility that the scalar field can couple with ordinary matter with different strengths (different coupling constants) depending on the clustering state of matter components in the considered gravitational structures and that a possible correlation with the evolutionary state of gravitational systems is possible. These results are extremely important when compared to the theoretical scenario they are inspired by, namely the chameleon or the symmetron theory: they have so far only been considered only on cosmological scales, as possible explanations for dark energy. We showed in this work that their properties also make them suitable for explaining astrophysical phenomena on smaller scales, thus mimicking dark matter.
We point out that this work is part of a larger project where we want to test our model and parametrization by using other different cosmological and astrophysical probes, and its main goal is to strengthen the idea that such a model can work as a consistent unifying scenario for all the dark sectors.
A challenging but decisive test will be to treat the lensing theory in the Newtonian and post-Newtonian formalism. A comprehensive and formally corrected approach, from the theoretical point of view, is needed to fully test the theory against lensing observables. In fact, by simply adopting the Newtonian limit and the standard of general relativity, it is easily shown that the same outcome of Einstein theory is obtained (Lubini et al. 2011). This is straightforward because the Newtonian limit recovered from general relativity does not take the further degrees of freedom of alternative gravities into account. On the other hand, considering that alternative gravities usually contain further degrees of freedom with respect to general relativity, a more accurate treatment has to be adopted for the lensing problem. As shown in Stabile & Stabile (2012), differences emerge as soon as as the Newtonian and the post-Newtonian formalisms are fully considered assuming also the perturbation theory of more gravitational degrees of freedom. In this perspective, differences between alternative gravity and dark matter pictures could emerge giving the signature for the final theory. For these reasons we searched for and collected from literature data regarding the mass profiles of clusters of galaxies, reconstructed by both strong and weak lensing, and we will use them in the near future.
Moreover, on the astrophysical side, we will also explore the possible correlations between classical models (NFW or generalized NFW profiles) for dark matter and the effective contribution from our scalar field. Concerning spiral galaxies, it will be interesting to verify if and how our model is able to reproduce the universal rotation curve scenario (Persic et al. 1997; Salucci 2011).
After this preliminary analysis of the static properties of gravitational structures, we will go deeper in our study of the nature of a scalar field with the properties we considered in this work by studying its influence on the formation and the evolution of the same structures. We will explore the non-linear effects in clustering processes, and on the cosmological side, we will study the feasibility of this model with the cosmic microwave background radiation data and matter power spectrum features.
To be certain that our results are free of this particular choice, we performed our analysis changing the length parameter ra from the chosen best value, ra ≃ 14Reff, to ra ≃ 1.4Reff (as discussed in Mamon & Lokas 2005b), spanning a wide range of values. We can conclude that our results are completely unaffected by this choice.
It is obtained from the extragalactic database Hyperleda, http://leda.univ-lyon1.fr/
Acknowledgments
D.F.M. thanks the Research Council of Norway FRINAT grant 197251/V30. D.F.M. is also partially supported by project CERN/FP/123618/2011 and CERN/FP/123615/2011. V.S. is now working at the UPV/EHU in the project “Gravitación, Cosmología Relativista y otros aspectos de la Estructura del Universo”. S.C. acknowledges the support of INFN (Sez. di Napoli, iniziative specifiche NA12 and OG51) and the ERASMUS/SOCRATES European programme. V.S. thanks L. Coccato for giving important suggestions for managing elliptical galaxy data, Y. Fukazawa for providing data about X-ray emission of NGC 4374, and P. Brownstein for interesting comments and suggestions.
References
- Acquaviva, V., Baccigalupi, C., Leach, S. M., Liddle, A. R., & Perrotta, F. 2005, Phys. Rev. D, 71, 104025 [NASA ADS] [CrossRef] [Google Scholar]
- Bekenstein, J. D. 2004, Phys. Rev. D, 70, 083509 [NASA ADS] [CrossRef] [Google Scholar]
- Bekenstein, J. D. 2005, Phys. Rev. D, 71, 069901 [NASA ADS] [CrossRef] [Google Scholar]
- Bergond, G., Zepf, S. E., Romanowsky, A. J., Sharples, R. M., & Rhode, K. L. 2006, A&A, 448, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertone, G., Hooper, D., & Silk, J. 2005, Phys. Rept., 405, 279 [Google Scholar]
- Bertschinger, E., & Zukin, P. 2008, Phys. Rev. D, 78, 024015 [NASA ADS] [CrossRef] [Google Scholar]
- Binetruy, P. 2006, Supersymmetry: Theory, experiment and cosmology (Oxford, UK: Oxford Univ. Pr.) [Google Scholar]
- Brax, P., van de Bruck, C., Davis, A.-C., Khoury, J., & Weltman, A. 2004, Phys. Rev. D, 70, 123518 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Brax, P., Davis, A.-C., Li, B., Winther, H. A., & Zhao, G.-B. 2012, J. Cosmol. Astropart. P., 10, 002 [Google Scholar]
- Bryan, G. L., & Norman, M. L. 1998, ApJ, 495, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Capozziello, S. 2002, Int. J. Mod. Phys. D, 11, 483 [Google Scholar]
- Capozziello, S., & De Laurentis, M. 2011, Phys. Repts., 509, 167 [Google Scholar]
- Capozziello, S., & Francaviglia, M. 2008, Gen. Rel. Grav., 40, 357 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Capozziello, S., & Tsujikawa, S. 2008, Phys. Rev. D, 77, 107501 [NASA ADS] [CrossRef] [Google Scholar]
- Capozziello, S., Carloni, S., & Troisi, A. 2003, Recent Res. Dev. Astron. Astrophys., 1, 625 [Google Scholar]
- Cappellari, M., Bacon, R., Bureau, M., et al. 2006, MNRAS, 366, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Carroll, S. M., Press, W. H., & Turner, E. L. 1992, ARA&A, 30, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Cavaliere, A., & Fusco-Femiano, R. 1978, A&A, 70, 677 [NASA ADS] [Google Scholar]
- Clifton, T., Mota, D. F., & Barrow, J. 2005, MNRAS, 358, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Coccato, L., Gerhard, O., Arnaboldi, M., et al. 2009, MNRAS, 394, 1249 [NASA ADS] [CrossRef] [Google Scholar]
- Copeland, E. J., Sami, M., & Tsujikawa, S. 2006, Int. J. Mod. Phys. D, 15, 1753 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Davis, A.-C., Li, B., Mota, D. F., & Winther, H. 2012, ApJ, 748, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., Stoehr, F., Mamon, G. A., et al. 2005, Nature, 437, 707 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Diehl, S., & Statler, T. S. 2007, ApJ, 668, 150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Douglas, N. G. 2007, ApJ, 664, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Douglas, N. G., Arnaboldi, M., & Freeman, K. C., et al. 2002, PASP, 114, 1234 [NASA ADS] [CrossRef] [Google Scholar]
- Dunkley, J., Bucher, M., Ferreira, P. G., Moodley, K., & Skordis, C. 2005, MNRAS, 356, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Esposito-Farese, G., & Polarski, D. 2001, Phys. Rev. D, 63, 063504 [NASA ADS] [CrossRef] [Google Scholar]
- Evrard, A. E., Metzler, C. A., & Navarro, J. F. 1996, ApJ, 469 [Google Scholar]
- Fukazawa, Y., Betoya-Nonesa, J. G., Pu, J., Ohto, A., & Kawano, N. 2006, ApJ, 636, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Gannouji, R., Moraes, B., & Polarski, D. 2009 [arXiv:0907.0393] [Google Scholar]
- Gultekin, K., Richstone, D. O., Gebhardt, K., et al. 2009, ApJ, 698, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Hinterbichler, K., & Khoury, J. 2010, Phys. Rev. Lett., 104, 231301 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, W., & Sawicki, I. 2007, Phys. Rev. D, 76, 064004 [CrossRef] [Google Scholar]
- Humphrey, P. J., Buote, D. A., Gastaldello, F., et al. 2006, ApJ, 646, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Jing, Y. P., & Suto, Y. 2000, ApJ, 529, L69 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Khoury, J., & Weltman, A. 2004, Phys. Rev. D, 69, 044026 [CrossRef] [Google Scholar]
- Klypin, A., & Prada, F. 2009, ApJ, 690, 1488 [NASA ADS] [CrossRef] [Google Scholar]
- Koivisto, T., & Mota, D. F. 2006, Phys. Rev. D, 73, 083502 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Koivisto, T. S., Mota, D. F., & Pitrou, C. 2009, J. High Energy Phys., 0909, 092 [Google Scholar]
- Kormendy, J., Fisher, D. B., Cornell, M. E., & Bender, R. 2009, ApJS, 182, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Krauss, L. M. 2006 [arXiv:hep-ph/0702051] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Li, B., Barrow, J. D., & Mota, D. F. 2007, Phys. Rev. D, 76, 104047 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- LimaNeto, G. B., Gerbal, D., & Márquez, I. 1999, MNRAS, 309, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Linde, A. D. 2008, Lect. Notes Phys., 738, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Lubini, M., Tortora, C., Naef, J., Jetzer, Ph., & Capozziello, S. 2011, Eur. Phys. J. C, 71, 1834 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McGaugh, S. S. 2012, AJ, 143, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Mamon, G. A., & Lokas, E. L. 2005a, MNRAS, 362, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Mamon, G. A., & Lokas, E. L. 2005b, MNRAS, 363, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Mamon, G. A., & Lokas, E. L. 2006, MNRAS, 370, 1581 [NASA ADS] [CrossRef] [Google Scholar]
- Manera, M., & Mota, D. F. 2006, MNRAS, 371, 1373 [NASA ADS] [CrossRef] [Google Scholar]
- Mathews, W. G., & Brighenti, F. 2003, ARA&A, 41, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Méndez, R. H., Riffeser, A., & Kudritzki, R.-P., et al. 2001, ApJ, 563, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 1983, ApJ, 270, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Mota, D. F. 2008, J. Cosmology Astropart. Phys., 09006 [Google Scholar]
- Mota, D. F., & Shaw, D. J. 2006, Phys. Rev. Lett., 97, 151102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mota, D. F., Salzano, V., & Capozziello, S. 2011, Phys. Rev. D, 83, 084038 (Paper I) [NASA ADS] [CrossRef] [Google Scholar]
- Napolitano, N. R., Arnaboldi, M., Freeman, K. C., & Capaccioli, M. 2001, A&A, 377, 784 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Napolitano, N. R., Arnaboldi, M., & Capaccioli, M. 2002, A&A, 383, 791 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Napolitano, N. R., Romanowsky, A. J., Coccato, L., et al. 2009, MNRAS, 393, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Napolitano, N. R., Romanowsky, A. J., & Capaccioli, M., et al. 2011, MNRAS, 411, 2035 (N+11) [NASA ADS] [CrossRef] [Google Scholar]
- Napolitano, N. R., Capozziello, S., Romanowsky, A. J., Capaccioli, M., & Tortora, C. 2012, ApJ, 748, 87 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Hayashi, E., Power, C., et al. 2004, MNRAS, 349, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Olive, K. A., & Pospelov, M. 2008, Phys. Rev. D, 77, 043524 [NASA ADS] [CrossRef] [Google Scholar]
- Oyaizu, H., Lima, M., & Hu, W. 2008, Phys. Rev. D, 78, 123524 [NASA ADS] [CrossRef] [Google Scholar]
- Padmanabhan, T. 2003, Phys. Rep., 380, 235 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Planck Collaboration 2014, A&A, in press [arXiv:1303.5076] [Google Scholar]
- Peebles, P. J. E., & Rathra, B. 2003, Rev. Mod. Phys., 75, 559 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Peng, E. W., Ford, H. C., & Freeman, K. C. 2004, ApJ, 602, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Persic, M., Salucci, P., & Stel, F. 1997, MNRAS, 281, 27 [Google Scholar]
- Prugniel, P., & Simien, F. 1994, A&A, 321, 111 [Google Scholar]
- Puzia, T. H., Kissler-Patig, M., Thomas, D., et al. 2004, A&A, 415, 123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romanowsky, A. J., Douglas, N. G., Arnaboldi, M., et al. 2003, Science, 301, 1696 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Romanowsky, A. J., Strader, J., Spitler, L. R., et al. 2009, AJ, 137, 4956 [NASA ADS] [CrossRef] [Google Scholar]
- Sahni, V., & Starobinski, A. 2000, Int. J. Mod. Phys. D, 9, 373 [NASA ADS] [Google Scholar]
- Salucci, P., Frigerio Martins, C., & Lapi, A. 2011 [arXiv:1102.1184] [Google Scholar]
- Sanchez, A. G., Baugh, C. M., Percival, W. J., et al. 2006, MNRAS, 366, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. H. 2005, MNRAS, 363, 459 [NASA ADS] [Google Scholar]
- Schuberth, Y., Richtler, T., Hilker, M., et al. 2010, A&A, 513, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seljak, U., Makarov, A., McDonald, P., et al. 2005, Phys. Rev. D, 71, 043511 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, J., & Gebhardt, K. 2010, ApJ, 711, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Stabile, A., & Stabile, A. 2012, Phys. Rev. D, 85, 044014 [NASA ADS] [CrossRef] [Google Scholar]
- Starobinsky, A. A. 2007, JETP Lett., 86, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Swaters, R. A., Sanders, R. H., & McGaugh, S. S. 2010, ApJ, 718, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Tegmark, M., Strauss, M., Blanton, M., et al. 2004, Phys. Rev. D, 69, 103501 [CrossRef] [Google Scholar]
- Teodorescu, A. M., Méndez, R. H., Bernardi, F., Riffeser, A., & Kudritzki, R. P. 2010, ApJ, 721, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J. L., Dressler, A., & Blakeslee, J. P., et al. 2001, ApJ, 546, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Markevitch, M., Murray, S. S., et al. 2005, ApJ, 628, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Woodley, K. A, Gómez, M., Harris, W. E., Geisler, D., & Harris, G. L. H. 2010, AJ, 139, 1871 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Mock elliptical galaxy analysis. Left panel: velocity dispersion profile; Right panel: circular velocity profile. Dark lines: solid − scalar field with two coupling constants; dot-dashed − scalar field with one coupling constant; dashed − classical NFW dark matter profile. Light lines: dashed − stellar velocity dispersion (circular velocity) in the classical dark matter approach; dotted − gas velocity dispersion (circular velocity) in the classical dark matter approach; dot-dashed − dark matter velocity dispersion (circular velocity). Vertical lines: dotted − effective radius Reff, limit achievable with only stellar photometry; dashed − 5−6 Reff, limit achievable with PNe reconstructed kinematics; solid: virial radius rvir. |
| In the text | |
 |
Fig. 2 Left panel: velocity dispersion curve of NGC4374. Dark lines: solid line is the total velocity dispersion in the scalar field approach, i.e. scalar field + baryons; dot-dashed line is the total velocity dispersion in the classical approach, i.e. dark matter + baryons. Light lines: dashed line is the stellar velocity dispersion in the NFW approach; dotted line is the dark matter velocity dispersion. Right panel: the same as before but on a logarithmic scale. |
| In the text | |
 |
Fig. 3 Dark matter profile vs. radii for clusters of galaxies. Dashed line is the observationally derived estimation of dark matter; solid line is the theoretical estimation for the effective dark matter component; dot-dashed lines are the 1σ confidence levels given by errors on fitting parameters plus statistical errors on mass profiles. |
| In the text | |
 |
Fig. 3 continued. |
| In the text | |
 |
Fig. 4 Scalar field length plotted versus mean (gas-density weighted) cluster temperature and the radius r500 defined in the text. |
| In the text | |
 |
Fig. 5 Comparison between the Hubble function H(z) calculated from the fiducial model described in the text and the Hubble function obtained by the empirical relation H(z) ∝ L0.27. Error bars are calculated from the errors on the interaction length L. |
| In the text | |
 |
Fig. 6 Temperature profiles for all clusters plotted as a function of distance from the centre and in units of the scalar field length L. The temperatures are scaled to the mean (gas-density weighted) cluster temperature. Dashed line is for high temperature clusters (⟨ T ⟩ > 5 keV); solid line is for intermediate temperature clusters (2.5 < ⟨ T ⟩ < 5 keV); dotted line is for low temperature clusters (⟨ T ⟩ < 2.5 keV). |
| In the text | |
 |
Fig. 7 Rotation curves of LSB galaxies. Dots are velocities from data; solid line is the theoretical model, |
| In the text | |
 |
Fig. 7 continued. |
| In the text | |
 |
Fig. 8 Correlation among the scalar field coupling constants and the central surface brightness of spiral galaxies. |
| In the text | |
 |
Fig. 9 Correlation among scalar field coupling constants and the maximum stellar velocity. |
| In the text | |
 |
Fig. 10 Correlation among scalar field coupling constants and the gas mass. |
| In the text | |
 |
Fig. 11 Correlation among scalar field coupling constants and the total baryonic mass. |
| In the text | |
 |
Fig. 12 Baryonic Tully-Fisher relation for our galaxy sample: contributions from different velocity components. |
| In the text | |
 |
Fig. 13 Baryonic Tully-Fisher relation for our galaxy sample: total rotational velocity. |
| In the text | |
 |
Fig. 14 Correlation among the scalar field parameters Spirals are LSB spiral galaxies; filled squares are clusters of galaxies; filled circle is the elliptical galaxy NGC 4374. The dashed line is the best fit for clusters only; dotted line is the best fit for spiral galaxies only; dot-dashed line is the best fit for the total sample. Objects in brackets are the peculiar cases described in the text and not considered in the fits. |
| In the text | |
 |
Fig. 15 Correlation among the scalar field parameters and the gas density. Spirals are LSB spiral galaxies; the filled squares are clusters of galaxies; filled circle is the elliptical galaxy NGC 4374. Dashed line is the best fit only for clusters; the dotted line is the best fit for spiral galaxies only; the dot-dashed line is the best fit for the total sample. Objects in brackets are the peculiar cases described in the text and not considered in the fits. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.