| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 7 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201220935 | |
| Published online | 14 January 2014 | |
An independent planet search in the Kepler dataset
II. An extremely low-density super-Earth mass planet around Kepler-87
Institut für Astrophysik, Georg-August-Universität,
Friedrich-Hund-Platz 1,
37077
Göttingen,
Germany
e-mail:
avivofir@astro.physik.uni-goettingen.de
Received: 17 December 2012
Accepted: 7 October 2013
Context. The primary goal of the Kepler mission is the measurement of the frequency of Earth-like planets around Sun-like stars. However, the confirmation of the smallest of Kepler’s candidates in long periods around FGK dwarfs is extremely difficult or even beyond the limit of current radial velocity technology. Transit timing variations (TTVs) may offer the possibility for these confirmations of near-resonant multiple systems by the mutual gravitational interaction of the planets.
Aims. We previously detected the second planet candidate in the KOI 1574 system. The two candidates have relatively long periods (about 114 d and 191 d) and are in 5:3 resonance. We therefore searched for TTVs in this particularly promising system.
Methods. The full Kepler data was detrended with the proven SARS pipeline. The entire data allowed one to search for TTVs of the above signals, and to search for additional transit-like signals.
Results. We detected strong anti-correlated TTVs of the 114 d and 191 d signals, dynamically confirming them as members of the same system. Dynamical simulations reproducing the observed TTVs allowed us to also determine the masses of the planets. We found KOI 1574.01 (hereafter Kepler-87 b) to have a radius of 13.49 ± 0.55 R⊕ and a mass of 324.2 ± 8.8 M⊕, and KOI 1574.02 (Kepler-87 c) to have a radius of 6.14 ± 0.29 R⊕ and a mass of 6.4 ± 0.8 M⊕. Both planets have low densities of 0.729 and 0.152 g cm-3, respectively, which is non-trivial for such cold and old (7−8 Gyr) planets. Specifically, Kepler-87 c is the lowest-density planet in the super-Earth mass range. Both planets are thus particularly amenable to modeling and planetary structure studies, and also present an interesting case where ground-based photometric follow-up of Kepler planets is very desirable. Finally, we also detected two more short-period super-Earth sized (<2 R⊕) planetary candidates in the system, making the relatively high multiplicity of this system notable against the general paucity of multiple systems in the presence of giant planets like Kepler-87 b.
Key words: methods: data analysis / planetary systems
© ESO, 2014
1. Introduction
It is very difficult to detect, and even more difficult to confirm the detection of small planets orbiting in long periods around their host stars where the liquid-water habitable zone (HZ) lies. This is easier for M dwarf host stars since they are both smaller and lighter than Sun-like stars, making the respective transit and radial velocity signals larger. These considerations, coupled with the M dwarfs’ prevalence in the stellar population, are behind the great interest in M dwarfs and their HZ planets (e.g., Anglada-Escudé et al. 2012). However, for more massive stars, like the Sun and the bulk of the Kepler target stars, small HZ planets remain elusive targets. The few small HZ planets that have been detected so far (e.g., Kepler-22, Borucki et al. 2012) are all either around M dwarfs or with no dynamical confirmation (i.e., no mass measured). One way to positively detect these objects is by using transit timing variations (TTVs): in near-resonant systems the amplitude of these variations can allow small planets to be detected in the Kepler data, even down to Earth-mass (Holman & Murray 2005).
Kepler target KOI 1574 was flagged in Batalha et al. (2013) as having a relatively deep (~0.5%) candidate with a period of P01 ≈ 114 d (hereafter KOI 1574.01). Ofir & Dreizler (2013, hereafter OD13) re-analyzed all of Kepler’s KOIs and found 84 new transiting planet candidates in these light curves. Among them, OD13 identified an additional candidate in the KOI 1574 system using data from quarters 0 through 6. The additional outer candidate is in 5:3 resonance with KOI 1574.01, or a period of P02 ≈ 191 d (hereafter also KOI 1574.02). In this work we describe the KOI 1574 planetary system, and KOI 1574.02 in particular, as the first detection of a transiting super-Earth mass in a long period (near the HZ of KOI 1574). We present the spectral analysis of the host star in Sect. 2, light curve processing in Sect. 3, the observed TTVs and the resultant derived masses in Sect. 4, and conclude.
2. Spectral analysis
2.1. Observed spectra
We used two spectra of KOI 1574 for spectral analysis. The first one has been downloaded from the Kepler Community Follow-up Observing Program (CFOP) website1. The spectrum was taken by Erik Brugamyer and William Cochran using the Tull Coudé spectrograph at the 2.7 m Harlan J. Smith telescope at the McDonald Observatory on JD 2455703.83350 with an exposure time of 2900 s. The spectrograph has a resolution of 60 000 and covers a spectral range from about 3750 Å up to 10 000 Å. The useful range is, however, restricted to 4250−9000 Å because of low signal-to-noise outside this range. The spectrum has been reduced with IRAF applying standard processing.
The second spectrum has been taken with the Hobby-Eberly Telescope (HET; Ramsey et al. 1998) with the High Resolution Spectrograph (HRS; Tull et al. 1995) in a setup (15k central 600g5271 2as 2sky IS0 GC0 2x5) that provides a resolution of 15 000 and a wavelength coverage from 4260 Å to 6220 Å. It was obtained on 2012-09-23 (JD = 2 456 193.705981) with an exposure time of 2400 s. Using the IDL based REDUCE package (Piskunov & Valenti 2002) the spectrum was bias corrected, flat-fielded, optimally extracted, and finally wavelength calibrated using a ThAr lamp.
2.2. Model atmosphere fitting
At the Kepler-CFOP web page Sam Quinn provided the following analysis for the McDonald coudé spectrum: Teff = 5750 K, log (g) = 4.0, Vrot = 4 km s-1 at solar metallicity. It has to be noted that the uncertainties are estimated to be ±125 K, ±0.25 dex, and ±1 km s-1 for the effective temperature surface gravity and rotational velocity. Because of the correlation between metallicity and effective temperature, a variation of the metallicity of 0.2 dex would result in an additional uncertainty of the effective temperature of about 200 K. From a comparison of these values with stellar evolution models, the mass determination of the central star would be uncertain by 20−30%.
To improve the parameter determination we performed a model atmosphere fitting using the newest PHOENIX model grid (Husser et al. 2012). Models are available in steps of 100 K, 0.5 dex, and 0.5 dex in effective temperature, surface gravity, and metallicity. Microturbulence is not a free parameter but is derived from a scaling law using the mean convective velocity with each model. This scaling relation has been calibrated using 3D radiative transport on 3D hydrodynamical simulations. Other improvements compared to earlier models is a new equation of state as well as spherical symmetry for all models. We used a Levenberg-Marquardt optimization to fit the effective temperature, surface gravity, metallicity, and rotational velocity (only in the more highly resolved McDonald spectrum) simultaneously with a polynomial for the continuum for each spectral order. The surface gravity, however, was allowed to vary in a small interval log (g) = [3.9,4.0] only, which can be derived from the ratio of the stellar radius and the orbital period of the planet taken from the light curve analysis (Sect. 3), Kepler’s third law, and stellar evolution models. The final values and errors are weighted means over all spectral orders. It should be noted that we multiplied the errors by a factor of two in order to account for systematic errors, for example from the fact that the model atmospheres have to be calculated in 1D, allowing us to treat convection only in the mixing length approximation, or from the fact that the instrumental broadening was approximated with a Gaussian profile.
The stellar parameters determined from the two spectra (see Table 1 and also Fig. 1) marginally agree within their 1σ errors. For the final stellar parameters we adopt a mean from the two determinations. The parameters reported in CFOP reveal a slightly higher effective temperature. It should be noted that a solar abundance was assumed in that case. With our slightly sub-solar metallicity a somewhat lower effective temperature is needed to achieve similar line strengths of the mainly neutral metal lines.
We used the stellar parameters to compare KOI 1574 with Padova stellar evolution models (mass fraction for hydrogen X = 72.3%, helium 26% and metals Z = 1.7%; Bertelli et al. 2008) as well as with Y2 models (mass fraction for hydrogen X = 71%, helium 27% and metals Z = 2%; Yi et al. 2001; Kim et al. 2002; Yi et al. 2003; Demarque et al. 2004). The star KOI 1574 is at the end of its main sequence phase. The slightly sub-solar metallicity is consistent with an age of about 7−8 Gyr. We derived a stellar mass of 1.1 M⊙ ± 0.05 M⊙, which takes into account the dependence of the chemical composition as well as possible systematic errors in the evolution models. This results in a stellar radius of 1.82 R⊙ ± 0.04 R⊙.
Stellar parameters derived from our model atmosphere fit for the McDonald 2.7 m spectrum and the HET High Resolution Spectrograph.
 |
Fig. 1 Stellar parameters from Table 1 (shaded area) compared to Padova stellar evolution models (solid line) and Y2 models (dashed line). We note that the models differ slightly in their chemical composition. The bold regions on the tracks indicate the ratio of the stellar radius to the semi-major axis of the planetary orbit derived from its orbital period, the mass of the stellar model, and Kepler’s third law. The “+” symbols indicate 1 Gyr time steps. |
3. Light curve analysis
3.1. Preprocessing and detection
We use the full Kepler data – quarters 1 through 16 – in our analysis. The additional data includes a few more transits of KOI 1574.01 relative to OD13, and importantly the third and forth transit events of KOI 1574.02; unfortunately the star fall on the inactive Module 3 during quarters 7, 11, and 15 and transits that did occur were not observed. We applied nearly the same processing as in OD13 to the entire dataset. In short, it includes the removal of long-term trends by the application of a median filter to each continuous section individually, and the identification and removal of both additive and relative systematic effects in the data simultaneously with the SARS algorithm (Ofir et al. 2010). The only differences were (a) the inclusion of a correction for crowding and flux ratio effects as in Eq. (2) of Stumpe et al. (2012); (b) the use of the newly available target-specific status indicator to identify continuous sections instead of a global anomalies table; and (c) active avoidance of variable stars (KOIs, eclipsing binaries, and red giants) from the SARS learning set.
We re-searched the KOI 1574 system for transit signals and found the previous two signals to be very significant. We then searched for TTVs for each signal by fiting the linear-ephemeris model (computed using the Mandel and Agol 2002 formalism) to each one of the individual transits, allowing only for the time of mid-transit to vary. Indeed, KOIs 1574.01 and 1574.02 show strongly anti-correlated TTVs (see Fig. 3 and discussion in Sect. 4). These anti-correlated TTVs, coupled with the dynamical simulations that give strong limits on the masses of the two objects, allow us to dynamically confirm the KOIs 1574.01 and 1574.02 signals as true planets in the same planetary system. We therefore name these planets Kepler-87 b and c, respectively.
After the above initial TTVs-corrected modeling removed the planets’ model from the data, re-calculated the background long-term trends, and re-fitted the planets iteratively until convergence. We then removed the Kepler-87 b and c models completely and applied the optimal BLS (box least squares) technique (Ofir 2014) to search for additional transit signals in the residuals, and detected two additional short-period transit-like signals with periods of P03 ≈ 5.83 d and P04 ≈ 8.97 d above the 7.1σ significance threshold, hereafter KOI 1574.03 and KOI 1574.04, respectively. We note that the 1574.03 signal was also identified by the Kepler team in the Q0-Q8 data2. The new signals also passed all the other tests described in OD13. At this point we custom-fitted the long-term filter for this particular object. We changed the general segmented median filter to a segmented Savitzky-Golay filter (Savitzky & Golay 1964) of second order, in a two-day window span with iterative 3σ clipping, which is better than a simple median filter, and repeated all the above. We note that KOI 1574.03 and KOI 1574.04 show no significant TTVs, but the error bars are quite large for such shallow and short-period candidates.
Timing results of the perturbed circular orbit fit for the Kepler-87 b and Kepler-87 c planets.
Predicted transit times for the Kepler-87 b and c planets for the next few years of the adopted model.
Observed and derived parameters for the Kepler-87 (KOI 1574) system.
3.2. Global fit
We derived the final system parameters (given in Tables 2 and 4, illustrated in Fig. 2) by simultaneously fitting all four signals. We iterated the procedure below and the background long-term trends fitting several times untill convergence, and report the final iteration here. We used circular orbits for all signals, but we allowed the phase of all Kepler-87 b and c transits to be set relative to the closest time of mid-transit, and optimized for these times as well. This perturbed-circular fit is valid in the small TTVs regime only, and indeed the largest TTVs detected are about 7.5 × 10-5 of P01 and 6 × 10-4 of P02. The scaled semi-major axis a/R∗ parameter was common to all candidates: as in OD13 we scaled it by Kepler’s third law for each candidate. The final fit therefore included these parameters: one a/R∗, four planet radii rp/R∗, four impact parameters bp/R∗, eleven Tmid for Kepler-87 b, four Tmid for Kepler-87 c, and two linear parameters (P and Tmid) for KOIs 1574.03 and 1574.04, a total of 28 floating parameters. Once initial results suggested the proximity of Kepler-87 c to the HZ (below), and since the relevant parameter a/R∗ is usually both the most difficult to fit (has the largest error) and may have some sensitivity to the initial starting point, we ran twelve 5 × 105-step Markov Chain Monte Carlo (MCMC) fits that allowed all the variables to float, each with a different a/R∗ starting point evenly sampled between half and twice our initial estimate. We then checked that all twelve parameter sets converge on consistent values to 1σ on all parameters. The total of the 12 chains exhibited a smooth distribution of values up to Δχ2 < 100 (relative to the global minimum) so we considered as “burn-in” of each MCMC chain all the steps before the first time Δχ2 < 100 was reached, relative to the global minimum, and concated all these truncated chains (as in Tegmark et al. 2004) to one very large chain, nearly 6 × 106 steps long, that was used for parameter estimation. The final linear ephemeris for Kepler-87 b and c and their error bars were computed from the distribution of fits to the different Tmid along the MCMC chain. We note that the final a01/R∗ is smaller than the linear one (given in OD13), as expected: the linear ephemeris fit caused the average signal to appear smeared, and therefore with artificially higher a01/R∗.
 |
Fig. 2 Phased and binned (to half-hour bins) light curves of the Kepler-87 system components relative to the time of mid transit, with over plotted best-fitting models. From top to bottom: transiting exoplanets Kepler-87 b and c and planetary candidates KOIs 1574.03 and 1574.04. Above each light curve we show the model residuals, shifted for clarity. We note the vertical scale in each panel may be different. |
The equilibrium temperature of exoplanet Kepler-87 c is mostly derived from the above model’s a/R∗ axis and the host star Teff using ![\begin{equation} T_{\rm eq}=T_{\rm eff}\left(\frac{R_*}{2a}\right)^{1/2}[f(1-A_{\rm B})]^{1/4}. \end{equation}](/articles/aa/full_html/2014/01/aa20935-12/aa20935-12-eq164.png) (1)However, the planetary atmospheric parameters flux redistribution factor f and Bond albedo AB are completely unknown, and have a large effect on the resultant Teq. Conventional values would assume efficient redistribution of the stellar flux (f = 1) and Earth-like albedo (AB = 0.3), and these lead to Teq,02 = 403.3, or just hotter than the inner edge of the habitable zone. However, f and AB are completely unknown and can vary considerably. These changes in f or AB can lower the Teq,02 to well within the HZ.
(1)However, the planetary atmospheric parameters flux redistribution factor f and Bond albedo AB are completely unknown, and have a large effect on the resultant Teq. Conventional values would assume efficient redistribution of the stellar flux (f = 1) and Earth-like albedo (AB = 0.3), and these lead to Teq,02 = 403.3, or just hotter than the inner edge of the habitable zone. However, f and AB are completely unknown and can vary considerably. These changes in f or AB can lower the Teq,02 to well within the HZ.
4. Transit timing variations
Figure 3 shows the observed TTVs for Kepler-87 b and c with their error bars (relative to linear ephemeris). A search for the best-fitting sine for the TTVs of Kepler-87 b (which has enough data points to perform this analysis), gave a single peak with a super-period of 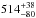 d, which agrees with the expected 5 × P01 = 573.69 to 1.5σ, further showing that the TTVs are indeed caused by the interaction between Kepler-87 b and c. Finally, one can prove that these TTVs are from planet-planet interaction by looking for anti-correlation between the TTVs of Kepler-87 b and c (Ford et al. 2012; Steffen et al. 2012 and Fabrycky et al. 2012), and they do exists, which means that (a) Kepler-87 b and Kepler-87 c are interacting planets in the same system; and (b) we can try to determine the masses of both planets.
d, which agrees with the expected 5 × P01 = 573.69 to 1.5σ, further showing that the TTVs are indeed caused by the interaction between Kepler-87 b and c. Finally, one can prove that these TTVs are from planet-planet interaction by looking for anti-correlation between the TTVs of Kepler-87 b and c (Ford et al. 2012; Steffen et al. 2012 and Fabrycky et al. 2012), and they do exists, which means that (a) Kepler-87 b and Kepler-87 c are interacting planets in the same system; and (b) we can try to determine the masses of both planets.
 |
Fig. 3 Observed transit timing variations relative to a linear ephemeris (black) over plotted with the best model closest to the parameters of Table 4 (red squares). Top and bottom panels are for Kepler-87 b and c, respectively. The error bars for Kepler-87 c are smaller than the size of the symbols. |
 |
Fig. 4 Residuals between observed and calculated TTVs. |
We used the hybrid symplectic integrator within the Mercury package (Chambers 1999), which we have run with a constant time step of 0.5 days, i.e., less than 1% of the orbital period of the P01 planet. We assume co-planar orbits, well justified from the transit fitting (see Table 4), which together with the stellar and the two planetary masses result in 11 free parameters for the 15 measured transit timings. The two inner planet candidates KOI 1574.03 and KOI 1574.04 have not been taken into account for the dynamical analysis.
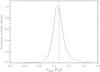 |
Fig. 5 Histogram of the stellar mass obtained from Levenberg-Marquardt fits starting at 2500 random initial values (full line) fitted with a Gaussian (dotted line). The mean (dotted) and the median (dashed) of the distribution are indicated as long vertical lines, the 1σ error as short vertical lines. |
 |
Fig. 6 Histogram of the mass of the inner planet obtained from Levenberg-Marquardt fits starting at 2500 random initial values (full line) fitted with a Gaussian (dotted line). The mean (dotted) and the median (dashed) of the distribution are indicated as long vertical lines, the 1σ error as short vertical lines. |
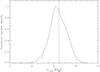 |
Fig. 7 Histogram of the mass of the outer planet obtained from Levenberg-Marquardt fits starting at 2500 random initial values (full line) fitted with a Gaussian (dotted line). The mean (dotted) and the median (dashed) of the distribution are indicated as long vertical lines, the 1σ error as short vertical lines. |
Given the stellar mass from the spectral analysis and the orbital periods from the light curve, a reasonable set of start parameters can be estimated from the ratio of the TTV amplitudes and the phase of the TTV variations. From preliminary stability calculations the eccentricity could also be limited to be less than or equal to about 0.1. We used the IDL routine mpfit, a Levenberg-Marquardt optimization, to fit the calculated TTVs as a function of the stellar and the two planetary masses, the semi-major axes, eccentricities, lengths of peri-astron, as well as mean anomalies at t = 0. We then used this fit to generate 2500 random starting values within the error range provided by mpfit and converged them as well. From the resulting sample we derive histograms of the parameters which allows us to obtain mean values and uncertainties. Figures 5−7 show the resulting distribution of the stellar and the planetary masses.
We would like to note that the mean stellar mass derived from the TTV analysis is close to the spectroscopic mass derived with the stellar density constraint (Sect. 2). The fit parameters are listed in Table 4. The mean masses for the two planets are 6.4 ± 0.8 M⊕ and 324.2 ± 8.8 M⊕ for the Kepler-87 c and b planets, respectively. The bulk densities of the planets are determined to be ρ01 = 0.729 ± 0.026 and be ρ02 = 0.152 ± 0.019 g cm-3, so the inner planet is a Jupiter-mass planet with a Saturn-like density while the outer planet is a very low density planet in the super-Earth mass regime. The eccentricities are low, i.e., the 3σ errors are within the stable regime which allows eccentricities below about 0.1. Within the uncertainties, the lengths of periastron of the two orbits are aligned.
While the total number of measurements is larger than the free parameters, the number of TTV measurements for the outer planet (4) is low. The TTVs of the outer planet are mainly constraining the mass of the inner planet (TTV amplitude), the eccentricity, and periastron length of the outer planet (phase shift against TTV of inner planet and shape of TTV), by the mean anomaly of the outer planet (time of first transit), and by the mean orbital period of the outer planet. At first it seems that the problem is over-determined, but these parameters are also constrained by the TTVs of the inner planet, however, more indirectly from the overall dynamical behavior of the three-body system. We therefore also analyzed the TTVs with a restricted set of parameters, i.e., we fixed the eccentricity and the length of periastron of the outer planet to their mean values. This does not change the results.
The deviations of the observed and simulated transit timings of the fit are presented in Figs. 3 and 4, the latter showing the residuals. The reduced χ2 is 0.8. We also risk and attempt to predict the times of mid-transit for the next few years (see Table 3). We note that the seemingly over-determined solution to Kepler-87 c makes it difficult for us to put reliable error bars on the prediction. By comparing future observations with the predicted timings given here one can quickly check if corrections to the model given in this paper are needed. This is quite likely, since the current observations cover the ≈550-day short term interaction cycle, but do not cover the longer term interaction cycle of >3000 days.
The minimum mutual Hill distance for the mean fit parameters is 4.7, which makes a long-term stable configuration plausible. Nevertheless, we integrated the orbit for 8 Gyr, i.e., the expected age of the system to ensure the dynamical stability, and found it to be stable.
 |
Fig. 8 Mass-radius relation for all known planets with masses below 30 M⊕ with overplotted bulk density contours. It is obvious that Kepler-87 c occupies a unique position on this parameter space as the lowest-density planet for its super-Earth mass range. Some planet names were shortened so that “K-X” stands for the planet Kepler-X, and similarly “C-X” and “H-X” stand for “CoRoT-X” and “HAT-P-X”. Solar system planets are designated with a letter with no error bars. We note Kepler-87 b is beyond the scope of this figure (see discussion in the main text). |
5. Discussion
We presented the dynamical confirmation of two long-period low-density transiting planets using transit timing variation, as well as the initial detection of two transiting super-Earth-sized planet candidates, all in the Kepler-87 system. Kepler-87 c is the longest-period confirmed transiting planet around a single star, and Kepler-87 b has the third-longest period, after the previous record holder Kepler-30 d (Fabrycky et al. 2012). Batalha et al. (2013) strengthened the case for the paucity of short-period (<10 d) giant planets in multiple systems (Latham et al. 2011). However, this paucity seems to be less severe for longer period giant planets such as Kepler-87 b. Particularly, planet candidate KOI 1574.04 was detected neither in the Q0-Q6 data (Batalha et al. 2013) nor in the Q1-Q12 data (Tenenbaum et al. 2012).
The most important feature of the Kepler-87 system is its two low-density planets (Fig. 8). While Kepler-87 b (ρ01 = 0.729 ± 0.026) has mass and radius that put it directly in the center of the general distribution of giant planets, Kepler-87 c (ρ02 = 0.152 ± 0.019) is anomalously low-density for its mass, similar to that of the least dense very hot Jupiters (e.g., Hartman et al. 2011). However, the Kepler-87 planets are rarefied although they are neither strongly irradiated nor young. Such low densities suggest that a significant mass fraction can be attributed to Hydrogen and Helium. While common for giant planets, such a composition is non-trivial for planets less massive than 10 M⊕ such as Kepler-87 c which at no point in its history had the canonical critical mass for the starting of gas accretion of 10 M⊕. Comparing these low densities to previously known planets is difficult since there are very few similarly long-period transiting planets, but the few known circumbinary planets already include Kepler-35 b (Welsh et al. 2012) which has a density of 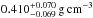 , between the Kepler-87 planets. Importantly, there is no simple analogue to the low density of Kepler-87 c.
, between the Kepler-87 planets. Importantly, there is no simple analogue to the low density of Kepler-87 c.
Initially this result was baffling to us. However, the above solution exhibits strong self-consistency between different determinations of some of the variables: the stellar mass from the spectroscopy agrees with the stellar mass from the dynamical modeling, and the semi-major axes from the light curve fitting + stellar model agree with the semi-major axes from dynamical model. From a theoretical stand point, Rogers et al. (2011) attempted to put limits on the masses of similarly sized Kepler candidates and found that even low-mass low-density planets were possible in the general framework of core-nucleated accretion using plausible disk configurations. They found that a planet with a radius of 6 R⊕ like Kepler-87 c and an equilibrium temperature of 500 K would have a mass of 6.4 M⊕ if ≈20% of its mass were made of a gaseous envelope (assuming an ice-rock interior, and H/He in protosolar proportions). Correcting for the lower equilibrium temperature of Kepler-87 c (Teq = 403.3), its envelope mass fraction is probably even higher than that. Planets such as Kepler-87 c, as well as the highly irradiated Kepler-11 and -36 systems (Lissauer et al. 2011 and Carter et al. 2012), demonstrate that the great compositional variety that was found for gas giants also extends down to planets with intermediate masses between Earth and Uranus.
We believe that the two large planets of the Kepler-87 system present an opportunity for detailed study of exoplanet interior structure: residing at a relatively large orbital distance they are significantly less affected by the extreme insolation that on shorter period planets may produce inflated radii on the one hand and mass loss due to irradiation driven atmospheric escape on the other hand. Furthermore, the host star is at a stage of its evolution that is age sensitive, making the system age relatively well determined. This benign and constrained environment should make the two planets more amenable to modeling.
The end of the Kepler mission also presents an interesting case where ground-based photometric follow-up of Kepler planets is very desirable: the systematic uncertainty associated with the low number of data points means that additional observations are of significant value. On the one hand, Kepler-87 b is an easy target (0.5% depth) to better Kepler’s two-plus minutes timing precision, and almost any-precision detection of Kepler-87 c will be worthwhile owing to its very large amplitude TTVs. On the other hand, because of their long periods and large host star, both planets exhibit long transits of about 12hr and 15hr, which means full transits probably need a multi-site campaign. We note that the accumulated effect of TTVs is large and can be even more than a day already in the near future (see Table 3).
As cataloged at the Exoplanet Archive http://exoplanetarchive.ipac.caltech.edu/index.html
Acknowledgments
A.O. acknowledges financial support from the Deutsche Forschungsgemeinschaft under DFG GRK 1351/2. M.Z. acknowledges support by the European Research Council under the FP7 Starting Grant agreement number 279347. We thank Guillem Anglada-Escudé for discussing at length this system with us. We thank Bill Cochran and the rest of his team who observed KOI 1574 and made the data available on CFOP. We would like to thank the team of the Hobby-Eberly Telescope for taking the data of KOI 1574. This paper includes data collected by the Kepler mission. Funding for the Kepler mission is provided by the NASA Science Mission directorate. Some of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST). STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. Support for MAST for non-HST data is provided by the NASA Office of Space Science via grant NNX09AF08G and by other grants and contracts. This research has made use of the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program.
References
- Anglada-Escudé, G., Arriagada, P., Vogt, S. S., et al. 2012, ApJ, 751, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2013, ApJS, 204, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D. G., Batalha, N., et al. 2012, ApJ, 745, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, J. A., Agol, E., Chaplin, W. J., et al. 2012, Science, 337, 556 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Demarque, P., Woo, J.-H., Kim, Y.-C., & Yi, S. K. 2004, ApJS, 155, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrycky, D. C., Ford, E. B., Steffen, J. H., et al. 2012, ApJ, 750, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, E. B., Fabrycky, D. C., Steffen, J. H., et al. 2012, ApJ, 750, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Torres, G., et al. 2011, ApJ, 742, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, M. J., & Murray, N. W. 2005, Science, 307, 1288 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Howett, C. J. A., Spencer, J. R., Pearl, J., & Segura, M. 2010, Icarus, 206, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, Y.-C., Demarque, P., Yi, S. K., & Alexander, D. R. 2002, ApJS, 143, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Latham, D. W., Rowe, J. F., Quinn, S. N., et al. 2011, ApJ, 732, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J., Fabrycky, D. C., Ford, E. B., et al. 2011, Nature, 470, 53 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Ofir, A. 2014, A&A, in press, DOI: 10.1051/0004-6361/201220860 [Google Scholar]
- Ofir, A., & Dreizler, S. 2013, A&A, 555, A5 [Google Scholar]
- Ofir, A., Alonso, R., Bonomo, A. S., et al. 2010, MNRAS, 404, L99 [NASA ADS] [Google Scholar]
- Piskunov, N. E., Valenti, J. A. 2002, A&A, 385, 1095 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramsey, L. W., Adams, M. T., Barnes, T. G., et al. 1998, Proc. SPIE, 3352, 34 [Google Scholar]
- Rogers, L. A., Bodenheimer, P., Lissauer, J. J., & Seager, S. 2011, ApJ, 738, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Savitzky, A., & Golay, M. J. E. 1964, Analytical Chemistry, 36, 1627 [Google Scholar]
- Steffen, J. H., Fabrycky, D. C., Ford, E. B., et al. 2012, MNRAS, 421, 2342 [NASA ADS] [CrossRef] [Google Scholar]
- Stumpe, M. C., Smith, J. C., Van Cleve, J. E., et al. 2012, PASP, 124, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Tegmark, M., Strauss, M. A., Blanton, M. R., et al. 2004, Phys. Rev. D, 69, 103501 [CrossRef] [Google Scholar]
- Tenenbaum, P., Jenkins, J. M., Seader, S., et al. 2012, ApJS, submitted [arXiv:1212.2915] [Google Scholar]
- Tull, R. G., MacQueen, P. J., Sneden, C., & Lambert, D. L. 1995, PASP, 107, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Veverka, J., Helfenstein, P., Hapke, B., & Goguen, J. D. 1988, Mercury (University of Arizona Press), 37 [Google Scholar]
- Welsh, W. F., Orosz, J. A., Carter, J. A., et al. 2012, Nature, 481, 475 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Yi, S., Demarque, P., Kim, Y.-C., et al. 2001, ApJS, 136, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Yi, S. K., Kim, Y.-C., & Demarque, P. 2003, ApJS, 144, 259 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Stellar parameters derived from our model atmosphere fit for the McDonald 2.7 m spectrum and the HET High Resolution Spectrograph.
Timing results of the perturbed circular orbit fit for the Kepler-87 b and Kepler-87 c planets.
Predicted transit times for the Kepler-87 b and c planets for the next few years of the adopted model.
All Figures
 |
Fig. 1 Stellar parameters from Table 1 (shaded area) compared to Padova stellar evolution models (solid line) and Y2 models (dashed line). We note that the models differ slightly in their chemical composition. The bold regions on the tracks indicate the ratio of the stellar radius to the semi-major axis of the planetary orbit derived from its orbital period, the mass of the stellar model, and Kepler’s third law. The “+” symbols indicate 1 Gyr time steps. |
| In the text | |
 |
Fig. 2 Phased and binned (to half-hour bins) light curves of the Kepler-87 system components relative to the time of mid transit, with over plotted best-fitting models. From top to bottom: transiting exoplanets Kepler-87 b and c and planetary candidates KOIs 1574.03 and 1574.04. Above each light curve we show the model residuals, shifted for clarity. We note the vertical scale in each panel may be different. |
| In the text | |
 |
Fig. 3 Observed transit timing variations relative to a linear ephemeris (black) over plotted with the best model closest to the parameters of Table 4 (red squares). Top and bottom panels are for Kepler-87 b and c, respectively. The error bars for Kepler-87 c are smaller than the size of the symbols. |
| In the text | |
 |
Fig. 4 Residuals between observed and calculated TTVs. |
| In the text | |
 |
Fig. 5 Histogram of the stellar mass obtained from Levenberg-Marquardt fits starting at 2500 random initial values (full line) fitted with a Gaussian (dotted line). The mean (dotted) and the median (dashed) of the distribution are indicated as long vertical lines, the 1σ error as short vertical lines. |
| In the text | |
 |
Fig. 6 Histogram of the mass of the inner planet obtained from Levenberg-Marquardt fits starting at 2500 random initial values (full line) fitted with a Gaussian (dotted line). The mean (dotted) and the median (dashed) of the distribution are indicated as long vertical lines, the 1σ error as short vertical lines. |
| In the text | |
 |
Fig. 7 Histogram of the mass of the outer planet obtained from Levenberg-Marquardt fits starting at 2500 random initial values (full line) fitted with a Gaussian (dotted line). The mean (dotted) and the median (dashed) of the distribution are indicated as long vertical lines, the 1σ error as short vertical lines. |
| In the text | |
 |
Fig. 8 Mass-radius relation for all known planets with masses below 30 M⊕ with overplotted bulk density contours. It is obvious that Kepler-87 c occupies a unique position on this parameter space as the lowest-density planet for its super-Earth mass range. Some planet names were shortened so that “K-X” stands for the planet Kepler-X, and similarly “C-X” and “H-X” stand for “CoRoT-X” and “HAT-P-X”. Solar system planets are designated with a letter with no error bars. We note Kepler-87 b is beyond the scope of this figure (see discussion in the main text). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


