| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A107 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201322094 | |
| Published online | 16 December 2013 | |
Decay-less kink oscillations in coronal loops⋆
1
Institute of Solar-Terrestrial Physics, 664033
Irkutsk, Russia
e-mail:
anfinogentov@iszf.irk.ru
2
Centre for Fusion, Space and Astrophysics, Department of Physics, University of
Warwick, CV4 7AL, UK
e-mail:
g.nistico@warwick.ac.uk
3
School of Space Research, Kyung Hee University,
446-701
Yongin, Gyeonggi, Korea
4
Central Astronomical Observatory at Pulkovo of the Russian Academy
of Sciences, 196140
St Petersburg,
Russia
Received: 17 June 2013
Accepted: 2 August 2013
Context. Kink oscillations of coronal loops in an off-limb active region are detected with the Imaging Assembly Array (AIA) instruments of the Solar Dynamics Observatory (SDO) at 171 Å.
Aims. We aim to measure periods and amplitudes of kink oscillations of different loops and to determinate the evolution of the oscillation phase along the oscillating loop.
Methods. Oscillating coronal loops were visually identified in the field of view of SDO/AIA and STEREO/EUVI-A: the loop length was derived by three-dimensional analysis. Several slits were taken along the loops to assemble time-distance maps. We identified oscillatory patterns and retrieved periods and amplitudes of the oscillations. We applied the cross-correlation technique to estimate the phase shift between oscillations at different segments of oscillating loops.
Results. We found that all analysed loops show low-amplitude undamped transverse oscillations. Oscillation periods of loops in the same active region range from 2.5 to 11 min, and are different for different loops. The displacement amplitude is lower than 1 Mm. The oscillation phase is constant along each analysed loop. The spatial structure of the phase of the oscillations corresponds to the fundamental standing kink mode. We conclude that the observed behaviour is consistent with the empirical model in terms of a damped harmonic resonator affected by a non-resonant continuously operating external force.
Key words: Sun: corona / Sun: oscillations / methods: observational
A movie is available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Kink oscillations of solar coronal plasma structures are one of the most debated examples of the magnetohydrodynamic (MHD) wave activity of the solar corona (see, e.g. De Moortel & Nakariakov 2012, for a recent review). Kink oscillations are transverse displacements of field-aligned plasma non-uniformities, typically observed in the EUV band with imaging telescopes. Kink oscillations have a broad range of periods, from several seconds (e.g. Williams et al. 2001) to several hours (e.g. Hershaw et al. 2011). This mode of MHD oscillations is usually detected in warm (i.e. 1 MK) and hot (i.e. 10 MK) coronal loops, (e.g. Aschwanden et al. 1999; Nakariakov et al. 1999; White et al. 2012, respectively). It is also found in prominence fibrils (e.g. Arregui et al. 2012), in hot jets (e.g. Cirtain et al. 2007; Vasheghani Farahani et al. 2009), and in post-flare supra-arcade non-uniformities (Verwichte et al. 2005). Kink oscillations are detected in both standing (e.g. Nakariakov et al. 1999; White & Verwichte 2012) and propagating (e.g. Williams et al. 2001; Tomczyk et al. 2007; McIntosh et al. 2011) forms. Standing oscillations are mainly horizontally polarised, but several examples of the vertically polarised mode have been found as well (Wang & Solanki 2004; White et al. 2012). Most often, one sees the fundamental mode (in the longitudinal direction), with the maximum displacement at the loop top and oscillations at the footpoints. However, higher spatial harmonics have also been detected (e.g. Verwichte et al. 2004; De Moortel & Brady 2007).
Theoretical modelling of kink oscillations is commonly based upon a straight magnetic cylinder model (Edwin & Roberts 1983; Zaitsev & Stepanov 2008). Linear fast magnetoacoustic perturbations of the cylinder with the azimuthal wave number m = 1, confined to its boundary in the external medium, are described by the Bessel function inside the cylinder and the Macdonald function outside it. A transcendental dispersion relation that links the frequency and the longitudinal wave number of the kink perturbation to the parameters of the plasma inside and outside the cylinder shows that this mode exists for all wave numbers. The mode is dispersive. In the long-wavelength limit the phase speed of the kink mode is a so-called kink speed, CK, that is the density-weighed average Alfvén speed inside and outside the oscillating plasma non-uniformity. More specifically, 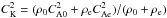 , where ρ0 and ρe are the density, and CA0 and CAe are the Alfvén speeds, inside and outside the cylinder, respectively. In the long-wavelength limit, the kink mode is weakly compressive and weakly dispersive, and hence is sometimes referred to as “Alfvénic” to highlight its “magnetic” nature. In some recent papers these modes were also called “Alfvén”, which is inconsistent with the commonly accepted interpretation of this phenomenon (see the discussion in Edwin & Roberts 1983; Van Doorsselaere et al. 2008a,b; Goossens et al. 2012). The importance of the correct interpretation, especially for the estimation of the wave energetics, was recently pointed out by Goossens et al. (2013).
, where ρ0 and ρe are the density, and CA0 and CAe are the Alfvén speeds, inside and outside the cylinder, respectively. In the long-wavelength limit, the kink mode is weakly compressive and weakly dispersive, and hence is sometimes referred to as “Alfvénic” to highlight its “magnetic” nature. In some recent papers these modes were also called “Alfvén”, which is inconsistent with the commonly accepted interpretation of this phenomenon (see the discussion in Edwin & Roberts 1983; Van Doorsselaere et al. 2008a,b; Goossens et al. 2012). The importance of the correct interpretation, especially for the estimation of the wave energetics, was recently pointed out by Goossens et al. (2013).
The main interest in kink oscillations is connected with seismological diagnostics of coronal plasmas. Nakariakov & Ofman (2001) developed a technique for estimating the Alfvén speed and the absolute value of the magnetic field in an oscillating loop. Andries et al. (2005) showed that the period ratio of different spatial harmonics allows for estimating the density scale height. Van Doorsselaere et al. (2008a) demonstrated the fine structuring of diffuse coronal loops. Ruderman et al. (2008) designed a technique for the estimating the loop expansion factor. Also, Verwichte et al. (2006) demonstrated that properties of kink oscillations can be used for estimating the steepness of radial density structuring.
An intriguing feature of standing kink oscillations is their rapid decay. Kink oscillations excited by a flare or an eruption nearby are usually observed to damp in about 3–4 oscillation periods. This behaviour remains stable for periods ranging from a few minutes to several hours (see, e.g., Fig. 12 in White & Verwichte 2012). The physical mechanism responsible for the rapid damping has been the subject of a number of theoretical studies, and now it is generally accepted that it is resonant absorption: linear coupling of the kink mode to unresolved torsional motions at a very thin resonant layer (e.g. Ruderman & Roberts 2002; Goossens et al. 2002, 2011).
Very recently, it was found that there are two kinds of standing kink oscillations of loops: in addition to the high-amplitude rapidly decaying oscillations known since Aschwanden et al. (1999) and Nakariakov et al. (1999), there are decay-less low-amplitude oscillations (Nisticò et al. 2013). These different regimes were found in the same loop. Moreover, no significant change in the oscillation periods was detected during the transition from one regime to the other. This behaviour indicates that both regimes could be responses of the same loop to two different non-resonant drivers, one operating continuously, and the other one being localised in time. Moreover, an example of a gradually growing kink oscillation was found in Wang et al. (2012), and spectroscopic signatures of persistent Doppler shifts, arguably associated with kink waves, were also discussed in Tian et al. (2012). Thus, there is a need for a systematic study of this new regime, which is the aim of this paper.
2. Observations
We analysed transverse oscillations of loops that belong to the active region (AR) NOAA 11654 at the time when it was on the western solar limb. The AR appears to be filled with many overlaying loops. We collected EUV images on 22 January 2013, between 00:00–06:00 UT, with the SDO/AIA instrument (Lemen et al. 2012) at 171 Å. The data were retrieved from the JSOC data centre1. We downloaded subframes extracted from the full-size images with a field-of-view (FOV) of 600 × 600 arcsec, spatial resolution of 0.6′′, and a time cadence of 12 s. A snapshot of the off-limb AR is shown in Fig. 1 (left). This AR is also clearly seen from the Solar TErrestrial RElations Observatory (STEREO) Ahead spacecraft. The corresponding image obtained with the Extreme Ultra Violet Imager (EUVI) telescope (Howard et al. 2008) on-board STEREO at 195 Å is presented in Fig. 1 (right). Many bright spots and long loops with the associated footpoints can be easily seen. The red line in Fig. 1 (right) marks the position of the limb as seen from the SDO point of view: the left loop footpoints are not visible from SDO, but they are close to the limb. During the six hours of observations, the AR does not show any impulsive activity such as flares or coronal mass ejections (CMEs): we consulted the RHESSI catalogue and no flare was registered from this AR during this time. Flares that occurred in other ARs during this observation period were below the class C. In this work, we focus on the 171 Å data set. We identified several oscillating loops and took a number of slits across and along them to study and analyse kink oscillations observed in the spatial structure of the EUV emission intensity.
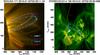 |
Fig. 1 Left: snapshot of the AR NOAA 11654 from SDO/AIA at 171 Å. The analysed loops are labelled with different colours and by increasing numbers.The solid circle on the loops with numbers mark the position of the slits where time-distance maps have been extracted. Right: a view from STEREO/EUVI-A at 195 Å of the active region of interest. The red meridian marks the limb position as seen from the SDO (or Earth) perspective. |
Parameters of transverse loop oscillations.
3. Analysis and results
3.1. Slit analysis
We inspected the image sequences related to the region of interest, and chose some loops that clearly exhibited oscillations. The highest cadence possible in STEREO/EUVI was 5 min and it was provided only at 195 Å. In conjunction with STEREO/EUVI-195 Å, we used SDO/AIA 193 Å, since the temperature responses of these two bands are rather similar. Running difference images were used to highlight EUV emission intensity variations in time and highlight the loop shape (see Fig. 2 and online movie).
To assess the loop’s 3D shape and estimate its length, we made a 3D reconstruction of the loop with the procedure scc_measure.pro from the SolarSoft (SSW) package. The technique for obtaining the loop length and the 3D loop shape is not described here but will be subject of a future paper. Here we restrict ourselves to giving some estimates of the parameters only. For simplicity, we projected the 3D points by highlighting the loops to the FOV of both the instruments (see Fig. 1). Then we fitted the points, projected to the SDO/AIA-171 FOV, by an elliptical curve using the mpfitellipse.pro procedure. In this way, we defined the loop shape as seen from the observer and stacked several equidistant slits perpendicular to the loop path to depict oscillations at different positions. We made this for four different loops (or, rather, bundles of loops), whose locations are over-plotted in Fig. 1 (left) with different symbols and colours.
 |
Fig. 2 Running difference images of coronal loops. The left panel shows the active region NOAA 11654 from SDO/AIA in the 193 Åband. The right panel shows a running difference image computed from STEREO/EUVI-A observing the same active region in the 195 Åband at the same time, but at a different angle. The green lines in both panels show the position of the limb as seen from SDO. Red solid circles in both panels mark the same points on the loop visible from both spacecraft. A movie showing the temporal evolution between 00:10 and 05:50 UT on 22. Jan. 2013 is available online. |
We selected 100 slits perpendicular to the fitted loop path. Each slit was three AIA pixels wide and 76 pixels long, which corresponds to almost 32 Mm. To increase the signal-to-noise ratio we calculated an average intensity value over the slit width. This procedure is justified because the apparent projected wavelengths of the studied oscillations was comparable with the whole length of the oscillating loops. Typical time-distance maps are presented in Fig. 3. Characteristic wave-like patterns are clearly seen in the maps. The oscillations seem to last in time, without any remarkable decay: some oscillations show only three/four periods lasting about 20 min, while others are extended in time for more than one hour (e.g., see the right-bottom panel of Fig. 3). We need to point out that in some cases different oscillatory patterns are simultaneously seen in the dynamics of different plasma threads forming a specific loop that can be considered as a bundle of the threads (see, e.g. the bottom panels of Fig. 3).
Amplitudes and periods of the transverse oscillations were estimated from the most pronounced oscillatory patterns visually identified in Fig. 3. In the time-distance plots there are many overlaying loops. In most cases it was impossible to fit the transverse shape of the loop with a Gaussian profile. Because of that, we used loop edges to track the oscillations. We also calculated partial derivatives in the direction perpendicular to the loop (the direction of the highest spatial gradient) to determine the instant position of the loop boundaries. The displacements of the loop boundaries (and hence of the loop itself, assuming that its minor radius does not change) were determined for each instant of time by fitting the spatial derivatives of the transverse profile of the EUV intensity across the loop by a Gaussian function. This was made with the GAUSSFIT routine from the IDL library. The positions of the loop edges determined by this method are marked with red dots in Fig. 3. The loop edge positions were then fitted with a sine function to obtain its periods and amplitudes with the CURVEFIT function. The fitted oscillations are shown with white lines in Fig. 3.
The measured oscillation parameters are presented in Table 1. The displacement amplitudes of the oscillations are found to be below 1 Mm in all cases. The periods range between 260–620 s (4−11 min). If one considers the displacement to follow the simple harmonic pattern, ~ξsin(2πt/P), where ξ is the displacement amplitude and P is the period, then the time derivative of this dependence gives the velocity amplitude of the oscillation, 2πξ/P. For the observed periods and displacements, the velocity amplitude ranges from 0.7 to 4.2 km s-1 for different loops. This value is consistent with the previous estimate, for instance about 30 km s-1 in Tomczyk et al. (2007), 5 km s-1 in McIntosh et al. (2011), and 1.6 km s-1 in Tian et al. (2012).
3.2. Cross-correlation analysis
The determination of the oscillation phase at different segments of the loops allows us to assess whether the oscillations are standing or propagating, and to distinguish between the fundamental (also called global) mode (with the highest perturbation at the loop apex) and the second longitudinal harmonic (with a node at the loop apex and two anti-phase maxima in the loop legs). This requires measuring the phase delay between the signals measured in different slits taken along the loop. To perform this we employed the cross-correlation analysis. From each slit (see Sect. 3.1) we extracted the intensity profile measured at a spatial location near the edge of the loop, as shown in Fig. 4. The periodic loop movement causes brightness variation at these locations when the loop crosses the line-of-sight. We used this brightness variation to estimate the oscillation periods and phases in different parts of the loop. The intensity profile from the slit with the highest observed amplitude of the oscillation was used as the reference in computing the cross-correlation function.
We performed the cross-correlation analysis for each loop highlighted in Fig. 1. The typical cross-correlation functions obtained are shown in Fig. 4. One can see that for all these loops the position of the cross-correlation function maximum does not depend on the distance along the loop and corresponds to the zero lag relative to the reference position. There are some irregular perturbations in the cross-correlation maximum positions. However, their irregularity suggests that they are likely to be caused by the noise. If these phase shifts were caused by a propagating wave, the phase shifts would increase or decrease monotonically with the distance from the loop footpoints. Thus, the observed oscillations are most likely standing, and the observed spatial distribution of the oscillation phase corresponds to the fundamental kink mode.
 |
Fig. 3 Time-distance maps for the analysed loops at different positions (slit number) along the loop paths. The most noticeable oscillations were fitted with a sine function to define their parameters. Red dots indicate the positions of the loop edge estimated by the Gaussian fitting to the partial derivative of the time-distance plot in transverse direction. The white lines show the best-fitting sinusoidal functions. |
 |
Fig. 4 Cross-correlation coefficient for loops marked in Fig. 1. The vertical axis corresponds to the distance along the loop. The horizontal axis shows the time lag relatively to the reference location. |
4. Discussion and conclusion
We analysed dynamics of coronal loops in a non-flaring active region observed with SDO/AIA in 171 Å. It was found that the loops experience low-amplitude undamped periodic displacements. We chose several specific loops from the dataset and analysed their transverse oscillations with time-distance maps corresponding to spatial slits chosen at different positions across the loops. The slits covered the whole length of the analysed loops, from almost the footpoints to the loop top. The lengths of the analysed loops were determined by comparing two different views taken from SDO and STEREO-A by at 193 and 195 Å images. We summarise our conclusions as follows:
-
1
Clear oscillatory patterns that correspond to the periodicdisplacements of the analysed coronal loops in the plane-of-skyare observed. These oscillations last from three or four periods tomore than ten periods without any visible decay or amplification.The beginning and end times of the oscillations observed indifferent loops are different. Typically, the oscillations becomevisible and then invisible when there is some major topologicalchange in the observed topology, for instance two loops graduallymerge or split in the line-of-sight. The detected oscillationamplitude does not exceed 1 Mm, while it shouldbe corrected for the projection effect.
-
2
Different loops are observed to oscillate with different periods, ranging from 2 min to 11 min. Longer loops seem to oscillate with longer periods, while this conclusion cannot be taken as statistically significant because of the small number of the analysed loops and requires a dedicated study. Moreover, in different time intervals the same loop can have different oscillation periods.
-
3
Different segments of the analysed loops are seen to displace harmonically and in phase. The highest amplitudes are observed at the tops of the loops. This spatial structure of the oscillations corresponds to the standing fundamental mode.
Online material
Movie of Fig. 2 Access here
Acknowledgments
The data used are courtesy of the STEREO/SECCHI and SDO/AIA consortia. The work is supported by the Marie Curie PIRSES-GA-2011-295272 RadioSun project, the European Research Council under the SeismoSun Research Project No. 321141 (VMN), the Russian Ministry of Education and Science project No. 8524, State agreement No. 8407; the Russian Foundation of Basic Research under grants 12-02-33110-mol-a-ved, 12-02-31746-mol-a, 13-02-00044-a and 13-02-90472-ukr-f-a; the Kyung Hee University International Scholarship (VMN), and the UK-Science and Technology Facilities Council (STFC) for the CFSA Rolling Grant (GN).
References
- Andries, J., Arregui, I., & Goossens, M. 2005, ApJ, 624, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Arregui, I., Oliver, R., & Ballester, J. L. 2012, Liv. Rev. Sol. Phys., 9, 2 [Google Scholar]
- Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Cirtain, J. W., Golub, L., Lundquist, L., et al. 2007, Science, 318, 1580 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- De Groof, A., & Goossens, M. 2000, A&A, 356, 724 [NASA ADS] [Google Scholar]
- De Moortel, I., & Brady, C. S. 2007, ApJ, 664, 1210 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., & Nakariakov, V. M. 2012, Roy. Soc. London Philos. Trans. Ser. A, 370, 3193 [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Goossens, M., Andries, J., & Aschwanden, M. J. 2002, A&A, 394, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goossens, M., Erdélyi, R., & Ruderman, M. S. 2011, Space Sci. Rev., 158, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Goossens, M., Andries, J., Soler, R., et al. 2012, ApJ, 753, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Goossens, M., Van Doorsselaere, T., Soler, R., & Verth, G. 2013, ApJ, 768, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Hershaw, J., Foullon, C., Nakariakov, V. M., & Verwichte, E. 2011, A&A, 531, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howard, R. A., Moses, J. D., Vourlidas, A., et al. 2008, Space Sci. Rev., 136, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
- McIntosh, S. W., de Pontieu, B., Carlsson, M., et al. 2011, Nature, 475, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., & Ofman, L. 2001, A&A, 372, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Ofman, L., Deluca, E. E., Roberts, B., & Davila, J. M. 1999, Science, 285, 862 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nakariakov, V. M., Aschwanden, M. J., & van Doorsselaere, T. 2009, A&A, 502, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nisticò, G., Nakariakov, V. M., & Verwichte, E. 2013, A&A, 552, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruderman, M. S., & Roberts, B. 2002, ApJ, 577, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., Verth, G., & Erdélyi, R. 2008, ApJ, 686, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, H., McIntosh, S. W., Wang, T., et al. 2012, ApJ, 759, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Tomczyk, S., McIntosh, S. W., Keil, S. L., et al. 2007, Science, 317, 1192 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Van Doorsselaere, T., Brady, C. S., Verwichte, E., & Nakariakov, V. M. 2008a, A&A, 491, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Doorsselaere, T., Nakariakov, V. M., & Verwichte, E. 2008b, ApJ, 676, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Vasheghani Farahani, S., Van Doorsselaere, T., Verwichte, E., & Nakariakov, V. M. 2009, A&A, 498, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verwichte, E., Nakariakov, V. M., Ofman, L., & Deluca, E. E. 2004, Sol. Phys., 223, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Verwichte, E., Nakariakov, V. M., & Cooper, F. C. 2005, A&A, 430, L65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verwichte, E., Foullon, C., & Nakariakov, V. M. 2006, A&A, 452, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, T. J., & Solanki, S. K. 2004, A&A, 421, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, T., Ofman, L., Davila, J. M., & Su, Y. 2012, ApJ, 751, L27 [Google Scholar]
- White, R. S., & Verwichte, E. 2012, A&A, 537, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, R. S., Verwichte, E., & Foullon, C. 2012, A&A, 545, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, D. R., Phillips, K. J. H., Rudawy, P., et al. 2001, MNRAS, 326, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Zaitsev, V. V., & Stepanov, A. V. 2008, Phys. Uspekhi, 51, 1123 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left: snapshot of the AR NOAA 11654 from SDO/AIA at 171 Å. The analysed loops are labelled with different colours and by increasing numbers.The solid circle on the loops with numbers mark the position of the slits where time-distance maps have been extracted. Right: a view from STEREO/EUVI-A at 195 Å of the active region of interest. The red meridian marks the limb position as seen from the SDO (or Earth) perspective. |
| In the text | |
 |
Fig. 2 Running difference images of coronal loops. The left panel shows the active region NOAA 11654 from SDO/AIA in the 193 Åband. The right panel shows a running difference image computed from STEREO/EUVI-A observing the same active region in the 195 Åband at the same time, but at a different angle. The green lines in both panels show the position of the limb as seen from SDO. Red solid circles in both panels mark the same points on the loop visible from both spacecraft. A movie showing the temporal evolution between 00:10 and 05:50 UT on 22. Jan. 2013 is available online. |
| In the text | |
 |
Fig. 3 Time-distance maps for the analysed loops at different positions (slit number) along the loop paths. The most noticeable oscillations were fitted with a sine function to define their parameters. Red dots indicate the positions of the loop edge estimated by the Gaussian fitting to the partial derivative of the time-distance plot in transverse direction. The white lines show the best-fitting sinusoidal functions. |
| In the text | |
 |
Fig. 4 Cross-correlation coefficient for loops marked in Fig. 1. The vertical axis corresponds to the distance along the loop. The horizontal axis shows the time lag relatively to the reference location. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


