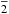| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 8 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201322053 | |
| Published online | 05 December 2013 | |
Proposal for a Laue lens relying on hybrid quasi-mosaic curved crystals
1 Department of Physics and Earth SciencesUniversity of Ferrara, via Saragat 1/c, 44122 Ferrara, Italy
2 CNR – IDASC SENSOR Lab., Italy
e-mail: guidi@fe.infn.it
Received: 4 June 2013
Accepted: 11 October 2013
A promising method of concentrating X- and soft γ-rays from celestial sources is a Laue lens. A new scheme for this lens, relying on diffraction in curved Si and Ge crystals, is introduced here. The proposed Laue lens is based on high-efficiency diffraction of curved (111) or (22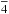 ) crystalline planes, which are bent through quasi-mosaic effect. While diffraction in curved (111) quasi-mosaic crystals is well known and has recently been proposed for a Laue lens, diffraction by quasi-mosaic (22
) crystalline planes, which are bent through quasi-mosaic effect. While diffraction in curved (111) quasi-mosaic crystals is well known and has recently been proposed for a Laue lens, diffraction by quasi-mosaic (22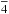 ) planes is suggested and demonstrated here through experimental work carried out at the Institut Laue-Langevin (ILL, Grenoble, France) at DIGRA, a facility specifically built for characterizing instrumentation in Astrophysics. Results show that the diffraction efficiency in the (22
) planes is suggested and demonstrated here through experimental work carried out at the Institut Laue-Langevin (ILL, Grenoble, France) at DIGRA, a facility specifically built for characterizing instrumentation in Astrophysics. Results show that the diffraction efficiency in the (22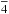 ) quasi-mosaic sample is amplified by more than one order of magnitude with respect to an equivalent crystal without quasi-mosaic effect. The lens has been designed in such a way as to maximize and smoothen its sensitivity, thanks to a custom-made code based on a genetic algorithm.
) quasi-mosaic sample is amplified by more than one order of magnitude with respect to an equivalent crystal without quasi-mosaic effect. The lens has been designed in such a way as to maximize and smoothen its sensitivity, thanks to a custom-made code based on a genetic algorithm.
Key words: techniques: high angular resolution / telescopes / techniques: imaging spectroscopy
© ESO, 2013
1. Introduction
Loosely speaking, observing hard X-ray or soft γ-ray astronomical sources in the energy range of 100–1000 keV is more like old-fashioned naked-eye observation of the sky than to modern device-assisted astronomy with a telescope because high-energy photons cannot be concentrated. Strictly speaking, the lack of optical components working in this energy range means that one cannot focus, which in turn leads to a poor signal-to-noise ratio recorded by the detectors. Indeed, multilayer optics proved that they are capable of high-efficiency X-ray focusing of up to 70 keV photons, though beyond this limit the efficiency of these optics critically deteriorates (Madsen et al. 2009).
There is a wealth of experiments that could be performed provided that a suitable sensitivity of detection devices were accomplished. Indeed, γ-ray emission takes place in several places in the Universe, starting from our Sun to the γ-ray bursts (GRBs) at redshifts z > 8 and to the cosmic γ-ray background radiation of the early Universe. Cosmic rays originate locally in solar flares, within our Galaxy in compact binary systems, pulsars, supernova remnants, and in extremely distant objects such as active galactic nuclei and GRBs.
Accordingly, the scientific community is seeking for methods to make these experiments come true (von Ballmoos 2013). One proposal for a nonfocusing method of detection is using geometrical optics concepts, such as collimators or coded masks. However, since the total interaction cross-section for γ-rays attains its minimum within 100–1000 keV, the efficiency of geometrical optics decreases while at the same time the background noise increases with respect to the signal because of the growing importance of shield leakage and/or nβ activation. Another nonfocusing solution consists of quantum optics based on Compton effect and tracking detectors. Indeed, using focusing methods probably has great potential because of the possibility of concentrating the signal from a large collector onto a small detector to beat the instrumental backgrounds that may hamper the observation.
A Laue lens is the typical means of focusing hard X- or γ-rays. It is conceived as an ensemble of many crystals arranged in such a way that as much radiation as possible is diffracted onto the lens focus over a selected energy band (Smither 1982; Lund 1992; von Ballmoos et al. 2005; Knödlseder et al. 2009). Perfect and flat mono-crystals diffract within a very narrow energy range, so that they are not adequate for a Laue lens. Mosaic crystals can be viewed as an assembly of crystallites, that is, very small slightly misaligned perfect crystals (Zachariasen 1945). Crystallite orientation is normally distributed, which leads to a Gaussian-like energy bandpass. Several crystals can be grown with the mosaic structure, which makes them good candidates for the realization of a broad-band Laue lens. However, mosaic crystals have two limitations. Firstly, their mosaicity (FWHM of the angular distribution of the crystallites) is poorly controlled during the growth, which results in the rejection of many crystals immediately after they have been cut from the ingot. Secondly, their diffraction efficiency is ultimately limited to 50% by the dynamical theory of diffraction in crystals.
Crystals with curved diffracting planes (CDP crystals) represent an alternative to mosaic crystals with the potential to overcome these two drawbacks. Their energy bandpass can be very well controlled, because it is proportional to the curvature, and their diffraction efficiency is not limited to 50% (Keitel et al. 1999; Malgrange 2002) because the continuous change of the incidence angle on bent crystalline planes prevents re-diffraction of a diffracted beam. The energy bandpass of the photons diffracted by these crystals is orders of magnitude broader than for a flat crystal, featuring a uniform transfer function provided that the crystal curvature is homogeneous. Indeed, a scheme relying on Laue diffraction with CDP crystals proved to work for hard X-rays with a diffraction efficiency ideally close to unity (Barrière et al. 2010; Bellucci et al. 2011b). A particular kind of CDP crystals was recently also proposed as optical components for focusing hard X-rays, namely a crystal exploiting the so-called quasi-mosaic (QM) effect (Guidi et al. 2011b).
In this paper we present a simulated prototype of a Laue lens relying on curved Si and Ge QM crystals, which are bent through QM effect, exploiting (111) and (22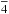 ) planes for X-ray diffraction. Diffraction of QM crystals through (111) planes has previously been proved experimentally (Camattari et al. 2013a; Guidi et al. 2013), showing that QM curvature amplifies the diffraction efficiency by more than one order of magnitude with respect to an equivalent crystal without quasi-mosaic curvature, that is, with flat diffracting planes. The use of diffraction through (22
) planes for X-ray diffraction. Diffraction of QM crystals through (111) planes has previously been proved experimentally (Camattari et al. 2013a; Guidi et al. 2013), showing that QM curvature amplifies the diffraction efficiency by more than one order of magnitude with respect to an equivalent crystal without quasi-mosaic curvature, that is, with flat diffracting planes. The use of diffraction through (22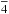 ) planes in a QM crystal has never been observed to date, and therefore needed to be validated by experimental work, as shown in Sect. 3.1. As we explain in Sect. 4, the combined use of Si and Ge exploiting (111) and (22
) planes in a QM crystal has never been observed to date, and therefore needed to be validated by experimental work, as shown in Sect. 3.1. As we explain in Sect. 4, the combined use of Si and Ge exploiting (111) and (22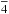 ) QM CDPs leads to an unprecedented resolution for a Laue lens.
) QM CDPs leads to an unprecedented resolution for a Laue lens.
2. Mathematical derivations
2.1. Quasi-mosaic crystals
For the sake of better understanding the usage of QM crystals for diffraction, we briefly summarize some features, which will be also useful to explain the behavior of (22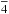 ) crystals in the experimental part.
) crystals in the experimental part.
QM crystals belong to a class of CDP crystals featuring two curvatures of two different lying of crystallographic planes (see Figs. 1 and 2). As a crystal is bent to a primary curvature by external forces, under specific orientations, another curvature (secondary curvature) is generated within the crystal, viz. the QM curvature (Lekhnitskii et al. 1956; Sumbaev 1957). Quasi-mosaicity is a mechanical property driven by anisotropy and is fully explained by the theory of linear elasticity in an anisotropic medium. In contrast to a Laue lens, which is based on mosaic crystals, using QM crystals allows focusing the incident beam on a spot smaller than the dimension of the diffracting elements, attaining very high resolution and sensitivity together with a wide-bandpass response (Guidi et al. 2011b; Camattari et al. 2011).
A Laue lens with QM crystals is an arrangement of curved plates whose primary curvature lies on a spherical calotte of radius RP. Due to Bragg diffraction, focusing of each QM sample converges on a focal spot at a distance f = RP/2 on the symmetry axes of the calotte (see Fig. 1). By using QM crystals, it is possible to combine the focusing action due to primary curvature with the high reflectivity of CDP built up by quasi-mosaicity. Indeed, if there were no QM effect, the reflectivity of the whole lens would be the same as for an unbent mono-crystal, that is a relatively poor figure.
Low weight is mandatory for a Laue lens built for astrophysical observations, that is, for operating in satellite-borne experiments. Self-standing curved crystals would be a great advantage because of they do not need an external holding system to maintain the curvature, which would otherwise increase the weight of the structure. In the literature, there are examples manufacturing a self-standing QM crystals (Camattari et al. 2013a).
A simple technique to fabricate a self-standing crystal with CDP, starting from an unbent mono-crystal, is the technique of superficial grooving (Bellucci et al. 2011a; Camattari et al. 2013b; Neri et al. 2013, 2012). Self-standing curved crystals bent by superficial grooves were recently shown to exhibit a uniform angular distribution with a total bandpass proportional to the curvature and a diffraction efficiency close to 90% at 150 keV (Barrière et al. 2010; Bellucci et al. 2011b). Diffraction from a QM crystal manufactured by a mesh of superficial grooves was recently tested by X-ray diffraction in transmission geometry, producing results in line with theoretical expectations (Camattari et al. 2013a; Guidi et al. 2013).
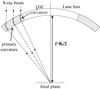 |
Fig. 1 Schematic representation of a cross section of a Laue lens based on QM crystals. Gray rectangles represent the crystals. The primary curvature leads to a secondary curvature of the planes affected by quasi-mosaicity. In this configuration the QM diffracting planes are perpendicular to the main surface of the plates. The primary curvature allows focalizing diffracted radiation onto the focal plane, while the QM curvature increases the diffraction efficiency. |
2.2. QM curvature calculation
Since the QM curvature is a consequence of crystal anisotropy, its radius of curvature is strictly linked to the crystal orientation. It is possible to calculate the ratio between primary and QM curvatures thanks to the linear theory of elasticity. The curvatures of internal planes can be calculated through the displacement field as a function of u(r), v(r) and w(r), which are the deformations along the x, y, and z axes, respectively. A complete treatment of the subject can be found in Lekhnitskii et al. (1956).
 |
Fig. 2 Schematic representation of a crystal plate with the coordinate system used for the modeling. In a) two moments are applied, while in b) a single moment is applied. Crystallographic orientation and QM curvature for the two cases are highlighted. |
We considered the two problems described in Figs. 2a and 2b. For the first case (Fig. 2a), it is demonstrated that spherical bending of (22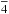 )1 Si or Ge plates as a primary curvature results in a QM curvature of the (111) planes, so that we need to obtain a spherical curvature by applying two momenta Mx and My to the sample. The curvature of the largest face along x and y, that is, the principal curvature on the two perpendicular directions, is
)1 Si or Ge plates as a primary curvature results in a QM curvature of the (111) planes, so that we need to obtain a spherical curvature by applying two momenta Mx and My to the sample. The curvature of the largest face along x and y, that is, the principal curvature on the two perpendicular directions, is 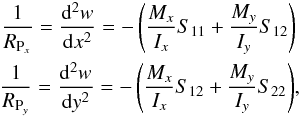 (1)where Sij are the components of compliance matrix referred to the (x,y,z) Cartesian system, and Ix and Iy the momentum of inertia. Choosing y as the focusing direction, the QM curvature is
(1)where Sij are the components of compliance matrix referred to the (x,y,z) Cartesian system, and Ix and Iy the momentum of inertia. Choosing y as the focusing direction, the QM curvature is 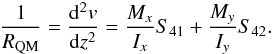 (2)Then, if the curvature is spherical, that is,
(2)Then, if the curvature is spherical, that is, 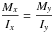 , the ratio between primary and QM curvatures holds
, the ratio between primary and QM curvatures holds 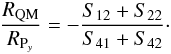 (3)Therefore, because the stress is uniform over the largest surface, the ratio is independent of the crystal plate dimensions.
(3)Therefore, because the stress is uniform over the largest surface, the ratio is independent of the crystal plate dimensions.
For the second case (Fig. 2b), it is demonstrated that cylindrical bending of (111) Si or Ge plates as a primary curvature results in a QM curvature of the (22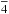 ) planes, so that we have to apply only one momentum M to the sample. In this case, the primary curvature along the y-axis holds
) planes, so that we have to apply only one momentum M to the sample. In this case, the primary curvature along the y-axis holds 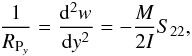 (4)while the secondary QM in the focusing direction is
(4)while the secondary QM in the focusing direction is 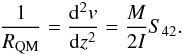 (5)Finally, the ratio between QM and primary curvatures can be obtained as
(5)Finally, the ratio between QM and primary curvatures can be obtained as 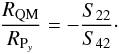 (6)The ratios for the cases of interest are reported in Table 1.
(6)The ratios for the cases of interest are reported in Table 1.
Ratios between QM curvatures and principal curvatures, the latter calculated along the y-axis.
2.3. Simulation of a Laue lens with QM crystals
A Laue lens based on QM crystals can work over a wide energy range. Si and Ge crystals were chosen because they can be commercially found with high crystalline perfection and mostly because they exhibit the QM effect. A photon beam with energy between 100 and 300 keV was considered to impinge onto the crystals parallel to the axis of the lens because Si and Ge diffract X-rays at high efficiency in this energy range. Since (111) and (22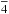 ) planes can diffract photons of the same energy, though at very different Bragg angles, the crystals could be arranged at different positions to build up a Laue lens, featuring significant enhancement of the geometric area undergoing diffraction.
) planes can diffract photons of the same energy, though at very different Bragg angles, the crystals could be arranged at different positions to build up a Laue lens, featuring significant enhancement of the geometric area undergoing diffraction.
We considered the crystal tiles to be disposed as concentric rings onto the spherical calotte of a Laue lens with a focal distance f = 20 m. Thus, the primary radius of curvature of the tiles must be twice the focal length of the lens, namely 40 m (Frontera et al. 2006, 2012; Camattari et al. 2012). The thickness of the tile, T0, affects both the focusing capability and the reflectivity of the lens. High values of T0 lead to higher reflectivity and lower spatial resolution on the focal plane, while lower values of T0 decrease the reflectivity but increase the focusing strength. The crystals were chosen all with the same tile size 20 × 10 mm2, with the longer side parallel to the direction where focalization occurs, that is, the radial direction. This tile size reduces the blank space between tiles, while T0 was chosen to be 5 mm to guarantee high reflectivity.
For a CDP crystal, the ratio between diffracted beam intensity and incident beam intensity, that is, the crystal reflectivity rQM, is given by the formula (Malgrange 2002) 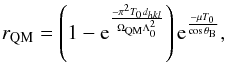 (7)where the first factor is the diffraction efficiency and the latter is the attenuation factor due to absorption throughout the sample, μ is the linear absorption coefficient, dhkl the d-spacing of planes (hkl), θB the Bragg angle, and Λ0 the extinction length as defined by (Authier 2001) for the Laue symmetric case. ΩQM represents the bending angle of the CDPs, namely of the QM planes. ΩQM can be calculated as a function of the primary curvature through Eqs. (3) and (6).
(7)where the first factor is the diffraction efficiency and the latter is the attenuation factor due to absorption throughout the sample, μ is the linear absorption coefficient, dhkl the d-spacing of planes (hkl), θB the Bragg angle, and Λ0 the extinction length as defined by (Authier 2001) for the Laue symmetric case. ΩQM represents the bending angle of the CDPs, namely of the QM planes. ΩQM can be calculated as a function of the primary curvature through Eqs. (3) and (6).
The energy bandpass of a crystal in a ring is given by the formula (Barrière et al. 2007) 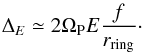 (8)Here rring is the radius of a selected ring, ΩP is the bending angle induced in the tile by primary curvature, planer and E the mean energy diffracted by the ring. This latter depends on the material, crystallographic plane, and the distance from the axes of the lens, that is, the radius of the ring, as given by the formula
(8)Here rring is the radius of a selected ring, ΩP is the bending angle induced in the tile by primary curvature, planer and E the mean energy diffracted by the ring. This latter depends on the material, crystallographic plane, and the distance from the axes of the lens, that is, the radius of the ring, as given by the formula 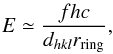 (9)where h and c are the Planck constant and the light speed, respectively. The small-angle approximation was considered in the last two formulae.
(9)where h and c are the Planck constant and the light speed, respectively. The small-angle approximation was considered in the last two formulae.
The effective area of an instrument at a certain energy is defined as its geometric area, as seen by the X-ray beam, times the diffraction efficiency at that energy. This parameter is important for quantifying the number of events that an ideal detector located on the focus of the Laue lens would count under exposure to a certain photon flux. As for any tile in the lens, the effective area at a given energy is defined as the geometric area exposed to the photon flux times the reflectivity of the tile at the energy of interest. Because of the finite angle ΩQM exposed to photon flux, only a part of the tile is capable of diffracting a certain photon energy. Thus, the effective area AEff for a single tile is given by 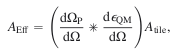 (10)
where the first function in the convolution is the normalized distribution of diffracting planes due to the primary curvature, the second function is the distribution of reflectivity due to the QM curvature as function of the diffracting angle Ω, and Atile is the geometric area of each tile. The effective area of the whole lens is the sum of the effective areas of the tiles composing the lens itself. For the simulation, the effective area was calculated as a discrete function of energy, the step being 0.5 keV. This value was selected because it is a good compromise between accuracy and computational time.
(10)
where the first function in the convolution is the normalized distribution of diffracting planes due to the primary curvature, the second function is the distribution of reflectivity due to the QM curvature as function of the diffracting angle Ω, and Atile is the geometric area of each tile. The effective area of the whole lens is the sum of the effective areas of the tiles composing the lens itself. For the simulation, the effective area was calculated as a discrete function of energy, the step being 0.5 keV. This value was selected because it is a good compromise between accuracy and computational time.
As an estimator of the smoothness of the effective area vs. photon energy, the quantity smoothing was defined in the following way. Firstly, the moving average of the effective area function aws calculated for five sequential values of energy by starting from the minimum (100 keV). Then, the distance between these five values of AEff to their average value was calculated and the largest one was selected. This procedure was repeated by shifting the section under analysis along the energy axis, up to the maximum energy (300 keV). Consequently, the quantity smoothing is the sum of all the collected contributions of maximum distances.
To maximize and smoothen the effective area of the simulated Laue lens, a genetic algorithm was implemented. As a first step, a Laue lens was generated, composed of Si and Ge QM crystalline tiles. A tile of the lens was chosen arbitrarily and was randomly transformed into a tile of different species by changing the material and/or the crystallographic orientation.
It is possible to define a quantifier k [i] of both the effective area for all the energies and of the smoothness of the effective area itself. ![\begin{eqnarray} \label{genetic} k[i]=w_1\frac{\int_{E_{\min}}^{E_{\max}} A_{\rm Eff}[i+1]\, {\rm d}E}{\int_{E_{\min}}^{E_{\max}} A_{\rm Eff}[i]\, {\rm d}E}-w_2\frac{{\rm smoothing}[i+1]}{{\rm smoothing}[i]}, \end{eqnarray}](/articles/aa/full_html/2013/12/aa22053-13/aa22053-13-eq52.png) (11)where the index [i] represents the configuration before crystal transformation, while the index [i + 1] represents the configuration after crystal transformation. w1 and w2 are weights to be assigned to the two terms in Eq. (11). By increasing w1 it is possible to achieve a high value of the total effective area, while an increase of w2 favors a better smoothness. The minus sign before the second term indicates that the second quantity has to be minimized, while the first has to be maximized.
(11)where the index [i] represents the configuration before crystal transformation, while the index [i + 1] represents the configuration after crystal transformation. w1 and w2 are weights to be assigned to the two terms in Eq. (11). By increasing w1 it is possible to achieve a high value of the total effective area, while an increase of w2 favors a better smoothness. The minus sign before the second term indicates that the second quantity has to be minimized, while the first has to be maximized.
If k [i + 1] > k [i], the crystal exchange is held, otherwise it is rejected. This procedure is was iterated until the system reached thermalization, that is, the maximum of k [i] was attained.
3. Results
3.1. Experimental results
Self-standing QM crystals have previously been proved to efficiently diffract through (111) planes (Camattari et al. 2013a). In contrast, the diffraction efficiency of (22 ) CDP has never been tested in QM crystals and needed to be experimentally tested prior to simulating the lens.
) CDP has never been tested in QM crystals and needed to be experimentally tested prior to simulating the lens.
A cylindrical curvature was produced on a Si crystal by inducing a superficial strained layer. The tile size was 20 × 100 × 3 mm3, the crystallographic orientation was the same as in Fig. 2b. The sample curvature was measured by using an optical profilometer (VEECOTM NT1100) with 1 μm lateral and 1 nm vertical resolution at the Sensor and Semiconductor Laboratory (Ferrara, Italy). The primary radius of curvature, measured along y, was 21.2 m. Using the results listed in Table 1, the radius of curvature of the (22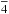 ) QM planes (secondary curvature) was 74.6 m.
) QM planes (secondary curvature) was 74.6 m.
Diffraction efficiency of the (22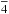 ) CDP was tested by γ-ray diffraction in transmission geometry at the Institut Laue-Langevin (ILL, Grenoble, France) at the facility named DIffractometer for Gamma Ray Astrophysics (DIGRA), a facility specifically built for characterizing instrumentation in Astrophysics. The γ-ray beam energy was E = 181.931 keV with monochromaticity ΔE/E ≈ 10-6. Gamma quanta were produced by neutron capture in a gadolinium target (
) CDP was tested by γ-ray diffraction in transmission geometry at the Institut Laue-Langevin (ILL, Grenoble, France) at the facility named DIffractometer for Gamma Ray Astrophysics (DIGRA), a facility specifically built for characterizing instrumentation in Astrophysics. The γ-ray beam energy was E = 181.931 keV with monochromaticity ΔE/E ≈ 10-6. Gamma quanta were produced by neutron capture in a gadolinium target (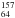 Gd) inserted close to the nuclear reactor of ILL at a temperature of 400 °C. The beam divergence after the Si (220) monochromator was 1 arcsec, measured by recording a rocking curve (RC) of the monochromator itself. The collimated-beam size was 1 mm on the diffraction plane and 3 mm on the perpendicular plane. A standard electrode coaxial Ge detector with 25% relative efficiency supplied by Canberra was used. The main features of the experiment are reported in Table 2.
Gd) inserted close to the nuclear reactor of ILL at a temperature of 400 °C. The beam divergence after the Si (220) monochromator was 1 arcsec, measured by recording a rocking curve (RC) of the monochromator itself. The collimated-beam size was 1 mm on the diffraction plane and 3 mm on the perpendicular plane. A standard electrode coaxial Ge detector with 25% relative efficiency supplied by Canberra was used. The main features of the experiment are reported in Table 2.
Experimental features.
We characterized the samples by performing RCs, that is, by recording either the transmitted or diffracted beam intensity while the crystal was being rotated around the position where the Bragg condition was met. Thus, the photon beam hit the (111) surface of the sample. The diffraction efficiency was measured at the center of the sample and its RC is reported in Fig. 3. The gray area in the figure represents the theoretical expectation as calculated through a custom-made code specifically designed for simulating the performance of diffraction through broad-band crystals such as mosaic or CDP crystals. The code has previously been tested in experiments in previous papers (Bellucci et al. 2011b; Guidi et al. 2011b,a). In the simulation, both primary and secondary curvatures were accounted for. From the theory of elasticity, the ratio of the QM curvature, RQM, to the primary one, RP, was set at 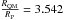 for the orientation we used (see Table 1). The angular distribution after diffraction consists of the convolution between the distribution due to the portion of primary curvature seen by the beam, and the distribution due to secondary curvature. The primary curvature seen by the beam was calculated by taking into account the width of the collimated beam (1 mm) and the radius of curvature measured with the profilometer (21.2 m). To calculate the diffraction efficiency, the dynamical theory was considered (Authier & Malgrange 1998). Moreover, the divergence of the beam was included by convolving the obtained distribution with a Gaussian of σ = 1 arcsec. Figure 3 highlights the very good agreement between the theoretical expectation relying on quasi-mosaicity and the experimental results.
for the orientation we used (see Table 1). The angular distribution after diffraction consists of the convolution between the distribution due to the portion of primary curvature seen by the beam, and the distribution due to secondary curvature. The primary curvature seen by the beam was calculated by taking into account the width of the collimated beam (1 mm) and the radius of curvature measured with the profilometer (21.2 m). To calculate the diffraction efficiency, the dynamical theory was considered (Authier & Malgrange 1998). Moreover, the divergence of the beam was included by convolving the obtained distribution with a Gaussian of σ = 1 arcsec. Figure 3 highlights the very good agreement between the theoretical expectation relying on quasi-mosaicity and the experimental results.
 |
Fig. 3 Experimental and theoretical RCs of a [22 |
As a result of the above experiment, the quasi-mosaicity of (22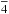 ) planes proved true and therefore it can be used for the implementation in the construction of a Laue lens composed of QM crystalline tiles.
) planes proved true and therefore it can be used for the implementation in the construction of a Laue lens composed of QM crystalline tiles.
3.2. Simulation results
A Laue lens composed of Ge and Si QM crystals was simulated. The crystals were arranged in the lens according to the described custom-made genetic algorithm. The genetic algorithm was set to maximize the effective area in the energy range 100–300 keV and to make it as smooth as possible with respect to the energy variation. We initialized the algorithm by starting with an a priori initial guess for the tile arrangement in the Laue lens, taking into account the different Bragg angles. Figure 4 shows a possible arrangement of the QM tiles in a Laue lens, and quantitative results are listed in Table 5. Figure 5 represents the spectral effective area of the lens, in which the contributions of the four species are visible.
To verify that the final arrangement was not affected by the initial guess and to control possible interference of local maxima in the quantifier in Eq. (11), we re-initialized the algorithm by a fully casual disposition of the tiles. After a much longer computing time, we arrived at a similar arrangement to the previous simulation.
Lens features.
Crystals features.
Number of tiles per type normalized to the number of samples per ring.
 |
Fig. 4 Arrangement of crystalline tiles over the calotte of the simulated Laue lens. The legend describes the diffracting plane employed. The crystals are 20 × 10 × 5 mm3 Ge tiles. The disposition of the tiles is optimized with a specifically written genetic code. |
 |
Fig. 5 Effective area per unit energy of the lens. The contributions of the tiles of different species is visible. Tiles were positioned in the lens to maximize effective area in the energy range 100–300 keV and made the profile as smooth as possible with respect to energy variation. The histogram is calculated analytically, while the continuous lines are calculated with a Monte Carlo simulation. |
Finally, the lens was composed of QM tiles 20 × 10 × 5 mm3 of size with the focusing curvature along the wider dimension. Because of this choice, all the photons diffracted by the lens were enclosed in a circle of 10 mm in diameter. To evaluate the capability of focalization of this Laue lens, a Monte Carlo code was written to simulate an on-axis photon beam hitting the lens within the energy range of 100–300 keV. The concentration of photons is high at the center of the spot and rapidly decreases close to the borders, as is clearly visible in Figs. 6, 7.
 |
Fig. 6 Photon distribution onto the focal plane of the lens in arbitrary units. Concentration of photons is high in the focal point and rapidly decreases far from the center. The distribution is obtained with a Monte Carlo code. |
4. Discussion
Diffraction from (22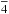 ) CDP occurs at a Bragg angle much larger than for the (111) planes at the same energy. This means that the crystalline tiles implementing (111) CDP occupy the innermost part of the lens because of the small Bragg angle. In contrast, tiles using (22
) CDP occurs at a Bragg angle much larger than for the (111) planes at the same energy. This means that the crystalline tiles implementing (111) CDP occupy the innermost part of the lens because of the small Bragg angle. In contrast, tiles using (22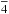 ) CDP occupy the outermost part of the lens because of the large Bragg angle. Although the reflectivity for (22
) CDP occupy the outermost part of the lens because of the large Bragg angle. Although the reflectivity for (22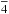 ) CDP is lower than for (111) CDP, the external position guarantees a large geometric area, resulting in a large effective area. Moreover, this configuration works with Ge and Si crystals simultaneously owing to their different d-spacing, that is, still more locations for crystalline tiles are generated. In summary, building up a lens with very large geometric area that concentrates a range of energies can be envisaged. Si provides the largest part of the effective area at low energies, as expected for a light material. Ge tiles, which are composed of a material with higher atomic number, maximize their reflectivity for high energies, providing the largest part of effective area in this zone.
) CDP is lower than for (111) CDP, the external position guarantees a large geometric area, resulting in a large effective area. Moreover, this configuration works with Ge and Si crystals simultaneously owing to their different d-spacing, that is, still more locations for crystalline tiles are generated. In summary, building up a lens with very large geometric area that concentrates a range of energies can be envisaged. Si provides the largest part of the effective area at low energies, as expected for a light material. Ge tiles, which are composed of a material with higher atomic number, maximize their reflectivity for high energies, providing the largest part of effective area in this zone.
The photon distribution on the focal plane are well-collimated as a result of focusing through QM tiles. This peculiarity is expected to provide high-quality focusing. A quantifier of the focusing capability is the focusing factor G, defined as 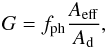 (12)where Aeff is the effective area of the lens and Ad is the area of the focal spot that contains a fraction fph of photons reflected by the lens. Physically, it represents the number of photons enclosed in a focal spot divided by the area of the focal spot and normalized with respect to the photon flux impinging on the lens. To calculate the focusing factor, the radius of the focal spot Rspot was chosen to enclose 90% of the photons, cutting the tails of the distribution., that is, Rspot = 4.66 mm. Figure 8 shows the focusing factor of the lens as a function of the energy of impinging photons.
(12)where Aeff is the effective area of the lens and Ad is the area of the focal spot that contains a fraction fph of photons reflected by the lens. Physically, it represents the number of photons enclosed in a focal spot divided by the area of the focal spot and normalized with respect to the photon flux impinging on the lens. To calculate the focusing factor, the radius of the focal spot Rspot was chosen to enclose 90% of the photons, cutting the tails of the distribution., that is, Rspot = 4.66 mm. Figure 8 shows the focusing factor of the lens as a function of the energy of impinging photons.
 |
Fig. 7 Fraction of enclosed photons vs. radius of the focal spot enclosing the photons on the focal plane. The radius Rspot corresponding to 90% of the enclosed photons was chosen for the simulation to cut the tails of the focal distribution. Rspot = 4.66 mm. |
For the sake of comparison, we simulated the performance of a Laue lens consisting solely of Si and Ge QM (111) tiles and optimized for the purpose. The dimension of QM tiles, the curvature radius and the energy bandpass of the lens are the same as in the previous case. A lens made of (111) QM crystals results in a smaller effective area and then in a smaller focusing factor, as visible in Fig. 8.
 |
Fig. 8 Focusing factor of a lens composed of QM (22 |
 |
Fig. 9 Predicted 3σ detection sensitivities for continuum (black) and narrow line (blue) emission, assuming an exposure time of 100 ks and Δ E/E = 1/2 for the continuum and Δ E/E = 3% for the line sensitivity. |
Finally, we expressed the performance of the lens in terms of the most often acknowledged quantifier recognized by the community of astrophysicists, namely the sensitivity, that is, the lowest flux detectable with 3 sigma significance, for the cases of continuum- and narrow-line emissions. The results are shown in Fig. 9, which are in line with the sensitivity of the proposed Laue lens for the Gamma Ray Imager (GRI, Knödlseder et al. 2009). Indeed, the smaller effective area of the QM-based Laue lens, which is intrinsic in the usage of QM crystals, is abundantly compensated for by the strong focusing exerted by QM effect. In fact, the property of QM crystals to focus on a spot smaller than the dimension of the diffracting crystals themselves raises the sensitivity of the lens. Another advantage of the proposed lens is that its focal length is expected to allow the lens to be accommodated in one spacecraft only despite its relatively large diameter, resulting in a modest weight (292 kg) of the diffracting crystals. If a longer focal length were considered, with two satellites flying in formation as for the GRI, a still better figure of merit would be attained (effective area increases to 1000 cm2 at 100 m focal length).
5. Conclusions
The idea of a Laue lens to focalize X- and γ-rays was proposed about thirty years ago with a scheme entirely based on mosaic crystals. Compared to the initial formulation, significant progress has been made, which brings the concept of a Laue lens within reach. In this paper we proposed a novel configuration, based on quasi-mosaicity, with hybrid Si and Ge crystals exploiting traditional (111) planes and (22 ) diffracting planes as an innovative concept. In this way, it is possible to enhance the capability of the lens by a factor larger than two compared with a Laue lens with only one species of QM crystals. High sensitivity was obtained as a result of the strong focusing capability due to the QM effect.
) diffracting planes as an innovative concept. In this way, it is possible to enhance the capability of the lens by a factor larger than two compared with a Laue lens with only one species of QM crystals. High sensitivity was obtained as a result of the strong focusing capability due to the QM effect.
Acknowledgments
This work has been partially supported by the LAUE project of ASI. The authors thank Michael Jentschel (Institut Laue-Langevin, Grenoble) for assistance in experimental measurements.
References
- Authier, A. 2001, Dynamical theory of X-ray diffraction (Oxford University Press) [Google Scholar]
- Authier, A., & Malgrange, C. 1998, Acta Cryst., A54, 806 [Google Scholar]
- Barrière, N., von Ballmoos, P., Bastie, P., et al. 2007, Optics for EUV, X-Ray, and Gamma-Ray Astronomy III., eds. L. S. O’Dell, & G. Pareschi, Proc. SPIE 6688, 66880 [Google Scholar]
- Barrière, N., Guidi, V., Bellucci, V., et al. 2010, J. Appl. Cryst., 43, 1519 [CrossRef] [Google Scholar]
- Bellucci, V., Camattari, R., Guidi, V., & Mazzolari, A. 2011a, Thin Solid Films, 520, 1069 [NASA ADS] [CrossRef] [Google Scholar]
- Bellucci, V., Camattari, R., Guidi, V., Neri, I., & Barrière, N. 2011b, Exp Astron, 31, 45 [Google Scholar]
- Camattari, R., Bellucci, V., Guidi, V., & Neri, I. 2011, Optics for EUV, X-Ray, and Gamma-Ray Astronomy V, eds. L. S. O’Dell, & G. Pareschi, Proc. SPIE, 8147, 81471 [Google Scholar]
- Camattari, R., Guidi, V., & Neri, I. 2012, Space Telescopes and Instrumentation 2012: Ultraviolet to Gamma Ray, Proc. SPIE 8443, 844335 [Google Scholar]
- Camattari, R., Guidi, V., Bellucci, V., Neri, I., & Jentschel, M. 2013a, Rev. Sci. Instrum., 84, 053110 [Google Scholar]
- Camattari, R., Guidi, V., Lanzoni, L., & Neri, I. 2013b, Meccanica, 48, 1875 [CrossRef] [Google Scholar]
- Frontera, F., Pisa, A., Carassiti, V., et al. 2006, Proc. SPIE, 6266, 626 [Google Scholar]
- Frontera, F., Virgilli, E., Liccardo, V., et al. 2012, Space Telescopes and Instrumentation 2012: Ultraviolet to Gamma Ray, 8443, 84430 [Google Scholar]
- Guidi, V., Barrière, N., Bellucci, V., Camattari, R., & Neri, I. 2011a, Optics for EUV, X-Ray, and Gamma-Ray Astronomy V, eds. S. L. O’Dell, & G. Pareschi, 8147, 81471 [Google Scholar]
- Guidi, V., Bellucci, V., Camattari, R., & Neri, I. 2011b, J. Appl. Cryst., 44, 1255 [CrossRef] [Google Scholar]
- Guidi, V., Bellucci, V., Camattari, R., & Neri, I. 2013, Nucl. Instr. Meth. A, 309, 249 [Google Scholar]
- Keitel, S., Malgrange, C., Niemöller, T., & Schneider, J. R. 1999, Acta Cryst., A55, 855 [Google Scholar]
- Knödlseder, J., von Ballmoos, P., Frontera, F., et al. 2009, Exp. Astron., 23, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Lekhnitskii, S., Tsai, S., & Cheron, T. 1956, Anisotropic Plates (Gordon and Breach Science Publishers) [Google Scholar]
- Lund, N. 1992, Exp Astron, 2, 259 [Google Scholar]
- Madsen, K. K., Harrison, F. A., Mao, P. H., et al. 2009, Proc. SPIE, 7437, 743716 [CrossRef] [Google Scholar]
- Malgrange, C. 2002, Cryst. Res. and Tech., 37, 654 [Google Scholar]
- Neri, I., Camattari, R., Bellucci, V., Guidi, V., & Bastie, P. 2012, Space Telescopes and Instrumentation 2012: Ultraviolet to Gamma Ray, Proc. SPIE, 8443, 844334 [CrossRef] [Google Scholar]
- Neri, I., Camattari, R., Bellucci, V., Guidi, V., & Bastie, P. 2013, J. Appl. Cryst., 46, 953 [CrossRef] [Google Scholar]
- Smither, R. K. 1982, Rev. Sci. Instrum., 53, 131 [Google Scholar]
- Sumbaev, O. 1957, Sov. Phys. JETP, 5, 1042 [Google Scholar]
- von Ballmoos, P. 2013, Nucl. Instr. Meth. B, 309, 244 [CrossRef] [Google Scholar]
- von Ballmoos, P., Halloin, H., Evrad, J., et al. 2005, Exp. Astron., 20, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Zachariasen, W. H. 1945, Theory of X-ray diffraction in crystals (J. Wiley and sons, inc.) [Google Scholar]
All Tables
Ratios between QM curvatures and principal curvatures, the latter calculated along the y-axis.
All Figures
 |
Fig. 1 Schematic representation of a cross section of a Laue lens based on QM crystals. Gray rectangles represent the crystals. The primary curvature leads to a secondary curvature of the planes affected by quasi-mosaicity. In this configuration the QM diffracting planes are perpendicular to the main surface of the plates. The primary curvature allows focalizing diffracted radiation onto the focal plane, while the QM curvature increases the diffraction efficiency. |
| In the text | |
 |
Fig. 2 Schematic representation of a crystal plate with the coordinate system used for the modeling. In a) two moments are applied, while in b) a single moment is applied. Crystallographic orientation and QM curvature for the two cases are highlighted. |
| In the text | |
 |
Fig. 3 Experimental and theoretical RCs of a [22 |
| In the text | |
 |
Fig. 4 Arrangement of crystalline tiles over the calotte of the simulated Laue lens. The legend describes the diffracting plane employed. The crystals are 20 × 10 × 5 mm3 Ge tiles. The disposition of the tiles is optimized with a specifically written genetic code. |
| In the text | |
 |
Fig. 5 Effective area per unit energy of the lens. The contributions of the tiles of different species is visible. Tiles were positioned in the lens to maximize effective area in the energy range 100–300 keV and made the profile as smooth as possible with respect to energy variation. The histogram is calculated analytically, while the continuous lines are calculated with a Monte Carlo simulation. |
| In the text | |
 |
Fig. 6 Photon distribution onto the focal plane of the lens in arbitrary units. Concentration of photons is high in the focal point and rapidly decreases far from the center. The distribution is obtained with a Monte Carlo code. |
| In the text | |
 |
Fig. 7 Fraction of enclosed photons vs. radius of the focal spot enclosing the photons on the focal plane. The radius Rspot corresponding to 90% of the enclosed photons was chosen for the simulation to cut the tails of the focal distribution. Rspot = 4.66 mm. |
| In the text | |
 |
Fig. 8 Focusing factor of a lens composed of QM (22 |
| In the text | |
 |
Fig. 9 Predicted 3σ detection sensitivities for continuum (black) and narrow line (blue) emission, assuming an exposure time of 100 ks and Δ E/E = 1/2 for the continuum and Δ E/E = 3% for the line sensitivity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.