| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A64 | |
| Number of page(s) | 9 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201321947 | |
| Published online | 06 December 2013 | |
Probing the cosmic-ray content of galaxy clusters by stacking Fermi-LAT count maps
1 Physik-Institut, Universität Zürich, Winterthurerstrasse 190, 8057 Zürich, Switzerland
e-mail: ben.huber@physik.uzh.ch
2 Department of Astronomy, University of Geneva, ch. d’Écogia 16, 1290 Versoix, Switzerland
e-mail: celine.tchernin@unige.ch; dominique.eckert@unige.ch
3 The Oskar Klein Centre for Cosmoparticle Physics, Department of Physics, Stockholm University, Albanova, 10691 Stockholm, Sweden
e-mail: christian.farnier@fysik.su.se
Received: 23 May 2013
Accepted: 2 October 2013
Aims. Radio observations have shown that galaxy clusters are giant reservoirs of cosmic rays (CR). Although a gamma-ray signal from the cluster volume is expected to arise through interactions of CR protons with the ambient plasma, a confirming observation is still missing.
Methods. We searched for a cumulative gamma-ray emission in the direction of galaxy clusters by analysing a collection of stacked Fermi-LAT count maps. Additionally, we investigated possible systematic differences in the emission between cool-core and non-cool-core cluster populations.
Results. Making use of a sample of 53 clusters selected from the HIFLUGCS catalog, we do not detect a significant signal from the stacked sample. The upper limit on the average flux per cluster derived for the total stacked sample is at the level of a few 10-11 ph cm-2 s-1 at a 95% confidence level in the 1–300 GeV band, assuming power-law spectra with photon indices 2.0, 2.4, 2.8, and 3.2. Separate stacking of the cool-core and non-cool-core clusters in the sample lead to similar values of around 5 × 10-11 ph cm-2 s-1 and 2 × 10-11 ph cm-2 s-1, respectively.
Conclusions. Under the assumption that decaying π0, produced in collisions between CRs and the ambient thermal gas, are responsible for gamma-ray emission, we set upper limits on the average CR content in galaxy clusters. For the entire cluster population, our upper limit on the gamma-ray flux translates into an upper limit on the average CR-to-thermal energy ratio of 4.6% for a photon index of 2.4, although it is possible for individual systems to exceed this limit. Our 95% upper limits are at the level expected from numerical simulations, which most likely suggests that the injection of CR at cosmological shocks is less efficient than previously assumed.
Key words: galaxies: clusters: general / gamma rays: galaxies: clusters / methods: data analysis / astroparticle physics / cosmic rays
© ESO, 2013
1. Introduction
Galaxy clusters are the largest gravitationally bound structures in the Universe and have been successfully observed in radio, optical, UV, and X-ray wavelengths (see e.g. Sarazin 1986; Voit 2005, for reviews). These observations indicate that galaxy clusters are not only large-scale accumulations of galaxies, gas, and dark matter, but are also giant reservoirs of relativistic cosmic rays (CRs), i.e. relativistic electrons and protons, confined in the cluster volume through large-scale magnetic fields (Völk et al. 1996; Berezinsky et al. 1997; Völk & Atoyan 1999). Cosmic rayss are accelerated in shock waves induced by cluster mergers and during the accretion of material from the cluster environment. These shocks also contribute to the thermalization of substructures in the hot intra-cluster gas. Cosmic rays can also be injected into the cluster volume by central active galactic nuclei (AGN) and supernovae (SNe).
The presence of relativistic electrons is demonstrated by observations in the radio band attributed to large-scale synchrotron radiation (e.g. Feretti 2005; Ferrari et al. 2008; Brunetti 2011; Feretti et al. 2012) and possibly by observed emissions in the extreme UV and hard X-ray range attributed to inverse-Compton scattering (ICS) with photons of the cosmic microwave background (CMB; e.g. Rephaeli et al. 2008; Eckert et al. 2008; Nevalainen et al. 2009; Ajello et al. 2010). Cosmic-ray protons are expected to be confined in galaxy clusters for very long timescales, which may lead to proton-proton (p-p) collisions between CR protons and the ambient thermal plasma. Gamma rays may then arise from the decay of neutral pions produced in these interactions (e.g. Blasi et al. 2007; Pfrommer et al. 2008; Pinzke & Pfrommer 2010), with an interaction rate for p − p collisions that is expected to be highest close to the gravitational centre of the cluster where the target proton density is enhanced.
In addition, accretion shocks expected to be powerful enough to boost electrons up to 100 TeV and protons up to 1000 TeV could be an alternative source of high-energy gamma rays (Vannoni et al. 2011; Timokhin et al. 2004). At these energies, primary and secondary electrons could undergo ICS and transform CMB photons into high-energy gamma rays (e.g. Blasi et al. 2007). Another possibility considers ultra-high-energy protons with energies >106 TeV, that interact with the CMB producing electron-positron pairs leading to hard X-ray and gamma-ray emission via synchrotron and ICS (Inoue et al. 2005).
Galaxy clusters are also strong candidates to search for an exotic signature, since a large quantity of dark matter is attested in galaxy clusters. Some observational evidence suggest that dark matter could be formed of weakly interactive massive particles. A potential gamma-ray signal observable with Fermi-LAT could then arise from the annihilation of dark-matter particles (e.g. Colafrancesco et al. 2006; Jeltema et al. 2009; Pinzke et al. 2011).
Numerous observational studies (e.g. Reimer et al. 2003; Perkins 2008; Aharonian et al. 2009; Aleksić et al. 2010; Ackermann et al. 2010; Arlen et al. 2012; Dutson et al. 2013) have resulted in upper limits on the gamma-ray emission from clusters of galaxies, but a definite observation is still missing (see also Pinzke et al. 2011).
In this work, we searched for gamma-ray emission from galaxy clusters using the stacking method described in Huber et al. (2012), applying a maximum likelihood analysis on stacked count maps of galaxy clusters obtained with the Large Area Telescope (LAT). The LAT is the main instrument aboard the Fermi Gamma Ray Space Telescope spacecraft. It is a pair conversion telescope with an effective area of ~1 m2 and a field of view of about 2.4 sr, generally operating in survey mode and providing an all-sky coverage every two orbits. The instrument is sensitive to gamma-ray events with energies between 20 MeV to 300 GeV (Atwood et al. 2009).
We took into account that galaxy clusters can be subdivided into two classes, cool-core (CC) and non-cool-core (NCC) galaxy clusters (Cavagnolo et al. 2009), which may correspond to different stages of a cyclical cluster evolution (e.g. Rossetti et al. 2011). In this evolutionary scenario, CC galaxy clusters are relaxed systems that host AGN at their centre, powered by the accretion of intra-cluster gas (e.g. McNamara & Nulsen 2007, 2012; Fabian 2012). On the other hand, NCC galaxy clusters are disturbed systems in which merger events lead to particle acceleration (e.g. Brunetti et al. 2009; Cassano et al. 2010; Rossetti et al. 2011) through large-scale shocks (Markevitch & Vikhlinin 2007; Markevitch 2010).
The paper is structured as follows. In Sect. 2, we describe the selection of galaxy clusters that we use to search for gamma-ray emission. The data processing and analysis method used to stack the emission from the selected galaxy clusters is described in Sect. 3. In Sect. 4, we present our results on the gamma-ray emissivity obtained for the entire cluster sample and separately for the CC and NCC subsamples. In Sect. 5, we use our observational results to set constraints on the average CR energy density in galaxy clusters. We conclude the paper with a discussion in Sect. 6.
2. Cluster selection
From the extensive catalog of high X-ray luminosity galaxy clusters HIFLUGCS (Reiprich & Böhringer 2002), a list of 53 clusters (Table 3) has been retained to fulfill selection criteria that would lead to an enhanced signal-to-noise ratio. Our selection criteria are as follows:
-
Because of the decrease in gamma-ray flux with increasingdistance of the emitting object, only galaxy clusters located at lowredshift z < 0.2 have been retained.
-
To avoid false signal detection due to a possible mismodelling of the observed strong diffuse emission along the galactic plane and in the galactic centre region, galaxy clusters located at latitudes |b| < 25° and longitudes −30 < l < +30° have been discarded. Additionally, because of the strong emission detected around the Taurus molecular cloud, the galaxy cluster A400 was also excluded.
-
Finally, to avoid false signals from residual emission of powerful gamma-ray sources listed in the second year Fermi-LAT (2FGL) catalog (Nolan et al. 2012) in the close vicinity of the galaxy clusters, A1650, A1651, A1689, A2065, A2199, A2589, A3376, HCG94, M49, NGC 4636, UGC 03957, and ZwCl1215 have also been removed from the selection.
3. Analysis
3.1. Data preparation
In this study, we make use of the gamma-ray events collected by the Fermi-LAT satellite from 2008-08-04 to 2013-01-31 analysed using the version v9r27p1 of the Fermi Science Tools1 in conjunction with the P7SOURCE_V6 instrument response functions. To reduce the large number of events due to diffuse emissions and to improve the point spread function of the instrument, an energy threshold of 200 MeV was applied to the event selection. For each source listed in Table 3, SOURCE class photon-like events were extracted from a circular region of interest (ROI) with ~10° radius centred on the galaxy cluster. Good time intervals were generated using the recommended selection expression2 and a ROI-based maximum zenith angle cut was applied to exclude photons coming from the Earth limb. A binned likelihood analysis is first performed on each individual ROI to determine the parameters of the gamma-ray emission model. The expected gamma-ray signal within the ROI is modelled using a combination of the galactic3 (GB) and isotropic4 (EGB) diffuse emission models, and also incorporates all point-like sources listed in the 2FGL catalog within 20° around the galaxy cluster. To prevent genuine variability or statistical fluctuations of the signal from nearby sources from affecting the analysis, the overall flux normalizations of sources within 10° radius of the target were treated as free parameters during the likelihood analysis. The normalizations of the GB and EGB components were also free to vary during the fitting procedure to improve any local mismodelling of the diffuse emission in this particular ROI. All other parameters were fixed to the best fitting values published in the 2FGL. The parameters maximizing the likelihood function are then used to simulate all Fermi-LAT detected sources, with the exception of the GB and EGB components, and to subtract them from the data to simplify the model used for the stacking analysis (see Huber et al. 2012).
3.2. Stacking analysis
Following the procedure described in Huber et al. (2012), the stacking of the sources is performed by adding step by step the point-source subtracted count maps of the selected ROIs. At each stacking step, the co-added map is analysed using a binned maximum likelihood approach (Mattox et al. 1996), in which two alternative model hypotheses are compared by maximizing their respective likelihoods with respect to the obtained count map. The null hypothesis corresponds to gamma-ray events originating from the GB and EGB components only, whereas the alternative hypothesis includes an additional test source, corresponding to a point-like emission with power-law spectral shape parametrized as 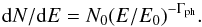 As the signal is expected to be faint, only the flux normalization parameter is allowed to vary during the fitting procedure, whereas the photon spectral index Γph was fixed to a set of values 2.0,2.4,2.8, and 3.2, and the energy scale E0 was set to 1 GeV. We performed the spectral fit in the energy range between 1 and 300 GeV where a power law is a good approximation of the gamma-ray spectrum resulting from neutral pion decay arising in proton-proton collisions (see Sect. 5 and Appendix A). This particular choice of gamma-ray spectral indices allows us to bracket the range of indices of the injected proton spectrum (Pinzke & Pfrommer 2010; Vazza et al. 2012).
As the signal is expected to be faint, only the flux normalization parameter is allowed to vary during the fitting procedure, whereas the photon spectral index Γph was fixed to a set of values 2.0,2.4,2.8, and 3.2, and the energy scale E0 was set to 1 GeV. We performed the spectral fit in the energy range between 1 and 300 GeV where a power law is a good approximation of the gamma-ray spectrum resulting from neutral pion decay arising in proton-proton collisions (see Sect. 5 and Appendix A). This particular choice of gamma-ray spectral indices allows us to bracket the range of indices of the injected proton spectrum (Pinzke & Pfrommer 2010; Vazza et al. 2012).
The probability of the presence of the additional test source is obtained from a likelihood ratio test defined as 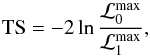 where
where 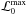 and
and 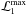 are the maximum likelihood values for the null and alternative hypotheses, respectively. If the null hypothesis is true, then the detection significance of the additional source is approximately given by
are the maximum likelihood values for the null and alternative hypotheses, respectively. If the null hypothesis is true, then the detection significance of the additional source is approximately given by 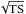 . In the following, we use a detection threshold of TS = 25 to report the flux of the source. When there is a lower TS value, a 95% confidence level (CL) upper limit on the gamma-ray flux divided by the sample size (SUL/N) is reported. Namely, the corresponding upper limit represents the maximum allowed average flux per system in the sample (at 95% CL). We stress that, since this is an average value, this limit does not hold on an individual-object basis, and it is possible for some systems to exhibit a higher gamma-ray flux. For the upper limits on individual systems, we refer the reader to Ackermann et al. (2010).
. In the following, we use a detection threshold of TS = 25 to report the flux of the source. When there is a lower TS value, a 95% confidence level (CL) upper limit on the gamma-ray flux divided by the sample size (SUL/N) is reported. Namely, the corresponding upper limit represents the maximum allowed average flux per system in the sample (at 95% CL). We stress that, since this is an average value, this limit does not hold on an individual-object basis, and it is possible for some systems to exhibit a higher gamma-ray flux. For the upper limits on individual systems, we refer the reader to Ackermann et al. (2010).
3.3. Stacking order
In hierarchical formation scenarios, galaxy clusters with large masses imply a long formation history, which in turn allows CRs to be accumulated in the cluster volume over time (Berezinsky et al. 1997). It is therefore reasonable to expect that the gamma-ray luminosity correlates with the galaxy cluster mass (see Pinzke & Pfrommer 2010). On the other hand, since the measured flux is inversely proportional to the square of the distance of the source, it is less likely that objects with a similar mass located at a larger distance will be detected. For these reasons, we stack the galaxy clusters in a sorted sequence defined by descending values of M500/z2, where M500 is the galaxy cluster mass encompassed in the volume for which the density is 500 times larger than the critical density of the Universe and z is the cluster redshift.
We also tested other stacking orders, and found that the TS or flux upper-limit developments were not greatly modified.
4. Results
In this section we present the results of the TS and flux upper limits (SUL/N) obtained for the additional point-like emission after each stacking step on the whole set of galaxy clusters listed in Table 3. Since the evolution histories of CC and NCC galaxy clusters are different we also provide results for these two populations of galaxy clusters.
4.1. Stacking of 53 clusters
 |
Fig. 1 Evolution of the TS corresponding to the additional presence of a point-like emission at the centre of the ROIs as a function of the number of stacked galaxy clusters obtained from the whole sample (plain line), as well as for cool-core (star-dashed line) and non-cool-core (circle-dashed line) populations. The TS values are obtained for a power-law spectrum with photon index Γph = 2.4 and galaxy cluster ordered by descending values of M500/z2. |
 |
Fig. 2 95% CL upper-limits on the average photon flux (SUL/N) in the 1–300 GeV energy band for a potential point-like emission at the centre of the ROIs versus the number of stacked clusters. The stacking analysis is performed using a power-law spectrum with photon index 2.4 and a stacking order of descending M500/z2-values. |
Flux upper limits divided by the sample size (SUL/N) on the stacked emission in the 1–300 GeV energy band.
The TS development obtained after each stacking step of our 53 galaxy clusters ordered by descending M500/z2-values is shown in Fig. 1. For every stacking step the resulting TS value remains below the detection threshold TS = 25, with a final TS value of 3.8 after 52 stacking steps for a photon index of 2.4, not leading to any significant signal after any stacking step.
Since no significant signal was detected, we computed the corresponding 95% CL gamma-ray flux upper limit (SUL/N) integrated between 1 and 300 GeV, shown in Fig. 2. Stacking all 53 clusters from Table 3 and analysing them with photon indices Γph = 2.0, 2.4, 2.8, and 3.2 yield final upper limits on the gamma-ray emissivity of the galaxy cluster sample of the order of a few 10-11 ph cm-2 s-1 in the 1 to 300 GeV range. In comparison, the individual flux upper limit obtained for a power law with spectral index Γph = 2.0 and translated in the same energy range published in Ackermann et al. (2010) range between 1.5 and 28.2 × 10-10 ph cm-2 s-1, not considering the comparatively high values for the Ophiuchus and Perseus clusters.
4.2. Separate stacking of cool-core and non-cool-core clusters
In the following, we separate the CC and NCC populations from our sample of 53 clusters and perform independent analyses on the two subsamples. Because of the presence of a central radio-loud AGN in CCs (Mittal et al. 2009), gamma-rays could originate, for instance, from CRs ejected by the AGN, that interact with the ambient cluster gas (e.g. Mathews 2009; Colafrancesco & Marchegiani 2008; Fujita & Ohira 2011). Instead, NCCs are expected to be disturbed systems with ongoing dynamical activity, that could lead to the presence of CRs accelerated through merger shocks and large-scale turbulence. The separate treatment of the two types of galaxy clusters could resolve intrinsic differences in their gamma-ray emissivity. The class of each cluster is indicated in Table 3, following the classification of Cavagnolo et al. (2009) when available, and Chen et al. (2007) otherwise. Though not significant, the largest discrepancy in the resulting TS development between both samples is found for a stacking sequence defined by descending values of M500/z2.
4.2.1. Stacking cool-core clusters
From our selection of galaxy clusters, 21 objects belong to the CC class. The development of the TS of the stacked CC galaxy clusters sub-sample ordered by descending M500/z2 is presented in Fig. 1. The TS values remain below 4 during the whole stacking process and thus no significant signal was detected. The 21 stacked CC galaxy clusters result in final flux SUL/N 5.7 × 10-11 ph cm-2 s-1 for an intermediate photon index Γph = 2.4.
4.2.2. Stacking non-cool-core clusters
We repeated the same analysis for our sample of 32 NCC galaxy clusters. The sample is again sorted by descending M500/z2 values, and the corresponding TS development during the stacking procedure is shown in Fig. 1. In contrast to the result obtained for the CC sample, the largest value of the TS, though not statistically significant, is obtained after the stacking of few large and nearby objects. The final TS value is, however, below 1. The 95% CL flux SUL/N obtained for the final sample of 32 stacked NCC galaxy clusters is 2.7 × 10-11 ph cm-2 s-1 for Γph = 2.4.
In all investigated cases, the TS values remain below the detection threshold. The final 95% CL flux upper limits obtained for power laws with photon indices Γph = 2.0,2.4,2.8, and 3.2 integrated from 1 to 300 GeV, as well as the final TS values, are summarized in Table 1.
5. Constraints on the cosmic-ray energy density
The gamma-ray data explored in this paper can be combined with X-ray observations to extract constraints and limits on the averaged CR energy density in galaxy clusters. Indeed, theoretical models generally agree in reporting that the gamma-ray emission from clusters should be dominated by the decay of π0 produced in p − p interactions between the CR and the ambient intracluster medium (ICM; e.g. Colafrancesco & Blasi 1998; Pfrommer & Enßlin 2004; Pfrommer et al. 2008) 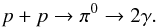 (1)Assuming that the gamma-ray flux results from this process, constraints on the energy density stored in CRs can be obtained. The distribution of the ambient gas for the systems is known from X-ray observations (e.g. Reiprich & Böhringer 2002; Chen et al. 2007), and thus upper limits on the CR-to-thermal energy ratio can be derived.
(1)Assuming that the gamma-ray flux results from this process, constraints on the energy density stored in CRs can be obtained. The distribution of the ambient gas for the systems is known from X-ray observations (e.g. Reiprich & Böhringer 2002; Chen et al. 2007), and thus upper limits on the CR-to-thermal energy ratio can be derived.
5.1. Method
We describe here the method used to determine upper limits on the average CR-to-thermal energy ratio, ϵ, in our galaxy cluster sample. For more details about the calculation, we refer the reader to Appendix A.
We consider a CR population with a power-law energy spectrum with index Γp. To cover the range of spectral indices predicted by simulations, we vary the spectral index of the underlying proton population between ~2 (corresponding to the strong shock limit, i.e. Mach numbers M ≥ 10) and ~3.2 (corresponding to weak shocks with M ~ 2). Through π0 decay, this CR population produces a gamma-ray signal with a slightly harder effective photon spectrum (see Appendix A). We consider only the protons with an energy higher than the threshold for π0 production. In other terms, we set a low-energy cut to the proton population at a kinetic energy of 1 GeV, since protons with lower energies are not observable. We assume that the density of the thermal gas follows an isothermal beta model (Cavaliere & Fusco-Femiano 1976), with parameters for each cluster obtained from the literature (Chen et al. 2007). The produced gamma-ray luminosity is then obtained by integrating the photon production rate over the cluster volume, 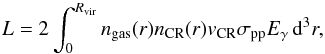 (2)
(2)
where ngas(r) and nCR(r) are the densities of thermal gas and CR at radius r from the cluster centre, vCR ~ c is the velocity of the CR, σpp is the proton-proton interaction cross section, and Eγ is the energy of the produced photons. For the radial dependence of the CR density, we first assume that the CR follow the same radial distribution as the thermal gas (referred to as the isobaric case). As alternative possibilities, we also consider a profile where the CR-to-thermal energy ratio increases with radius as ϵ(r) ~ r0.5 (referred to as flatter), as expected from the acceleration of CR at cosmological shocks (see e.g. Vazza et al. 2012; Pinzke & Pfrommer 2010; Donnert et al. 2010), and a decreasing radial profile (ϵ(r) ~ r-0.5, referred to as steeper) to model the injection of CR by a central AGN (e.g. Colafrancesco & Marchegiani 2008; Mathews 2009; Fujita & Ohira 2011). Finally, upper limits on the CR energy density were derived for the three different cases and compared with the average thermal energy in our population, which was computed using the parameters given in Chen et al. (2007).
Among the 53 systems comprising our sample, 32 are classified as NCC, while 21 exhibit CC properties. As an estimate of the virial radius Rvir, we used the scaling relations of Arnaud et al. (2005), making the approximation Rvir ~ R200. We note that among our sample CC clusters typically exhibit a lower temperature (Tav,CC ~ 3.2 keV), and thus a lower mass and thermal energy, than NCC systems (Tav,NCC ~ 5.5 keV).
Upper limits on the CR-to-thermal energy ratio of the parent proton population.
5.2. Results
Our results regarding the CR-to-thermal energy ratio are given in Table 2. We report the results obtained for the entire sample, as well as for the CC and NCC cluster populations independently, for the three different CR radial distributions described above. As can be seen in Table 2, for a photon index of 2.0 our upper limits on the CR-to-thermal energy ratio for the whole sample are in the range 3–6%. We stress that these values represent average values for the sample and cannot be used on a single-object basis. For comparison, using data obtained by the EGRET experiment on board the Compton Gamma-Ray Observatory, Reimer et al. (2003) performed a similar study to the one presented in this paper, reaching upper limits on the CR-to-thermal energy ratio of the order of 10–20% also for a photon index of 2.0. Thanks to the excellent sensitivity of Fermi-LAT, our upper limit lies a factor of 3–4 below the upper limits obtained in this study. Recently, Ackermann et al. (2010) performed a similar analysis on individual systems and obtained stringent gamma-ray upper limits. This study allowed the authors to constrain the CR energy density at the level of a few percent of the thermal energy density in the best cases. Similar results were recently obtained on the Coma cluster through a combination of Fermi-LAT and VERITAS data (Arlen et al. 2012), which lead to an upper limit of the order of 2% on the CR-to-thermal pressure ratio. Compared to these studies, our analysis puts constraints on the average population which are slightly below the few best cases for individual systems. The stacking method therefore allows us to bring the constraints on the typical cluster population to the level of the few best individual cases. Recently, Dutson et al. (2013) stacked a sample of 114 clusters including a central radio galaxy with Fermi-LAT, and did not find any evidence of a signal in the stacked population, in agreement with the results presented here.
In the fully relativistic case, the limits provided here can be readily transformed into the pressure ratio using the relation 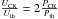 . This assumption is approximately valid, since we are considering only protons with kinetic energies >1 GeV. Thus in the isobaric case, for the average population we obtain an upper limit on the pressure ratio of PCR/Pth ≲ 2.2%. It has been claimed from numerical simulations (e.g. Ando & Nagai 2008) that the presence of a significant CR component in galaxy clusters could introduce a bias in cluster masses estimated assuming hydrostatic equilibrium. Our results indicate that the pressure contribution from CR is small, and thus that the bias in cluster masses induced by the presence of CR, if existing, would be negligible.
. This assumption is approximately valid, since we are considering only protons with kinetic energies >1 GeV. Thus in the isobaric case, for the average population we obtain an upper limit on the pressure ratio of PCR/Pth ≲ 2.2%. It has been claimed from numerical simulations (e.g. Ando & Nagai 2008) that the presence of a significant CR component in galaxy clusters could introduce a bias in cluster masses estimated assuming hydrostatic equilibrium. Our results indicate that the pressure contribution from CR is small, and thus that the bias in cluster masses induced by the presence of CR, if existing, would be negligible.
Sample of 53 clusters used for the stacking.
6. Discussion
6.1. CR injection at merger shocks
Numerical simulations modelling the formation of large-scale structures always report the presence of strong accretion shocks (i.e. with a Mach number M ~ 10) in the outer regions of galaxy clusters, and weaker (2 ≤ M ≤ 5) and more energetic merger shocks induced by structure-formation processes in the innermost cluster regions (e.g. Miniati et al. 2000, 2001; Ryu et al. 2003; Pfrommer et al. 2008; Vazza et al. 2012). These shocks are expected to inject a population of CR protons, which should accumulate in the cluster’s volume starting from the formation epoch (Berezinsky et al. 1997; Völk & Atoyan 1999). The data explored here thus allow us to constrain the overall amount of CR protons injected at cosmological shocks. Recently, using pure hydrodynamical simulations Vazza et al. (2012) estimated that the CR-to-thermal pressure ratio should slightly increase with radius, from ~1% in the core to ~10% around R200, without any important differences between relaxed and dynamically-active systems. Similar results were obtained by Pinzke & Pfrommer (2010). Since the bulk of the CR are produced in merger shocks with Mach number in the range 2–4, we expect the photon index of the resulting proton population to be in the range 2.3 to 2.8. Comparing these predictions with our computation of the CR-to-thermal pressure ratio (see Sect. 5.2 and Table 2), for a flatter CR distribution we can see that our 95% upper limits on the pressure ratio for the entire sample are in the range 3 − 5% for Γp in the range 2.3–2.8. These values are similar to the expectations of numerical simulations, and thus our observational results are starting to probe the particle acceleration models assumed in these simulations. For the NCC subpopulation, our upper limits are at the level of 2 − 3% of the thermal pressure for Γp in the range 2.3–2.8, which is in slight disagreement with the predictions. Therefore, although these predictions cannot be firmly ruled out yet, it is likely that the acceleration efficiency assumed in these simulations is overestimated.
Given that the simulations presented by Vazza et al. (2012) and Pinzke & Pfrommer (2010) are non-radiative and neglect the injection of CR by other processes (AGN, SNe), the predicted level of CR energy density should be treated as a lower bound to the expectations from numerical simulations, which reinforces our result. As discussed in Vazza et al. (2013), a possible explanation for this result is the little-known acceleration efficiency of CR at weak shocks. Vazza et al. (2012) used the efficiency of CR injection expected from diffuse shock acceleration theory (DSA), following Kang & Jones (2007). Since the DSA theory is tailored to reproduce the acceleration efficiency of high-Mach number shocks in galactic supernova remnants, our results could indicate that CR acceleration at weak shocks is significantly less efficient than expected from DSA. Moreover, recent results regarding supernova remnants have shown that the accelerated CR spectra are steeper than expected from DSA (Caprioli 2012; Kang 2012), even in the high-Mach number regime. Therefore, it appears likely that the acceleration efficiency used in existing numerical simulations is overestimated in the case of cosmological shocks.
Alternatively, cosmic rays could have been transported outwards to lower-density regions, which would make them unobservable to us (Enßlin et al. 2011; Keshet 2010). As we can see in Table 2, our constraints are less tight when assuming a flat radial distribution for the CR, since the density of target protons drops sharply in the outer regions (Eckert et al. 2012). Therefore, an efficient transport of cosmic rays towards the outskirts could be responsible for making the CR distribution even flatter than considered here, resulting in a lower gamma-ray flux.
6.2. AGN feedback in cool-core clusters
One of the main discoveries of Chandra has been the discovery of X-ray cavities at the centre of relaxed galaxy clusters, which are thought to be inflated by powerful AGN outbursts (see McNamara & Nulsen 2007, 2012; Fabian 2012, for reviews). Indeed, radio-loud AGN are found to be ubiquitous at the centre of CC clusters (Burns 1990; Mittal et al. 2009), and in many cases CR electrons are filling the volume of X-ray cavities, providing strong evidence of the interplay between the central engine and the surrounding plasma. The energy injected by the central AGN can be large, preventing the gas from cooling below X-ray emitting temperatures and forming stars. While the general picture is clear, the details of the heat transfer mechanism are still not understood. One of the proposed mechanisms (e.g. Colafrancesco & Marchegiani 2008; Mathews 2009; Fujita & Ohira 2011) considers the interaction of a population of relativistic CR with the gas as heat conveyor. In this framework, it has been shown that the observed X-ray properties can be recovered if the CR energy density is large enough. Our upper limit on the CR-to-thermal energy ratio in CC clusters thus allows us to put constraints on this model.
For a proton spectral index of 2.7, Colafrancesco & Marchegiani (2008) found that they could explain the observed X-ray temperature profile and the radio halo, when observed, in CC clusters if the CR radial distribution is steeper than that of the gas and if the pressure ratio is of the order of ~0.4–1.2, depending on the considered clusters. The typical expected gamma-ray fluxes exceed 10-10 ph cm-2 s-1 when converted in the [1–300] GeV band, which is several times larger than our upper limit. Fujita & Ohira (2012) used a model where the CR are injected in the ICM during AGN intermittent explosions whose outgoing shock waves, followed by the formation of bubbles, heat the gas. This model was applied to the observations made on Perseus. Again, in this case a CR radial distribution more peaked than that of the gas and a pressure ratio of the order of 1–25% (depending on the distance to the cluster centre) were required to explain the observations.
Comparing these models with our observational results, in the case of a CR profile decreasing with radius and for proton indices between 2.5 and 3.0, we obtain an upper limit on the CR-to-thermal pressure ratio of 3–5% which is well below the values required to offset cooling. We note that because of the large target densities in the central regions, our analysis is very sensitive to the CR energy density in the inner regions, especially in the case of a steep CR radial profile. Therefore, we conclude that the energy density in the central regions of CC clusters is probably lower than what is needed in these models to offset radiative cooling, and heating through cavity expansion and/or shocks is preferred.
In this framework, we note that the upper limit obtained here also has implications on the typical gamma-ray luminosity of the central AGN itself. Indeed, in the case of Perseus (Abdo et al. 2009) a bright variable gamma-ray source was detected by Fermi-LAT, corresponding to the central AGN NGC 1275/3C 84 (see also Eckert & Paltani 2009; Colafrancesco et al. 2010; Aleksić et al. 2012). Our non-detection of the stacked CC cluster population with an upper limit ~3 orders of magnitude below the gamma-ray flux of NGC 1275 thus shows that the central AGN of Perseus is significantly more active than the typical radio-loud AGN which are at work at the centre of CC clusters. A similar conclusion has recently been reached by Dutson et al. (2013).
7. Summary
Making use of a maximum likelihood analysis of stacked Fermi-LAT count maps, we searched for gamma-ray emission from a sample of 53 galaxy clusters selected from the extended HIFLUGCS sample. Our results can be summarized as follows:
-
Assuming power-law spectra with a photon index ofΓph = 2.0,2.4,2.8, and 3.2, we obtained 95% CL upper limits on the average photon flux per system (SUL/N) of a few 10-11 ph cm-2 s-1 in the [1–300] GeV energy band for the total sample. This upper limit is an order of magnitude lower than the typical upper limits for individual clusters (Ackermann et al. 2010).
-
Performing separate analyses for the CC and NCC populations, we do not find evidence of differences in their gamma-ray emissivity. The 95% CL flux upper limits (SUL/N) obtained for our CC and NCC sample are 5.7 and 2.7 × 10-11 ph cm-2 s-1, respectively, for a photon index of Γph = 2.4.
-
Assuming that the gamma-ray signal comes entirely from the decay of π0 produced in p − p collisions between CR protons and the ambient thermal gas, we derived upper limits of 4 to 10% on the average CR energy density for a photon indices of Γph = 2.0,2.4,2.8, and 3.2 (corresponding to a proton index of Γp = 2.05,2.45,2.85, and 3.25). Upper limits were also obtained for flatter and steeper radial distributions of the CR with respect to the thermal gas.
-
Comparing our upper limits on the CR energy density with the expectations of numerical simulations modelling the injection of CR at cosmological shocks (Vazza et al. 2012; Pinzke & Pfrommer 2010), and taking into account that these simulations neglect the potential contribution of AGN and SNe to the global CR budget, our results are in disagreement with the CR level predicted by these simulations. Although we cannot completely rule out these models, this probably indicates that the injection of CR at low Mach number shocks is lower than expected from DSA. Alternatively, a very flat radial CR distribution (e.g. resulting from CR streaming), may reconcile our data with the expectations.
Acknowledgments
We thank Franco Vazza and the anonymous referee for useful discussions and comments.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 699, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2010, ApJ, 717, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Anton, G., et al. 2009, A&A, 495, 27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ajello, M., Rebusco, P., Cappelluti, N., et al. 2010, ApJ, 725, 1688 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Antonelli, L. A., Antoranz, P., et al. 2010, ApJ, 710, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Alvarez, E. A., Antonelli, L. A., et al. 2012, A&A, 539, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ando, S., & Nagai, D. 2008, MNRAS, 385, 2243 [NASA ADS] [CrossRef] [Google Scholar]
- Arlen, T., Aune, T., Beilicke, M., et al. 2012, ApJ, 757, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, M., Pointecouteau, E., & Pratt, G. W. 2005, A&A, 441, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 1978, MNRAS, 182, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Berezinsky, V. S., Blasi, P., & Ptuskin, V. S. 1997, ApJ, 487, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P., Gabici, S., & Brunetti, G. 2007, Int. J. Mod. Phys. A, 22, 681 [Google Scholar]
- Brunetti, G. 2011, Mem. Soc. Astron. It., 82, 515 [NASA ADS] [Google Scholar]
- Brunetti, G., Cassano, R., Dolag, K., & Setti, G. 2009, A&A, 507, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burns, J. O. 1990, AJ, 99, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Caprioli, D. 2012, , J. Cosmol. Astropart. Phys., 7, 38 [Google Scholar]
- Cassano, R., Ettori, S., Giacintucci, S., et al. 2010, ApJ, 721, L82 [NASA ADS] [CrossRef] [Google Scholar]
- Cavagnolo, K. W., Donahue, M., Voit, G. M., & Sun, M. 2009, ApJS, 182, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Cavaliere, A., & Fusco-Femiano, R. 1976, A&A, 49, 137 [NASA ADS] [Google Scholar]
- Chen, Y., Reiprich, T. H., Böhringer, H., Ikebe, Y., & Zhang, Y.-Y. 2007, A&A, 466, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colafrancesco, S., & Blasi, P. 1998, Astropart. Phys., 9, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Colafrancesco, S., & Marchegiani, P. 2008, A&A, 484, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colafrancesco, S., Profumo, S., & Ullio, P. 2006, A&A, 455, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colafrancesco, S., Marchegiani, P., & Giommi, P. 2010, A&A, 519, A82 [Google Scholar]
- Donnert, J., Dolag, K., Cassano, R., & Brunetti, G. 2010, MNRAS, 407, 1565 [NASA ADS] [CrossRef] [Google Scholar]
- Dutson, K. L., White, R. J., Edge, A. C., Hinton, J. A., & Hogan, M. T. 2013, MNRAS, 429, 2069 [NASA ADS] [CrossRef] [Google Scholar]
- Eckert, D., & Paltani, S. 2009, A&A, 495, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eckert, D., Produit, N., Paltani, S., Neronov, A., & Courvoisier, T. J.-L. 2008, A&A, 479, 27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eckert, D., Vazza, F., Ettori, S., et al. 2012, A&A, 541, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Enßlin, T., Pfrommer, C., Miniati, F., & Subramanian, K. 2011, A&A, 527, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C. 2012, ARA&A, 50, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Feretti, L. 2005, Adv. Space Res., 36, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Feretti, L., Giovannini, G., Govoni, F., & Murgia, M. 2012, A&ARv, 20, 54 [Google Scholar]
- Ferrari, C., Govoni, F., Schindler, S., Bykov, A. M., & Rephaeli, Y. 2008, Space Sci. Rev., 134, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Fujita, Y., & Ohira, Y. 2011, ApJ, 738, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Fujita, Y., & Ohira, Y. 2012, ApJ, 746, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, B., Farnier, C., Manalaysay, A., Straumann, U., & Walter, R. 2012, A&A, 547, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inoue, S., Aharonian, F. A., & Sugiyama, N. 2005, ApJ, 628, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Jeltema, T. E., Kehayias, J., & Profumo, S. 2009, Phys. Rev. D, 80, 023005 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, H. 2012, J. Kor. Astron. Soc., 45, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, H., & Jones, T. W. 2007, Astropart. Phys., 28, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Kelner, S. R., Aharonian, F. A., & Bugayov, V. V. 2006, Phys. Rev. D, 74, 034018 [NASA ADS] [CrossRef] [Google Scholar]
- Keshet, U. 2010 [arXiv:1011.0729] [Google Scholar]
- Markevitch, M. 2010 [arXiv:1010.3660] [Google Scholar]
- Markevitch, M., & Vikhlinin, A. 2007, Phys. Rep., 443, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathews, W. G. 2009, ApJ, 695, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. R., & Nulsen, P. E. J. 2007, ARA&A, 45, 117 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- McNamara, B. R., & Nulsen, P. E. J. 2012, New J. Phys., 14, 055023 [NASA ADS] [CrossRef] [Google Scholar]
- Miniati, F., Ryu, D., Kang, H., et al. 2000, ApJ, 542, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Miniati, F., Ryu, D., Kang, H., & Jones, T. W. 2001, ApJ, 559, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Mittal, R., Hudson, D. S., Reiprich, T. H., & Clarke, T. 2009, A&A, 501, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nevalainen, J., Eckert, D., Kaastra, J., Bonamente, M., & Kettula, K. 2009, A&A, 508, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nolan, P. L., Abdo, A. A., Ackermann, M., et al. 2012, ApJS, 199, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Perkins, J. S. 2008, in AIP Conf. Ser. 1085, eds. F. A. Aharonian, W. Hofmann, & F. Rieger, 569 [Google Scholar]
- Pfrommer, C., & Enßlin, T. A. 2004, A&A, 413, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfrommer, C., Enßlin, T. A., & Springel, V. 2008, MNRAS, 385, 1211 [NASA ADS] [CrossRef] [Google Scholar]
- Pinzke, A., & Pfrommer, C. 2010, MNRAS, 409, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Pinzke, A., Pfrommer, C., & Bergström, L. 2011, Phys. Rev. D, 84, 123509 [NASA ADS] [CrossRef] [Google Scholar]
- Reimer, O., Pohl, M., Sreekumar, P., & Mattox, J. R. 2003, ApJ, 588, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Reiprich, T. H., & Böhringer, H. 2002, ApJ, 567, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Rephaeli, Y., Nevalainen, J., Ohashi, T., & Bykov, A. M. 2008, Space Sci. Rev., 134, 71 [Google Scholar]
- Rossetti, M., Eckert, D., Cavalleri, B. M., et al. 2011, A&A, 532, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryu, D., Kang, H., Hallman, E., & Jones, T. W. 2003, ApJ, 593, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L. 1986, Rev. Mod. Phys., 58, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Timokhin, A. N., Aharonian, F. A., & Neronov, A. Y. 2004, A&A, 417, 391 [Google Scholar]
- Vannoni, G., Aharonian, F. A., Gabici, S., Kelner, S. R., & Prosekin, A. 2011, A&A, 536, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazza, F., Brüggen, M., Gheller, C., & Brunetti, G. 2012, MNRAS, 421, 3375 [NASA ADS] [CrossRef] [Google Scholar]
- Vazza, F., Brüggen, M., & Gheller, C. 2013, MNRAS, 428, 2366 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Völk, H. J., & Atoyan, A. M. 1999, Astropart. Phys., 11, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Völk, H. J., Aharonian, F. A., & Breitschwerdt, D. 1996, Space Sci. Rev., 75, 279 [Google Scholar]
Appendix A: Computation of the CR energy density
Appendix A.1: Proton-proton interaction model
We consider a population of relativistic CR which interact with the ambient thermal gas. For each interaction, if the CR energy is larger than the threshold energy for pion production, its interaction with a thermal proton will produce pions and trigger a particle shower, 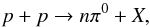 (A.1)where n is the π0 multiplicity and X are the hadronic showers. The π0 then decay into two photons, producing an observable signature in the gamma-ray range. We remark that in galaxy clusters, the gas density, magnetic fields, and radiation fields of the ambient medium are low such that all the produced pions will decay before interacting with the medium and the observed gamma-ray flux can be directly related to their parent protons.
(A.1)where n is the π0 multiplicity and X are the hadronic showers. The π0 then decay into two photons, producing an observable signature in the gamma-ray range. We remark that in galaxy clusters, the gas density, magnetic fields, and radiation fields of the ambient medium are low such that all the produced pions will decay before interacting with the medium and the observed gamma-ray flux can be directly related to their parent protons.
In this work, we use the parametrization given by Kelner et al. (2006) to describe the produced photon spectrum. Since this parametrization is optimized for energies larger than 100 GeV, we apply the delta approximation at lower energy (see Kelner et al. 2006, for details).
The collision rate of protons with the gas can be described as 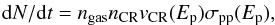 (A.2)where nCR and vCR are the number density and velocity of the CRs, respectively, and ngas is the density of target protons. The interaction cross section σpp(Ep) can be parametrized by the equation (Kelner et al. 2006)
(A.2)where nCR and vCR are the number density and velocity of the CRs, respectively, and ngas is the density of target protons. The interaction cross section σpp(Ep) can be parametrized by the equation (Kelner et al. 2006) ![\appendix \setcounter{section}{1} \begin{equation} \label{eq:sigma} \sigma_{\rm pp}(E_{\rm p})=(34.3+1.88L+0.25L^2)\left[1-\left(\frac{E_{\rm th}}{E_{\rm p}}\right)\right] \mbox{mb}, \end{equation}](/articles/aa/full_html/2013/12/aa21947-13/aa21947-13-eq119.png) (A.3)with L = ln(Ep/1 TeV) and
(A.3)with L = ln(Ep/1 TeV) and 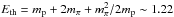 GeV, where mπ and mp are the masses of the π0 and the proton, respectively. It grows logarithmically for energies larger than 100 GeV and is approximatively constant in the range Ep ∈ [5;100] GeV. In the energy range where the cross section is constant, the produced photon spectra follow the spectral shape of the parent proton population, whereas at lower energies, close to the threshold energy for pion production, the resulting spectra are harder.
GeV, where mπ and mp are the masses of the π0 and the proton, respectively. It grows logarithmically for energies larger than 100 GeV and is approximatively constant in the range Ep ∈ [5;100] GeV. In the energy range where the cross section is constant, the produced photon spectra follow the spectral shape of the parent proton population, whereas at lower energies, close to the threshold energy for pion production, the resulting spectra are harder.
The observational constraints from Fermi-LAT data were obtained by assuming that the spectral shape of the observed photons follows a single power law. However, below the threshold energy for pion production (<1 GeV), the predicted spectrum differs significantly from a power law. To alleviate this issue, we restrict to the photons with energies >1 GeV where the spectrum can be well-represented by a power law, and we fit the model spectrum with a simple power law over the energy range of interest. The best-fit photon index is used as an effective photon index. For instance, for a parent proton spectrum of Γ = 2, we find an effective photon index of 1.94. This is illustrated in Fig. A.1, where we represent in blue the photon spectrum produced by the interaction of the primary protons (in black) with the ambient gas. We can see that the effective photon index (red curve) is harder than the spectral index of the parent protons. Observationally, we obtained upper limits on the cluster emission for effective photon indices Γph = 2.0, 2.4, 2.8, and 3.2, which correspond to parent CR populations with Γp = 2.05, 2.45, 2.85, and 3.25.
As for each interaction, 2 photons of energy 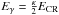 are produced (where κ ~ 0.17 is the fraction of energy transferred from the proton to the pion Eπ = κECR, Kelner et al. 2006), the total gamma-ray luminosity is given by the product of the interaction rate with the photon energy,
are produced (where κ ~ 0.17 is the fraction of energy transferred from the proton to the pion Eπ = κECR, Kelner et al. 2006), the total gamma-ray luminosity is given by the product of the interaction rate with the photon energy, 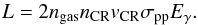 (A.4)
(A.4)
 |
Fig. A.1 Produced photon spectrum (blue) for a proton injected spectrum of Γp = 2 and Ecut,p = 1015 eV (black, scaled by an arbitrary factor). The red dotted line represents the best fit of the photon spectra with a simple power law in the energy range [1–300] GeV. The behaviour at low energy follows the increase in the cross section at Ep ~ 1 GeV (see Eq. (A.3)). Note that the proton spectrum is expressed as function of the kinetic energy, Ecin = Etot − mpc2, with mp ~ 1 GeV/ c2. |
Appendix A.2: Application to galaxy clusters
We assume that the produced gamma-rays follow a power-law distribution with the same spectral index in all systems (see Pinzke & Pfrommer 2010). In other terms, we assume that the CR are accelerated by the same mechanism, such that the CR content is expected to be of the same order of magnitude in all clusters. We assume that the CR distribution follows a power-law shape with an exponential cut-off at high energy, a choice motivated by the shock acceleration mechanism (e.g. Bell 1978), 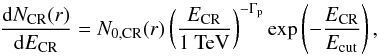 (A.5)where Γp is the proton spectral index, N0,CR(r) is the normalization of the spectrum at distance r from the cluster centre, and Ecut is the cut-off energy. For proton indices larger than 2, the total CR energy density depends very weakly on the cut-off energy, and thus we fix Ecut to 1019 eV. Since protons with kinetic energies <1 GeV are unobservable to us, we set a low-energy threshold of 1 GeV to the distribution.
(A.5)where Γp is the proton spectral index, N0,CR(r) is the normalization of the spectrum at distance r from the cluster centre, and Ecut is the cut-off energy. For proton indices larger than 2, the total CR energy density depends very weakly on the cut-off energy, and thus we fix Ecut to 1019 eV. Since protons with kinetic energies <1 GeV are unobservable to us, we set a low-energy threshold of 1 GeV to the distribution.
For simplicity, we assume that the density of the thermal gas follows an isothermal beta model (Cavaliere & Fusco-Femiano 1976), where the gas density can be parametrized by the function 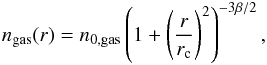 (A.6)where n0,gas is the central density, rc is the cluster core radius, and β is the slope of the density profile in the outer regions. The thermal energy density at a radius r is given by
(A.6)where n0,gas is the central density, rc is the cluster core radius, and β is the slope of the density profile in the outer regions. The thermal energy density at a radius r is given by 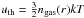 , where the temperature is assumed to be constant over the cluster volume. The total gamma-ray luminosity is then obtained by integrating Eq. (A.4) over the entire cluster volume,
, where the temperature is assumed to be constant over the cluster volume. The total gamma-ray luminosity is then obtained by integrating Eq. (A.4) over the entire cluster volume, 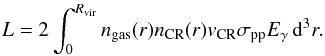 (A.7)We express the total energy stored into CR as a fraction of the thermal energy, UCR = ϵ·Uth. Given that CR have been accumulating in the cluster volume since the formation epoch, we expect the CR energy density to be roughly constant from one system to another. Thus, ϵ is assumed to be similar in all galaxy clusters, independently of their dynamical state. To determine ϵ, we first assume that the CR are in equipartition with the gas (i.e. we set ϵ = 1) and determine the gamma-ray flux that should be observed under this assumption. The ratio of the observed UL to the flux expected when assuming equipartition then gives the value of ϵ.
(A.7)We express the total energy stored into CR as a fraction of the thermal energy, UCR = ϵ·Uth. Given that CR have been accumulating in the cluster volume since the formation epoch, we expect the CR energy density to be roughly constant from one system to another. Thus, ϵ is assumed to be similar in all galaxy clusters, independently of their dynamical state. To determine ϵ, we first assume that the CR are in equipartition with the gas (i.e. we set ϵ = 1) and determine the gamma-ray flux that should be observed under this assumption. The ratio of the observed UL to the flux expected when assuming equipartition then gives the value of ϵ.
Under the assumption of equipartition, we derive for each cluster the emitted photon spectrum per unit time and volume. The equipartition flux of cluster i produced within these assumptions is then given by ![\appendix \setcounter{section}{1} \begin{equation} F_i=\frac{1}{4\pi d_{L,i}^2}\int_{V_i}\mbox{d}^3r \int_{1\mbox{\scriptsize{ GeV}}}^{300\mbox{\scriptsize{ GeV}}} E_{\gamma}\,\mbox{d}E_{\gamma} {\, \left[\frac{{\rm d}N_{\gamma}}{{\rm d}V{\rm d}E_{\gamma}{\rm d}t}\right]_{i} } \cdot \label{eq:equipartitionflux} \end{equation}](/articles/aa/full_html/2013/12/aa21947-13/aa21947-13-eq150.png) (A.8)To compare this with our upper limits on the stacked populations, we define the expected equipartition flux Fequip as the mean of the equipartition fluxes of individual systems,
(A.8)To compare this with our upper limits on the stacked populations, we define the expected equipartition flux Fequip as the mean of the equipartition fluxes of individual systems, 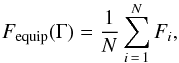 (A.9)where N is the total number of galaxy clusters in the sample. Then, an upper limit on the CR-to-thermal energy ratio can simply be obtained by taking the ratio of the observed flux to the equipartition flux,
(A.9)where N is the total number of galaxy clusters in the sample. Then, an upper limit on the CR-to-thermal energy ratio can simply be obtained by taking the ratio of the observed flux to the equipartition flux, 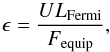 (A.10)where ULFermi is the upper limit obtained in Sect. 4.
(A.10)where ULFermi is the upper limit obtained in Sect. 4.
All Tables
Flux upper limits divided by the sample size (SUL/N) on the stacked emission in the 1–300 GeV energy band.
All Figures
 |
Fig. 1 Evolution of the TS corresponding to the additional presence of a point-like emission at the centre of the ROIs as a function of the number of stacked galaxy clusters obtained from the whole sample (plain line), as well as for cool-core (star-dashed line) and non-cool-core (circle-dashed line) populations. The TS values are obtained for a power-law spectrum with photon index Γph = 2.4 and galaxy cluster ordered by descending values of M500/z2. |
| In the text | |
 |
Fig. 2 95% CL upper-limits on the average photon flux (SUL/N) in the 1–300 GeV energy band for a potential point-like emission at the centre of the ROIs versus the number of stacked clusters. The stacking analysis is performed using a power-law spectrum with photon index 2.4 and a stacking order of descending M500/z2-values. |
| In the text | |
 |
Fig. A.1 Produced photon spectrum (blue) for a proton injected spectrum of Γp = 2 and Ecut,p = 1015 eV (black, scaled by an arbitrary factor). The red dotted line represents the best fit of the photon spectra with a simple power law in the energy range [1–300] GeV. The behaviour at low energy follows the increase in the cross section at Ep ~ 1 GeV (see Eq. (A.3)). Note that the proton spectrum is expressed as function of the kinetic energy, Ecin = Etot − mpc2, with mp ~ 1 GeV/ c2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


