EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 559 (November 2013) A&A, 559 (2013) A128 Full HTML
Free Access
Issue
A&A
Volume 559, November 2013
Article Number A128
Number of page(s) 10
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201321884
Published online 26 November 2013

© ESO, 2013

1. Introduction

The equation of state (EoS) of dense matter, i.e. the relation between the average baryon number density n, the pressure P, and the mass-energy density ρ is an essential ingredient for modelling the structure and the dynamics of neutron stars (NSs), the stellar remnants of type II supernova explosions (see e.g. Haensel et al. 2007).

With average densities ranging from a few grams per cubic centimeter at their surface to about 1015 g cm-3 in their core, the interior of NSs is expected to exhibit very different phases of matter. Because nuclei in the iron region are the most strongly bound, the surface of a NS is expected to be mostly composed of iron, possibly with a small admixture of other elements as a result of the accretion of matter or the fallback of material from the envelope ejected during the supernova explosion. Below the surface in the so-called outer crust, at densities above ρ ~ 104 g cm-3, matter consists of a body-centred cubic crystal of fully ionised atoms coexisting with a degenerate electron gas. With increasing density, nuclei become progressively more neutron rich as a result of electron capture; under terrestrial conditions these nuclei would be highly unstable, but in the outer crust of the NS their stability is ensured by the degeneracy of the electron gas. At a density of about ~4 × 1011 g cm-3, neutrons begin to drip out of the nuclei, marking the transition to the inner crust, which is composed of an inhomogeneous assembly of neutron-proton clusters immersed in a neutron liquid and neutralised by the degenerate electron gas (see e.g. Chamel & Haensel 2008). When the density reaches about ~1014 g cm-3 (about half the density found at the centre of heavy nuclei), the crust dissolves into a homogeneous mixture of neutrons with a small admixture of protons, neutralised by electrons and, at slightly higher densities, muons, thus forming the so-called outer core. The inner core of massive NSs may contain other particles like hyperons, meson condensates, or even deconfined quarks (see e.g. Page & Reddy 2006; Weber et al. 2007).

Determining the transition between these various phases is of particular importance for interpreting some astrophysical observations. For instance, quasiperiodic oscillations detected in giant flares from soft-gamma ray repeaters (Barat et al. 1983; Israel et al. 2005; Strohmayer & Watts 2005, 2006; Watts & Strohmayer 2006) are believed to be the signatures of starquakes induced by magnetic stresses, as proposed by Duncan (1998). If this interpretation is correct, the observed frequencies can be used to probe the interior of NSs provided suitable microscopic models are available (see e.g. Watts 2012 for a recent review). In particular, the frequency spectrum of seismic modes depends on the location of the crust-core boundary (Piro 2005; Strohmayer & Watts 2006), which in turn requires a unified treatment of dense matter. The transition between the outer and inner parts of the crust of a NS is also important for modelling pulsar glitches (Espinoza et al. 2011), which are generally thought to be related to the dynamics of the neutron ocean in the crust (see e.g. Sect. 12.4 in Chamel & Haensel 2008 for a review).

For these reasons, we have recently developed a family of three different unified EoSs reflecting the current lack of knowledge of high-density matter (Goriely et al. 2010; Pearson et al. 2011, 2012; Chamel et al. 2012). Our EoSs are based on the nuclear energy density functional (EDF) theory, which has proved to be very successful for describing the properties of medium-mass and heavy nuclei (Bender et al. 2003; Stone & Reinhard 2007). However, the EDF theory is not restricted to finite systems but can also be applied to describe infinite systems, either homogeneous (like NS cores) or inhomogeneous (like NS crusts). Even though existing functionals are phenomenological, they can provide a convenient interpolation of microscopic calculations using realistic nucleon-nucleon potentials, which have usually been restricted to symmetric nuclear matter and pure neutron matter only. The EDF theory is, therefore, particularly well-suited for a unified description of the different regions inside a NS. Such a unified EoS is the popular SLy EoS developed by Douchin & Haensel (2001) for the inner crust and for the core (supplemented with the EoS of Haensel & Pichon 1994 for the outer crust). However, the compressible liquid drop approximation used to calculate the EoS of the inner crust does not take into account quantum shell effects that play a critical role in determining the equilibrium composition of the crust. In addition, the SLy4 functional underlying the SLy EoS was only constrained so as to obtain what Chabanat et al. (1998a,b) considered a “reasonable reproduction” of the neutron-matter EoSs UV14+UVII from Wiringa et al. (1988). However, many other microscopic calculations of the neutron-matter EoS using realistic forces have been carried out over the past decades.

The paper is organised as follows. The models underlying the unified Brussels-Montreal EoSs are briefly reviewed in Sect. 2. In Sect. 3, we discuss the various properties of rotating and non-rotating NSs, as obtained with these unified EoSs, and we compare them with astrophysical observations. These include the binding energy inferred from SN1987A in Sect. 3.1, the gravitational surface redshift in Sect. 3.2, the relation between the gravitational mass and the baryonic mass in the context of the double pulsar J0737−3039 in Sect. 3.3, the constraints on the NS masses and radii obtained from observations of low-mass X-ray binaries in Sect. 3.4, the minimum NS mass for the direct Urca process to occur in Sect. 3.5, the maximum NS mass and PSR J0348+0432 in Sect. 3.6, the Keplerian frequency limit in Sect. 3.7, and the moment of inertia of the Crab pulsar in Sect. 3.8. Finally, in Sect. 4, we will give our conclusions.

2. Unified equations of state

The interior of a NS is assumed to be made of cold catalysed matter, i.e. matter in full thermodynamic equilibrium at zero temperature. This assumption is generally satisfied in the core of mature NSs. However this approximation may be less accurate in the crust (see e.g. Chamel & Haensel 2008 for a discussion). In particular, the temperature in the interior of a NS is not zero; however, thermal effects mostly affect the surface layers of the star (see e.g. Yakovlev & Pethick 2004; Page & Reddy 2006). Moreover, the composition of the crust of a real NS may deviate from that obtained in full equilibrium because of the accretion of matter. Therefore, the EoSs considered here are mostly suitable for non-accreting NSs. For simplicity, we will assume that the entire core is composed of nucleons and leptons only and we will therefore drop the distinction between the outer core and the inner core. The unified EoSs that we employ here provide a consistent description of both the crust and the core using the nuclear EDF theory with the same Brussels-Montreal functionals BSk19, BSk20, and BSk21 (Goriely et al. 2010) but different approximations, as briefly reviewed below.

2.1. Brussels-Montreal nuclear energy density functionals

The functionals underlying the unified EoSs considered here are based on generalised Skyrme effective nucleon-nucleon interactions (Chamel et al. 2009; Goriely et al. 2010), supplemented with a microscopic contact pairing interaction (Chamel 2010). These EDFs were fitted to the 2149 measured masses of nuclei with N and Z ≥ 8 given in the 2003 Atomic Mass Evaluation (Audi et al. 2003), with an rms deviation of 0.58 MeV. At the same time, an optimal fit to charge radii was ensured. The masses of bound nuclei were obtained by adding to the Hartree-Fock-Bogoliubov (HFB) energy a phenomenological Wigner term and a correction term for the collective energy. The fit to the mass data is essential to obtain reliable estimates of the masses of the unmeasured neutron-rich nuclei, thus making the functionals well-suited for describing the properties of nuclei found in the outer crust of a NS. On the other hand, the SLy4 functional was fitted to only six nuclear masses; moreover, three of these nuclei had N = Z (even), and since no Wigner term was included in the model the symmetry energy must inevitably be too large. Possibly for this reason, the rms deviation from the mass data (only even-even nuclei were considered) is quite large, 5.1 MeV (Dobaczewski et al. 2004).

The Brussels-Montreal EDFs were also constrained to reproduce various properties of homogeneous nuclear matter as obtained from many-body calculations using realistic two- and three-nucleon interactions. In particular, the isoscalar effective mass to nucleon mass ratio in symmetric nuclear matter at saturation was set to the realistic value of 0.8 (see the discussion by Goriely et al. 2003). More importantly, the three different functionals BSk19, BSk20, and BSk21 were fitted to three different neutron-matter EoSs, reflecting the current lack of knowledge of the high-density behaviour of dense matter. More specifically, BSk19 was adjusted to the soft EoS of neutron matter of Friedman & Pandharipande (1981) obtained from the realistic Urbana v14 nucleon-nucleon force with the three-body force TNI; BSk20 was fitted to the EoS of Akmal et al. (1998) labelled “A18 + δv + UIX”; whereas BSk21 was constrained to reproduce the stiff EoS labelled “V18” taken from Li & Schulze (2008). All three neutron-matter EoSs are consistent at the low densities prevailing in NS crusts and agree quite well with the results obtained from more recent microscopic calculations, as illustrated in Fig. 1 where the shaded area corresponds to the quantum Monte Carlo calculations by Gandolfi et al. (2012). With this neutron-matter constraint combined with the excellent fit to nuclear masses, the Brussels-Montreal EDFs are well-suited for the description of the inner crust of a NS where neutron-proton clusters coexist with a neutron liquid.

thumbnail Fig. 1

Neutron-matter energy per particle as a function of baryon number density for the EDFs BSk19-20-21. For comparison, we show the calculations by Gandolfi et al. (2012, shaded area).

Furthermore, (i) we imposed a value of J = 30 MeV on the symmetry coefficient, a value that yields an optimum fit to nuclear masses (Goriely et al. 2013; see also e.g. Goriely et al. 2010; Lattimer 2012; Tsang et al. 2012 for a discussion of experimental and theoretical estimates of J); (ii) the incompressibility Kv of symmetric nuclear matter at saturation was required to fall in the experimental range 240 ± 10 MeV (Colò et al. 2004); (iii) the isovector effective mass was found to be smaller than the isoscalar effective mass, in agreement with both experiments and many-body calculations (see Goriely et al. 2010 for a detailed discussion); (iv) a qualitatively realistic distribution of the potential energy among the four spin-isospin channels in nuclear matter was obtained; and (v) spurious spin and spin-isospin instabilities in nuclear matter that generally plague existing Skyrme functionals have been eliminated for all densities and temperatures prevailing in NSs and supernova cores by extending the Skyrme functional (Chamel et al. 2009; Chamel & Goriely 2010).

With these features, we believe that our EDFs can be reliably applied to all regions of a NS: the outer crust, the inner crust, and the liquid core.

2.2. Outer crust

The EoSs of the outer crust were calculated in the framework of the standard BPS model (Baym et al. 1971). In this model, it is assumed that the outer crust is made of fully ionised atoms arranged in a body-centred cubic lattice at zero temperature. In addition, the outer crust is supposed to contain homogeneous crystalline structures, i.e. structures made of only one type of nuclides with proton number Z and atomic number A. The values of Z and A in each layer of pressure P were found by minimising the Gibbs free energy per nucleon g = e + P/n, e being the internal energy per nucleon and n the average baryon number density. The only microscopic inputs of this model are atomic masses. The EoSs were determined using experimental atomic masses complemented with theoretical atomic masses obtained from the HFB atomic mass models discussed above (see Pearson et al. 2011 for details). These EoSs have recently been extended to include the effects of a strong magnetic field on the degenerate electron gas (Chamel et al. 2012). However, we will consider only non-magnetised NSs in this paper.

With increasing density, the equilibrium nucleus becomes progressively more neutron-rich, until neutrons start to drip out. This transition, which delimits the boundary between the outer crust and the inner crust, occurs when the neutron chemical potential (which coincides with g at equilibrium) exceeds the neutron rest mass energy. The presence of unbound neutrons in the inner crust contributes to the pressure and has an impact on nuclear masses, effects not taken into account in the BPS model. A different treatment was therefore adopted, and will be discussed in the next section.

2.3. Inner crust

Beyond the neutron-drip threshold, the Thomas-Fermi method extended up to the fourth order was applied, with the same Skyrme functionals as those underlying the HFB atomic mass models used for the outer crust (Pearson et al. 2012). Proton quantum shell corrections were added perturbatively via the Strutinsky integral theorem. Neutron quantum shell corrections, which were shown to be much smaller than proton quantum shell corrections (Oyamatsu & Yamada 1994; Chamel et al. 2007), were neglected. This method, called the extended Thomas-Fermi+Strutinsky integral (ETFSI) method, is a computationally high-speed approximation to the fully self-consistent Hartree-Fock equations (Onsi et al. 2008). Since nuclear clusters are essentially spherical, except possibly near the crust-core interface where so-called nuclear pastas might exist (see e.g. Sect. 3.3 in Chamel & Haensel 2008 for a brief review), the Wigner-Seitz (WS) approximation was adopted to calculate the Coulomb energy. To further optimise the computations, the nucleon density distributions in the WS cell were parameterised as nq(r) = nBq + nΛqfq(r), where q = n,p for neutrons or protons respectively, nBq is a constant background term, nΛq a constant term, and fq a damped Fermi profile which ensures that all density derivatives vanish at the surface of the cell, thus providing a smooth matching of the nucleon distributions between adjacent cells.

In principle, the EoS of the inner crust should be determined by minimising at constant pressure P the Gibbs free energy per nucleon g with respect to all the parameters of the WS cell. However, this procedure would be computationally extremely costly. A numerically much more convenient approach consists in minimising the energy e per nucleon at constant average baryon number density n with respect to the same parameters. The error thereby introduced was found to be negligible (Pearson et al. 2012).

Even though two different codes were used to calculate the EoS in the outer crust and in the inner crust, the pressure (energy per nucleon) at the boundary was found to differ by less than 3% (5%), while the deviations in the proton number amounted to about 5%. This disagreement can be accounted for by the several approximations made in our ETFSI method, compared to the HFB method adopted in our outer-crust calculations, as discussed by Pearson et al. (2012).

2.4. Liquid core

With increasing density, matter was found to become progressively more homogeneous until the clusters dissolve into a plasma of nucleons and electrons, thus delimiting the boundary between the inner crust and the core (Pearson et al. 2012). The density at which the transition occurs was found to be in excellent agreement with the density below which homogeneous beta-equilibrated matter becomes unstable against the formation of clusters, thus demonstrating the consistency of our code. Muons were found to appear at higher densities. The EoS of homogeneous beta-equilibrated matter made of nucleons and leptons was calculated by Goriely et al. (2010) for the same functionals as those employed in the outer and inner regions of the crust.

3. Neutron star properties

We have applied the unified EoSs based on the Brussels-Montreal EDFs BSk19, BSk20, and BSk21 to compute the global structure of non-rotating and rigidly rotating NSs. For this purpose, we have solved Einstein’s equations of general relativity for stationary axisymmetric spacetimes (Bonazzola et al. 1993; Gourgoulhon et al. 1999; Grandclément & Novak 2009) using the LORENE library (http://www.lorene.obspm.fr, Gourgoulhon 2010). The NS properties calculated with the Brussels-Montreal EoSs have been compared with those obtained from the popular SLy EoS (Douchin & Haensel 2001). The results will be discussed in the following sections.

3.1. Binding energy

The detection of neutrinos from SN1987A allows the energy released during the supernova core-collapse to be evaluated. The energy of the neutrinos is estimated to be Eν ≃ (3 ± 1.5) × 1053 erg (see e.g. Haensel et al. 2007, Chap. 9). Since 99% of the energy of the supernova was carried away by neutrinos of all flavours, Eν can be considered a measurement of the binding energy of the newly born NS. To compare this measurement with theoretical predictions, we define Ebind as the mass defect with respect to a cloud of iron dust (Douchin & Haensel 2001)1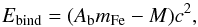(1)where Ab is the number of nucleons in the NS; mFe is the mass of iron per nucleon; mFe = 55.845  u (Wieser et al. 2013) with u = 1.6605 × 10-24 g (CODATA 2010, http://physics.nist.gov/cuu/Constants/index.html); M is the NS gravitational mass; and c is the speed of light. Bearing in mind that Ebind ≃ Eν leads to the constraint shown in Fig. 2 for a NS mass ~1.4 M⊙. All EoSs are found to be compatible with this constraint.

thumbnail Fig. 2

Binding energy versus NS mass for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF. The shaded area corresponds to the constraint inferred from the neutrino detection of SN1987A.

3.2. Gravitational surface redshift

Of particular astrophysical interest is the gravitational redshift of photons emitted from the NS surface. This quantity, denoted by zsurf, is related to the compactness ratio rg/R where rg = 2GM/c2 is the Schwarzschild radius, G being the gravitational constant and R the star radius. For non-rotating NS, zsurf is given by (see e.g. Haensel et al. 2007) 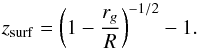(2)As shown in Fig. 3, which displays the gravitational redshift as a function of the gravitational mass up to the maximum mass consistent with causality, for a given NS mass the gravitational redshift decreases with the stiffness of EoS. For the canonical NS mass ~1.4 M⊙, zsurf thus decreases from ~0.27 to ~0.23 from the softest EoS (BSk19) to the stiffest EoS (BSk21) (Fantina et al. 2012). The shaded area is excluded by general relativity and causality (Haensel et al. 2007). The horizontal band bounded by dashed lines corresponds to the range of redshifts inferred from the spectroscopic study of the gamma-ray burst GRB 790305 from the soft gamma-ray repeater SGR 0526−066 (Higdon & Lingenfelter 1990). Interpreting the emission line at 430 ± 30 keV with the annihilation of electron-positron pairs leads to zsurf = 0.23 ± 0.07. This range of values is consistent with the gravitational redshift expected at the surface of a NS. A few years ago, Cottam et al. (2002) reported the detection of absorption lines in the spectra of several X-ray bursts from the low-mass X-ray binary EXO 0748−676. By identifying these lines with the Fe XXVI and XXV n = 2−3 and O VIII n = 1−2 transitions, they obtained zsurf = 0.35. Nevertheless, the detection of these lines has not been confirmed by subsequent observations (Cottam et al. 2008). Moreover, it has been recently argued that the widths of the absorption lines found by Cottam et al. (2002) are incompatible with the measured rotational frequency of this NS (Lin et al. 2010).

thumbnail Fig. 3

Gravitational redshift at the surface of a NS as a function of the NS mass for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF. The shaded area is excluded by general relativity and causality (Haensel et al. 2007). The horizontal band bounded by dashed lines indicates the range of redshifts inferred from the spectroscopic analysis of the gamma-ray burst GRB 790305 (Higdon & Lingenfelter 1990).

3.3. Gravitational mass versus baryonic mass

A few years ago, Podsiadlowski et al. (2005) proposed probing the EoS of dense matter using the observations of J0737−3039. This system is composed of two pulsars (Kramer et al. 2005, 2006): J0737−3039A, with a spin period of 22.7 ms and a mass 1.3381 ± 0.0007 M⊙, and J0737−3039B, with a spin period of 2.77 s and a mass 1.2489 ± 0.0007 M⊙ (the lowest NS mass measured with the highest accuracy). The low mass of pulsar B, the small eccentricity, and the low transverse velocity of this system suggest that pulsar B was not formed from a conventional iron core-collapse supernova. Instead, it is believed that pulsar B was born after the accretion-induced collapse of an oxygen-neon-magnesium core. Because of accretion, the central density of the core increased until magnesium became unstable against electron capture. The lack of electron degeneracy pressure thus led to the gravitational collapse of the core. The threshold density 4.5 × 109 g cm-3 for the onset of electron captures corresponds to a critical baryonic mass of Mb,0 = 1.375 M⊙ (Podsiadlowski et al. 2005). Taking into account the uncertainties in the composition and in the central temperature of the pre-collapse core, Podsiadlowski et al. (2005) estimated that the baryonic mass of pulsar B should lie in the range 1.366 < Mb,0 < 1.375 M⊙. Assuming that this scenario is correct, the knowledge of both the gravitational mass of pulsar B (estimated from pulsar timing) and its baryonic mass leads to a constraint on the EoS of dense matter. As shown in Fig. 4, only the EoS based on the BSk19 EDF is compatible with this constraint. On the other hand, Podsiadlowski et al. (2005) discussed various caveats in their analysis (e.g. neglect of mass loss during the supernova, variation of the critical mass due to carbon flashes), which can considerably change the constraint on the EoS. In particular, Kitaura et al. (2006) carried out hydrodynamical simulations of stellar collapse taking mass loss into account and found Mb,0 = 1.360 ± 0.002 M⊙. The SLy EoS fulfills this constraint, whereas the EoSs based on the EDFs BSk19 and BSk20 are ruled out. On the other hand, the EoS based on the BSk21 EDF is marginally compatible with the observations of PSR J0737−3039.

thumbnail Fig. 4

Gravitational mass M of non-rotating NSs versus baryonic mass Mb for the unified Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF. The filled and empty rectangles indicate the constraints inferred from the assumption that pulsar J0737–3039B was formed in an electron-capture supernova as obtained by Kitaura et al. (2006) and by Podsiadlowski et al. (2005), respectively.

3.4. Mass-radius relation

Observations of the thermal emission from NSs can provide valuable constraints on their masses and radii. The most reliable constraints are expected to be inferred from observations of transient low-mass X-ray binaries (LMXBs) in globular clusters because their distances can be accurately determined and their atmospheres, most presumably weakly-magnetised and primarily composed of hydrogen, can be reliably modelled.

The mass and radius of a NS can also be constrained from observations of type I X-ray bursts. These bursts are the manifestations of explosive thermonuclear fusion reactions triggered by the accretion of matter onto the NS surface. More precisely, the unstable burning of helium ash produced by the fusion of accreted hydrogen is thought to be at the origin of type I X-ray bursts. In some cases, the bursts are luminous enough to substantially expand the photosphere until the Eddington limit is reached. Measurements of the Eddington flux, the angular area of the photosphere, and the distance, combined with NS atmosphere models, allow a determination of the NS mass and radius.

Recently, Steiner et al. (2010) determined a probability distribution of masses and radii analysing astrophysical observations of six NSs: three type I X-ray bursters with photospheric radius expansion, and three transient LMXBs in globular clusters. We show this constraint on the mass versus radius plot in Fig. 5, together with the mass-radius relation obtained with the Brussels-Montreal and the SLy EoSs. All but the EoS based on the BSk19 EDF satisfy this constraint, although the EoS based on the BSk21 EDF is marginally compatible. However, it should be pointed out that the analysis of type I X-ray bursts is still a matter of debate (Lattimer 2012). We note that the constraint shown in Fig. 5, as well as the mass-radius relations, were obtained considering non-rotating stars.

thumbnail Fig. 5

Mass-radius relation of NSs for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF. The dark (light) shaded regions correspond to the 1σ (2σ) probability distributions implied by observations of transient LMXBs in globular clusters and type I X-ray bursters, as shown in the upper right panel of Fig. 9 of Steiner et al. (2010).

3.5. Direct Urca constraint

The density dependence of the proton fraction Yp = np/n in dense matter is very important for determining the thermal evolution of a NS. During the first 105−106 yr, a NS cools down mainly via neutrino emission. The most efficient neutrino emission mechanism is the so-called direct Urca (dUrca) process: a sequence of neutron decays 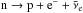and electron captures p + e− → n + νe. However, this process can only occur if the proton fraction exceeds some critical value 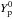. Indeed, momentum conservation leads to the triangle inequality (Heron’s formula) 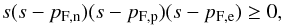(3)where s = (pF,n + pF,p + pF,e)/2, pF,i = ħ(3π2ni)1/3 being the Fermi momentum of particle species i. Since the core of a NS is highly degenerate, we have neglected the neutrino and antineutrino momenta, which are of order kBT/c ≪ pF,i (with kB the Boltzmann constant). In neutron-rich matter, Eq. (3) reduces to 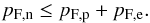(4)Imposing electric charge neutrality, np = ne + nμ, Eq. (4) can be expressed as 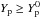with the critical proton fraction 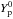given by (Klähn et al. 2006) 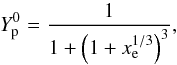(5)where xe = ne/(ne + nμ) is the leptonic electron fraction. The actual value of xe and therefore of 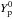are determined by the equilibrium conditions μe = μμ and μn = μp + μe, where μi denotes the chemical potential of the particle species i. In particular, 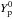is mainly determined by the symmetry energy (Lattimer et al. 1991). In the absence of muons, xe = 1 and 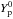reaches its lowest value 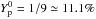. The presence of muons increases the value of 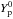. In the limit of ultrarelativistic muons, xe = 1/2 and 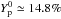(Lattimer et al. 1991).

Only the EoS based on the BSk21 EDF allows the dUrca process to occur in the core of stable NSs, and then only at baryon densities n > 0.45 fm-3 (xe ≃ 0.614, 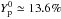) or equivalently for NSs whose gravitational mass is M > 1.59  M⊙ (Chamel et al. 2011). All the EoSs considered here are therefore compatible with the constraint of Klähn et al. (2006) that no dUrca process should occur in NSs with typical masses in the range M ~ 1−1.5 M⊙. On the other hand, the pulsar in CTA1, the transiently accreting millisecond pulsar SAX J1808.4−3658, and the soft X-ray transient 1H 1905+000 appear to be very cold, thus suggesting that these NSs cool very fast via the dUrca process (Jonker et al. 2007; Heinke et al. 2009; Page et al. 2009). Moreover, the low luminosity from several young supernova remnants likely to contain a still unobserved NS (Kaplan et al. 2004, 2006) provides further evidence for a dUrca process (Shternin & Yakovlev 2008; Page et al. 2009). If the interpretations of these observations are correct, the EoSs based on the BSk19 and BSk20 EDFs, as well as the SLy EoS, would be ruled out since they forbid the dUrca process in NS cores.

thumbnail Fig. 6

Gravitational mass of non-rotating NSs versus central baryon number density for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF. The horizontal band corresponds to the measurement of the mass of PSR J0348+0432 (Antoniadis et al. 2013).

3.6. Maximum mass with and without rotation

Figure 6 shows the gravitational mass of non-rotating NSs as a function of the central baryon number density, up to the maximum mass consistent with causality. Until very recently, the largest NS mass measured was that of PSR J1614−2230 (Demorest et al. 2010), namely 1.97 ± 0.04 M⊙. As can be deduced from this figure, this observation seems to rule out our softest EoS BSk19. However, taking into account the measured value of PSR J1614−2230 at 3σ accuracy, 1.97 ± 0.11 M⊙ (Demorest et al. 2010), the EoS based on the BSk19 EDF is found to be marginally compatible with this observation. Very recently, the mass of another massive NS in a compact binary system has been deduced. As shown in Fig. 6, the value of 2.01 ± 0.04 M⊙ at 1σ accuracy (2.01 ± 0.11 M⊙ at 3σ accuracy) for the mass of PSR J0348+0432 (Antoniadis et al. 2013) rules out the EoS based on BSk19.

On the other hand, rotation can increase the maximum mass of NSs (see e.g. Stergioulas 2003 for a review, and references therein) and therefore the question arises as to whether the EoS based on the BSk19 EDF could still be compatible with the existence of massive NSs. However, as already pointed out by Chamel et al. (2011), the increase in the maximum mass due to rotation is negligibly small (~0.005 M⊙) for rotational frequencies comparable to that of PSR J1614−2230 (namely ν = 317 Hz). In the case of PSR J0348+0432, the rotational frequency is even lower (ν = 25.6 Hz, Antoniadis et al. 2013), thus leaving our conclusions unchanged. As a consequence, the EoS based on BSk19 appears too soft to support massive NSs. However, as discussed by Chamel et al. (2013), it would be premature to conclude that the EoS of purely nucleonic matter has to be much stiffer than the EoS obtained from BSk19 because the core of a NS could be made of non-nucleonic matter. Considering the possibility of a transition to an exotic phase in NS cores, we showed that a 2 M⊙ NS is not necessarily incompatible with a purely nucleonic EoS as soft as BSk19.

As indicated in Tables 1 and 2, even for PSR J1748−2446ad (Hessels et al. 2006), which is the fastest spinning pulsar known (ν = 716 Hz), rotation increases the maximum mass by only 2% (5%) for BSk19 (BSk21). Kaaret et al. (2007) claimed that the X-ray transient XTE J1739−285 is rotating at a frequency of 1122 Hz, but their observations have not been confirmed. Even though rotation has a minor impact on the maximum NS mass, it can substantially affect the structure of less massive NSs, as illustrated in Fig. 7, which displays the mass-radius relation up to the maximum mass point consistent with causality. In particular, accounting for rotation at 716 Hz increases the radius of a 1  M⊙ NS by ~10%, ~14%, and ~18%, for the EoSs based on the EDFs BSk19, BSk20, and BSk21, respectively.

thumbnail Fig. 7

Gravitational mass versus circumferential radius relation for non-rotating and rigidly rotating NSs for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21. The horizontal band corresponds to the measurement of the mass of PSR J0348+0432 (Antoniadis et al. 2013). The dashed line represents the mass-shedding limit for PSR J1748−2446ad (Hessels et al. 2006). The shaded area in the top left-hand corner, delimited by R > 2.9GM/c2, is excluded by causality (Glendenning 2000).

Table 1

Global properties of non-rotating NSs for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF.

Table 2

Global properties of NSs rotating at rotational frequency ν = 716 Hz for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF.

thumbnail Fig. 8

Keplerian frequency versus gravitational mass for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF. The horizontal dashed lines correspond to the rotational frequency of PSR J1748−2446ad (Hessels et al. 2006) and the claimed rotational frequency of XTE J1739−285 (Kaaret et al. 2007).

3.7. Keplerian frequency

The rotational frequency ν of any stable NS is limited by the Keplerian frequency νK beyond which the star will be disrupted as a result of mass shedding. The Keplerian frequencies associated with the Brussels-Montreal and SLy EoSs are plotted in Fig. 8 as a function of the gravitational mass M, up to the maximum mass consistent with causality. Because the observed rotational frequency of a NS must be lower than νK, a lower limit on the NS mass can be inferred. This limiting mass increases with frequency. Therefore, the most stringent constraints are found for the most rapidly rotating NSs. For instance, the mass of PSR J1748−2446ad, which rotates at a rotational frequency of 716 Hz, cannot be lower than ~0.7 M⊙. On the other hand, only NSs with masses larger than 1.6 M⊙ (2 M⊙) can rotate at a frequency of 1122 Hz for the EoS based on BSk20 (BSk21).

As discussed in the previous section, the maximum mass is barely affected by rotation even for PSR J1748−2446ad, the fastest spinning pulsar known, because the rotational frequency still remains very small compared to the Keplerian frequency (Bejger et al. 2007). Figure 9 shows the mass-radius relation for non-rotating NSs (thick dashed lines) and NSs rigidly rotating at a frequency of 716 Hz, 1122 Hz, and at the Keplerian frequency (thick solid lines). The configurations stop at the maximum mass consistent with causality. We find that the increase in the maximum mass is substantial only for fast rotation (ν > 1 kHz). Table 3 lists the properties of the most massive and most rapidly rotating NSs (requiring the speed of sound at the NS centre to be lower than the speed of light). Rotation increases the maximum mass by about 17−20% at most. We also find that the highest possible rotational frequency for the maximum mass configuration lies in the range between ~1650 Hz and ~1980 Hz depending on the stiffness of the EoS at high densities. These results are in reasonable agreement with those obtained by Krastev et al. (2008) and Haensel et al. (2009).

Table 3

Global structure of the most massive and rapidly rotating NSs for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF.

thumbnail Fig. 9

Gravitational mass versus circumferential radius for static and rigidly rotating NSs at rotational frequencies of 716 Hz, 1122 Hz, and at the Keplerian frequency, for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21.

3.8. Moment of inertia

The mass and radius of a rotating NS can be constrained by measuring its moment of inertia (see e.g. Lattimer & Schutz 2005; Worley et al. 2008). Lattimer & Schutz (2005) found that the moment of inertia I of a slowly rotating NS with a mass M ≳ 1 M⊙, as determined from Einstein’s equations of general relativity, can be well approximated by the following empirical formula: (6)This relation holds for a wide class of EoSs, except for the very soft ones. Even though the moment of inertia of a rotating NS has not yet been measured, a lower bound can be inferred from the timing observations of the Crab pulsar (see e.g. Bejger & Haensel 2003; Haensel et al. 2007, and references therein). Assuming that the loss 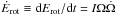of the pulsar spin energy goes mainly into accelerating the nebula leads to 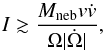(7)where Mneb is the mass of the nebula, v its expansion velocity, 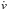its acceleration, Ω the angular frequency of the Crab pulsar, and 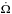its time derivative. The main uncertainty in Eq. (7) lies in the mass of the nebula, whose estimated value is Mneb = 4.6 ± 1.8 M⊙ (Fesen et al. 1997). Following the same procedure as described in Haensel et al. (2007)2, we obtain the following lower limits for the Crab moment of inertia ICrab for different masses of the nebula: 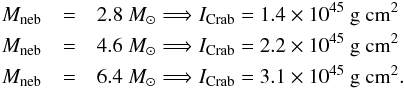(8)Inserting these values into Eq. (6), we thus obtain the constraints on the mass and radius of the Crab pulsar displayed in Fig. 10. For comparison, we also show the mass-radius relation of slowly rigidly rotating NSs with a period equal to that of the Crab pulsar, for the unified Brussels-Montreal and SLy EoSs. The configurations stop at the maximum mass consistent with causality.

thumbnail Fig. 10

Gravitational mass versus circumferential radius for slowly rigidly rotating NSs (with the same period as that of the Crab pulsar) for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF. The thick dashed lines labelled by 2.8 M⊙, 4.6 M⊙, and 6.4 M⊙ correspond to the constraint in Eq. (6) (see text for details); the region below each line is excluded. The shaded area in the top left-hand corner, delimited by R > 2.9GM/c2, is excluded by causality (Glendenning 2000).

According to Eq. (7), only the EoSs predicting a value of I higher than ICrab are acceptable. Only the EoSs based on BSk20 and BSk21 are found to be compatible with this constraint for the mass of the nebula Mneb = 4.6 M⊙. The corresponding mass of the Crab pulsar, as predicted by these EoSs, is very high ~2  M⊙. On the other hand, the observed nebular chemical abundances indicate that the Crab pulsar was not formed from an iron core-collapse supernova but most presumably from an electron-capture supernova (Hillebrandt 1982; Nomoto et al. 1982), whose remnant is expected to be a low-mass NS with a typical mass ~1.3  M⊙ (Podsiadlowski et al. 2004; van den Heuvel 2004). Increasing the mass of the nebula leads to higher values of the NS mass. This suggests that Mneb is probably lower than 4.6 M⊙. Considering the errors on the estimated mass of the nebula, the lowest acceptable value is Mneb = 2.8 M⊙ (Fesen et al. 1997). For this value of Mneb, the EoSs based on SLy4, BSk20, and BSk21 are now consistent with both the constraint in Eq. (7) and the expectation of a low mass NS. In particular, for the EoS based on BSk21 the predicted mass of the Crab pulsar ~1.3  M⊙ is in excellent agreement with the mass expected from a NS born in an electron-capture supernova. The EoS based on BSk19 is not ruled out by Eq. (7), but leads to a substantially higher NS mass ~1.6 M⊙, which is hardly compatible with the Crab pulsar formation scenario discussed above.

4. Conclusions

Using the recently developed unified Brussels-Montreal EoSs based on the generalised Skyrme functionals BSk19, BSk20, and BSk21, as well as the popular SLy EoS, we have determined the global properties of both non-rotating and rigidly rotating NSs (see also Tables 1 and 2), and we have compared them with various astrophysical constraints, summarised in Table 4. These include: (i) estimated binding energy of SN1987A; (ii) the measurement of the gravitational redshift in GRB 790305; (iii) the estimated baryonic mass of J0737−3039B; (iv) the measurements of the mass and radius of three transient LMXBs in globular clusters and three type I X-ray bursters; (v) the very low surface temperature inferred in the transiently accreting millisecond pulsar SAX J1808.4−3658, the soft X-ray transient 1H 1905+000, and the pulsar in CTA1, and the low luminosity from supernova remnants suggesting the occurrence of the dUrca process in NS cores; (vi) the measured mass of PSR J0348+0432; and (vii) the lower limit on the moment of inertia of the Crab pulsar from the kinetics of the expanding nebula. We note that except for the accurate measurement of the mass of PSR J0348+0432, the remaining constraints are more uncertain and model-dependent. Therefore, they should be treated with some skepticism. Having said that, it appears that the EoS based on BSk21 is the only EoS that is at least marginally compatible with all these constraints. The BSk21 EDF is also favoured by recent measurements of atomic masses (Chamel et al. 2011). Although the functional underlying the softest EoS based on the EDF BSk19 seems to be favoured by the analysis of heavy-ion collision experiments (Fuchs et al. 2001; Sturm et al. 2001; Hartnack et al. 2006; Xiao et al. 2009), the corresponding EoS appears to be ruled out by astrophysical observations. However, as discussed by Chamel et al. (2013), this apparent discrepancy could be easily resolved by considering the occurrence of a transition to an exotic phase in NS cores. It is, therefore, premature to rule out the BSk19 EDF and to conclude that the EoS of purely nucleonic matter has to be much stiffer than the EoS based on BSk19.

Table 4

Summary of astrophysical constraints for the unified Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF.

1

This definition is not unique, as discussed e.g. by Haensel et al. (2007) in Chapter 6.

2

We note that the second term on the right-hand side of Eq. (9.41) for Rneb in Haensel et al. (2007) should be written with a plus sign, as in Eq. (23) from Bejger & Haensel (2003).

Acknowledgments

The financial support of the F.R.S.-FNRS (Belgium) and the NSERC (Canada) is gratefully acknowledged. We would like to thank J. Novak & M. Bejger for fruitful discussions.

References

  1. Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
  2. Antoniadis, J., Freire, P. C. C., Wex, N., et al. 2013, Science, 340, 1233232 [Google Scholar]
  3. Audi, G., Wapstra, A. H., & Thibault, C. 2003, Nucl. Phys. A, 729, 337 [NASA ADS] [CrossRef] [Google Scholar]
  4. Barat, C., Hayles, R. I., Hurley, K., et al. 1983, A&A, 126, 400 [NASA ADS] [Google Scholar]
  5. Baym, G., Pethick, C., & Sutherland, P. 1971, ApJ, 170, 299 [Google Scholar]
  6. Bender, M., Heenen, P.-H., & Reinhard, P.-G. 2003, Rev. Mod. Phys., 75, 121 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bejger, M., & Haensel, P. 2003, A&A, 405, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bejger, M., Haensel, P., & Zdunik, J. L. 2007, A&A, 464, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bonazzola, S., Gourgoulhon, E., Salgado, M., & Marck, J.-A. 1993, A&A, 278, 421 [NASA ADS] [Google Scholar]
  10. Chabanat, E., Bonche, P., Haensel, P., Meyer, J., & Schaeffer, R. 1998a, Nucl. Phys. A, 635, 231 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chabanat, E., Bonche, P., Haensel, P., Meyer, J., & Schaeffer, R. 1998b, Nucl. Phys. A, 643, 441 [CrossRef] [Google Scholar]
  12. Chamel, N. 2010, Phys. Rev. C, 82, 061307 [NASA ADS] [CrossRef] [Google Scholar]
  13. Chamel, N., & Goriely, S. 2010, Phys. Rev. C, 82, 045804 [NASA ADS] [CrossRef] [Google Scholar]
  14. Chamel, N., & Haensel, P. 2008, Liv. Rev. Relativity 11, 10 [NASA ADS] [Google Scholar]
  15. Chamel, N., Naimi, S., Khan, E., & Margueron, J. 2007, Phys. Rev. C, 75, 055806 [NASA ADS] [CrossRef] [Google Scholar]
  16. Chamel, N., Goriely, S., & Pearson, J. M. 2009, Phys. Rev. C, 80, 065804 [NASA ADS] [CrossRef] [Google Scholar]
  17. Chamel, N., Fantina, A. F., Pearson, J. M., & Goriely, S. 2011, Phys. Rev. C, 84, 062802(R) [NASA ADS] [CrossRef] [Google Scholar]
  18. Chamel, N., Pavlov, R. L., Mihailov, L. M., et al. 2012, Phys. Rev. C, 86, 055804 [NASA ADS] [CrossRef] [Google Scholar]
  19. Chamel, N., Fantina, A. F., Pearson, J. M., & Goriely, S. 2013, A&A, 553, A22 [Google Scholar]
  20. Colò, G., van Giai, N., Meyer, J., Bennaceur, K., & Bonche, P. 2004, Phys. Rev. C, 70, 024307 [NASA ADS] [CrossRef] [Google Scholar]
  21. Cottam, J., Paerels, F., & Mendez, M. 2002, Nature, 420, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  22. Cottam, J., Paerels, F., Méndez, M., et al. 2008, ApJ, 672, 504 [NASA ADS] [CrossRef] [Google Scholar]
  23. Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., & Hessels, J. W. T. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  24. Dobaczewski, J., Stoitsov, M. V., & Nazarewicz, W. 2004, AIP Conf. Ser., 726, 51 [Google Scholar]
  25. Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Duncan, R. C. 1998, ApJ, 498, L45 [NASA ADS] [CrossRef] [Google Scholar]
  27. Espinoza, C. M., Lyne, A. G., Stappers, B. W., & Kramer, M. 2011, MNRAS, 414, 1679 [NASA ADS] [CrossRef] [Google Scholar]
  28. Fantina, A. F., Chamel, N., Pearson, J. M., & Goriely, S. 2012, Electromagnetic Radiation from Pulsars and Magnetars, ASP Conf. Ser., 466, 195 [NASA ADS] [Google Scholar]
  29. Fesen, R. A., Shull, J. M., & Hurford, A. P. 1997, AJ, 113, 354 [NASA ADS] [CrossRef] [Google Scholar]
  30. Friedman, B., & Pandharipande, V. R. 1981, Nucl. Phys. A, 361, 502 [NASA ADS] [CrossRef] [Google Scholar]
  31. Fuchs, C., Faessler, A., Zabrodin, E., & Zheng, Y.-M. 2001, Phys. Rev. Lett., 86, 1974 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  32. Gandolfi, S., Carlson, J., & Reddy, S. 2012, Phys. Rev. C, 85, 032801 [NASA ADS] [CrossRef] [Google Scholar]
  33. Glendenning, N. K. 2000, Compact stars: nuclear physics, particle physics, and general relativity, Astronomy and astrophysics library (Springer: New York) [Google Scholar]
  34. Goriely, S., Samyn, M., Bender, M., & Pearson, J. M. 2003, Phys. Rev. C, 68, 054325 [NASA ADS] [CrossRef] [Google Scholar]
  35. Goriely, S., Chamel, N., & Pearson, J. M. 2010, Phys. Rev. C, 82, 035804 [NASA ADS] [CrossRef] [Google Scholar]
  36. Goriely, S., Chamel, N., & Pearson, J. M. 2013, Phys. Rev. C, 88, 024308 [NASA ADS] [CrossRef] [Google Scholar]
  37. Gourgoulhon, E. 2010, lectures given at the Compstar 2010 School [arXiv:1003.5015v1] [Google Scholar]
  38. Gourgoulhon, E., Haensel, P., Livine, R., et al. 1999, A&A, 349, 851 [Google Scholar]
  39. Grandclément, P., & Novak, J. 2009, Liv. Rev. Relativity, 12, 1 [NASA ADS] [Google Scholar]
  40. Haensel, P., & Pichon, B. 1994, A&A, 283, 313 [NASA ADS] [Google Scholar]
  41. Haensel, P., Potekhin, A. Y., & Yakovlev, D. G. 2007, in Neutron Stars 1: Equation of State and Structure (New York: Springer), Astrophys. Space Sci. Lib., 326 [Google Scholar]
  42. Haensel, P., Zdunik, J. L., Bejger, M., & Lattimer, J. M. 2009, A&A, 502, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Hartnack, C., Oeschler, H., & Aichelin, J. 2006, Phys. Rev. Lett., 96, 012302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  44. Heinke, C. O., Jonker, P. G., Wijnands, R., Deloye, C. J., & Taam, R. E. 2009, ApJ, 691, 1035 [NASA ADS] [CrossRef] [Google Scholar]
  45. Hessels, J. W. T., Ransom, S. M., Stairs, I. H., et al. 2006, Science, 311, 1901 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  46. Higdon, J. C., & Lingenfelter, R. E. 1990, ARA&A, 28, 401 [NASA ADS] [CrossRef] [Google Scholar]
  47. Hillebrandt, W. 1982, A&A, 110, L3 [NASA ADS] [Google Scholar]
  48. Israel, G. L., Belloni, T., Stella, L., et al. 2005, ApJ, 628, L53 [NASA ADS] [CrossRef] [Google Scholar]
  49. Jonker, P. G., Steeghs, D., Chakrabarty, D., & Juett, A. M. 2007, ApJ, 665, L147 [NASA ADS] [CrossRef] [Google Scholar]
  50. Kaaret, P., Prieskorn, Z., in ’t Zand, J. J. M., et al. 2007, ApJ, 657, L97 [Google Scholar]
  51. Kaplan, D. L., Frail, D. A., Gaensler, B. M., et al. 2004, ApJS, 153, 269 [NASA ADS] [CrossRef] [Google Scholar]
  52. Kaplan, D. L., Gaensler, B. M., Kulkarni, S. R., & Slane, P. O. 2006, ApJS, 163, 344 [NASA ADS] [CrossRef] [Google Scholar]
  53. Kitaura, F. S., Janka, H.-T., & Hillebrandt, W. 2006, A&A, 450, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Klähn, T., Blaschke, D., Typel, S., et al. 2006, Phys. Rev. C, 74, 035802 [NASA ADS] [CrossRef] [Google Scholar]
  55. Kramer, M., Lorimer, D. R., Lyne, A. G., et al. 2005, 22nd Texas Symposium on Relativistic Astrophysics, 142 [Google Scholar]
  56. Kramer, M., Stairs, I. H., Manchester, R. N., et al. 2006, Science, 314, 97 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  57. Krastev, P. G., Li, B.-A., & Worley, A. 2008, ApJ, 676, 1170 [NASA ADS] [CrossRef] [Google Scholar]
  58. Lattimer, J. M. 2012, Ann. Rev. Nucl. Sc., 62, 485 [Google Scholar]
  59. Lattimer, J. M., & Schutz, B. F. 2005, ApJ, 629, 979 [NASA ADS] [CrossRef] [Google Scholar]
  60. Lattimer, J. M., Prakash, M., Pethick, C. J., & Haensel, P. 1991, Phys. Rev. Lett., 66, 2701 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  61. Li, Z. H., & Schulze, H.-J. 2008, Phys. Rev. C, 78, 028801 [NASA ADS] [CrossRef] [Google Scholar]
  62. Lin, J., Özel, F., Chakrabarty, D., & Psaltis, D. 2010, ApJ, 723, 1053 [NASA ADS] [CrossRef] [Google Scholar]
  63. Nomoto, K., Sugimoto, D., Sparks, W. M., et al. 1982, Nature, 299, 803 [NASA ADS] [CrossRef] [Google Scholar]
  64. Onsi, M., Dutta, A. K., Chatri, H., et al. 2008, Phys. Rev. C, 77, 065805 [Google Scholar]
  65. Oyamatsu, K., & Yamada, M. 1994, Nucl. Phys. A, 578, 181 [NASA ADS] [CrossRef] [Google Scholar]
  66. Page, D., & Reddy, S. 2006, Annu. Rev. Nucl. Part. Sci., 56, 327 [Google Scholar]
  67. Page, D., Lattimer, J. M., Prakash, M., & Steiner, A. W. 2009, ApJ, 707, 1131 [NASA ADS] [CrossRef] [Google Scholar]
  68. Pearson, J. M., Goriely, S., & Chamel, N. 2011, Phys. Rev. C, 83, 065810 [NASA ADS] [CrossRef] [Google Scholar]
  69. Pearson, J. M., Chamel, N., Goriely, S., & Ducoin, C. 2012, Phys. Rev. C, 85, 065803 [NASA ADS] [CrossRef] [Google Scholar]
  70. Piro, A. L. 2005, ApJ, 634, L153 [NASA ADS] [CrossRef] [Google Scholar]
  71. Podsiadlowski, P., Langer, N., Poelarends, A. J. T., et al. 2004, ApJ, 612, 1044 [NASA ADS] [CrossRef] [Google Scholar]
  72. Podsiadlowski, P., Dewi, J. D. M., Lesaffre, P., et al. 2005, MNRAS, 361, 1243 [NASA ADS] [CrossRef] [Google Scholar]
  73. Shternin, P. S., & Yakovlev, D. G. 2008, Astron. Lett., 34, 675 [NASA ADS] [CrossRef] [Google Scholar]
  74. Steiner, A. W., Lattimer, J. M., & Brown, E. F. 2010, ApJ, 722, 33 [NASA ADS] [CrossRef] [Google Scholar]
  75. Stergioulas, N. 2003, Liv. Rev. Relativity, 6, 3 [Google Scholar]
  76. Stone, J. R., & Reinhard, P.-G. 2007, Prog. Part. Nucl. Phys., 58, 587 [NASA ADS] [CrossRef] [Google Scholar]
  77. Strohmayer, T. E., & Watts, A. L. 2005, ApJ, 632, L111 [NASA ADS] [CrossRef] [Google Scholar]
  78. Strohmayer, T. E., & Watts, A. L. 2006, ApJ, 653, 593 [NASA ADS] [CrossRef] [Google Scholar]
  79. Sturm, C., Böttcher, I., Dȩbowski, M., et al. 2001, Phys. Rev. Lett., 86, 39 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
  80. Tsang, M. B., Stone, J. R., Camera, F., et al. 2012, Phys. Rev. C, 86, 015803 [NASA ADS] [CrossRef] [Google Scholar]
  81. van den Heuvel, E. P. J. 2004, 5th INTEGRAL Workshop on the INTEGRAL Universe, 552, 185 [Google Scholar]
  82. Watts, A. L. 2012, Neutron starquakes and the dynamic crust in Neutron Star Crust, eds. C. Bertulani, & J. Piekarewicz (Nova Science Publishers) [Google Scholar]
  83. Watts, A. L., & Strohmayer, T. E. 2006, ApJ, 637, L117 [NASA ADS] [CrossRef] [Google Scholar]
  84. Weber, F., Negreiros, R., Rosenfield, P., & Stejner, M. 2007, Prog. Part. Nucl. Phys., 59, 94 [NASA ADS] [CrossRef] [Google Scholar]
  85. Wieser, M. E., Holden, N., Copler, T. B., et al. 2013, Pure Appl. Chem., 85, 1047 [CrossRef] [Google Scholar]
  86. Wiringa, R. B., Fiks, V., & Fabrocini, A. 1988, Phys. Rev. C, 38, 1010 [NASA ADS] [CrossRef] [Google Scholar]
  87. Worley, A., Krastev, P. G., & Li, B.-A. 2008, ApJ, 685, 390 [NASA ADS] [CrossRef] [Google Scholar]
  88. Xiao, Z., Li, B.-A., Chen, L.-W., Yong, G.-C., & Zhang, M. 2009, Phys. Rev. Lett., 102, 062502 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  89. Yakovlev, D. G., & Pethick, C. J. 2004, ARA&A, 42, 169 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]

All Tables

Table 1

Global properties of non-rotating NSs for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF.

In the text
Table 2

Global properties of NSs rotating at rotational frequency ν = 716 Hz for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF.

In the text
Table 3

Global structure of the most massive and rapidly rotating NSs for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF.

In the text
Table 4

Summary of astrophysical constraints for the unified Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF.

In the text

All Figures

thumbnail Fig. 1

Neutron-matter energy per particle as a function of baryon number density for the EDFs BSk19-20-21. For comparison, we show the calculations by Gandolfi et al. (2012, shaded area).
In the text
thumbnail Fig. 2

Binding energy versus NS mass for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF. The shaded area corresponds to the constraint inferred from the neutrino detection of SN1987A.
In the text
thumbnail Fig. 3

Gravitational redshift at the surface of a NS as a function of the NS mass for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF. The shaded area is excluded by general relativity and causality (Haensel et al. 2007). The horizontal band bounded by dashed lines indicates the range of redshifts inferred from the spectroscopic analysis of the gamma-ray burst GRB 790305 (Higdon & Lingenfelter 1990).

In the text
thumbnail Fig. 4

Gravitational mass M of non-rotating NSs versus baryonic mass Mb for the unified Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF. The filled and empty rectangles indicate the constraints inferred from the assumption that pulsar J0737–3039B was formed in an electron-capture supernova as obtained by Kitaura et al. (2006) and by Podsiadlowski et al. (2005), respectively.

In the text
thumbnail Fig. 5

Mass-radius relation of NSs for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF. The dark (light) shaded regions correspond to the 1σ (2σ) probability distributions implied by observations of transient LMXBs in globular clusters and type I X-ray bursters, as shown in the upper right panel of Fig. 9 of Steiner et al. (2010).
In the text
thumbnail Fig. 6

Gravitational mass of non-rotating NSs versus central baryon number density for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF. The horizontal band corresponds to the measurement of the mass of PSR J0348+0432 (Antoniadis et al. 2013).
In the text
thumbnail Fig. 7

Gravitational mass versus circumferential radius relation for non-rotating and rigidly rotating NSs for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21. The horizontal band corresponds to the measurement of the mass of PSR J0348+0432 (Antoniadis et al. 2013). The dashed line represents the mass-shedding limit for PSR J1748−2446ad (Hessels et al. 2006). The shaded area in the top left-hand corner, delimited by R > 2.9GM/c2, is excluded by causality (Glendenning 2000).
In the text
thumbnail Fig. 8

Keplerian frequency versus gravitational mass for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF. The horizontal dashed lines correspond to the rotational frequency of PSR J1748−2446ad (Hessels et al. 2006) and the claimed rotational frequency of XTE J1739−285 (Kaaret et al. 2007).
In the text
thumbnail Fig. 9

Gravitational mass versus circumferential radius for static and rigidly rotating NSs at rotational frequencies of 716 Hz, 1122 Hz, and at the Keplerian frequency, for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21.
In the text
thumbnail Fig. 10

Gravitational mass versus circumferential radius for slowly rigidly rotating NSs (with the same period as that of the Crab pulsar) for the Brussels-Montreal EoSs based on the EDFs BSk19-20-21, and for the SLy EoS based on the SLy4 EDF. The thick dashed lines labelled by 2.8 M⊙, 4.6 M⊙, and 6.4 M⊙ correspond to the constraint in Eq. (6) (see text for details); the region below each line is excluded. The shaded area in the top left-hand corner, delimited by R > 2.9GM/c2, is excluded by causality (Glendenning 2000).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.