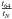| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 12 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201321499 | |
| Published online | 18 November 2013 | |
Radiation hydrodynamics integrated in the PLUTO code
1
Institute for Astronomy and Astrophysics, Section Computational
Physics, Eberhard Karls Universität Tübingen, Auf der Morgenstelle 10, 72076
Tübingen,
Germany
e-mail: kolb.stefan@gmail.com;
matthias.stute@uni-tuebingen.de; wilhelm.kley@uni-tuebingen.de
2
Dipartimento di Fisica, Università degli Studi di
Torino, via Pietro Giuria
1, 10125
Torino,
Italy
Received:
18
March
2013
Accepted:
6
September
2013
Aims. The transport of energy through radiation is very important in many astrophysical phenomena. In dynamical problems the time-dependent equations of radiation hydrodynamics have to be solved. We present a newly developed radiation-hydrodynamics module specifically designed for the versatile magnetohydrodynamic (MHD) code PLUTO.
Methods. The solver is based on the flux-limited diffusion approximation in the two-temperature approach. All equations are solved in the co-moving frame in the frequency-independent (gray) approximation. The hydrodynamics is solved by the different Godunov schemes implemented in PLUTO, and for the radiation transport we use a fully implicit scheme. The resulting system of linear equations is solved either using the successive over-relaxation (SOR) method (for testing purposes) or using matrix solvers that are available in the PETSc library. We state in detail the methodology and describe several test cases to verify the correctness of our implementation. The solver works in standard coordinate systems, such as Cartesian, cylindrical, and spherical, and also for non-equidistant grids.
Results. We present a new radiation-hydrodynamics solver coupled to the MHD-code PLUTO that is a modern, versatile, and efficient new module for treating complex radiation hydrodynamical problems in astrophysics. As test cases, either purely radiative situations, or full radiation-hydrodynamical setups (including radiative shocks and convection in accretion disks) were successfully studied. The new module scales very well on parallel computers using MPI. For problems in star or planet formation, we added the possibility of irradiation by a central source.
Key words: radiative transfer / hydrodynamics / accretion, accretion disks
© ESO, 2013
1. Introduction
Radiative effects play a very important role in nearly all astrophysical fluid flows, ranging from planet and star formation to the largest structures in the Universe. Coupling the equations of radiation transport to those of (magneto-)hydrodynamics (MHD) has been studied for decades, and comprehensive treatments can be found for example in textbooks by Mihalas & Mihalas (1984) or Pomraning (1973). The numerical implementation of two-temperature radiation hydrodynamics (in the diffusion approximation) into multi-dimensional MHD/HD-codes has been made over twenty years ago in various implementations, for example by Eggum et al. (1988), Kley (1989), in the ZEUS-code (Stone et al. 1992), and more recently by Turner & Stone (2001).
To study the dynamics and characteristics of stellar atmospheres together with convection, for example, more accurate solvers for the radiation transport based on the method of short characteristics have been developed, see Davis et al. (2012) and Freytag et al. (2012) for the current status. This can then be coupled to the hydrodynamics using the Variable Eddington Tensor method (Jiang et al. 2012). Another approach is the M1 closure model where the radiative moment equations are closed at a higher level (González et al. 2007; Aubert & Teyssier 2008). Despite this progress, it is still useful and desirable to have a method at hand that solves the interaction of matter and radiation primarily within the bulk part of the matter, which may be optically thick. In this type of applications, the method of flux-limited diffusion (FLD, see Levermore & Pomraning 1981) has its clear merits and is still implemented into existing MHD-codes, for example in NIRVANA (Kley et al. 2009) to study the planet formation process, in RAMSES (Commerçon et al. 2011) for protostellar collapse simulations, and in combination with a multi-frequency irradiation tool into PLUTO (Kuiper et al. 2010) for massive star formation.
Since the 3D-MHD code PLUTO (Mignone et al. 2007) is becoming increasingly popular within the astrophysics community, we added a publicly available radiation module that is based on the two-temperature FLD-approximation, as described by Commerçon et al. (2011). PLUTO solves the equations of hydrodynamics and magnetohydrodynamics including the non-ideal effects of viscosity, thermal conduction, and resistivity by means of shock-capturing Godunov-type methods. Several Riemann solvers, time-stepping methods and interpolation schemes can be chosen. Additionally, we added a ray-tracing routine that allows for additional irradiation by a point source in the center. Treating the irradiation in a ray-tracing approach guarantees the long-range character of the radiation better than FLD (Kuiper et al. 2012; Kuiper & Klessen 2013).
The paper is organized as follows. In Sect. 2.1, we briefly introduce the equations of hydrodynamics including radiation transport. Additionally, we describe the general idea behind the flux-limited diffusion approximation. In Sect. 3, we present the discretization of the equations, the solver of the resulting matrix equation, and our numerical implementation of irradiation. In Sect. 4, we present six different test cases to show the correctness of the implemented equations: four test cases with an analytical solution (Sects. 4.1 to 4.4) and two others in which our results are compared with those from other codes (Sects. 4.5 and 4.6). We conclude with a summary and conclusions.
2. Radiation hydrodynamics
2.1. Equations
Even though the PLUTO-environment includes the full MHD-equations and nonideal effects
such as viscosity, we restrict ourselves here to the Euler equations of ideal
hydrodynamics. Radiation effects are included in the two-temperature approximation, which
implies an additional equation for the radiation energy. To follow the transport of
radiation, we applied the flux-limited diffusion approximation and treated the exchange of
energy and momentum between the gas and the radiation field with additional terms in the
gas momentum and energy equations. The system of equations then reads ![\begin{eqnarray} \label{eqn:continuity_equation} &&\pdl{\rho}{t} + \nabla \cdot (\rho \vec{v}) = 0 \\ \label{eqn:momentum_equation_coupled} &&\pdl{\rho \vec{v}}{t}+\nabla \cdot \left(\rho \vec{v} \otimes \vec{v}\right) + \nabla p = +~ \rho (\accExt + \accRad) \\ \label{eqn:gas_energy_equation_coupled} &&\pdl{e}{t}+\nabla\cdot\left[\left(e + p\right)\vec{v}\right] = +~ \rho \vec{v} \cdot (\accExt + \accRad) \\ &&\phantom{\pdl{e}{t}+\nabla\cdot\left[\left(e + p\right)\vec{v}\right]=}\hspace{3pt} -\kappa_\mathrm{P} \rho c ( a_\mathrm{R} T^4 - E) \nonumber \\ \label{eqn:radiation_energy_equation_coupled} &&\pdl{E}{t} + \nabla \cdot \vec{F} = \kappa_\mathrm{P}\rho c \left( a_\mathrm{R} T^4 - E\right) . \end{eqnarray}](/articles/aa/full_html/2013/11/aa21499-13/aa21499-13-eq2.png) The first three Eqs. ((1)–(3)) describe the evolution of the gas motion, where ρ is the
gas density, p the thermal pressure, v the velocity,
e = ρ ϵ + 1/2 ρ v2
the total energy density (i.e., the sum of internal and kinetic) of the gas without
radiation, and aext an acceleration caused by external forces
(e.g. gravity), not induced by the radiation field (see below). This system of equations
is closed by the ideal gas relation
The first three Eqs. ((1)–(3)) describe the evolution of the gas motion, where ρ is the
gas density, p the thermal pressure, v the velocity,
e = ρ ϵ + 1/2 ρ v2
the total energy density (i.e., the sum of internal and kinetic) of the gas without
radiation, and aext an acceleration caused by external forces
(e.g. gravity), not induced by the radiation field (see below). This system of equations
is closed by the ideal gas relation 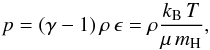 (5)where γ is the ratio of
specific heats, T the gas temperature, kB the
Boltzmann constant, μ the mean molecular weight, and
mH the mass of hydrogen. The specific internal energy can be
written as ϵ = cV T, with
the specific heat capacity given by
(5)where γ is the ratio of
specific heats, T the gas temperature, kB the
Boltzmann constant, μ the mean molecular weight, and
mH the mass of hydrogen. The specific internal energy can be
written as ϵ = cV T, with
the specific heat capacity given by 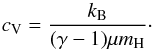 (6)Here, we assumed constant γ
and μ, which also implies a constant cV.
(6)Here, we assumed constant γ
and μ, which also implies a constant cV.
The evolution of the radiation energy density E is given by Eq. (4), where F denotes the radiative
flux, κP the Planck mean opacity, c the speed
of light, and aR the radiation constant. The fluid is
influenced by the radiation in two different ways. First, the radiation may be absorbed or
emitted by the fluid, leading to variation of its energy density. This variation is given
by the expression 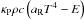 , see the right-hand side of Eqs. (3)and (4). The second effect is that of radiation pressure. We included this term as an
additional acceleration to the momentum equation,
, see the right-hand side of Eqs. (3)and (4). The second effect is that of radiation pressure. We included this term as an
additional acceleration to the momentum equation, 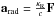 . The present implementation does not
include the advective transport terms for the radiation energy and radiative pressure work
in Eqs. (3)and (4). For the relatively low temperature
protoplanetary disk application that we consider here, these terms are of minor
importance. If required, these terms can be treated in our implementation
straightforwardly within PLUTO by adding source terms.
. The present implementation does not
include the advective transport terms for the radiation energy and radiative pressure work
in Eqs. (3)and (4). For the relatively low temperature
protoplanetary disk application that we consider here, these terms are of minor
importance. If required, these terms can be treated in our implementation
straightforwardly within PLUTO by adding source terms.
2.2. Flux-limited diffusion approximation
The system of equations shown cannot be solved without additional assumptions for the
radiative flux F. Here we used the flux-limited diffusion approximation (FLD)
where the radiation flux is given by a diffusion approximation 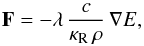 (7)with the Rosseland mean opacity
κR. The flux-limiter λ describes
approximately the transition from very optically thick regions with
λ = 1/3 to optically thin regimes, where
(7)with the Rosseland mean opacity
κR. The flux-limiter λ describes
approximately the transition from very optically thick regions with
λ = 1/3 to optically thin regimes, where
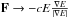 . This leads to the formal definition of
the flux-limiter, which is a function of the dimensionless quantity
. This leads to the formal definition of
the flux-limiter, which is a function of the dimensionless quantity 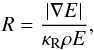 (8)with the following behavior:
(8)with the following behavior: ![\begin{equation} \lambda(R) = \left\{\begin{array}{ll}\frac{1}{3}, & R \to 0 \\[2mm] \frac{1}{R}, & R \to \infty. \end{array}\right. \label{eqn:fluxlimiter_limits} \end{equation}](/articles/aa/full_html/2013/11/aa21499-13/aa21499-13-eq30.png) (9)Physically sensitive flux-limiters thus have
to fulfill the Eq. (9)in the given limits
and describe the behavior between the limits approximately. We implemented three different
flux-limiters:
(9)Physically sensitive flux-limiters thus have
to fulfill the Eq. (9)in the given limits
and describe the behavior between the limits approximately. We implemented three different
flux-limiters: 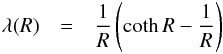 (10)
(10)![\begin{eqnarray} \label{eqn:fluxlimiter_minerbo} \lambda(R) &=& \left\{ \begin{array}{l l} \dfrac{2}{3 + \sqrt{9+12 R^2}} & \quad 0 \leq R \leq \dfrac{3}{2}\\[3mm] \dfrac{1}{1+R+\sqrt{1+2R}} & \quad \dfrac{3}{2} < R \leq \infty\\ \end{array} \right. \end{eqnarray}](/articles/aa/full_html/2013/11/aa21499-13/aa21499-13-eq32.png) (11)
(11)![\begin{eqnarray} \label{eqn:fluxlimiter_kley} \lambda(R) &=& \left\{ \begin{array}{l l} \dfrac{2}{3 + \sqrt{9+10 R^2}} & \quad 0 \leq R \leq 2\\[3mm] \dfrac{10}{10 R+ 9 + \sqrt{180 R + 81}} & \quad 2 < R \leq \infty\\ \end{array} \right. \end{eqnarray}](/articles/aa/full_html/2013/11/aa21499-13/aa21499-13-eq33.png) (12)from Levermore & Pomraning (1981), Minerbo
(1978), and Kley (1989), respectively. A
comparison of them is presented in Kley (1989).
(12)from Levermore & Pomraning (1981), Minerbo
(1978), and Kley (1989), respectively. A
comparison of them is presented in Kley (1989).
In general, it is necessary to solve the equations for each frequency that appears in the physical problem. However, here we used the gray approximation in which all radiative quantities including the opacities are integrated over all frequencies. Scattering is not accounted for directly in our treatment, but it is included in the effective isotropic absorption and emission coefficients.
3. Solving the radiation part
3.1. Reformulation of the equations
Instead of solving the system of Eqs. ((1)–(4)) directly as a whole, the problem is split into two steps. In the first step, PLUTO is used to solve the equations of fluid dynamics with the additional force caused by the radiation. This corresponds to Eqs. (1)to (3)with the additional acceleration, arad, but without the interaction term between the matter and radiation (last term in Eq. (3)). By using PLUTO for solving the non-radiative part of the equations, we are not limited to the Euler equations, but are able to use the full capabilities of PLUTO for solving the equations of hydrodynamics or magnetohydrodynamics, including the effects of viscosity and magnetic resistivity.
In a second additional step the radiation energy Eq. (4)is solved together with the corresponding heating-cooling term in the
internal energy of the fluid 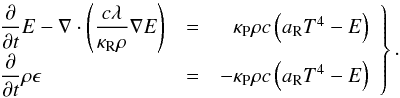 (13)To obtain the radiation energy density, the
system of coupled Eq. (13)is solved.
Within one time step PLUTO advances the hydrodynamical quantities, that is, the density
ρ, the velocity v, and a temporary pressure
p from time tn to time
tn + 1, where the time step,
Δt = tn + 1−tn,
is determined by PLUTO using the CFL conditions, currently without the radiation pressure.
These depend on the used time-stepping method in PLUTO; for more information see Mignone et al. (2007) and the userguide of PLUTO.
(13)To obtain the radiation energy density, the
system of coupled Eq. (13)is solved.
Within one time step PLUTO advances the hydrodynamical quantities, that is, the density
ρ, the velocity v, and a temporary pressure
p from time tn to time
tn + 1, where the time step,
Δt = tn + 1−tn,
is determined by PLUTO using the CFL conditions, currently without the radiation pressure.
These depend on the used time-stepping method in PLUTO; for more information see Mignone et al. (2007) and the userguide of PLUTO.
The physical process of radiation transport takes place on timescales much shorter than the one in hydrodynamics. To use the same time step for hydrodynamics and the radiation transport, we applied an implicit scheme to handle the radiation diffusion and the coupling between matter and radiation described by Eq. (13). Because of the coupling of the equations, the method updates T and E simultaneously, which formally leads to a nonlinear set of coupled equations. As outlined below, the system is solved for the radiation energy density E. From the new values for E, the new fluid temperature (see Eq. (17) below) is computed and the fluid pressure is updated by using the ideal gas relation from Eq. (5). This is then used within PLUTO to calculate a new total gas energy e.
3.2. Discretization
To discretize the Eqs. (13), we applied a
finite-volume method. For that purpose we integrated over the volume of a grid cell and
transformed the divergence into a surface integral. Furthermore, we replaced the gradient
of E by finite differences and applied an implicit scheme. The
discretization scheme was implemented in 3D for Cartesian, cylindrical, and spherical
polar coordinates including all the necessary geometry terms for the divergence and
gradient. Since the density has been updated already in the hydrodynamical part of the
solver, we can replace 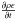 with
with
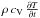 , which is valid for a constant heat
capacity. Then the resulting discretized equations for the radiative part can be written
as
, which is valid for a constant heat
capacity. Then the resulting discretized equations for the radiative part can be written
as 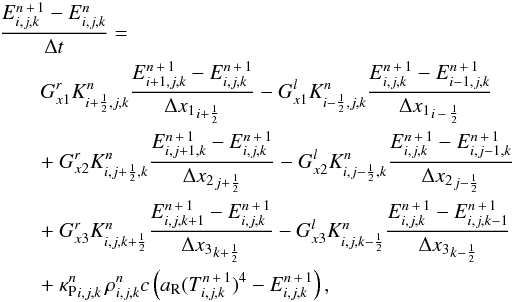 (14)and for the thermal energy (or temperature,
respectively)
(14)and for the thermal energy (or temperature,
respectively)  (15)Here, the superscript n
refers to the values of all variables after the most recent update from the hydrodynamical
step. To simplify the notation for the separate radiation module, it is assumed that the
update takes place from time n to n + 1. The subscripts
i,j,k refer to the three spatial directions of the computational grid,
where all variables are located at the cell centers. Half-integer indices refer to cell
interfaces. The physical sizes (proper length) of each cell in the three spatial
directions m (m = 1,2,3) are given by
Δxm, where we additionally allowed for
non-equidistant grids. The effective radiative diffusion coefficient (defined at cell
centers) is given by
(15)Here, the superscript n
refers to the values of all variables after the most recent update from the hydrodynamical
step. To simplify the notation for the separate radiation module, it is assumed that the
update takes place from time n to n + 1. The subscripts
i,j,k refer to the three spatial directions of the computational grid,
where all variables are located at the cell centers. Half-integer indices refer to cell
interfaces. The physical sizes (proper length) of each cell in the three spatial
directions m (m = 1,2,3) are given by
Δxm, where we additionally allowed for
non-equidistant grids. The effective radiative diffusion coefficient (defined at cell
centers) is given by 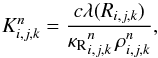 where
Ri,j,k is calculated from Eq. (8)by central differencing. Values at cell
interfaces are obtained by linear interpolation. The factors
where
Ri,j,k is calculated from Eq. (8)by central differencing. Values at cell
interfaces are obtained by linear interpolation. The factors
 are geometrical terms defined,
respectively, as the left and right surface areas divided by the cell volume in the
direction given by m = 1,2,3. In the recent work by Bitsch et al. (2013b) the difference equations have been written out in
more detail for Cartesian equidistant grids. The required opacities are evaluated using
the values of ρ and T after the hydrodynamical update at
time tn.
are geometrical terms defined,
respectively, as the left and right surface areas divided by the cell volume in the
direction given by m = 1,2,3. In the recent work by Bitsch et al. (2013b) the difference equations have been written out in
more detail for Cartesian equidistant grids. The required opacities are evaluated using
the values of ρ and T after the hydrodynamical update at
time tn.
As mentioned before, Eqs. (13)constitute
a set of coupled nonlinear equations. The nonlinear term
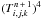 that appears in Eq. (15)is linearized using the method outlined in
Commerçon et al. (2011),
that appears in Eq. (15)is linearized using the method outlined in
Commerçon et al. (2011),
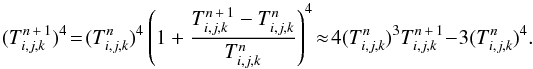 (16)Using this approximation, we obtained an
equation for computing the new temperature in terms of the new radiation energy density,
(16)Using this approximation, we obtained an
equation for computing the new temperature in terms of the new radiation energy density,
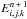 , and the old temperatures,
, and the old temperatures,
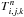
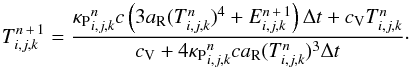 (17)The expression can be substituted into Eq.
(14)to obtain a linear system of
equations for the new radiation energies
(17)The expression can be substituted into Eq.
(14)to obtain a linear system of
equations for the new radiation energies 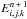 , which can be solved using standard matrix
solvers, see Sect. 3.4. The new temperature can then
be calculated from Eq. (17). We
implemented several boundary conditions for the radiation energy density including
periodic, symmetric, and fixed values.
, which can be solved using standard matrix
solvers, see Sect. 3.4. The new temperature can then
be calculated from Eq. (17). We
implemented several boundary conditions for the radiation energy density including
periodic, symmetric, and fixed values.
3.3. Irradiation
To couple possible irradiation to the radiation transport equations, a new source term,
S, has to be added to the right-hand side of the thermal energy
equation in system (13)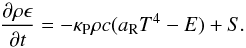 (18)This results in an additional term,
Si,j,k/(ρi,j,kcV),
in Eq. (15), correspondingly in Eq. (17), and in a modification of the right-hand
side of the resulting matrix equation for
(18)This results in an additional term,
Si,j,k/(ρi,j,kcV),
in Eq. (15), correspondingly in Eq. (17), and in a modification of the right-hand
side of the resulting matrix equation for 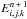 .
.
For the present implementation, we assumed that the irradiating source is located at the
center of a spherical coordinate system. Therefore it is straightforward to compute the
optical depth τi,j,k even for simulations
using parallel computers. Assuming that a ray of light travels along the radial direction
from the origin to the grid cell i,j,k under consideration, the optical
depth from the inner radius r0 to the ith
grid cell with radius ri can be simply
expressed as the integral along the radial coordinate, 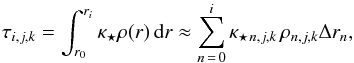 (19)where
Δrn is the radial length of the
nth grid cell, and κ⋆ the
opacity used for irradiation. For the sake of readability, we write
τi instead of
τi,j,k in the following. We used
κ⋆ = κP in the
test case with irradiation as presented in Sect. 4.3. Additionally, κ⋆ can be defined
by the user, as can the other opacities. Re-emission of the photons that were absorbed in
the cell volume is handled in our treatment by the heating-cooling term, see Eq. (13).
(19)where
Δrn is the radial length of the
nth grid cell, and κ⋆ the
opacity used for irradiation. For the sake of readability, we write
τi instead of
τi,j,k in the following. We used
κ⋆ = κP in the
test case with irradiation as presented in Sect. 4.3. Additionally, κ⋆ can be defined
by the user, as can the other opacities. Re-emission of the photons that were absorbed in
the cell volume is handled in our treatment by the heating-cooling term, see Eq. (13).
The luminosity of the source is given by
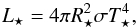 (20)where σ denotes the
Stefan-Boltzmann constant, T⋆ is the
temperature of the star, and R⋆ its radius.
To compute the amount of irradiated energy that is absorbed by a specific grid cell we
have to know the surface area A of a grid cell oriented perpendicular to
the radiation from the star and the flux f at the radius
r. This surface area A is given by the expression
(20)where σ denotes the
Stefan-Boltzmann constant, T⋆ is the
temperature of the star, and R⋆ its radius.
To compute the amount of irradiated energy that is absorbed by a specific grid cell we
have to know the surface area A of a grid cell oriented perpendicular to
the radiation from the star and the flux f at the radius
r. This surface area A is given by the expression
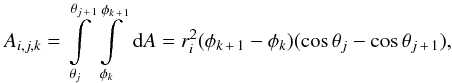 (21)where θ is the azimuthal and
φ the polar angle in the spherical coordinate system. Without
absorption, the flux f is given by the expression
(21)where θ is the azimuthal and
φ the polar angle in the spherical coordinate system. Without
absorption, the flux f is given by the expression
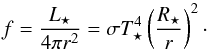 (22)The amount of energy per time that arrives at
the surface of the grid cell (i,j,k) is
(22)The amount of energy per time that arrives at
the surface of the grid cell (i,j,k) is
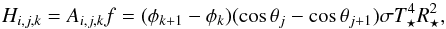 (23)again without absorption. If the irradiated
energy is partly absorbed, the remaining amount of energy per time is then
Hi,j,ke−τi,j,k.
Using these results, we can compute the energy density per time, S, that
is absorbed by one grid cell (i,j,k)
(23)again without absorption. If the irradiated
energy is partly absorbed, the remaining amount of energy per time is then
Hi,j,ke−τi,j,k.
Using these results, we can compute the energy density per time, S, that
is absorbed by one grid cell (i,j,k) 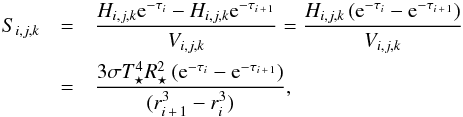 (24)with the volume of a grid cell
(24)with the volume of a grid cell
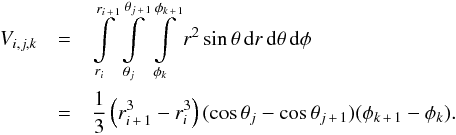 (25)The absorbed energy density per time,
Si,j,k, is computed for each grid cell
before solving the matrix equation. A similar treatment of irradiation has been described
recently by Bitsch et al. (2013b), for a
multi-frequency implementation see Kuiper et al.
(2010).
(25)The absorbed energy density per time,
Si,j,k, is computed for each grid cell
before solving the matrix equation. A similar treatment of irradiation has been described
recently by Bitsch et al. (2013b), for a
multi-frequency implementation see Kuiper et al.
(2010).
3.4. Matrix solver
We implemented two different solvers for the matrix equation. The first one uses the
method of successive over-relaxation (SOR), and as a faster and more flexible solver the
PETSc1 library is used. From the PETSc library the
Krylov subspace iterative method and a preconditioner is used to solve the matrix
equation. For all test cases described we used gmres (generalized minimal residual) as
iterative method and bjacobi (block Jacobi) as preconditioner. Among others, the
convergence of the SOR algorithm and the PETSc library can be estimated using the
following criteria: 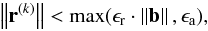 (26)where b is the right-hand side
of the matrix equation Ax = b,
r(k) = b−Ax(k)
is the residual vector for the kth iteration of the solver and
x is the solution vector (here the radiation energy density). As the norm
we used the L2 norm here. The quantities
ϵr and ϵa are the relative and
absolute tolerance, respectively, and are problem dependent, with a common value of
10-50 for ϵa. For the test cases in Sect. 4 we used relative tolerances
ϵr between 10-5 and 10-8. The
criterion (26)is the default one used by
the PETSc library. For more information about the convergence test in PETSc we refer to
Sect. 4.3.2. of Balay et al. (2012). The solver
performance in a parallel environment is described in Sect. 4.6.4.
(26)where b is the right-hand side
of the matrix equation Ax = b,
r(k) = b−Ax(k)
is the residual vector for the kth iteration of the solver and
x is the solution vector (here the radiation energy density). As the norm
we used the L2 norm here. The quantities
ϵr and ϵa are the relative and
absolute tolerance, respectively, and are problem dependent, with a common value of
10-50 for ϵa. For the test cases in Sect. 4 we used relative tolerances
ϵr between 10-5 and 10-8. The
criterion (26)is the default one used by
the PETSc library. For more information about the convergence test in PETSc we refer to
Sect. 4.3.2. of Balay et al. (2012). The solver
performance in a parallel environment is described in Sect. 4.6.4.
4. Test cases
To verify the implemented method, we simulated several test problems and compared the results with either corresponding analytical solutions or calculations made with different numerical codes. Most of the tests correspond to one-dimensional problems. To model these, we used quasi-one-dimensional domains, with a very long cuboid with the height h, width w, and length l. The length l is much longer than the width or height, and for simplicity we used w = h. We performed some of the tests in all three implemented coordinate systems (Cartesian, cylindrical, and spherical) and in three different alignments of the cuboid along each coordinate direction. This was made to check whether the geometry factors are correct. For a non-Cartesian coordinate system we placed the cuboid at large distances r from the origin such that the domain approximately describes a Cartesian setup.
We used the solver based on the PETSc library for all test cases with the default iterative solver gmres and the pre-conditioner bjacobi.
4.1. Linear diffusion test
The following test was adapted from Commerçon et al.
(2011). The initial profile of the radiation energy density was set to a delta
function that was evolved in time and compared with the analytical one-dimensional
solution. We performed this test in all implemented coordinate systems (Cartesian,
cylindrical, and spherical coordinates) as described above, which resulted in nine
different simulations. The used domain is quasi-one-dimensional and the equations of
hydrodynamics are not solved in this test. Only the radiation diffusion equation
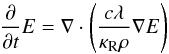 (27)is solved, which we obtained from Eqs. (13)by setting
κP = 0. An analytical solution to Eq. (27)can be calculated in the one-dimensional
case with a constant flux-limiter
(27)is solved, which we obtained from Eqs. (13)by setting
κP = 0. An analytical solution to Eq. (27)can be calculated in the one-dimensional
case with a constant flux-limiter 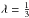 and a constant product of the Rosseland
opacity and density, here we set . The equation to solve is then given by
and a constant product of the Rosseland
opacity and density, here we set . The equation to solve is then given by 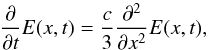 (28)with the solution
(28)with the solution 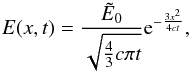 (29)where
(29)where 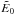 is the integral over the initial profile
of the energy density, E(x,t = 0). Note that in the
quasi-one-dimensional case (using a stretched three-dimensional domain)
is the integral over the initial profile
of the energy density, E(x,t = 0). Note that in the
quasi-one-dimensional case (using a stretched three-dimensional domain)
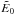 has the unit .
has the unit .
4.1.1. Setup
The domain is a cuboid with a length of and a width and height of . We used here
301 × 3 × 3 grid cells. The initial profile of the radiation energy density in the quasi
one-dimensional case is set by ![\begin{equation} E_i =\begin{cases} 1{\dfrac{erg}{cm^3}}, & i = 1,2,\dots,N \text{ with } i\neq \dfrac{N}{2}\\[4mm] \hspace{10pt}\dfrac{\tilde{E}_0}{\Delta x},& i = \dfrac{N}{2}\\ \end{cases} , \end{equation}](/articles/aa/full_html/2013/11/aa21499-13/aa21499-13-eq117.png) (30)where Δx is the length of
a grid cell. For numerical reasons, we set
Ei for
(30)where Δx is the length of
a grid cell. For numerical reasons, we set
Ei for
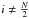 to the value instead of . This choice is
not problematic, since for our chosen value of . The initial values for pressure and
density are and . Furthermore, we used for the Rosseland opacity. All boundary
conditions were set to periodic except for the boundary conditions at the beginning and
end of the quasi-one-dimensional domain, which were set to outflow. For the matrix
solver we used a relative tolerance of
ϵr = 10-8. The simulation
started at with a constant time step of and stopped at .
to the value instead of . This choice is
not problematic, since for our chosen value of . The initial values for pressure and
density are and . Furthermore, we used for the Rosseland opacity. All boundary
conditions were set to periodic except for the boundary conditions at the beginning and
end of the quasi-one-dimensional domain, which were set to outflow. For the matrix
solver we used a relative tolerance of
ϵr = 10-8. The simulation
started at with a constant time step of and stopped at .
 |
Fig. 1 Linear diffusion test at time . The simulated (read dots) and the analytical (black line) solutions are plotted. We also plot the solution with the absolute value of the relative error (blue dashed line) that belongs to the axis on the right. |
 |
Fig. 2 Time evolution for the linear diffusion test from time to at three different positions: at (black lines), at (blue lines) and at (red lines). The dotted lines for each position belong to the simulated solution, the solid lines to the analytical solution, and the dashed lines show the relative error that belongs to the axis on the right. |
4.1.2. Results
The numerical solution En and the analytical solution Ea from Eq. (29)are plotted in Figs. 1 and 2 together with the absolute value of the relative error. In Fig. 1 the radiation energy density is plotted against the position at time . The relative error in the relevant range from to is always lower than one percent. In Fig. 2 the time evolution from to is shown for the positions coded in black, blue, and red, respectively. The results shown in this figure strongly depend on the position. For the position the error is lower than one percent for all times later than , and decreases with time. For the other positions, the behavior is different. The relative error rises and after a while it decreases. This behavior can be explained by looking at Fig. 1. The error is higher at the diffusion front. This region moves with time and causes the effect for the other positions. The test shows that the time evolution of the radiation energy density is reproduced correctly. As described, this test was performed in different coordinate systems and orientations, with the same results.
4.2. Coupling test
The purpose of this test from Turner & Stone
(2001) is to check the coupling between radiation and the fluid. For this purpose
we simulated a stationary fluid that is initially out of thermal equilibrium. In this
simulation the radiation energy density is the dominant energy, which is constant over the
whole simulation. The system of Eqs. (13)decouples in this case and, in addition, it is not necessary to solve the
matrix equation for E. By setting
σP = κPρ and
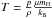 from Eq. (5)with the assumption that σP and
ρ are constant, we can rewrite the thermal energy equation of the
system (13)as
from Eq. (5)with the assumption that σP and
ρ are constant, we can rewrite the thermal energy equation of the
system (13)as 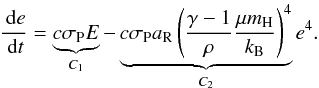 (31)With these approximations, the coefficients
C1 and C2 are constant. The
solution to Eq. (31)can be calculated
analytically in terms of an algebraic equation that would have to be solved iteratively.
Here, we integrated Eq. (31)numerically
using a Runge Kutta solver of fourth-order scheme with adaptive step size. In the
following we refer to this solution as the reference solution.
(31)With these approximations, the coefficients
C1 and C2 are constant. The
solution to Eq. (31)can be calculated
analytically in terms of an algebraic equation that would have to be solved iteratively.
Here, we integrated Eq. (31)numerically
using a Runge Kutta solver of fourth-order scheme with adaptive step size. In the
following we refer to this solution as the reference solution.
Information on the expected behavior of the solution can be obtained directly from the
differential equation. It is clear that in the final equilibrium state (with
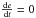 ) the gas temperature has to be equal to
the radiation temperature
) the gas temperature has to be equal to
the radiation temperature ![\hbox{$T=\sqrt[4]{\frac{E}{a_\mathrm{R}}}$}](/articles/aa/full_html/2013/11/aa21499-13/aa21499-13-eq150.png) , thus the final gas energy density will be
, thus the final gas energy density will be
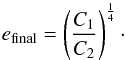 (32)If the initial gas energy density
e0 is much lower than efinal, we
can neglect the second term in Eq. (31)at
the beginning, thus
e(t) = C1 t + e0.
The corresponding coupling time can be estimated to
(32)If the initial gas energy density
e0 is much lower than efinal, we
can neglect the second term in Eq. (31)at
the beginning, thus
e(t) = C1 t + e0.
The corresponding coupling time can be estimated to 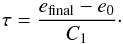 (33)On the other hand, if
e0 ≫ efinal, we can neglect the
first term in Eq. (31)and derive
(33)On the other hand, if
e0 ≫ efinal, we can neglect the
first term in Eq. (31)and derive
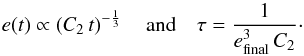 (34)
(34)
 |
Fig. 3 Coupling test from to with three different initial gas energy densities. The reference solution (black lines) and the simulated results for the initial energy density (red dots), (blue dots), and (green dots) are plotted. |
4.2.1. Setup
The computational domain was identical to that of the linear diffusion test in Sect. 4.1. For the grid we used a resolution of 25 × 3 × 3 grid cells. As before, we did not solve the equations of hydrodynamics, and the boundary conditions were quite simple. All boundaries were set to periodic boundary conditions. The constants we used were set to radiation energy density , density , opacity , mean molecular weight μ = 0.6, and the ratio of specific heats γ = 5/3. The simulations started at with an initial time step of and evolved until . After each step the time step was increased by 1% to speed up the computation. The simulation was performed with three different initial gas energy densities, , and, .
4.2.2. Results
Figure 3 shows the numerical gas energy density and the reference solution plotted against time for the three different initial values of e. The agreement of both results is excellent for all initial values. From the figure we see that in the limit of low and high initial e0, we find exactly the behavior predicted by the estimates for Eq. (31). The analytic estimates for the coupling time τ from Eq. (33)agree very well with our results. The estimate for is and for we calculated . For efinal < e0, the estimate in Eq. (34)is approximately . We have to mention here that this test primarily verifies the correctness of Eq. (17). As in the linear diffusion test, this test was performed in three different coordinate systems in different orientations, with the same results.
4.3. Coupling test with irradiation
 |
Fig. 4 Coupling test with enabled irradiation from to at three different distances d from the inner boundary of the domain. The reference solution (black lines) and the simulated results for the energy density are plotted at distances (red dots), (blue dots) and (green dots). |
This test is in its basic setup the same as that from Sect. 4.2, but with irradiation enabled, that is, Eq. (18)is solved instead of the second equation in
(13). As described in Sect. 3.3, irradiation is limited to the spherical coordinates
we used for this test. With the same assumptions as in Sect. 4.2, that is, σP and ρ are
constant, and with the definitions for σP, e,
p as well as for T, it is possible to rewrite
S from Eq. (24)as
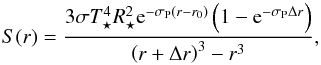 (35)and obtain for Eq. (18)
(35)and obtain for Eq. (18)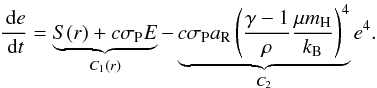 (36)The reference solution was computed in the
same way as before, although it now depends on the distance r from the
star. The quasi-one-dimensional domain started at and ended at , and we used 300 × 3 × 3
grid cells. The domain size in θ and φ direction was
chosen in a way such that the grid cells were nearly quadratic. For the simulation we used
a constant radiation energy density of , a density of , a Rosseland opacity of , and a
Planck opacity of κP = κR, which
corresponds to . The opacity for the irradiation
κ⋆ was set to
κP. For the star, the temperature was set to and the radius
to . Additionally, we assumed that there is no absorption in the region between the
surface of the star and the inner boundary of the computation domain. Figure 4 shows the gas energy density plotted against time with
an initial gas energy of at three different positions , , and where d is
measured relative to the inner boundary of the quasi-one-dimensional domain. In Fig. 5 the radial dependency of the gas energy density is
plotted for the same simulation at five different times. As expected, the results show
that the gas energy density at a time later than becomes constant and depends on the
distance from the star. The simulated and reference solution agree excellently.
(36)The reference solution was computed in the
same way as before, although it now depends on the distance r from the
star. The quasi-one-dimensional domain started at and ended at , and we used 300 × 3 × 3
grid cells. The domain size in θ and φ direction was
chosen in a way such that the grid cells were nearly quadratic. For the simulation we used
a constant radiation energy density of , a density of , a Rosseland opacity of , and a
Planck opacity of κP = κR, which
corresponds to . The opacity for the irradiation
κ⋆ was set to
κP. For the star, the temperature was set to and the radius
to . Additionally, we assumed that there is no absorption in the region between the
surface of the star and the inner boundary of the computation domain. Figure 4 shows the gas energy density plotted against time with
an initial gas energy of at three different positions , , and where d is
measured relative to the inner boundary of the quasi-one-dimensional domain. In Fig. 5 the radial dependency of the gas energy density is
plotted for the same simulation at five different times. As expected, the results show
that the gas energy density at a time later than becomes constant and depends on the
distance from the star. The simulated and reference solution agree excellently.
 |
Fig. 5 Radial dependency of the gas energy density for the coupling test with enabled irradiation. The gas energy density is plotted at different times, (red dots), (blue dots), (green dots), (yellow dots), and (magenta dots). The dots represent the numerical solution and the solid black lines the reference solution. Position d is again measured relatively to the inner boundary of the quasi one-dimensional domain. |
4.4. Steady-state test
The original version of this test was published in Flaig
(2011). We considered a one-dimensional stationary setup with a given density
stratification. In steady-state, the time derivatives in Eqs. (13)vanish and the system is reduced to the
following equation for the radiation energy density: 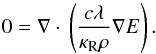 (37)A further reduction is obtained when we
rewrite this equation in one dimension along the z-axis in Cartesian
coordinates. The equation is then much simpler and can be written as
(37)A further reduction is obtained when we
rewrite this equation in one dimension along the z-axis in Cartesian
coordinates. The equation is then much simpler and can be written as 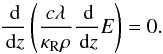 (38)In general, the expression
(38)In general, the expression
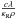 is not known analytically for realistic
opacities. To circumvent this problem, we defined the effective optical depth
is not known analytically for realistic
opacities. To circumvent this problem, we defined the effective optical depth
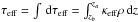 , where
za and
zb are the lower and upper boundaries of
the quasi-one-dimensional domain, respectively, and κeff is
the effective opacity given by
, where
za and
zb are the lower and upper boundaries of
the quasi-one-dimensional domain, respectively, and κeff is
the effective opacity given by 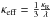 . By using
dτeff = κeffρ dz,
Eq. (38)can be rewritten as
. By using
dτeff = κeffρ dz,
Eq. (38)can be rewritten as
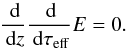 (39)The solution of this equation is then given
by
(39)The solution of this equation is then given
by 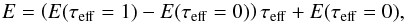 (40)where
E(τeff = 0) and
E(τeff = 1) are the radiation energy
density at the position where the effective optical depth has the values zero or one,
respectively. Thus, in the static case the radiation energy has a linear dependence on the
optical depth τeff for all opacity laws.
(40)where
E(τeff = 0) and
E(τeff = 1) are the radiation energy
density at the position where the effective optical depth has the values zero or one,
respectively. Thus, in the static case the radiation energy has a linear dependence on the
optical depth τeff for all opacity laws.
 |
Fig. 6 Comparison between the numerical (red dots) and the analytical (black line) solutions of the steady-state test after . In addition, the absolute value of the relative error (blue dashed line) is plotted relatively to the axis on the right side. This axis is logarithmic. |
4.4.1. Initial setup
The domain was chosen to have an arbitrary length of , and a width and height of and 300 × 3 × 3 grid cells were used. This test was performed without solving the hydrodynamical equations, but instead we solved Eqs. (13)for a fixed density and opacity law and evolved the solution, until a stationary state had been reached. For the radiation boundary conditions, we used boundary conditions with fixed values of E at the lower and upper boundary of the domain. At the lower boundary we chose E = aRT4 with a temperature of .
Because the stratification is optically thin at the upper boundary, we want to allow the radiation to escape freely from the domain. For this reason we simply set the temperature to a very low value at the upper boundary, here .
All other boundary conditions were set to periodic. The density stratification is given
by 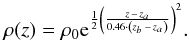 (41)The initial temperature profile can be
chosen randomly in principle, but to speed up the computation, we used a linear
temperature profile starting at za with and
ending at zb with . From this temperature
profile we assigned pressure values using Eq. (5). The radiation energy density E inside the domain was also
set using the gas temperature profile and
E = aRT4. The
ratio of specific heats and the mean molecular weight were set to
γ = 1.43 and μ = 0.6, respectively. As flux-limiter we
chose Eq. (11), for the Rosseland mean
opacity κR we used data from Lin & Papaloizou (1985), and the Planck mean opacity was set to
κP = κR. The initial time step
was and increased slightly with time to speed up the computation and keep the number of
iterations performed by the matrix solver nearly constant. This simulation was preformed
with a relative tolerance of
ϵr = 10-6 for the matrix
solver.
(41)The initial temperature profile can be
chosen randomly in principle, but to speed up the computation, we used a linear
temperature profile starting at za with and
ending at zb with . From this temperature
profile we assigned pressure values using Eq. (5). The radiation energy density E inside the domain was also
set using the gas temperature profile and
E = aRT4. The
ratio of specific heats and the mean molecular weight were set to
γ = 1.43 and μ = 0.6, respectively. As flux-limiter we
chose Eq. (11), for the Rosseland mean
opacity κR we used data from Lin & Papaloizou (1985), and the Planck mean opacity was set to
κP = κR. The initial time step
was and increased slightly with time to speed up the computation and keep the number of
iterations performed by the matrix solver nearly constant. This simulation was preformed
with a relative tolerance of
ϵr = 10-6 for the matrix
solver.
4.4.2. Results
Steady-state was reached approximately after . In Fig. 6, we plot the radiation energy density against the effective optical depth τeff from our numerical solution (red dots) together with the analytical solution from Eq. (40). The parameters E(τeff = 1) − E(τeff = 0) and E(τeff = 0) were obtained by fitting Eq. (40)to the numerical solution. We note here that E(τeff = 0) was determined by interpolation between ghost cells and active cells near the upper boundary zb. Hence, the radiation temperature in the active region can be much higher than ; the value was specifically chosen to be very low. We also plot the absolute value of the relative error |(En − Ea)/Ea|. The results from the simulation agree very well with the analytical prediction. As we can see from Fig. 6, the strongest deviation from the analytical solution is at low values of τeff with an relative error of about one percent. As the linear diffusion and the coupling test, this test was performed in all three coordinate systems and in different orientations, with the same results.
4.5. Radiation shock
In this section we extend the previous tests and solve now the full equations of hydrodynamics and radiation transport simultaneously, testing the complete new module within the PLUTO-environment.
4.5.1. Initial setup
Following the set-up from Ensman (1994), a shock was generated in a quasi-one-dimensional domain. This test case is more complex than the others, and it is not possible to derive an analytical solution. Instead we compare our results with the simulations of Commerçon et al. (2011). The computational domain was chosen to have a length of and a width and height of with 2048 × 4 × 4 grid cells. The initial density and temperature were set to and . The initial radiation energy density was set by the equation E = aRT4. For the flux-limiter we employed the Minerbo-formulation according to Eq. (11), and for the opacity we used . Furthermore, the ratio of specific heats was set to γ = 7/5 and the mean molecular weight to μ = 1, in analogy to Commerçon et al. (2011). The time step was computed through the CFL condition of PLUTO, for which we used a value of 0.4. As solver we used a medium-accurate, but robust solver named tvdlf, which uses a simple Lax-Friedrichs scheme. To generate the radiative shock, the following boundary conditions were used: in the direction of the shock propagation, we employed a reflective boundary condition at the lower boundary and a zero-gradient at the upper boundary of the domain. The remaining boundaries were set to periodic. For the relative tolerance used by the matrix solver we chose a value of ϵr = 10-5. The shock was generated by applying an initial velocity v to the gas. The velocity was directed toward the reflecting boundary condition, which acts as a wall. The shock then propagated from the wall back into the domain. Depending on the velocity, the shock was sub- or supercritical, that is, the temperature behind the shock front was higher than or equal to the temperature upstream (in front of the shock front), respectively. In this test we simulated both cases: the subcritical shock with a velocity of , and the supercritical shock with .
 |
Fig. 7 Sub- and supercritical shock tests. In both cases we plot the radiation temperature (blue line) and the gas temperature (red line) against s = z − v × t, where z is the position along the quasi-one-dimensional domain and v is the piston velocity. The subcritical shock a) is shown at time and the supercritical shock b) at . |
Comparison of the results from the radiation shock test with analytical estimates and the results from Commerçon et al. (2011) for the pre-shock T− and post-shock T2 gas temperatures as well as the spike temperature T+.
4.5.2. Results
For a better comparison with the results of simulations, where the material is at rest
and a moving piston causes the shock, we introduced the quantity s.
This quantity is given by the relation
s = z − v × t,
where z is the position along the quasi-one-dimensional domain. Note
that this quantity is called z in Commerçon et al. (2011). Figure 7 shows
the radiation temperature (blue line) and the gas temperature (red line) against the
previously defined quantity s for both the subcritical (at ) and
supercritical case (at ). In the supercritical case the pre- and post-shock gas
temperature are equal, as expected. In the subcritical case these temperatures can be
estimated analytically (Ensman 1994; Mihalas & Mihalas 1984; Commerçon et al. 2011). In Table 1, the analytical estimates and the numerical values from our simulations and
the results from Commerçon et al. (2011) are shown
together. Here T2 is the post-shock temperature,
T− the pre-shock temperature and
T+ the spike temperature. In the equations,
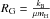 is the perfect gas constant,
is the perfect gas constant,
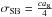 the Stefan-Boltzmann constant, and
u is the velocity of the shock relative to the upstream material (or
vice versa) in our case .
the Stefan-Boltzmann constant, and
u is the velocity of the shock relative to the upstream material (or
vice versa) in our case .
The results agree in general with the analytical estimates and the results from Commerçon et al. (2011). The analytical estimate for the post-shock temperature is higher than the numerical results with both codes. We note here that the analytical estimate depends on u and therefore differs from the values given in Commerçon et al. (2011). The pre-shock and spike temperatures agree reasonably well with the analytical estimates in our simulations but are higher than the results from Commerçon et al. (2011). The differences of our numerical solution to the analytical estimates may arise because we ignored the advective terms in the radiation energy density in Eq. (4), which may play a role in this dynamic situation. Additionally, it is noteworthy that the position of the shock front is very well reproduced. This test was performed in Cartesian coordinates.
4.6. Accretion disk
The goal of this last test is to compare the results of different codes on a more complex two-dimensional physical problem that involves the onset of convective motions. For this purpose we modeled a section of an internally heated, viscous accretion disk in spherical coordinates (r,θ,φ), where r is the distance to the center of the coordinate system, θ the polar angle measured from the z-axis in cylindrical coordinates, and φ the azimuth angle. The setup follows the standard disk model as used in Kley et al. (2009). The tests proceeded in two steps. In a first setup we reduced the complexity of the problem and considered a static problem, that is, without solving the equations of hydrodynamics. This will demonstrate that the equilibrium between viscous heating and radiative cooling is treated correctly in our implementation. In the second setup we considered the full hydrodynamic problem and studied the onset of convection in disks.
4.6.1. Initial setup
For both the static and the dynamical case we used the same initial setup. The radial
extent ranged from rmin = 0.4 to
rmax = 2.5, where all lengths are given in units of the
semi-major axis of Jupiter . In the vertical direction the domain extended from to and
in φ direction from to . In the three coordinate directions
(r,θ,φ) we used 256 × 32 × 4 grid cells. The disk aspect ratio
h was set to , where
s = rsinθ describes the (radial)
distance from the z-axis in cylindrical coordinates, and
H is the disk’s vertical scale height. The viscosity
ν was set to a value of , and the mean molecular weight to . For the
ratio of specific heats we used different values, as specified below. The density
stratification can be obtained from vertical hydrostatic equilibrium, assuming a
temperature that is constant on cylinders,
T = T(s). From this follows (Masset et al. 2006)
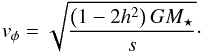 (42)where the quantity
ρ0 was chosen such that the total mass of the disk is
Mdisk = 0.01M⋆,
where M⋆ is the mass of the central star of
the system, which is set to the mass of the sun,
M⋆ = M⊙.
The mass within the computational domain is then 1/2 Mdisk,
because we only computed the upper half of the disk. The radial variation leads to a
surface density profile of Σ ∝ r−1/2, which is the
equilibrium profile for constant viscosity, and vanishing mass flux through the disk.
The pressure p is set by the isothermal relation
(42)where the quantity
ρ0 was chosen such that the total mass of the disk is
Mdisk = 0.01M⋆,
where M⋆ is the mass of the central star of
the system, which is set to the mass of the sun,
M⋆ = M⊙.
The mass within the computational domain is then 1/2 Mdisk,
because we only computed the upper half of the disk. The radial variation leads to a
surface density profile of Σ ∝ r−1/2, which is the
equilibrium profile for constant viscosity, and vanishing mass flux through the disk.
The pressure p is set by the isothermal relation
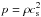 , with the speed of sound
cs = HΩK and the Keplerian
angular velocity
, with the speed of sound
cs = HΩK and the Keplerian
angular velocity 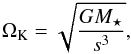 with the gravitational constant
G. The temperature can be computed through Eq. (5)and results in
with the gravitational constant
G. The temperature can be computed through Eq. (5)and results in
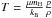 . The initial velocities are set to zero
except for the angular velocity vφ, which
is set to
. The initial velocities are set to zero
except for the angular velocity vφ, which
is set to 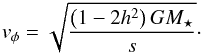 For the Rosseland mean opacity
κR we used data from Lin
& Papaloizou (1985), and the Planck mean opacity was set to
κP = κR. The displayed
simulations were performed in the rotating frame in which the coordinate system rotates
with the constant angular velocity of ΩK at ajup,
but for non rotating systems identical results are obtained. As before, the radiation
energy density was initialised to
E = aRT4.
For the Rosseland mean opacity
κR we used data from Lin
& Papaloizou (1985), and the Planck mean opacity was set to
κP = κR. The displayed
simulations were performed in the rotating frame in which the coordinate system rotates
with the constant angular velocity of ΩK at ajup,
but for non rotating systems identical results are obtained. As before, the radiation
energy density was initialised to
E = aRT4.
For density, pressure, and radial velocity we applied reflective radial boundary conditions and set the angular velocity to the Keplerian values. In the azimuthal direction periodic boundary conditions were used for all variables. In the vertical direction we applied an equatorial symmetry and reflective boundary condition for θmin. The radiation boundary conditions were set to reflective for the r direction (both lower and upper), in θ-direction we used a fixed value of E = aRT4 with at θmin (which denotes the disk surface), and a symmetric boundary condition holds at the disk’s midplane θmax. For the φ-direction we used periodic boundary conditions.
In both cases we used a relative tolerance of ϵr = 10-8 for the matrix solver. In the simulation with hydrodynamics we used the Riemann-solver hllc2.
4.6.2. Static case
In this test case only the radiative equations were solved without the hydrodynamics.
To account for the viscous heating in this case, we added an additional dissipation
contribution, D, to the right-hand side of the internal energy equation
in Eqs. (13). We considered standard
viscous heating, and included only the main contribution from the approximately
Keplerian shear flow. At the individual grid points the dissipation is then given by
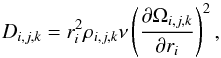 (43)where ν is the constant
viscosity and Ωi,j,k the angular velocity at the individual
grid points. In summary, we solved the same equations as in the case with irradiation,
where we substituted Si,j,k with
Di,j,k.
(43)where ν is the constant
viscosity and Ωi,j,k the angular velocity at the individual
grid points. In summary, we solved the same equations as in the case with irradiation,
where we substituted Si,j,k with
Di,j,k.
 |
Fig. 8 Radial mid-plane temperature profile in the simulations with PLUTO (red dots) and with RH2D (black line) after a) and b) , together with the absolute value of the relative error (blue dashed line) that belongs to the log axis on the right. |
 |
Fig. 9 Radial mid-plane temperature profile in the simulation with PLUTO (red line), RH2D (black line) and NIRVANA (blue line) in the quasi-equilibrium state after a) for γ = 5/3 without convection and b) in the strongly convective case with γ = 1.1 . We added the results of a simulation performed with PLUTO where we used a logarithmic grid in r-direction (green line). |
In steady-state, the time derivatives in the Eqs. (13)vanish and the system is reduced to the following equation for
the radiation energy density 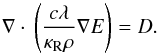 (44)In optically thick regions,
E = aRT4 and
Eq. (44)determines the temperature
stratification within the disk.
(44)In optically thick regions,
E = aRT4 and
Eq. (44)determines the temperature
stratification within the disk.
The simulation starts at and is evolved until are reached, where one orbit corresponds to the Keplerian orbital period at the distance of ajup, which is given here by . The initial and overall time step was chosen as . The results for the static case are shown in Fig. 8 for a value of γ = 7/5 for the adiabatic index. The plots show the radial temperature profile of the accretion disk in the mid-plane for the simulations after 10 orbits (top panel) and after 100 orbits (bottom panel). We display the results of two different simulations, one performed with the PLUTO code (red dots) using the described methods, and the second (black lines) run with the RH2D code (Kley 1989). The results from both codes are nearly identical. Even after the absolute value of the relative error is always lower than 2%. The test shows that the time scale of the radiative evolution, and the equilibrium state are captured correctly. We note that the RH2D code uses the one-temperature approach of radiation transport in this case.
4.6.3. Dynamical case
The final equilibrium of the described static case does not depend on the magnitude of γ, because the viscous heating is independent of it, see Eq. (44). The situation is different, however, for the dynamical cases, where the hydrodynamical evolution of the flow is taken into account. Since the timescale of the radiative transport depends on γ (through Eq. 6), one might expect the possibility of convective instability, see for example the recent work by Bitsch et al. (2013a). This is indeed the case for low enough values of γ. To demonstrate the correctness of our implementation also for the full dynamical problem, we modeled two disks, one with γ = 5/3, which clearly shows no convection, and the other with γ = 1.1, which shows strong convection. The initial setup was identical to that described before, but now we solved the equations of viscous hydrodynamics with radiation transport, but without irradiation and explicit dissipation. For viscous flows the energy generation due to viscous dissipation is automatically included in the total energy equation. The Eqs. (1)to (3)were solved with PLUTO, and the system of Eqs. (13)where solved as described in Sect. 3. Since this setup is very dynamical and requires a more complex interplay of hydrodynamics and radiative transport, we used a third code, NIRVANA, for comparison. The NIRVANA code has been used in Kley et al. (2009) and Bitsch et al. (2013a) on very similar setups. The results of the two cases are shown in Fig. 9. In the top panel (a) we display the result for γ = 5/3, which is not convective. Here, the agreement between the codes is excellent with the maximum deviation in the percentage range. In the lower panel (b) we display the results for γ = 1.1. Here the radiative transport timescale is prolonged, which leads to a strongly convective situation, as can be seen in the raggedness of the curves. In this simulation we doubled the spatial resolution compared with γ = 5/3, such that the convection cells are reasonably well resolved, see Fig. 10. The agreement between the three different codes is very good, despite the very different solution methods for the hydrodynamics equations: PLUTO uses the total energy equation with a Riemann solver, while RH2D and NIRVANA use a second-order upwind scheme and the thermal energy equation. Additionally, the latter two codes use the full dissipation function and the one-temperature approach.
 |
Fig. 10 Vertical slice of the disk temperature at in the dynamical case with γ = 1.1 showing convection cells. Also plotted in the inset is the enlarged region from r = 0.4 ajup to 0.6 ajup with the velocity field in the r − θ plane (black arrows). |
4.6.4. Parallel scaling
To test the parallel scaling of our new implementation, we used the same setup as in Sect. 4.6.3 and increased the number of grid cells to 1024 × 64 × 256. The computations were only run until , and we used the solver PETSc. In this way, we were able to run the test on 64 to up to 1024 processor cores within a reasonable time. The simulations were run on clusters of the bwGRiD, which are equipped with Intel Xeon E5440 cpus and have a low-latency InfiniBand network. In Fig. 11 we show the results of the simulations performed with full hydrodynamics and radiation transport. The run-time increases nearly by a factor of two when doubling the number of cores. With this setup, solving the hydrodynamics equations needs between 40% and 50% of the computation time and the radiation transport the remaining 60% to 50%, but these numbers are strongly problem-dependent. Therefore, even for up to 1024 cores, we see good agreement with ideal scaling. According to Amdahl’s law, the full code, including the original part of PLUTO and our implementation of the radiation transport, is well parallelized.
5. Summary and conclusions
We described the implementation of a new radiation module to the PLUTO code. The module solves for the flux-limited diffusion approximation in the two-temperature approach. For discretization the finite-volume method was used, and the resulting difference equations couple the updates of the temperature and radiation energy density. Because of potentially severe time-step limitations, the set of equations is solved implicitly. To treat the non linearity of the temperature in the matter-radiation coupling term, we used the method of Commerçon et al. (2011).
The accuracy of the implementation was verified using different physical and numerical setups. The first set of tests delt with purely radiative problems that included the purely diffusive evolution toward an equilibrium, and special setups for testing the coupling terms between radiative and thermal energy. A newly developed setup checked the correct inclusion of the irradiation from a central source in a spherical coordinate system.
In the second test suite we studied the full simultaneous evolution of hydrodynamics and radiation. First, sub- and supercritical radiative shock simulations were performed, whose resulte agreed very well with previously published results of identical setups. Finally, we studied the onset of convection in internally heated viscous disks and found very good agreement between three different independent hydrodynamical codes. This last test also allowed us to test the correct implementation in a spherical coordinate system and a non-equidistant logarithmic grid. Our numerical performance tests indicate excellent parallel scaling for up to at least 1024 processors.
 |
Fig. 11 Parallel scaling benchmark results for the static-accretion disk test case. We plot
here the number of processor cores against |
The current version of the radiation module includes routines for the Rosseland mean opacity from Lin & Papaloizou (1985) and Bell & Lin (1994). Additionally, it is possible to use the Rosseland and Planck mean opacities from Semenov et al. (2003).
The described radiation module can be easily used within the PLUTO-environment. It can be found on the webpage3 as a patch for version 4.0 of PLUTO.
For more information visit the website http://www.mcs.anl.gov/petsc or see Balay et al. (2012).
bwGRiD (http://www.bw-grid.de), member of the German D-Grid initiative, funded by the Ministry for Education and Research (Bundesministerium für Bildung und Forschung) and the Ministry for Science, Research and Arts Baden-Württemberg (Ministerium für Wissenschaft, Forschung und Kunst Baden-Württemberg).
Acknowledgments
We gratefully thank the bwGRiD project4 for the computational resources. We gratefully acknowledge support from the German Research Foundation (DFG) through grant KL 650/11 within the Collaborative Research Group FOR 759: The formation of Planets: The Critical First Growth Phase. We thank Rolf Kuiper for many stimulating discussions, physical as well as technical.
References
- Aubert, D., & Teyssier, R. 2008, MNRAS, 387, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Balay, S., Brown, J., et al. 2012, PETSc Users Manual, Tech. Rep. ANL-95/11 – Revision 3.3, Argonne National Laboratory [Google Scholar]
- Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Bitsch, B., Boley, A., & Kley, W. 2013a, A&A, 550, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Crida, A., Morbidelli, A., Kley, W., & Dobbs-Dixon, I. 2013b, A&A, 549, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Commerçon, B., Teyssier, R., Audit, E., Hennebelle, P., & Chabrier, G. 2011, A&A, 529, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davis, S. W., Stone, J. M., & Jiang, Y.-F. 2012, ApJS, 199, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Eggum, G. E., Coroniti, F. V., & Katz, J. I. 1988, ApJ, 330, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Ensman, L. 1994, ApJ, 424, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Flaig, M. 2011, Ph.D. Thesis, Universität Tübingen [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2012, J. Comput. Phys., 231, 919 [Google Scholar]
- González, M., Audit, E., & Huynh, P. 2007, A&A, 464, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiang, Y.-F., Stone, J. M., & Davis, S. W. 2012, ApJS, 199, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W. 1989, A&A, 208, 98 [NASA ADS] [Google Scholar]
- Kley, W., Bitsch, B., & Klahr, H. 2009, A&A, 506, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuiper, R., & Klessen, R. S. 2013, A&A, 555, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuiper, R., Klahr, H., Dullemond, C., Kley, W., & Henning, T. 2010, A&A, 511, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuiper, R., Klahr, H., Beuther, H., & Henning, T. 2012, A&A, 537, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levermore, C. D., & Pomraning, G. C. 1981, ApJ, 248, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1985, in Protostars and Planets II, eds. D. C. Black, & M. S. Matthews (Tucson: University of Arizona press), 981 [Google Scholar]
- Masset, F. S., D’Angelo, G., & Kley, W. 2006, ApJ, 652, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mihalas, D., & Mihalas, B. W. 1984, Foundations of radiation hydrodynamics (New York: Oxford University Press) [Google Scholar]
- Minerbo, G. N. 1978, J. Quant. Spec. Radiat. Transf., 20, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Pomraning, G. C. 1973, The equations of radiation hydrodynamics (Oxford: Pergamon Press) [Google Scholar]
- Semenov, D., Henning, T., Helling, C., Ilgner, M., & Sedlmayr, E. 2003, A&A, 410, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stone, J. M., Mihalas, D., & Norman, M. L. 1992, ApJS, 80, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, N. J., & Stone, J. M. 2001, ApJS, 135, 95 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Comparison of the results from the radiation shock test with analytical estimates and the results from Commerçon et al. (2011) for the pre-shock T− and post-shock T2 gas temperatures as well as the spike temperature T+.
All Figures
 |
Fig. 1 Linear diffusion test at time . The simulated (read dots) and the analytical (black line) solutions are plotted. We also plot the solution with the absolute value of the relative error (blue dashed line) that belongs to the axis on the right. |
| In the text | |
 |
Fig. 2 Time evolution for the linear diffusion test from time to at three different positions: at (black lines), at (blue lines) and at (red lines). The dotted lines for each position belong to the simulated solution, the solid lines to the analytical solution, and the dashed lines show the relative error that belongs to the axis on the right. |
| In the text | |
 |
Fig. 3 Coupling test from to with three different initial gas energy densities. The reference solution (black lines) and the simulated results for the initial energy density (red dots), (blue dots), and (green dots) are plotted. |
| In the text | |
 |
Fig. 4 Coupling test with enabled irradiation from to at three different distances d from the inner boundary of the domain. The reference solution (black lines) and the simulated results for the energy density are plotted at distances (red dots), (blue dots) and (green dots). |
| In the text | |
 |
Fig. 5 Radial dependency of the gas energy density for the coupling test with enabled irradiation. The gas energy density is plotted at different times, (red dots), (blue dots), (green dots), (yellow dots), and (magenta dots). The dots represent the numerical solution and the solid black lines the reference solution. Position d is again measured relatively to the inner boundary of the quasi one-dimensional domain. |
| In the text | |
 |
Fig. 6 Comparison between the numerical (red dots) and the analytical (black line) solutions of the steady-state test after . In addition, the absolute value of the relative error (blue dashed line) is plotted relatively to the axis on the right side. This axis is logarithmic. |
| In the text | |
 |
Fig. 7 Sub- and supercritical shock tests. In both cases we plot the radiation temperature (blue line) and the gas temperature (red line) against s = z − v × t, where z is the position along the quasi-one-dimensional domain and v is the piston velocity. The subcritical shock a) is shown at time and the supercritical shock b) at . |
| In the text | |
 |
Fig. 8 Radial mid-plane temperature profile in the simulations with PLUTO (red dots) and with RH2D (black line) after a) and b) , together with the absolute value of the relative error (blue dashed line) that belongs to the log axis on the right. |
| In the text | |
 |
Fig. 9 Radial mid-plane temperature profile in the simulation with PLUTO (red line), RH2D (black line) and NIRVANA (blue line) in the quasi-equilibrium state after a) for γ = 5/3 without convection and b) in the strongly convective case with γ = 1.1 . We added the results of a simulation performed with PLUTO where we used a logarithmic grid in r-direction (green line). |
| In the text | |
 |
Fig. 10 Vertical slice of the disk temperature at in the dynamical case with γ = 1.1 showing convection cells. Also plotted in the inset is the enlarged region from r = 0.4 ajup to 0.6 ajup with the velocity field in the r − θ plane (black arrows). |
| In the text | |
 |
Fig. 11 Parallel scaling benchmark results for the static-accretion disk test case. We plot
here the number of processor cores against |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.