| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201321846 | |
| Published online | 07 October 2013 | |
Differential asteroseismic study of seismic twins observed by CoRoT⋆
Comparison of HD 175272 with HD 181420
1
Institut d’Astrophysique et de Géophysique de l’Université de
Liège, Allée du 6 Août
17, 4000
Liège, Belgium
e-mail: benoit.mosser@obspm.fr
2
Department of Astronomy and Space Science, Erciyes
University, 38039
Melikgazi, Kayseri,
Turkey
3
LESIA, CNRS, Université Pierre et Marie Curie, Université Denis
Diderot, Observatoire de Paris, 92195
Meudon Cedex,
France
4
Department of Physics and Astronomy, Aarhus
University, 8000
Aarhus C,
Denmark
5
Université de Toulouse, UPS-OMP, IRAP, 31400
Toulouse,
France
6
Laboratoire AIM, CEA/DSM, CNRS – Université Paris Diderot,
IRFU/SAp,
91191
Gif-sur-Yvette Cedex,
France
7
Institut d’Astrophysique Spatiale, UMR 8617, Université Paris Sud,
91405
Orsay Cedex,
France
8
Space Science Institute, 4750 Walnut street Suite# 205, Boulder, CO
80301,
USA
9
Instituto de Astrofisica de Canarias, 38205, La
Laguna, Tenerife, Spain
10
Université de Nice-Sophia Antipolis, CNRS UMR 7293, Observatoire
de la Côte d’Azur, Laboratoire J.L. Lagrange, BP 4229, 06304
Nice Cedex 04,
France
11
Universidad de La Laguna, Dpto de Astrofisica, 38206, La
Laguna, Tenerife, Spain
12
NRS, IRAP, 14
avenue Édouard Belin, 31400
Toulouse,
France
Received:
6
May
2013
Accepted:
2
September
2013
Context. The CoRoT short asteroseismic runs give us the opportunity to observe a large variety of late-type stars through their solar-like oscillations. We report the observation and modeling of the F5V star HD 175272.
Aims. Our aim is to define a method for extracting as much information as possible from a noisy oscillation spectrum.
Methods. We followed a differential approach that consists of using a well-known star as a reference to characterize another star. We used classical tools such as the envelope autocorrelation function to derive the global seismic parameters of the star. We compared HD 175272 with HD 181420 through a linear approach, because they appear to be asteroseismic twins.
Results. The comparison with the reference star enables us to substantially enhance the scientific output for HD 175272. First, we determined its global characteristics through a detailed seismic analysis of HD 181420. Second, with our differential approach, we measured the difference of mass, radius and age between HD 175272 and HD 181420.
Conclusions. We have developed a general method able to derive asteroseismic constraints on a star even in case of low-quality data. This method can be applied to stars with interesting properties but low signal-to-noise ratio oscillation spectrum, such as stars hosting an exoplanet or members of a binary system.
Key words: asteroseismology / stars: interiors / techniques: photometric / stars: evolution / stars: individual: HD 175272 / stars: individual: HD 181420
© ESO, 2013
1. Introduction
Asteroseismology allows us to investigate the interior of stars. The most detailed analysis of a star is based on the determination of the largest possible number of oscillation frequencies, which requires a high-quality oscillation spectrum (e.g., Deheuvels et al. 2010; Metcalfe et al. 2012). When only global seismic parameters are determined, the output is poorer, but nevertheless allows us to gain information that is not given by classical spectrometric observations (e.g., García et al. 2009; Mathur et al. 2010). The output is limited for a low-quality oscillation spectrum. However, because many interesting stars, for instance those hosting an exoplanet, may present such a low-quality oscillation spectrum (e.g., Gaulme et al. 2010), it is necessary to find a method that optimizes the seismic information even in unfavorable cases.
The seismic program of the CoRoT mission (Michel et al. 2008) provides short runs in between five-month-long runs, which allow us to study a larger set of variable stars. HD 175272, a solar-like star suspected to show measurable solar-like oscillations, was a secondary target of the first short run centered on HD 175726 (Mosser et al. 2009b). It was observed for 27 days in October 2007. Despite the dim magnitude of the star and the limited duration of the observation, we show that we can benefit from the scaling relations observed in asteroseismology (Kjeldsen & Bedding 1995) to enhance the accuracy of the asteroseismic output. The comparison with a close reference star with a high signal-to-noise (S/N) oscillation spectrum (HD 181420, Barban et al. 2009) makes it possible to benefit from the higher-precision models that can be derived from the higher-quality oscillation spectrum.
Studying solar-like stars, solar analogs, or solar twins has proved to be fruitful for investigating the influence of small differences compared with the well-known solar case, as for example τ Ceti (Teixeira et al. 2009), α Cen B (Kjeldsen et al. 2005), or 16 Cyg A and B (Metcalfe et al. 2012). Similarly, studying 1-M⊙ evolutionary sequences is of great interest (Silva Aguirre et al. 2011). With the large increase of stars showing solar-oscillations, we can now exploit the concept of a differential seismic analysis between stellar twins and extend it to references other than the Sun. We present this for the typical case where, due to different S/N properties, a poorly constrained star can benefit from the observations and the modeling of a reference star.
The method presented here involves a differential analysis between two stars with similar seismic properties. It avoids the possible uncertainties caused by the extrapolation of the solar case, where the Sun is used as a far-away reference. It is aimed at constraining differences in internal physical processes of very well constrained stellar twins, both seismically and spectroscopically, from main-sequence stars to red giants. This method helps avoiding the high inaccuracy in the forward-modeling approach of poorly constrained stars. Indeed, when the parameter space is too small, all models in this subspace significantly differ from the real star. In contrast, a differential study is less subject to systematic errors. An accurate measurement of the differences between the target and a reference star is thus possible.
In Sect. 2, we discuss the physical parameters of HD 175272 and the prediction of the asteroseismic signal by scaling the star to a close reference, HD 181420. Observations are presented in Sect. 3. The analysis of the power spectrum is analyzed in Sect. 4, with the identification of the large separation and of its variation with frequency. In Sect. 5, we first describe the physics of our models and perform a seismic modeling of HD 181420, the reference star. We finally explain our differential asteroseismic method and apply it to the study of the second star HD 175272. In Sect. 6, we address the problem of using the frequency νmax of the maximum oscillation amplitude in scaling relations, especially for stars that are not close to the solar type. We also examine how seismic references can be defined. Section 7 is devoted to conclusions.
Primary parameters of HD 175272
2. Stellar parameters
HD 175272, or HIP 92794, is known as an F5 dwarf. Its V magnitude has been derived from Strömgren photometry by Olsen (1994). From medium-resolution stellar spectra, Prugniel & Soubiran (2001) have estimated the effective temperature to be about 6500 K and log g = 4.09; these estimates are presented as poor. Nordström et al. (2004), who performed the Geneva-Copenhagen survey of the solar neighborhood, have inferred the stellar mass to be about 1.44 ± 0.06 M⊙ and the metallicity about −0.06 dex. They also estimated the age to be about 1.8 ± 0.2 Gyr. Poretti et al. (2003) have measured vsini≃ 23 km s-1. They also found that HD 175272 does not show any evident trace of variability.
We have revised the spectroscopic observations with a high-resolution spectrum of HD 175272 recorded with the spectrometer ELODIE at OHP. The updated values of Teff and log g are given in Table 1, with large uncertainties related to the S/N of the recorded spectrum. The abundances for 16 elements are given in Table 2. They were analyzed according to the method presented by Bruntt et al. (2004), considering a microturbulence of 1.70 ± 0.23 km s-1. This provides a mean metallicity [Me/H] = 0.077 ± 0.111. This metallicity is the mean abundance of metals with at least ten lines: Si, Fe, and Ni. The uncertainty on [Me/H] includes the contributions from the uncertainties on Teff, log g, and microturbulence.
According to these parameters, the seismic scaling relations can be used to infer the expected global seismic parameters (e.g., Michel et al. 2008; Belkacem et al. 2011; White et al. 2011). The mean large frequency separation scales as the square root of the mean density and is expected to be in the range [70, 90 μHz]. The frequency νmax of maximum oscillation signal scales as the acoustic cutoff frequency and is expected to be in the range [1.4, 1.9 mHz]. The maximum bolometric amplitude of the radial modes is expected to be in the range [3, 6 ppm] (Samadi et al. 2007; Huber et al. 2011).
Abundance of 16 elements in HD 175272.
 |
Fig. 1 Level-2 light curve of HD 175272. The gray curve shows a low-pass filtering, keeping one point per CoRoT orbit. |
 |
Fig. 2 Power density spectrum in log-scale axes. The peak around 4 μHz is probably the signature of the stellar rotation; the peak at 23.2 μHz is an artifact due to the low-Earth orbit. The black curve corresponds to a box-car-averaged spectrum, with a varying smoothing window (the size of the window increases linearly with frequency). The dashed line represents the white-noise component; the background is modeled with two Harvey-like components indicated by the dotted lines. |
3. Seismic observations
3.1. Time series
This first short CoRoT run lasted 27.2 days in October 2007 with HD 175726 as the principal solar-like target (Mosser et al. 2009b). At the usual 32-s sampling of CoRoT seismic data, the whole time series includes 73 426 points, and the mean flux is about 5.22 × 107 photoelectrons (Fig. 1). The gaps due to data loss when the satellite crossed the South Atlantic Anomaly are responsible for the duty cycle of about 89.8%, with 65 944 original data points, and the remainders obtained from interpolation.
When smoothed with one point per CoRoT orbit (Fig. 1), the time series shows rapid variation with a typical amplitude of about 200 ppm, much greater than the expected standard deviation (≃10 ppm). The stellar origin of these variations is most probable since similar features are absent from the other times series recorded during the same CoRoT run, even if the rapid variation with a period close to one day occuring during the last third of the run may be instrumental artifacts. The spot-modeling of the unperturbed light curve, performed with the method developed by Mosser et al. (2009a), derives a surface rotation of the order of 2.8 ± 0.4 days. Compared with previously analyzed stars (e.g., Mosser et al. 2009a; Ballot et al. 2011), we note that the precision is limited by a poorer S/N.
3.2. Low-frequency pattern
The unfiltered power density spectrum of HD 175272 is given in Fig. 2. As presented in Auvergne et al.
(2009), it is affected by artifacts at the orbital and diurnal frequencies. We
had to correct these undesired signatures, and performed a similar correction as in Mosser et al. (2009b). Following Michel et al. (2009), we propose a fit for the stellar background
component in the low-frequency pattern, with two Lorentzian-like components in the
low-frequency range (below 1 mHz): 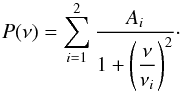 (1)Contrary to Michel et al. (2009), who introduced a denominator varying as
ν4, we note that an exponent of 2 provides a better fit.
Because the time series shown in Fig. 1 is quiet
compared to HD 175726, two components are enough to provide an acceptable fit (Table 3).
(1)Contrary to Michel et al. (2009), who introduced a denominator varying as
ν4, we note that an exponent of 2 provides a better fit.
Because the time series shown in Fig. 1 is quiet
compared to HD 175726, two components are enough to provide an acceptable fit (Table 3).
Parameters of the two-component background.
 |
Fig. 3 Smoothed power density spectrum (with an apodized 300-μHz FWHM window) in log-scale axes. The dashed line represents the contributions of the granulation signal and of the photon noise. The dotted line is a Gaussian fit of the excess power envelope. The mixed line is the smoothed spectrum of HD 181420, with the same treatment and an offset accounting for the different photon-noise levels. |
3.3. Excess power at high frequency
The high-frequency variations of the time series, after high-pass filtering above the frequency range where oscillations are expected, present a standard deviation of about 154 ppm, in agreement with the 132 ppm value expected from pure photon noise for such a star. Photon-noise-limited performance gives an observed high-frequency power density of about 0.56 ppm2 μHz-1, in agreement with the expected value.
A strong smoothing of the spectrum with an apodized 300-μHz window was applied to show the evidence of excess power around 1.6 mHz (Fig. 3), as determined with several methods (Verner et al. 2011). In the expected range, this signature cannot be confused with the low-frequency contribution described by Eq. (1). It corresponds to a height-to-background ratio of about 45%, which compares the asteroseismic power with the background power at νmax, both integrated over one large separation. We note that the excess power in the spectrum of HD 175272 is similar to what has been observed in HD 181420 after correcting for the continuous background levels caused by the photon noise. The locations of the maximum power and its amplitude coincide.
 |
Fig. 4 Automatic determination of the large separation. Dark squares indicate the values of EACF tested in 13 frequency ranges between 2 and 220 μHz. Gray values are artifacts cause by the CoRoT low Earth orbit and must be excluded. The horizontal dashed line indicates the threshold level for a detection at the 1% rejection level. The vertical dark gray line indicates the observed signature at Δν ≃ 75 μHz, and the dash-dotted lines the spurious signatures of the daily aliases (11.6 and 23.2 μHz). |
4. Data analysis
4.1. Mean seismic global parameters
Despite the observed power excess, the Fourier spectrum does not exhibit the regular
pattern expected for solar-like oscillations around 1.6 mHz (Fig. 2). Therefore, we used the formalism (EACF) and the automated procedure
for a blind detection of the large separation developed by Mosser & Appourchaux (2009). According to the global seismic parameters of
the spectrum and to the scaling of the EACF, we expect a maximum of the envelope
autocorrelation amplitude 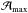 of about 20, hence a fully reliable detection of the large separation. We found a maximum
amplitude
of about 20, hence a fully reliable detection of the large separation. We found a maximum
amplitude 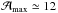 (Fig. 4), lower than expected, but above the 1%
rejection level, which is at eight for a blind detection of solar-like oscillations in
solar-like stars (Mosser & Appourchaux 2009).
(Fig. 4), lower than expected, but above the 1%
rejection level, which is at eight for a blind detection of solar-like oscillations in
solar-like stars (Mosser & Appourchaux 2009).
The blind analysis was followed by a more detailed study. The most precise value of the mean large separation was derived from its measurement in a broad frequency range around νmax, with a filter of the same width as the envelope where oscillations are detected. We measured 74.9 ± 0.4 μHz. Other methods, similar to those used by Verner et al. (2011), converge on the same value. Comparison of different methods has shown that the EACF provides reliable results. The recent work by Mosser et al. (2013) and Hekker et al. (2013) helps in understanding this: the measurement of the large separation in global conditions over a broad radial-order range is less sensitive than local methods to the influence of the glitches superimposed on the regular agency of the oscillation pattern. Local methods can be precise, but do not necessary reach accuracy.
In similar conditions, the mean large separation of HD 181420 is 75.2 ± 0.04 μHz. The ratio between the two stars, defined as the comparison of the low-S/N target with the reference, is about 0.996 ± 0.005. Accordingly, we can derive that the stars have very similar mean densities.
The maximum amplitude in the oscillation spectrum, estimated with a Gaussian fit of the energy excess envelope, is at 1.60 ± 0.03 mHz. With the maximum for HD 181420 reported at 1.61 ± 0.01 mHz, we derive a ratio of about 0.994 ± 0.020. This ratio is close to the ratio of the large separations. This agrees with the scaling relation between νmax and Δν reported in many stars (e.g., Stello et al. 2009; Mosser et al. 2010). We note that these error bars are internal uncertainties only: they rely on the assumption that the energy excess envelope has a Gaussian form. Even if this is an usual assumption, it does not rely on a firm theoretical basis. For a more evolved star such as Procyon, this form is clearly not verified (Bedding et al. 2010). The comparison of the different methods used for measuring νmax has shown that there are small systematic bias. Here, only internal uncertainties are relevant, because we perform a differential analysis on twin stars with the same method.
 |
Fig. 5 Smoothed density spectrum of HD 175272 (Gaussian filter of width 5 μHz). Gray and white domains indicate frequency ranges with a width equal to the mean large separation. The dot-dashed line gives the spectrum of HD 181420, with frequencies multiplied by a factor 0.996, also smoothed and corrected for the difference between the white-noise contributions. |
4.2. P-mode pattern
Owing to the low S/N, it is impossible to identify the oscillation pattern precisely. A strong smoothing of the spectrum is required to reveal it in the spectrum, which is incompatible with a precise mode identification. The H0 test gives only a few eigenvalues at the 10% rejection level (Appourchaux 2004). Despite this, the identification of the radial and dipole ridge is possible, based in Fig. 7 of Mosser et al. (2013). This work shows that the observed εobs term describing the location of radial modes is mainly a function of the ratio νmax/Δν, modulated by the stellar mass, which is also a function of the global parameters Δν and νmax. For HD 175272, εobs is about 1.0, so that the closest radial mode to νmax has a radial order n = 21 and a frequency ν21,0 ≃ 1.57 mHz. The comparison with the Fourier spectrum of HD 181420, again based on a scaling factor of 0.996, agrees with this identification (Fig. 5).
4.3. Mode amplitudes
The mode amplitude, determined according to the global recipe reported in Michel et al. (2009), is about 3.0 ± 0.3 ppm. The major contribution to the uncertainty comes from the photon noise and granulation signal. This value is similar to the value 3.6 ppm expected from Samadi et al. (2007). This shows that the difficulty of observing the oscillation pattern of HD 175272 is mainly due to its faint magnitude (HD 175272 is twice as far as HD 181420) and to a limited observing run (one month versus five months).
 |
Fig. 6 Amplitude per radial mode determined according to Michel et al. (2009) for HD 175272 (solid line + dashed lines indicating the ±1 − σ uncertainty) and for the reference HD 181420 (mixed lines indicating the uncertainty). Error bars are principally due to the uncertainty in the power density of the background. |
Seismic constraints and their standard errors for HD 181420 and HD 175272.
5. Differential seismic modeling for seismic twins
5.1. Stellar models
Models were constructed using the CESAM2k stellar evolution code (Morel 1997; Morel & Lebreton 2008) for stellar structure and evolution. To establish the oscillation frequencies, we used the adiabatic oscillation code LOSC (Scuflaire et al. 2008). Following the identification of solar-like oscillation properties of HD 181420 (Barban et al. 2009), modes with n = 16–25 and ℓ ≤ 3 were computed.
Three different cases for modeling HD 181420.
We used the EFF equation of state (Eggleton et al. 1973), the OPAL opacity tables (Iglesias & Rogers 1996), complemented at low temperatures with the opacities of Alexander & Ferguson (1994). The nuclear reaction rates were computed using the NACRE compilation (Angulo et al. 1999). The atmosphere was derived assuming a gray Eddington atmosphere. The adopted physical description for the convective zone is the standard mixing-length theory (MLT Böhm-Vitense 1958). We computed two grids of models, one assuming the mixture of Grevesse & Noels (1993) and the other the more recent mixture of Asplund et al. (2005), respectively denoted GN93 and AGS05 hereafter. Diffusion was not considered in the computation of the models.
We divided the problem into two parts. In a first step, we found a reference model that best satisfied the set of observational constraints for HD 181420. The second step was to characterize the lower-S/N target HD 175272 by comparing it with the reference star HD 181420 through a differential analysis.
5.2. Seismic modeling of the reference star HD 181420
In our search for the best model of HD 181420, we considered different sets of constraints. This allowed us to determine the importance of each of them in determining the stellar parameters and to identify the problems that might be related to some of them.
In case I, we only used the seismic constraints
(Δν,νmax) and two free parameters: the age
t and the mass M. The other parameters
(Y,α) were fixed to solar-calibrated values and we adopted the
metallicity given in Table 1. For the relation
between νmax and structure parameters, we adopted the scaling
relation 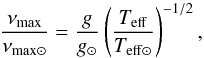 (2)with the unbiased calibration provided by
Mosser et al. (2013). To our surprise, we did not
succeed in finding an acceptable solution in this simple case, since the inferred mass and
radius differed too much from the values expected from the photometric and spectrometric
parameters. This problem and its origin will become clear after the study of the other
cases.
(2)with the unbiased calibration provided by
Mosser et al. (2013). To our surprise, we did not
succeed in finding an acceptable solution in this simple case, since the inferred mass and
radius differed too much from the values expected from the photometric and spectrometric
parameters. This problem and its origin will become clear after the study of the other
cases.
In case II, we took the three constraints
(Δν,νmax,Teff)
and three parameters (M,t,Y0). We did not
consider the luminosity constraint because of its large uncertainty with a relative error
of about 9% (see Table 1). The best solution found
in this case was M = 1.58 M⊙,
t = 1.47 Gyr, Y0 = 0.1982. However, the
agreement between model and observations is still not satisfying in this case. To clarify
this, we simplified the problem even more by adopting the scaling relation for
Δν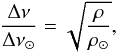 (3)knowing from the modeling by White et al. (2011) that a calibration factor close to
1 is justified here. Adopting the effective temperature given in Table 1 and the two seismic constraints then leads to the
solution: M = 1.58 M⊙,
R = 1.69 R⊙, which are unrealistic values
in view of the effective temperature and standard stellar evolution theory.
(3)knowing from the modeling by White et al. (2011) that a calibration factor close to
1 is justified here. Adopting the effective temperature given in Table 1 and the two seismic constraints then leads to the
solution: M = 1.58 M⊙,
R = 1.69 R⊙, which are unrealistic values
in view of the effective temperature and standard stellar evolution theory.
Finally, in case III, we performed a minimization with four constraints (Δν,νmax, Teff, L/L⊙) and four parameters (M,t,Y0,α): M = 1.53 M⊙, t = 1.46 Gyr, Y0 = 0.1948, α = 1.05. However, some of the stellar parameters we found, such as the mass, the radius, and the luminosity, were unrealistic for solar-like stars.
These results are summarized in Table 5. As a consequence of this preliminary study, a clear difficulty appeared to be finding a model that reproduced a set of constraints including νmax. This could come from an inaccurate measurement of νmax or could indicate that the scaling relation (Eq. (2)) for νmax calibrated on the Sun is too inaccurate for an F2 star such as HD 181420. Again, the case of Procyon justifies that the scaling relations cannot be considered to be accurate for such a star, since the seismic and modeled masses differ by about 25% (see, e.g., Table 1 of Mosser et al. 2013). We note that, because of the stellar mass higher than 1.3 M⊙, the oscillation spectrum of HD 181420 is less accurately described by the asymptotic expansion, the value of the offset ε being significantly lower than expected (Mosser et al. 2013). This may also explain why the scaling relations are not as accurate as for lower-mass stars. The departure from both the νmax and ε scaling relations is caused by the significant changes of the physical properties of the external layers with increasing effective temperature.
Hence, we finally chose to remove this constraint for the seismic modeling of HD 181420. However, we retained it for the differential analysis (see next section). The final set of three constraints adopted for determining the best model is thus Δν, Teff, L/L⊙ (see Tables 1 and 4 for the observed values). We assumed as free parameters the mass M, the age t, and the initial helium abundance Y. For our models, we used the solar mixture of Grevesse & Noels (1993) as well as the new one of Asplund et al. (2005). We used a solar-calibrated value of the mixing-length parameter thoughout. We determined the best models that minimized the χ2 fitting function. Table 6 gives their parameters for the two chemical mixtures. To determine the uncertainty of the model parameters of HD 181420, we used the singular value decomposition method (SVD; for a detailed description, see e.g., Ozel et al. 2011, and references therein).
Best models of HD 181420.
5.3. Differential analysis for HD 175272 with the scaling relation for Δν
As indicated above, the second step was performing a differential seismic analysis of the star HD 175272, based on its similarity with the reference star HD 181420. From Table 1, we see that the estimated luminosities of the two stars are different. This seems unrealistic in view of their very similar other characteristics. Moreover, the luminosity error bar for HD 175272 is very large. We therefore decided to exclude the luminosity difference as a constraint in our differential analysis. The relative differences of observational constraints used as input for our differential analysis are given in Table 7. These values are deduced from Tables 1 and 4. For Z/X0, slight differences are found depending on the adopted solar mixture. With the subscript 1 referring to HD 181420 and 2 to HD 175272, we have (Z/X0)1 = 0.0218 ± 0.0030 and (Z/X0)2 = 0.0295 ± 0.0075 for the mixture of Grevesse & Noels (1993). For the more recent mixture of Asplund et al. (2005), we have (Z/X)⊙ = 0.0165, which leads to (Z/X0)1 = 0.0147 ± 0.0020 and (Z/X0)2 = 0.0198 ± 0.0050.
As previously mentioned, we decided to exclude the constraint νmax in obtaining the reference model of the star HD 181420. Also, both stars, HD 181420 and HD 175272, are very different from the Sun in terms of their mass, radius, and luminosity. Therefore, we assume that Eq. (2) is not accurate enough for comparison of the two stars with the Sun. However, these two stars are similar to each other with respect to their seismic properties. In this situation we can expect that, although the scaling relation is not valid for a comparison with the Sun, it is valid for the comparison between two stars that have similar properties,
Observed relative differences between the two stars used as input for the differential analysis.
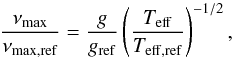 (4)where the index “ref” refers to the values of
the reference star. As a first step, we also assumed that the mean large separation
Δν is proportional to the square root of the stellar density,
(4)where the index “ref” refers to the values of
the reference star. As a first step, we also assumed that the mean large separation
Δν is proportional to the square root of the stellar density,
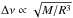 . We therefore used the following scaling
relations:
. We therefore used the following scaling
relations: 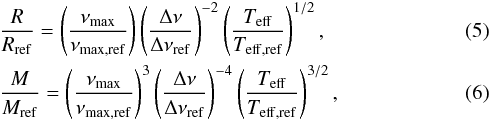 where Teff,
R, M are the effective temperature, radius, and mass
of the stars, respectively. If Δν, νmax and
Teff are known, Eqs. (5) and (6) directly
yield the stellar mass and radius. From Eqs. (5) and (6), we obtain the
differential equations
where Teff,
R, M are the effective temperature, radius, and mass
of the stars, respectively. If Δν, νmax and
Teff are known, Eqs. (5) and (6) directly
yield the stellar mass and radius. From Eqs. (5) and (6), we obtain the
differential equations 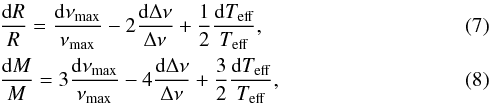 where dR/R
and dM/M are the relative difference in radius and mass
between the two stars, related to the relative differences
dνmax/νmax,
dΔν/Δν and
dTeff/Teff given by the
observations (Table 7). The solutions of Eqs.
(7) and (8) for these input values are given in Table 8. Note that the mass and radius differences found using scaling
relations are independent of stellar evolutionary models. Then, by differentiating the
relations
L = L(M,t,Y0,Z/X0)
and Teff
= Teff(M,t,Y0,Z/X0)
given by the stellar evolutionary tracks and using Stefan-Boltzmann’s law,
where dR/R
and dM/M are the relative difference in radius and mass
between the two stars, related to the relative differences
dνmax/νmax,
dΔν/Δν and
dTeff/Teff given by the
observations (Table 7). The solutions of Eqs.
(7) and (8) for these input values are given in Table 8. Note that the mass and radius differences found using scaling
relations are independent of stellar evolutionary models. Then, by differentiating the
relations
L = L(M,t,Y0,Z/X0)
and Teff
= Teff(M,t,Y0,Z/X0)
given by the stellar evolutionary tracks and using Stefan-Boltzmann’s law,
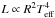 , we obtained the following equations:
, we obtained the following equations:
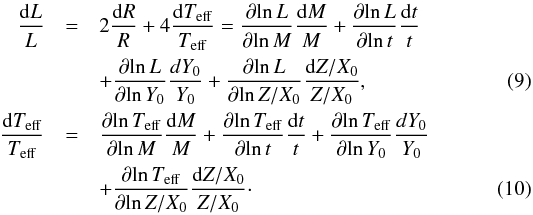 The value of the first term
dR/R on the left-hand side of Eq. (9) and that of the term
dM/M are obtained from previous step (Eqs. (7) and (8)), and the term
dTeff/Teff is obtained from the
observations. Thus, we have a linear system of equations with two unknowns
(dY0/Y0,dt/t),
which then allows us to determine the differences in initial helium abundance and age
between the two stars.
The value of the first term
dR/R on the left-hand side of Eq. (9) and that of the term
dM/M are obtained from previous step (Eqs. (7) and (8)), and the term
dTeff/Teff is obtained from the
observations. Thus, we have a linear system of equations with two unknowns
(dY0/Y0,dt/t),
which then allows us to determine the differences in initial helium abundance and age
between the two stars.
Relative differences between the two stars deduced from our differential analysis, using the scaling relation for Δν.
5.4. Differential analysis for HD 175272 with the full computation of adiabatic frequencies
Relations (7) and (8), which were used in Sect. 5.3, have the advantage of being model independent.
However, scaling relations are known to be approximate. We accordingly also applied a
differential approach that does not use the scaling relation for Δν. As
before, we differentiated the relations
L = L(M,t,Y0,Z/X0)
and
Teff = Teff(M,t,Y0,Z/X0)
given by the stellar evolutionary tracks. We now also differentiated the relation
Δν = Δν(M,t,Y0,Z/X0)
given by complete adiabatic oscillations computations. Finally, we eliminated
dL/L, which is poorly constrained, by differentiating
Stefan-Boltzmann’s law and Eq. (4):
dL/L = dM/M −dνmax/νmax + 7/2 dTeff/Teff.
This finally gave the following linear system (observational constraints are on the
left-hand side and unknowns on the right-hand side): 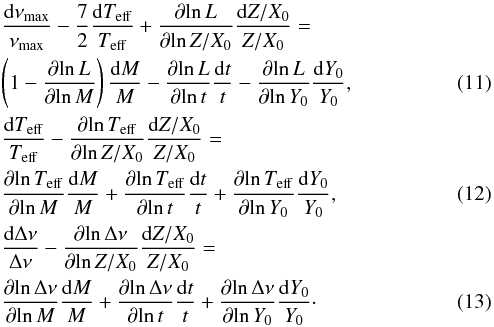 The solutions of these equations are given in
Table 9. We explain below how the relative
differences in radius were obtained (Eq. (17)). Equations (11)–(13) can be formulated in matrix form, which
helps in determining the standard errors on the parameter relative differences. Let
Aij be the 3 × 3 matrix of the linear
system and
xi = (dM/M,dt/t,dY0/Y0)
the three unknowns. With these notations, we have
The solutions of these equations are given in
Table 9. We explain below how the relative
differences in radius were obtained (Eq. (17)). Equations (11)–(13) can be formulated in matrix form, which
helps in determining the standard errors on the parameter relative differences. Let
Aij be the 3 × 3 matrix of the linear
system and
xi = (dM/M,dt/t,dY0/Y0)
the three unknowns. With these notations, we have
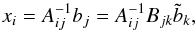 (14)with
(14)with
![\begin{eqnarray} B_{jk}\tilde{b}_{k} = \left( \begin{array}{cccc} 1 & -7/2 & 0 & \displaystyle{\frac{\partial \!\ln L}{\partial \!\ln Z/X_0}} \\[0.3cm] 0 & 1 & 0 & -\displaystyle{\frac{\partial \!\ln T_{\rm eff}}{\partial \!\ln Z/X_0}} \\[0.3cm] 0 & 0 & 1 & -\displaystyle{\frac{\partial\!\ln \Delta \nu}{\partial\! \ln Z/X_0}} \end{array} \right) \left( \begin{array}{c} \displaystyle{\frac{\diff \nu_{\rm max}}{\nu_{\rm max}}} \\[0.3cm] \displaystyle{\frac{\diff \Teff}{\Teff}} \\[0.3cm] \displaystyle{\frac{\diff\Delta\nu}{\Delta\nu}} \end{array} \right). \end{eqnarray}](/articles/aa/full_html/2013/10/aa21846-13/aa21846-13-eq177.png) (15)The variances of
xi are obtained assuming independence of
the constraints
(15)The variances of
xi are obtained assuming independence of
the constraints 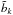 , which gives
, which gives 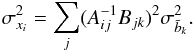 (16)To obtain the relative differences in radii,
we simply differentiated the νmax scaling relation:
(16)To obtain the relative differences in radii,
we simply differentiated the νmax scaling relation:
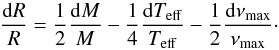 (17)The term
dM/M in the above equation is obtained from the first
line of Eq. (14), which gives
(17)The term
dM/M in the above equation is obtained from the first
line of Eq. (14), which gives ![\begin{equation} \label{dRvector} \frac{\diff R}{R} = \left(\frac{1}{2}({\bf A}^{-1}{\bf B})_{1} + \left(\frac{-1}{2}, \frac{-1}{4}, 0,0\right)\right) \left( \begin{array}{c} \displaystyle{\frac{\diff \nu_{\rm max}}{\nu_{\rm max}}} \\[3mm] \displaystyle{\frac{\diff \Teff}{\Teff}} \\[3mm] \displaystyle{\frac{\diff \Delta\nu}{\Delta\nu}} \\ \end{array} \right). \end{equation}](/articles/aa/full_html/2013/10/aa21846-13/aa21846-13-eq182.png) (18)The variance of
dR/R is thus given by
(18)The variance of
dR/R is thus given by 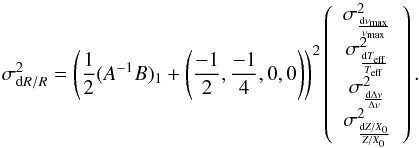 (19)Finally, in Tables 10 and 11, our parameter
estimates for the second star with a low S/N are shown, using the Δν
scaling relation and the full computation of adiabatic frequencies for the two solar
mixtures (GN93 and AGS05), respectively. Through the differential analysis, it is
impossible to determine the parameter uncertainties of HD 175272 alone, because of the
correlation between the constraints y1 and
δy = 2(y2 − y1)/(y1 + y2).
Therefore, we proceeded differently, obtaining the parameter uncertainties by the SVD
method applied to HD 175272 alone. Using the scaling relation for Δν, the
uncertainties on R2 and M2 are
obtained from the propagation of the uncertainties on the observational constraints,
(19)Finally, in Tables 10 and 11, our parameter
estimates for the second star with a low S/N are shown, using the Δν
scaling relation and the full computation of adiabatic frequencies for the two solar
mixtures (GN93 and AGS05), respectively. Through the differential analysis, it is
impossible to determine the parameter uncertainties of HD 175272 alone, because of the
correlation between the constraints y1 and
δy = 2(y2 − y1)/(y1 + y2).
Therefore, we proceeded differently, obtaining the parameter uncertainties by the SVD
method applied to HD 175272 alone. Using the scaling relation for Δν, the
uncertainties on R2 and M2 are
obtained from the propagation of the uncertainties on the observational constraints,
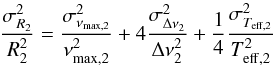 (20)and
(20)and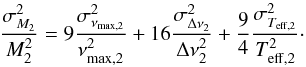 (21)
(21)
Parameters of HD 175272 obtained by adding the results of the differential analysis to those obtained for HD 181420, and using the Δν scaling relation.
6. Discussion
6.1. Using νmax in detailed seismic analysis
Using νmax to establish the best model for the reference star, HD 181420, was not successful. This failure can have been caused by possible observational and theoretical uncertainties. Indeed, νmax may not be the most appropriate quantity for a precise characterization of stars that are very different from the Sun in terms of their stellar parameters such as mass, radius, luminosity, and effective temperature. First of all, from a theoretical point of view, the explanation of the scaling relation νmax − νc remains a matter of debate. Belkacem et al. (2011) have shown that this scaling relation can be understood by assuming a resonance at oscillation frequencies around thermal frequency 1/τ in the super-adiabatic region of the convective envelope. Nevertheless, in addition to a linear relation between the thermal frequency and the cutoff frequency νc, these authors highlighted a strong dependence with respect to the Mach number and the parametrization of convection for instance through the mixing-length parameter. The stars considered in this paper have a significantly higher effective temperature than the Sun, and therefore the characteristics of their convective envelope are very different from that of the Sun: larger Mach numbers and maybe shorter mixing lengths. Hence, it is not surprising that the scaling relations calibrated on the Sun yield poor results for these stars.
Another difficulty that may appear in modeling the reference star is a poor measurement of νmax. The duration of the observations and thus the limited frequency resolution as well as the data analysis methods of the stellar oscillation spectrum can add to the uncertainty on the location of the maximum height in the oscillation power spectrum envelope (Baudin et al. 2011). The solar-like power spectrum shows an excess of power in a broad envelope. The profile of this envelope is assumed to be represented by a Gaussian. Even if this is the common assumption, it is not based on a firm theoretical explanation. For example, this shape is clearly not identified for Procyon (see Fig. 10 from Arentoft et al. 2008).
However, we were able to use νmax when characterizing a second star, HD 175272, with a poor S/N through differential analysis. Indeed, these two stars, HD 181420 and HD 175272, are very similar and we can assume that this is the same for their convection zones. Thus, it appears reasonable to accept the scaling relation νmax − νc as a local scaling for stars with similar convective envelopes.
6.2. Choosing a reference
HD 175272, with an EACF just above the threshold level for detecting solar-like oscillations, corresponds typically to a low-quality oscillation spectrum (Table 3 of Mosser & Appourchaux 2009). As a comparison, the reference HD 181420 has an EACF of about 240, high enough to allow a precise identification of the modes over more than nine radial orders. Even though Barban et al. (2009) proposed two options for the mode identification because this star may be affected by the HD 49933 misidentification syndrome (Appourchaux et al. 2008; Benomar et al. 2009), the ridge identification in HD 181420 is unambiguous (Mosser & Appourchaux 2009; White et al. 2012). Much higher EACF are easily observed in CoRoT and Kepler targets, such as HD 49933 (Benomar et al. 2009), HD 49385 (Deheuvels et al. 2010), or the solar analogs 16 Cyg A and B (Metcalfe et al. 2012). This means that there are a large number of main-sequence stars and subgiants that can serve as seismic references. We consider that an EACF of 100 is enough for the reference, so that we currently identify more than 80 possible references for subgiants and main-sequence stars, according to previous CoRoT and Kepler observations (e.g., Verner et al. 2011). The only domain where the set of reference stars appears to be loose in the main sequence for stars with a lower mass than the Sun is for νmax ≥ 3.6 mHz. In the red giant domain, the number of potential references is huge because it benefits from long observation runs with both CoRoT and Kepler (e.g., Mosser et al. 2010; di Mauro et al. 2011; Stello et al. 2013).
7. Conclusion
We have presented a new approach to determine stellar properties of solar-like stars that we call differential seismology of twins. This method makes it possible to constrain the global characteristics of stars with a low S/N from reference stars observed with a higher S/N.
We applied this method to two CoRoT solar-like stars: HD 181420 with a high S/N oscillation spectrum served as a reference for modeling the secondary target of the first CoRoT short run, HD 175272. This opened a positive perspective for the analysis of low S/N asteroseismic data from the CoRoT and Kepler missions, or for those observed during a short period of time, such as the Kepler one-month time series (Chaplin et al. 2011). These targets can benefit from a comparative analysis. This can be the case for targets showing a peculiar interest, such as members of a double system or stars hosting an exoplanet.
To obtain information on the less-known star HD 175272 from the well-known reference star HD 18142, we first found the best stellar model of HD 181420. We note that a difficulty appeared when we tried to find the best model of the reference star taking into account all observational constraints including νmax. In fact, the two stars considered in this study, HD 181420 and HD 175272, are very different from the Sun in terms of their mass, radius, luminosity, and effective temperature and therefore their seismic properties. This difficulty might originate from either a departure from the linear relation between νmax and νc or an inaccurate measurement of νmax.
Then, we performed a differential analysis to characterize the lower S/N target HD 175272 based on its seismic similarity with the reference star HD 181420. Although the calibration relying on νmax is not appropriate for the reference star HD 181420 compared with the Sun, the two stars HD 181420 and HD 175272 are so close to each other that the scaling relation can be used locally for nearby stars. We therefore decided to assume here that the physical mechanism is the dominant factor in the failure to scale νmax from the Sun to HD 181420.
The results of our differential analysis presented in Tables 8 and 9 show that the standard errors are significant compared with the relative differences. This simply results from the large measurement errors given in Table 7. The differential approach decreases the inaccuracies of the forward seismic analysis, but the precision of the results remains intrinsically related to the precision of the measurements. The very large standard error found for dY0/Y0 is striking. We checked carefully that this is indeed the correct result of our analysis. Degeneracies are often present in the stellar parameters – constraints relation, so that some parameters cannot be determined precisely. This is the case for Y0 in the specific region of the Hertzsprung-Russel diagram corresponding to the twin stars.
Comparing the results found using the scaling relation for Δν (Table 8) with those obtained from a full computation of adiabatic frequencies (Table 9) shows that they are very close. This clearly shows that the inaccuracy of the Δν scaling relation does not affect the results of the differential analysis significantly. For measurement precisions similar to those of this study, it is therefore fully justified to use Eqs. (7) and (8) for an easy and rapid determination of the radius and mass relative differences. Comparing the results obtained with the two solar mixtures gives a lower bound on the inaccuracies of the differential seismic study. Here, the inaccuracies resulting from the choice of the solar mixture are smaller than the imprecisions resulting from the measurements, but not negligible.
With our differential method, the scientific output of many asteroseismic objects with a poor S/N might benefit from the accurate modeling of nearby reference stars with a high S/N. Owing to the large number of asteroseismic targets observed with a high S/N in the many regions of the Hertzsprung-Russel diagram where solar-like oscillations are present, this type of differential seismic analysis allows us to characterize a large number of different types of stars with a low S/N, from red giants to main-sequence stars, and to enhance the precision of the asteroseismic output.
This method is not just useful for characterizing the lower S/N targets. It can can also be applied to very well constrained stars. In this case, it would give a very precise determination of the structural differences between nearby stars. The strength of the differential method is here that the results are less sensitive to the systematic errors coming from both the modeling and the data analysis method.
Acknowledgments
N.O. acknowledges support from the Scientific and Technological Research Council of Turkey (TUBITAK). R.A.G. acknowledges the financial support of the CNES/CoRoT grant at the SAp.
References
- Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Appourchaux, T. 2004, A&A, 428, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Appourchaux, T., Michel, E., Auvergne, M., et al. 2008, A&A, 488, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arentoft, T., Kjeldsen, H., Bedding, T. R., et al. 2008, ApJ, 687, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes III, & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballot, J., Gizon, L., Samadi, R., et al. 2011, A&A, 530, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barban, C., Deheuvels, S., Baudin, F., et al. 2009, A&A, 506, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baudin, F., Barban, C., Belkacem, K., et al. 2011, A&A, 529, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bedding, T. R., Kjeldsen, H., Campante, T. L., et al. 2010, ApJ, 713, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Belkacem, K., Goupil, M. J., Dupret, M. A., et al. 2011, A&A, 530, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benomar, O., Baudin, F., Campante, T. L., et al. 2009, A&A, 507, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
- Bruntt, H., Bikmaev, I. F., Catala, C., et al. 2004, A&A, 425, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaplin, W. J., Kjeldsen, H., Christensen-Dalsgaard, J., et al. 2011, Science, 332, 213 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Deheuvels, S., Bruntt, H., Michel, E., et al. 2010, A&A, 515, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- di Mauro, M. P., Cardini, D., Catanzaro, G., et al. 2011, MNRAS, 415, 3783 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P., Faulkner, J., & Flannery, B. P. 1973, A&A, 23, 325 [NASA ADS] [Google Scholar]
- García, R. A., Régulo, C., Samadi, R., et al. 2009, A&A, 506, 41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaulme, P., Deheuvels, S., Weiss, W. W., et al. 2010, A&A, 524, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, eds. N. Prantzos, E. Vangioni-Flam, & M. Casse, 15 [Google Scholar]
- Hekker, S., Elsworth, Y., Basu, S., et al. 2013, MNRAS, 434, 1668 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Kjeldsen, H., Bedding, T. R., Butler, R. P., et al. 2005, ApJ, 635, 1281 [NASA ADS] [CrossRef] [Google Scholar]
- Mathur, S., García, R. A., Catala, C., et al. 2010, A&A, 518, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Metcalfe, T. S., Chaplin, W. J., Appourchaux, T., et al. 2012, ApJ, 748, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, E., Baglin, A., Auvergne, M., et al. 2008, Science, 322, 558 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Michel, E., Samadi, R., Baudin, F., et al. 2009, A&A, 495, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morel, P. 1997, A&AS, 124, 597 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Morel, P., & Lebreton, Y. 2008, Ap&SS, 316, 61 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mosser, B., & Appourchaux, T. 2009, A&A, 508, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Baudin, F., Lanza, A. F., et al. 2009a, A&A, 506, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Michel, E., Appourchaux, T., et al. 2009b, A&A, 506, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Belkacem, K., Goupil, M.-J., et al. 2010, A&A, 517, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Michel, E., Belkacem, K., et al. 2013, A&A, 550, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olsen, E. H. 1994, A&AS, 106, 257 [NASA ADS] [Google Scholar]
- Ozel, N., Dupret, M.-A., & Baglin, A. 2011, A&A, 532, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poretti, E., Garrido, R., Amado, P. J., et al. 2003, A&A, 406, 203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prugniel, P., & Soubiran, C. 2001, A&A, 369, 1048 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samadi, R., Georgobiani, D., Trampedach, R., et al. 2007, A&A, 463, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scuflaire, R., Montalbán, J., Théado, S., et al. 2008, Ap&SS, 316, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Silva Aguirre, V., Chaplin, W. J., Ballot, J., et al. 2011, ApJ, 740, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Stello, D., Chaplin, W. J., Basu, S., Elsworth, Y., & Bedding, T. R. 2009, MNRAS, 400, L80 [NASA ADS] [CrossRef] [Google Scholar]
- Stello, D., Huber, D., Bedding, T. R., et al. 2013, ApJ, 765, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Teixeira, T. C., Kjeldsen, H., Bedding, T. R., et al. 2009, A&A, 494, 237 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verner, G. A., Elsworth, Y., Chaplin, W. J., et al. 2011, MNRAS, 415, 3539 [NASA ADS] [CrossRef] [Google Scholar]
- White, T. R., Bedding, T. R., Stello, D., et al. 2011, ApJ, 742, L3 [NASA ADS] [CrossRef] [Google Scholar]
- White, T. R., Bedding, T. R., Gruberbauer, M., et al. 2012, ApJ, 751, L36 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Observed relative differences between the two stars used as input for the differential analysis.
Relative differences between the two stars deduced from our differential analysis, using the scaling relation for Δν.
Parameters of HD 175272 obtained by adding the results of the differential analysis to those obtained for HD 181420, and using the Δν scaling relation.
All Figures
 |
Fig. 1 Level-2 light curve of HD 175272. The gray curve shows a low-pass filtering, keeping one point per CoRoT orbit. |
| In the text | |
 |
Fig. 2 Power density spectrum in log-scale axes. The peak around 4 μHz is probably the signature of the stellar rotation; the peak at 23.2 μHz is an artifact due to the low-Earth orbit. The black curve corresponds to a box-car-averaged spectrum, with a varying smoothing window (the size of the window increases linearly with frequency). The dashed line represents the white-noise component; the background is modeled with two Harvey-like components indicated by the dotted lines. |
| In the text | |
 |
Fig. 3 Smoothed power density spectrum (with an apodized 300-μHz FWHM window) in log-scale axes. The dashed line represents the contributions of the granulation signal and of the photon noise. The dotted line is a Gaussian fit of the excess power envelope. The mixed line is the smoothed spectrum of HD 181420, with the same treatment and an offset accounting for the different photon-noise levels. |
| In the text | |
 |
Fig. 4 Automatic determination of the large separation. Dark squares indicate the values of EACF tested in 13 frequency ranges between 2 and 220 μHz. Gray values are artifacts cause by the CoRoT low Earth orbit and must be excluded. The horizontal dashed line indicates the threshold level for a detection at the 1% rejection level. The vertical dark gray line indicates the observed signature at Δν ≃ 75 μHz, and the dash-dotted lines the spurious signatures of the daily aliases (11.6 and 23.2 μHz). |
| In the text | |
 |
Fig. 5 Smoothed density spectrum of HD 175272 (Gaussian filter of width 5 μHz). Gray and white domains indicate frequency ranges with a width equal to the mean large separation. The dot-dashed line gives the spectrum of HD 181420, with frequencies multiplied by a factor 0.996, also smoothed and corrected for the difference between the white-noise contributions. |
| In the text | |
 |
Fig. 6 Amplitude per radial mode determined according to Michel et al. (2009) for HD 175272 (solid line + dashed lines indicating the ±1 − σ uncertainty) and for the reference HD 181420 (mixed lines indicating the uncertainty). Error bars are principally due to the uncertainty in the power density of the background. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


