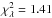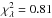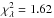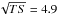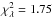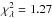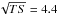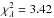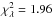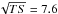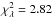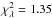| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 11 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201321767 | |
| Published online | 02 October 2013 | |
Calibration of AGILE-GRID with in-flight data and Monte Carlo simulations
1 INAF/IASF-Milano, via E. Bassini 15, 20133 Milano, Italy
e-mail: chen@iasf-milano.inaf.it
2 INAF/IAPS, via Fosso del Cavaliere 100, 00133 Roma, Italy
3 INAF/IASF-Bologna, via Gobetti 101, 40129 Bologna, Italy
4 INFN-Pavia, via Agostino Bassi 6, 27100 Pavia, Italy
5 ASI Science Data Center, via Galileo Galilei, 00044 Frascati Roma, Italy
6 INAF OAR, via di Frascati 33, 00040 Monteporzio Catone, Roma, Italy
7 ENEA Frascati, via Enrico Fermi 13, 00044 Frascati (Roma), Italy
8 Dip. di Fisica, Univ. Tor Vergata, via della Ricerca Scientifica 1, 00133 Roma, Italy
9 CIFS, Villa Gualino – v.le Settimio Severo 63, 10133 Torino, Italy
10 INAF-OAC, localita’ Poggio dei Pini, strada 54, 09012 Capoterra (CA), Italy
11 Dip. Fisica, Univ. Trieste and INFN Trieste, via A. Valerio 2, 34127 Trieste, Italy
12 School of Physics, University of the Witwatersrand, Johannesburg Wits 2050, South Africa
13 Dip. Fisica, Universitá di Torino, via Giuria 1, 10125 Torino, Italy
14 ENEA – Bologna, via Martiri Montesole 4, 40129 Bologna, Italy
15 INFN – Roma La Sapienza, P.le A. Moro 2, 00185 Roma, Italy
16 INFN Roma Tor Vergata, via della Ricerca Scientifica 1, 00133 Roma, Italy
17 Dip. di Fisica, Univ. Dell’Insubria, via Valleggio 11, 22100 Como, Italy
18 Agenzia Spaziale Italiana, Viale Liegi 26, 00198 Roma, Italy
19 INAF – IASF Palermo, via Ugo La Malfa 153, 90146 Palermo, Italy
20 ASTRON, the Netherlands Institute for Radio Astronomy, Postbus 2, 7990 AA, Dwingeloo, The Netherlands
21 Royal Institute of Technology (KTH), Stockholm, Sweden
22 The Oskar Klein Centre for Cosmoparticle Physics, Stockholm, Sweden
Received: 24 April 2013
Accepted: 27 August 2013
Context. AGILE is a γ-ray astrophysics mission which has been in orbit since 23 April 2007 and continues to operate reliably. The γ-ray detector, AGILE-GRID, has observed Galactic and extragalactic sources, many of which were collected in the first AGILE Catalog.
Aims. We present the calibration of the AGILE-GRID using in-flight data and Monte Carlo simulations, producing instrument response functions (IRFs) for the effective area (Aeff), energy dispersion probability (EDP), and point spread function (PSF), each as a function of incident direction in instrument coordinates and energy.
Methods. We performed Monte Carlo simulations at different γ-ray energies and incident angles, including background rejection filters and Kalman filter-based γ-ray reconstruction. Long integrations of in-flight observations of the Vela, Crab and Geminga sources in broad and narrow energy bands were used to validate and improve the accuracy of the instrument response functions.
Results. The weighted average PSFs as a function of spectra correspond well to the data for all sources and energy bands.
Conclusions. Changes in the interpolation of the PSF from Monte Carlo data and in the procedure for construction of the energy-weighted effective areas have improved the correspondence between predicted and observed fluxes and spectra of celestial calibration sources, reducing false positives and obviating the need for post-hoc energy-dependent scaling factors. The new IRFs have been publicly available from the AGILE Science Data Center since November 25, 2011, while the changes in the analysis software will be distributed in an upcoming release.
Key words: instrumentation: detectors / methods: data analysis / techniques: image processing / telescopes / gamma rays: general
© ESO, 2013
1. Introduction
AGILE (Tavani et al. 2009) is an Italian Space Agency (ASI) small scientific mission for high-energy astrophysics launched on April 23, 2007, composed of a pair-production Gamma Ray Imager (GRID) sensitive in the energy range 30 MeV−50 GeV (Barbiellini et al. 2002; Prest et al. 2003), an X-ray Imager (Super-AGILE) sensitive in the energy range 18−60 keV (Feroci et al. 2007), and a mini-calorimeter sensitive to γ-rays and charged particles with energies between 300 keV and 100 MeV (Labanti et al. 2009). AGILE has detected both persistent and variable sources, many of which were collected in the first AGILE Catalog (Pittori et al. 2009) and in a recent study of bright sources variability (Verrecchia et al. 2013).
2. Pre-flight calibration of on-board trigger
The AGILE-GRID is a pair-production telescope with 12 planes of silicon strip detectors, the first 10 of which lie under a pair-conversion tungsten layer (Bulgarelli et al. 2010). The size of the tungsten-silicon tracker is 38.06 × 38.06 × 21.078 cm3 and its on-axis depth totals 0.8 radiation lengths. Monte Carlo simulations (Cocco et al. 2002; Longo et al. 2002) with GEANT3 (Brun & Carminati 1993) were used to determine which on-board filter strategy would produce the reduction in particle and albedo background required by telemetry constraints while maintaining an acceptable effective area for γ-rays, resulting in hardware on-board triggers (Argan et al. 2008) and on-board simplified Kalman filter (Giuliani et al. 2006) for event reconstruction and albedo rejection. These simulations were validated with pre-flight tests with cosmic-ray muons in the clean rooms of Laben (Milan) and CGS (Tortona) (Argan et al. 2008) and with γ-rays at INFN Laboratori Nazionali di Frascati (Cattaneo et al. 2011, 2012).
3. On-ground background rejection filter
The effective area (Aeff), the three-dimensional point spread function (PSF), and the energy dispersion probability (EDP) of AGILE-GRID, collectively referred to as the instrument response functions (IRFs), depend on the direction of the incoming γ-ray in instrument coordinates. Throughout this paper, we will refer to this direction by the angular coordinate Ω = (Θ,Φ), where Θ is the off-axis (polar) angle and Φ the azimuth angle in spherical coordinates (see also Pittori & Tavani 2002).
3.1. Description
Additional processing is required on-ground in order to further reduce the particle background. Detailed analysis of event morphology is used to distinguish γ-rays from charged particles. The first on-ground filter to be used with real flight data F4, used a hard decision tree and severe cuts for γ-rays with Θ > 40° to limit contamination by cosmic-ray electrons and positrons. Since AGILE public data release v2.0 in October 6, 2009, F4 has been replaced by two new filters. A more permissive filter using multivariate analysis, FT3ab, was developed. Further development of the multivariate analysis technique combined with some of the F4 criteria produced a more advanced filter, FM3.119 (also known as FM), which provides a good tradeoff between effective area and background rejection (Bulgarelli et al., in prep.). Each event is classified as a likely gamma-ray (G), uncertain (L), a particle (P) or a single-track event (S). In practice, all scientific analyses other than pulsar timing and gamma-ray bursts have used G events exclusively.
 |
Fig. 1 AGILE effective areas as a function of energy. Effective area = geometric area × fraction of surviving events. The top plot is for Θ = 0°, the bottom plot for Θ = 40°. AGILE curves are for filters FT3ab and FM3.119, event class G. |
 |
Fig. 2 AGILE and Fermi effective areas as a function of energy. The top plot is for Θ = 0°, the bottom plot for Θ = 40°. AGILE curves are for filters FT3ab and FM3.119, event class G. Fermi Pass 7 curves are for version 6, SOURCE event class, front and back events. Fermi IRFs are taken from the Fermi Science Tools, version v9r23p1. The current version is available for public download at http://fermi.gsfc.nasa.gov/ssc/data/analysis/software/. |
3.2. Monte Carlo simulations
To improve and extend the IRFs, we performed additional Monte Carlo simulations after the launch of AGILE. For each set of instrument coordinates (Θ = 1, 30, 35, 40, 45, 50, 60° and Φ = 0, 45°), Ctot = 59 × 106 events were generated from a source with a power-law spectrum whose spectral index is α = −1.7, with energies ranging from 4 MeV to 50 GeV. The events were processed using both the on-board filter and the on-ground event reconstruction procedures, including the background rejection filters.
3.3. Effective area
For the effective area matrix as a function of Ω, the events for each event class were separated into Nm = 16 energy bins, whose boundaries are 10, 35, 50, 71, 100, 141, 200, 283, 400, 632, 1000, 1732, 3000, 5477, 10 000, 20 000, and 50 000 MeV. For each energy bin i containing γ-rays with energies between Ei and Ei + 1, the number of events classified as event class V, is C(i,Ω,V). The effective area Aeff(i,Ω,V) is then defined as 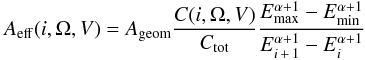 (1)where Ageom is the geometric area of the instrument, Ctot is the total number of events as defined in Sect. 3.2, Emax = ENm + 1 = 50 GeV and Emin = E1 = 10 MeV. Some results are shown in Fig. 1 and compared to the effective area of Fermi-LAT in Fig. 2(Ackermann et al. 2012).
(1)where Ageom is the geometric area of the instrument, Ctot is the total number of events as defined in Sect. 3.2, Emax = ENm + 1 = 50 GeV and Emin = E1 = 10 MeV. Some results are shown in Fig. 1 and compared to the effective area of Fermi-LAT in Fig. 2(Ackermann et al. 2012).
 |
Fig. 3 EDPs for filter FMG at various energy bins (71−100, 100−141, 400−632, and 3000−5477 MeV) at Θ = 30°. Within each bin the true energy follows a power-law distribution (see Sect. 3.2). The solid vertical line is the lower boundary of the true energy bin, while the dotted lines are fixed at 100, 400, and 1000 MeV. |
3.4. Energy dispersion probability
The AGILE energy dispersion matrices use the same energy bins for the true and reconstructed energies. For each event class and set of instrument coordinates, the EDP is the fraction of events within a given true energy bin whose reconstructed energy lies within a given reconstructed energy bin. The EDPs for the G event class of the FM3.119 filter (hereafter referred to as FMG) for selected energy bins at Θ = 30° are shown in Fig. 3. Note that a substantial fraction of γ-rays with true energy below 100 MeV have reconstructed energies above 100 MeV, implying that a substantial fraction of events with reconstructed energies above 100 MeV will have true energies below 100 MeV for most astrophysical γ-ray sources, which tend to have spectral indices α ≈ −2. Any γ-ray source which emits primarily below 100 MeV will also be detected in the nominal E > 100 MeV band. Meanwhile, a majority of γ-rays with true energy above 1 GeV have reconstructed energies below 1 GeV. Any γ-ray source which emits primarily above 1 GeV will have most of its flux reconstructed in the 400 MeV < E < 1000 MeV band. Both of these effects are due to the limitations of multiple scattering as the primary method of energy reconstruction; at lower energies, a certain fraction of events will nevertheless be scattered at small angles (where the peak of the angular distribution lies; see the description in the next section), while at high energies the pitch of the silicon microstrips, 121 μm, is too coarse to measure the scattering angle and the Mini-Calorimeter reaches its saturation point. The relationship between true and observed energy is shown in Figs. 3 and 4. The AGILE-GRID analysis software takes these factors into account, but discrepancies may arise if the spectral index is fixed to the wrong value or if the spectrum diverges significantly from a power law.
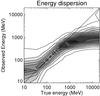 |
Fig. 4 EDP for filter FMG at Θ = 30°. Note the deviations from linearity below 100 MeV and above 400 MeV. |
3.5. Point spread function
A series of γ-rays from the same direction in instrument coordinates will have a distribution of reconstructed directions, an effect known as point spread dispersion (PSD). The PSF, which also depends on the γ-ray energy and event class, is defined as the probability distribution of the angular distance θ between the reconstructed and the true direction. The PSF is estimated from Monte Carlo simulations. Some examples of PSFs are shown in Figs. 5 and 6.
 |
Fig. 5 Monoenergetic PSFs at Θ = 30° with filter FMG at 100, 400, and 1000 MeV. The I0007 PSF matrices were created by directly binning the Monte Carlo data, dividing the raw histogram by sinθ, and normalizing. The I0010 PSF matrices are identical to those of I0007. |
 |
Fig. 6 Monoenergetic PSFs at Θ = 30° with filter FMG at 100, 400, and 1000 MeV. The I0023 PSF matrices were created by first fitting Eq. (8) to the Monte Carlo data, then binning the values of the King function and normalizing. |
4. Fluxes, spectra and PSFs of real sources
The flux and spectrum of any physical point source can be decomposed into a series of monoenergetic point sources whose fluxes are equal to the differential flux of the point source at each energy. Each monoenergetic point source has a well-defined Aeff, EDP, and PSF. These quantities are used to calculate the composite effective area and PSF of the physical source depending on its spectrum and coordinates in the instrument frame.
Several versions of the IRFs have been used for the AGILE-GRID analysis. Version I0007, used internally since the beginning of 2009 and released publicly on May 22, 2009 in software release 3.0 by the AGILE Data Center1, part of the ASI Science Data Center (ASDC), used histograms directly binned from Monte Carlo data for the PSFs, without fitting to any analytic function. Version I0010, used internally from August 2009 until the end of 2010 and never released in public software packages, used the same directly binned PSFs, but introduced correction factors into the effective area matrices in a first attempt to account for energy dispersion when calculating the effective area for real sources. Finally, the latest version (I0023), used internally by the AGILE team since the end of 2010, and publicly included in ASDC software release 5.0 on November 25, 2011, fills the PSFs with an analytic King function fit to the Monte Carlo data, while removing the effective area correction factors introduced into I0010. A new exposure generation procedure which accounts for energy dispersion will be included in an upcoming software release. These characteristics are summarized in Table 1.
Versions of the AGILE-GRID IRFs.
4.1. Effective area
Suppose that a γ-ray source has a power-law spectrum dN/dE = NEα. Then the flux in the energy bin i is 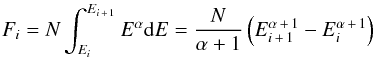 (2)and the total flux between energies Ea and Eb is
(2)and the total flux between energies Ea and Eb is 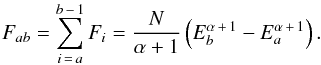 (3)If an instrument with Aeff(i,Ω,V) for γ-rays whose true energy lies within energy bin i is exposed to the source for time t, the number of counts in each energy bin is
(3)If an instrument with Aeff(i,Ω,V) for γ-rays whose true energy lies within energy bin i is exposed to the source for time t, the number of counts in each energy bin is 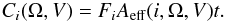 If EDP(i,j,Ω,V) is the fraction of γ-rays whose true energy lies in energy bin i which have reconstructed energy within energy bin j, the number of counts from the full source spectrum whose reconstructed energy lies in energy bin j is
If EDP(i,j,Ω,V) is the fraction of γ-rays whose true energy lies in energy bin i which have reconstructed energy within energy bin j, the number of counts from the full source spectrum whose reconstructed energy lies in energy bin j is 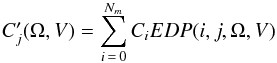 with Nm defined as in Sect. 3.3. Therefore the total number of counts whose observed energies lie between Ea and Eb is
with Nm defined as in Sect. 3.3. Therefore the total number of counts whose observed energies lie between Ea and Eb is  (4)where both the effective areas and EDPs for individual energy bins and the observed effective areas are functions of the γ-ray direction Ω in instrument coordinates and event type V.
(4)where both the effective areas and EDPs for individual energy bins and the observed effective areas are functions of the γ-ray direction Ω in instrument coordinates and event type V.
The effective area with respect to an interval of observed energies Ea and Eb is defined as the number of counts whose observed energies lie between Ea and Eb (Eq. (4)) divided by the true flux between Ea and Eb (Eq. (3)) divided by the time of observation t as follows: 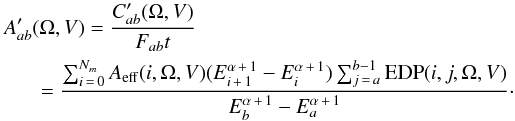 (5)Note that
(5)Note that 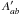 can be expressed as a weighted sum of Aeff(i,Ω,V) as follows:
can be expressed as a weighted sum of Aeff(i,Ω,V) as follows: 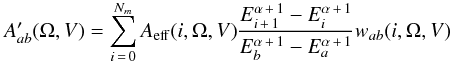 where
where 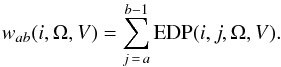 (6)As of this writing, a simpler formula for the energy weight, not taking into account the EDPs, has been used, where the scaling factors wab(i,Ω,V) were set equal to 1 for the first version of the IRFs (I0007), and determined post-hoc as a function of instrument coordinates Ω according to the procedure in Sect. 5.1. These post-hoc scaling factors were incorporated directly into the effective area matrices in version I0010 of the IRFs.
(6)As of this writing, a simpler formula for the energy weight, not taking into account the EDPs, has been used, where the scaling factors wab(i,Ω,V) were set equal to 1 for the first version of the IRFs (I0007), and determined post-hoc as a function of instrument coordinates Ω according to the procedure in Sect. 5.1. These post-hoc scaling factors were incorporated directly into the effective area matrices in version I0010 of the IRFs.
However, we have found too limited the range of spectral indices for which this simplified formula is applicable, and are implementing the correct formula in the soon-to-be-released BUILD 22 of the software.
4.2. Point spread function
The PSF for a physical source observed in an interval of reconstructed energies is the weighted average of the PSFs in individual energy bins, where the weight of each energy bin is proportional to the product of the effective area, the flux in the energy bin (determined by the source spectrum), and the fraction of γ-rays from the energy bin whose reconstructed energy lies within the observed reconstructed energy interval (determined by the EDP). If the source has power-law index α between energies Ea and Eb, the PSF is 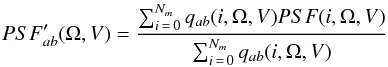 (7)where
(7)where 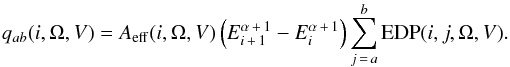 Earlier versions (I0007/I0010) of the PSF matrices used histograms taken directly from the Monte Carlo simulations. The updated PSF matrices (I0023) contain values derived from a fit to the Monte Carlo data using a modified King function (King 1962) used to characterize high-energy PSFs (Kirsch et al. 2004; Read et al. 2011) f(θ), which has three parameters, B, the (arbitrary) normalization, δ, the characteristic width, and γ, which is related to the relative strength of the core vs. the tail, as follows:
Earlier versions (I0007/I0010) of the PSF matrices used histograms taken directly from the Monte Carlo simulations. The updated PSF matrices (I0023) contain values derived from a fit to the Monte Carlo data using a modified King function (King 1962) used to characterize high-energy PSFs (Kirsch et al. 2004; Read et al. 2011) f(θ), which has three parameters, B, the (arbitrary) normalization, δ, the characteristic width, and γ, which is related to the relative strength of the core vs. the tail, as follows: 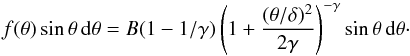 (8)The PSF matrices are then filled with the values derived from the King function with a bin size of 0.1°.
(8)The PSF matrices are then filled with the values derived from the King function with a bin size of 0.1°.
We compare the 68% γ-ray containment radii (CRs) of the PSFs in single, true energy bins (Table 2) with those of the composite PSFs in broad, reconstructed energy intervals (Table 3). Note that the CR for the reconstructed E > 1 GeV interval is broader than that of the true E = 1 GeV bin. This is because, as we showed in Sect. 3.4, the reconstructed E > 1 GeV interval is dominated by γ-rays whose true energy is actually below 1 GeV.
68% γ-ray Containment Radii (CRs) of monoenergetic PSFs.
68% γ-ray Containment Radii (CRs) of composite PSFs.
 |
Fig. 7 Observed flux of the source at the position of the Vela pulsar for E > 100 MeV as a function of Θ with the I0007 IRFs. The linear fit to these fluxes were used to calculate the effective area correction factors in the I0010 IRFs. |
5. Comparison to in-flight data
We generated long-term integrations of AGILE-GRID in-flight data in both pointing (2007/07/09−2009/10/15) and spinning (2009/11/04−2010/10/31) modes of the Vela and anti-center regions, generating counts and exposure maps with a bin size of 0.3°. The AGILE maximum likelihood analysis (Bulgarelli et al. 2012) was performed taking into account the Galactic diffuse emission and the isotropic background, and the following bright point sources: the Vela point source, which comprises both the pulsar and the pulsar wind nebula (PWN), and the Crab and Geminga point sources and IC443 in the anti-center region, where the Crab point source also comprises both the pulsar and the PWN, all with fixed source locations and fixed, power-law spectra. Model counts were compared to data to validate the PSF, while spectra and fluxes were compared to those published in the Third EGRET catalog (hereafter 3EG, Hartman et al. 1999) in order to determine the post-hoc scaling factors introduced in 4.1 that were incorporated into the I0010 effective area matrices and calculated according to the procedure described in the following subsection.
5.1. Fluxes and spectra: correction factors
To create the I0010 version of the effective area matrices, we compared the fluxes for E > 100 MeV obtained using the I0007 effective areas with the AGILE likelihood analysis of the Vela pulsar at different off-axis angles with those expected from the fluxes and spectra reported in the Fermi Large Area Telescope First Source Catalog (hereafter 1FGL, Abdo et al. 2010). A linear fit was performed on the fluxes produced by the analysis (Fig. 7). The correction factors were set equal to the inverse of the ratio between the fluxes implied by the fit parameters and the 1FGL fluxes for Θ < 60° and set equal to the value at 60° for Θ ≥ 60°. These were applied to the original effective areas to produce new effective areas to be used in AGILE analysis.
However, when attempting to reproduce this procedure for the updated IRFs, we discovered that the fluxes and spectra of the softer spectrum of the Crab were overestimated. In fact, the likelihood analysis of the Crab pulsar using IRFs with no correction factors applied produces fluxes not far from the desired value, albeit with distortions in the spectrum.
 |
Fig. 8 Fluxes of the source at the position of the Vela pulsar found using the new effective area calculation (I0023) and the new PSF (I0023) for long integrations in pointing (red diamonds) and spinning (blue squares) mode. The black curve represents the flux and spectrum listed in 1FGL. No curve fitting was performed. |
 |
Fig. 9 Fluxes of the source at the position of the Crab pulsar found using the new effective area calculation (I0023) and the new PSF (I0023) for long integrations in pointing (red diamonds) and spinning (blue squares) mode. The black curve represents the flux and spectrum listed in 1FGL. No curve fitting was performed. |
 |
Fig. 10 Observed counts vs. model with PSF at the Vela source, E > 100 MeV, pointing mode. The error bars are Poisson errors around the sum of the counts within 10° × 0.25° slices in galactic longitude (top) and galactic latitude (bottom). The data are compared to a model (solid curve) composed of an isotropic component (dash-dot), a galactic diffuse component (dash), and a point source (dash-dot-dot-dot) with reduced |
5.2. Fluxes and spectra: a new routine for generating exposure
As a result, we concluded that scaling factors alone were unable to correct for the flux and spectra simultaneously for sources with both hard and soft spectra. We have revised the exposure generation routines to use the true effective area formula in Eq. (5). We compare the results to the 1FGL spectra of Vela in Fig. 8 and the Crab in Fig. 9. In both cases, the AGILE analysis software assumes an unbroken power law with a single spectral index and is therefore unable to model the exponential cutoff above 2.9 GeV in the case of Vela and 5.8 GeV in the case of the Crab. Also, because 1FGL and the AGILE observations cover slightly different epochs, the Crab flux and spectrum may be affected by variability (Tavani et al. 2011; Abdo et al. 2011).
5.3. Point spread function
The PSFs as calculated in Eq. (7) were compared to the count maps generated by the long integrations in pointing and spinning mode for all three pulsars, Vela, Crab, and Geminga, both as a function of energy bin and for the full energy range from 100 MeV to 50 GeV. The PSFs show varying levels of agreement with the data. Examples are shown in Figs. 10−13. In each of these figures, the number of counts were integrated within 10° × 0.25° slices in galactic longitude and galactic latitude and compared to a model comprising an isotropic component, a galactic diffuse component, and a point source component (see Eq. (7)). The coefficients of the components were determined using the AGILE analysis software.
 |
Fig. 11 Observed counts vs. model with PSF at the Vela source, E > 400 MeV, pointing mode. The error bars are Poisson errors around the sum of the counts within 10° × 0.25° slices in galactic longitude (top) and galactic latitude (bottom). The data are compared to a model (solid curve) composed of an isotropic component (dash-dot), a galactic diffuse component (dash), and a point source (dash-dot-dot-dot) with reduced |
To estimate the goodness of fit, we calculated the maximum likelihood ratio statistic (Baker & Cousins 1984), ![\begin{equation} \chi_{\lambda}^2 = 2 \sum_{i\,=\,1}^{N}\left[ M_i - C_i + C_i \ln\left(\frac{C_i}{M_i}\right)\right], \label{eq_ml} \end{equation}](/articles/aa/full_html/2013/10/aa21767-13/aa21767-13-eq90.png) (9)where Ci is the number of counts and Mi the number predicted by the model in each 10° × 0.25° slice. The reduced
(9)where Ci is the number of counts and Mi the number predicted by the model in each 10° × 0.25° slice. The reduced 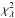 is found by dividing by the number of degrees of freedom, which in this case is 38 (43 slices −3 free parameters).
is found by dividing by the number of degrees of freedom, which in this case is 38 (43 slices −3 free parameters).
 |
Fig. 12 Observed counts vs. model with PSF at the Vela source, E > 100 MeV, spinning mode. The error bars are Poisson errors around the sum of the counts within 10° × 0.25° slices in galactic longitude (top) and galactic latitude (bottom). The data are compared to a model (solid curve) composed of an isotropic component (dash-dot), a galactic diffuse component (dash), and a point source (dash-dot-dot-dot) with reduced |
 |
Fig. 13 Observed counts vs. model with PSF at the Vela source, E > 400 MeV, spinning mode. The error bars are Poisson errors around the sum of the counts within 10° × 0.25° slices in galactic longitude (top) and galactic latitude (bottom). The data are compared to a model (solid curve) composed of an isotropic component (dash-dot), a galactic diffuse component (dash), and a point source (dash-dot-dot-dot) with reduced |
In some cases, the real PSF appears to be broader than the model predicts, particularly in spinning mode. One possible source of this broadening is systematic error in the measurement of the spacecraft orientation. For each AGILE observation in both pointing and spinning mode, we smoothed the two-dimensional model with a simple Gaussian and found the Gaussian width σ which minimized 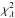 . The difference
. The difference 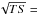 unreduced
unreduced 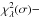 unreduced
unreduced 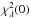 should be distributed as χ2 with one degree of freedom and therefore be statistically significant when it is greater than 5. Best fit Gaussian smoothed model PSFs are shown in Figs. 10−13. Figures 14 and 15 show the reduced
should be distributed as χ2 with one degree of freedom and therefore be statistically significant when it is greater than 5. Best fit Gaussian smoothed model PSFs are shown in Figs. 10−13. Figures 14 and 15 show the reduced 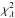 with and without Gaussian smoothing.
with and without Gaussian smoothing.
 |
Fig. 14 Reduced |
 |
Fig. 15 Reduced |
Figure 16 shows the best fit σ as a function of Θ. The values of σ are roughly consistent with ≈0.3°. However, in Fig. 17, we see that 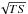 shows a statistically significant improvement only in the case of the observations in spinning mode. These results are consistent with the hypothesis of a systematic error in the measurement of the spacecraft orientation in spinning mode.
shows a statistically significant improvement only in the case of the observations in spinning mode. These results are consistent with the hypothesis of a systematic error in the measurement of the spacecraft orientation in spinning mode.
 |
Fig. 16 Best-fit Gaussian smoothing width σ for AGILE observations of E > 100 MeV (top) and E > 400 MeV (bottom). Galactic longitude slices in pointing (solid black) and spinning (red dotted) mode; Galactic latitude slices in pointing (magenta dashed) and spinning (blue dot-dash) mode. The widths are roughly consistent with ≈0.3°. |
 |
Fig. 17 Significance of improvement |
A refined attitude reconstruction method using Kalman filtering techniques, optimized for the AGILE spinning observation mode, has been recently developed by the Compagnia Generale per lo Spazio (CGS), in joint collaboration with the ASDC. CGS is the prime industrial contractor of the AGILE mission, being in charge of design development and integration of the complete satellite. Star Sensor data in spinning mode are noisier, and present short gaps due to occasional blinding. The new attitude reconstruction improves the efficiency and the quality of the attitude measurement. A new analysis of in-flight spinning data reprocessed with the new attitude reconstruction is in progress at ASDC, and the results will be presented elsewhere.
6. Conclusions
The on-ground background rejection filters used by AGILE-GRID have been optimized a number of times to increase the effective area while maintaining a reasonable level of instrumental and cosmic-ray background. To validate and keep pace with these changes, the monoenergetic PSFs and EDPs produced by Monte Carlo simulations and validated by pre-launch tests were compared to in-flight data.
The effective area calculations in narrow and wide reconstructed energy bands show extreme sensitivity to the assumed spectral index due to the large energy dispersion. As a result, for day-to-day analysis, correction factors were calculated and introduced into the effective area matrices as a substitute for the full energy dispersion calculation.
These correction factors produced valid results only for a limited range of source spectra. A new version of the analysis software, soon to be released by the ASDC, properly takes into account the energy dispersion when calculating the energy-dependent effective area. The software may now be used to calculate the spectral index through simultaneous analysis of the data divided into energy intervals. By comparing the calculated index to the index initially assumed to generate the exposure files and PSFs and iterating, the true flux and spectral index of the source may then be found. Strong deviations from power-law spectral behavior are not implemented and may lead to distortions, particularly at low and high energies where a large portion of the flux may come from outside the nominal energy bins.
The in-flight PSFs for real sources in pointing mode agree with those predicted by the Monte Carlo simulations, while those in spinning mode differ significantly. This effect is probably due to systematic error in the Star Sensor measurement of the spacecraft orientation in spinning mode. A new optimized attitude reconstruction method currently under testing at ASDC should be able to correct this systematic error, which broadens the PSF by ≈0.3° for spinning mode observations.
AGILE and Fermi have different pointing strategies and are sensitive to variability on different timescales. In addition, at any given time AGILE and Fermi pointed toward different areas on the sky. AGILE-GRID therefore remains a completely complementary instrument for the detection of rapid transient phenomena.
Acknowledgments
We would like to thank the Istituto Nazionale di Astrofisica, the Agenzia Spaziale Italiana, the Consorzio Interuniversitario per la Fisica Spaziale, and the Istituto Nazionale di Fisica Nucleare for their generous support of the AGILE mission and this research, including ASI contracts N. I/042/10/1 and I/028/12/0. We would also like to thank the journal referee, whose comments helped to substantially improve this paper.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJS, 188, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, Science, 331, 739 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2012, ApJS, 203, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Argan, A., Tavani, M., Trois, A., et al. 2008, in Nucl. Sci. Symp. Conf. Record, 2008. NSS ’08. IEEE (IEEE), 774 [Google Scholar]
- Baker, S., & Cousins, R. D. 1984, Nucl. Instrum. Methods Phys. Res., 221, 437 [Google Scholar]
- Barbiellini, G., Fedel, G., Liello, F., et al. 2002, Nucl. Instr. Meth. A, 490, 146 [Google Scholar]
- Brun, R., & Carminati, F. 1993, GEANT – Detector Description and Simulation Tool, CERN Program Library Long Writeup W5013, CERN Geneva, Switzerland, CH-1211 Geneva 23, Switzerland [Google Scholar]
- Bulgarelli, A., Argan, A., Barbiellini, G., et al. 2010, Nucl. Instr. Meth. A, 614, 213 [Google Scholar]
- Bulgarelli, A., Chen, A. W., Tavani, M., et al. 2012, A&A, 540, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cattaneo, P. W., Argan, A., Boffelli, F., et al. 2011, Nucl. Instr. Meth. A, 630, 251 [Google Scholar]
- Cattaneo, P. W., Argan, A., Boffelli, F., et al. 2012, Nucl. Instr. Meth. A, 674, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Cocco, V., Longo, F., & Tavani, M. 2002, Nucl. Instr. Meth. A, 486, 623 [Google Scholar]
- Feroci, M., Costa, E., Soffitta, P., et al. 2007, Nucl. Instr. Meth. A, 581, 728 [Google Scholar]
- Giuliani, A., Cocco, V., Mereghetti, S., Pittori, C., & Tavani, M. 2006, Nucl. Instr. Meth. A, 568, 692 [Google Scholar]
- Hartman, R. C., Bertsch, D. L., Bloom, S. D., et al. 1999, ApJS, 123, 79 [NASA ADS] [CrossRef] [Google Scholar]
- King, I. 1962, AJ, 67, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Kirsch, M. G. F., Altieri, B., Chen, B., et al. 2004, in SPIE Conf. Ser. 5488, eds. G. Hasinger, & M. J. L. Turner, 103 [Google Scholar]
- Labanti, C., Marisaldi, M., Fuschino, F., et al. 2009, Nucl. Instr. Meth. A, 598, 470 [Google Scholar]
- Longo, F., Cocco, V., & Tavani, M. 2002, Nucl. Instr. Meth. A, 486, 610 [Google Scholar]
- Pittori, C., & Tavani, M. 2002, Nucl. Instr. Meth. A, 488, 295 [Google Scholar]
- Pittori, C., Verrecchia, F., Chen, A. W., et al. 2009, A&A, 506, 1563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prest, M., Barbiellini, G., Bordignon, G., et al. 2003, Nucl. Instr. Meth. A, 501, 280 [Google Scholar]
- Read, A. M., Rosen, S. R., Saxton, R. D., & Ramirez, J. 2011, A&A, 534, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tavani, M., Barbiellini, G., Argan, A., et al. 2009, A&A, 502, 995 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tavani, M., Bulgarelli, A., Vittorini, V., et al. 2011, Science, 331, 736 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Verrecchia, F., Pittori, C., Chen, A. W., et al. 2013, A&A, in press, DOI: 10.1051/0004-6361/201321452 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 AGILE effective areas as a function of energy. Effective area = geometric area × fraction of surviving events. The top plot is for Θ = 0°, the bottom plot for Θ = 40°. AGILE curves are for filters FT3ab and FM3.119, event class G. |
| In the text | |
 |
Fig. 2 AGILE and Fermi effective areas as a function of energy. The top plot is for Θ = 0°, the bottom plot for Θ = 40°. AGILE curves are for filters FT3ab and FM3.119, event class G. Fermi Pass 7 curves are for version 6, SOURCE event class, front and back events. Fermi IRFs are taken from the Fermi Science Tools, version v9r23p1. The current version is available for public download at http://fermi.gsfc.nasa.gov/ssc/data/analysis/software/. |
| In the text | |
 |
Fig. 3 EDPs for filter FMG at various energy bins (71−100, 100−141, 400−632, and 3000−5477 MeV) at Θ = 30°. Within each bin the true energy follows a power-law distribution (see Sect. 3.2). The solid vertical line is the lower boundary of the true energy bin, while the dotted lines are fixed at 100, 400, and 1000 MeV. |
| In the text | |
 |
Fig. 4 EDP for filter FMG at Θ = 30°. Note the deviations from linearity below 100 MeV and above 400 MeV. |
| In the text | |
 |
Fig. 5 Monoenergetic PSFs at Θ = 30° with filter FMG at 100, 400, and 1000 MeV. The I0007 PSF matrices were created by directly binning the Monte Carlo data, dividing the raw histogram by sinθ, and normalizing. The I0010 PSF matrices are identical to those of I0007. |
| In the text | |
 |
Fig. 6 Monoenergetic PSFs at Θ = 30° with filter FMG at 100, 400, and 1000 MeV. The I0023 PSF matrices were created by first fitting Eq. (8) to the Monte Carlo data, then binning the values of the King function and normalizing. |
| In the text | |
 |
Fig. 7 Observed flux of the source at the position of the Vela pulsar for E > 100 MeV as a function of Θ with the I0007 IRFs. The linear fit to these fluxes were used to calculate the effective area correction factors in the I0010 IRFs. |
| In the text | |
 |
Fig. 8 Fluxes of the source at the position of the Vela pulsar found using the new effective area calculation (I0023) and the new PSF (I0023) for long integrations in pointing (red diamonds) and spinning (blue squares) mode. The black curve represents the flux and spectrum listed in 1FGL. No curve fitting was performed. |
| In the text | |
 |
Fig. 9 Fluxes of the source at the position of the Crab pulsar found using the new effective area calculation (I0023) and the new PSF (I0023) for long integrations in pointing (red diamonds) and spinning (blue squares) mode. The black curve represents the flux and spectrum listed in 1FGL. No curve fitting was performed. |
| In the text | |
 |
Fig. 10 Observed counts vs. model with PSF at the Vela source, E > 100 MeV, pointing mode. The error bars are Poisson errors around the sum of the counts within 10° × 0.25° slices in galactic longitude (top) and galactic latitude (bottom). The data are compared to a model (solid curve) composed of an isotropic component (dash-dot), a galactic diffuse component (dash), and a point source (dash-dot-dot-dot) with reduced |
| In the text | |
 |
Fig. 11 Observed counts vs. model with PSF at the Vela source, E > 400 MeV, pointing mode. The error bars are Poisson errors around the sum of the counts within 10° × 0.25° slices in galactic longitude (top) and galactic latitude (bottom). The data are compared to a model (solid curve) composed of an isotropic component (dash-dot), a galactic diffuse component (dash), and a point source (dash-dot-dot-dot) with reduced |
| In the text | |
 |
Fig. 12 Observed counts vs. model with PSF at the Vela source, E > 100 MeV, spinning mode. The error bars are Poisson errors around the sum of the counts within 10° × 0.25° slices in galactic longitude (top) and galactic latitude (bottom). The data are compared to a model (solid curve) composed of an isotropic component (dash-dot), a galactic diffuse component (dash), and a point source (dash-dot-dot-dot) with reduced |
| In the text | |
 |
Fig. 13 Observed counts vs. model with PSF at the Vela source, E > 400 MeV, spinning mode. The error bars are Poisson errors around the sum of the counts within 10° × 0.25° slices in galactic longitude (top) and galactic latitude (bottom). The data are compared to a model (solid curve) composed of an isotropic component (dash-dot), a galactic diffuse component (dash), and a point source (dash-dot-dot-dot) with reduced |
| In the text | |
 |
Fig. 14 Reduced |
| In the text | |
 |
Fig. 15 Reduced |
| In the text | |
 |
Fig. 16 Best-fit Gaussian smoothing width σ for AGILE observations of E > 100 MeV (top) and E > 400 MeV (bottom). Galactic longitude slices in pointing (solid black) and spinning (red dotted) mode; Galactic latitude slices in pointing (magenta dashed) and spinning (blue dot-dash) mode. The widths are roughly consistent with ≈0.3°. |
| In the text | |
 |
Fig. 17 Significance of improvement |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.