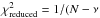| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321664 | |
| Published online | 10 October 2013 | |
Physical properties of asteroid 308635 (2005 YU55) derived from multi-instrument infrared observations during a very close Earth approach ⋆
1 Max-Planck-Institut für extraterrestrische Physik, Giessenbachstraße, Postfach 1312, 85741 Garching, Germany
e-mail: tmueller@mpe.mpg.de
2 Institute of Astronomy, School of Science, the University of Tokyo, 2-21-1 Osawa, Mitaka, 181-0015 Tokyo, Japan
e-mail: tmiyata@ioa.s.u-tokyo.ac.jp
3 Konkoly Observatory, Research Center for Astronomy and Earth Sciences, Hungarian Academy of Sciences, Konkoly Thege 15-17, 1121 Budapest, Hungary
4 Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
5 Institute of Space and Astronautical Science, Japan Aerospace Exploration Agency, 3-1-1 Yoshinodai, Sagamihara, 229-8510 Kanagawa, Japan
6 Department of Astronomy, Graduate School of Science, The University of Tokyo, Hongo 7-3-1, Bunkyo-ku, 113-0033 Tokyo, Japan
7 Planetary Plasma and Atmospheric Research Center, Tohoku University, Aramaki, Aoba-ku, 980-8578 Sendai, Japan
8 Astronomical Institute, Graduate School of Science, Tohoku University, Aramaki, Aoba-ku, 980-8578 Sendai, Japan
9 European Space Astronomy Centre (ESAC), European Space Agency, Apartado de Correos 78, 28691 Villanueva de la Cañada, Madrid, Spain
Received: 8 April 2013
Accepted: 29 July 2013
The near-Earth asteroid 308635 (2005 YU55) is a potentially hazardous asteroid which was discovered in 2005 and passed Earth on Nov. 8, 2011 at 0.85 lunar distances. This was the closest known approach by an asteroid of several hundred metres in diameter since 1976 when an object of similar size passed at 0.5 lunar distances. We observed 2005 YU55 from the ground with a recently developed mid-IR camera (miniTAO/MAX38) in N and Q bands and with the Submillimeter Array (SMA) at 1.3 mm. In addition, we obtained space observations with Herschel/PACS at 70, 100, and 160 μm. Our thermal measurements cover a wide range of wavelengths from 8.9 μm to 1.3 mm and were taken after opposition at phase angles between –97° and –18°. We performed a radiometric analysis via a thermophysical model and combined our derived properties with results from radar, adaptive optics, lightcurve observations, speckle, and auxiliary thermal data. We find that 308635 (2005 YU55) has an almost spherical shape with an effective diameter of 300 to 312 m and a geometric albedo pV of 0.055 to 0.075. Its spin axis is oriented towards celestial directions (λecl, βecl) = (60° ± 30°, –60° ± 15°), which means it has a retrograde sense of rotation. The analysis of all available data combined revealed a discrepancy with the radar-derived size. Our radiometric analysis of the thermal data together with the problem to find a unique rotation period might be connected to a non-principal axis rotation. A low to intermediate level of surface roughness (rms mean slope in the range 0.1–0.3) is required to explain the available thermal measurements. We found a thermal inertia in the range 350−800 Jm-2 s-0.5 K-1, very similar to the rubble-pile asteroid 25 143 Itokawa and indicating a surface with a mixture of low conductivity fine regolith with larger rocks and boulders of high thermal inertia.
Key words: minor planets, asteroids: individual: (308635) 2005 YU55 / radiation mechanisms: thermal / techniques: photometric / infrared: planetary systems
Table 2 is available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
The Apollo- and C-type asteroid 308635 (2005 YU55) is on a Mars-Earth-Venus crossing orbit1 (Vodniza & Pereira 2010; Hicks et al. 2010; Somers et al. 2010). Arecibo radar measurements in April 2010 have shown that 2005 YU55 is a very dark, nearly spherical object2. They estimated a diameter of about 400 m, in contradiction to earlier calculations based on the V-magnitude in combination with a low albedo which led to a diameter estimation of only 250 m.
2005 YU55 had a very close Earth approach in Nov. 2011 when it passed within 0.85 lunar distances (0.85 LD) of the Earth. In January 2029, the asteroid will pass about 0.0023 AU (equivalent to 0.89 LD) from Venus. This close encounter with Venus will determine how close the object will pass the Earth in 2041 and 20453. The JPL Horizons system gives the absolute magnitude of 2005 YU55 as H = 21.1 mag4. No other asteroid with H < 23 mag has been observed to pass inside 1 LD. According to recent orbit simulations it does not pose any risk of an impact with Earth for the next 100 years5. The closest recorded approach by an asteroid of similar characteristics was that of 2004 XP14 (H = 19.4 mag) to 1.1 LD on July 3, 2006, hence the encounter with 2005 YU55 was an exceptional event.
The close Earth approach in Nov. 2011 offered an observing opportunity from ground that lasted several days and also a brief (~16 h) observing window for the Herschel6 Space Observatory located in the Lagrangian point L2 at about 1.5 Mio km from Earth. This was a unique opportunity to study a potentially hazardous asteroid (PHA) in great detail to derive physical and thermal properties which are needed to make long-term orbit predictions and to improve our knowledge of Apollo asteroids in general. We observed this near-Earth asteroid from the ground at mid-IR N and Q bands (miniTAO/MAX38 camera), at millimetre wavelengths (Smithsonian Astrophysical Observatory Submillimeter Array, or SMA), and from space with Herschel/PACS at far-IR wavelengths. We present our observations (Sect. 2), the thermophysical model (TPM) analysis (Sect. 3) and discuss the results (Sect. 4). In this work, we also considered a set of auxiliary data (radar, optical, UV, and thermal measurements) which were only available via unrefereed abstracts, astronomical circulars, and telegrams.
2. Observations
2.1. Groundbased mid-IR observations with MAX38
 |
Fig. 1 Mid-infrared images of 2005 YU55 obtained by the miniTAO/MAX38 camera in the 18.7 μm filter during the time of the closest Earth approach. North is up and west is right. The asteroid moved from right (west) to left (east). |
We observed the asteroid 2005 YU55 in the period Nov. 8−10, 2011 with the mid-IR camera MAX38 (Miyata et al. 2008; Nakamura et al. 2010; Asano et al. 2012) attached on the mini-TAO 1-m telescope (Sako et al. 2008) which is located at 5640 m on the summit of Co. Chajnantor in Chile, which is part of the University of Tokyo Atacama Observatory Project (PI: Yuzuru Yoshii; Yoshii et al. 2010). The MAX38 camera has a 128 × 128 Si:Sb BIB detector with a pixel scale of 1.26 arcsec and a field of view of 2 × 2.5 arcmin determined by the rectangular field stop in the cold optics (the remaining 0.5 × 2.5 arcmin of the detector array is used for spectroscopy). The MAX38 observing periods (Nov. 8 23:04 to Nov. 9 01:51, 2011 UT and from Nov. 9 23:56 to Nov. 10 02:04, 2011 UT) covered the time of the closest approach (Nov. 8 23:24, 2011 UT) and about 24 h later. The weather conditions were excellent through the observations. Imaging observations in the 8.9 μm (Δλ ~ 0.9 μm), 12.2 μm (0.5 μm), and 18.7 μm (0.9 μm) bands were carried out. The star α Tuc (IRAS 22150-6030, HR 8502, HD 211416) was also observed after the observations of the asteroid as a flux standard. The absolute flux value of the standard star was obtained via the α Tuc template spectrum (Cohen et al. 1999).
Since the distance to the asteroid from the Earth was very short, the asteroid had a very high apparent motion on the sky. We pointed the telescope at repeated intervals to follow the asteroid’s movement. The intervals were set to 1 min and 3 min on Nov. 8 and 9, respectively. Normal sidereal tracking was applied in the period between the telescope pointings. Images were taken at a frame rate of 3.8 Hz with an effective integration time of 0.197 s. The frame rate is fast enough not to extend the image of the asteroid on each frame. Chopping technique7 was not applied because the background can be canceled out by using frames just before or after an object frame. The observation parameters are summarised in Table 1 and three examples of reduced images taken at the time of the closest approach are shown in Fig. 1.
MAX38 observation parameters.
Observing geometries (Herschel-centric) and final calibrated flux densities.
On Nov. 8, the asteroid was so bright (observatory-centric distance was about 0.0021–0.0023 AU) that it was detectable in each frame. Sky frames, composed by averaging 7 frames taken within 2 s, were subtracted. This successfully canceled out sky variation similar to observations taken in chopping technique. Aperture photometry with an aperture radius of 3 arcsec was applied for each frame. Photometric values were determined by averaging frames taken in a period of 5 min. Errors were estimated as standard deviation of the photometric values.
On Nov. 9 the asteroid was already at about 0.0084–0.0089 AU distance and it was difficult to detect the asteroid on each frame. Here, we added 92 frames into one image by shifting the frames to compensate for the asteroid’s movement on the sky and subtracted the averaged sky frames. The frame-to-frame shifts were calculated from the ephemeris provided by the NASA Horizons web page8. The asteroid images in the co-added frames appeared nearly point-like and no noticeable extensions were detected. We applied aperture photometry on the final sky-subtracted images. The final flux and error values were again obtained by averaging all individual photometric values.
In addition to the photometric error we also added a 5% absolute flux calibration error for the N-band data and a 7% error for the Q-band data based on the radiometric tolerance discussion in Cohen et al. (1999) and the information given in the stellar template. These errors also include possible colour-terms (estimated to be below 2%) due to the different spectral shapes of the star and the asteroid in the N- and Q-band filters. In the first night (Nov. 8/9) α Tuc and the asteroid were observed at similar airmass and similar precipitable water vapour (PWV) levels9 (based on APEX measurements) and no additional corrections were needed. In the second night (Nov. 9/10) 2005 YU55 was observed in Q band at a large airmass close to 2.0 and a PWV of around 0.5 mm, while α Tuc was taken at an airmass of around 1.6 and a PWV-level of about 0.3 mm. Based on ATRAN10 model calculations of the atmospheric transmittance vs. PWV for the 18 μm filter, we estimated that the derived Q-band flux for 2005 YU55 must be about 5–10% too low. We increased the derived 18.7 μm flux of the second night by 8% and gave a 10% absolute flux calibration error (instead of 7%) to compensate for the additional source of uncertainty. The final calibrated flux densities are given in Table 2.
2.2. Space far-IR observations with Herschel/PACS
The far-IR observations with the Herschel Space Observatory were reported by Müller et al. (2011b). The asteroid 2005 YU55 crossed the entire visibility window (~60° to ~115° solar elongation) in about 16 h and its apparent motion was between 2.8 and 3.8 °/h, far outside the technical tracking limit of the satellite. Therefore, we performed two standard scan-map observations of 240 s length each, one in the 70/160 μm (Nov. 10 14:52–14:56, 2011 UT, OBSID 1342232729) and one in the 100/160 μm filter combination (Nov. 10 14:57–15:01, 2011 UT, OBSID 1342232730), at fixed times at pre-calculated positions on the sky. Each scan-map consisted of four scan-legs of 14 arcmin length and separated by 4 arcsec parallel to the apparent motion of the target and with a scan-speed of 20′′/s. During both scan-map observations 2005 YU55 crossed the observed field of view and the target was seen in each scan-leg. Figure 2 (top) shows the sky-projected image of the 70 μm band observations. The PACS photometer takes data frames with 40 Hz, but binned onboard by a factor of 4 before downlink. We re-centred/stacked all frames where the satellite was scanning with constant speed (about 1700 frames in each of the two dual-band measurements) on the expected position of 2005 YU55. The results are shown in Fig. 2 (bottom). This technique worked extremely well and one can clearly see many details of the tripod-dominated point spread function (PSF). We performed aperture photometry on the final calibrated images and estimated the flux error via photometry on artificially implemented sources in the clean vicinity around our target. The fluxes were finally corrected for colour terms to obtain monochromatic flux densities at the PACS reference wavelengths. These corrections are due to the differences in spectral energy distribution between 2005 YU55 and the assumed constant energy spectrum ν Fν = const. in the PACS calibration scheme. The colour-corrections for objects in the temperature range of ≈250–400 K are 1.01, 1.03, and 1.06 (±0.01) in the blue, green, and red band, respectively11. The photometric error of the artificial sources were combined quadratically with the absolute flux calibration errors (5% in all three bands based on the model uncertainties of the fiducial stars used in the PACS photometer flux calibration scheme) and the error related to the colour-correction (1%). The final monochromatic flux densities and their absolute flux errors at the PACS reference wavelengths 70.0, 100.0, and 160.0 μm are listed in Table 3.
 |
Fig. 2 Top: sky-projected PACS image of 2005 YU55 at 70 μm. Each of the four scan-legs shows the target at a different position. Bottom: object-centred images of the target in the three filters: blue (70 μm), green (100 μm), and red (160 μm). The tripod-dominated PSF is clearly visible. |
2.3. Groundbased millimetre observations with the SMA
Observing geometries (SMA-centric) and final calibrated flux densities.
 |
Fig. 3 SMA image of 2005 YU55 at 1.3 mm. The ellipse represents the two-dimensional full width at half maximum of the synthesized beam of the array, which is effectively the PSF of the instrument for the observations of an unresolved target. |
We performed observations of 2005 YU55 a few hours past the closest Earth approach on Nov. 9, 2011 using the Submillimeter Array (SMA) located near the summit of Mauna Kea in Hawaii. The SMA was operated in separated sideband mode with 2 GHz continuum bandwidth per sideband. The lower sideband was tuned to 220.596 GHz and the upper sideband (USB) at 230.596 GHz, providing a mean frequency of 225.596 GHz, or 1328.9 μm (covering the range from 1300.1 to 1359.0 μm). Complex gains were obtained from several different quasars as the asteroid moved across the sky. The amplitude scale was corrected for Earth’s atmospheric opacity through standard system temperature calibration, and then corrected to the absolute (Jansky) scale by referencing to observations of Uranus and Callisto, astronomical sources with flux densities known to within ~5% at this frequency.
The measurements were difficult because of poor weather, particularly atmospheric phase stability, and were further hampered by the exceptionally rapid motion of the object. The asteroid’s apparent position at its fastest changed by ~7′′/s relative to sidereal, which is significantly faster than the SMA phase tracking system (the digital delay software, or DDS) was designed for. To compensate, a special version of the DDS was created which attempted to track the phase on much shorter timescales. However, this was only partly successful and there were obvious signs of decorrelation (loss of signal caused by the motion of the source relative to the tracked phase centre) on most baselines. This required extensive data flagging and secondary self-calibration of the amplitude, which introduced significant systematic errors in the flux density scale.
Despite these challenges, we obtained a clear detection of the object. Figure 3 shows the 1.3 mm image of 2005 YU55 after both phase reference calibrations and additional self-calibration. The target itself was unresolved and the oblong image of the asteroid in Fig. 3 is simply due to the PSF of the instrument for the observations, which is shown in the lower-left corner as an ellipse of 3.73′′ × 2.58″ in size, with a major axis position angle of 83.66° East of North. Over the 3.5 h of observation (Nov. 9, 2011 09.16–12.46 h UT) we also see the expected drop in flux density as the source recedes, consistent with the apparent size decrease with time. While the detection is of high signficance (SNR ~ 35), the systematic problems of compensating for the tracking-induced decorrelation combined with the poor weather dominated the flux-density error budget. Taking all effects into account, we obtained a flux density of 75 ± 25 mJy at observation mid-time (Nov. 9, 2011 10:49 UT, see Table 4).
2.4. Auxiliary data sets
Radar measurements.
Nolan et al. (2010), Busch et al. (2012), and Taylor et al. (2012a,b) presented results obtained by radar measurements using the Arecibo S-band, the Deep Space Network Goldstone DSS-14 and DSS-13, Green Bank Telescope, and Arecibo/VLBA (radar speckle tracking). They found 2005 YU55 to be a dark (at radar/radio wavelengths), spherical object of about 400 m in diameter and with a rotation period of roughly 18 h (Nolan et al. 2010; Taylor et al. 2012a). Busch et al. (2012) confirmed the nearly spheroidal shape and determined the maximum dimensions of the object to be 360 ± 40 m in all directions. The radar team estimated the pole direction from the motion of the radar speckle pattern during three days of observations after the fly-by. Combining the radar images and the speckle data excluded all prograde pole directions, and restricted the possible retrograde poles to (λecl, βecl) = (20°, –74°) ± 20° with a rotation period of 19.0 ± 0.5 h.
Thermal infrared observations from Gemini-North/Michelle.
Lim et al. (2012a,b) obtained thermal infrared photometry and spectroscopy in N and Q bands using the Michelle instrument at Gemini-North. According to their thermal model analysis (Tss = 360–370 K; η ≈ 1.25–1.5) the thermal measurements are consistent with an object diameter of 400 m, but the best fit to their data was found for a size of 322 ± 18 m and a maximum subsolar temperature Tss of 409 ± 12 K (thermal model η ≈ 0.93). More recently, Lim et al. (2012c) combined their thermal data with results from radar measurements and found an equatorial diameter of 380 ± 20 m and a thermal inertia Γ ≈ 500–1500 Jm-2 s-0.5 K-1. They also calculated values for the effective diameter via radiometric techniques and only based on their thermal data. They found an effective diameter of 310 m for a low thermal inertia of 350 Jm-2 s-0.5 K-1 and of 350 m for a thermal inertia of 1000 Jm-2 s-0.5 K-1 (DPS meeting #44, #305.01 presentation).
Keck adaptive-optics (AO) imaging.
Merline et al. (2011; 2012) reported on adaptive optics (AO) imaging of 2005 YU55 during its close fly-by on 2011 Nov. 9 UT with the Keck II AO system NIRC2. The preliminary results were derived under the assumption of a smooth triaxial ellipsoid having a principle-axis rotation of 18 h. They found a preference for poles in the southern sub-latitudes and an effective object diameter of 307 ± 15 m. This would be consistent with the radar-favoured retrograde sense of rotation meaning that the object presented a warm terminator during its close approach. In addition, they give two explicit solutions: (a) a prograde pole with (λecl, βecl) = (339°, +84°) ± 6° and object dimensions of 337 × 324 × 267 m (±15 m in each dimension), corresponding to a spherical equivalent diameter of 308 ± 9 m; (b) a retrograde pole with (λecl, βecl) = (22°, –35°) ± 15° and object dimensions of 328 × 312 × 245 m (±15, 15, 30 m), corresponding to a spherical equivalent diameter of 293 ± 14 m.
VLT-NACO speckle imaging observations.
Sridharan et al. (2012) performed VLT-NACO speckle imaging in the Ks band in no-AO mode. The observations on 2005 YU55 were carried out one hour (10-min block) and two hours (15-min block) after the closest Earth approach, interleaved by sky background and calibration observations. The planned closed-loop AO observations failed because of poor observing conditions and only no-AO mode (speckle imaging mode) observations were possible. They found that 2005 YU55 has a spherical shape with a mean diameter of about 270 m. At the same time they extracted a mean diameter of 261 ± 20 m × 310 ± 30 m from edge-enhanced image reconstructions. The large uncertainties are due to the theoretical resolution of 95 m at the distance of the object and the final image quality.
CCD photometric observations.
CCD lightcurve measurements from different observers were analysed by Warner et al. (2012a,b). Their analysis resulted in two possible synodic periods of 16.34 ± 0.01 h with an amplitude of 0.24 ± 0.02 mag (9–17 Nov., 2011) and 19.31 ± 0.02 h with an amplitude of 0.20 ± 0.02 mag. The first one was supported by the initial radar analysis, while the second one is now the currently favoured solution by the radar team. The 19.31 h lightcurve has a bimodal shape and there seem to be indications for a non-principal axis rotation. Because of the large phase angle coverage of the CCD data they were also able to derive the absolute R-band magnitude HR = 20.887 ± 0.042 and the phase slope parameter G = −0.147 ± 0.014. With an assumed V − R value of 0.38 they calculated the absolute V-band magnitude HV = 21.27 ± 0.05.
Absolute magnitude and phase curve.
Based on Bessel R-band photometry and long-slit CCD spectrograms during the 2010 and 2011 apparitions, Hicks et al. (2010; 2011) reported an absolute R-band magnitude of HR = 20.73 and a phase slope parameter G = −0.12 describing a very steep phase curve which is typically found for low-albedo C- and P-type asteroids. They measured a V − R colour of 0.37 mag leading to an absolute V-band magnitude of HV = 21.1 ± 0.1. An indpendent work by Bodewits et al. (2011) presented a V-band absolute magnitude of HV = 21.2 when applying a phase curve derived from UV measurements (GUV = −0.13).
3. Thermophysical model analysis
For the analysis of our thermal data (miniTAO/MAX38, SMA, Herschel/PACS) we applied a thermophysical model (TPM) that is based on the work by Lagerros (1996; 1997; 1998). This model is frequently and successfully applied to near-Earth asteroids (e.g. Müller et al. 2004; 2005; 2011a; 2012), to main-belt asteroids (e.g. Müller & Lagerros 1998; Müller & Blommaert 2004), and also to more distant objects (e.g. Horner et al. 2012; Lim et al. 2010). The TPM takes into account the true observing and illumination geometry for each observational data point, a crucial aspect for the interpretation of our 2005 YU55 observations that cover a wide range of phase angles. The TPM allows the implementation of a shape model and spin-vector properties. The heat conduction into the surface is controlled by the thermal inertia Γ. The observed mid- and far-IR fluxes are connected to the hottest regions on the asteroid surface and dominated by the diurnal heat wave. The seasonal heat wave is less important and therefore not considered here. The infrared beaming effects are calculated via a surface roughness model, described by segments of hemispherical craters. Here, mutual heating is included and the true crater illumination and the visibility of shadows is considered. The level of roughness is driven by the rms mean surface slope which correspond to a given crater depth-to-radius value combined with the fraction of the surface covered by craters, see also Lagerros (1996) for further details. We used a constant emissivity of 0.9 at all wavelengths, knowing that the emissivity can decrease beyond ~200 μm in some cases (e.g. Müller & Lagerros 1998; 2002). All of our data, except the SMA data point with its large error bar, have been taken at wavelength <200 μm and the constant emissivity is therefore a valid assumption. The TPM input parameters and applied variations are listed in Table 5.
Summary of general TPM input parameters and applied ranges.
3.1. Using a spherical model
We started our analysis with a spherical model to see which spin-axis orientations, sizes, geometric albedos, and thermal properties produce acceptable solutions with reduced χ2 values12 around or below 1.0. For the spin-axis solutions we used all values specified in the literature and many additional orientations to cover the entire λecl-βecl space. For the calculation of the reduced χ2-curves we consider the true observing and illumination constellation (helio-centric and observer-centric distances, phase angle, spin-axis orientation) for each epoch and we then compare it with the corresponding measurement. These calculations are done for a wide range of thermal inertias and different levels of surface roughness as specified in Table 5. An example for the application of this technique can be found in Müller et al. (2011a). Each model setup produces a curve of reduced χ2 values as a function of thermal inertia. Figure 4 shows these curves for all different spin-axis orientations, a rotation period of 19.31 h, and an intermediate level of surface roughness (rms mean slope of 0.3). Reduced χ2 values around or below 1.0 correspond to TPM solutions which explain all observed fluxes in a statistically acceptable way. There are several spin-axis orientations that produce an excellent match to all our thermal measurements at thermal inertia values in the range between approximately 200 and 1500 Jm-2 s-0.5 K-1.
 |
Fig. 4 Calculation of reduced χ2 values for all specified spin-axis orientations, a fixed rotation period of 19.31 h, and an intermediate surface roughness level (rms mean slope of 0.3). The prograde AO solution (solid line) and the radar solution (dashed line) for the spin-vector are indicated in the figure. |
The distribution of the reduced χ2 minima along the ecliptic longitudes and latitudes is shown in Fig. 5. There are large zones in the λecl.-βecl space which can be excluded with high probability (light blue, green, yellow, and red zones), but there remain several possible spin-axis orientations compatible with our data set (dark blue zones), including the radar and AO solutions.
 |
Fig. 5 The χ2 minima calculated for all spin-axis orientations listed in Table 5 and for an intermediate level of roughness (rms mean slope of 0.3). The dark blue zones indicate spin-poles which allow us to obtain an acceptable match to all thermal data simultaneously (reduced χ2 values around or below 1.0). The radar and both AO solutions are indicated by the crossed circles. We note that the size, albedo, and thermal inertia are free parameters and only the best possible solution for each spin axis has been considered. |
Figures 4 and 5 both have a slight dependency on the selected surface roughness (for both figures we have used rms mean slope of 0.3). In general, lower roughness (rms mean slope of 0.1) produces lower χ2 minima and at smaller thermal inertia values going down to about 200 Jm-2 s-0.5 K-1. Higher values for the surface roughness (rms mean slope ≥0.5) shift the χ2 minima to values well above 1.0 and towards higher thermal inertia going up to about 1500 Jm-2 s-0.5 K-1. It is interesting to note that the prograde AO solution (solid line in Fig. 4) works very well (χ2 minima very close to 1.0) for a low surface roughness, while the radar solution produces a better match when a high surface roughness is applied.
3.2. Influence of the spin-axis orientation
As a next step, we investigated the influence of different spin-axis orientations on the size and albedo solutions. We determined the χ2 minima for all listed spin-axis orientations and for four different levels of roughness (rms mean slope of 0.1, 0.3, 0.5, and 0.8). Figure 6 shows how the corresponding radiometric sizes and geometric albedos are distributed in the reduced χ2 picture. We connected the four χ2 minima belonging to the AO solution (solid line) and the ones belonging to the radar solution (dashed line) in Fig. 6. These lines show that the connected size and albedo values remain stable, only the fit gets better (lower χ2 minima) for specific roughness settings. We also found that the derived thermal inertias change significantly with roughness at similar χ2 values, indicating that we cannot resolve the degeneracy between roughness and thermal inertia with our data set. A smoother surface is connected to lower values for the thermal inertia, the rougher surfaces require higher thermal inertias.
 |
Fig. 6 Distribution of the χ2 minima and the related effective diameter (top) and geometric albedos (bottom). The four different levels of roughness are indicated by different symbols. The values for the prograde AO solution (solid line) and the radar solution (dashed line) are connected in the figures. |
The thermal data are compatible with different spin-axis orientations, but the size, the geometric albedo, and also the possible thermal inertias are very well constrained by our thermal data set. The best solutions are found for an effective diameter of about 310 m, if we include the best solutions for the prograde AO spin axis and the radar spin-axis orientations, then the possible diameter range goes from 295 to 335 m (see Fig. 6, top). For the geometric albedo we find a value of about 0.062 and a possible range between 0.053 to 0.067 (see Fig. 6, bottom). Figure 7 shows how our best TPM solution translates the insolation during the epoch of the Herschel measurement into a thermal picture of the surface as seen from Herschel. For the calculations we used a spin-axis orientation of (λecl, βecl) = (60°, –60°) and a spherical shape model with a total of 800 facets. The large influence of the thermal inertia in combination with the object’s rotation is the reason for the warm temperatures also in regions without direct illumination.
 |
Fig. 7 TPM picture of 2005 YU55 as seen from Herschel on Nov. 10 14:55, 2011 UT in the object-centred reference frame (z-axis along the object’s rotation axis), with the Sun at a phase angle of –71°, spin-axis orientation (λecl, βecl) = (60°, –60°), and a spherical shape model with a total of 800 facets. Top: insolation in W/m2. Bottom: temperature in K. |
4. Discussions
4.1. Comparison with the radar results
The comparison between the radar results (Busch et al. 2012) and our findings is very interesting. If we use the radar diameter (360 ± 40 m, close to a spheroidal shape) and the spin-axis properties ([λecl, βecl] = [20°, –74°] ± 20°, Psid = 19.0 ± 0.5 h), it is not possible to find an acceptable match to our thermal measurements. The reduced χ2 minima always stay well above 2.0 and the match between TPM-predictions and observed fluxes is very poor. Even for the lowest diameter limit of 320 m the model calculations would exceed the measured fluxes systematically by 15–25%. At a diameter of 360 m the model fluxes are already 30–40% above the measurements. The radar size estimates are, as the radiometric size estimates, model dependent. The spin-axis orientation and the rotation rate have a larger influence on the radar solution (e.g. Ostro et al. 2002) than they have on the radiometric solution. The radar images are dominated by the surface part that is closest to the antenna while the thermal data are tightly connected to the entire cross-section at the moment of observation. This might explain the differences between both techniques.
However, we do find an acceptable match to all thermal data if we just use the radar spin-properties combined with a high level of surface roughness (rms mean slope of 0.8). But the corresponding diameter is only 299 m, well outside the radar derived range, with a pV = 0.067 and a thermal inertia of 400 Jm-2 s-0.5 K-1. In fact, all high obliquity cases with βecl ≤ −60° (retrograde sense of rotation) produce small diameters in the range 300–310 m, while only the low obliquity cases with βecl ≥ +60° (prograde sense of rotation) produce larger effective diameters of 325–340 m.
4.2. Comparison with AO and speckle results
The Keck AO results presented by Merline et al. (2012) compare better with our findings. Table 6 summarises the AO and our radiometric results.
Comparison between AO results and our findings.
The southern rotational poles are not specified in detail by Merline et al. (2012), but here we see for the first time an agreement between the derived sizes. The originally specified retrograde pole towards an ecliptic latitude of –35° is very unlikely: acceptable TPM solutions (with reduced χ2 minima below 2.0) are only found if the thermal inertia is well above 2000 Jm-2 s-0.5 K-1, an unrealistically high value which has never been measured before. It should be noted here that the highest derived thermal inertias are still below 1000 Jm-2 s-0.5 K-1 (e.g. Delbo et al. 2007) and that our mid- to far-IR data originate in the top layer of the surface. We do not see any signatures of sub-surface layers where the thermal inertia could be significantly higher (Keihm et al. 2012).
The speckle observation in no-AO mode presented by Sridharan et al. (2012) revealed a roughly spheroidal shape with a mean diameter of 270 m. By using a more sophisticated reconstruction technique they estimated a mean diameter of 261 ± 20 m × 310 ± 30 m, corresponding to an object-averaged size of approximately 285 ± 25 m. Within the error bars, this value agrees with our radiometrically derived diameter of 300–310 m and it also creates doubts whether the large radar size is realistic. The indications for a diameter close to 300 m also makes the various prograde solutions more unlikely, which all require diameters in the range 325–340 m.
4.3. Spin-axis properties
Combining the spin-axis information given by Busch et al. (2012), Merline et al. (2012), and our findings (see Fig. 4), our analysis supports a retrograde sense of rotation with a possible spin-axis orientation of (λecl, βecl) = (60° ± 30°, –60° ± 15°). The relatively large errors in (λecl, βecl) also cover the possible solutions connected to the different roughness levels mentioned before. If we use this solution, then the size estimate from AO observations matches our radiometrically derived optimal size and we also have an agreement with the radar derived spin-pole. The discrepancy with the radar size remains.
Our thermal observations cover a wide range of phase angles, wavelengths, and different illumination and observing geometries. This allowed us to exclude many spin-axis orientations (see Fig. 5). Nevertheless, we could not find a strong preference for a single spin-axis orientation nor for the sense of rotation. Even very extreme solutions like the retrograde radar solution and the prograde AO solution seem to explain the data equally well. This is very surprising. Based on our previous modelling experiences for 1999 JU3 (Müller et al. 2011a) and 1999 RQ36 (Müller et al. 2012) based on much smaller sets of thermal data, we expected to find a unique spin-axis solution. This might be an indication that 2005 YU55 is a tumbler with a strongly time-dependent orientation of the spin axis (for further details on tumbling asteroids see Pravec et al. 2005). Busch et al. (2012) have already speculated about the possibility that terrestrial tides might have torqued the object into a non-principal axis spin state. However, their observations are consistent with a principle-axis rotation. Warner et al. (2012b) found two non-commensurate solutions for the rotation period (16.34 ± 0.01 h; 19.31 ± 0.02 h) that they could not fully explain. They suggest that a non-principal axis rotation should be considered. After the radar and lightcurve analysis, the thermal analysis now also points towards the possibility of a non-principle axis rotation.
We also looked into the influence of the two published rotation periods, but the ≈3 h difference between the two available periods did not affect our radiometric solutions significantly. The longer rotation period typically requires slightly higher inertias to produce the same disk-integrated flux, but this is a marginal effect here in this case.
4.4. Comparison with other thermal measurements
Instead of comparing our TPM radiometric results with the preliminary results produced by Lim et al. (2012a–c) via a simple thermal model, we predicted flux densities for the epochs and the wavelength bands of the Michelle/Gemini North observations shown in Fig. 2 in Lim et al. (2012b). For the TPM prediction we simply used our best effective diameter (310 m) and albedo (pV = 0.062) solution connected to our preferred spin-axis orientation of (λecl, βecl) = (60°, –60°). The thermal inertia and roughness levels are less well constrained and our data set does not allow the degeneracy between these two parameters to be broken. A low roughness (rms mean slope of 0.1) combined with small values of the thermal inertia of about 200 Jm-2 s-0.5 K-1 would explain our measurements, as does higher roughness levels (rms mean slope of 0.5) combined with higher thermal inertia around 800 Jm-2 s-0.5 K-1. We selected an intermediate solution (rms mean slope of 0.3; thermal inertia =500 Jm-2 s-0.5 K-1).
The Gemini-North/Michelle photometry shown in Fig. 2 in Lim et al. (2012b) was taken on 09-Nov.-2011 11:02–11:15 UT (α = −34.0°, r = 0.994 AU, Δ = 0.004 AU) and on 10-Nov.-2011 09:32–11:52 UT (α = −15.5°, r = 1.001 AU, Δ = 0.012 AU). Since the calibrated flux densities and errors are not explicitly given, we could only do a qualitative comparison. Table 7 shows our TPM prediction for both epochs and the Michelle reference wavelengths in Jansky and W/m2/μm.
TPM flux predictions for the Michelle bands and both observing epochs in 2011.
Our TPM-predictions agree very well with the observed fluxes and error bars presented in Lim et al. (2012b). For the first epoch we estimated that the agreement is within about 10% at all wavelengths, while for the second epoch the TPM prediction seems to be about 5–15% below the observed fluxes.
We also tested the low-roughness/low-inertia case mentioned above and indeed it produces very similar fluxes and the agreement is on a similar level. The high-roughness/high-inertia case is less convincing, the TPM predictions are systematically lower by 5–20%. The Michelle/Gemini North data favour a thermal inertia value in the range 200–700 Jm-2 s-0.5 K-1, combined with an intermediate to low roughness level (rms mean slope in the range 0.1–0.5), also in agreement with the lowest reduced χ2 values in Fig. 4.
4.5. Overall fit to the measurements
We tested the quality of the final solution for 2005 YU55 against the observed and calibrated flux densities by calculating the TPM predictions for each data point listed in Tables 2–4. The observed and calibrated mono-chromatic flux densities are shown in Fig. 8 together with the TPM predictions for the specific observing geometries. The observation/TPM ratios are very sensitive to wavelength-dependent effects (related surface roughness and thermal inertia), phase-angle dependent effects (an incorrect thermal inertia would cause before/after opposition asymmetries), and shape effects (ratios as a function of rotational phase). An overall ratio close to 1.0 indicates that the size and thermal properties (and in second order also albedo) are correctly estimated. Figure 9 shows how well our final TPM solution explains our thermal data covering a wide range of wavelengths from 8.9 μm to 1.3 mm and taken at very different phase angles ranging from –97° to –18°. No trends with wavelength nor with phase angle can be seen.
 |
Fig. 8 Observered and calibrated flux densities together with the corresponding TPM prediction. The model predictions for the MAX38 data are shown at the start and end time of each observing day. The distance between observer and target and also the phase angle changed rapidly during the close encounter period of three days. For the PACS data the model prediction from 5 to 1500 μm is shown. |
 |
Fig. 9 Observered and calibrated flux densities divided by the corresponding TPM prediction. Top: as a function of wavelength. Middle: as a function of phase angle. Bottom: as a function of rotational phase. |
Figure 9 also shows that 2005 YU55 must be close to a sphere. An elongated or strangely shaped body would produce a thermal lightcurve, but our data set does not show any significant deviations at specific rotational phases (bottom figure). Not all rotational phases have been covered by our thermal measurements, however, and some of the observational errors are large. There is also the possibility that effects of an ellipsoidal shape could have been compensated by roughness effects (a larger cross-section combined with a low surface roughness could produce the same flux levels as a smaller cross-section combined with high surface roughness). Figure 9 (bottom) would then also show a constant ratio at all rotational phases. But since the roughness influences the flux in a wavelength-dependent manner (see e.g. Müller 2002, Fig. 3), one should then see a larger scatter in Fig. 9 (top) at short wavelengths where the roughness has the greatest influence on the observed fluxes. At long wavelengths (beyond ~20 μm) the effects of roughness are much smaller and the shape effects are dominating. Shape effects or combined shape/roughness variations are not seen in our data set.
We also did an additional test to see if the optical lightcurve amplitude of 0.20 ± 0.02 mag (Warner et al. 2012a,b) is compatible with our findings. An amplitude of this size would mean that the flux at lightcurve maximum is about 1.2 times the flux at lightcurve minimum, which would require a SNR > 10 time series data set for confirmation. The PACS data are of sufficient quality, but they are taken at a single epoch. The miniTAO/MAX38 measurements have error bars that are too large, related mainly to systematic errors in the absolute flux calibration scheme. However, we looked at the relative variation of the 22 miniTAO/MAX38 data points taken at 18.7 μm with respect to the spherical shape model flux predictions. The deviations never exceed 10%, but these data cover only a very limited range of rotational phases (from 195 to 245° and a single point at 305° in the bottom of Fig. 9). The thermal data are therefore perfectly compatible with the optical lightcurve results and there are no indications of large deviations from a spherical shape.
4.6. Error calculations
We combine the constraints from the radar measurements (retrograde sense of rotation, estimate of spin-axis orientation), the AO findings (effective diameter of 307 ± 15 m for southern poles), and the speckle technique (object-averaged diameter of 285 ± 25 m) with the χ2 analysis for the possible spin-axis orientations (see Figs. 4, 5, and corresponding figures for different roughness levels which are not shown here). For a good fit the reduced χ2 values should be close to 1 and we estimated for our data set that the 3-σ confidence level for the reduced χ2 is around 1.6. This leads to an estimated spin-axis orientation of (λecl, βecl) = (60° ± 30°, –60° ± 15°).
We can also use the 3-σ threshold in reduced χ2 for the derivation of the corresponding size and albedo range. Figure 10 shows the size and albedo solutions for the full range of thermal inertias (from 0 to 3000 Jm-2 s-0.5 K-1), the four different levels of roughness (rms mean slope of 0.1, 0.3, 0.5, and 0.8, shown with different symbols), and for all spin-axis solutions compatible with (λecl, βecl) = (60° ± 30°, –60° ± 15°). Based on the 3-σ confidence level we derived a possible diameter range of 295 to 322 m, 0.057 to 0.068 for the geometric albedo, and a thermal inertia larger than 150 Jm-2 s-0.5 K-1.
As a second step we looked in more details at the derived size, albedo, and thermal inertia ranges. The solutions close to the 3-σ threshold in our χ2 analysis are very problematic in the sense that they produce strong trends in the observation/model figures (see Fig. 9) either with wavelengths and/or with phase angle. These trends are very difficult to catch in an automatic χ2 analysis. We therefore moved back to the 1-σ solutions, corresponding to a possible diameter range of 300–312 m, a geometric albedo range of 0.062–0.067, and a thermal inertia range of 350–1000 Jm-2 s-0.5 K-1. The smallest thermal inertia values are connected to low roughness values (rms mean slope ≤0.3) and the largest thermal inertia values to very rough surface levels (rms mean slope ≥0.5). The calculations for the Michelle/Gemini North data put another constraint on the thermal inertia and reduce the possible range to 350–800 J m-2 s-0.5 K-1. The derived radiometric albedo range of 0.062–0.067 is connected to the HV magnitude of 21.2 m, if we include the ±0.15 mag, then the possible range is significantly bigger: from 0.055 to 0.075.
 |
Fig. 10 Size and albedo solutions for the full range of thermal inertias, for the four different levels of roughness, and for the most likely spin-axis solutions. |
5. Conclusions
Here is a short summary of our findings for the near-Earth asteroid 2005 YU55:
-
1.
Our thermal data can be explained via a spherical shape modelwithout seeing significant offsets at specific rotational phases,showing that 2005 YU55 is almost spherical.
-
2.
Our best spin-axis solution can be specified by (λecl, βecl) = (60° ± 30°, –60° ± 15°). However, the analysis of the thermal data alone would also allow for specific spin-axis orientations in the northern ecliptic hemisphere with a prograde rotation of the object.
-
3.
The radiometric analysis of our thermal data that span a wide range of phase angles and wavelengths (best visible in the χ2 picture in Fig. 5) is compatible with changing spin-axis orientations, which might be an indication for a non-principal axis rotation of 2005 YU55.
-
4.
2005 YU55 has a possible effective diameter range of Dequ = 300–312 m (equivalent diameter of an equal volume sphere); this range was derived under the assumption that the spin axis is indeed as specified above.
-
5.
The analysis of all available data combined revealed a discrepancy with the radar-derived size.
-
6.
The geometric visual albedo pV was radiometrically derived to be in the range 0.062 to 0.067 (HV = 21.2 mag) or 0.055−0.075 if we include the ±0.15 mag error in HV, in agreement with the C-type taxonomic classification.
-
7.
2005 YU55 has a thermal inertia in the range 350−800 Jm-2 s-0.5 K-1, very similar to the value found for the rubble-pile asteroid 25 143 Itokawa by Müller et al. (2005). We also expect, therefore, the surface of 2005 YU55 to look very similar and to be composed of low conductivity fine regolith mixed with larger rocks and boulders that have much higher thermal inertias.
-
8.
The observed thermal emission can be best reproduced when considering a low to intermediate roughness with an rms mean slope of 0.1–0.3; the lower roughness (or smoother surface) is connected to the lower thermal inertias, while a higher roughness would also require the higher inertia values.
Online material
Observing geometries (miniTAO-centric) and final calibrated flux densities.
2005, M.P.E.C. 2005-Y47: http://www.minorplanetcenter.org/mpec/K05/K05Y47.html
NASA Near Earth Object Program News: http://neo.jpl.nasa.gov/news/news171.html
JPL Horizons: http://ssd.jpl.nasa.gov/horizons.cgi
JPL’s NEO Radar Detection Program Webpage: http://echo.jpl.nasa.gov/asteroids/index.html
JPL Horizons: http://ssd.jpl.nasa.gov/horizons.cgi
PACS report PICC-ME-TN-038: http://herschel.esac.esa.int/twiki/pub/Public/PacsCalibrationWeb/cc_report_v1.pdf
Acknowledgments
We would like to thank the Herschel operations team who supported the planning and scheduling of our fixed-time observations. Without their dedication and enthusiasm these measurements would not have been possible. The Submillimeter Array is a joint project between the Smithsonian Astrophysical Observatory and the Academia Sinica Institute of Astronomy and Astrophysics and is funded by the Smithsonian Institution and the Academia Sinica. The work of C.K. has been supported by the PECS-98073 contract of the European Space Agency and the Hungarian Space Office, the K-104607 grant of the Hungarian Research Fund (OTKA), and the Bolyai Research Fellowship of the Hungarian Academy of Sciences. E. Vilenius acknowledges the support of the German DLR project number 50 OR 1108. S.H. is supported by the Space Plasma Laboratory, ISAS/JAXA. A.P. is supported by the Hungarian grant LP2012-31/2012.
References
- Asano, K., Miyata, T., Sako, S., et al. 2012, Proc. SPIE, 8446, 115 [Google Scholar]
- Bodewits, D., Campana, S., Kennea, J., et al. 2011, Central Bureau Electronic Telegrams, 2937, 1 [NASA ADS] [Google Scholar]
- Busch, M. W., Benner, L. A. M., Brozovic, M., et al. 2012, in Asteroids, Comets, Meteors, Conf. Proc., LPI Contribution 1667, 6179 [Google Scholar]
- Cohen, M., Walker, R. G., Carter, B., et al. 1999, AJ, 117, 1864 [NASA ADS] [CrossRef] [Google Scholar]
- Delbo, M., dell’Oro, A., Harris, A. W., et al. 2007, Icarus 190, 236 [Google Scholar]
- Hicks, M., Lawrence, K., & Benner, L. 2010, The ATel, 2571 [Google Scholar]
- Hicks, M., Somers, J., Truong, T., & Teague, S. 2011, The ATel, 3763 [Google Scholar]
- Horner, J., Müller, T. G., & Lykawka, P. S. 2012, MNRAS, 423, 2587 [NASA ADS] [CrossRef] [Google Scholar]
- Keihm, S., Tosi, F., Kamp, L., et al. 2012, Icarus, 221, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Lagerros, J. S. V. 1996, A&A, 310, 1011 [NASA ADS] [Google Scholar]
- Lagerros, J. S. V. 1997, A&A, 325, 1226 [NASA ADS] [Google Scholar]
- Lagerros, J. S. V. 1998, A&A, 332, 1123 [NASA ADS] [Google Scholar]
- Lim, T. L., Stansberry, J., Müller, T. G., et al. 2010, A&A, 518, 148 [Google Scholar]
- Lim, L. F., Emery, J. P., Moskovitz, N. A., & Granvik, M. 2012a, in 43rd Lunar and Planetary Science Conf., LPI Contribution 1659, 2202 [Google Scholar]
- Lim, L. F., Emery, J. P., Moskovitz, N. A., & Granvik, M. 2012b, in Asteroids, Comets, Meteors, Conf. Proc., LPI Contribution 1667, 6295 [Google Scholar]
- Lim, L. F., Emery, J. P., Moskovitz, N. A.., et al. 2012c, DPS Meeting 44, 305.01 [Google Scholar]
- Merline, W. J., Drummond, J. D., Tamblyn, P. M., et al. 2011, IAU Circular, 9242, http://www.cbat.eps.harvard.edu/iauc/09200/09242.html [Google Scholar]
- Merline, W. J., Drummond, J. D., Tamblyn, P. M., et al. 2012, in Asteroids, Comets, Meteors 2012, Conf. Proc., LPI Contribution 1667, 6372 [Google Scholar]
- Miyata, T., Sako, S., Nakamura, T., et al. 2008, in Ground-based and Airborne Instrumentation for Astronomy II, Proc. SPIE, 7014, 701428 [CrossRef] [Google Scholar]
- Müller, T. G. 2002, M&PS, 37, 1919 [Google Scholar]
- Müller, T. G., & Blommaert, J. A. D. L. 2004, A&A, 418, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, T. G., & Lagerros, J. S. V. 1998, A&A, 338, 340 [NASA ADS] [Google Scholar]
- Müller, T. G., Sterzik, M. F., Schütz, O., et al. 2004, A&A, 424, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, T. G., Sekiguchi, T., Kaasalainen, M., et al. 2005, A&A, 443, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, T. G., Ďurech, J., Hasegawa, S., et al. 2011a, A&A, 525, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, T. G., Altieri, B., & Kidger, M. 2011b, IAU Circular, 9241, http://www.cbat.eps.harvard.edu/iauc/09200/09241.html [Google Scholar]
- Müller, T. G., O’Rourke, L., Barucci, A. M., et al. 2012, A&A, 548, 36 [Google Scholar]
- Nakamura, T., Miyata, T., Sako, S., et al. 2010, in Ground-based and Airborne Instrumentation for Astronomy III, Proc. SPIE, 7735, 773561 [CrossRef] [Google Scholar]
- Nolan, M. C., Vervack, R. J., Howell, E. S., et al. 2010, DPS Meeting 42, 13.19, BAAS, 42, 1056 [NASA ADS] [Google Scholar]
- Ostro, S., Hudson, R. S., Benner, L. A. M., et al. 2002, in Asteroids III, eds. W. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel, 151 [Google Scholar]
- Pravec, P., Harris, A. W., Scheirich, P., et al. 2005, Icarus, 173, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Sako, S., Aoki, T., Doi, M., et al. 2008, in Ground-based and Airborne Telescopes II, Proc. SPIE, 7012, 70122T [CrossRef] [Google Scholar]
- Somers, J. M., Hicks, M., Lawrence, K., et al. 2010, DPS Meeting 42, 13.16, BAAS, 42, 1055 [NASA ADS] [Google Scholar]
- Sridharan, R., Girard, J. H. V., Lombardi, G., Ivanov, V. D., & Dumas, C. 2012, in Optical and Infrared Interferometry III, Proc. SPIE, 8445 [Google Scholar]
- Taylor, P. A., Nolan, M. C., Howell, E. S., et al. 2012a, AAS Meeting 219, 432.11 [Google Scholar]
- Taylor, P. A., Howell, E. S., Nolan, M. C., et al. 2012b, in Asteroids, Comets, Meteors, Conf. Proc., LPI Contribution 1667, 6340 [Google Scholar]
- Vodniza, A. Q., & Pereira, M. R. 2010, DPS Meeting 42, 13.25, BAAS, 42, 1057 [NASA ADS] [Google Scholar]
- Warner, B. D., Stephens, R. D., Brinsfield, J. W., et al. 2012a, The Minor Planet Bulletin, Association of Lunar and Planetary Observers, 39, 84 [Google Scholar]
- Warner, B. D., Stephens, R. D., Brinsfield, J. W., et al. 2012b, in Asteroids, Comets, Meteors 2012, Conf. Proc., LPI Contribution 1667, 6013 [Google Scholar]
- Yoshii, Y., Aoki, T., Doi, M, et al. 2010, in Ground-based and Airborne Instrumentation for Astronomy III, Proc. SPIE, 7733, 773308 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Mid-infrared images of 2005 YU55 obtained by the miniTAO/MAX38 camera in the 18.7 μm filter during the time of the closest Earth approach. North is up and west is right. The asteroid moved from right (west) to left (east). |
| In the text | |
 |
Fig. 2 Top: sky-projected PACS image of 2005 YU55 at 70 μm. Each of the four scan-legs shows the target at a different position. Bottom: object-centred images of the target in the three filters: blue (70 μm), green (100 μm), and red (160 μm). The tripod-dominated PSF is clearly visible. |
| In the text | |
 |
Fig. 3 SMA image of 2005 YU55 at 1.3 mm. The ellipse represents the two-dimensional full width at half maximum of the synthesized beam of the array, which is effectively the PSF of the instrument for the observations of an unresolved target. |
| In the text | |
 |
Fig. 4 Calculation of reduced χ2 values for all specified spin-axis orientations, a fixed rotation period of 19.31 h, and an intermediate surface roughness level (rms mean slope of 0.3). The prograde AO solution (solid line) and the radar solution (dashed line) for the spin-vector are indicated in the figure. |
| In the text | |
 |
Fig. 5 The χ2 minima calculated for all spin-axis orientations listed in Table 5 and for an intermediate level of roughness (rms mean slope of 0.3). The dark blue zones indicate spin-poles which allow us to obtain an acceptable match to all thermal data simultaneously (reduced χ2 values around or below 1.0). The radar and both AO solutions are indicated by the crossed circles. We note that the size, albedo, and thermal inertia are free parameters and only the best possible solution for each spin axis has been considered. |
| In the text | |
 |
Fig. 6 Distribution of the χ2 minima and the related effective diameter (top) and geometric albedos (bottom). The four different levels of roughness are indicated by different symbols. The values for the prograde AO solution (solid line) and the radar solution (dashed line) are connected in the figures. |
| In the text | |
 |
Fig. 7 TPM picture of 2005 YU55 as seen from Herschel on Nov. 10 14:55, 2011 UT in the object-centred reference frame (z-axis along the object’s rotation axis), with the Sun at a phase angle of –71°, spin-axis orientation (λecl, βecl) = (60°, –60°), and a spherical shape model with a total of 800 facets. Top: insolation in W/m2. Bottom: temperature in K. |
| In the text | |
 |
Fig. 8 Observered and calibrated flux densities together with the corresponding TPM prediction. The model predictions for the MAX38 data are shown at the start and end time of each observing day. The distance between observer and target and also the phase angle changed rapidly during the close encounter period of three days. For the PACS data the model prediction from 5 to 1500 μm is shown. |
| In the text | |
 |
Fig. 9 Observered and calibrated flux densities divided by the corresponding TPM prediction. Top: as a function of wavelength. Middle: as a function of phase angle. Bottom: as a function of rotational phase. |
| In the text | |
 |
Fig. 10 Size and albedo solutions for the full range of thermal inertias, for the four different levels of roughness, and for the most likely spin-axis solutions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.