EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 557 (September 2013) A&A, 557 (2013) A119 Full HTML
Free Access
Issue
A&A
Volume 557, September 2013
Article Number A119
Number of page(s) 8
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201322195
Published online 18 September 2013

© ESO, 2013

1. Introduction

The eclipsing nature of LL Aqr was detected by using the Hipparcos satellite (Perryman et al. 1997; Kazarovets et al. 1999), photometry from which showed two eclipses of clearly different depth separated by roughly two years. The spectral type of the system has been classified as G1 V (Houk & Swift 1999).

Otero & Dubovsky (2004) used the Hipparcos observations plus photometry from the NSVS (Woźniak et al. 2004) and ASAS (Pojmański 1997) surveys to determine an orbital period of 20.1784 d. The orbit is quite eccentric, resulting in a secondary eclipse near phase 0.3. The eclipses are short compared to the orbital period, so LL Aqr is a detached eclipsing binary (dEB).

Ibanoǧlu et al. (2008, hereafter I08) presented extensive UBV photometry which nevertheless does not cover the ingress or egress of secondary minimum. They also obtained twelve spectra from which radial velocities (RVs) were measured – ten from the 91 cm telescope at the Catania Astrophysical Observatory, Italy, and two from the 150 cm telescope at TÜBITAK National Observatory, Turkey. I08 used these data to determine the physical properties of the system, obtaining masses and radii to precisions of 5% and 1.5%, respectively. The primary is a slightly evolved 1.2 M⊙ star whereas the secondary is a solar twin. A third component was also detected in the two TÜBITAK spectra, with an RV close to the systemic velocity of the dEB, but not in the ten Catania spectra.

Most recently, Griffin (2013, hereafter G13) presented 25 high-precision RVs for the two eclipsing components obtained with the Cambridge CORAVEL instrument, which directly observes cross-correlation functions of objects using a spectrum of Arcturus as the template (Griffin 1967). No trace of the putative third component was identified. The RVs of the two eclipsing stars are of sufficient quality to give their masses to better than 1%, making a definitive characterisation of the two stars possible if combined with sufficient photometry. Numerous photometric observations are available from the SuperWASP database.

Analyses of low-mass dEBs usually yield radii which are too large to match the predictions of theoretical stellar models (Hoxie 1973; López-Morales 2007), a phenomenon which is attributed to enhanced stellar activity due to tidal effects. The wide separation of the two components of LL Aqr means they should be relatively unaffected by tides, so their properties are important indicators of the reliability of theoretical models in this mass range. In this work we present a determination of the physical properties of LL Aqr.

thumbnail Fig. 1

Full light curves of LL Aqr from SuperWASP and I08. The jktebop best fits are plotted as black lines and the residuals of the fits are shown in the lower panel.

2. Observations

An extensive light curve of LL Aqr has been obtained by the SuperWASP consortium (Pollacco et al. 2006) in the course of a survey to detect new transiting extrasolar planets. Over 25 000 observations have been obtained to date, yielding coverage of all orbital phases and the potential for a precise measurement of the physical properties of the system. The observations were taken through the SuperWASP wide filter, which has a response function close to that of Gunn g+r. Data were obtained using four of the cameras: 14 576 points from camera 141, 87 from camera 142, 1054 from camera 147 (all part of the SuperWASP-North installation at La Palma, Spain), and finally 9364 points from camera 223 (at the SuperWASP-South installation, Sutherland, South Africa). Cameras 142 and 147 did not obtain any data during eclipse, so we did not involve these data in the analysis.

After inspecting the raw and detrended light curves, we selected those which had been detrended using the sysrem algorithm (Tamuz et al. 2005) for further study. The 23 940 datapoints from cameras 141 and 223 have a median photometric precision of approximately 0.01 mag, but have many outliers due to weather or technical issues. We therefore calculated a preliminary fit to the light curve and iteratively rejected those datapoints lying greater than 3σ from the best fit, finishing with 21 362 datapoints. This was done using the jktebop code (see below) and ten iterations. We tested the use of a 4σ clipping threshold, and found that this did not have a significant effect on our results but caused the retention of several groups of datapoints taken on the same nights and systematically offset in magnitude from the remaining data. The full photometric data are given in Table 1.

Finally, we obtained the published UBV light curves from I08 and RVs from Griffin (2013) for inclusion in our analysis. We did not include the RVs measured by I08 due to their lower number and precision compared to those from Griffin (2013). We also searched the literature for measured times of minimum light in order to refine the orbital period of LL Aqr, finding six. Table 2 gives these times of minimum along with their residual versus the best fit obtained below. The full light curves from SuperWASP and I08 are shown in Fig. 1.

Table 1

SuperWASP photometric data for LL Aqr.

Table 2

Published times of minimum light for LL Aqr.

thumbnail Fig. 2

SuperWASP light curve of the primary (top) and secondary eclipse (middle) and Griffin (2013) RVs (bottom) of LL Aqr. The datapoints are shown in red and the solid lines show the best fits found using jktebop. The residuals are shown below each fit.

thumbnail Fig. 3

UBV light curves of the primary (top) and secondary eclipse (bottom) of LL Aqr. The datapoints are shown in blue (U), green (B) and red (V), and the solid lines show the best fits found using jktebop. The residuals are shown below each fit.

3. Data analysis

The component stars of LL Aqr are well-detached and almost spherical, making the system well-suited to analysis using the jktebop code1, as originally presented by Southworth et al. (2004) and with significant extensions by Southworth et al. (2007) and Southworth (2008). jktebop is based on the ebop code (Etzel 1981; Popper & Etzel 1981) with the nde model (Nelson & Davis 1972). It represents the star and planet as biaxial spheroids but adopts the spherical approximation for the calculation of light lost during eclipse.

Important parameters of the jktebop model are the fractional radii of the two stars, (1)where a is the orbital semimajor axis, and RA and RB are the true radii of the stars. We fitted for their sum and ratio: 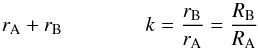(2)plus the orbital inclination (i), the central surface brightness ratio of the two stars (J), and the nuisance parameter the out-of-eclipse magnitude.

The orbital period (Porb) and the time of primary mid-eclipse (Tpri) were also included as fitted quantities. The orbital ephemeris was further constrained by including the six published times of minimum light as observational quantities, using the method of Southworth et al. (2007).

For limb darkening we adopted the quadratic law with coefficients2 taken from Claret & Bloemen (2011). The precise values of the limb darkening coefficients are not important to the results, but the light curve contains sufficient information for the linear coefficient for each star (uA and uB) to be fitted. The quadratic coefficients (vA and vB) were held fixed.

We checked for the possibility of contaminating “third” light, motivated by the detection of a third signal in two of the 12 spectra obtained by I08, by including it as a fitted parameter. We obtained a value which was very close to zero and much smaller than its uncertainty, so we fixed third light at zero for subsequent calculations.

LL Aqr presents a significant orbital eccentricity which we accounted for by fitting for the quantities ecosω and esinω, where e is eccentricity and ω is the longitude of periastron. This is because e and ω can be strongly correlated (e.g. Pavlovski et al. 2009), compromising their utility as fitted parameters. Light curves of eccentric dEBs typically allow the quantity ecosω to be determined precisely, as it primarily affects the time difference between primary and secondary eclipse (e.g. Kopal 1959). The main indicator of esinω is the ratio of the eclipse durations, which are generally less precise. The inclusion of RVs in an analysis can allow a significantly improved measurement of esinω (see Wilson 1979). We therefore decided to modify jktebop to allow simultaneous fitting to the SuperWASP light curve and the RVs of both stars3.

We included the velocity amplitudes of the two stars (KA and KB) and the systemic velocities (γA and γB) as fitted parameters. We allowed the stars to have different systemic velocities in order to avoid possible systematic effects due to mismatch between their spectra and the template used to observe the cross-correlation function (see also Popper & Hill 1991). The fitted values of γA and γB differ by an acceptable 1.5σ. We checked the consequences of this approach by computing an alternative solution where the two stars have a common systemic velocity. This yielded values for KA, KB and esinω which were larger by 0.3σ, and had a smaller effect on all other parameters.

Measurement errors are not available for the RVs (they were all accorded unit weight by Griffin 2013), and are far too small for the SuperWASP data, so all datapoints in individual datasets were assigned the same weight. We incorporated the iterative adjustment of weights for the individual datasets in jktebop, in order to appropriately combine the different sources of information. This was done by forcing the reduced χ2 (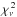) for each dataset to be unity; by doing this we are implicitly assuming that the best fit we find is a good representation of the data.

Uncertainties were calculated using a Monte Carlo (MC) approach (Southworth et al. 2004) with 1000 synthetic datasets per run. Whilst this does a good job for well-behaved data (Southworth et al. 2005b), we have found that it underestimates the true uncertainties in the presence of correlated noise such as occurs in the SuperWASP data (Southworth et al. 2011). We therefore ran residual-permutation (RP) simulations (see Southworth 2008), after modifying the implementation of this algorithm in jktebop such that the residuals are permuted only within datasets. To account for the much smaller number of RV compared to photometric datapoints, we set the residuals for smaller datasets to cycle multiple times whilst the residuals for the largest dataset cycle exactly once.

The final results of this analysis are contained in Table 3 and are precisely and accurately measured. The uncertainties on individual parameters were assessed in three ways: from the covariance matrix, from MC and from RP. The parameters primarily determined by the photometry (rA, rB, J, i, Porb, Tpri) show uncertainties from the RP analysis which are roughly twice those from the MC approach. The formal errors agree well with the MC results, which is sensible because the solution does not suffer from the strong correlations between parameters which formal errors do not account for.

We find an orbital ephemeris of

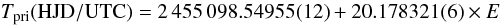where each bracketed quantity represents the uncertainty in the last digit of the preceding number, and E is the number of orbital cycles since the reference epoch. This orbital period is in good agreement with the value obtained by Griffin (2013). The period found by I08 has a higher quoted precision than our own, despite being based on fewer data, and is in formal but unexceptional disagreement with our result.

Table 3

Individual parameters of the fits to the SuperWASP light curve of LL Aqr, including several alternative sets of errorbars.

Table 4

Individual parameters of the fits to the UBV light curves of LL Aqr, including two alternative sets of errorbars.

We also modelled the UBV light curves presented by I08, each of which contains 1925 datapoints with full coverage of the primary eclipse but only partial coverage of the secondary eclipse. We fixed the orbital ephemeris at that determined to high precision from the preceding analysis, and also fixed esinω at the value found above to make up for not including RVs in this step. The limb darkening coefficients were also not adjusted after it was established that the light curves have insufficient precision to constrain them to within useful limits. The best fits are shown in Fig. 3. Errorbars were calculated via the MC and RP algorithms and both are shown in Table 4. The errorbars for e and ω are underestimated because esinω was fixed in these analyses. For all three light curves the RP uncertainties are at least a factor of two larger than the MC uncertainties, showing that dedicated observations can be as strongly affected by correlated noise as robotic survey data. We adopted the larger of the MC and RP errorbars for each parameter.

For calculating the final photometric and spectroscopic parameters we adopted the weighted mean of the individual values of rA + rB, k, i, rA and rB. The results for the U light curve are outwardly slightly discrepant, but in fact their large uncertainties make them consistent with the other values to within 1−2σ. We calculated weighted means both with and without the U results and found them to differ insignificantly, so we adopted those including the U results. The 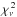of the values around the weighted means are 3.5 for i, 1.5 for rA and 1.7 for rB. These disagreements are not big enough to indicate a problem with the data (or analysis), and have been accounted for by inflating the uncertainties in the affected parameters to enforce 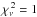. The final parameters are given in Table 5; those not already discussed in this paragraph have been adopted unchanged from individual analyses. The final light ratios in UBV were calculated by repeating the fits to these light curves whilst fixing the geometrical parameters to the values given in Table 5. A model light curve calculated for the geometrical properties in Table 5 shows that the primary eclipse is total but that the secondary eclipse is partial.

4. Physical properties and distance

The physical properties of LL Aqr have been calculated from the values of Porb, rA, rB, i, e, KA and KB measured in the preceding section. This was done using the jktabsdim code originally developed by Southworth et al. (2005a), which propagates the uncertainty in each input parameter by a perturbation approach. Results are calculated for each input parameter, and plus and minus its errorbar, yielding the effect of its uncertainty on each output parameter. The individual contributions are then added in quadrature to generate the final errorbar for each output quantity. The adopted physical constants are listed in Southworth (2011).

The masses and radii of the two stars (Table 6) are all measured to high precision (less than 1%), thanks to the high quality of the RVs from Griffin (2013) and the large quantity of photometric observations4. LL Aqr is therefore an excellent check and calibrator of theoretical models in the region of the Sun; the mass and radius of the secondary component are almost identical to those of the Sun. This will be exploited in the next section. The synchronous rotational velocities of the stars are only 3 km s-1. Tidal effects move the rotational velocities towards a pseudosynchronous state, i.e. synchronous with the orbital motion at periastron when the stars have their smallest separation (Hut 1981). The pseudosynchronous rotational velocities of the stars are 6.64 ± 0.04 km s-1 for the primary star and 5.04 ± 0.04 km s-1 for the secondary star.

The distance to the system is also straightforwardly measurable. For this we adopted the Teff values from I08 and the 2MASS JHK apparent magnitudes5 (Skrutskie et al. 2006). I08 measured standard magnitudes for LL Aqr of V = 9.206, B − V = 0.559 and U − B = 0.085. The V-band measurement does not agree well with the values of V = 9.32 ± 0.02 and 9.86 ± 0.03 obtained from Tycho observations (Høg et al. 1997). There is a multitude of different (but often related) alternatives listed by Vizier6 and these show a spread from V = 9.2 to V = 9.4 so cannot break the deadlock. The B magnitudes are (surprisingly) more concordant.

Table 5

Final photometric and spectroscopic parameters for LL Aqr.

Our favoured method for determining the distance to the system is via surface brightness relations (Southworth et al. 2005a), using the empirical calibrations provided by Kervella et al. (2004). When adopting this method, the UBV magnitudes from I08 and the 2MASS JHK magnitudes, we were able to find a consistent distance of 135–139 pc in each of the BVJHK passbands. The U passband yields a distance about 6 pc shorter, which is well within its uncertainty. We were able to obtain distances to the individual stars in UBV as we possess flux ratios between the stars in these passbands; their consistency shows that the Teff measurements (or at least their ratio) from I08 are reliable.

For our distance measurement we required an interstellar reddening excess of E(B − V) = 0.12 ± 0.05 (conservative errorbar) to align the distances found in the BV and JHK passbands. We adopt the final distance value of 137.8 ± 2.7 pc from the K band, as this value is least affected by the uncertainties in Teff and E(B − V). The revised Hipparcos parallax (van Leeuwen 2007) of 8.62 ± 1.15 mas corresponds to a distance of 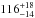 pc, which agrees with our final distance measurement to within 1.4σ.

Table 6

The physical properties of the LL Aqr system.

5. Comparison with theoretical stellar models

thumbnail Fig. 4

Mass–radius and mass–Teff plots comparing the physical properties of LL Aqr (points with errorbars) with the predictions of four sets of theoretical stellar models (points without errorbars show the tabulated predictions and lines show a quadratic interpolation between these for each set of models).

We have compared the physical properties of LL Aqr to several sets of tabulated theoretical predictions in the mass–radius and mass–Teff planes. Such comparisons are informative because the physical properties of the two stars are precisely measured and very different: the unevolved secondary star is a good indicator of bulk metal abundance, Z, whereas the properties of the slightly evolved primary indicate the age of the system, τ, for a given Z. The long orbital period also means that tidal interactions have had an insignificant effect on the evolution of the two stars, so they are reliably representative of single stars.

One important caveat is that the measured Teff values of the two stars are not independent. I08 determined the Teff of the primary star from its colour index, and fixed this when analysing the light curve. The Teff of the secondary star was thus determined relative to that of the primary. In the case of LL Aqr the ratio of the Teffs is well-determined, but the absolute values are less precise. This situation is common in the analysis of dEBs (e.g. Claret 2003; Southworth & Clausen 2007).

Armed with the Yonsei-Yale models (Demarque et al. 2004) and adopting a scaled-solar chemical composition, we find that predictions for Z = 0.01 and τ = 2.9 Gyr match the masses and radii well but under-predict the Teff values by 1σ. Adopting a lower Z = 0.007 and τ = 2.6 Gyr matches the mass and radius of the primary star and the Teff values of both stars, but predicts a modestly larger radius for the mass of the secondary star. The mean of the two sets of predictions provides a good match to the properties of LL Aqr.

The equivalent VRSS (VandenBerg et al. 2006) models for Z = 0.01 and τ = 2.5 Gyr also match both masses and radii well, but under-predict the temperatures by 1σ. The Teramo (Pietrinferni et al. 2004) models for Z = 0.01 and the PARSEC models (Bressan et al. 2012) for Z = 0.008, both for age τ = 2.5 Gyr, are almost identical and good matches to both stars. They fit the radii well and under-predict the Teff values by about 0.7σ. They are therefore in formally good agreement with the properties of LL Aqr.

thumbnail Fig. 5

Spectrum of LL Aqr in the region of the Ca H and K lines, showing the lack of chromospheric emission in the line cores. One pixel suffered from a cosmic ray event and has been greyed out.

We conclude that it is possible to find theoretical predictions which are consistent with the physical properties of the LL Aqr system for metallicities of Z = 0.007–0.010 and ages in the interval 2.5–2.9 Gyr, although the majority of theoretical models tested would prefer the stars to be cooler by about 100 K. The dereddened B − V indices found in Sect. 3 yield Teff values (Boyajian et al. 2013) which are lower than those found by I08, but not by a statistically significant amount. A definitive confrontation with theoretical model predictions could be performed once precise spectroscopic Teffs and chemical abundances have been obtained for the two stars.

6. Indications of stellar activity

Table 7

Échelle spectrum of LL Aqr.

Low-mass stars often exhibit signs of stellar activity such as modulated brightness due to starspots, enhanced UV and X-ray flux, and emission lines at optical wavelengths. We checked for each of these possibilities.

Firstly, the residuals of the SuperWASP data versus the best fit were subjected to a period analysis using the period04 package (Lenz & Breger 2004). A Fourier transform for periods below 1 d shows no evidence for sinusoidal variation, with a 3σ limit of 3 mmag. The limits for the individual stars are 5 mmag (primary) and 7 mmag (secondary) as they both contribute to the flux in the SuperWASP passband.

Secondly, LL Aqr was not detected in the ROSAT Point Source Catalogue (Voges et al. 1999) to a limit of 0.1 counts s-1 in the 0.1–2.5 keV band. It has been detected in the FUV and NUV bands by the GALEX satellite (Morrissey et al. 2007), at magnitudes 20.45 and 14.18 respectively. These measurements do not point to an enhanced X-ray or UV flux arising from the system.

Finally, the best indicators of chromospheric activity at optical wavelengths are the calcium H and K lines at 3933 Å and 3967 Å (Wilson 1968; Duncan et al. 1991). These were not in the wavelength range of the spectra obtained by I08, so we acquired a single spectrum of LL Aqr using the 3 m Shane Telescope at the Lick Observatory, US. We used the Hamilton échelle spectrograph to obtain a spectrum covering the full optical range at a resolving power of approximately 60 000 (Table 7). The Ca H and K lines show no emission, except for a mischievously placed cosmic ray event (Fig. 5). Whilst Ca H and K emission is generally weak at the temperatures of the components of LL Aqr (e.g. Knutson et al. 2010), spot and chromospheric activity is seen in our own Sun for which the mass and radius of LL Aqr B is a good match. We also see no emission at Hα. We conclude that LL Aqr shows no evidence of stellar activity or magnetism.

We also used the spectrum to measure the projected rotational velocities of the two stars. The spectrum was taken at phase 0.011 (just after the end of primary eclipse) when the velocity difference of the stars was 43 km s-1 and their spectral lines were well separated. We first measured an instrumental broadening of 0.09 Å from the emission lines in the thorium-argon calibration exposures. We then modelled selected spectral lines using the uclsyn code (Smalley et al. 2001; Smith 1992), finding Vsini = 4 ± 2 km s-1 for the primary star and Vsini = 4 ± 2 km s-1 for the secondary star. These values are consistent with both synchronous and pseudo-synchronous rotation.

7. Conclusions

The eclipsing nature of the binary system LL Aqr was discovered from Hipparcos photometry. Its joint properties of a solar-twin secondary star and a long orbital period make it ideal for studying the evolution of solar-type stars where the complicating effects of tidal interactions are weak.

We measured the physical properties of LL Aqr to high precision based on high-quality published radial velocity measurements from Griffin (2013) and extensive photometry obtained by the SuperWASP instruments located at La Palma and South Africa. The jktebop code was modified to simultaneously fit RVs and light curves for this work. These data were augmented by published UBV light curves from I08, allowing the SuperWASP results to be checked and refined. The resulting masses and radii are model-independent and have precisions of better than 1%.

Theoretical models are able to match the measured physical properties of LL Aqr for an approximately half-solar chemical composition and an age of 2.5 Gyr. More sensitive tests of stellar theory could be achieved through obtaining precise spectroscopic Teff and chemical abundance measurements. LL Aqr displays no evidence of spot activity or chromospheric emission, and both components are rotating slowly.

Tidal effects act to alter the rotational velocities and orbital eccentricity of the stars. Using the tidal friction theory of Zahn (1977) we find a rotational synchronisation timescale of approximately 1.5 Gyr and an orbital circularisation timescale which is greater by three orders of magnitude. Both timescales are consistent with the properties of LL Aqr at an age of 2.5 Gyr: the stars have rotational velocities consistent with both synchronous and pseudo-synchronous rotation, and the orbit has not been circularised.

The comparison with theoretical models shows that the components of LL Aqr do not exhibit the anomalously large radii typical for low-mass dEBs (Ribas 2006; Ribas et al. 2008; López-Morales 2007; Southworth 2009). Such inflated radii are explained by invoking fast rotation in short-period binary systems due to tidal effects. This enhances the magnetic activity of the star, which in turn inhibits convective heat transport and thus causes the star to be larger and cooler. A prediction of this concept is that long-period dEBs will not show inflated radii. LL Aqr does not, in line with KIC 6131659 (Porb = 17.5 d, Bass et al. 2012) and RW Lac (Porb = 10.4 d, Lacy et al. 2005). LSPM J1112+7626 (Porb = 41.0 d, Irwin et al. 2011) is an M-dwarf dEB which shows spot activity and inflated radii; its discord with the picture outlined above could easily be due to a young age.

1

jktebop is written in fortran77 and the source code is available at http://www.astro.keele.ac.uk/jkt/codes/jktebop.html

2

The adopted limb darkening coefficients were the average of the values for the Gunn g and r passbands.

3

The modified jktebop code was also used by Frandsen et al. (2013) in the study of the giant dEB system KIC 8410637.

4

The properties of LL Aqr have been entered into the DEBCat catalogue of well-studied detached eclipsing binary star systems: http://www.astro.keele.ac.uk/jkt/debcat/

5

The 2MASS magnitudes are J = 8.145 ± 0.023, H = 7.872 ± 0.033 and Ks = 7.819 ± 0.023. These observations were taken at epoch JD 2 451 315.9260, corresponding to phase 0.54 for LL Aqr, so are representative of its out-of-eclipse brightness.

Acknowledgments

J.S. acknowledges funding from STFC in the form of an Advanced Fellowship. We are grateful to the SuperWASP Consortium for obtaining the main light curve used in this work, to Roger Griffin and Serdar Evren for supplying published observations of LL Aqr, to Kelsey Clubb for obtaining the Hamilton spectrum of LL Aqr, and to Barry Smalley and Roger Griffin for discussions. We thank the anonymous referee for a helpful report. The following internet-based resources were used in research for this paper: the NASA Astrophysics Data System; and the SIMBAD database operated at CDS, Strasbourg, France.

References

  1. Bahcall, J. N., Pinsonneault, M. H., & Wasserburg, G. J. 1995, Rev. Mod. Phys., 67, 781 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bakan, S. 2009, BAV Rundbrief, 58, 9 [Google Scholar]
  3. Bass, G., Orosz, J. A., Welsh, W. F., et al. 2012, ApJ, 761, 157 [NASA ADS] [CrossRef] [Google Scholar]
  4. Boyajian, T. S., von Braun, K., van Belle, G., et al. 2013, ApJ, 771, 40 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
  6. Claret, A. 2003, A&A, 399, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Demarque, P., Woo, J.-H., Kim, Y.-C., & Yi, S. K. 2004, ApJS, 155, 667 [NASA ADS] [CrossRef] [Google Scholar]
  9. Duncan, D. K., Vaughan, A. H., Wilson, O. C., et al. 1991, ApJS, 76, 383 [NASA ADS] [CrossRef] [Google Scholar]
  10. Etzel, P. B. 1981, in Photometric and Spectroscopic Binary Systems, eds. E. B. Carling, & Z. Kopal (Dordrecht: Kluwer), NATO ASI Ser. C., 69, 111 [Google Scholar]
  11. Frandsen, S., Lehmann, H., Hekker, S., et al. 2013, A&A, 556, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Griffin, R. F. 1967, ApJ, 148, 465 [NASA ADS] [CrossRef] [Google Scholar]
  13. Griffin, R. F. 2013, The Observatory, 133, 156 [Google Scholar]
  14. Høg, E., Bässgen, G., Bastian, U., et al. 1997, A&A, 323, L57 [NASA ADS] [Google Scholar]
  15. Houk, N., & Swift, C. 1999, Michigan catalogue of two-dimensional spectral types for the HD Stars, 5 (Department of Astronomy, University of Michigan) [Google Scholar]
  16. Hoxie, D. T. 1973, A&A, 26, 437 [NASA ADS] [Google Scholar]
  17. Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
  18. Ibanoǧlu, C., Evren, S., Taş, G., et al. 2008, MNRAS, 390, 958 (I08) [NASA ADS] [CrossRef] [Google Scholar]
  19. Irwin, J. M., Quinn, S. N., Berta, Z. K., et al. 2011, ApJ, 742, 123 [NASA ADS] [CrossRef] [Google Scholar]
  20. Kazarovets, E. V., Samus, N. N., Durlevich, O. V., et al. 1999, IBVS, 4659, 1 [Google Scholar]
  21. Kervella, P., Thévenin, F., Di Folco, E., & Ségransan, D. 2004, A&A, 426, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Knutson, H. A., Howard, A. W., & Isaacson, H. 2010, ApJ, 720, 1569 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kopal, Z. 1959, Close binary systems, The International Astrophysics Series (London: Chapman & Hall) [Google Scholar]
  24. Lacy, C. H. S., Torres, G., Claret, A., & Vaz, L. P. R. 2005, AJ, 130, 2838 [NASA ADS] [CrossRef] [Google Scholar]
  25. Lenz, P., & Breger, M. 2004, in The A-Star Puzzle, eds. J. Zverko, J. Žižnovsky, S. J. Adelman, & W. W. Weiss (Cambridge UK: Cambridge University Press), IAU Symp., 224, 786 [Google Scholar]
  26. López-Morales, M. 2007, ApJ, 660, 732 [NASA ADS] [CrossRef] [Google Scholar]
  27. Morrissey, P., Conrow, T., Barlow, T. A., et al. 2007, ApJS, 173, 682 [NASA ADS] [CrossRef] [Google Scholar]
  28. Nelson, B., & Davis, W. D. 1972, ApJ, 174, 617 [NASA ADS] [CrossRef] [Google Scholar]
  29. Otero, S. A., & Dubovsky, P. A. 2004, IBVS, 5557, 1 [NASA ADS] [Google Scholar]
  30. Pavlovski, K., Tamajo, E., Koubský, P., et al. 2009, MNRAS, 400, 791 [NASA ADS] [CrossRef] [Google Scholar]
  31. Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
  32. Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
  33. Pojmański, G. 1997, AcA, 47, 467 [Google Scholar]
  34. Pollacco, D. L., Skillen, I., Cameron, A. C., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
  35. Popper, D. M., & Etzel, P. B. 1981, AJ, 86, 102 [NASA ADS] [CrossRef] [Google Scholar]
  36. Popper, D. M., & Hill, G. 1991, AJ, 101, 600 [NASA ADS] [CrossRef] [Google Scholar]
  37. Ribas, I. 2006, Ap&SS, 304, 89 [NASA ADS] [CrossRef] [Google Scholar]
  38. Ribas, I., Morales, J. C., Jordi, C., et al. 2008, Mem. Soc. Astron. It., 79, 562 [Google Scholar]
  39. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  40. Smalley, B., Smith, K. C., & Dworetsky, M. M. 2001, UCLSYN Userguide [Google Scholar]
  41. Smith, K. C. 1992, Ph.D. Thesis, University of London [Google Scholar]
  42. Southworth, J. 2008, MNRAS, 386, 1644 [NASA ADS] [CrossRef] [Google Scholar]
  43. Southworth, J. 2009, MNRAS, 394, 272 [NASA ADS] [CrossRef] [Google Scholar]
  44. Southworth, J. 2011, MNRAS, 417, 2166 [NASA ADS] [CrossRef] [Google Scholar]
  45. Southworth, J., & Clausen, J. V. 2007, A&A, 461, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Southworth, J., Maxted, P. F. L., & Smalley, B. 2004, MNRAS, 351, 1277 [NASA ADS] [CrossRef] [Google Scholar]
  47. Southworth, J., Maxted, P. F. L., & Smalley, B. 2005a, A&A, 429, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Southworth, J., Smalley, B., Maxted, P. F. L., Claret, A., & Etzel, P. B. 2005b, MNRAS, 363, 529 [NASA ADS] [CrossRef] [Google Scholar]
  49. Southworth, J., Bruntt, H., & Buzasi, D. L. 2007, A&A, 467, 1215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Southworth, J., Pavlovski, K., Tamajo, E., et al. 2011, MNRAS, 414, 3740 [NASA ADS] [CrossRef] [Google Scholar]
  51. Tamuz, O., Mazeh, T., & Zucker, S. 2005, MNRAS, 356, 1466 [NASA ADS] [CrossRef] [Google Scholar]
  52. van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. VandenBerg, D. A., Bergbusch, P. A., & Dowler, P. D. 2006, ApJS, 162, 375 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  54. Voges, W., Boller, T., Dennerl, K., et al. 1999, in Highlights in X-ray Astronomy, eds. B. Aschenbach, & M. J. Freyberg, 282 [Google Scholar]
  55. Wilson, O. C. 1968, ApJ, 153, 221 [NASA ADS] [CrossRef] [Google Scholar]
  56. Wilson, R. E. 1979, ApJ, 234, 1054 [NASA ADS] [CrossRef] [Google Scholar]
  57. Woźniak, P. R., Vestrand, W. T., Akerlof, C. W., et al. 2004, AJ, 127, 2436 [NASA ADS] [CrossRef] [Google Scholar]
  58. Zahn, J. 1977, A&A, 57, 383 [Google Scholar]
  59. Zombeck, M. V. 1990, Handbook of space astronomy and astrophysics (Cambridge University Press), 2nd edn. [Google Scholar]

All Tables

Table 1

SuperWASP photometric data for LL Aqr.

In the text
Table 2

Published times of minimum light for LL Aqr.

In the text
Table 3

Individual parameters of the fits to the SuperWASP light curve of LL Aqr, including several alternative sets of errorbars.

In the text
Table 4

Individual parameters of the fits to the UBV light curves of LL Aqr, including two alternative sets of errorbars.

In the text
Table 5

Final photometric and spectroscopic parameters for LL Aqr.

In the text
Table 6

The physical properties of the LL Aqr system.

In the text
Table 7

Échelle spectrum of LL Aqr.

In the text

All Figures

thumbnail Fig. 1

Full light curves of LL Aqr from SuperWASP and I08. The jktebop best fits are plotted as black lines and the residuals of the fits are shown in the lower panel.
In the text
thumbnail Fig. 2

SuperWASP light curve of the primary (top) and secondary eclipse (middle) and Griffin (2013) RVs (bottom) of LL Aqr. The datapoints are shown in red and the solid lines show the best fits found using jktebop. The residuals are shown below each fit.
In the text
thumbnail Fig. 3

UBV light curves of the primary (top) and secondary eclipse (bottom) of LL Aqr. The datapoints are shown in blue (U), green (B) and red (V), and the solid lines show the best fits found using jktebop. The residuals are shown below each fit.
In the text
thumbnail Fig. 4

Mass–radius and mass–Teff plots comparing the physical properties of LL Aqr (points with errorbars) with the predictions of four sets of theoretical stellar models (points without errorbars show the tabulated predictions and lines show a quadratic interpolation between these for each set of models).
In the text
thumbnail Fig. 5

Spectrum of LL Aqr in the region of the Ca H and K lines, showing the lack of chromospheric emission in the line cores. One pixel suffered from a cosmic ray event and has been greyed out.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.