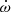EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 665 (September 2022) A&A, 665 (2022) A13 Full HTML
Open Access
Issue
A&A
Volume 665, September 2022
Article Number A13
Number of page(s) 15
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202244287
Published online 01 September 2022

© D. Baroch et al. 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

1. Introduction

Well-detached double-lined eclipsing binaries are the basic source of information for stellar dimensions, such as masses and radii, to high precision (Andersen 1991; Torres et al. 2010). Moreover, eccentric systems that show apsidal motion, that is, the precession of the line of apsides, yield additional unique information about the stellar internal density distribution through the log k2 parameter. This can only be accurately determined for this type of eclipsing binary, where the masses and radii of their components can be measured to a precision better than ∼2% (Claret et al. 2021).

Observed apsidal motion rates have two main components: a secular variation due to the non-spherical shape of the stars, called the quadrupole or classical term, and a contribution due to the effect in the two-body equations of motion given by general relativity, the relativistic term. Both components have recently been studied in Baroch et al. (2021) and Claret et al. (2021) for those systems with precise times of minimum light determinations based on photometric measurements obtained with the Transiting Exoplanet Survey Satellite (TESS) space mission (Ricker et al. 2015), which we also use in this paper. An additional element of the apsidal motion rate can be caused by the presence of a perturbing third body (Borkovits et al. 2007, 2019). Although this term is generally negligible when compared to the other terms, it may become relevant in precise determinations of the apsidal motion rate or when the classical term is relatively small.

Two well-known cases of eclipsing binaries that show apsidal motion and with TESS data were not included in Baroch et al. (2021) and Claret et al. (2021) because of the lack of sufficiently precise absolute dimensions. These are V889 Aql and V402 Lac. Both systems show quite eccentric orbits, with e ∼ 0.4, but different orbital periods. This leads to different dominant terms of the apsidal motion: relativistic for V889 Aql and classical for V402 Lac.

The system V889 Aql was identified four decades ago as the first known case of relativistic apsidal motion (Giménez & Scaltriti 1982), based on the comparison of the displacement of the secondary eclipse compared with a previous light curve by Semeniuk (1967). A value of 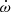= 0.00046 ± 0.00015 deg cycle−1 was obtained by adopting an orbital eccentricity of 0.37, which was deduced from light curve analysis. Khaliullin & Khaliullina (1989) obtained a new light curve and confirmed the apsidal motion rate given by Giménez & Scaltriti (1982). A deeper analysis of the light curve yielded a refined determination of the orbital eccentricity and the presence of significant third light (L3 = 18.5% of the total light) as well as indications of the presence of a third body. This was later confirmed, with more precise times of minimum light, by Wolf et al. (2005), who established a period for the third body orbit of 52 yr. Nevertheless, the estimated mass of the third body, assuming a co-planar orbit, could not explain the observed L3 value. In any case, the comparison of the observed apsidal motion rate with theoretical predictions requires a good radial velocity (RV) curve, which would allow a precise determination of the stellar masses and eccentricity. A more recent study by Kıran et al. (2019) included spectroscopic measurements but could not achieve the required precision. Moreover, the authors used an incomplete light curve, with no consideration of L3. A new, more precise light curve, with no phase gaps, as well as a better RV curve are clearly needed.

The system V402 Lac was studied using Hipparcos photometry by Bulut & Demircan (2008), who obtained initial results with the EBOP light curve analysis tool. Herrero (2010) presented new photometry and analysed the available RV curves; however, the degeneracy between the eccentricity, flux ratio, and ratio of radii could not be solved, and the presence of third light was not considered. New photometry by Hoyman et al. (2018) produced an additional light curve, and they analysed the times of eclipse available, leading to an apsidal motion period of 213 years and the detection of a third body, with an orbital period of 20.5 yr around the eclipsing binary. Unfortunately, a constraint of L2/L1 from spectroscopy could not be established, and the presence of third light in the crowded field of view was not analysed. To address these issues, TESS measurements have been used, which provide additional times of minima and a precise light curve, and new spectroscopic observations allowed the possible solutions to be constrained.

In this work, new spectroscopic measurements have been obtained for both stars. Their TESS light curves, as well as new eclipse timings, have been analysed. As a result, we present new absolute dimensions and orbital parameters. We show the general properties and sidereal orbital periods (Ps) of the two objects in Table 1.

Table 1.

General properties of V889 Aql and V402 Lac.

Section 2 presents the observational data, both from spectroscopy and photometry. Section 3 describes the analysis of the RV curves and the times of eclipse, leading to the orbital parameters. Section 4 presents the modelling of the TESS light curves, which yield the corresponding absolute dimensions of the system. Finally, Sect. 5 compares the results with theoretical predictions and summarises the conclusions.

2. Observations

2.1. Spectroscopy

We obtained new spectroscopic observations of V899 Aql and V402 Lac with four different spectrographs. Observations of the two targets between September and October 2020 were acquired with CAFE (Aceituno et al. 2013), a high resolution échelle spectrograph mounted on the 2.2 m telescope at Calar Alto observatory, Spain, which covers a wavelength range between 365 nm and 980 nm with a spectral resolution of 70 000. V889 Aql was also observed between March and April 2021 with the échelle spectrograph mounted on the 1.2 m telescope TIGRE (Schmitt et al. 2014) at la Luz observatory, Mexico. The spectrograph at TIGRE has a spectral resolution of 20 000 and covers a wavelength range between 350 nm and 880 nm in two channels, the blue channel between 350 nm and 560 nm, and the red channel between 580 nm and 880 nm. Here we only use data from the blue channel of TIGRE, since it is closer to the emission peak of V889 Aql.

Additionally, we also observed V402 Lac between October 2001 and August 2006, and between September and November 2009 with the Robert G. Tull Coudé Spectrograph (Tull et al. 1995) and with the STELLA échelle spectrograph (Strassmeier et al. 2001), respectively. The Tull spectrograph is mounted on the 2.7 m telescope at the McDonald Observatory, USA, and covers a wavelength range between 375 nm and 1020 nm at a resolving power of about 60 000. The STELLA échelle spectrograph is mounted on the two 1.2 m telescopes at Izana Observatory, Spain, and covers a wavelength range between 390 nm and 870 nm with a spectral resolution of about 55 000. Data from these two instruments were already used in the analysis of Herrero (2010). We summarise the number of available spectra from each instrument in Table 2, together with the time span of each dataset.

Table 2.

Number and time span of the available spectra for each target from different instruments, with the number of RVs used in the analysis in parentheses.

The RVs of the components of each system were computed by searching for their signature in the spectra using todmor (Zucker et al. 2003), an implementation for multi-order spectra of the two-dimensional cross-correlation method todcor (Zucker & Mazeh 1994). In this technique, two different template spectra are used for each component, scaled according to their flux ratio in the wavelength range of the observations. The two spectra are simultaneously Doppler-shifted, constructing a two-dimensional cross-correlation function (CCF) map from which the RVs of the two components are computed. As templates for the calculation of the CCFs, we employed synthetic Phoenix stellar models (Husser et al. 2013) for the observations of V889 Aql. However, since the expected temperature of V402 Lac is close to the limit of the Phoenix models, 12 000 K (Herrero 2010; Hoyman et al. 2018), we instead decided to use models from the Coelho synthetic stellar library (Coelho 2014), which covers temperatures up to 25 000 K, and allowed us to explore a wider grid of template temperatures. We adopted solar metallicities for all the spectra. For each target and instrument, we checked all the échelle orders of the spectra with the highest signal-to-noise ratio with todmor, and discarded those with no signals in their CCFs due to telluric contamination or lack of spectral lines.

The parameters of the best templates were found by exploring a grid of values for effective temperatures (Teff), luminosity ratios (L2/L1), and spectral line broadening (vb) due to rotation, spectral resolution, and other effects such as macroturbulence, seeking the combination that maximised the CCF peak of each spectrum. In the case of V889 Aql, a luminosity ratio of L2/L1 = 0.98 ± 0.06 was derived, together with the Teff and vb values for each instrument given in Table 3, and with the weighted mean values listed in the last row. In the case of V402 Lac, however, we found strong degeneracies between L2/L1 and vb, probably due to the lack of clear and deep lines in the spectra caused by the large rotational velocities of the components. Therefore, we decided to fix the luminosity ratio to 1 based on the results found in Sects. 3.2 and 4.2, which point towards two equal-mass stars of similar luminosities. Teff and vb values derived for V402 Lac, with the adopted L2/L1 = 1, are listed in Table 4.

Table 3.

Template parameters of V889 Aql found from the maximisation of the CCF peak of all available spectra with todmor and their weighted means with uncertainties.

Table 4.

Same as Table 3 but for V402 Lac.

Finally, RV curves were computed consistently with todmor using as templates for each instrument the ones with their parameters closer to those listed in Tables 3 and 4. The RVs of spectra taken during any of the eclipses or at orbital phases close to conjunction, where the spectral lines of the components could not be separated due to rotational broadening, were not further considered. The final number of RVs used in this analysis is shown in parenthesis in Table 2. We list the derived RVs of each object in Tables A.1 and A.2.

Concerning the possibility to check rotational velocities using the Rossiter-McLaughlin effect (Rossiter 1924; McLaughlin 1924), we could obtain eight CAFE spectra within the primary eclipse of V889 Aql but not for the shorter period case of V402 Lac. Observations showed that the rotational effect on the RVs during eclipse could not provide any indication of misalignment of the rotational axes of V889 Aql, although more observations during both eclipses are needed to confirm the actual alignment of all components.

2.2. Photometry

The two systems studied in this work have been observed by the TESS mission (Ricker et al. 2015), which is an all-sky photometric survey obtaining densely covered light curves at very high precision of the nearest and brightest stars, aimed at detecting exoplanets. The excellent quality of TESS data make them ideal for the study of stellar eclipse events (Baroch et al. 2021; Claret et al. 2021; Southworth 2021b), which are much more prominent than exoplanet transits.

V402 Lac was one of the TESS targets included in Sector 16, which was observed in September 2019. We collected the 2-min cadence simple aperture photometry (SAP) produced by the Science Process Operation Centre (Jenkins et al. 2016), available at the Mikulski Archive for Space Telescopes1 (MAST). We show in Fig. 1 the mask used for the computation of the SAP and the brightest neighbours to V402 Lac. As it can be seen in the figure, the mask contains a star (BD+44 4060, label #2) with Gaia magnitude G = 9.87, which we estimate to contribute 5.2% of the total flux in the Gaia band. In addition, the bright visual companion to V402 Lac, HD 210387 (label #3, G = 6.72), has a point spread function that extends several pixels inside the mask, which would also significantly contribute to the total flux through an undetermined amount.

thumbnail Fig. 1.

TESS target pixel file of V402 Lac in Sector 16 (created with tpfplotter; Aller et al. 2020), with the colour code indicating the flux measured by each pixel. We show the pixels included in the computation of the SAP as orange bordered pixels. The size of the red circles indicates the TESS magnitudes of the three brightest stars contained in the field, with V402 Lac marked with a white cross.

On the other hand, V889 Aql was not included as a TESS target in any of the sectors, though it fell within the TESS field of view during Sectors 14 and 40, which were observed between July and August 2019 and between June and July 2021, with a cadence of 30 and 10 min, respectively. Therefore, we downloaded the TESS full frame images (FFIs) from MAST, and used the public TESS aperture photometry tool Eleanor2 (Feinstein et al. 2019) to extract the SAP of V889 Aql with a mask defined by the pixels shown in Fig. 2. The mask was modified to avoid the addition of a visual companion (label #2, G = 11.21), which was included in the default mask computed by Eleanor.

thumbnail Fig. 2.

Portion of the TESS FFI containing V889 Aql in Sector 40 (created with tpfplotter; Aller et al. 2020), with the colour code indicating the flux measured by each pixel. We show the pixels used to extract the photometry as orange bordered pixels. The size of the red circles indicates the TESS magnitudes of the two brightest stars contained in the field, with V889 Aql marked with a white cross.

The out-of-eclipse TESS photometry of both stars, shown in Figs. 3 and 4, present long-term trends produced by effects such as pointing jitter and scattered light from the Earth and Moon (Hattori et al. 2022), which can bias the resulting orbital parameters and measured times of minimum light. To mitigate the effects of these trends, we employed the Python package george (Ambikasaran et al. 2015) to model the out-of-eclipse photometry using a Gaussian process correlated-noise model with a squared-exponential covariance function (see e.g., Gibson et al. 2012; Aigrain et al. 2016, for more details). The length-scale hyperparameter was set to a value of 2 days for V889 Aql, while for V402 Lac was set to a value of 20 days to avoid fitting the modulations produced by geometric effects, observed with a periodicity of 3.78 d, the orbital period of the system. The resulting model, shown as red lines in the upper panels in Figs. 3 and 4, were used to normalise the entire light curve, including the eclipses.

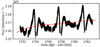thumbnail Fig. 3.

Model (red) used to detrend the out-of-eclipse TESS photometry (black dots) of V402 Lac in the second part of Sector 16.

thumbnail Fig. 4.

Model (red) used to detrend the out-of-eclipse TESS photometry (black dots) of V889 Aql in the second part of Sector 40.

In the photometric analysis presented in Sect. 4, in order to speed up the optimisation of the orbital parameters, we reduced the number of photometric points by only using the last part (i.e. after intermediate data downlink) of the TESS light curve in Sector 16 for V889 Aql and Sector 40 in V402 Lac, which in both cases seem to be the portions less affected by TESS systematics. The data used in the analysis represent ∼37% of the available data for V889 Aql, containing one pair of primary and secondary eclipses, and a ∼50% of the available data for V402 Lac, containing three pairs of primary and secondary eclipses.

2.3. Times of minimum light

Following the same approach as in Baroch et al. (2021), we determined the time of minimum light of the TESS photometry using the Kwee & van Woerden (1956, KvW) method, considering only eclipses where both the ingress and egress are well sampled, and using the same orbital phase interval for all primary and secondary eclipses for consistency. We discarded eclipses with strong asymmetries in their bisectors (see Baroch et al. 2021, for more details), which could be indicative of biased timing determinations due to, for example, systematic trends remaining in the data after our modelling. As a result of this procedure, we obtained 7 useful eclipse timings of V889 Aql (4 primary and 3 secondary) and 12 of V402 Lac (6 primary and 6 secondary).

In addition, we collected numerous photoelectric times of eclipse of V889 Aql and V402 Lac that have been measured over the last decades, and listed them in Tables 5 and 6. In total, 40 eclipse timings (20 primary and 20 secondary) are available for V889 Aql and 50 (31 primary and 19 secondary) for V402 Lac.

Table 5.

Times of eclipse for V889 Aql.

Table 6.

Times of eclipse for V402 Lac.

Preliminary attempts to fit the ephemeris of the eclipse timings of V402 Lac yielded residuals with a median deviation ten times larger than the published uncertainties, with some timings deviating up to 100 times the stated error. Although several works have shown that in the presence of systematic deviations from an ideal eclipse the KvW method may produce exceedingly optimistic errors (Breinhorst et al. 1973; Mikulášek et al. 2014; Torres et al. 2017), the deviations are much larger that those usually observed (cf. the timings of V889 Aql have a median deviation ∼1.5 times larger than their errors). For this reason, we decided to use errors of 0.005 and 0.010 days to primary and secondary timings, respectively, and errors of 0.0001 and 0.0004 days to primary and secondary TESS timings, respectively. These values are set to approximately match the dispersion shown by the residuals of the fit described in Sect. 3.2.

3. Study of the orbital parameters

For the determination of the orbital parameters from RVs we usually need good knowledge of the orbital period, which is generally constrained to high precision from the times of minimum light. At the same time, the analysis of the eclipse timings in eccentric orbits require a good determination of the orbital eccentricity, which can be highly correlated with the apsidal motion (Torres et al. 2015). Therefore, a combined solution of the RVs and the times of minimum was obtained, allowing a precise simultaneous determination of the anomalistic orbital period and the eccentricity. This procedure has been already successfully followed in the somewhat similar binary systems V501 Mon (Torres et al. 2015) and V541 Cyg (Torres et al. 2017).

For the RV model we assumed a Keplerian orbital motion, and solved for the sidereal period (Ps), the semi-amplitudes of the components (K1 and K2), the eccentricity (e), the apsidal motion (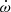), the argument of periastron (ω0) and time of periastron passage (Tperi) defined at a reference time of the primary eclipse TI, and the systemic velocity of each instrument (γInst.). Additionally, we also allowed an adjustable RV jitter term for each instrument (JitInst.), which was added in quadrature to the errors as described in Baluev (2009). Simultaneously, the times of eclipse were modelled using Eq. (11) in Giménez & Bastero (1995), solving for Pa, TI, e, ω0 and 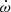. We also modelled the light travel time effect over the times of eclipse due to a potential third body with Eq. (2) of Irwin (1959). This additional effect yields the orbital parameters of the third body, as well as the time semi-amplitude (τ), from which we can estimate the minimum mass.

The optimisation of all orbital parameters and computation of uncertainties was done by sampling the posterior probability distribution with the emcee sampler (Foreman-Mackey et al. 2013), an implementation of the affine-invariant ensemble sampler Markov chain Monte Carlo (Goodman & Weare 2010).

3.1. V889 Aql

We used the model described above to simultaneously fit the RVs in Table A.1 and eclipse timings in Table 5. We show the best fits in Figs. 5 and 6. The parameters of the best joint fit are given in Table 7. The value of the orbital inclination, needed to fit the eclipse timings with Eq. (11) in Giménez & Bastero (1995), was adopted from the preliminary solution of the light curve to be 89 deg (see Sect. 4.1), and the fitted parameters were found to be very robust to variations of the adopted value. As expected, the simultaneous fit of both eclipse timings and RVs allowed us to obtain tight constrains on the anomalistic orbital period and the eccentricity, with Pa = 11.120771 ± 0.000004 d and e = 0.3750 ± 0.0013, which otherwise would be impossible to determine without fixing one of the values. The velocity semi-amplitude values obtained in the best fit indicate that the two stars have very similar masses, but not identical, with a mass ratio q = 0.978 ± 0.005. In addition, we also obtained a precise determination of the apsidal motion, of 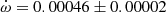deg cycle−1, in agreement with previous determinations (Giménez & Scaltriti 1982; Khaliullin & Khaliullina 1989; Wolf et al. 2005) and consistent within mutual uncertainties with the value of 0.000487 ± 0.000013 deg cycle−1 obtained by Kıran et al. (2019), who modelled the eclipse timings with a free value for the eccentricity. The effect of the apsidal motion on the eclipse timings is clearly seen in Fig. 6. In the upper-left panel, we show the eclipse timings once the linear ephemeris (i.e. the first three terms in Eq. (11) in Giménez & Bastero 1995) are subtracted, leaving only the effects of the apsidal motion and the third body, while the lower-left panel show the effect of the apsidal motion alone (i.e. after the linear ephemeris and the third body effect are subtracted).

thumbnail Fig. 5.

Best fit to the CAFE (circles) and TIGRE (triangles) RVs of V889 Aql, phase-folded to the orbital period. Blue and red colours correspond to the primary and secondary components, respectively. The bottom panels show the residuals of the best fit.

thumbnail Fig. 6.

Best fit to the primary (blue) and secondary (red) times of minimum light of V889 Aql, after subtracting the linear ephemeris (top left), after subtracting the linear ephemeris and the effect of the third body (bottom left), and after subtracting the linear ephemeris and the apsidal motion (top right). The panel at the bottom-right shows the residuals from all the fits.

Table 7.

Parameters of the best joint fit to the RVs and eclipse timings of V889 Aql.

Similarly, in the upper-right panel in Fig. 6 we show the eclipse timings after linear ephemeris and apsidal motion contribution are subtracted, leaving a clear indication of the presence of a third body around V889 Aql, as already found by Wolf et al. (2005) and Kıran et al. (2019). The best-fit parameters indicate a third body orbital period of 67 ± 4 a and an eccentricity of 0.24 ± 0.04. The third body induces a semi-amplitude over the eclipse timing residuals from a linear ephemeris of 0.047 ± 0.002 d, from which we derive a mass function of 0.122 ± 0.012 M⊙, or equivalently, a minimum mass of ∼1.6 M⊙.

As a sanity check to confirm that the presence of a third body is not affecting the measured value of the apsidal motion term, we used Eq. (7) in Baroch et al. (2021) to compute the apsidal motion from a linear fit to the difference between secondary and primary eclipse timings (T2 − T1), from which we derive an apsidal motion of 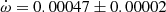deg cycle−1, confirming the value found previously.

3.2. V402 Lac

Following the same approach as for V889 Aql, we simultaneously modelled the RVs and eclipse timings of V402 Lac, listed in Tables A.2 and 6, respectively. In this case, however, the RV observations span almost 20 years, covering a non-negligible portion of the apsidal motion period, which we expect to cause a significant deviation of the RVs from a Keplerian orbit due to periastron precession. For this reason, we modelled the RVs with a Keplerian orbit, but allowing the argument of periastron, ω, to vary according to the apsidal motion rate 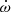as 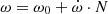, with N representing the number of cycles since TI and with ω0 defined at the same reference time of primary eclipse TI used in the fit to the eclipse timings. We list the obtained best fitting parameters of the joint model in Table 8. We obtained an anomalistic orbital period Pa = 3.782138 ± 0.000006 d with an eccentricity of e = 0.376 ± 0.003. The obtained values of the semi-amplitudes are compatible within the uncertainties, indicating that the two component stars are nearly indistinguishable, with a mass ratio of q = 0.995 ± 0.008. The improvement in the precision of the eccentricity value with respect to other works (Bulut 2013; Hoyman et al. 2018) allows us to precisely determine the apsidal motion rate of the system, yielding a value of 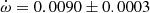deg cycle−1.

Table 8.

Parameters of the best joint fit to the RVs and eclipse timings of V402 Lac.

As can be seen in Fig. 7, which shows the best fit to the RVs phase-folded to the orbital period, the relatively fast apsidal motion rate has noticeable effects over the available RVs, arising from the change of the argument of periastron with time. The upper-left panel in Fig. 8 shows the best fit to the times of eclipse of V402 Lac, with the bottom-left and upper-right panels showing the apsidal motion and third body effects separately, as in Fig. 6. While the apsidal motion effect produces a clear deviation of the eclipse timings from a linear ephemeris, the effect of a hypothetical third body is more dubious. The relatively low precision of the secondary minimum timings, the low amplitude of the modulation produced by the third body, and a period at least as long as the baseline of the observations, makes it impossible to derive precise and non-degenerate orbital parameters. For this reason, we decided to fix the eccentricity to zero, and give only a lower limit to the orbital period of the third body. Although the best fit yields an orbital period of 46 yr and an amplitude of 0.015 d, which is shown in the upper-right panel in Fig. 8, we obtain comparable fits for periods and amplitudes as low as 20 years and 0.004 d, respectively. This lower limit to the orbital period of the third body is comparable to the period determined by Hoyman et al. (2018), of 20.54 yr, although they obtained an amplitude five times larger than the one we obtain fixing the same period. Finally, to check the significance of the third body signal and the effect that it may have over the determined orbital parameters, we repeated the analysis of the eclipse timings without including the light travel time effect in the model. We obtained a best-fit with a log-likelihood 20 units lower than the obtained with the full model, giving significant evidence in favour of the presence of a third body. Furthermore, the orbital parameters derived with the model without the effect of a third body do not differ by more than one sigma from those of the full model.

thumbnail Fig. 7.

Best fit to the CAFE (circles), STELLA (triangles), and Tull (squares) RVs of V402 Lac, phase-folded to the anomalistic period, and with the argument of periastron precessing according to . Blue hues and red hues correspond to the primary and secondary components, respectively, while the colour code indicates the date of the measurements and fit. The bottom panels show the residuals from the best fit.

thumbnail Fig. 8.

Same as Fig. 6, but for V402 Lac.

4. Light curve analysis and absolute dimensions

As mentioned before, in this type of eclipsing binaries with similar components there is an intrinsic degeneracy between the orbital parameters and the ratio of radii. Therefore, in the following analysis of the light curves, we adopt the orbital eccentricity and the sidereal period derived in Sect. 3 from the study of the RV curves and the eclipse timings.

4.1. V889 Aql

In order to obtain reliable photometric parameters of V889 Aql, we analysed the TESS photometry with the JKTEBOP3 code, a modern implementation written by J. Southworth of the Nelson–Davis–Etzel eclipsing binary model used in the code EBOP (Nelson & Davis 1972; Etzel 1981; Popper & Etzel 1981). In our analysis, we adopted the sidereal period and orbital eccentricity given in Table 7, and solved for the reference time of the primary eclipse (TI), the sum of the fractional radii normalised to the semi-major axis (rA + rB) and their ratio (k ≡ rB/rA), the orbital inclination (i), argument of periastron (ω), the central surface brightness ratio of the two stars (J), the fraction of light from a third body divided by the total light (L3/L), and a magnitude zero-point (m0).

As shown by other authors, a well-known and common problem in the analysis of partial eclipses with similar components is that the solutions for the ratio of radii, k, and the surface flux ratio, J, are highly degenerated, and yielding solutions above and below k = 1 (Torres et al. 2015; Southworth 2021a). This situation is more acute in the case of a significant amount of third light. To avoid such correlations, given that the spectroscopic analysis provided us with information about the luminosity ratio between the components, we used the resulting value, 0.98 ± 0.06, as a prior in the light curve analysis with JKTEBOP. The gravity darkening and quadratic limb darkening coefficients were adopted from Claret (2017), specifically computed for the TESS wavelength range for identical components with an effective temperature of 9200 K and log g = 4.20. To compute the errors, we generated 10 000 synthetic light curves with JKTEBOP by adding random noise according to the observational uncertainties. We then computed the best fit and determined the standard deviation of the parameters. In addition, to determine more realistic uncertainties, we repeated the analysis fixing e at the upper and lower value of the error bar in Table 7, computed the dispersion of the results, and added them quadratically to the uncertainties determined with JKTEBOP. This process had the highest impact over the uncertainties of k, i, and ω, which were increased by a factor of ∼10. We show the best fit parameters and uncertainties in Table 9, and show the corresponding best fit in Fig. 9 together with the original TESS measurements. We computed the individual fractional radii from the values of k and rA + rB, obtaining rA = 0.0549 ± 0.0012 and rA = 0.0544 ± 0.0012. The value of the argument of periastron we find, of 126.1 ± 0.2 deg, is in perfect agreement with the 126.14 deg value obtained in Sect. 3.1.

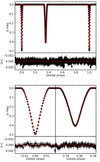thumbnail Fig. 9.

TESS photometry of V889 Aql from the second orbit of Sector 40 (black dots) and its best fit computed with JKTEBOP (red). The top panel shows the photometry phase-folded to the sidereal period, while the bottom panel shows the details of the primary (left) and secondary (right) eclipses. The residuals of the fits are shown in the bottom part of all panels.

Table 9.

Parameters of the fit to the TESS light curve of V889 Aql.

It should be noted that the L3 value of 19.1% confirms that found in the light curve analysis of Khaliullin & Khaliullina (1989), who also obtained an eccentricity in perfect agreement with our value in Table 7. However, our value may be overestimated due to the large pixel size of TESS, which may be including light from other close sources. Assuming a mass-luminosity relation of L ∝ M3.5, the measured third light would correspond to a third body with a mass of ∼1.75 M⊙, which is slightly higher than the minimum mass found from the light travel time effect analysis. This could suggest that the inclination of the third body orbit is close to that of the eclipsing system. However, with a third light of 19.1% of the total light in the TESS band, we expect a third light of around 14% in the band at which we obtained the spectra with CAFE. With this contribution to the total light, the spectral lines of the third body should be detected by analysing the spectra with todmor. However, we could not see any additional signal that could be attributed to the third body. This could suggest that the light from the third body is actually coming from two stars in a binary system. In this case, the outer binary system should be composed of two stars with masses ∼1.4 M⊙, each one contributing about 9.5% to the total light in the TESS band, or ∼5% in the CAFE band, which should be challenging to detect with todmor. In this case, the mutual inclination between the inner and the outer binary would be close to 50 deg, thus increasing the effect that the outer system may have over the orbital parameters and apsidal motion of the inner system (Borkovits et al. 2019) through the Lidov-Kozai mechanism (Lidov 1962; Kozai 1962). Nevertheless the timescale of the Lidov-Kozai induced oscillations, around 50 000 yr, would not have a significant effect in our measurement of the orbital eccentricity.

Using the results presented in Tables 7 and 9, the absolute dimensions of the eclipsing components of V889 Aql are given in Table 10.

Table 10.

Absolute dimensions of V889 Aql and V402 Lac.

4.2. V402 Lac

As in the case of V889 Aql, we modelled the TESS light curves of V402 Lac adopting the sidereal period and the orbital eccentricity from the study in Sect. 3.2. Given the larger stellar deformation of the components of V402 Lac, apparent in the out-of-eclipse photometry, and the relatively long duration of the eclipses, we used the same JKTEBOP code only for preliminary solutions, while the final parameters were computed using the Wilson-Devinney (WD; Wilson & Devinney 1971) code instead. This code represents the stars using Roche geometry and takes into account reflection and proximity effects accordingly. We fixed the effective temperature to the values indicated in Table 4, and adopted the quadratic limb-darkening coefficients by Claret (2017) corresponding to these temperatures. We also adopted the mass ratio from the spectroscopic solution, and fixed the bolometric albedo and the gravity darkening exponent to 1, as usual for radiative envelopes. The rotation of the components was assumed to be pseudo-synchronised at periastron (Hut 1981), although we also checked that the results obtained assuming the broadening values listed in Table 4 did not change significantly. We solved for the time of primary eclipse, the argument of periastron, the orbital inclination, the gravitational potentials of each component (ΩA and ΩB), the luminosity of the component A (as a parameter depending on the light curve normalisation), and the third light contribution. Unlike for V889 Aql, we could not fix the value of LB/LA from the spectroscopic analysis, since we could not find a precise value different from 1. Therefore, we opted for constraining its value by fixing the effective temperature of star B and assuming radiative coupling between the components for the I band in the WD code. LB/LA is finally reported in the table, and justifies the equal-luminosity assumption we made in the spectroscopic analysis.

We evaluated the uncertainties following the same process done for V889 Aql. We reanalysed the light curve with the eccentricity fixed at the value found in the spectroscopic solution and at the upper and lower values of the error bar in Table 7, computed the dispersion of the solutions, and added them quadratically to the formal uncertainties determined with the WD code. We obtained errors much larger than the formal uncertainties computed by the WD code, as expected. We list in Table 11 the parameters of the best solution and the corresponding uncertainties, and shown in Fig. 10 the best fit to the data.

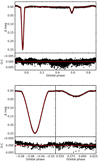thumbnail Fig. 10.

TESS photometry of V402 Lac from the second orbit of Sector 16 (black dots) and its best fit computed with the WD code (red). The top panel shows the photometry phase-folded to the sidereal period, while the bottom panel shows the details of the primary (left) and secondary (right) eclipses. The residuals of the fits are shown in the bottom part of all panels.

Table 11.

Parameters of the fit to the TESS light curve of V402 Lac.

As can be seen in the residuals of the best fit, there is a systematic deviation of the model at the beginning of the primary eclipse. This systematic effect is repeated when using the two parts of the TESS light curve individually, which rules out that it is produced by trends in the data processing. We attribute this systematic deviation to a lack of accuracy in the WD code in modelling the stellar deformations producing the reflection effect. It should be mentioned that the phase of periastron coincides with the beginning of the primary eclipse in the light curve of V402 Lac. Therefore, to prevent the underestimation of the errors due to any bias that may arise from this systematic deviation, we inflated the errors by a factor of two. In any case, all solutions agree with a system of almost identical components.

We obtained an argument of periastron of 58.1 ± 1.4 d, fully compatible with the value corresponding to the same reference time derived by the joint fit to RVs and times of minima. From the values of the gravitational potential we derive individual fractional radii of rA = 0.1315 ± 0.0018 and rB = 0.1304 ± 0.0014. The luminosity ratio as derived with the WD code is 0.99 ± 0.02, which is compatible with the value of 1 that we fixed in the spectroscopic analysis with todmor. In addition, we detect a significant third light contribution of 15 ± 4%. Although some of this light may be coming from a third companion, as seen in by the mask used by TESS shown in Fig. 1, a significant part of it might have its origin in the star (label #2) inside the TESS mask and in the bright star (label #3) close to V402 Lac.

5. Discussion and conclusions

Absolute dimensions of the components of V889 Aql and V402 Lac, as derived from the above orbital elements and light curve solutions, are given in Table 10, with relative errors between 0.8 and 2.1%. These absolute dimensions are sufficiently precise for a meaningful comparison with theoretical models and the analysis of the observed apsidal motion rates. Nevertheless, a reliable comparison with the distance given by Gaia, as shown in Table 1, was not possible due to the uncertainties in the contribution of the third light components measured with TESS in the V-band photometry and the computation of the extinction coefficients, which are expected to be relatively large. We could only verify that a reasonable combination of adopted third light and extinction could reproduce the Gaia measurements.

We computed the theoretical values of the k2 using the theoretical models published by Claret (2019), which are based on the Modules for Experiments in Stellar Astrophysics package (Paxton et al. 2011, 2013, 2015). These models assume convective core overshooting following the semi-empirical dependence on mass given by Claret & Torres (2018). We homogeneously derived k2 values and their errors from interpolation in the models, using M and log g as input parameters. However, since there are no previous determinations of the metallicity of any of the two systems, we tuned them until the derived mean effective temperature derived was compatible with the mean effective temperatures listed in Tables 3 and 4. This was achieved by assuming a metallicity of [Fe/H] = +0.10 ± 0.02 for V889 Aql and [Fe/H] = 0.00 ± 0.05 for V402 Lac, as can be seen in Figs. 11 and 12. Additional cross-checks were carried out by comparing the derived ages of the two components and obtaining compatible values in both systems, which provided additional reassurance. The uncertainties of the theoretical values were computed from the standard deviations of the results obtained from 105 random re-samplings of the input parameters, M, log g, and [Fe/H], employing their quoted uncertainties.

thumbnail Fig. 11.

Teff − log g relationship for the primary (blue) and secondary (red) components of V889 Aql, together with the theoretical models from Claret (2019) corresponding to the mass of each component and metallicities of 0.0 (dashed lines) and 0.1 (dotted lines).

thumbnail Fig. 12.

Teff − log g relationship for the primary (blue) and secondary (red) components of V402 Lac, together with the theoretical models from Claret (2019) corresponding to the mass of each component and metallicities of 0.0 (dashed lines) and 0.1 (dotted lines).

Using the absolute dimensions and orbital parameters of V889 Aql, we obtain a theoretical apsidal motion rate of 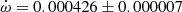deg cycle−1, with a classical term of 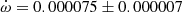deg cycle−1 and a relativistic term of 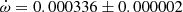deg cycle−1. Additionally, the third body companion, hypothetically composed of two stars of 1.4 M⊙ and with a mutual inclination of 50 deg, contributes with an estimated value of 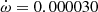deg cycle−1 (Borkovits et al. 2019), which increases the theoretical apsidal motion value to 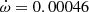deg cycle−1. This value is in good agreement with the observed value of 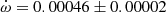deg cycle−1, although the assumption on the third body mass and inclination remains a source of significant uncertainty.

Using the absolute dimensions and orbital parameters of V402 Lac, we obtain a theoretical apsidal motion of 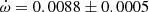deg cycle−1, with a classical term of 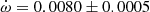deg cycle−1 and a relativistic term of 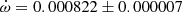deg cycle−1. Despite us not considering the effect of the potential third body, which is nevertheless not expected to be significant given the large classical term, the predicted value is compatible with the observed 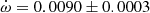deg cycle−1 within errors.

In conclusion, both systems are now part of the select group of eclipsing binaries with precise absolute dimensions, necessary for the improvement of empirical calibrations (Torres et al. 2010) or the testing of apsidal rates (Baroch et al. 2021). The case of V889 Aql is a clear example of apsidal motion dominated by the relativistic term, 75% of the total, with a significant third body contribution. On the other hand, V402 Lac shows a rather fast apsidal motion dominated by the classical term, with negligible relativistic and third body contributions. In the light curves, significant third light contributions were identified as was the presence of a third body through the variations in the eclipse timings, particularly in the case of V889 Aql.

Acknowledgments

This article has made use of observations collected at the Centro Astronómico Hispano Alemán (CAHA) at Calar Alto, operated jointly by the Junta de Andalucía and the Instituto de Astrofísica de Andalucía (CSIC). Data were partly obtained with the TIGRE telescope, located at La Luz observatory, México. TIGRE is a collaboration of the Hamburger Sternwarte, the Universities of Hamburg, Guanajuato and Liège. This paper includes data collected by the TESS mission. Funding for the TESS mission is provided by the NASA’s Science Mission Directorate. STELLA was made possible by funding through the State of Brandenburg (MWFK) and the German Federal Ministry of Education and Research (BMBF). The facility is a collaboration of the AIP in Brandenburg with the IAC in Tenerife. The construction of the 2.7 m telescope and Tull spectrograph was supported by contract NASr-242 with the National Aeronautics and Space Administration. This work has made use of data from the European Space Agency (ESA) mission Gaia. Gaia data are being processed by the Gaia Data Processing and Analysis Consortium (DPAC). Funding for the DPAC is provided by national institutions, in particular the institutions participating in the Gaia MultiLateral Agreement (MLA). The Gaia mission website is https://www.cosmos.esa.int/gaia. The Gaia archive website is https://archives.esac.esa.int/gaia. This publication has been made possible by grant PGC2018-098153-B-C33 funded by MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe”, by the program Unidad de Excelencia María de Maeztu CEX2020-001058-M, and by the Generalitat de Catalunya/CERCA programme.

References

  1. Abt, H. A. 2004, ApJS, 155, 175 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aceituno, J., Sánchez, S. F., Grupp, F., et al. 2013, A&A, 552, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Aigrain, S., Parviainen, H., & Pope, B. J. S. 2016, MNRAS, 459, 2408 [NASA ADS] [Google Scholar]
  4. Aller, A., Lillo-Box, J., Jones, D., Miranda, L. F., & Barceló Forteza, S. 2020, A&A, 635, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Ambikasaran, S., Foreman-Mackey, D., Greengard, L., Hogg, D. W., & O’Neil, M. 2015, IEEE Trans. Pattern Anal. Mach. Intell., 38, 252 [Google Scholar]
  6. Andersen, J. 1991, A&ARv, 3, 91 [Google Scholar]
  7. Badenas-Agustí, M. 2012, Analysis of the Eclipsing Binary Star System V402 Lac, unpublished [Google Scholar]
  8. Baluev, R. V. 2009, MNRAS, 393, 969 [Google Scholar]
  9. Baroch, D., Giménez, A., Ribas, I., et al. 2021, A&A, 649, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Biro, I. B., Borkovits, T., Hegedus, T., et al. 2007, Inf. Bull. Var. Stars, 5753, 1 [NASA ADS] [Google Scholar]
  11. Borkovits, T., Forgács-Dajka, E., & Regály, Z. 2007, A&A, 473, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Borkovits, T., Forgács-Dajka, E., & Rappaport, S. A. 2019, EAS Publ. Ser., 82, 99 [CrossRef] [EDP Sciences] [Google Scholar]
  13. Bozkurt, Z. 2011, Inf. Bull. Var. Stars, 5978, 1 [NASA ADS] [Google Scholar]
  14. Brát, L., Šmelcer, L., Kuèáková, H., et al. 2008, Open Eur. J. Var. Stars, 0094, 1 [Google Scholar]
  15. Brát, L., Trnka, J., Lehky, M., et al. 2009, Open Eur. J. Var. Stars, 107, 1 [Google Scholar]
  16. Brát, L., Trnka, J., Smelcer, L., et al. 2011, Open Eur. J. Var. Stars, 137, 1 [Google Scholar]
  17. Braune, W. 2014, BAV Circ., 63, 58 [Google Scholar]
  18. Breinhorst, R. A., Pfleiderer, J., Reinhardt, M., & Karimie, M. T. 1973, A&A, 22, 239 [NASA ADS] [Google Scholar]
  19. Bulut, İ. 2013, New A, 21, 22 [NASA ADS] [CrossRef] [Google Scholar]
  20. Bulut, İ., & Demircan, O. 2003, Inf. Bull. Var. Stars, 5476, 1 [NASA ADS] [Google Scholar]
  21. Bulut, İ., & Demircan, O. 2008, New A, 13, 252 [NASA ADS] [CrossRef] [Google Scholar]
  22. Claret, A. 2017, A&A, 600, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Claret, A. 2019, A&A, 628, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Claret, A., & Torres, G. 2018, ApJ, 859, 100 [Google Scholar]
  25. Claret, A., Giménez, A., Baroch, D., et al. 2021, A&A, 654, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Coelho, P. R. T. 2014, MNRAS, 440, 1027 [Google Scholar]
  27. de Bernardi, C., & Scaltriti, F. 1978, Acta. Astron., 28, 221 [NASA ADS] [Google Scholar]
  28. Diethelm, R. 1985, BBSAG Bull., 77, 2 [Google Scholar]
  29. Diethelm, R. 1990, BBSAG Bull., 96, 2 [NASA ADS] [Google Scholar]
  30. Diethelm, R. 1996, BBSAG Bull., 113, 4 [NASA ADS] [Google Scholar]
  31. Diethelm, R. 2012, Inf. Bull. Var. Stars, 6029, 1 [NASA ADS] [Google Scholar]
  32. Diethelm, R. 2014, Inf. Bull. Var. Stars, 6093, 1 [NASA ADS] [Google Scholar]
  33. Etzel, P. B. 1981, in Photometric and Spectroscopic Binary Systems, eds. E. B. Carling, & Z. Kopal, NATO ASI Ser. C, 69, 111 [NASA ADS] [CrossRef] [Google Scholar]
  34. Feinstein, A. D., Montet, B. T., Foreman-Mackey, D., et al. 2019, PASP, 131, 094502 [Google Scholar]
  35. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  36. Gaia Collaboration 2020, VizieR Online Data Catalog: I/350 [Google Scholar]
  37. Gibson, N. P., Aigrain, S., Roberts, S., et al. 2012, MNRAS, 419, 2683 [NASA ADS] [CrossRef] [Google Scholar]
  38. Giménez, A., & Bastero, M. 1995, Ap&SS, 226, 99 [Google Scholar]
  39. Giménez, A., & Scaltriti, F. 1982, A&A, 115, 321 [Google Scholar]
  40. Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
  41. Hattori, S., Foreman-Mackey, D., Hogg, D. W., et al. 2022, AJ, 163, 284 [NASA ADS] [CrossRef] [Google Scholar]
  42. Hegedus, T., Biro, I. B., Borkovits, T., & Paragi, Z. 1996, Inf. Bull. Var. Stars, 4340, 1 [NASA ADS] [Google Scholar]
  43. Hegedus, T., Borkovits, T., Biro, I. B., et al. 2003, Inf. Bull. Var. Stars, 5372, 1 [NASA ADS] [Google Scholar]
  44. Herrero, E. 2010, Master’s Thesis, Universitat de Barcelona, Spain [Google Scholar]
  45. Hoňková, K., Juryšek, J., Lehký, M., et al. 2013, Open Eur. J. Var. Stars, 160, 1 [Google Scholar]
  46. Hoyman, B., Kalomeni, B., & Yakut, K. 2018, New A, 60, 65 [NASA ADS] [CrossRef] [Google Scholar]
  47. Hubscher, J. 2017, Inf. Bull. Var. Stars, 6196, 1 [NASA ADS] [Google Scholar]
  48. Hubscher, J., Lehmann, P. B., Monninger, G., Steinbach, H.-M., & Walter, F. 2010, Inf. Bull. Var. Stars, 5941, 1 [NASA ADS] [Google Scholar]
  49. Husser, T. O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
  51. Irwin, J. B. 1959, AJ, 64, 149 [Google Scholar]
  52. Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, in Software and Cyberinfrastructure for Astronomy IV, eds. G. Chiozzi, & J. C. Guzman, SPIE, 9913, 99133E [Google Scholar]
  53. Khaliullin, K. F., & Khaliullina, A. I. 1989, Sov. Ast., 33, 41 [NASA ADS] [Google Scholar]
  54. Kıran, E., Bakış, V., Bakış, H., & Değirmenci, Ö. L. 2019, Ap&SS, 364, 214 [CrossRef] [Google Scholar]
  55. Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
  56. Kwee, K. K., & van Woerden, H. 1956, Bull Astron. Inst. Neth., 12, 327 [NASA ADS] [Google Scholar]
  57. Lidov, M. L. 1962, Planet Space Sci., 9, 719 [NASA ADS] [CrossRef] [Google Scholar]
  58. McLaughlin, D. B. 1924, ApJ, 60, 22 [Google Scholar]
  59. Mikulášek, Z., Chrastina, M., Liška, J., et al. 2014, Contrib. Astron. Obs. Skalnate Pleso, 43, 382 [Google Scholar]
  60. Nelson, B., & Davis, W. D. 1972, ApJ, 174, 617 [NASA ADS] [CrossRef] [Google Scholar]
  61. Pagel, L. 2020, BAV J., 033, 1 [NASA ADS] [Google Scholar]
  62. Paschke, A. 2019, BAV J., 031, 1 [NASA ADS] [Google Scholar]
  63. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  64. Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
  65. Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
  66. Popper, D. M., & Etzel, P. B. 1981, AJ, 86, 102 [NASA ADS] [CrossRef] [Google Scholar]
  67. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
  68. Rossiter, R. A. 1924, ApJ, 60, 15 [Google Scholar]
  69. Schmitt, J. H. M. M., Schröder, K. P., Rauw, G., et al. 2014, Astron. Nachr., 335, 787 [NASA ADS] [CrossRef] [Google Scholar]
  70. Semeniuk, I. 1967, Acta. Astron., 17, 223 [NASA ADS] [Google Scholar]
  71. Skillman, D. R. 1982, J. Am. Assoc. Var. Star Obs., 11, 57 [NASA ADS] [Google Scholar]
  72. Southworth, J. 2021a, Universe, 7, 369 [NASA ADS] [CrossRef] [Google Scholar]
  73. Southworth, J. 2021b, The Observatory, 141, 190 [NASA ADS] [Google Scholar]
  74. Strassmeier, K. G., Granzer, T., Weber, M., et al. 2001, Astron. Nachr., 322, 287 [NASA ADS] [CrossRef] [Google Scholar]
  75. Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
  76. Torres, G., Sandberg Lacy, C. H., Pavlovski, K., Fekel, F. C., & Muterspaugh, M. W. 2015, AJ, 150, 154 [Google Scholar]
  77. Torres, G., McGruder, C. D., Siverd, R. J., et al. 2017, ApJ, 836, 177 [Google Scholar]
  78. Tull, R. G., MacQueen, P. J., Sneden, C., & Lambert, D. L. 1995, PASP, 107, 251 [NASA ADS] [CrossRef] [Google Scholar]
  79. Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 [Google Scholar]
  80. Wolf, M., Diethelm, R., & Zejda, M. 2005, Ap&SS, 296, 109 [NASA ADS] [CrossRef] [Google Scholar]
  81. Wolf, M., Claret, A., Kotková, L., et al. 2010, A&A, 509, A18 [CrossRef] [EDP Sciences] [Google Scholar]
  82. Zasche, P., Uhlar, R., Kucakova, H., & Svoboda, P. 2011, Inf. Bull. Var. Stars, 6007, 1 [NASA ADS] [Google Scholar]
  83. Zasche, P., Uhlar, R., Kucakova, H., Svoboda, P., & Masek, M. 2014, Inf. Bull. Var. Stars, 6114, 1 [NASA ADS] [Google Scholar]
  84. Zasche, P., Uhlar, R., Svoboda, P., et al. 2017, Inf. Bull. Var. Stars, 6204, 1 [NASA ADS] [Google Scholar]
  85. Zucker, S., & Mazeh, T. 1994, ApJ, 420, 806 [NASA ADS] [CrossRef] [Google Scholar]
  86. Zucker, S., Mazeh, T., Santos, N. C., Udry, S., & Mayor, M. 2003, A&A, 404, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Appendix A: RV data

Tables A.1 and A.2 list the RVs used in this work, as computed with todmor. The RVs from each instrument are labelled as C (CAFE), T (TIGRE), Tu (Tull), and S (STELLA).

Table A.1.

Radial velocities of V889 Aql.

Table A.2.

Radial velocities of V402 Lac.

All Tables

Table 1.

General properties of V889 Aql and V402 Lac.

In the text
Table 2.

Number and time span of the available spectra for each target from different instruments, with the number of RVs used in the analysis in parentheses.

In the text
Table 3.

Template parameters of V889 Aql found from the maximisation of the CCF peak of all available spectra with todmor and their weighted means with uncertainties.

In the text
Table 4.

Same as Table 3 but for V402 Lac.

In the text
Table 5.

Times of eclipse for V889 Aql.

In the text
Table 6.

Times of eclipse for V402 Lac.

In the text
Table 7.

Parameters of the best joint fit to the RVs and eclipse timings of V889 Aql.

In the text
Table 8.

Parameters of the best joint fit to the RVs and eclipse timings of V402 Lac.

In the text
Table 9.

Parameters of the fit to the TESS light curve of V889 Aql.

In the text
Table 10.

Absolute dimensions of V889 Aql and V402 Lac.

In the text
Table 11.

Parameters of the fit to the TESS light curve of V402 Lac.

In the text
Table A.1.

Radial velocities of V889 Aql.

In the text
Table A.2.

Radial velocities of V402 Lac.

In the text

All Figures

thumbnail Fig. 1.

TESS target pixel file of V402 Lac in Sector 16 (created with tpfplotter; Aller et al. 2020), with the colour code indicating the flux measured by each pixel. We show the pixels included in the computation of the SAP as orange bordered pixels. The size of the red circles indicates the TESS magnitudes of the three brightest stars contained in the field, with V402 Lac marked with a white cross.
In the text
thumbnail Fig. 2.

Portion of the TESS FFI containing V889 Aql in Sector 40 (created with tpfplotter; Aller et al. 2020), with the colour code indicating the flux measured by each pixel. We show the pixels used to extract the photometry as orange bordered pixels. The size of the red circles indicates the TESS magnitudes of the two brightest stars contained in the field, with V889 Aql marked with a white cross.
In the text
thumbnail Fig. 3.

Model (red) used to detrend the out-of-eclipse TESS photometry (black dots) of V402 Lac in the second part of Sector 16.
In the text
thumbnail Fig. 4.

Model (red) used to detrend the out-of-eclipse TESS photometry (black dots) of V889 Aql in the second part of Sector 40.
In the text
thumbnail Fig. 5.

Best fit to the CAFE (circles) and TIGRE (triangles) RVs of V889 Aql, phase-folded to the orbital period. Blue and red colours correspond to the primary and secondary components, respectively. The bottom panels show the residuals of the best fit.
In the text
thumbnail Fig. 6.

Best fit to the primary (blue) and secondary (red) times of minimum light of V889 Aql, after subtracting the linear ephemeris (top left), after subtracting the linear ephemeris and the effect of the third body (bottom left), and after subtracting the linear ephemeris and the apsidal motion (top right). The panel at the bottom-right shows the residuals from all the fits.
In the text
thumbnail Fig. 7.

Best fit to the CAFE (circles), STELLA (triangles), and Tull (squares) RVs of V402 Lac, phase-folded to the anomalistic period, and with the argument of periastron precessing according to . Blue hues and red hues correspond to the primary and secondary components, respectively, while the colour code indicates the date of the measurements and fit. The bottom panels show the residuals from the best fit.
In the text
thumbnail Fig. 8.

Same as Fig. 6, but for V402 Lac.
In the text
thumbnail Fig. 9.

TESS photometry of V889 Aql from the second orbit of Sector 40 (black dots) and its best fit computed with JKTEBOP (red). The top panel shows the photometry phase-folded to the sidereal period, while the bottom panel shows the details of the primary (left) and secondary (right) eclipses. The residuals of the fits are shown in the bottom part of all panels.
In the text
thumbnail Fig. 10.

TESS photometry of V402 Lac from the second orbit of Sector 16 (black dots) and its best fit computed with the WD code (red). The top panel shows the photometry phase-folded to the sidereal period, while the bottom panel shows the details of the primary (left) and secondary (right) eclipses. The residuals of the fits are shown in the bottom part of all panels.
In the text
thumbnail Fig. 11.

Teff − log g relationship for the primary (blue) and secondary (red) components of V889 Aql, together with the theoretical models from Claret (2019) corresponding to the mass of each component and metallicities of 0.0 (dashed lines) and 0.1 (dotted lines).
In the text
thumbnail Fig. 12.

Teff − log g relationship for the primary (blue) and secondary (red) components of V402 Lac, together with the theoretical models from Claret (2019) corresponding to the mass of each component and metallicities of 0.0 (dashed lines) and 0.1 (dotted lines).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.