EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 557 (September 2013) A&A, 557 (2013) A122 Full HTML
Free Access
Issue
A&A
Volume 557, September 2013
Article Number A122
Number of page(s) 11
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201322057
Published online 18 September 2013

© ESO, 2013

1. Introduction

Subluminous B stars (sdBs) have similar colours and spectral characteristics to main sequence stars of spectral type B, but are much less luminous. Strong line broadening and the early confluence of the Balmer series is caused by the high surface gravities (log  g ≃ 5.0−6.0) of these compact stars (RsdB ≃ 0.1−0.3 R⊙). SdBs are considered to be core helium-burning stars with very thin hydrogen envelopes and masses of about half a solar mass (Heber 1986) located at the extreme end of the horizontal branch (EHB).

The origin of these stars is unclear. A mass loss mechanism must manage to remove all but a tiny fraction of the hydrogen envelope at about the same time as the helium core has attained the mass (≃0.5 M⊙) required for the helium flash. The reason for this mass loss is still unknown. Several single star scenarios invoke enhanced stellar winds or interaction with the stellar environment (see Heber 2009 for a review).

However, Mengel et al. (1976) showed that the required strong mass loss can occur in a close-binary system. The progenitor of the sdB star has to fill its Roche lobe near the tip of the red-giant branch (RGB) to lose most of its hydrogen-rich envelope. The merger of binary white dwarfs (WDs) was investigated by Webbink (1984) who showed that an EHB star can form when two helium core white dwarfs merge and the product is sufficiently massive to ignite helium.

Maxted et al. (2001) determined a very high fraction of radial velocity variable sdB stars (see also Morales-Rueda et al. 2003; Napiwotzki et al. 2004a; Copperwheat et al. 2011). Han et al. (2002; 2003) used binary population synthesis models and studied the stable Roche lobe overflow (RLOF) channel, the common envelope ejection (CE) channel, where the mass transfer to the companion is dynamically unstable, and the He-WD merger channel.

The formation of sdBs has also been related to the origin of the even more enigmatic He-sdO/Bs (Ahmad & Jeffery 2003; Naslim et al. 2010; Ströer et al. 2007; Hirsch & Heber 2009). The so-called late hot flasher scenario was proposed to form these objects (Lanz et al. 2004; Miller-Bertolami et al. 2008).

At first glance, determining the helium abundance in sdB atmospheres seems to be the best diagnostic tool to distinguish between the different formation channels. While the merger of two He-WDs would form a pure He-star, a wide range of helium abundances is predicted by the late hot flasher scenario. Different mass-loss on the RGB, either triggered via single-star or binary evolution, may also leave an imprint on the helium abundance of the formed sdB.

Unfortunately, the primordial helium abundance of sdB stars is significantly affected by processes in the hot and very dense atmospheres of these stars. Sargent & Searle (1966) found sdB stars to be helium deficient for the first time. Greenstein et al. (1967) suggested that diffusion might cause the observed helium deficiency. However, theoretical diffusion models yielded only little success (e.g. Michaud et al. 1983), since the timescales for the gravitational settling were predicted to be too short. The atmospheres of sdBs should not only be depleted in helium, but essentially helium-free. Several attempts have been made to model the atmospheres of sdBs by invoking radiative levitation and mass loss caused by stellar winds to counteract the gravitational settling (Bergeron et al. 1988; Michaud et al. 1989; Fontaine & Chayer 1997; Ohl et al. 2000; Unglaub & Bues 2001).

Diffusion not only affects the elemental abundances, but can also lead to a separation of different isotopes. When a heavier isotope is significantly affected by gravitational settling, the lighter one appears to be enriched in the atmosphere. An enrichment of 3He has initially been found in main sequence B stars with subsolar helium abundance (Sargent & Jugaku 1961; Hartoog & Cowley 1979) and explained by diffusion processes (Vauclair et al. 1974). Feige 86 was the first horizontal branch star showing this anomaly (Hartoog 1979). Eventually Heber (1987) detected strong line shifts in the sdB star SB 290 and the blue horizontal branch star PHL 25 indicating that basically the whole helium content of the atmosphere consists of 3He. Later, Edelmann et al. (2001) and Heber & Edelmann (2004) found another three sdBs (Feige 36, BD +48 2721, PG 0133+114) where 3He is enriched in the atmosphere.

Finally, diffusion may change the atmospheres of hot subdwarfs in an even more substantial way. Miller-Bertolami et al. (2008) argued that due to diffusion processes He-sdOs will turn into hydrogen rich subdwarfs before they evolve towards the white dwarf graveyard. The discovery of sdBs with He abundances between the normal sdBs and the He-rich ones seems to be consistent with this scenario (Ahmad et al. 2007; Vennes et al. 2007; Naslim et al. 2011; 2012).

In this paper, we determine the helium abundances and isotopic shifts caused by enrichment of 3He of 44 sdBs from high-resolution spectroscopy. Previous papers of this series dealt with the rotational properties of sdB binaries (Geier et al. 2010, Paper I), the rotational properties of single sdBs (Geier & Heber 2012, Paper II) and the metal abundances of sdBs in the context of diffusion (Geier 2013, Paper III).

In Sect. 2 we give an overview of the observations taken with different instruments. The determination of the atmospheric parameters and helium abundances as well as an evaluation of the uncertainties are described in Sect. 3. In Sects. 4–6 we present our results regarding the atmospheric parameters, helium abundances and isotopic shifts, which are discussed further in Sect. 7. Finally, a summary is given in Sect. 8.

2. Observations and data reduction

39 bright subdwarf B stars were observed with the FEROS spectrograph (R = 48 000, 3750−9200  Å) mounted at the ESO/MPG 2.2 m telescope in La Silla. The spectra were downloaded from the ESO science archive and reduced with the FEROS-DRS pipeline under the ESO MIDAS context in optimum extraction mode. The single spectra of all programme stars were RV-corrected and co-added in order to achieve higher signal-to-noise.

Five stars were observed with the FOCES spectrograph (R = 30 000, 3800−7000  Å) mounted at the CAHA 2.2 m telescope and the spectra were also reduced with the MIDAS package.

Medium resolution spectra of 12 stars were obtained with the ISIS spectrograph (R ≃ 4000,λ = 3440−5270  Å) mounted at the WHT. Nine sdBs discovered in the course of the Edinburgh-Cape blue object survey (Stobie et al. 1997; Kilkenny et al. 1997; O’Donoghue et al. 2013) have been observed with the grating spectrograph and intensified Reticon Photon Counting System on the 1.9 m telescope of the SAAO (R ≃ 1300,λ = 3300−5600  Å). Spectra of five sdBs have been taken with the CAFOS spectrograph mounted at the CAHA 2.2 m telescope (R ≃ 1000,λ = 3500−5800  Å). Table 1 provides a detailed overview of the observed sample and the data.

3. Atmospheric parameter determination and systematic effects

3.1. High-resolution echelle spectra – known issues

Most spectroscopic studies of sdB stars have relied on low and medium-resolution data (R ≃ 500−4000). Fitting model atmospheres to high signal-to-noise ratio (S/N) data allows us to determine Teff and log g with formal uncertainties lower than the systematic effects between different model grids (Green et al. 2008; Heber et al. 2000). This standard technique yielded key results on which our current understanding of sdB formation and evolution is founded (e.g. Heber 1986; Heber & Langhans 1986; Saffer et al. 1994; Maxted et al. 2001; Edelmann et al. 2003; Green et al. 2008; Østensen et al. 2010; Copperwheat et al. 2011; Vennes et al. 2011; Geier et al. 2011b; Németh et al. 2012).

On the other hand, high resolution echelle spectrographs (R > 10 000) are widely used in astronomy today. However, data reduction and analysis of echelle spectra is difficult. Even if sophisticated data reduction pipelines are available, issues such as fringing, extraction errors, insufficient order merging and normalisation remain. Due to the low luminosity of sdBs, echelle spectroscopy of these objects is rather challenging, as only a few of them have magnitudes brighter than 10th. Furthermore, sdBs are hot stars and the most important lines for their analysis are found in the bluest parts of optical spectra; unfortunately, echelle spectrographs are often not very sensitive in the blue, particularly where fibre-feeds are used.

The spectra of sdBs are dominated by strong and broad hydrogen Balmer lines, which are the key to deriving their atmospheric parameters. Since these lines are usually broader than the single echelle orders, merging errors can severely affect the parameter determination and suspicious features can be hard to spot, particularly in low S/N data. However, Lisker et al. (2005) successfully analysed high resolution spectra of sdBs observed in the course of the ESO-SPY project (Napiwotzki et al. 2003). In this case, the UVES spectrograph at the ESO-VLT was used, which is very sensitive in the blue wavelength range. Furthermore, rectification of the data was done by dividing by the featureless spectra of DC-type white dwarfs. However, most of the known DC white dwarfs are too faint to be observed with 2 m-class telescopes and it is therefore not clear, in general, whether reliable atmospheric parameters of sdBs can be derived from medium S/N (30–50), high resolution echelle spectra.

3.2. Determination of atmospheric parameters

thumbnail Fig. 1

Example fit of LTE models to the Balmer and selected He i lines in the FEROS spectrum of EC 03591−3232.

Atmospheric parameters and helium abundances of our sample have been determined by fitting model spectra to the hydrogen Balmer and helium lines of the high-resolution spectra using the SPAS routine developed by H. Hirsch (see Fig. 1). The method is described in Copperwheat et al. (2011). To derive the atmospheric parameters we used local thermodynamic equilibrum (LTE) model with solar metallicity for stars with effective temperatures between 24 000 K and 30 000 K. The hottest stars with Teff > 30 000 K have been fitted with LTE models with supersolar metallicity (see Copperwheat et al. 2011).

Due to the high resolution of the spectra the formal errors derived with a bootstrapping algorithm are much smaller than the typical systematic offsets between different model grids (ΔTeff ≃ 500 K, Δlog g ≃ 0.05). However, these formal uncertainities must not be adopted as error estimates, because systematic shifts are the dominant error source in this case.

3.3. Comparison with medium resolution data

Due to the caveats discussed in Sect. 3.1, the parameter determination from the high-resolution spectra needs to be checked and systematic effects have to be quantified properly. We used medium-resolution spectra obtained with the ISIS, the SAAO-Reticon and the CAFOS spectrograph and analysed them in the same way as the high-resolution data.

The ISIS and CAFOS spectra have a very high S/N (>100) and cover the blue spectral range down to the Balmer jump. These spectra are perfectly suited for the determination of atmospheric parameters. Again, formal errors are much smaller than the typical systematic offsets between different model grids, which are adopted as error estimates in this case. The SAAO-Reticon spectra also cover the higher Balmer lines, but their quality is inhomogeneous. Although the formal fitting errors can be large – ranging from 700 K to 2000 K in Teff and from 0.12 to 0.28 in log g – they provide a valuable consistency check for the results derived from the high-resolution data.

Figures 2 and 3 show the comparison between the high-resolution and the medium-resolution parameters. In general, the consistency between the parameters derived from high- and medium-resolution data is reasonable.

thumbnail Fig. 2

Effective temperature derived from high-resolution spectra plotted against effective temperature derived from medium resolution spectra (ISIS, SAAO-Reticon, CAFOS). The dotted lines mark the average deviation between the two datasets. The size of the points scales with the data quality of the high-resolution spectra.

thumbnail Fig. 3

Surface gravity derived from high-resolution spectra plotted against surface gravity derived from medium-resolution spectra (see Fig. 2).

thumbnail Fig. 4

Teff − log g-diagram for the entire sample under study. The helium main sequence (HeMS) and the EHB band (limited by the zero-age EHB, ZAEHB, and the terminal-age EHB, TAEHB) are superimposed with EHB evolutionary tracks for solar metallicity taken from Dorman et al. (1993) labelled with their masses. Open symbols mark objects where isotopic shifts due to an enrichment of 3He were detected, filled symbols objects with atmospheres dominated by 4He. The diamonds mark stars belonging to the upper helium sequence, the circles stars belonging to the lower sequence (see Fig. 5). The triangles mark the three sdBs with enriched 3He from literature (Heber et al. 1984; Edelmann et al. 1999; Morales-Rueda et al. 2003).

In order to quantify the uncertainties in the parameter determination, the averages of the shifts with respect to the parameters derived from medium-resolution spectra have been calculated; these are ΔTeff ≃ 1100 K and Δlog g ≃ 0.12. The high resolution spectra of PG 1616+144, PG 1710+490 and PG 2205+023 have S/N values below 30 and hence show large deviations especially in Teff (up to 3500 K). These stars have been excluded before calculating the average. Although not perfect, the above uncertainties are consistent with values found in the literature (see Appendix A).

4. Atmospheric parameters

The atmospheric parameters of all 44 programme stars are shown in Table 2. The final parameters are derived either from high S/N ISIS and CAFOS spectra, if available, or from high-resolution spectra obtained with FEROS and FOCES. The Teff − log g-diagram of the whole sample under study is shown in Fig. 4. All stars are concentrated on or above the EHB, fully consistent with theory, and we therefore conclude that the atmospheric parameter determination is of sufficient quality (see also the comparison with independent determinations from the literature given in Table A.1).

5. Helium abundances

High resolution spectra are very well suited for measuring accurate elemental abundances of sdBs, because the rather weak lines of helium and metals are fully resolved. We therefore used the FEROS and FOCES spectra to determine the helium abundances of our programme stars. The formal uncertainties are very small (Δlog y = 0.01 − 0.07) and comparable to the deviations measured when analysing several single spectra of one object. Taking systematic effects into account the helium abundances should therefore be accurate to ≃0.1 dex. The results are given in Table 2.

Figure 5 shows the helium abundances of our sample plotted against effective temperature. All but two of our programme stars have the subsolar helium abundances typical of sdB stars. Edelmann et al. (2003) reported a correlation of helium abundance with temperature, which was subsequently confirmed by Lisker et al. (2005) and Németh et al. (2012). This correlation can be clearly seen in our sample as well.

Edelmann et al. (2003) also reported the discovery of two distinct sequences showing a similar correlation with temperature. The “low sequence” is offset by about 2 dex from the “high sequence”. Lisker et al. (2005) and Geier et al. (2011b) could not confirm this finding, but the sample size of these studies was smaller than that of Edelmann et al. (2003). Németh et al. (2012) studied a sample of bright hot subdwarfs spanning the whole temperature and helium abundance range from sdBs to He-sdOs and found indications for the two distinct sequences although, in their sample, the lower sequence appears to be less steep than reported by Edelmann et al. (2003).

The two distinct sequences are also visible in our data and combining these with the results of other studies (Saffer et al. 1994; Maxted et al. 2001; Edelmann et al. 2003; Morales-Rueda et al. 2003; Lisker et al. 2005; Østensen et al. 2010; Geier et al. 2011b; Németh et al. 2012) the underlying pattern becomes more apparent. In Fig. 5, all of these results are overplotted with the two regression lines calculated by Edelmann et al. (2003) as well as the regression line for the lower sequence calculated by Németh et al. (2012) based on their results spanning a larger range in effective temperatures and helium abundances. The two lines by Edelmann et al. (2003) match very well with the sequences seen in our sample, while the line by Németh et al. (2012) is slightly different. However, as has been correctly pointed out by Németh et al. (2012), those lines are only very crude tentative models, which certainly do not reflect the real complexity of the underlying data.

Defining a dividing line between the two helium sequences by eye, which follows the relation log y = 0.127 Teff/1000 K − 6.718, the numbers of stars belonging to the different sequences can be counted. From our sample of 44 stars, 31 of them (70%) are associated with the upper sequence while 13 (30%) belong to the lower one. The respective fractions of the full sample of 383 sdBs are 82% and 18%, but the full sample is likely to be biased against low helium abundances because most analyses are based on low- and medium-resolution spectra where weak He lines are often not detectable. We therefore regard the respective fractions derived from our sample to be more reliable.

6. The 3He isotopic anomaly

The high-resolution spectra are also perfectly suited to search for small shifts in the rest wavelengths of the helium lines due to the enrichment of 3He. Wavelength shifts can be caused by different effects (for example, the presence of magnetic fields or pressure shifts in high density environments), but the helium line shifts caused by the enrichment of 3He can be modelled quite accurately and show a typical pattern. While some lines like He i 5876 are only shifted by 0.04  Å towards redder wavelengths, the shifts of He i 4922 and He i 6678 are significant (0.33 and 0.50  Å respectively; Fred et al. 1951; given in Hartoog & Cowley 1979). Displacements of this order can be easily detected in high resolution spectra.

All of the stars in our sample have been examined and in 8 cases, isotopic shifts due to the presence of 3He are clearly visible (Figs. 6, 7). One of these (BD+48 2721) has already been discovered by Edelmann et al. (2001).

thumbnail Fig. 5

Helium abundance log y plotted against effective temperature. The filled symbols mark the results from our study. Filled diamonds mark objects where isotopic shifts due to an enrichment of 3He were detected, filled circles objects with atmospheres dominated by 4He. Upper limits are marked with triangles. The solid horizontal line is drawn at solar helium abundance. The two dashed lines are regression lines for the two distinct helium sequences taken from Edelmann et al. (2003). The dotted regression line for the lower sequence is taken from Németh et al. (2012). Measurements taken from literature are plotted as grey symbols.

7. Discussion

7.1. Helium sequences

The reasons for the correlation of the helium abundance with temperature and the bimodal structure in the Teff − log y diagram are unknown, although several suggestions have been made and are discussed briefly below.

Photospheric convection has been proposed as the cause of the relative enrichment of helium in sdB atmospheres towards higher temperature. Greenstein & Sargent (1974) suggested that a He+/He2+ convection zone could transport helium from deeper layers into the photosphere of subdwarfs hotter than 30 000 K (but see also Groth et al. 1985). However, Michaud et al. (2011) calculated complete stellar evolution models, including the effects of atomic diffusion and radiative acceleration, to study the abundance anomalies observed on the hot end of the HB. Their models, which assume extra mixing but no stellar-wind mass loss, are in general agreement with the observed metal abundances of sdB stars (Geier 2013) as well as the helium abundances for Teff > 25 000 K. Furthermore, they show that diffusion effects reach far deeper than the stellar atmospheres themselves and should also be dominant in the He+/He2+ convection zone (Moehler, Michaud, priv. comm.).

According to the Michaud et al. (2011) models, the observed scatter in helium abundance is caused by different HB ages and differences in the initial metallicity of the progenitor populations, but these models predict neither the observed correlation with temperature nor the two helium sequences. If the helium abundance does depend on the age of the sdB, one would expect to see a continuous distribution and not a concentration in distinct sequences.

Aznar Cuadrado & Jeffery (2002) argued that, due to tidal effects, sdBs residing in short-period binaries might have higher photospheric helium content than long-period systems or single stars. Edelmann et al. (2003) suggested that this effect could be responsible for the two helium sequences – and this can be directly tested with the available data. Our current sample of bright sdBs consists mostly of stars in which no radial velocity shifts have been detected and so these sdBs are not in close binaries with stellar mass companions. On the other hand, the target sample for the MUCHFUSS project (Geier et al. 2011b), which aims at finding sdBs with massive compact companions in close orbits, consists only of RV variable stars. From the 51 sdBs drawn from the MUCHFUSS sample, 15 belong to the lower helium sequence, so the fraction of these stars is almost exactly the same as in the sample presented here. The close binary hypothesis can therefore be excluded as an explanation of the helium sequences.

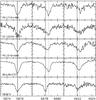thumbnail Fig. 6

Helium lines of sdB stars. The rest wavelengths of the 4He (solid) and 3He lines (dotted) are plotted as vertical lines. The rest wavelengths of the 3He lines have been taken from Hartoog & Cowley (1979). The stars are highly enriched in 3He, but also show a component of 4He. For comparison, the He lines of SB 815 are plotted in the lowest panel. This star does not show line shifts due to enrichment of 3He.

O’Toole (2008) proposed another possibility: whilst the stars belonging to the upper sequence might be core helium-burning (post-)EHB stars evolving in the way modelled by, for example, Dorman et al. (1993), the sdBs forming the lower sequence could be post-RGB objects without helium burning in their cores. The latter objects are direct progenitors of He-WDs with masses ranging from ~0.2 M⊙ to 0.33 M⊙ and are crossing the EHB on cooling tracks (e.g. Driebe et al. 1998). The only sdB for which the post-RGB nature could be proven unambiguously (using a trigonometric parallax) is HD 188112 (Heber et al. 2003) which also has the lowest helium abundance (log y =  −5) ever measured for an sdB. Two candidates of similar low mass have been discovered by Vennes at al. (2011) and Silvotti et al. (2012) but, even though these sdBs also show no detectable helium lines, their post-RGB nature is less well established than in the case of HD 188112. Observational evidence for particularly low helium abundance in post-RGB objects therefore remains weak.

Another way to probe the post-RGB scenario is the comparison of both helium populations in the Teff − log g diagram (O’Toole 2008). In Fig. 8, the stars associated with the upper sequence are plotted. Most sdBs are situated within or close to the EHB band but about 10% are above the EHB – consistent with the standard scenario in which most stars are core helium-burning and therefore residing on the EHB and only a minority are more evolved shell helium-burning objects (Dorman et al. 1993).

The distribution of the helium-poor sdBs is different (see Fig. 9) in that the number density of stars on and above the EHB is similar. In the classical picture, sdBs evolve from the EHB but such an even distribution is not expected because the evolutionary time on the EHB is significantly longer than that for post-EHB evolution (~10 times as long).

Comparing the distribution of the helium-poor sdBs with post-RGB tracks calculated by Driebe et al. (1998), one would expect these objects to be the progenitors of He-WDs with masses between 0.25 M⊙ and 0.3 M⊙. The evolutionary timescales on these tracks scale strongly with mass; while the evolution of an 0.25 M⊙ object takes of the order of 100 Myr, it shortens to only a few million years if the object is more massive (0.3 M⊙). Accordingly, one would expect a higher density of objects with low masses in the Teff-log g diagram (if the formation rate of post-RGB objects does not depend on the mass) but this is not the case – most objects are evenly distributed between the ~0.25 M⊙ and 0.3 M⊙ evolutionary tracks (see Fig. 9).

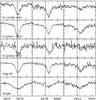thumbnail Fig. 7

Comments are as for Fig. 6 except that in these stars, the helium lines are entirely shifted to the 3He rest wavelength and no traces of 4He are visible. For comparison, the He lines of SB 290 are plotted in the lowest panel. This star is the prototype of sdBs enriched in 3He (Heber 1987) but note that the lines show significant rotational broadening (Geier et al. 2013).

thumbnail Fig. 8

Teff − log g-diagram for the sdBs associated with the upper helium sequence (see Fig. 4).

Being aware of this problem, O’Toole (2008) argued that many more He-WDs with masses close to 0.3 M⊙ are formed than objects with even lower masses (e.g. Liebert et al. 2005; De Gennaro et al. 2008) which could compensate for the difference in evolutionary timescales. Given that the 18–29% of the sdB population belonging to the helium poor sequence are all direct He-WD progenitors with an evolution about 100 times shorter than the lifetime on the EHB (≃100 Myr), the formation rate of these objects (neglecting selection effects) would be more than ~20 times higher than the formation rate of core helium-burning sdBs. Even so, the distribution of objects seen in Fig. 9 is still hard to explain with the post-RGB scenario. The crowding near the EHB remains especially suspicious, because evolution should be more or less uniform along the tracks given by Driebe et al. (1998). The lack of objects below the EHB poses a particular problem in this respect. In contrast, a significant number of He-WD progenitors with masses between 0.16 M⊙ and 0.4 M⊙ have been discovered at temperatures below ≃25 000 K and well below the HB (see Kilic et al. 2012 and references therein). We therefore conclude that post-RGB evolution, despite being a very interesting option, is not able to explain all of the observations in a conclusive way.

7.2. Isotopic anomaly

The enrichment of 3He in around 18% of our programme stars also remains unexplained. Figure 4 shows the distribution of these stars in the Teff–log g-diagram, including the three sdBs with isotopic shifts taken from the literature. It can be clearly seen that they cluster in a narrow temperature range between 27 000 K and 31 000 K, with BD+48 2721 (Teff = 24 800 K) being the only exception and – given the uncertainties – this 3He-strip could be pure. The fact that all 3He enriched sdBs belong to the upper helium sequence (Fig. 5) might be a selection effect, because the diagnostic helium lines are too weak to measure the isotopic shifts in the helium-poor stars.

Most 3He sdB stars show clear shifts of the He i line at 6678  Å, indicating that almost all the helium in the atmosphere is 3He. BD+48 2721, EC 12234−2607 and PG 1519+640 show strong lines of 3He blended with weak components of 4He (see Fig. 6) and these three stars cover the whole 3He temperature strip. The isotope ratio is therefore not correlated with effective temperature.

Michaud et al. (2011) predict a mild enrichment of 3He but, due to gravitational settling of the heavier isotope, this should be the case in all sdBs. Hartoog & Cowley (1979) studied the enrichment of 3He in main sequence B stars and discovered a pattern strikingly similar to our results: stars enriched in 3He were found at effective temperatures between 18 000 K and 21 000 K; stars with lower temperatures down to ~13 000 K show slight underabundances in helium with respect to the Sun, while the hotter stars up to ~32 000 K are slighty overabundant in helium. The two known BHB stars with detected 3He isotopic shifts (Feige 86, Teff = 16 400 K; Bonifacio et al. 1995; PHL 25, Teff = 19 500 K; Heber & Langhans 1986) have temperatures close to the strip detected by Hartoog & Cowley (1979).

thumbnail Fig. 9

Teff − log g-diagram for the sdBs associated with the lower helium sequence. The figure is similar to Fig. 4 with additional evolutionary tracks for post-RGB objects plotted as dotted lines (Driebe et al. 1998).

In Figs. 4 and 5 a similar pattern can be seen. The sdBs enriched in 3He occupy a small strip in Teff, within which the helium abundance decreases towards lower temperatures and increases towards higher temperatures.

Hartoog & Cowley (1979) argued that diffusion is responsible for this effect. At low temperatures, the radiation pressure is not strong enough to support helium in the atmosphere. As soon as the temperature reaches a certain threshold value, the less massive 3He can be supported, but not the more abundant 4He, which leads to an enrichment of 3He in the atmosphere. At even higher temperatures, both isotopes are enriched and the isotopic anomaly vanishes as the helium abundance rises (see also Vauclair et al. 1974).

A similar scenario might explain the more compact sdB stars. Focusing on the upper helium sequence in Fig. 5 one can see that the helium abundance is scattering around log y ≃  −2.5 for temperatures below 31 000 K. 3He is enriched at the border region. For temperatures higher than ≃31 000 K the helium abundance is rising.

Finally, radiatively driven stellar wind mass loss might play a role (see, for example, Babel 1996 and references therein), but Hu et al. (2011) derived upper limits for this mass loss to be of the order of 10-15 M⊙ yr-1 to allow sdBs to pulsate. However, even weak and fractionated winds might already affect the abundances in the atmospheres of sdB stars (Unglaub 2008).

8. Summary

Atmospheric parameters and helium abundances of 44 bright sdBs have been determined. We have shown that effective temperatures and surface gravities can be derived from high resolution echelle spectra with sufficient accuracy. Systematic uncertainties have been determined by comparing the parameters derived from the high resolution data with the ones derived from medium resolution spectra. Most stars are core helium-burning, but some sdBs are already in the shell helium-burning phase.

Helium abundances have been measured with high accuracy. Besides the known correlation of helium abundance with temperature, two distinct sequences in helium abundance have been confirmed. The reasons for both the increasing helium abundance with temperature and the bimodal distribution have been discussed, but we are left without a strong conclusion.

Significant isotopic shifts of helium lines due to an enrichment in 3He have been found in the spectra of 8 sdBs. Most of these stars cluster in a small temperature range between 27 000 K and 31 000 K very similar to the known 3He-rich main sequence B stars, which cluster at somewhat lower temperatures. This phenomenon is most probably related to diffusion processes in the atmosphere.

Online material

Table 1

Target sample and data.

Table 2

Atmospheric parameters.

Appendix A: Comparison of atmospheric parameters with the literature

Atmospheric parameters of 20 of the sdBs analysed here have also been found in the literature. All parameters derived from model fits to the spectral lines are listed in Table A.1. Given the fact that different methods, models and data were used to determine these parameters, our new results are in general agreement with the literature values. The lower temperature (− 2600 K) Saffer et al. (1994) derived for [CW83] 1758+36 may be more accurate, because our analysis is based on only one FOCES spectrum of mediocre quality, while the spectra used by Saffer et al. (1994) cover the Balmer jump. We reanalysed the spectrum used by Saffer et al. (1994) with our method and confirmed the parameters given in this study (Saffer refit).

The atmospheric parameters of the bright sdB, PG 0342+026, have been determined from its spectral energy distribution by Lamontagne et al. (1987), Theissen et al. (1995) and Aznar Cuadrado & Jeffery (2001). Given the higher uncertainties of this method the derived parameters are consistent with our results within the error limits.

Table A.1

Atmospheric parameters from the literature.

Acknowledgments

S.G. was supported by the Deutsche Forschungsgemeinschaft under grant He 1356/49-1. D.K. thanks the University of the Western Cape and the South African National Research Foundation for financial support. We thank R. A. Saffer for sharing his data with us as well as N. Hambly and H. McGillivray for their contributions to the EC survey. We also thank S. J. O’Toole, S. Moehler and N. Reindl for fruitful discussions. Finally, we want to thank the referee S. Vennes for helpful comments and suggestions. Based on observations at the La Silla Observatory of the European Southern Observatory for programmes number 073.D-0495(A), 074.B-0455(A), 076.D-0355(A), 077.D-0515(A) and 078.D-0098(A). Based on observations with the William Herschel Telescope and the Isaac Newton Telescope operated both by the Isaac Newton Group at the Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias on the island of La Palma, Spain. This paper uses observations made at the South African Astronomical Observatory (SAAO). Based on observations collected at the Centro Astronómico Hispano Alemán (CAHA) at Calar Alto, operated jointly by the Max-Planck Institut für Astronomie and the Instituto de Astrofísica de Andalucía (CSIC).

References

  1. Ahmad, A., & Jeffery, C. S. 2003, A&A, 402, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Ahmad, A., Behara, N. T., Jeffery, C. S., Sahin, T., & Woolf, V. M. 2007, A&A, 465, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Aznar Cuadrado, R., & Jeffery, C. S. 2001, A&A, 368, 994 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Aznar Cuadrado, R., & Jeffery, C. S. 2002, A&A, 385, 131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Babel, J. 1996, A&A, 309, 867 [NASA ADS] [Google Scholar]
  6. Bergeron, P., Wesemael, F., Michaud, G., & Fontaine, G. 1988, ApJ, 332, 964 [NASA ADS] [CrossRef] [Google Scholar]
  7. Blanchette, J.-P., Chayer, P., Wesemael, F., et al. 2008, ApJ, 678, 1329 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bonifacio, P., Castelli, F., & Hack, M. 1995, A&AS, 110, 441 [NASA ADS] [Google Scholar]
  9. Chayer, P., Fontaine, M., Fontaine, G., Wesemael, F., & Dupuis, J. 2006, Balt. Astron., 15, 131 [NASA ADS] [Google Scholar]
  10. Copperwheat, C. M., Morales-Rueda, L., Marsh, T. R., Maxted, P. F. L., & Heber, U. 2011, MNRAS, 415, 1381 [NASA ADS] [CrossRef] [Google Scholar]
  11. De Gennaro, S., von Hippel, T., Winget, D. E., et al. 2008, AJ, 135, 1 [NASA ADS] [CrossRef] [Google Scholar]
  12. Dorman, B., Rood, R. T., & O’Connell, R. W. 1993, ApJ, 419, 596 [CrossRef] [Google Scholar]
  13. Driebe, T., Schönberner, D., Bloecker, T., & Herwig, F. 1998, A&A, 339, 123 [NASA ADS] [Google Scholar]
  14. Edelmann, H., Heber, U., & Napiwotzki, R. 1999, ASP Conf. Ser., 169, 546 [NASA ADS] [Google Scholar]
  15. Edelmann, H., Heber, U., & Napiwotzki, R. 2001, Astron. Nachr., 322, 401 [NASA ADS] [CrossRef] [Google Scholar]
  16. Edelmann, H., Heber, U., Hagen, H.-J., et al. 2003, A&A, 400, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Edelmann, H., Heber, U., Altmann, M., Karl, C., & Lisker, T. 2005, A&A 442, 1023 [Google Scholar]
  18. Fontaine, G., & Chayer, P. 1997, in Proc. of Conference on Faint Blue Stars, eds. A. G. D., Philip, J., Liebert, R. A., Saffer, & D. S., Hayes, 169 [Google Scholar]
  19. Fred, M., Tomkins, F. S., Brody, J. K., & Hamermesh, M. 1951, Phys. Rev., 82, 406 [NASA ADS] [CrossRef] [Google Scholar]
  20. Geier, S. 2013, A&A, 549, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Geier, S., & Heber, U. 2012, A&A, 543, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Geier, S., Nesslinger, S., Heber, U., et al. 2007, A&A, 464, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Geier, S., Heber, U., Podsiadlowski, Ph., et al. 2010, A&A, 519, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Geier, S., Classen, L., & Heber, U. 2011a, ApJ, 733, L13 [NASA ADS] [CrossRef] [Google Scholar]
  25. Geier, S., Hirsch, H., Tillich, A., et al. 2011b, A&A, 530, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Geier, S., Heber, U., Heuser, C., et al. 2013, A&A, 551, A4 [Google Scholar]
  27. Green, E. M., Fontaine, G., Hyde, E. A., For, B.-Q., & Chayer, P. 2008, ASP Conf. Ser., 392, 75 [NASA ADS] [Google Scholar]
  28. Greenstein, J. L., & Sargent, A. I. 1974, ApJS, 28, 157 [NASA ADS] [CrossRef] [Google Scholar]
  29. Greenstein, J. L., Truran, J. W., & Cameron, A. G. W. 1967, Nature, 213, 871 [NASA ADS] [CrossRef] [Google Scholar]
  30. Groth, H. G., Kudritzki, R.-P., & Heber, U. 1985, A&A, 152, 107 [NASA ADS] [Google Scholar]
  31. Han, Z., Podsiadlowski, P., Maxted, P. F. L., Marsh, T. R., & Ivanova, N. 2002, MNRAS, 336, 449 [NASA ADS] [CrossRef] [Google Scholar]
  32. Han, Z., Podsiadlowski, P., Maxted, P. F. L., & Marsh, T. R. 2003, MNRAS, 341, 669 [NASA ADS] [CrossRef] [Google Scholar]
  33. Hartoog, M. R. 1979, ApJ, 231, 161 [NASA ADS] [CrossRef] [Google Scholar]
  34. Hartoog, M. R., & Cowley, A. P. 1979, ApJ, 228, 229 [NASA ADS] [CrossRef] [Google Scholar]
  35. Heber, U. 1986, A&A, 155, 33 [NASA ADS] [Google Scholar]
  36. Heber, U. 1987, MitAG, 70, 79 [NASA ADS] [Google Scholar]
  37. Heber, U. 2009, ARA&A, 47, 211 [NASA ADS] [CrossRef] [Google Scholar]
  38. Heber, U., & Edelmann, H. 2004, Ap&SS, 291, 341 [NASA ADS] [CrossRef] [Google Scholar]
  39. Heber, U., & Langhans, G. 1986, in Proc. New insights in astrophysics, ESA SP, 263, 279 [NASA ADS] [Google Scholar]
  40. Heber, U., Hunger, K., Jonas, G., & Kudritzki, R. P. 1984, A&A, 130, 119 [NASA ADS] [Google Scholar]
  41. Heber, U., Reid, I. N., & Werner, K. 2000, A&A, 363, 198 [NASA ADS] [Google Scholar]
  42. Heber, U., Edelmann, H., Lisker, T., & Napiwotzki, R. 2003, A&A, 411, 477 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Hirsch, H. A., & Heber, U. 2009, JPh Conf. Ser., 172, 012015 [Google Scholar]
  44. Hu, H., Tout, C. A., Glebbeek, E., & Dupret, M.-A. 2011, MNRAS, 418, 195 [NASA ADS] [CrossRef] [Google Scholar]
  45. Kilic, M., Brown, W. R., Allen de Prieto, C., et al. 2012, ApJ, 751, 141 [NASA ADS] [CrossRef] [Google Scholar]
  46. Kilkenny, D., O’Donoghue, D., Koen, C., Stobie, R. S., & Chen, A. 1997, MNRAS, 287, 867 [NASA ADS] [CrossRef] [Google Scholar]
  47. Lamontagne, R., Wesemael, F., & Fontaine, G. 1987, ApJ, 318, 844 [NASA ADS] [CrossRef] [Google Scholar]
  48. Lanz, T., Brown, T. M., Sweigart, A. V., Hubeny, I., & Landsman, W. B. 2004, ApJ, 602, 342 [NASA ADS] [CrossRef] [Google Scholar]
  49. Liebert, J., Bergeron, P., & Holberg, J. B. 2005, ApJS, 156, 47 [NASA ADS] [CrossRef] [Google Scholar]
  50. Lisker, T., Heber, U., Napiwotzki, R., et al. 2005, A&A, 430, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Maxted, P. F. L., Marsh, T. R., & North, R. C. 2000, MNRAS, 317, L41 [NASA ADS] [CrossRef] [Google Scholar]
  52. Maxted, P. F. L., Heber, U., Marsh, T. R., & North, R. C. 2001, MNRAS, 326, 139 [Google Scholar]
  53. Mengel, J. G., Norris, J., & Gross, P. G. 1976, ApJ, 204, 488 [NASA ADS] [CrossRef] [Google Scholar]
  54. Michaud, G., Vauclair, G., & Vauclair, S. 1983, ApJ, 267, 256 [NASA ADS] [CrossRef] [Google Scholar]
  55. Michaud, G., Bergeron, P., Heber, U., & Wesemael, F. 1989, ApJ, 338, 417 [NASA ADS] [CrossRef] [Google Scholar]
  56. Michaud, G., Richer, J., & Richard, O. 2011, A&A, 529, 60 [Google Scholar]
  57. Miller Bertolami, M. M., Althaus, L. G., Unglaub, K., & Weiss, A. 2008, A&A, 491, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Morales-Rueda, L., Maxted, P. F. L., Marsh, T. R., North, R. C., & Heber, U. 2003, MNRAS, 338, 752 [Google Scholar]
  59. Napiwotzki, R., Christlieb, N., Drechsel, H., et al. 2003, ESO Msngr, 112, 25 [Google Scholar]
  60. Napiwotzki, R., Karl, C. A., Lisker, T., et al. 2004a, Ap&SS, 291, 321 [NASA ADS] [CrossRef] [Google Scholar]
  61. Napiwotzki, R., Yungelson, L., Nelemans, G., et al. 2004b, ASP Conf. Ser., 318, 402 [Google Scholar]
  62. Naslim, N., Jeffery, C. S., Ahmad, A., Behara, N. T., & Sahin, T. 2010, MNRAS, 409, 582 [NASA ADS] [CrossRef] [Google Scholar]
  63. Naslim, N., Jeffery, C. S., Behara, N. T., & Hibbert, A. 2011, MNRAS, 412, 363 [NASA ADS] [CrossRef] [Google Scholar]
  64. Naslim, N., Geier, S., Jeffery, C. S., et al. 2012, MNRAS, 423, 3031 [NASA ADS] [CrossRef] [Google Scholar]
  65. Németh, P., Kawka, A., & Vennes, S. 2012, MNRAS, 427, 2180 [NASA ADS] [CrossRef] [Google Scholar]
  66. O’Donoghue, D., Kilkenny, D., Koen, C., et al. 2013, MNRAS, 431, 240 [NASA ADS] [CrossRef] [Google Scholar]
  67. Østensen, R. H., Silvotti, R., Charpinet, S., et al. 2010, MNRAS, 409, 1470 [NASA ADS] [CrossRef] [Google Scholar]
  68. Ohl, R. G., Chayer, P., & Moos, H. W. 2000, ApJ, 538, L95 [NASA ADS] [CrossRef] [Google Scholar]
  69. O’Toole, S. J. 2008, ASP Conf. Ser., 392, 67 [NASA ADS] [Google Scholar]
  70. O’Toole, S. J., & Heber, U. 2006, A&A, 452, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Saffer, R. A., Bergeron, P., Koester, D., & Liebert, J. 1994, ApJ, 432, 351 [NASA ADS] [CrossRef] [Google Scholar]
  72. Sargent, A. W. L. W., & Jugaku, J. 1961, ApJ, 134, 777 [NASA ADS] [CrossRef] [Google Scholar]
  73. Sargent, A. W. L. W., & Searle, L. 1966, ApJ, 145, 652 [NASA ADS] [CrossRef] [Google Scholar]
  74. Silvotti, R., Østensen, R. H., Bloemen, S., et al. 2012, MNRAS, 424, 1752 [NASA ADS] [CrossRef] [Google Scholar]
  75. Stobie, R. S., Kilkenny, D., O’Donoghue, D., et al. 1997, MNRAS, 287, 848 [NASA ADS] [CrossRef] [Google Scholar]
  76. Ströer, A., Heber, U., Lisker, T., et al. 2007, A&A, 462, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Theissen, A., Moehler, S., Heber, U., Schmidt, J. H. K., & de Boer, K. S. 1995, A&A, 298, 577 [NASA ADS] [Google Scholar]
  78. Unglaub, K. 2008, A&A, 486, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Unglaub, K., & Bues, I. 2001, A&A, 374, 570 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Vauclair, S., Michaud, G., & Charland, Y. 1974, A&A, 31, 381 [NASA ADS] [Google Scholar]
  81. Vennes, S., Kawka, A., & Smith, J. A. 2007, ApJ, 668, L59 [NASA ADS] [CrossRef] [Google Scholar]
  82. Vennes, S., Kawka, A., & Németh, P. 2011, MNRAS, 410, 2095 [NASA ADS] [Google Scholar]
  83. Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Target sample and data.

In the text
Table 2

Atmospheric parameters.

In the text
Table A.1

Atmospheric parameters from the literature.

In the text

All Figures

thumbnail Fig. 1

Example fit of LTE models to the Balmer and selected He i lines in the FEROS spectrum of EC 03591−3232.
In the text
thumbnail Fig. 2

Effective temperature derived from high-resolution spectra plotted against effective temperature derived from medium resolution spectra (ISIS, SAAO-Reticon, CAFOS). The dotted lines mark the average deviation between the two datasets. The size of the points scales with the data quality of the high-resolution spectra.
In the text
thumbnail Fig. 3

Surface gravity derived from high-resolution spectra plotted against surface gravity derived from medium-resolution spectra (see Fig. 2).
In the text
thumbnail Fig. 4

Teff − log g-diagram for the entire sample under study. The helium main sequence (HeMS) and the EHB band (limited by the zero-age EHB, ZAEHB, and the terminal-age EHB, TAEHB) are superimposed with EHB evolutionary tracks for solar metallicity taken from Dorman et al. (1993) labelled with their masses. Open symbols mark objects where isotopic shifts due to an enrichment of 3He were detected, filled symbols objects with atmospheres dominated by 4He. The diamonds mark stars belonging to the upper helium sequence, the circles stars belonging to the lower sequence (see Fig. 5). The triangles mark the three sdBs with enriched 3He from literature (Heber et al. 1984; Edelmann et al. 1999; Morales-Rueda et al. 2003).
In the text
thumbnail Fig. 5

Helium abundance log y plotted against effective temperature. The filled symbols mark the results from our study. Filled diamonds mark objects where isotopic shifts due to an enrichment of 3He were detected, filled circles objects with atmospheres dominated by 4He. Upper limits are marked with triangles. The solid horizontal line is drawn at solar helium abundance. The two dashed lines are regression lines for the two distinct helium sequences taken from Edelmann et al. (2003). The dotted regression line for the lower sequence is taken from Németh et al. (2012). Measurements taken from literature are plotted as grey symbols.
In the text
thumbnail Fig. 6

Helium lines of sdB stars. The rest wavelengths of the 4He (solid) and 3He lines (dotted) are plotted as vertical lines. The rest wavelengths of the 3He lines have been taken from Hartoog & Cowley (1979). The stars are highly enriched in 3He, but also show a component of 4He. For comparison, the He lines of SB 815 are plotted in the lowest panel. This star does not show line shifts due to enrichment of 3He.
In the text
thumbnail Fig. 7

Comments are as for Fig. 6 except that in these stars, the helium lines are entirely shifted to the 3He rest wavelength and no traces of 4He are visible. For comparison, the He lines of SB 290 are plotted in the lowest panel. This star is the prototype of sdBs enriched in 3He (Heber 1987) but note that the lines show significant rotational broadening (Geier et al. 2013).
In the text
thumbnail Fig. 8

Teff − log g-diagram for the sdBs associated with the upper helium sequence (see Fig. 4).
In the text
thumbnail Fig. 9

Teff − log g-diagram for the sdBs associated with the lower helium sequence. The figure is similar to Fig. 4 with additional evolutionary tracks for post-RGB objects plotted as dotted lines (Driebe et al. 1998).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.