| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 19 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201322047 | |
| Published online | 29 August 2013 | |
“TNOs are Cool”: A survey of the trans-Neptunian region
IX. Thermal properties of Kuiper belt objects and Centaurs from combined Herschel and Spitzer observations⋆,⋆⋆
1
LESIA-Observatoire de Paris, CNRS, UPMC Univ. Paris 6, Univ. Paris-Diderot,
5 Place J.
Janssen,
92195
Meudon Cedex,
France
e-mail:
emmanuel.lellouch@obspm.fr
2
Instituto de Astrofísica de Andalucía (CSIC),
Glorieta de la Astronomía
s/n, 18008
Granada,
Spain
3
Queen’s University, University Rd, Belfast
BT7 1NN,
UK
4
Deutsches Zentrum für Luft- und Raumfahrt (DLR), Institute of
Planetary Research, Rutherfordstrasse 2, 12489
Berlin,
Germany
5
Max-Planck-Institut für extraterrestrische Physik (MPE),
Postfach 1312,
Giessenbachstr., 85741
Garching,
Germany
6
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore
MD
21218,
USA
7
Konkoly Observatory, Research Centre for Astronomy and Earth
Sciences, Hungarian Academy of Sciences, Konkoly Thege 15-17, 1121
Budapest,
Hungary
8
SRON, Postbus 800, 9700 AV
Groningen, The
Netherlands
9
Center for Astrophysics of the University of Coimbra, Geophysical
and Astronomical Observatory, Almas
de Freire, 3040-004
Coimbra,
Portugal
10
Unidad de Astronomía, Universidad de Antofagasta,
Avenida Angamos
601, Antofagasta,
Chile
11
Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique
de Marseille) UMR 7326, 13388
Marseille,
France
Received:
10
June
2013
Accepted:
12
July
2013
Aims. The goal of this work is to characterize the ensemble thermal properties of the Centaurs / trans-Neptunian population.
Methods. Thermal flux measurements obtained with Herschel/PACS and Spitzer/MIPS provide size, albedo, and beaming factors for 85 objects (13 of which are presented here for the first time) by means of standard radiometric techniques. The measured beaming factors are influenced by the combination of surface roughness and thermal inertia effects. They are interpreted within a thermophysical model to constrain, in a statistical sense, the thermal inertia in the population and to study its dependence on several parameters. We use in particular a Monte-Carlo modeling approach to the data whereby synthetic datasets of beaming factors are created using random distributions of spin orientation and surface roughness.
Results. Beaming factors η range from values <1 to ~2.5, but high η values (>2) are lacking at low heliocentric distances (rh < 30 AU). Beaming factors lower than 1 occur frequently (39% of the objects), indicating that surface roughness effects are important. We determine a mean thermal inertia for Centaurs/ TNO of Γ = (2.5 ± 0.5) J m-2 s−1/2 K-1, with evidence of a trend toward decreasing Γ with increasing heliocentric (by a factor ~2.5 from 8–25 AU to 41–53 AU). These thermal inertias are 2–3 orders of magnitude lower than expected for compact ices, and generally lower than on Saturn’s satellites or in the Pluto/Charon system. Most high-albedo objects are found to have unusually low thermal inertias. Our results suggest highly porous surfaces, in which the heat transfer is affected by radiative conductivity within pores and increases with depth in the subsurface.
Key words: Kuiper belt: general / planetary systems / planets and satellites: surfaces / methods: observational / techniques: photometric
Herschel is an ESA space observatory with science instruments provided by European–led Principal Investigator consortia and with important participation from NASA.
Table 3 is available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Combined optical and thermal observations provide the most common approach to measuring the size and albedos of unresolved airless solar system bodies. Known as the radiometric method, this technique, which dates back to the 1970s (Allen 1970), has been applied to most families of small bodies, especially main-belt asteroids, near-Earth asteroids, and Jupiter Trojans. Initially limited in number by practical constraints on ground-based observations, thermal observations of asteroids have quickly expanded to large surveys, such as IRAS in 1983 (2200 objects in 1983, Tedesco et al. 2002), AKARI in 2006–2007 (about 5000 objects, Usui et al. 2013), Warm Spitzer ExploreNEO since 2009 (600 near-Earth objects, Trilling et al. 2012), and WISE/NEOWISE in 2009–2010, which observed over 150 000 small bodies at 3.4, 4.6, 12, and 22 μm, including some 100 000 main-belt asteroids (Masiero et al. 2011), over 400 NEOs (Mainzer et al. 2011a), and about 2000 Trojans (Grav et al. 2011).
More distant bodies, such as Centaurs and trans-Neptunian objects (TNOs), have been studied much less, due to their faintness and the increasing confusion due to sky emission in the wavelength range where they emit (peak radiation near 100 μm). Except for a handful of objects measured from ground-based radiometry – and several more from stellar occultation and direct imaging – Spitzer (2004–2009) provided the first significant dataset on the size/albedo in the Kuiper belt, with about 60 Centaurs/KBOs published measurements at 24 and/or 70 μm (Cruikshank et al. 2005; Grundy et al. 2005, 2007; Stansberry et al. 2006, 2008; Brucker et al. 2009). Building on these results, an observing program entitled “TNOs are Cool!” (Müller et al. 2009) was initiated on Herschel (Pilbratt et al. 2010) to observe 130 objects with the Photodetector Array Camera and Spectrometer (PACS; Poglitsch et al. 2010) operating in three bands at 70, 100, and 160 μm. A small subset (11) of the objects were also observed with the Spectral and Photometric Imaging Receiver (SPIRE; Griffin et al. 2010) at 250, 350 and 500 μm. Results for about 75% of the observed sample have been or are being published (Müller et al. 2010; Lim et al. 2010; Lellouch et al. 2010; Santos-Sanz et al. 2012; Mommert et al. 2012; Vilenius et al. 2012; Pàl et al. 2012; Fornasier et al. 2013; Kiss et al. 2013a and in prep.; Vilenius et al. 2013; Duffard et al. 2013).
Beyond the measure of sizes and albedos, multi-wavelength thermal radiometry provides
information on the surface temperature distribution, as the latter impacts the shape of the
emitted spectral energy distribution (SED), i.e. the objects’ color temperature. In addition
to the heliocentric distance, Bond bolometric albedo and bolometric emissivity, that
together define the mean surface temperature, the temperature distribution is determined by
the object’s rotation state (rate and spin-vector orientation), thermal inertia, and surface
roughness. The thermal inertia is usually the physical quantity of interest. However, in
many cases, the problem is under-determined, as the other parameters involved, particularly
the rotational parameters, are poorly or not constrained. Therefore, a simple and powerful
approach is to describe the temperature distribution across the object as similar to that
resulting from instantaneous equilibrium of a smooth spherical surface with solar radiation
(the “equilibrum” (EQM) model), but modified by a “beaming factor” (η) so
that the temperature at solar incidence i is given by 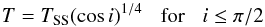 (1)where the subsolar
temperature TSS is given by:
(1)where the subsolar
temperature TSS is given by:  (2)where
F⊙ is the solar flux at 1 AU, rh
is the heliocentric distance in AU,
A = pV·q
is the bolometric albedo, and ϵb is the bolometric emissivity,
often assumed to be 0.9. Here pV is the
geometric albedo and q is the phase integral, and σ is
Stefan-Boltzmann’s constant. The beaming factor is then adjusted to fit the shape of the
SED; in essence, by varying the instantaneous equilibrium temperature it enables the model
to be matched to the color temperature of the object, as determined from multi-wavelength
thermal measurements. More accurate η estimates can be derived if the
measurements sample a broader fraction of the SED, and in particular cover both sides of the
peak of the Planck function. This approach was originally developed for near-Earth objects
(NEOs) – the NEATM model (Harris 1998) – but is
applicable to all atmosphereless bodies, and it has been amply demonstrated (e.g. Harris 2006, and references therein) to be vastly
superior to EQM (or to models with fixed η, such as the asteroid standard
model (STM) which has η = 0.756; Lebofsky
& Spencer 1989) for the purposes of deriving accurate diameters/albedos. In
the case of Centaurs/TNOs, the method was first presented by Stansberry et al. (2008) under the name of “hybrid-STM”, using
Spitzer/MIPS measurements at 24 and 70 μm. Although
strictly speaking the hybrid-STM assumes zero phase angle, while NEATM handles non-zero
phase angles, this is unimportant in the case of distant objects1, and the above papers analyzing Herschel data have
used equivalently both versions. Throughout this paper we ignored phase angle effects, i.e.
did not make the distinction between NEATM and “hybrid-STM”. In principle, therefore NEATM
solves for three parameters (diameter, albedo and beaming factor) by fitting at least
thermal measurements from at least two bands2, with
the optical magnitude HV providing a third
relation between diameter and albedo (Russell 1916).
(2)where
F⊙ is the solar flux at 1 AU, rh
is the heliocentric distance in AU,
A = pV·q
is the bolometric albedo, and ϵb is the bolometric emissivity,
often assumed to be 0.9. Here pV is the
geometric albedo and q is the phase integral, and σ is
Stefan-Boltzmann’s constant. The beaming factor is then adjusted to fit the shape of the
SED; in essence, by varying the instantaneous equilibrium temperature it enables the model
to be matched to the color temperature of the object, as determined from multi-wavelength
thermal measurements. More accurate η estimates can be derived if the
measurements sample a broader fraction of the SED, and in particular cover both sides of the
peak of the Planck function. This approach was originally developed for near-Earth objects
(NEOs) – the NEATM model (Harris 1998) – but is
applicable to all atmosphereless bodies, and it has been amply demonstrated (e.g. Harris 2006, and references therein) to be vastly
superior to EQM (or to models with fixed η, such as the asteroid standard
model (STM) which has η = 0.756; Lebofsky
& Spencer 1989) for the purposes of deriving accurate diameters/albedos. In
the case of Centaurs/TNOs, the method was first presented by Stansberry et al. (2008) under the name of “hybrid-STM”, using
Spitzer/MIPS measurements at 24 and 70 μm. Although
strictly speaking the hybrid-STM assumes zero phase angle, while NEATM handles non-zero
phase angles, this is unimportant in the case of distant objects1, and the above papers analyzing Herschel data have
used equivalently both versions. Throughout this paper we ignored phase angle effects, i.e.
did not make the distinction between NEATM and “hybrid-STM”. In principle, therefore NEATM
solves for three parameters (diameter, albedo and beaming factor) by fitting at least
thermal measurements from at least two bands2, with
the optical magnitude HV providing a third
relation between diameter and albedo (Russell 1916).
The beaming factor is thus a proxy for all combined effects causing a departure of the surface temperatures from the case of a smooth spherical surface in instantaneous equilibrium with insolation3. These include surface roughness and thermal inertia effects, which tend to increase and decrease, respectively, the surface temperatures. In a general sense, “high” η values indicate high thermal inertias, while values less than unity can occur only in presence of surface roughness. Although, for a given object, a physical interpretation of the η-value requires a knowledge of the spin state, the distribution of η values within a population allows one to draw conclusions about the ensemble-averaged thermal inertia of the targets. Such a statistical approach has been demonstrated in the case of near-Earth asteroids by Delbo’ et al. (2007), who inferred a mean thermal inertia for km-sized NEAs of 200 ± 40 J m-2 s−1/2 K-1 (hereafter MKS). In the case of Centaurs/TNOs, the Spitzer measurements have provided about 30 beaming factor values, indicating a mean value of η = 1.2 (Stansberry et al. 2008), but with large scatter due to the large error bars on the individual measurements, and possibly due to a range of spin orientations, spin rates and thermal characteristics. No interpretation of this mean η was presented by Stansberry et al.
In this paper, we take advantage of the broader wavelength coverage and larger sample afforded by the combined Spitzer–Herschel dataset to conduct a study of the thermal properties of Centaurs/TNOs, sampling the various population subclasses. Section 2 describes the data set. Section 3 describes the modeling approach. Inferences on thermal inertia are presented in Sect. 4 and discussed in Sect. 5.
2. The dataset
We consider a set of 85 Centaurs/TNOs for which Herschel/ Spitzer observations permit a determination of the beaming factor. This includes (i) published values of η, (ii) updated values of η based on published fluxes, (iii) new η values determined from yet-unpublished fluxes. Before describing the dataset, we briefly present the Herschel sample.
2.1. The Herschel Centaurs/TNO sample
The Herschel sample consists of 130 Centaurs/TNOs. For the most part, these objects were selected using source knowledge as of 2009. Flux predictions in the Herschel/PACS bands made use of NEATM and were based, whenever possible, on previous individual diameter/albedo results from Spitzer. However, in a more general way, flux estimates made use of HV magnitudes, assuming fixed values of the geometric albedo (pV = 0.08) and beaming factor (η = 1.25), based on mean results from Spitzer (Stansberry et al. 2008). Objects for which flux predictions exceeded a certain threshold – i.e. for which detection with PACS was expected – were retained in the sample.
An object’s brightness, as expressed by HV,
is proportional to
pVD2 where
D is diameter. The thermal flux, on the other hand, is essentially
proportional to D2/Δ2 (where Δ, the
observer-centric distance, is approximately equal to rh for
distant objects) times the Planck function at a temperature which scales as
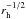 but
is mostly independent of pV. Because of the
thermal flux dependence on D2/Δ2, our sample has a
selection bias toward larger objects at greater distances. Smaller objects at great
distances would not have been included because their predicted fluxes would be too low.
This bias is worsened by the discovery bias against finding small objects at greater
distances. There is, in addition, a bias toward discovering preferentially high-albedo
objects at greater distances. Such objects, under our assumption of the same albedo for
all TNOs, would be “interpreted” as having a larger D (leading to a
larger predicted thermal flux), and so would be more likely to be included in our sample.
As will be seen below, the D vs. rh bias is
clearly visible in our results, and the pv
vs. rh bias may also be present. In contrast, there is no bias
on η, which enters absolute flux predictions in a rather insensitive way
and is essentially determined from the shape of the SED.
but
is mostly independent of pV. Because of the
thermal flux dependence on D2/Δ2, our sample has a
selection bias toward larger objects at greater distances. Smaller objects at great
distances would not have been included because their predicted fluxes would be too low.
This bias is worsened by the discovery bias against finding small objects at greater
distances. There is, in addition, a bias toward discovering preferentially high-albedo
objects at greater distances. Such objects, under our assumption of the same albedo for
all TNOs, would be “interpreted” as having a larger D (leading to a
larger predicted thermal flux), and so would be more likely to be included in our sample.
As will be seen below, the D vs. rh bias is
clearly visible in our results, and the pv
vs. rh bias may also be present. In contrast, there is no bias
on η, which enters absolute flux predictions in a rather insensitive way
and is essentially determined from the shape of the SED.
2.2. Published η values
A large fraction of the observations performed within the “TNOs are Cool!” program on Herschel has been published. Herschel/PACS measurements of 19 Classical Objects, 18 Plutinos, and 15 scattered-disk/detached objects were presented by Vilenius et al. (2012), Mommert et al. (2012) and Santos-Sanz et al. (2012) respectively. These measurements, combined with Spitzer data whenever available, provided diameter/albedo values for these 52 bodies (2 of which were only limits), as well as 30 (12 Classical + 11 Plutino + 7 scattered disk objects (SDO)/detached) η values4. Fornasier et al. (2013) presented flux measurements with Herschel/SPIRE for 10 objects, that were combined with Herschel/PACS and Spitzer, providing alternative η values for 9 of them (with one overlapping object – Huya – in Mommert et al. 2012 and another – Salacia – in Vilenius et al. 2012). We adopted the η values of Fornasier et al. (2013), however generally retaining values based on PACS and MIPS only, as the SPIRE fluxes appear affected by emissivity effects at the longest wavelengths. An extended study of the Classical Objects family by Vilenius et al. (2013) led to the addition of 18 objects, of which 9 have had their η values determined with enough accuracy for our purpose. Most recently, Duffard et al. (2013) analyzed Herschel/PACS measurements from 14 Centaurs, and again combined them with Spitzer (and WISE in some cases) data to determine the η. Those were included as such, as well as previous Spitzer results (Stansberry et al. 2008; Brucker et al. 2009) on four objects not observed by Herschel. Finally Kiss et al. (2013a) presented a portrait of the newly discovered and yet unclassified object 2012 DR30, including an η measurement based on Herschel/PACS and WISE. In total, this makes 64 objects for which we adopted the published diameters, albedos, and beaming factors without any modifications.
2.3. Updated η values
In a number of situations, we used published fluxes but re-derived new or updated values of η, using NEATM. First, this is the case for 4 SDO/detached whose Herschel fluxes were presented in Santos-Sanz et al. (2012) but for which the authors did not attempt to infer η values, in the absence of Spitzer measurements. Although Herschel-only η are admittedly much less accurate, they are still significant and so we derived them here for completeness. Note that for two of these objects (2007 OR10 and 2007 RW10, only HR magnitudes are available, so the resulting red albedos pR were converted into pV following Santos-Sanz et al. (2012) (i.e., assuming a color index V − R = 0.55 ± 0.11 – typical of SDO/detached objects – for 2007 RW10, and a Quaoar-like value, 0.67 ± 0.02, for 2007 OR10).
In a few cases, independent albedo/size estimates exist from stellar occultation
measurements. For those objects, a single thermal measurement is sufficient to derive the
beaming factor. Even in the case of multi-thermal wavelength measurements, the
diameter/albedo precision afforded by the occultation technique is superior to that of the
radiometric method, so using occultation-derived results will lead to an improved
determination of the thermal properties. This was done here for Eris and Makemake (and
2002 TX300, see below), i.e. running NEATM but with the diameter and albedo
fixed to their known values. The case for Makemake is peculiar, as its 24–500
μm SED cannot be fit with a NEATM (nor a thermophysical model) assuming
a homogeneous surface; it is suspected that the SED includes a contribution from a dark
and warmer component that dominates at the shortest wavelengths (Lim et al. 2010). For this reason, we considered only the SPIRE
measurements at 250–500 μm from Lim et
al. (2010), and those were modeled with D = 1430 ± 9 km and
pV = 0.77 ± 0.02 (Ortiz et al. 2012). The resulting η value
(2.29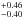 ,
see Table 3) is similar to that found by Lim et al.
(2010) for Makemake “bright terrain” (nominally, 1.9). For Eris, we used the 100
and 160 μm fluxes from Santos-Sanz et
al. (2012) updated by Kiss et al. (in prep.), and remodeled them using
D = 2326 ± 12 km and
pV = 0.96 ± 0.04 (Sicardy et al. 2011). Although the measurements did provide a 70
μm flux, it was not included in the modeling, as being probably
affected by Eris’ satellite Dysnomia or by a hot, dark terrain on Eris to a significant
degree.
,
see Table 3) is similar to that found by Lim et al.
(2010) for Makemake “bright terrain” (nominally, 1.9). For Eris, we used the 100
and 160 μm fluxes from Santos-Sanz et
al. (2012) updated by Kiss et al. (in prep.), and remodeled them using
D = 2326 ± 12 km and
pV = 0.96 ± 0.04 (Sicardy et al. 2011). Although the measurements did provide a 70
μm flux, it was not included in the modeling, as being probably
affected by Eris’ satellite Dysnomia or by a hot, dark terrain on Eris to a significant
degree.
Herschel color-corrected fluxes at 70, 100 and 160 μm and H-magnitudes for the “new” objects presented in this work.
Finally, Pàl et al. (2012) presented Herschel/PACS 70/100/ 160 μm fluxes of two prominent objects, Sedna and 2010 EK139, and inferred their diameter and albedo, mostly based on thermophysical analysis. For consistency, we here remodel their published fluxes with our NEATM (as described in Santos-Sanz et al. 2012). More details on the NEATM fits are given in Sect. 2.4.
2.4. New η measurements
In addition to the above objects, we include here 13 “new” bodies, i.e. observed by Herschel/PACS within the “TNOs are Cool!” program, but whose measurements have not been reported previously. These include two classical objects (Varuna and 2002 TX300, the latter being a Haumea-family member), four Plutinos (1994 TB, Ixion, 2004 TY364 and 1998 VG44), three non-Plutino resonant objects (1998 SM165, 2002 WC19 and 1999 DE9) and two SDOs (1999 OX3 and 1995 TL8). Finally we include Saturn’s irregular satellite Phoebe and Uranus’ Sycorax, both of which are thought to be captured Centaurs/TNOs.
Details on the observing technique, data reduction, measurement of the object fluxes, and modeling can be found in the previous “TNOs are Cool!” publications, particularly in Santos-Sanz et al. (2012), and only a brief summary is given here. Herschel/PACS observations were performed using the scan map mode, whereby the spacecraft is slewed at constant speed (20″/s) along 10 parallel lines, or “legs“, separated by 4″, and in two intersecting scanning directions. Each such scan-map is repeated two to five times, depending on the expected brightness of the objects. Within a single scan map, either the blue-red (70/160 μm) or the green-red channel (100/160 μm) combination is selected. Furthermore each target is visited twice, with identical observations repeated in both visits with a time interval chosen so that the target moves 30–50″ between visits. Data are reduced under the HIPE environment5, using a two-stage high-pass filtering procedure, producing one image per visit, filter and scan direction. The changing position of the source with respect to the background in the first vs second visit then allows the background in the individual maps to be determined and subtracted and a background-subtracted, combined image to be obtained. More details on the reduction techniques can be found in Kiss et al. (2013b). Fluxes are extracted from aperture photometry, where a priori knowledge of the source position (near the map center) facilitates its identification. The optimum synthetic aperture to measure the target flux is usually taken as 1.0–1.25 times the FWHM of the PSF in the corresponding filter, and photometric uncertainties are estimated from random implantation of artificial sources and attendant statistical photometry. Fluxes along with their error bars are finally color-corrected using a first guess of the object mean temperature (but the color-correction is only at the few percent level). Observing conditions and fluxes for the Herschel/PACS observations are given in Table 1.
Spitzer color-corrected fluxes at 23.68 and 71.42 μm for the “new” objects presented in this work.
Correlation results for η values.
Spitzer/MIPS (Rieke et al. 2004) observations of the same objects were used to complement the Herschel/PACS data. Out of the 13 objects, some have fluxes published (Stansberry et al. 2008; Brucker et al. 2009) while others are unpublished. Unpublished data have been processed in a similar way as in Stansberry et al. (2008) and Brucker et al. (2009), using the calibration (Gordon et al. 2007; Engelbracht et al. 2007) and color-correction procedure (Stansberry et al. 2007) described in references therein, and photometric uncertainties are being handled in the same manner. Some of the background subtraction techniques used for our Herschel data are in fact derived from techniques originally developed for the MIPS data reductions. The previously unpublished fluxes presented here are based on new reductions of the MIPS data, utilizing updated ephemeris positions for the targets. Observing conditions and fluxes for the Spitzer/MIPS observations are given in Table 2.
Color-corrected fluxes and their 1–σ error bars at 23.78 and 71.42
μm (MIPS), and 70, 100 and 160 μm (PACS) were modeled
within NEATM to determine best fit values and uncertainties for the objects diameter
D, visible geometric albedo
pV and beaming factor η.
In this task, a crucial parameter is the absolute
HV magnitude, for which depending on the
object, more or less information may be available (ranging from only rough magnitudes
compiled from MPC reports to cases with detailed lightcurve and phase curve information),
and we proceeded following Santos-Sanz et al. (2012). In NEATM, Eq. (2) requires some form or value for the phase
integral, and following the previous studies, we adopted the albedo-dependent expression
q = 0.336·pV + 0.479
(Brucker et al. 2009). Flux upper limits were
treated as non-detections (i.e. zero flux) with a 1-σ error bar equal to
the upper limit. Uncertainties on the three fitted parameters were estimated using the
Monte-Carlo method of Mueller et al. (2011), i.e. generating and fitting 1000 synthetic
datasets, and adopting the median and the central 68.2% of the solutions. When fits were
“bad”, i.e. characterized by a reduced χ2 significantly larger
than 1, we “inflated” the measurement error bars to obtain more realistic uncertainties,
using the procedure and the conditions outlined in Santos-Sanz et al. (2012). For one object of our sample (2002 TX300),
the diameter and geometric albedo have been measured to be D = 286 ± 10
km and  from stellar occultation (Elliot et al. 2010).
These values were therefore held fixed when running NEATM, with η as the
only free parameter.
from stellar occultation (Elliot et al. 2010).
These values were therefore held fixed when running NEATM, with η as the
only free parameter.
Phoebe, whose diameter, shape and albedo are known accurately after the Cassini
measurements, provides a validation of the NEATM approach. It was observed by
Spitzer (unpublished data, see Table 2), Herschel/PACS
(Table 1), Herschel/SPIRE, and also by WISE (Mainzer et al. 2011b). In a first step, we used the Spitzer
and Herschel/PACS data to solve for D,
pv, and η. This led to
D = 198 ± 4 km and  %.
The diameter is only 7% lower than the mean diameter inferred from Cassini
(213 ± 1.4 km; Thomas 2010). The albedo, on the other hand, is 27% larger than
the 0.6 μm albedo (8.2 ± 0.2%) reported from
Cassini/VIMS by Buratti et al.
(2008), a combination of the smaller diameter and probably of the spatial
variegation on the body. Fixing D and
pv to the Cassini
values, we then inferred
%.
The diameter is only 7% lower than the mean diameter inferred from Cassini
(213 ± 1.4 km; Thomas 2010). The albedo, on the other hand, is 27% larger than
the 0.6 μm albedo (8.2 ± 0.2%) reported from
Cassini/VIMS by Buratti et al.
(2008), a combination of the smaller diameter and probably of the spatial
variegation on the body. Fixing D and
pv to the Cassini
values, we then inferred  ,
in satisfactory agreement with the WISE value (1.23 ± 0.01). Further analyses of the
Phoebe thermal data, including the SPIRE measurements, will be published elsewhere in the
context a dedicated thermophysical model.
,
in satisfactory agreement with the WISE value (1.23 ± 0.01). Further analyses of the
Phoebe thermal data, including the SPIRE measurements, will be published elsewhere in the
context a dedicated thermophysical model.
 |
Fig. 1 Observed beaming factor η as a function of heliocentric distance rh for the entire sample. With two exceptions (objects observed by Herschel and WISE, see Table 3), blue (resp. green, red) symbols refer to objects with both Herschel and Spitzer (resp. only Herschel, only Spitzer) fluxes. |
 |
Fig. 2 Beaming factor η as a function of left: geometric albedo and right: diameter. Labels M, H, TX, E, Q refer to Makemake, Haumea, 2002 TX300, Eris and Quaoar, respectively. |
2.5. Qualitative description of the η results
Results for diameter, geometric albedo, and beaming factor for all objects in our sample (85 objects), including the various sources, are tabulated in Table 3, where the heliocentric distance at the time of observation is also given. In what follows, we focus on the distribution of η values and their variations with other parameters. Results on the size and albedo distributions will be published separately.
Table 4 presents the results of correlation searches between η and the other parameters, using the Spearman-rank correlation coefficients (Spearman 1904) and following the methods described by Santos-Sanz et al. (2012). In particular, we present correlation coefficients calculated by taking into account or not the error bars on the parameters. As in the above paper, for the case where error bars are accounted for, Table 4 includes the p-value (i.e. the significance level of no-correlation), and the Gaussian-σ level of the correlation significance. Correlations are calculated on the whole set of 85 objects, and on a reduced set of 56 “good” objects for which the η uncertainty (mean of “upward” and “downward” error bars) is less than 0.3.
Figure 1 shows the derived η factor for all objects as a function of heliocentric distance. A large dispersion of the η values is noticeable, ranging from <1 to ~2.5. A significant fraction of the objects (39%) have central η values lower than 1, indicating important surface roughness effects. The mean value of η is 1.175 if equal weight is given to all objects. When error-bar weighting is applied, a mean value of 1.07 is obtained, close to the median η value (1.09). Note that one object, the Centaur 2005 UJ438, exhibits an extremely low η value (nominally <0.5). This could plausibly result from coma activity, as emission of small and hot particles would enhance the short-wavelength flux, leading to a low apparent η, although Jewitt (2009) did not find any activity on this body. Although a visual inspection of Fig. 1 may suggest a general increase of η with rh, Table 4 indicates that correlation is weak and only significant at 1.4σ. However, it is noteworthy that within the “core” of the Kuiper belt, i.e. near rh = 40 AU where a large fraction of the sample occurs, the entire η = 0.6–2.5 interval is filled. In contrast, within 30 AU from the Sun, the η values are restricted to progressively narrower ranges, and no objects with η > 2 are seen at rh < 30 AU, nor with η > 1.5 at rh < 15 AU. As will be shown, this is an expected behavior for a set of objects with a generally low thermal inertia and a diversity of pole orientations.
Adopted rotational properties.
 |
Fig. 3 Beaming factor η as a function of left: lightcurve period (44 objects) middle: lightcurve amplitude (same 44 objects) and right: density (14 objects). Lightcurve information is taken from Table 5 and density values from literature (see text). |
Figure 2 shows η as a function of the other two parameters derived from NEATM, i.e. diameter D and geometric albedo pV. η and D appear to be weakly positively correlated (Table 4), but this may be a consequence of the fact that there is a very strong correlation between rh and D in our sample (itself a target discovery/selection bias, as discussed in Sect. 2.1). The η vs. pV plot indicates that while low-albedo objects explore the full range of η, high-albedo objects tend to have exclusively low-η values. In fact, all objects with geometric albedos higher than 20% have η < 1.5, with one exception (Makemake). No significant correlation is present beyond 1-σ between η and pV. This result is noticeable in view of the positive correlation (coefficient +0.45, 4.3σ) between rh and pV in our sample (which may reflect the selection bias discussed in Sect. 2.1). Rotational information (i.e. lightcurve period P and amplitude Δm) is available for 44 objects of the sample, as summarized in Table 5. Density (ρ) estimates are also available for 14 objects, mostly binary systems (Sicardy et al. 2011; Santos-Sanz et al. 2012; Vilenius et al. 2012; Mommert et al. 2012; Ortiz et al. 2012; Fornasier et al. 2013). Figure 3 shows plots of η vs. Δm, P and ρ, none of which shows trends beyond the 1.3σ confidence level.
In what follows, we present models to derive ensemble thermal properties of the population. We mostly focus on the interpretation of the η vs. rh behavior, but also study the η vs. pV relationship.
3. Model
3.1. Relating beaming factor to thermal parameter
As indicated in the Introduction, for a spherical object, the beaming factor includes the
combined effects of surface roughness and thermal inertia. Thermal inertia effects are not
only dependent on the value of the thermal inertia (Γ) but also on the rotation state
(i.e. spin orientation and rate) of the object. For a given spin orientation,
characterized by the subsolar latitude on the object β (which for distant
objects can be assumed identical to the subobserver latitude), the degree to which the
surface responds to insolation is fully characterized by the so-called “thermal
parameter”, Θ (Spencer et al. 1989). Θ is equal to
the ratio of the characteristic timescale for radiating heat from the subsurface to the
diurnal timescale, and is expressed as: 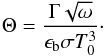 (3)Here
ω = 2π/P is the body rotation rate,
where P is the rotation rate, ϵb,
σ have been defined previously and T0 is
the instantaneous equilibrium subsolar temperature (given as
TSS per Eq. (2) but omitting the beaming factor). Objects
with the same value of Θ exhibit the same diurnal temperature profile, provided they have
the same spin orientation (i.e. β). More generally, local temperatures
can be written as (e.g. Lellouch et al. 2000):
(3)Here
ω = 2π/P is the body rotation rate,
where P is the rotation rate, ϵb,
σ have been defined previously and T0 is
the instantaneous equilibrium subsolar temperature (given as
TSS per Eq. (2) but omitting the beaming factor). Objects
with the same value of Θ exhibit the same diurnal temperature profile, provided they have
the same spin orientation (i.e. β). More generally, local temperatures
can be written as (e.g. Lellouch et al. 2000):
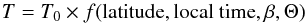 (4)where
f(latitude, local time, β,Θ) is a temperature
function, that depends on the thermal parameter and on local insolation (through latitude,
local time, and subsolar latitude); when Θ = 0, f = 1 at the subsolar
point.
(4)where
f(latitude, local time, β,Θ) is a temperature
function, that depends on the thermal parameter and on local insolation (through latitude,
local time, and subsolar latitude); when Θ = 0, f = 1 at the subsolar
point.
 |
Fig. 4 Model beaming factor η as a function of thermal parameter Θ for three values of the subsolar/subearth latitude β and five values of the instantaneous subsolar temperature T0. |
Thus, Θ and β control the temperature distribution at the surface, as does η semi-empirically. The first task is therefore to quantitatively relate η to Θ, for a given value of β. For this we first produced a series of thermophysically-based temperature distributions, entirely defined by the values of T0, Θ and β. For each model, and using an object of arbitrary radius, the object-integrated SED was calculated and then refit with NEATM to determine the equivalent value of the beaming factor. In practice, the emitted flux was calculated at the five wavelengths from which most of our observational determinations of η were obtained (i.e. 23.78, 70, 71.42, 100 and 160 μm). As the SED varies drastically in shape with the absolute temperatures, this was performed on a grid of five values of the subsolar temperatures encompassing the range of our measurements, given the heliocentric distances and determined albedos: T0 = 25, 50, 75, 100 and 150 K.
Results are shown in Fig. 4 for the five values of T0 and three values of β (0°, 32.7°, and 60°). Note that β = 32.7° (=(π/2−1) rad) is the mean value in the case of a uniform distribution of spin orientations on a sphere (in such a distribution, a particular βi value is weighted by cos βi). Unsurprisingly, results are strongly dependent on β. In contrast the η(Θ) relation is much less dependent on T0. This will permit us, for a particular object, to interpolate between the various T0 curves. Note that when β = 90° (not shown in Fig. 4), η = 1 for any Θ value, as the temperature distribution on a smooth sphere with pole-on orientation is identical to the instantaneous equilibrium case, regardless of thermal inertia.
3.2. Surface roughness effects
Figure 4 shows that in the limit of high values of the thermal parameter, the beaming factor reaches asymptotic values of 2.5–2.8 for equator-on orientations (β = 0°). This is consistent with the highest η values in our observational sample (e.g. Fig. 1). However, the data also indicate a number of η < 1 cases, not accounted for in Fig. 4. These are due to surface roughness effects, not included in the previous section.
Surface roughness is usually treated in models by adding craters of variable opening
angle and surface coverage on a smooth sphere, and by accounting for shadowing and
multiple scattering of solar and thermal radiation as well as heat conduction inside
craters (Spencer 1990; Lagerros 1996; Emery et al.
1998; Delbo’ et al. 2007; Davidsson et al. 2009). These models for the most part
have been applied to unresolved asteroid observations. More recently, Rozitis & Green (2011) presented models
describing the observed directional thermal emission from any atmosphereless planetary
surface. In addition to the description in terms of the above two crater parameters,
roughness can also be parameterized in terms of the mean surface slope angle
( ,
Hapke 1984; Emery
et al. 1998), or the rms surface slope (s, as defined by Spencer 1990), or the rms surface “roughness”
(ρ, defined by Lagerros 1998).
,
Hapke 1984; Emery
et al. 1998), or the rms surface slope (s, as defined by Spencer 1990), or the rms surface “roughness”
(ρ, defined by Lagerros 1998).
The work by Spencer (1990) is appropriate to our study as it directly links surface roughness to the beaming factor η of the NEATM. In particular, he showed that the effect of a roughness level s can be seen as a “negative” contribution to η, such as δη(Θ,s) = η(Θ,s) − η(Θ,0). The most important feature of δη is that it is a function of Θ; in particular δη decreases with Θ and converges to ~0 at Θ > 30. This can be explained by temperature profiles within craters becoming progressively isothermal at high values of Θ. Otherwise δη is to high accuracy constant with subsolar latitude β, and also largely independent of wavelength (especially longward of the Planck maximum).
Here we considered two of the roughness cases described by Spencer (1990): (i) the 50% coverage, 90° opening angle case, which we termed “moderate roughness” (ii) the 100% coverage, 90° opening angle case, a maximum roughness situation which we called “high roughness”. The two cases respectively give δη = 0.24 and δη = 0.38 at Θ = 0, decreasing with the thermal parameter. They approximately correspond to rms surface roughness ρ ~ 0.6 and ~0.9, respectively, in the formalism of Lagerros (1998; see his Fig. 2).
 |
Fig. 5 Model beaming factor η as a function of thermal parameter Θ for four values of the subsolar/subearth latitude β and three surface roughness levels: Solid line: no roughness. Dotted line: moderate roughness. Dashed line: high roughness. The instantaneous subsolar temperature T0 is 50 K. |
Implementing the δη(Θ) corrections as per Fig. 6 of Spencer (1990), Fig. 5 shows the beaming factor vs thermal parameter relationship with and without surface roughness, for four values of β, restricting ourselves to the T0 = 50 K for figure clarity. The presence of surface roughness allows us to account for low η values in the low Θ regime, down to a minimum of η = 0.62 for high roughness and η = 0.79 for moderate roughness, while high η values are maintained for high Θ (up to ~2.6 for β = 0° and 1.95 for β = 32.7°). Overall this behavior accounts for the majority of the observationally-derived η’s. Figure 5 also shows that for a given orientation, the interpretation of a particular η value depends on the assumed roughness scenario, illustrating the roughness/thermal parameter degeneracy.
4. Thermal inertia results
4.1. Fixed spin state and roughness
With the above model, we now invert the measured η in terms of individual values of the thermal inertia. For this, in a first step, we assume that all objects have the same spin orientation, spin rate and surface roughness. For spin orientation, we consider both β = 32.7° and β = 0°. As representing a more likely mean orientation of the population, the first value is preferred. Admittedly, β = 0° permits an easier fit of high (>1.95) η values, but given the error bars, there is no unambiguous evidence for such values in our sample. We consider both the “high roughness” and “moderate roughness” cases, preferring the first case given the lowest measured η values. For a given (β, roughness) scenario, the measured η are solved in terms of the thermal parameter Θ (interpolating between the relevant T0 curves – see Fig. 4 – where T0 is calculated for each object from its heliocentric distance and albedo). Θ is finally converted to the thermal inertia Γ using Eq. (3), assuming a rotation period P = 8 h, a reasonable representative value for the TNO / Centaur population (see Fig. 3). Note that as Γ/Θ depends only weakly (power 1/2) on P, the uncertainty on P for a given object has not a large impact.
 |
Fig. 6 Individual thermal inertia vs. heliocentric distance, as inferred from the measured η for two values of the subsolar latitude (β = 32.7° and 0°) and the two surface roughness cases (“high” and “moderate”). |
 |
Fig. 7 Individual thermal inertia vs. geometric albedo, as inferred from the measured η for a subsolar latitude β = 32.7° and the two surface roughness cases. Labels H, TX and E refer to Haumea, 2002 TX300, and Eris, respectively. |
 |
Fig. 8 Individual thermal inertia for 44 objects as a function of rotational period, as inferred from the measured η, for two values of the subsolar latitude (β = 32.7° and 0°) and two cases of surface roughness (“high” and “moderate”). |
Results are summarized in Fig. 6 for the four cases. Considering the nominal η values, i.e. not accounting for error bars, the model gives Θ solutions for 70–82 objects out of 85 (i.e. 82–96%), depending of the (β, roughness) case (for the remaining 3–15 objects, the nominal η values cannot be fit by the model). Moreover 66–78 objects (i.e. 78–92%) have thermal inertia Γ less than 20 J m-2 s−1/2 K-1 (MKS), and 45–63 objects (53–74%) have Γ < 5 MKS. For the four considered cases, the median value of Γ varies from 1.7 MKS (β = 0°, moderate roughness) to 4.2 MKS (β = 32.7°, high roughness). For a given orientation, the ratio of the “high roughness” to the “moderate roughness” thermal inertia is in the range 1.3–1.8 for most objects, illustrating the well-known partial degeneracy between thermal inertia and roughness properties in defining the thermal fluxes. Overall, the distribution of η is indicative of a low thermal inertia for most objects. All four cases of Fig. 6 give the visual impression of a decrease of thermal inertia with increasing heliocentric distance. This is confirmed by simple Spearman rank correlation calculations (i.e. not including error bars on Γ). The strongest correlation between Γ and rh is found for the (β = 32.7°, high roughness) case (coefficient: − 0.58; 5.0σ confidence), while the least significant is obtained for the (β = 0°, moderate roughness) case (coefficient: − 0.40; 3.5σ) Fitting the (rh, Γ) values with a power-law function in the form Γ (rh) = Γ(30 AU) × (rh/30)−α (accounting for error bars) yields a power exponent α in the range 1.40–1.94 for the various orientation, roughness cases, and Γ(30 AU) = 2.0–4.0 MKS. Hence this analysis suggests a rapid decrease of thermal inertia with increasing heliocentric distance over 8–50 AU where most of the measurements refer to.
For the mean β = 32.7° orientation and the two roughness cases, Fig. 7 shows the inferred thermal inertia as a function of geometric albedos. The data indicate a general trend of a decrease of Γ with increasing pV. The noted absence of high values of η for bright objects (see Fig. 2) translates into a lack of “high” Γ values (>5 MKS) for objects having pV higher than ~20%. The Spearman correlation coefficient between Γ and pV is − 0.47 and − 0.35 for the high and moderate roughness cases, with 4.0 and 2.9 σ significance respectively. For the β = 0° case (not shown in Fig. 7), the significance of a decrease of Γ with pV is of 3.6 and 2.6σ for the two roughness cases, respectively. Note that this moderate Γ vs. pV anticorrelation can also be seen as an anticorrelation (with similar magnitude and significance) between Γ and diameter. In fact, geometric albedo and diameter in our sample appear to be positively correlated at 2.6σ (see Table 4), and a (Γ, diameter) plot shows a lack of Γ values higher than 5 MKS for objects larger than ~700 km in diameter, with Quaoar and Makemake as exceptions.
4.2. Attempting to use rotational information
As indicated above, rotational information (i.e. lightcurve period P and amplitude Δm) is available for 44 objects of the sample. In a first step, we used the actual P of these objects to invert η in terms of Γ, still keeping the assumption of fixed orientation and roughness. Results are shown in Fig. 8 for the same four cases as in Fig. 6, but this time plotted as a function of rotational period. Similar to Fig. 6, and noting also that error bars are usually smaller for points with lower thermal inertia, the figure indicates low thermal inertia, with median values ranging from 2.0 MKS (β = 0°, moderate roughness) to 4.5 MKS (β = 32.7°, high roughness). Although Fig. 8 might visually suggest an increase of the thermal inertia with rotation period, the Spearman rank correlation indicates that such a correlation is not significant beyond the 1.0–1.6σ level, depending on the (β, roughness) case.
 |
Fig. 9 Individual thermal inertia for objects having rotational lightcurve amplitudes Δm> 0.10, using subsolar latitudes estimated from the assumption of Jacobi equilibrium figures, using two values of the density (1000 and 3000 kg m-3), and two cases of surface roughness (“high” and “moderate”). |
The above analyses are still limited by the unknown orientation (β). We attempted to further use rotational information by assuming that objects exhibiting a sufficiently marked lightcurve adopt Jacobi equilibrium figures, i.e. are ellipsoids with a > b > c axes. In this case, the shape (i.e. the axis ratios) is defined by the rotation period and density, and the lightcurve amplitude then defines the viewing angle (β). Specifically, upon an assumption on the object density (ρ), we used the rotation period P = 2π/ω to calculate ω2/(πGρ), where G is the gravitational constant. When lower than a limit of 0.3742, the latter quantity provides c/a and b/a by interpolation from Chandrasekhar’s (1987) tables (see also Lacerda & Jewitt 2007). We considered two density cases (ρ = 1000 and 3000 kg m-3) and restricted ourselves to objects with some minimum lightcurve amplitude (Δmmin), considering that lightcurves with lower amplitudes may instead be due to albedo markings on a MacLaurin spheroid. Once c/a and b/a are known, β was determined from equations given e.g. in Lacerda & Luu (2003) or Rabinowitz et al. (2006) (page 1250, with β = 90°−Φ). The conversion of the beaming factors to thermal inertia was then performed using the individual values of P and β, again considering the “moderate” and “high” roughness cases.
This approach was only moderately successful. We started with Δmmin = 0.10. This case leads to solutions in terms of Γ for only 13 (for ρ = 1000 kg m-3) to 18 objects (for ρ = 3000 kg m-3). Results, shown in Fig. 9, indicate somewhat more dispersed and higher Γ values than before. This mostly results from the fact that the mean values of β deduced from the Jacobi equilibrium assumptions (47° and 50° for ρ = 1000 and 3000 kg m-3 respectively) are higher than those considered before for the population as a whole (0° and 32°). The median values of the thermal inertia, very similar for the two density cases, are typically 5–7 MKS and 17–23 MKS for the moderate and high roughness cases. However, we are not inclined to trust the results too much, especially because of the high β values, even higher than would be produced by a random distribution of polar axes in the ecliptic plane (leading to a mean β of 45°). This probably means that Δmmin > 0.10 is not strict enough to isolate the Jacobi ellipsoids, which is supported by the conclusion of Duffard et al. (2009) that the majority of large TNOs are in fact MacLaurin spheroids, with a relative fraction increasing from 30% at low density (ρ = 500 kg m-3) to more than 90% for ρ = 2500 kg m-3. Using a more restrictive Δmmin = 0.20 criterion, only 7–10 objects have Γ solutions, with (still high) mean β values of 38° and 42° for ρ = 1000 and 3000 kg m-3, and median values of Γ of 3–5 MKS and 8–17 MKS for the moderate and high roughness cases, respectively.
 |
Fig. 10 Left: Kolmogorov-Smirnov distance d between the observed distribution of η and those calculated as a function of thermal inertia for the four roughness scenarios. In all cases, a uniform distribution of the polar axes over the sphere is assumed. The minimum of d indicates the best fit thermal inertia Γ0. Right: histograms showing the distribution of best fit Γ0, when accounting for uncertainties in the η measurements (see text). |
 |
Fig. 11 Beaming factor η as a function of heliocentric distance rh for the entire sample, compared with Monte-Carlo simulations assuming a rotation period of 8 h, a geometric albedo of 0.1, a uniform distribution of the polar axes on the sphere, and a random distribution of surface roughnesses. Thermal inertia Γ = 1, 2.5 and 8 MKS cases are shown here. Although Γ = 8 MKS may seem needed to account for the three points with η = 1.5–1.8 at 13–18 AU, this case underpredicts the number of low η values at rh> 25 AU, and Γ = 2.5 MKS provides the overall best fit. |
4.3. Monte-Carlo simulations
 |
Fig. 12 Left: Kolmogorov-Smirnov distance d and Monte-Carlo simulations for the two assumed alternative distributions of polar axes. Top: uniform distribution of βs between ±90° (i.e. spin axes in ecliptic plane). Bottom: all objects with β = 0° (i.e. spin axes perpendicular ecliptic plane). In each case, the K-S distance to the data is plotted (left panels) as a function of Γ for the four roughness cases. Right panels show Monte-Carlo simulations for the random roughness cases. |
In a second, somewhat less model-dependent approach, we calculated “synthetic” datasets under various assumptions and compared them to the observed distribution of beaming factors. In practice, we generated a family of objects characterized by their individual heliocentric distance, spin orientation (β) and surface roughness. In general we assumed all objects to have a fixed rotation period P = 8 h and a fixed geometric albedo of pV = 0.1. As discussed above, results on the thermal inertia are relatively insensitive to P, and except for high-albedo objects, also rather insensitive to pV (through T0, see Fig. 4). In contrast, as is obvious from Fig. 5, they are strongly dependent on β and surface roughness, which were handled as follows. For each object of the simulation, a β value was randomly generated. We nominally assumed a uniform distribution of the spin axes orientations on the sphere. As discussed below, an alternative distribution of spin axes was also tested. For surface roughness, we considered the three cases (“no roughness”, “moderate roughness” and “high roughness”) previously described, assuming that they apply to all objects of the family (“fixed roughness cases”). In addition, we considered a so-called “random roughness” scenario, in which for each object, a roughness level was assigned randomly – considering a uniform distribution between the no-roughness and high roughness limiting cases. In the model and for any of the three “fixed roughness” cases, the distribution of β values is responsible for the diversity of η values at a given heliocentric distance rh, and the η distribution is further broadened in the random roughness scenario.
Comparison to the data was performed by using the two-dimensional Kolmorogov-Smirov test (e.g. Press et al. 1992). For each observed object, we calculated a set of 100 artificial objects having the same observed rh, but random values of β (and roughness, for the latter scenario). The model was then run for a series of values of the thermal inertia Γ in the range 0.5–50 MKS. The fit quality was then assessed from the Kolmorogov-Smirov (K-S) distance d in the (rh, η) plane. In essence, this distance quantifies the extent to which two 2-D datasets are similar (the more similar they are, the smaller d is). The K-S test also returns a significance level pKS for the fact that the two datasets derive from different distributions (the smaller pKS, the more different the distributions are likely to be).
For each model distribution, the K-S test was run by using the nominal (i.e. central) values of the measured η, providing the K-S distance d(Γ), and therefore the best fit value for Γ, noted Γ0. In addition, the sensitivity of the results to the measurement uncertainties was assessed by varying the measured η values within their error bars (using normally distributed random noise at the level indicated by the measurements). This was done for 100 repetitions, each of which returned a value of Γ0, finally providing the mean value of Γ0 and its standard deviation. Overall, the approach is similar to that adopted by Delbo’ et al. (2007) for determining the thermal inertia of near-Earth asteroids, except that they analyzed the behavior of η vs. phase angle instead of η vs. rh.
Results for d(Γ) are shown in the left panel of Fig. 10 for the four considered cases. This panel shows that with a minimum d value of 0.35 (corresponding to pKS = 6 × 10-7 at best fit), the no-roughness case can be rejected. For comparison, the “high”, “moderate” and “random” roughness cases have similar minimum d of 0.15–0.18, i.e. pKS in the range 0.06–0.09. The right panel of Fig. 10 shows histograms of the best fit Γ0 values when measurement uncertainties are considered. Excluding the no-roughness case, the solution ranges of Γ0 values are (3 ± 0.7) MKS, (5 ± 0.5) MKS and (2.5 ± 0.5) MKS for the moderate, high and random roughness cases, respectively. This range of values is in general agreement with inferences from the first approach (Sect. 4.1).
For our preferred “random roughness” case, Fig. 11 presents the model-calculated η vs rh distribution, for three values of Γ (1, 2.5 and 8). Here 750 points have been generated randomly in the manner explained previously, except that for a better visualization, a regular grid in rh in the 5–50 AU range has been adopted instead of retaining the measurements rh. For a given Γ value, the general increase of η with rh is simply the consequence of the increasing thermal parameter Θ through decreasing T0 (Eq. (3) and Fig. 4). Low Γ values such as Γ = 1 do not permit to explain η values higher than ~1.3. Large Γ (Γ = 8) seems to be required to explain the highest measured η values, especially the three points with η = 1.5–1.8 at 13–18 AU and a few points with η ~2.0–2.5 at 35–50 AU. However, as can be seen for the density distribution of red points in Fig. 11, this case underpredicts the number of low η (<1.3) values at rh > 25 AU. Overall, Γ = 2.5 provides the best fit.
Continuing with the assumption of a unique Γ value, we studied the sensitivity of the results to the assumed distribution of the β values. Specifically, we considered two extreme cases: (i) a uniform distribution of | β | values between 0° and +90°, which occurs in a situation where all spin axes are in the ecliptic plane but objects are seen at a random “season”; and (ii) a single β = 0° value, i.e. all spin axes are perpendicular to the line-of-sight (i.e., ecliptic plane). Results are shown in Fig. 12. The uniform β models (top panels) also permit a satisfactory interpretation of the measurements. Actually, with a minimum distance d = 0.09 and a pKS value of 0.64 for the random roughness case, the fit is even better than with the previous nominal model (uniform spin axis distribution on the sphere). In this case, the best fit Γ values are typically twice higher than in the nominal model. The top right panel of Fig. 12 shows Monte-Carlo simulations for this β distribution and Γ = (2, 5 and 15) MKS. Comparing the Γ = 5 MKS model with the previous Γ = 2.5 MKS case of Fig. 11, the slight improvement in the fit can be seen in that the new case permits to account for more points with high η without underpredicting the number of points with low η (an effect of the increased number of high β values in the uniform distribution). In contrast, the β = 0° models (bottom panels of Fig. 12) can be excluded. In the random roughness case, the minimum K-S distance never drops below 0.25 (pKS ~ 4 × 10-4), the problem being that the single β value leads to too narrow a distribution of the η values for a given rh, as can be seen in the bottom right panel of Fig. 12. The situation is of course even worse for the other three roughness (“fixed”) cases (pKS ~ 10-5 at best) since in this case the η distribution for fixed rh is infinitely narrow (following Fig. 5). We conclude that our data can exclude the situation where all spin axes are perpendicular to the line-of-sight, i.e. all objects are seen equator-on. Regarding the other orientation distributions, although the scenario favoring higher obliquities (all spin axes in the ecliptic plane) permits improved fits compared to the uniform orientation on a sphere, we cannot formally reject the latter. While some planetesimal formation scenarios suggest the spins may have originally been aligned perpendicularly to the ecliptic (Johansen & Lacerda 2010) there are possible evolutionary pathways to high obliquity spins (Lacerda 2011).
 |
Fig. 13 Left: Kolmogorov-Smirnov distance d between observed and modeled distribution of η grouping data by bins of heliocentric distance (rh < 25 AU, 25 < rh < 41 AU, and rh > 41 AU). In all models, a uniform distribution of the polar axes over the sphere and the “random roughness” case are assumed. Right: histograms showing the distribution of best fit Γ0, when accounting for uncertainties in the measured η. |
Coming back to the uniform orientation of the polar axes on the sphere and random roughness cases, and to follow-up on the results suggested in Sect. 4.1, we investigated cases in which the thermal inertia was allowed to vary with heliocentric distance. Specifically, the KS test was done separately on three bins in heliocentric distance, namely rh < 25 AU, 25 < rh < 41 AU, and rh > 41 AU. The first bin corresponds to the region of Centaurs and closest SDOs, and the other two split the remaining TNOs in two groups of approximately equal size (most objects in the last bin have rh < 53 AU). Results, shown in Fig. 13 (left panel), indicate that the minimum KS distance between observations and models is achieved for higher values of the thermal inertia at lower heliocentric distances. The same behavior is shown by the histograms of best fit solutions Γ0 when measurement errors are considered (right panel). These histograms indicate mean values for Γ0 of 5 ± 1 MKS at rh < 25 AU, 2.5 ± 0.5 MKS at 25 < rh < 41 AU, and 2 ± 0.5 MKS at rh > 41 AU. Although the error bars for the nearest two distance bins overlap, the histograms are strongly suggestive of an actual decrease of the thermal inertia with increasing heliocentric distance, consistent with inferences from Sect. 4.1.
Finally we briefly studied the dependence of Γ on geometric albedo. For this the
Monte-Carlo calculations and the Kolmogorov-Smirnov test were performed in the
(pV, η) space. A
difference with all previous simulations is that this time, synthetic objects had the same
rhand
pV as the real ones. Fixing the
rh to the observational values was needed because the
η(Γ) relationship is so strongly
rh-dependent. Thus, for each of the 85 observed objects we
created 100 clones that differed only in their β value, chosen randomly
from a uniform distribution on the sphere. As before, a rotation period of 8 h and the
random roughness case were used. Figure 14 compares
results for the previous solution having Γ = 2.5 MKS for all objects (see Fig. 11) with a simulation in which all objects having
geometric albedos higher than 20% are assigned a much lower thermal inertia, Γ = 0.5 MKS.
The visual improvement brought by the latter case is supported by the K-S distance, which
in (pV, η) space, decreases
from 0.17 for constant Γ to 0.12 for
pV-dependent Γ. A qualitatively similar
result is achieved in tests in which the thermal inertia is imposed to drop at large
diameters, e.g. Γ = 1 at D > 700 km. Thus, the
trend of a decreasing thermal inertia already suggested from the fixed orientation cases
(Fig. 7) is confirmed by this analysis. Note that the
drop in Γ required from the bright objects – from 2.5 to 0.5 MKS – is much more drastic
than the general decrease of Γ with heliocentric distance. Thus, in spite of the
correlation between pv and
rh in our sample, this indicates a specific behavior of the
high-albedo objects. Makemake
(pv = 0.77 ± 0.02,
 )
appears to be an exception to the picture, as it cannot be fit with Γ = 0.5 MKS.
)
appears to be an exception to the picture, as it cannot be fit with Γ = 0.5 MKS.
 |
Fig. 14 Beaming factor η as a function of geometric albedo
pV for the entire sample, compared
with Monte-Carlo simulations assuming a rotation period of 8 h, a random orientation
of the polar axes, uniform on the sphere, and a random distribution of surface
roughnesses. The synthetic objects have the same rh
values as in the observations. Cases with (i) a constant thermal inertia Γ = 2.5 MKS
(red points) and (ii) Γ = 2.5 MKS for objects with
pV < 20%
and Γ = 0.5 MKS for objects with
pV > 20%
(green points) are shown. The latter case allows an improved match of the
observations, except for Makemake
(pv = 0.77 ± 0.02,
|
5. Discussion
We have used two different approaches to determine the thermal inertia of TNO/Centaurs using their measured beaming factors. The first method consists of considering cases with fixed object orientation and roughness, – four orientations/roughness combinations have been included. The second method is a Monte-Carlo simulation of the population with a random distribution of orientations and surface roughnesses, in which the calculated beaming factors are compared to the observed values by means of the Kolmogorov-Smirnov test. Both approaches converge to suggest that TNO/Centaurs have low thermal inertia. The first method indicates a median value of Γ in the range 1.7–4.2 MKS, while the second yields a best-fit value Γ = 2.5 MKS for the most likely case where spin axes have a uniform distribution of orientation over the sphere (and only twice greater if all spin axes are in the equatorial plane). In addition, the two methods qualitatively agree on a decrease of thermal inertia with heliocentric distance. The “fixed orientation/roughness” model indicates a steep variation, with power exponent of about − 1.7. The statistical approach points to a more gentle decrease of Γ, by a nominal factor of 2.5 from 8–25 to 41–53 AU, which is roughly equivalent to a power exponent of ~− 1.
Thermal inertias: comparison with previous work.
5.1. Comparison with results from thermophysical models
For a limited number of objects of the combined Spitzer/ Herschel sample, more detailed thermophysical modeling (TPM) has been performed to determine thermal inertia and the sensitivity of the results to pole orientation, rotation period and surface roughness. Such models have been presented especially by Müller et al. (2010) and Lim et al. (2010) using an early version of the Herschel fluxes, and more extensively by Fornasier et al. (2013). In the case of Haumea, an estimate of its thermal inertia was obtained by Santos-Sanz et al. (2010) from preliminary TPM of its thermal lightcurve (Lellouch et al. 2010). Results from six prominent objects are gathered in Table 6 and compared to values from our work. For the latter, the indicated range encompasses the four (orientation, roughness) cases but does not account for the measurement error bars (note also that although for most of them, the rotational period is known, the results quoted here are those obtained from P = 8 h). The overall agreement between this and previous work is heartening and lends support to our simpler method. The higher value of Γ found on 2003 AZ84 by Müller et al. (2010) results from their higher η (1.31 ± 0.08), based on preliminary observations and reductions. For Quaoar, Fornasier et al. (2013) quote a thermal inertia in the 2–10 MKS range, but as can be seen for their Fig. 13, fitting solutions (reduced χ2 < 1) include thermal inertias up to 25 MKS, in agreement with the 4–25 MKS range estimated in this work.
5.2. Thermal inertia and dependence with heliocentric distance
We now turn to comparing our population results to expectations based on the properties
of ices. The thermal inertia is expressed as 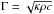 ,
where κ is the thermal conductivity, ρ is surface
density, and c in the specific heat. All of these quantities vary with
surface composition and temperature, but we here consider H2O-ice surfaces,
which are by far the most common in the Kuiper belt (e.g. de Bergh et al. 2013), and assume a constant ρ = 1000
kg m-3. The temperature dependence of c and
κ has been studied by a number of authors, and a recent compilation has
been presented by Castillo-Rogez et al. (2012). For
cristalline ice – which is the form of ice found on virtually all of the
H2O-ice objects – expressions given in Table C1 of that paper lead to an almost
constant thermal inertia over 150−30 K, increasing from 2100 to 2600 MKS. For amorphous
ice, litterature indicates conflicting results (by ~4 orders of magnitude!) on the thermal
conductivity. Using the expression given by Klinger
(1980) for κ in combination with that quoted for
c by Castillo-Rogez et al.
(2012) leads to a variation of the thermal inertia from 715 to 160 MKS over
150−30 K (i.e. a quasi-linear variation). Using instead the (assumed
temperature-independent) value of κ reported by Kouchi et al. (1992) (κ = 10-4
W m-1 K-1) would instead give Γ = 12−5 MKS over 150−30 K, but
according to Ross & Kargel (1998), the
Kouchi et al. (1992) measurements have been
refuted by Andersson & Suga (1994). Thus,
dismissing this latter case, the Γ value for compact H2O ice is typically two
(for amorphous ice) to three (cristalline) orders of magnitude higher than we determine on
TNO surfaces, and their expected variation with temperature is at most proportional to
T (i.e. to
,
where κ is the thermal conductivity, ρ is surface
density, and c in the specific heat. All of these quantities vary with
surface composition and temperature, but we here consider H2O-ice surfaces,
which are by far the most common in the Kuiper belt (e.g. de Bergh et al. 2013), and assume a constant ρ = 1000
kg m-3. The temperature dependence of c and
κ has been studied by a number of authors, and a recent compilation has
been presented by Castillo-Rogez et al. (2012). For
cristalline ice – which is the form of ice found on virtually all of the
H2O-ice objects – expressions given in Table C1 of that paper lead to an almost
constant thermal inertia over 150−30 K, increasing from 2100 to 2600 MKS. For amorphous
ice, litterature indicates conflicting results (by ~4 orders of magnitude!) on the thermal
conductivity. Using the expression given by Klinger
(1980) for κ in combination with that quoted for
c by Castillo-Rogez et al.
(2012) leads to a variation of the thermal inertia from 715 to 160 MKS over
150−30 K (i.e. a quasi-linear variation). Using instead the (assumed
temperature-independent) value of κ reported by Kouchi et al. (1992) (κ = 10-4
W m-1 K-1) would instead give Γ = 12−5 MKS over 150−30 K, but
according to Ross & Kargel (1998), the
Kouchi et al. (1992) measurements have been
refuted by Andersson & Suga (1994). Thus,
dismissing this latter case, the Γ value for compact H2O ice is typically two
(for amorphous ice) to three (cristalline) orders of magnitude higher than we determine on
TNO surfaces, and their expected variation with temperature is at most proportional to
T (i.e. to 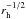 ) for
amorphous ice and nearly T– (i.e., rh–)
independent for the more likely case of cristalline ice.
) for
amorphous ice and nearly T– (i.e., rh–)
independent for the more likely case of cristalline ice.
Surface porosity and granularity strongly reduce the thermal conductivity, and are likely to be the cause of the measured low thermal inertias (e.g. Espinasse et al. 1991; Shoshany et al. 2002; Guilbert-Lepoutre et al. 2011). Based on a fractal porous model of cometary ice, Shoshany et al. (2002) propose an analytic expression for the effective thermal conductivity as a function of porosity p (defined as the fraction of the volume occupied by voids), in the form of a temperature-independent correction factor Φ = (1 − p/pc)4.1p+0.22, where pc = 0.7 the porosity at percolation threshold. This expression yields a steep decrease of Γ when p approaches pc, i.e. Φ = 0.01–0.001 for p = 0.58–0.64. This model (which reduces the surface density by only a factor of 2–3) therefore easily accounts for thermal inertias much lower than that of compact ices, without changing its temperature dependence.
However, the above expression ignores the effect of pore conductivity, which may become
dominant near the limiting porosity pc. Within empty pores,
heat is transferred through thermal radiation, inducing an effective conductivity
kpore = 4 rporeϵσT3.
In the most frequent case of cristalline ice, pore sizes of 25 μm (for
T = 150 K) – 3000 μm (for T = 30 K)
are required to produce a thermal inertia of 2.5 MKS. Comparing with the (vastly
uncertain) particle sizes invoked from modeling near-IR spectra, these numbers suggest
that the radiative contribution to conductivity may be important, especially for the high
temperature case. In this regime, κ scales as
T3, and combined with the temperature-dependence of the
specific heat (see Castillo-Rogez et al. 2012)
yields a Γ approximately proportional to T1.8 for cristalline
ice and to T2 for amorphous ice. Therefore, if the heat
transfer is dominated by radiative effects between particles, a
rh-1 dependence for Γ is expected. This behavior
is consistent with a factor-of-2.5 decrease of the thermal inertia from the Centaur (8–25
AU) region to the outer part of the Kuiper belt at 41–53 AU. It would still not be
sufficient to explain a steeper ~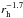 variation, as suggested from the “fixed orientation/roughness” approach.
variation, as suggested from the “fixed orientation/roughness” approach.
5.3. Comparison with other distant icy bodies and dependence with rotation period and albedo
While thermal inertia has been measured for a relatively large number of main-belt and near-Earth asteroids, revealing a convincing trend of a decrease with size (Delbo’ et al. 2007), measurements on icy bodies are more scarce. Spatially-resolved, spacecraft-borne observations of diurnal curves have provided values for Jupiter Galilean satellites and most of Saturn’s satellites (see Howett et al. 2010 and references therein). Inferred values, that refer to a skin depth associated with the diurnal timescale, are typically 50–70 MKS for Jupiter’s satellites and 5–20 MKS for Saturn’s (except in some specific regions of Mimas and Tethys, likely affected by electronic bombardement from Saturn’s magnetosphere, see Howett et al. 2011, 2012). This difference is probably indicative of a higher degree of compaction (enhanced density, reduced porosity) on the surface of Jupiter’s vs. Saturn’s icy moons. At greater distance from the Sun, the thermal inertia on Uranus moons is rather unconstrained, as their surface temperature, measured from the shape of the H2O ice bands in the near-IR (Grundy et al. 1999), is not determined with sufficient accuracy. No results are available for Neptune’s satellites (except for not directly comparable constraints on the seasonal thermal inertia of Triton’s surface based on seasonal pressure/polar cap models, e.g. Hansen & Paige 1992). In contrast, the thermal inertia of Pluto’s and Charon’s surfaces has been determined from the system thermal lightcurve, and found to be 25 ± 5 MKS for Pluto (relevant to the CH4/tholin areas), and most probably in the range 10–20 MKS for Charon (Lellouch et al. 2011).
The thermal inertia values determined in this study are, at comparable distances, lower
than both on the Saturn’s H2O-covered satellites and in the Pluto-Charon
system. We put aside the case of Pluto, whose surface texture may be affected by the
seasonal condensation/sublimation cycles of N2 and CH4, and where
thermal inertia may also be enhanced by gas conduction within surface pores (Lellouch et al. 2000). Nonetheless we argue that the
lower thermal inertia on the “average TNO” does not necessarily indicate different surface
properties compared to either Charon or Saturn’s moons. The skin depth, i.e. the depth
into the surface probed by the thermal measurements, can be expressed as
 .
The mean rotation period of TNOs is 8 h, vs. 1–5 days for most of the Saturn’s satellites
(except Phoebe and Iapetus) and 6.4 days for Charon. Hence, for equal density/thermal
properties, the diurnal wave probes shallower levels in the surface on fast rotating TNOs.
The order of magnitude of the thermal skin depth is 1 cm (e.g. 0.1 cm for the “average
TNO” and 2 cm for Charon, using the measured Γ). Hence, at least qualitatively, a thermal
inertia increasing with depth over the first cm into the surface would account for the
observed behavior. Such a behavior is actually observed on the regolith of the Moon (Keihm
1984) and Mercury (Mitchell & de Pater
1994), and has also been shown to occur on asteroid 21 Lutetia (Gulkis et al. 2012), with an increase of Γ from about 5
MKS to 30 MKS over a 5 cm depth. Another example of this situation is the fact that the
thermal inertia of Galilean satellites as determined from eclipse measurements, i.e. on a
~3 h timescale, is only 10–15 MKS, vs. 50–70 MKS inferred from diurnal curves (see Howett et al. 2010). Validating this scenario for TNOs
will require implementing models including a specific vertical profile of thermal
conductivity and density into the surface, coupled with a description of the absorbing
properties of the subsurface. For now, we caution on incorrect conclusions that might be
reached from oversimplified reasoning. For example, two objects with the same rotation
period but different measured values of thermal inertia must have different
surface/subsurface properties. Yet, based on a simple argument invoking different
ds (proportional to Γ) one might be tempted to conclude that
the two objects have the same surface/subsurfaces, but probed at different levels.
.
The mean rotation period of TNOs is 8 h, vs. 1–5 days for most of the Saturn’s satellites
(except Phoebe and Iapetus) and 6.4 days for Charon. Hence, for equal density/thermal
properties, the diurnal wave probes shallower levels in the surface on fast rotating TNOs.
The order of magnitude of the thermal skin depth is 1 cm (e.g. 0.1 cm for the “average
TNO” and 2 cm for Charon, using the measured Γ). Hence, at least qualitatively, a thermal
inertia increasing with depth over the first cm into the surface would account for the
observed behavior. Such a behavior is actually observed on the regolith of the Moon (Keihm
1984) and Mercury (Mitchell & de Pater
1994), and has also been shown to occur on asteroid 21 Lutetia (Gulkis et al. 2012), with an increase of Γ from about 5
MKS to 30 MKS over a 5 cm depth. Another example of this situation is the fact that the
thermal inertia of Galilean satellites as determined from eclipse measurements, i.e. on a
~3 h timescale, is only 10–15 MKS, vs. 50–70 MKS inferred from diurnal curves (see Howett et al. 2010). Validating this scenario for TNOs
will require implementing models including a specific vertical profile of thermal
conductivity and density into the surface, coupled with a description of the absorbing
properties of the subsurface. For now, we caution on incorrect conclusions that might be
reached from oversimplified reasoning. For example, two objects with the same rotation
period but different measured values of thermal inertia must have different
surface/subsurface properties. Yet, based on a simple argument invoking different
ds (proportional to Γ) one might be tempted to conclude that
the two objects have the same surface/subsurfaces, but probed at different levels.
Finally we find that objects with high albedos (>20%) tend to have lower beaming factors than the bulk of the population (Fig. 2), indicative of a lower thermal inertia (typically 0.5 MKS, see Figs. 7 and 14). A plausible explanation is that in addition to a specific composition (e.g. pure ice), a high albedo reflects a strongly scattering surface characterized by small grains. In a porous surface, the size of the pores is comparable to the size of the grains. Thus, in a regime where radiative conductivity is important and proportional to pore radius, one may expect that the thermal conductivity drops for high albedo objects. We note that given the positive correlation between diameter and geometric albedo in our sample, these low thermal inertias may also be viewed as being a characteristic of the large-sized objects (>700 km). The two aspects are probably related as large objects may be able to retain small grain regolith on their surfaces. This explanation is put forward by Delbo’ et al. (2007) to account for the trend of decreasing thermal inertia with increasing diameter in the asteroid belt. With a geometric albedo of 0.77 and a beaming factor of ~2.3, Makemake appears to be an outlier in this picture. In the “fixed orientation/roughness model” this η value indicates a thermal inertia of at least 5–7 MKS (obtained with β = 0°), and the Monte-Carlo simulations (Fig. 14) indicate that Γ = 0.5 MKS clearly provided a worse fit to this object than the mean 2.5 MKS value. The cause for this behavior is intriguing. Makemake is in the regime of volatile retention (Schaller & Brown 2007), and its 52 AU distance and the apparent presence of a dark and warm (~50 K) surface unit (Lim et al. 2010) make it an a priori plausible candidate for currently holding a CH4 or N2 atmosphere. Thus it might be tempting to attribute the anomalous thermal inertia to atmospheric conduction within surface pores. Based on Mendis & Brin (1977) equations for atmospheric-assisted thermal conductivity (proportional to atmospheric pressure), Lellouch et al. (2000) estimated that this process may contribute to the thermal inertia of Pluto, where the pressure is ~20 μbar. In the case of Makemake, however, stellar occultation observations provide an upper limit to any global atmosphere at the level of 4–12 nbar (Ortiz et al. 2012). This probably rules out the explanation, especially because the measured thermal inertia refers to Makemake’s bright terrains, where an atmosphere is not likely to exist. More detailed, multi-terrain, thermophysical models (as preliminary presented by Müller et al. 2011) are deferred to a future study.
6. Summary
In the framework of a NEATM model, Herschel/Spitzer thermal observations provide diameter, albedo and beaming factors for TNOs/Centaurs. We have used a set of published, updated or new values for 85 objects to characterize in a statistical sense the thermal properties of the population. For this, a thermophysical model including surface roughness and different assumptions on the objects rotation state was developed. We used (i) “fixed spin/roughness” models, in which all objects are assumed to have the same surface roughness, spin orientation and period and (ii) a Monte-Carlo approach whereby synthetic datasets of beaming factors are created from random distributions of spin orientation and surface roughness. The main conclusions can be summarized as follows:
-
Beaming factors η range from values <1 to ~2.5, but high η values are lacking at low heliocentric distances (e.g. there are no objects with η > 2 at rh < 30 AU). Beaming factors <1 are frequent and indicate that surface roughness effects are important.
-
The mean thermal inertia in the population is found to be Γ = (2.5 ± 0.5) J m-2 s−1/2 K-1
-
There is a strong suggestion that the thermal inertia decreases with heliocentric distance, from Γ0 of (5 ± 1) J m-2 s−1/2 K-1 at rh < 25 AU to (2.5 ± 0.5) J m-2 s−1/2 K-1 at 25 < rh < 41 AU, and (2 ± 0.5) J m-2 s−1/2 K-1 at rh = 41−53 AU.
-
These thermal inertias are 2–3 orders of magnitude lower than expected for compact ices and, for comparable distances, are generally lower than on Saturn’s satellites or in the Pluto/Charon system.
-
Objects with high albedos (>20%) have lower beaming factors than the rest of the population, i.e. unsually low thermal inertias. This possibly results from smaller grain size. An exception is Makemake.
-
While the measured thermal inertia cannot be directly associated to a specific surface composition, the ensemble of our results suggests strongly porous surfaces, in which the heat transfer is affected by radiative conductivity within pores and increases with depth in the subsurface.
Online material
Radiometric fit results.
Even for a 10° phase angle, larger than can occur in the Centaur/TNO region, phase effects reduce fluxes by less than 2% in the region of the Planck function peak (see Table 2 of Harris 1998).
HIPE is a joint development by the Herschel Science Ground Segment Consortium, consisting of ESA, the NASA Herschel Science Center, and the HIFI, PACS and SPIRE consortia members, see: http://herschel.esac.esa.int/DpHipeContributors.shtml
Acknowledgments
We acknowledge financial support by the French Program National de Planétologie and Centre National de la Recherche Scientifique (CNRS). M. Mommert acknowledges support through the DFG Special Priority Program 1385. E. Vilenius was supported by the German DLR project number 50 OR 1108. P. Santos-Sanz acknowledges financial support by Spanish grant AYA2008-06202-C03-01. The work of Cs. Kiss has been supported by the PECS-98073 grant of the European Space Agency and the Hungarian Space Office, the K-104607 grant of the Hungarian Research Fund (OTKA) and the Bolyai Research Fellowship of the Hungarian Academy of Sciences.
References
- Allen, D. A. 1970. Nature, 227, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Alvarez-Candal, A., Delsanti, A., et al. 2009, AJ, 137, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Andersson, O., & Suga, H. 1994, Phys. Rev. B, 50, 6583 [NASA ADS] [CrossRef] [Google Scholar]
- Bauer, J. M., Buratti, B. J., Simonelli, D. P., & Owen, W. M., Jr. 2004, ApJ, 610, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Bauer, J. M., Grav, T., Buratti, B. J., & Hicks, M. D. 2006, Icarus, 184, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Benecchi, S. D., Noll, K. S., Grundy, W. M., et al. 2009, Icarus, 200, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. E., & Schaller, E. L. 2007, Science, 316, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. E., & Trujillo, C. A. 2004, AJ, 127, 2413 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. E., Trujillo, C. A., & Rabinowitz, D. L. 2005, ApJ, 635, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. E., Schaller, E. L., Roe, H. G., Rabinowitz, D. L., & Trujillo, C. A. 2006, ApJ, 643, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. E., Burgasser, A. J., & Fraser, W. C. 2011, ApJ, 738, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Brucker, M. J., Grundy, W. M., Stansberry, J. A., et al. 2009, Icarus, 201, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Buratti, B., Soderlund, B., Bauer, J., et al. 2008, Icarus, 193, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Bus, S. J., Bowell, E., Harris, A. W., & Hewitt, A. V. 1989, Icarus, 77, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Castillo-Rogez, J. C., Johnson, T. V., Thomas, P. C., et al. 2012, Icarus, 219, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1987, Ellipsoidal figures of equilibrium (New York: Dover) [Google Scholar]
- Cruikshank, D. P., Stansberry, J. A., Emery, J. P., et al. 2005, ApJ, 624, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Davidsson, B. J. R., Gutierrez, P. J., Rickman, H. 2009, Icarus, 201, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, J. K., McBride, N., Ellison, S. L., Green, S. F., & Ballantyne, D. R. 1998, Icarus, 134, 213 [NASA ADS] [CrossRef] [Google Scholar]
- de Bergh, C., Schaller, E. L., Brown, M. E., et al. 2013, in The science of Solar System Ices ASSL, 356, 107 [Google Scholar]
- Delbo’, M., dell’Oro, A., Harris, A. W., Mottola, S., & Mueller, M. 2007, Icarus, 190, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Dotto, E., Perna, D., Barucci, M. A., et al. 2008, A&A, 490, 829 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duffard, R., Ortiz, J. L., Santos Sanz, P., et al. 2008, A&A, 479, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duffard, R., Ortiz, J. L., Thirouin, A., et al., 2009, A&A, 505, 1283 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duffard, R., Pinilla-Alonso, N., Santos-Sanz, P., et al. 2013, A&A, submitted [Google Scholar]
- Elliot, J. L., Kern, S. D., Clancy, K. B., et al. 2005, AJ, 129, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Elliot, J. L., Person, M. J., Zuluaga, C. A., et al. 2010, Nature, 465, 897 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Emery, J. P., Sprague, A. L., Witteborn, F. C, et al. 1998, Icarus, 136, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Engelbracht, C. W., Blaylock, M., Su, K. Y. L., et al. 2007, PASP, 119, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Espinasse, S., Klinger, J., Ritz, C., & Schmitt, B. 1991, Icarus, 92, 350 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farnham, T. L. 2001, Icarus, 152, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Fornasier, S., Lellouch, E., Müller, T., et al. 2013, A&A, 555, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaudi, B. S., Stanek, K. Z., Hartman, J. D., Holman, M. J., & McLeod, B. A. 2005, ApJ, 629, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Engelbracht, C. W., Fadda, D., et al. 2007, PASP, 119, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Grav, T., Mainzer, A. K., Bauer, J., et al. 2011, ApJ, 742, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2001 A&A, 518, L3 [Google Scholar]
- Grundy, W. M., Buie, M. W., Stansberry, J. A., Spencer, J. R., & Schmitt, B. 1999, Icarus, 142, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Grundy, W. M., Noll, K. S., & Stephens, D. C. 2005, Icarus, 176, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Grundy, W. M., Stansberry, J. A., Noll, K. S., et al. 2007, Icarus, 191, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Grundy, W. M., Noll, K. S., Virtanen, J., et al. 2008, Icarus, 197, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Grundy, W. M., Noll, K. S., Nimmo, F., et al. 2011, Icarus, 213, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Guilbert-Lepoutre, A., Lasue, J., Federico, C., et al. 2011, A&A, 529, A71 [Google Scholar]
- Gulkis, S., Keihm, S., Kamp, L., et al. 2012, Planet. Space Sci., 66, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, C., & Paige, D. A. 1992, Icarus, 99, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. W. 1984, Icarus, 59, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W. 1998, Icarus, 131, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, A. W. 2006, Proc. IAU Symp. 229 (Cambridge, UK: Cambridge Univ. Press), 449 [Google Scholar]
- Hoffmann, M., Fink, U., Grundy, W. M., & Hicks, M. 1992, Liège International Astrophysical Colloquia (Liège: Université de Liège), 30, 203 [NASA ADS] [Google Scholar]
- Howett, C. J. A., Spencer, J. R., Pearl, J., et al. 2010, Icarus, 206, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Howett, C. J. A., Spencer, J. R., Schenk, P., et al. 2011, Icarus, 216, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Howett, C. J. A., Spencer, J. R., Hurford, T., Verbiscer, A, & Segura, M. 2012, Icarus, 221, 1084 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D. C. 2009, AJ, 137, 4296 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., & Lacerda, P. 2010, MNRAS, 404, 475 [NASA ADS] [Google Scholar]
- Keihm, S. J. 1984, Icarus, 60, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Kern, S. D., McCarthy, D. W., Buie, M. W., et al. 2000, ApJ, 542, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Kiss, Cs., Szabó, Gy., Horner, J., et al. 2013a, A&A, 555, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kiss, Cs., Müller, T., Vilenius, E., et al. 2013b, Exp. Astron., submitted [Google Scholar]
- Klinger, J., 1980, Science, 209, 271 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kouchi, A., Greenberg, J. M., Yamamoto, T., & Mukai, T. 1992, ApJ, 388, L73 [Google Scholar]
- Lacerda, P. 2011, AJ, 142, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Lacerda, P., & Luu, J. 2003, Icarus, 161, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Lacerda, P., & Luu, J. 2006, AJ, 131, 2314 [NASA ADS] [CrossRef] [Google Scholar]
- Lacerda, P., & Jewitt, D. C. 2007, AJ, 133, 1393 [NASA ADS] [CrossRef] [Google Scholar]
- Lagerros, J. S. V. 1996, A&A, 310, 1011 [NASA ADS] [Google Scholar]
- Lagerros, J. S. V. 1998, A&A, 332, 1123 [NASA ADS] [Google Scholar]
- Lebofsky, L. A., & Spencer, J. R. 1989, in Asteroids II, 128 [Google Scholar]
- Lellouch, E., Laureijs, R., Schmitt, B., et al. 2000, Icarus, 147, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Lellouch, E., Kiss, C., Santos-Sanz, P., et al. 2010, A&A, 518, L147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lellouch, E., Stansberry, J., Emery, J., Grundy, W., & Cruikshank, D. P. 2011, Icarus, 214, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Lim, T. L., Stansberry, J., Müller, T. G., et al. 2010, A&A, 518, L148 [Google Scholar]
- Mainzer, A., Grav, T., Masiero, J., et al. 2011a, ApJ, 743, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Mainzer, A., Grav, T., Masiero, J., et al. 2011b, ApJ, 736, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Maris, M., Carraro, G., & Parisi, M. G. 2007, A&A, 472, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masiero, J. R., Mainzer, A. K., Grav, T., et al. 2011, ApJ, 741, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Mendis, D. A., & Brin, G. D. 1977, The Moon, 17, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, C., Verbiscer, A. J., Chanover, N. J., Holtzman, J. A., & Helfenstein, P. 2011, Icarus, 212, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Mitchell, D. L., & de Pater, I. 1994, Icarus, 110, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Mommert, M., Harris, A.W., Kiss, Cs., et al. 2012, A&A, 541, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mueller, M., Delbo’, M., Hora, J. L., et al. 2011, AJ, 141, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, T. G., Lellouch, E., Böhnhardt, H., et al. 2009, Earth Moon Planets, 105, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, T. G., Lellouch, E., Stansberry, J., et al. 2010, A&A, 518, L146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, T. G., Lellouch, E., Kiss, C., et al. 2011, EPSC-DPS Joint Meeting, 1416 [Google Scholar]
- Ortiz, J. L., Gutiérrez, P. J., Casanova, V., & Sota, A. 2003, A&A, 407, 1149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ortiz, J. L., Gutiérrez, P. J., Santos-Sanz, P., Casanova, V., & Sota, A. 2006, A&A, 447, 1131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ortiz, J. L., Morales, N., Duffard, R., et al. 2010, IAU Circ., 9184, 1 [NASA ADS] [Google Scholar]
- Ortiz, J.-L., Sicardy, B., Braga-Ribas, F., et al. 2012, Nature, 491, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Osip, D. J., Kern, S. D., & Elliot, J. L. 2003, Earth Moon Planets, 92, 409 [Google Scholar]
- Pàl, A., Kiss, Cs., Müller, T. G., et al. 2012, A&A, 541, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perna, D., Barucci, M. A., Fornasier, S., et al. 2010, A&A, 510, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, A., Teukchsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes (Cambridge: University Press) [Google Scholar]
- Rabinowitz, D. L., Barkume, K., Brown, M. E., et al. 2006, ApJ, 629, 1238 [NASA ADS] [CrossRef] [Google Scholar]
- Rabinowitz, D. L., Schaefer, B. E., & Tourtellotte, S. W. 2007, AJ, 133, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., Young, E. T., Engelbracht, C. W., et al. 2004, ApJS, 154, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Roe, H. G., Pike, R. E., & Brown, M. E. 2008, Icarus, 198, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Romanishin, W., & Tegler, S. C. 1999, Nature, 398, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Romon, J., de Bergh, C., Barucci, M. A., et al. 2001, A&A, 376, 310 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ross, R. G., & Kargel, J. S. 1998, in Solar System Ices (Kluwer Academic), ASSL, 227, 33 [NASA ADS] [Google Scholar]
- Rousselot, P., Petit, J.-M., Poulet, F., & Sergeev, A. 2005a, Icarus, 176, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Rousselot, P., Levasseur-Regourd, A.C., Muinonen, K., & Petit, J.-M. 2005b, Earth Moon Planets, 97, 353 [Google Scholar]
- Rozitis, B., & Green, S. F. 2011, MNRAS, 415, 2042 [NASA ADS] [CrossRef] [Google Scholar]
- Russell, H. N. 1916, ApJ, 43, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Santos-Sanz, P., Lellouch, E., Fornasier, S., et al. 2010, BAAS, 42, 1013 [NASA ADS] [Google Scholar]
- Santos-Sanz, P., Lellouch, E., Fornasier, S., et al. 2012, A&A, 541, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaller, E. L., & Brown, M. E. 2007, ApJ, 659, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Sheppard, S. S. 2007, AJ, 134, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Sheppard, S. S. 2010, AJ, 139, 1394 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sheppard, S. S., & Jewitt, D. C. 2002, AJ, 124, 1757 [NASA ADS] [CrossRef] [Google Scholar]
- Sheppard, S. S., & Jewitt, D. C. 2003, Earth Moon Planets, 92, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Shoshany, Y., Prialnik, D., & Podolak, M. 2002, Icarus, 157, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Sicardy, B., Ortiz, J. L., Assafin, M., et al. 2011, Nature, 478, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Spearman, C. 1904, Am. J. Psychol., 57, 72 [CrossRef] [Google Scholar]
- Spencer, J. R. 1990, Icarus, 83, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Spencer, J. R., Lebofsky, A. L., & Sykes, M. V. 1989, Icarus, 78, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Stansberry, J. A., Grundy, W. M., Margot, J. L., et al. 2006, ApJ, 643, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Stansberry, J. A., Gordon, K. D., Bhattacharya, B., et al. 2007, PASP, 119, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Stansberry, J., Grundy, W., Brown, M., et al. 2008, in The Solar System Beyond Neptune, eds. M. A. Barucci, et al. (Tucson: Univ. of Arizona Press), 161 [Google Scholar]
- Tedesco, E. F., Noah, P. V., Noah, M., & Price, S. D. 2002, AJ, 123, 1056 [Google Scholar]
- Tegler, S. C., Romanishin, W., Consolmagno, G. J., et al. 2005, Icarus, 175, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Thirouin, A., Ortiz, J. L., Duffard, R., et al. 2010, A&A, 522, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trilling, D. E.,Hora, J. L.,Mueller, M., et al. 2012, in Asteroids, Comets, Meteors 2012, Proc. Conf. LPI Contribution, 1667, 6485 [Google Scholar]
- Trujillo, C. A., & Brown, M. E. 2002, ApJ, 566, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Usui, F., Kasuga, T., Hasegawa, S., et al. 2013, ApJ, 752, 56 [Google Scholar]
- Vilenius, E., Kiss, Cs., Mommert, M., et al. 2012, A&A, 541, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vilenius, E., Kiss, Cs., Müller, T., et al. 2013, A&A, submitted [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [Google Scholar]
All Tables
Herschel color-corrected fluxes at 70, 100 and 160 μm and H-magnitudes for the “new” objects presented in this work.
Spitzer color-corrected fluxes at 23.68 and 71.42 μm for the “new” objects presented in this work.
All Figures
 |
Fig. 1 Observed beaming factor η as a function of heliocentric distance rh for the entire sample. With two exceptions (objects observed by Herschel and WISE, see Table 3), blue (resp. green, red) symbols refer to objects with both Herschel and Spitzer (resp. only Herschel, only Spitzer) fluxes. |
| In the text | |
 |
Fig. 2 Beaming factor η as a function of left: geometric albedo and right: diameter. Labels M, H, TX, E, Q refer to Makemake, Haumea, 2002 TX300, Eris and Quaoar, respectively. |
| In the text | |
 |
Fig. 3 Beaming factor η as a function of left: lightcurve period (44 objects) middle: lightcurve amplitude (same 44 objects) and right: density (14 objects). Lightcurve information is taken from Table 5 and density values from literature (see text). |
| In the text | |
 |
Fig. 4 Model beaming factor η as a function of thermal parameter Θ for three values of the subsolar/subearth latitude β and five values of the instantaneous subsolar temperature T0. |
| In the text | |
 |
Fig. 5 Model beaming factor η as a function of thermal parameter Θ for four values of the subsolar/subearth latitude β and three surface roughness levels: Solid line: no roughness. Dotted line: moderate roughness. Dashed line: high roughness. The instantaneous subsolar temperature T0 is 50 K. |
| In the text | |
 |
Fig. 6 Individual thermal inertia vs. heliocentric distance, as inferred from the measured η for two values of the subsolar latitude (β = 32.7° and 0°) and the two surface roughness cases (“high” and “moderate”). |
| In the text | |
 |
Fig. 7 Individual thermal inertia vs. geometric albedo, as inferred from the measured η for a subsolar latitude β = 32.7° and the two surface roughness cases. Labels H, TX and E refer to Haumea, 2002 TX300, and Eris, respectively. |
| In the text | |
 |
Fig. 8 Individual thermal inertia for 44 objects as a function of rotational period, as inferred from the measured η, for two values of the subsolar latitude (β = 32.7° and 0°) and two cases of surface roughness (“high” and “moderate”). |
| In the text | |
 |
Fig. 9 Individual thermal inertia for objects having rotational lightcurve amplitudes Δm> 0.10, using subsolar latitudes estimated from the assumption of Jacobi equilibrium figures, using two values of the density (1000 and 3000 kg m-3), and two cases of surface roughness (“high” and “moderate”). |
| In the text | |
 |
Fig. 10 Left: Kolmogorov-Smirnov distance d between the observed distribution of η and those calculated as a function of thermal inertia for the four roughness scenarios. In all cases, a uniform distribution of the polar axes over the sphere is assumed. The minimum of d indicates the best fit thermal inertia Γ0. Right: histograms showing the distribution of best fit Γ0, when accounting for uncertainties in the η measurements (see text). |
| In the text | |
 |
Fig. 11 Beaming factor η as a function of heliocentric distance rh for the entire sample, compared with Monte-Carlo simulations assuming a rotation period of 8 h, a geometric albedo of 0.1, a uniform distribution of the polar axes on the sphere, and a random distribution of surface roughnesses. Thermal inertia Γ = 1, 2.5 and 8 MKS cases are shown here. Although Γ = 8 MKS may seem needed to account for the three points with η = 1.5–1.8 at 13–18 AU, this case underpredicts the number of low η values at rh> 25 AU, and Γ = 2.5 MKS provides the overall best fit. |
| In the text | |
 |
Fig. 12 Left: Kolmogorov-Smirnov distance d and Monte-Carlo simulations for the two assumed alternative distributions of polar axes. Top: uniform distribution of βs between ±90° (i.e. spin axes in ecliptic plane). Bottom: all objects with β = 0° (i.e. spin axes perpendicular ecliptic plane). In each case, the K-S distance to the data is plotted (left panels) as a function of Γ for the four roughness cases. Right panels show Monte-Carlo simulations for the random roughness cases. |
| In the text | |
 |
Fig. 13 Left: Kolmogorov-Smirnov distance d between observed and modeled distribution of η grouping data by bins of heliocentric distance (rh < 25 AU, 25 < rh < 41 AU, and rh > 41 AU). In all models, a uniform distribution of the polar axes over the sphere and the “random roughness” case are assumed. Right: histograms showing the distribution of best fit Γ0, when accounting for uncertainties in the measured η. |
| In the text | |
 |
Fig. 14 Beaming factor η as a function of geometric albedo
pV for the entire sample, compared
with Monte-Carlo simulations assuming a rotation period of 8 h, a random orientation
of the polar axes, uniform on the sphere, and a random distribution of surface
roughnesses. The synthetic objects have the same rh
values as in the observations. Cases with (i) a constant thermal inertia Γ = 2.5 MKS
(red points) and (ii) Γ = 2.5 MKS for objects with
pV < 20%
and Γ = 0.5 MKS for objects with
pV > 20%
(green points) are shown. The latter case allows an improved match of the
observations, except for Makemake
(pv = 0.77 ± 0.02,
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


