| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 6 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201322039 | |
| Published online | 12 August 2013 | |
Astrometric results of observations of mutual occultations and eclipses of the Uranian satellites in 2007
1 Institut de Mécanique Céleste et de
Calcul des Éphémérides, Observatoire de Paris, UPMC, USTL, UMR 8028 du CNRS,
77 avenue
Denfert-Rochereau, 75014
Paris,
France
e-mail: arlot@imcce.fr
2 Lomonosov Moscow State University,
Sternberg Astronomical Institute, 13 Universitetskij prospect,
119992
Moscow,
Russia
e-mail: emelia@sai.msu.ru
3 TUBITAK National Observatory, Akdeniz
Universitesi Yerleskesi, 07058
Antalya,
Turkey
4 Ager, Lleida, Spain
5 Indian Institute of Astrophysics,
Bangalore,
India
6 Institut de Ciències de l’Espai
(CSIC-IEEC), Campus UAB, Facultat de Ciències, Torre C5 parell 2n pis, 08193 Bellaterra,
Catalunya,
Spain
7 Marseille, France
8 ESO, Chile
9 Covington,
Seattle,
WA,
USA
10 L’Ampolla, Tarragona, Spain, E. Forné died in September
2011
11 Apache Point Observatory,
2001 Apache Point Road, PO Box
59, Sunspot,
NM,
USA
12 Indian Hill Observatory,
Huntsburg,
Ohio,
USA
13 LESIA-Observatoire de Paris, CNRS,
Université Pierre et Marie Curie, Université Paris-Diderot,
11 rue Marcelin
Berthelot, 92195
Meudon Cedex,
France
14 Laboratoire Lagrange, UMR 7293,
Université de Nice Sophia-Antipolis, CNRS, Observatoire de la Côte
d’ Azur,
France
15 Observatório Nacional/MCTI,
R. General José Cristino 77, CEP
20.921-200
Rio de Janeiro, RJ, Brazil
e-mail: camargo@on.br;ribas@on.br;rvm@on.br
16 Universidad de Monterrey, Departamento de Fisica y
Matematicas, Av. I. Morones Prieto 4500 Pte., San Pedro Garza Garcia, N.L., CP 66238,
Mexico
17 Planétarium de Saint-Etienne, 28
rue Ponchardier, 42100
Saint-Étienne,
France
18 Observatório do Valongo/UFRJ, Ladeira Pedro Antonio 43, CEP
20.080-090 Rio de Janeiro-RJ, Brazil .
e-mail: massaf@astro.ufrj.br
19 Department of Astronomy and
Geodesy, Kazan Federal University, Kremlevskaya Str., 18, Kazan, 420008,
Russia
Received:
7
June
2013
Accepted:
27
June
2013
Context. The photometry of mutual occultations and eclipses of natural planetary satellites can be used to infer very accurate astrometric data. This can be achieved by processing the light curves of the satellites observed during international campaigns of photometric observations of these mutual events.
Aims. This work focuses on processing the complete database of photometric observations of the mutual occultations and eclipses of the Uranian satellites made during the international campaign in 2007. The final goal is to derive new accurate astrometric data.
Methods. We used an accurate photometric model of mutual events that explicitly depends on parameters that these accurate observations should be sensitive to, including the albedos of the satellites. Our original method is applied to derive astrometric data in relative positions from photometric observations of mutual occultations and eclipses of the Uranian satellites.
Results. We process the 41 light-curves obtained during the international campaign of photometric observations of the Uranian satellites in 2007. The root-mean-square (rms) of the residuals “observations minus calculations” (O–C) with respect to theory for the best 34 observations are equal to 10.3 and 17.7 mas in right ascension and declination, respectively. For five observations only the position angle was derived. Topocentric or heliocentric angular differences for satellites pairs were obtained from 25 central instant offsets between observation and theory during the time period from May 4, 2007 to January 4, 2008.
Conclusions. The rms of the residuals is from 10 to 20 mas that corresponds in situ to 10 to 20 km. These mutual event observations appear to be the most accurate astrometric ground-based observations of the major Uranian satellites to-date and should be used for dynamical purposes.
Key words: ephemerides / planets and satellites: general
© ESO, 2013
1. Introduction
Photometric observations of mutual occultations and eclipses of natural satellites of planets offer an efficient source of new astrometric data. The accuracy of the observation of phenomena depends mainly on our knowledge of the size of the objects and their shadows. This accuracy is provided in kilometers and does not depend on the distance between the objects and the Earth, which means that the farther away the object is, the better the angle accuracy is. This especially true for the Uranian satellites.
2. The mutual events
The Earth and the Sun cross the equatorial plane of Uranus every 42 years (at the equinox). The Uranocentric declinations of the Earth and the Sun then become zero and, since the orbital plane of the satellites is close to the equatorial plane of Uranus, the satellites occult and eclipse each other.
Fortunately, this equinox occurred in 2007. The period was particularly favourable because the equatorial plane crossing occurred near the opposition of Uranus and the Sun.
Arlot et al. (2006) compiled predictions of all 2006–2009 events using the LA07 ephemerides based on recent observations. About 280 possible mutual events were computed but only 170 were easily observable. These observations are difficult because of the proximity of the satellites to Uranus. Special infrared filters were recommended to increase the feasibility of the observations. However, our goal was to observe as many events as possible and recommendations were given (Arlot & Sicardy 2008). At least two independent observations of each event were desirable to eliminate any biases in the observation.
Since no thick atmosphere surrounds any of the Uranian satellites, the photometric observations of these phenomena are extremely accurate for astrometric purposes. Moreover, the large distance to the Earth will make the accuracy in angle much better than that obtained from direct imaging astrometric observations. This fact allows us to provide data to improve the theoretical models of the orbital motions and the dynamics of the Uranian satellites.
3. The PHEURA07 campaign
We coordinated an international PHEURA07 campaign to acquire a significant number of events. These events occur in a short period of time, so numerous observers located in several sites were necessary to help avoid meteorological problems and to observe different events from different longitudes. However, observations were more difficult than with the Galilean satellites which present similar events: the proximity of Uranus to its satellites prevents one from observing events occurring close to the planet. Infrared techniques allowing such observations will require large telescopes. Special image treatment was also an alternative to overcome the planetary glare (Assafin et al. 2009). Note that the negative value of the declination of Uranus (around –8 degrees) favoured the Southern hemisphere observers. We added to our dataset for analysis the observations made at Faulkes North, Faulkes South, SALT and Athens and published by Christou et al. (2009) and Hidas et al. (2008).
3.1. Detectors
When observing mutual events, only relative photometry can be completed. Since the elevation of Uranus above the horizon may be small, the air mass is often too high and absolute photometry is then impossible. Telescopes were equipped with the receptors listed in Table 1.
Receptors used for the observations.
3.2. Sites of observation
Coordinated by the Institut de Mécanique Céleste et de Calcul des Éphémérides (IMCCE), this campaign involved the different locations given in Table 2. This table gives the names, longitudes, latitudes, and elevations of the observational sites and the telescopes used (T means reflector, followed by the aperture in cm).
Sites of observation for the PHE-URA07 campaign.
4. Light-curve reduction procedure
Light-curves were reduced from photometric measurements performed with CCD cameras. For observations completed with CCD cameras in analogic video mode, the signal was digitized with digitizing boards. For observations recorded with video cameras special software was used for extracting the separate video frames before photometric analysis. The light-curves were obtained most of the time by aperture photometry. Two-dimensional measurements generally allow us to calibrate the signal from a particular satellite to that from a nearby satellite and sometimes to acquire data under difficult conditions such as twilight or light clouds (Arlot & Stavinschi 2007). We will provide in the next sections two different results: first, the photometric results as the magnitude drops and the timing of the minimum of light (which is not the minimum of distance because of the phase effect), and second, the astrometric relative positions of the satellites deduced from the light-curves.
5. The photometric data
The determination of both the time of minimum light and the extent of the magnitude drop were based on a fit to the light-curve of a sample polynomial. The errors in these determinations are also given. The error in the timing of the minimum is determined as follows. We calculate the noise in magnitudes and transform it into a time error using the highest value of the magnitude decrease speed during the event. The largest errors occur for the faint noisy events and the smallest for the most rapid. The errors remain comparable only if the integration times are the same. Table 3 provides the filters used for each observation. Note that filter L (or Large filter) often correspond often to no filter at all. In this case, the light is filtered by the sensitivity profile of the target CCD. The satellites involved in the events are indicated in the last column1. The next section will provide the astrometric data extracted from the light-curves.
Filters and observed satellites.
6. General assumptions about extracting astrometric data from the photometry of mutual events
We used our original method to derive positional and astrometric data from the measurements of satellite fluxes during their mutual occultations and eclipses. The main idea of the method consists in modelling the deviation of the observed relative satellite motion from the theoretical motion provided by the relevant ephemeris, rather than analysing the apparent relative motion of one satellite with respect to the other.
The measured flux E during an event at a given time t may be expressed by 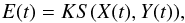 (1)where X(t) and Y(t) are the projections of the differences of planetocentric Cartesian coordinates of the two satellites onto the tangent plane of the event. The function S(x,y) describes a model of the phenomenon, with S(x,y) = 1 off event. The parameter K is a scale factor for the light drop during the event and is equal to the total flux outside the event.
(1)where X(t) and Y(t) are the projections of the differences of planetocentric Cartesian coordinates of the two satellites onto the tangent plane of the event. The function S(x,y) describes a model of the phenomenon, with S(x,y) = 1 off event. The parameter K is a scale factor for the light drop during the event and is equal to the total flux outside the event.
Given appropriate theories of the motion of planets and satellites, one can compute the theoretical values of functions X(t) and Y(t), i.e., Xth(t) and Yth(t) for the time ti(i = 1,2,....m) of each photometric measurement. Here m is the number of photometric measurements during a single event. The real values of X(ti) and Y(ti) differ from Xth(t) and Yth(t) by corrections Dx and Dy. Our method consists of solving the conditional equations 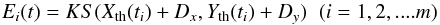 (2)for parameters Dx, Dy, and K. Here Ei is the photometric flux recorded at the time ti. We linearize conditional equations with respect to parameters Dx and Dy and then solve them using the least-squares method.
(2)for parameters Dx, Dy, and K. Here Ei is the photometric flux recorded at the time ti. We linearize conditional equations with respect to parameters Dx and Dy and then solve them using the least-squares method.
The function S(x,y) is calculated as an integral of the flux from each point of the satellite over the hemisphere facing the Earth. For each point we consider the wavelength-dependent reflective properties of the satellites, various laws of light scattering by a rough surface, variation of reflective properties over the satellite surface, and wavelength-dependent solar limb darkening. We consider also a wavelength-dependent sensitivity of the detector. See (Emel’yanov 2000, 2003; Emel’yanov & Gilbert 2006) for a description of the method, which we have already used in our works (Emel’yanov 2009).
7. Adopted photometric model of the satellites
The most comprehensive available data on the photometric properties of the major satellites of Uranus are published in Karkoschka (2001). In this paper, the results of the direct photometric measurements of the satellites for different phase angles and for the different wavelengths, as well as the parameters of the Hapke phase function are given. This allowed us to test the application of two light scattering laws, the Lommel-Seeliger and the Hapke laws. As we have not found a reliable dataset for the variation of reflective properties over the satellite surface, we assumed a uniform surface for the satellites.
In the application of the Lommel-Seeliger law we searched for a dependence of satellite albedo on the phase angle and light wavelength. According to Karkoschka (2001) this dependence can be: ![\begin{equation} \label{AlbedoA} A=A_0 [1+\gamma(\lambda-0.55)] \times 10^{-0.4(\beta\alpha+0.5 \alpha/(\alpha_0+\alpha))}, \end{equation}](/articles/aa/full_html/2013/09/aa22039-13/aa22039-13-eq34.png) (3)where α is the phase angle measured in degrees, λ the light wavelength measured in μm, and A0,γ,β and α0 the photometric parameters of the satellite. We can identify A with the observed reflectivity that includes the dependence of albedo for the phase angle and also the phase effect considered by the Lommel-Seeliger law. Values of the photometric parameters are given in Karkoschka (2001). Nevertheless, we preferred to make the independent fit of the parameters to the observed reflectivities given in Table 5 by Karkoschka (2001).
(3)where α is the phase angle measured in degrees, λ the light wavelength measured in μm, and A0,γ,β and α0 the photometric parameters of the satellite. We can identify A with the observed reflectivity that includes the dependence of albedo for the phase angle and also the phase effect considered by the Lommel-Seeliger law. Values of the photometric parameters are given in Karkoschka (2001). Nevertheless, we preferred to make the independent fit of the parameters to the observed reflectivities given in Table 5 by Karkoschka (2001).
In 2007 the phase angle for Uranus was less than only 0.21 degree from September 6, 2007 to September 13, 2007. There is no observation of the mutual events on this time interval. Therefore, the observed reflectivities at the phase angles 0.21, 1.10 and 2.82 degrees could only be taken from the fit of the parameters. The results of our fit are given in Table 4. For the satellite U1 Ariel the fit of all parameters was not successful and we took the parameters A0,β and α0 from Karkoschka (2001), but refined γ.
Using the obtained values of the parameters and the function in Eq. (3) we could apply the Lommel-Seeliger law to deduce astrometric results from the photometric observations of the mutual events of the satellites. However, it is necessary to explain which of the two light scattering laws, the Lommel-Seeliger or the Hapke laws, is better to use.
From all the available observations, we selected the most precise photometric observations that were made in the observatory Apache-Point on August 15, 2007. The occultation of Titania by Umbriel was observed there. From these photometric observations, astrometric data are derived via an advanced method incorporating light scattering laws in two cases, the Lommel-Seeliger and the Hapke laws. In the case of Hapke law the relevant parameters were taken from Karkoschka (2001), but the albedos of the satellites were reduced to the wavelength of filter I used in the Apache-Point observatory. The minimum distance rmin between the centres of the apparent discs of the satellites during the event was used as the astrometric result for the comparison.
To estimate the quality of the agreement of the observations with the model, the root-mean-square (rms) value σS of the deviations of the normalized measured flux S from the model light-curve was calculated for the measurement instants inside the phenomenon. In the case of mutual occultation the astrometric result depends directly on the relation of the albedo of the two satellites. In the two cases of the light scattering law, these relations were calculated and they proved to differ by a coefficient of 0.88. Therefore the second comparison was made after correction of the albedo for this coefficient. The results of the comparison are given in Table 5.
Results of the fit of the photometric parameters to the observed reflectivities.
Agreement of observations with the model (σS) and the resulting minimum of the apparent distance between the satellites (rmin) for different light scattering laws adopted.
It is evident from the table that the astrometric result strongly depends on the albedo of the satellites and considerably less on the accepted light scattering law. With the parameters given by Karkoschka (2001), the Hapke law does not give a good agreement for the photometric measurements with the model. As emphasized in Karkoschka (2001), “different combinations of parameters of the five-parameter model can yield almost identical phase curves, making a fit very sensitive to observational errors”. Therefore, we cannot consider the Hapke parameters to be reliable. We decided to use the Lommel-Seeliger law with the function in Eq. (3) for the albedo and the parameters from Table 4. The observed rotational features given in Karkoschka (2001) for the albedo dependence on the rotation of the satellite are not sufficiently precise to be used in our application.
8. Astrometric parameters
Along with Cartesian coordinates X and Y one can also consider angular coordinates X′′ and Y′′ defined by the equations 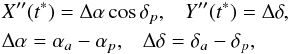 where αa and δa are the right ascension and declination of the occulting or eclipsing satellite, and αp and δp the corresponding coordinates of the occulted or eclipsed satellite. In the case of mutual eclipses these coordinates are heliocentric.
where αa and δa are the right ascension and declination of the occulting or eclipsing satellite, and αp and δp the corresponding coordinates of the occulted or eclipsed satellite. In the case of mutual eclipses these coordinates are heliocentric.
Astrometric results
(X′′(t∗),
Y′′(t∗): results;
σx,
σy: random errors; 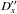 ,
, 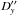 : O–C).
: O–C).
Precise relationships between X′′,Y′′ and X,Y are found in (Emel’yanov 1999). Given the topocentric or heliocentric distances R of the satellites one can compute X′′,Y′′ from X,Y using approximate relations 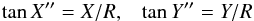 which are accurate for the considered observations to 0.00001 arcseconds. In a similar way, we designate by
which are accurate for the considered observations to 0.00001 arcseconds. In a similar way, we designate by 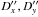 the angular values corresponding to the corrections Dx,Dy.
the angular values corresponding to the corrections Dx,Dy.
After the solution of Eq. (2), the astrometric result of the observation is derived as the corrected relative position of satellites 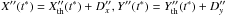 together with the associated time instant t∗ inside the time interval of the event. Although this is not rigorously true, we assume that t∗ is the time instant when
together with the associated time instant t∗ inside the time interval of the event. Although this is not rigorously true, we assume that t∗ is the time instant when 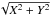 takes its minimum value, i.e. t∗ is the time of the closest apparent approach of the satellites.
takes its minimum value, i.e. t∗ is the time of the closest apparent approach of the satellites.
The errors σx and σy of the parameters 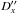 and
and 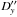 estimated via the least-squares method can be interpreted as internal errors resulting from the astrometric results following from the random errors of the photometry.
estimated via the least-squares method can be interpreted as internal errors resulting from the astrometric results following from the random errors of the photometry.
The derived values 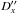 and
and 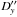 are the residuals “observations-calculations” (O–C) with respect to the applied theory of satellite motion. In our applications we used the theory by Lainey (2008). This model was made with the numerical integration over a long series of observations.
are the residuals “observations-calculations” (O–C) with respect to the applied theory of satellite motion. In our applications we used the theory by Lainey (2008). This model was made with the numerical integration over a long series of observations.
9. Derived astrometric results
We subdivided our final astrometric results into two sections. The first includes the results obtained from the observations where two coordinates X′′(t∗) and Y′′(t∗) could be successfully determined. The second section contains the results obtained in the cases where only the position angle could be determined.
In the first section, every final result of the observation of a single mutual phenomenon at a given observatory consists of the following fields: date, the type of the phenomenon (eclipse or occultation) including the satellite numbers, observatory code, the time instant t∗ in the UTC scale, X′′(t∗), Y′′(t∗), σx, σy, 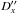 and
and 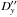 . The type of phenomenon is coded as naonp or naenp for a mutual occultation or eclipse, respectively. Here, na is the number of the occulting or eclipsing satellite and np is the number of the occulted or eclipsed satellite. We give the results in the form of the angular separation s (in arcseconds) and position angle A (in degrees) corresponding to X′′(t∗), Y′′(t∗). The minimum level Smin of the normalized flux is also given. We assign flag Q to each observation in order to indicate the quality and the reliability of the result. Flag Q may be one of the following values: 0 for satisfactorily determined coordinates or 1 for the results obtained from poor photometric data.
. The type of phenomenon is coded as naonp or naenp for a mutual occultation or eclipse, respectively. Here, na is the number of the occulting or eclipsing satellite and np is the number of the occulted or eclipsed satellite. We give the results in the form of the angular separation s (in arcseconds) and position angle A (in degrees) corresponding to X′′(t∗), Y′′(t∗). The minimum level Smin of the normalized flux is also given. We assign flag Q to each observation in order to indicate the quality and the reliability of the result. Flag Q may be one of the following values: 0 for satisfactorily determined coordinates or 1 for the results obtained from poor photometric data.
Right ascensions and declinations are measured in the International Celestial Reference Frame (ICRF). All angular quantities are in arcseconds. In the case of a mutual occultation, t∗ is the time of topocentric observation of satellites. In the case of a mutual eclipse, t∗ is the time of topocentric observation of the eclipsed satellite. Table 6 gives the first section of astrometric results.
The data in the second section consists of the following set of fields: date, the type of the phenomenon (eclipse or occultation) including the satellite numbers, the code of observatory, moment of time t∗ in the UTC scale, position angle A, and precision σalong of the apparent position along the apparent relative trajectory of the satellite, obtained with the least-squares method. The position angle A is given in degrees and σalong is given in arcseconds. In these cases, the apparent relative position of the satellite measured across the apparent trajectory cannot be determined accurately enough. Therefore position angles can only be determined up to ±180° (A ± 180°). Table 7 gives the second section of the astrometric results.
Tables 6 and 7 are available in electronic form from the Natural Satellites Data Center service2.
Second section of astrometric results.
10. Estimation of the accuracy of the derived astrometric results
The following estimates of the accuracy of the derived astrometric results were made. The least-squares method yields standard errors for the parameters 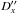 and
and 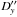 derived from the observed light-curves. These errors are due to random errors of the photometry and characterize the internal accuracy of the astrometric results. We have calculated the rms values of these estimates for all the light-curves reduced to determine the two coordinates X′′(t∗) and Y′′(t∗). Only 34 good results with Q = 0 were taken into consideration. These estimates are listed in Table 8 as total random errors. We have also calculated the total rms. of all
derived from the observed light-curves. These errors are due to random errors of the photometry and characterize the internal accuracy of the astrometric results. We have calculated the rms values of these estimates for all the light-curves reduced to determine the two coordinates X′′(t∗) and Y′′(t∗). Only 34 good results with Q = 0 were taken into consideration. These estimates are listed in Table 8 as total random errors. We have also calculated the total rms. of all 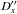 and
and 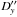 computed over all events and all observatories for the 34 cases where the two coordinates X′′(t∗), Y′′(t∗) were derived with Q = 0. These estimates are given in Table 8 as rms of O–C. The rms of the residuals calculated with the last ephemerides may be compared with rms of other sets of observations calculated in a similar way. For 4258 CCD observations made by Veiga & Vieira-Martins (1995, 1999) at Itajuba in 1989–1998, the calculated rms is 76 mas; for 514 observations made by Jones et al. (1998) at la Palma in 1990–1991, the calculated rms is 65 mas; for 2358 observations made by Qiao et al. (2013) at Sheshan, the calculated rms is 138 mas; and for the 445 observations made by Voyager 2 in 1985–1986 (Jacobson 1992), the rms is 26 mas. These results show the quality of mutual events: observations are unfortunately too rare.
computed over all events and all observatories for the 34 cases where the two coordinates X′′(t∗), Y′′(t∗) were derived with Q = 0. These estimates are given in Table 8 as rms of O–C. The rms of the residuals calculated with the last ephemerides may be compared with rms of other sets of observations calculated in a similar way. For 4258 CCD observations made by Veiga & Vieira-Martins (1995, 1999) at Itajuba in 1989–1998, the calculated rms is 76 mas; for 514 observations made by Jones et al. (1998) at la Palma in 1990–1991, the calculated rms is 65 mas; for 2358 observations made by Qiao et al. (2013) at Sheshan, the calculated rms is 138 mas; and for the 445 observations made by Voyager 2 in 1985–1986 (Jacobson 1992), the rms is 26 mas. These results show the quality of mutual events: observations are unfortunately too rare.
Estimates of the accuracy of the results of astrometric reduction performed to determine the two coordinates X′′(t∗), Y′′(t∗).
11. Conclusions
We reduced the entire database of photometric observations of the mutual occultations and eclipses of the Uranian satellites made during the international campaign in 2007 and determined the topocentric or heliocentric angular differences for satellites pairs at 27 time instants in the time interval from May 4, 2007 to January 4, 2008. The standard errors of the relative satellite coordinates due to the random errors of the photometry are equal to 6.5 and 4.1 mas in right ascension and declination, respectively. The rms of the O–C residuals with respect to the theory by Lainey (2008) are equal to 10.3 and 17.7 mas in right ascension and declination, respectively, for successful observations that put these observations among the best astrometric data of the Uranian satellites. For five observations, only the position angle was derived.
All the photometric data will be available on www/imcce/fr/nsdc
Acknowledgments
This work was supported by the FP7 ESPACE European Programme, the GRAM-INSU CNRS program, the Scientific Council of Paris Observatory, and by the Russian Foundation for Basic Research, project no. 12-02-00294. We thank the Indian Hill Observatory at Huntsburg, Ohio, for allowing us to make these observations. M.A., J.I.B.C., and R.V.M. acknowledge CNPq/Brazil grants 482080/2009-4, 306028/2005-0, 478318/2007-3, 151392/2005-6, and 304124/2007-9. M.A. and J.I.B.C. thank FAPERJ/Brazil for grants E-26/170.686/2004 and E-26/110.177/2009. F.B.R. thanks the CAPES/Brazil for its financial support. Z. Aslan and I. Khamitov thank TUBITAK for partial support in using RTT150 (Russian-Turkish 1.5-m telescope at TUG) with the project number TUG RTT150.07.0128. We also thank A. Christou from Armagh Observatory, T. Brown, and M. Hidas from Las Cumbres Observatory, E. Gomez and F. Lewis from the Faulkes Telescope Project, K. Gourgouliatos from the Institute of Astronomy of the University of Cambridge, V. Tsamis from the Hellenic Astronomical Association, and H. Worters from the Southern African Large Telescope Foundation for providing us with their previously published observations.
References
- Arlot, J. E., & Sicardy, B. 2008, Planet. Space Sci., 56, 1778 [NASA ADS] [CrossRef] [Google Scholar]
- Arlot, J. E., & Stavinschi M. 2007, in Solar and Stellar Physics Through Eclipses, ASP Conf. Ser., 370, 58 [Google Scholar]
- Arlot, J.E., Lainey, V., & Thuillot, W. 2006, A&A, 456, 1173 [Google Scholar]
- Assafin, M., Vieira-Martins, R., Braga-Ribas, F., et al. 2009, AJ, 137, 4046 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Christou, A. A., Lewis, F., Roche, P., et al. 2009, A&A, 497, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Emel’yanov, N. V. 1999, Sol. Sys. Res., 33, 133 [NASA ADS] [Google Scholar]
- Emel’yanov, N. V. 2000, Sol. Sys. Res., 34, 226 [NASA ADS] [Google Scholar]
- Emel’yanov, N. V. 2003, Sol. Sys. Res., 37, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Emel’yanov, N. V. 2009, MNRAS, 394, 1037 [NASA ADS] [CrossRef] [Google Scholar]
- Emel’yanov, N. V., & Gilbert, R. 2006, A&A, 453, 1141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hidas, M. G., Christou, A. A., & Brown, T. M. 2008, MNRAS, 384, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobson, R. A. 1992, A&AS, 96, 549 [NASA ADS] [Google Scholar]
- Jones, D. H. P., Taylor, D. B., & Williams, I. P. 1998, A&AS, 130, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karkoschka, E. 2001, Icarus, 151, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Lainey, V. 2008, Planet. Space Sci., 56, 1766 [Google Scholar]
- Qiao, R. C., Cheng, X., Dourneau, G., et al. 2013, MNRAS, 428, 2755 [NASA ADS] [CrossRef] [Google Scholar]
- Veiga, C. H., & Vieira Martins, R. 1995, A&AS, 113, 557 [NASA ADS] [Google Scholar]
- Veiga, C. H., & Vieira Martins, R. 1999, A&AS, 138, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Results of the fit of the photometric parameters to the observed reflectivities.
Agreement of observations with the model (σS) and the resulting minimum of the apparent distance between the satellites (rmin) for different light scattering laws adopted.
Astrometric results
(X′′(t∗),
Y′′(t∗): results;
σx,
σy: random errors; 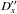 ,
, 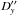 : O–C).
: O–C).
Estimates of the accuracy of the results of astrometric reduction performed to determine the two coordinates X′′(t∗), Y′′(t∗).
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


