| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201322005 | |
| Published online | 26 August 2013 | |
High-resolution modelling of meteoroid ablation
1 Department of Physics and Astronomy, University of Western Ontario, London ON, Canada
e-mail: margaret.campbell@uwo.ca
2 Astronomical Institute of the Academy of Sciences of the Czech Republic, Ondřejov observatory, Czech Republic
3 Centre for Planetary Science and Exploration, London ON, Canada
Received: 31 May 2013
Accepted: 8 July 2013
Context. The structure and composition of meteoroids is of great interest because of the insight it provides into their parent asteroids and comets.
Aims. Recently acquired, high-resolution video measurements of meteors will be used to evaluate two models of meteoroid ablation.
Methods. Ten meteors were observed with the Canadian Automated Meteor Observatory (CAMO), which uses pairs of mirrors to track meteors telescopically in the sky with a resolution of up to 3 meters per pixel. Two meteoroid ablation models were used to fit the wide-field light curves and deceleration measurements of the meteors, and the wakes predicted by each model were compared to the wakes measured in the telescopic system.
Results. Both models produced satisfactory fits to the wide field measurements, but both were very poor at predicting the narrow field brightness profiles of the meteors.
Conclusions. Models of meteoroid fragmentation in the atmosphere need significant improvement to match observations. Data from the CAMO observatory mirror systems provide significant constraints and can be used in the development of a new model of meteoroid ablation.
Key words: meteorites, meteors, meteoroids
© ESO, 2013
1. Introduction
Meteoroids, being fragments of comets and asteroids, are proxies for studying these primitive solar system bodies. The structure of millimeter-sized meteoroids is very interesting: whether they are single solid particles or fragment into smaller pieces, they give us information about the grain composition of their parent bodies, and the mechanism by which they fragment gives clues as to how the grains are bound together.
The question of fundamental grain size is especially interesting in the case of comets. Based on observations of micron-sized dust in comet tails, comets were originally thought to be composed of presolar grains (Greenberg & Li 1999): tiny grains of silicates coated with a thin layer of organics and ice, which formed in interstellar space. These sub-micron-sized grains were thought to form loose agglomerations in comets, possibly annealed together with mild heating and aqueous alteration. The Stardust sample return mission to comet Wild 2, however, showed an abundance of grains (ranging in size from tens to hundreds of microns) which were solid and refractory (Brownlee et al. 2012). These grains formed at high temperatures, like those in the early inner solar system, and are similar to the chondrules and calcium-aluminum-rich inclusions found in primitive meteorites of asteroidal origin. Their presence in a Jupiter family comet, thought to have formed beyond the orbit of Neptune, raises questions about mixing in the early solar nebula. Unfortunately, there are no Stardust samples in the millimeter size range, where most of the mass loss from comets occurs. Therefore, the size and distribution of fundamental grains in this size range is of particular interest.
The first clue that small meteoroids fragment in flight came from Super-Schmidt photographic observations (Jacchia 1955), in which the mass calculated from the light emitted by meteors, the photometric mass, was found to be much larger than the mass as deduced from deceleration (the dynamic mass). Hawkes & Jones (1975) developed a quantitative dustball model, where stony or metallic grains were embedded in a non-radiating “glue” of lower boiling point. This model predicted that faint meteors would completely dissociate before the onset of ablation (explaining the independence of beginnig and ending heights of faint meteors on their mass); brighter ones would fragment during ablation, and very bright meteors would fragment very little. Some of the predictions of this model have been verified: for example, the light curves of faint meteors tend to be symmetrical (e.g. Faloon et al. 2004). Also, small meteoroids tend to have trail lengths which are independent of mass (Murray et al. 1999). The dustball model also predicts that faint meteors should show significant physical wake by the end of the luminous portion of the trail: Fisher et al. (2000) searched for wake in faint meteors and found it in some, but not all; however, the apparatus used in the study had a resolution of order 50 m per pixel and could therefore only detect wake of several hundred meters.
 |
Fig. 1 Meteor 20101016_070052 observed with a) influx camera, b) wide field mirror camera, and c) narrow field mirror camera at the Tavistock site. The images have been inverted so that detail can be seen. The three frames are simultaneous. In the narrow field c), a trailed star is visible just in front of the meteor. |
There are many ways to model the fragmentation of a meteoroid. The entire body may disrupt into small constituent grains; this is essentially the model used by Campbell-Brown & Koschny (2004) to fit the light curves of Leonid meteors. Kikwaya et al. (2011) used the same model to determine meteoroid densities. In this implementation of the dustball model, thermal disruption, the fragments are released when the surface of the meteoroid reaches a designated temperature. There may be several bursts of fragmentation, but typically all the fragments are released close to the onset of luminosity. Another mechanism is thermal erosion (also known as quasi-continuous fragmentation), in which small grains continuously detach from the surface of the main body. Borovička et al. (2007) have successfully modelled Draconid meteors using a thermal erosion model, when a disruption model failed to match the light curves. Finally, the meteoroid may fragment into a few pieces of similar size, each of which continues to fragment in a similar way; this has been used to model the behaviour of the Sikhote-Alin fireball (Popova & Nemtchinov 1996), and the Benešov bolide (Borovička et al. 1998), among others. For large meteoroids producing bright fireballs like the last two examples, pressure is often linked to fragmentation events. In other words, when the pressure on the meteoroid from the atmosphere exceeds its material strength, it will fragment. Pressure cannot, however, be the cause of fragmentation in faint meteoroids like those in this study, since they ablate in the free molecular flow regime, where pressure is negligible.
Observations of meteors: the number of frames observed on each of the six cameras for each meteor.
Trajectories of the meteors.
A meteoroid which fragments should show wake, if the fragments are not of precisely identical size. Smaller fragments experience greater drag, and therefore fall behind larger fragments.Borovička et al. (2007) used this to evaluate their ablation model for Draconid meteors, which showed significant wake even on relatively low-resolution intensified video. They found qualitative agreement between the wake predicted by their model and the observed wake. In this paper, we test two models (thermal erosion and thermal disruption) against observations of 10 meteors with the high resolution CAMO mirror system.
2. Observations
2.1. Cameras
The ten meteors analysed in this paper were observed with the Canadian Automated Meteor Observatory (CAMO). CAMO (described in detail in Weryk et al. 2013), consists of two stations, located 44.6 km apart: Elginfield (43.193° N, 81.315° W) and Tavistock (43.264° N, 81.772° W). Each site has two camera systems. The first (the influx system) is a high spatial resolution intensified video camera. It has a pco.1600 camera, which is operated at 20 frames per second, each 1K × 1K and with an optical depth of 14-bits. The camera is lens coupled to an ITT image intensifier: the events in this work were collected with an 18 mm NiteCam. The objective lens is a 50 mm, f/0.95 Navitar lens, which gives a field of view of 20 × 20 degrees.
The second system (the tracking system) uses two intensified video cameras, both ImperX vga120 ccd cameras, with 640 × 480 pixel progressively scanned frames, and 12 bit image depth. Each is lens coupled to an 18 mm NiteCam image intensifier. One of the cameras has a 25 mm, f/0.85 objective lens, and a field of view 26 × 19°. It runs at 80 frames per second, and real time detection of meteors is done with the ASGARD software package (Weryk et al. 2008). Meteors detected in the wide field are tracked with a pair of mirrors rotating on orthogonal axes, which direct the meteor’s light into the second camera, which uses a William Optics Zenithstar 80 II ED APO f/6.8 refractor (the mirrors reduce the effective aperture to 50 mm). This tracking camera has a field of view of just over one degree, and runs at 110 frames per second; the mirrors track smoothly, so that the image of the meteor is smeared as little as possible. The field of view of the influx and tracking systems partly overlap, so meteors are often detected simultaneously in both systems. Data from all six cameras are time stamped using GPS time.
Figure 1 shows the same meteor (20101016_070052) at one instant from the three cameras at the Tavistock site. In the narrow image, it is obvious that the meteor is fragmenting.
Meteoroid orbits.
2.2. Data
The data used in this study were taken from October 16–November 7, 2010. A total of 356 events were tracked on the five selected nights, 90 of which were observed on both stations and produced solutions. Ten of these were selected for the current analysis: they were chosen for the small residuals in their solutions, complete light curves, and to represent a range of speeds and orbital parameters. Of the ten meteors used, six were observed with both the influx and wide field tracking cameras, and were tracked in both narrow field cameras. One event was observed on both systems but only tracked at one site; two were observed only in the wide and narrow tracking cameras at both sites, and one was observed by both influx cameras but only one wide and narrow tracking camera. Table 1 shows the number of frames of useful video on each of the six cameras. The narrow field tracking camera always began at least 6 frames after the wide field tracking camera, because of the delay in calculating the path of the meteor. Note that, in spite of this, the narrow field camera may observe the meteor for longer than the wide field camera, since the field of view of the mirrors is slightly larger (40 × 40 degrees) than the wide field camera, and tracking may continue after the meteor has left the field of view of the wide camera.
3. Analysis
3.1. Meteor trajectories, light curves and orbits
The images from each of the influx and wide field tracking cameras were reduced using the METAL software package (Weryk & Brown 2012) to obtain the position and brightness of the meteor in each frame by comparison with the background stars. Two station trajectory solutions were then obtained with the Milig algorithm (Borovička 1990). Careful analysis of the positions and light curves revealed a slight time offset between the influx cameras and the tracking system cameras. We attribute the offset to the difference in the time required to ingest the video from the two different models of camera, since data from the same type of camera (like the ImperX cameras on the wide and narrow field tracking systems at the two sites) show no significant (less than one frame) time offset. The time offset between the influx and tracking cameras was determined for each meteor, and was typically 0.06 to 0.07 s, slightly more than one frame in the influx system. The data from each meteor was slightly adjusted to account for this. Table 2 gives the speed (extrapolated to the top of the atmosphere), radiant, height, and peak magnitude of each meteor. It also shows the convergence angle, which is the angle made by the intersection of the planes which contain the line of the meteor and each of the stations. Very small convergence angles produce large errors in the solution. Most of the convergence angles were over 5 degrees, and the errors are reasonable even for the one meteor with a smaller convergence angle.
The brightness of the meteor was measured in each frame on all the cameras which observed it, by comparison with background stars; the apparent magnitude was then corrected to a range of 100 km to obtain the absolute magnitude. Most of the light curves have observations from multiple cameras for all or most of the trail, and in all cases the brightness measured on each camera agreed with the others to within the measurement uncertainty.
The orbits of the meteoroids were calculated with the method of Ceplecha (1987). Table 3 shows the orbital elements for each of the meteors. In some cases, the uncertainty in semi-major axis is large due to the uncertainty in the speed, but the type of orbit is well described in each case by the Tisserand parameter. Four of the meteors have Tj < 2, and are clearly from long period comets (one is an Orionid, from Comet 1P/Halley). One has a Tisserand parameter between 2 and 3, consistent with a Jupiter family comet; in fact, it and one meteor with a Tj > 3 are members of the North Taurid stream, and are both JFC material. The remaining orbits are asteroidal by the Tisserand parameter, though we note that the inclinations of all but the North Taurids are quite high for asteroidal orbits, and these objects may have large Tisserand parameters either due to observational uncertainties or non-gravitational forces. Radiation forces, for example, can circularize the orbits of meteoroids in this size range, increasing their Tisserand parameter.
3.2. High resolution meteor track lengths
The brightness of the meteor as a function of distance behind the head in the narrow field images was measured using the open-source image analysis software ImageJ (Rasband 2012). First, the angle of the line made by the meteor in the frame was determined using a two-dimensional Hough transform (Duda & Hart 1972). A measurement line oriented perpendicular to the meteor’s trail was moved along the meteor in one pixel increments, starting five pixels in front of the meteor’s head. Each measurement produced a curve of pixel brightness as a function of pixel perpendicular to the meteor, at that particular position along the meteor. Any pixel that was found to be two standard deviations above the background mean was counted as being part of the meteor, and all of these pixels were summed to obtain an integrated brightness for each frame of narrow field video. In cases where more than one fragment was present, the total light of all the fragments was added across the trail, even if the fragments were displaced from one another in the direction perpendicular to the direction of motion, as in Fig. 1.
Narrow field measurements.
 |
Fig. 2 Narrow field images from each of the events, with scale bar. The meteors show a range of different characteristics, including different amounts of wake and fragmentation. |
The integrated brightness curve was then converted to correspond to true linear distance along the meteor, from pixel distance. This was done by calculating the pixel scale, accounting for the range from camera to meteor, as well as perspective angle, as meteors rarely travel at right angles to the camera’s line of sight. Pixel scale typically varied between 3 and 12 m per pixel. Curves of meteor brightness versus linear distance along the meteor tended to agree between stations within measurement uncertainty. After these corrections, the brightness as a function of distance as measured on each of the two cameras generally agreed to within measurement uncertainty.
Two factors can increase the apparent length of the meteor on the frame. The first is blooming of the image, where point sources are approximately two-dimensional gaussians due to blooming in the intensifier and camera, distortion effects in the lenses and the (probably minor) contribution from diffraction. To characterize these effects, the gaussian profiles of stationary stars observed in the narrow field cameras were measured, and a characteristic sigma was found for each night which described the point spread function. The sigma was typically about a pixel and a half; it was slightly greater on the Elginfield camera than the Tavistock camera. The second factor is the failure of the cameras to track smoothly, which can spread the image of the meteor laterally and along the trail. The position of the front of the meteor was measured in each frame, and the drift from frame to frame was measured. This drift was not always constant in time. The tracking smear varied from half a pixel to eleven pixels per frame, and varied by as much as four pixels over the course of a single meteor. Table 4 shows the pixel scale, the characteristic sigma and the average tracking smear for each event.
Rather than attempt to correct the data for the spreading and smearing effects, they were quantified for each meteor and the modelled data (described in the following section) was modified to mimic the effects so that a useful comparison could be made. A constant value was used for the tracking smear, for simplicity.
In two cases (20101103_061856 and 20101103_071855), the narrow field observation ended when the meteor drifted out of the field of view, so that the end of the trajectory was not recorded. In every other case, the narrow field observation ended with the meteor brightness dropping below the background. Note that the limiting brightness of the narrow field varies as the mirrors track, since the orientation of the mirrors changes the effective aperture of that camera. Near the edges of the trackable area, the mirrors are closer to edge-on, and reflect less light onto the intensifier.
Figure 2 shows one frame from the narrow field camera for each of the meteors. Some of the meteors show clear fragmentation, some show significant wake, and some are nearly point sources with very faint wake.
4. Modelling
Two meteoroid ablation models were used to produce plots of predicted brightness as a function of distance from the meteoroid head. Neither of these models attempted to simulate the distribution of light produced by ablated atoms in the trail. We expect, given that meteoric atoms ablating from the surface of the meteoroid undergo several collisions before thermalizing with the atmosphere (see, e.g. Jones 1995), that there will be a small chemical wake behind even a nonfragmenting meteor. In the models described below, all light was assumed to come from meteoroid fragments directly; the only spread in the light was due to spreading of fragments as they decelerate. In all cases, meteors were modelled based only on their light curves and trajectories, including deceleration: the narrow field results were only compared after the modelling was complete.
4.1. Thermal disruption model
The first model is the thermal disruption model of Campbell-Brown & Koschny (2004), in which the full details may be found. The model simulates each meteor beginning at 180 km altitude. When a shell of material (the depth of which depends on the chosen thermal conductivity) reaches a threshold temperature, the shell fragments, leaving an unheated core if the meteoroid is large. The temperature at which fragmentation occurs and the grain distribution are adjusted to match the observations. A polynomial fit to the atmospheric density from the MSIS-E 90 model (Hedin 1991) from the appropriate date and location was used.
The temperature equation (derived from conservation of energy) used in the model characterizes three effects: the heat transferred from the kinetic energy of collisions with air molecules, the heat lost in blackbody radiation, the heat carried away with evaporating material:
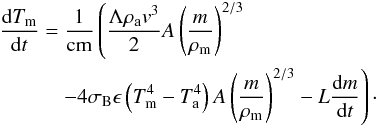 (1)Here, Tm is the meteoroid temperature, c the specific heat of the meteoroid, m the meteoroid mass, Λ the heat transfer coefficient, ρa the atmospheric density, v the meteoroid speed, A the shape factor, ρm the meteoroid density, σB the Stefan-Boltzmann constant, ϵ the emissivity of the meteoroid, Ta the atmospheric temperature, and L the heat of ablation. The initial temperature of each meteor was assumed to be 280 K (the approximate temperature of a blackbody at 1 AU); the specific heat was 1000 J kg-1 K-1; the heat transfer coefficient was 0.4; the shape factor 1.21; the emissivity 0.9; and the heat of ablation 6 × 106 J kg-1. The mass, speed and density of the meteoroid were adjusted to fit the observations.
(1)Here, Tm is the meteoroid temperature, c the specific heat of the meteoroid, m the meteoroid mass, Λ the heat transfer coefficient, ρa the atmospheric density, v the meteoroid speed, A the shape factor, ρm the meteoroid density, σB the Stefan-Boltzmann constant, ϵ the emissivity of the meteoroid, Ta the atmospheric temperature, and L the heat of ablation. The initial temperature of each meteor was assumed to be 280 K (the approximate temperature of a blackbody at 1 AU); the specific heat was 1000 J kg-1 K-1; the heat transfer coefficient was 0.4; the shape factor 1.21; the emissivity 0.9; and the heat of ablation 6 × 106 J kg-1. The mass, speed and density of the meteoroid were adjusted to fit the observations.
The speed is calculated based on conservation of momentum: 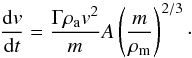 (2)
(2)
Γ is the drag coefficient (the fraction of momentum transferred to the meteoroid from the atmosphere); in this model it was assumed to be 1. This gives a constant ablation coefficient (σ = Λ/2ΓL) of 0.033 s2 km-2.
The mass loss is based on the Clausius-Clapeyron equation (which gives the partial vapour pressure of the meteoroid material) and the Knudsen-Langmuir formula (which gives the evaporation rate). When the temperature approaches the melting point of the material, a second term is added to simulate spallation of liquid drops: this term is simply proportional to the kinetic energy transferred from collisions with air molecules. 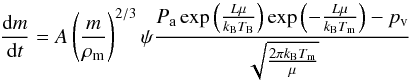 (3)
(3)
where ψ is the condensation coefficient (assumed to be 0.5), μ is the average atomic mass (set to 30), kB is the Boltzmann constant, Pa is the atmospheric pressure, TB is the boiling temperature of the meteoroid material, and pv is the vapour pressure of the meteoroid material near the surface of the meteoroid (negligible in free molecular flow).
The luminosity produced is assumed to be proportional to the kinetic energy lost by the meteoroid: 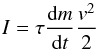 (4)
(4)
where I is the luminous intensity, and τ is the luminous efficiency. As in Campbell-Brown & Koschny (2004), the luminous efficiency was assumed to be 0.7%, with no velocity dependence. Given the uncertainties in luminous efficiency (see, e.g. Campbell-Brown et al. 2012), greater precision is not necessary.
The grain distribution in this case was manually adjusted to match the light curve and deceleration as closely as possible: there were up to four different sizes of grains. This sometimes causes unphysical effects in the brightness profile of the meteor, since grains of the same size have the same deceleration behaviour when released simultaneously, but is numerically faster and does not significantly affect the light curve or deceleration fits. Since the spread in the light produced by the ablating meteor depends on the difference between the smallest and largest grains, that can be evaluated without adding intermediate grain sizes. The bulk and grain density used for each meteor, the fragmentation temperature, and the number and sizes of grains used are shown in Table 5.
Parameters from thermal disruption model.
4.2. Thermal erosion model
The second model simulates thermal erosion (or quasi-continuous fragmentation) and is described in detail in its original form in Borovička et al. (2007). The equation for speed (deceleration) is the same as for the thermal disruption model. For luminosity, the deceleration term is included: 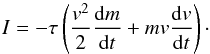 (5)The luminous efficiency is taken from Pecina & Ceplecha (1983). For velocities above 15 km s-1, τ is nearly proportional to the velocity, being about 0.6% at 20 km s-1 and 2.1% at 70 km s-1. Note that the selection of τ and inclusion/non-inclusion of the deceleration term only affects the mass scale of the grains, and does not change the general behaviour of the meteoroid in the model (e.g. the intensity profile).
(5)The luminous efficiency is taken from Pecina & Ceplecha (1983). For velocities above 15 km s-1, τ is nearly proportional to the velocity, being about 0.6% at 20 km s-1 and 2.1% at 70 km s-1. Note that the selection of τ and inclusion/non-inclusion of the deceleration term only affects the mass scale of the grains, and does not change the general behaviour of the meteoroid in the model (e.g. the intensity profile).
For mass loss, the classical concept of ablation coefficient, σ, is used (Ceplecha et al. 1998). In addition, thermal erosion of constituent grains begins at some point in the trajectory. The erosion rate is described by the erosion coefficient σe. The mass loss during the erosion phase is therefore described by the equation: 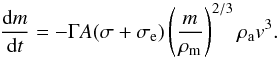 (6)After the separation from the main meteoroid, each grain is assumed to behave independently with its own deceleration, mass loss and radiation, but without further fragmentation (σe = 0). The total luminosity of the meteor at any time is computed as the sum of the contributions of the original body and all grains. After the erosion begins, the meteor becomes elongated due to differential deceleration of the grains. To compare the meteor position with the observation on low resolution cameras (to evaluate deceleration), the meteor position has to be defined. For this purpose, the meteor brightness profile along the trajectory is computed, assuming that each grain produces an image with instrumental Gaussian width corresponding to 50 meters (the same procedure was later used for the tracking cameras with the actual instrumental widths). The meteor position was defined at the brightest point of the profile.
(6)After the separation from the main meteoroid, each grain is assumed to behave independently with its own deceleration, mass loss and radiation, but without further fragmentation (σe = 0). The total luminosity of the meteor at any time is computed as the sum of the contributions of the original body and all grains. After the erosion begins, the meteor becomes elongated due to differential deceleration of the grains. To compare the meteor position with the observation on low resolution cameras (to evaluate deceleration), the meteor position has to be defined. For this purpose, the meteor brightness profile along the trajectory is computed, assuming that each grain produces an image with instrumental Gaussian width corresponding to 50 meters (the same procedure was later used for the tracking cameras with the actual instrumental widths). The meteor position was defined at the brightest point of the profile.
The grain masses were assumed to lie in some defined range, and to have a power law mass distribution within that range. The mass distribution index is assumed to be s = 2. In practice, the grains were grouped into mass bins. A single mass for all grains was also an option. The grain releases are allowed at fixed time intervals set to 0.00912 s (the interframe interval of high resolution cameras). The evolution of all grains of the same mass released at the same time is computed only once and the output luminosity is multiplied by the number of grains. The air density profile is taken from the NRLMSISE-00 model (Picone et al. 2002).
The optimisation of the parameters was done by a combination of trial-and-error and a numerical algorithm. To reduce the number of free parameters, the drag coefficient was fixed to Γ = 1 and shape coefficient was fixed to A = 1.21 for both the original meteoroid and the grains. Only two values of grain densities were considered, 3000 or 7500 kg m-3. In each case, the same ablation coefficient was used for all grains and the original meteoroid. The other parameters to be determined were: initial mass, height, velocity, and bulk density, height of the start of erosion, erosion coefficient, and grain mass range. In cases of meteors with more complex light curves, a formalism of two stage erosion was used. The first erosion was applied only to a certain fraction of the meteoroid. The rest was subject to the second erosion which started later. Parameters for the model are shown in Table 6.
Parameters from thermal erosion model.
For both models, a profile of the meteor brightness as a function of position along the trail was produced for closely spaced time intervals along the trail. Since it was difficult to subtract the gaussian spreading and tracking smear from the measured data, the model results were blurred and smeared by the amount appropriate to each event, generating a profile for each of the tracking cameras which observed the meteor. No attempt was made to adjust either model to fit the narrow field.
 |
Fig. 3 Model fits to light curves and positional data. The shaded area shows the heights where narrow field observations were made. Length difference refers to the difference between the predicted position of the meteor (given a constant speed) and the measured position. |
 |
Fig. 4 Model fits to light curves and positional data. The shaded area shows the heights where narrow field observations were made. |
 |
Fig. 5 Model fits to light curves and positional data. The shaded area shows the heights where narrow field observations were made. |
5. Results
The thermal erosion model produced good fits for both the light curve and the deceleration curve for all 10 meteors. The thermal disruption model produced acceptable fits in most cases, though in general the fits did not match the data as well as the thermal erosion model (Figs. 3, 4, and 5). The deceleration predicted by the thermal disruption model was a poor match in several cases, because cannot be tuned as precisely, since fragmentation can only occur near the beginning of the light curve. In the figures, the length difference refers to the difference between the predicted position of the meteor (given a constant speed) and the measured position.
The densities and grain distributions these two models used to fit the meteors are very different. In most cases, the bulk density is higher in fits with the thermal disruption model than the thermal erosion model; the constituent grains also tend to be larger, although the total mass is similar in all cases.
The brightness profiles from the narrow field were plotted with each model’s prediction at the corresponding height. Recall that the models do not predict the brightness in the wake of the meteor; all light produced is considered to come from the position of the meteoroid or its fragments. The cloud of ionized atoms in the meteoroids’ wake will certainly contribute to the total light, and this luminosity will persist behind the current meteoroid position, with a length dependent on the distance travelled by excited atoms before they thermalize. It is expected that this effect will be greater at higher altitudes, where the atmospheric density is lower and it will take longer for the atoms to thermalize. No attempt has been made in this work to estimate the amount of chemical wake, but it likely contributes to the total wake, particularly for the highest observed altitudes.
To address this, we examine whether the predicted wake from each model fits within the envelope of the observed wake. If the predicted wake is shorter or fainter at a given distance from the head, the difference might be due to light emission by atoms in the trail. If the predicted wake is longer and brighter, the model has failed. Figure 6 shows the brightness profiles at the lowest height observed in the narrow field, with the corresponding predictions from each model. In most cases, the predicted wake was largest toward the end of the trail, where the model is therefore more likely to fail.
 |
Fig. 6 Observed and predicted brightness profiles at the lowest observed height. The red line labelled JB is the thermal erosion model; the blue line labelled MCB is the thermal disruption model. Note that, in several cases, models consistent with the observations in this lowest height are not consistent at some earlier point in the trail. |
For each frame, the brightness profile from each camera was plotted against the model predicted brightness profile. The thermal disruption model was consistent with the observed brightness profile in two of the ten cases. The thermal erosion model was inconsistent with all the observed brightness profiles, although it came close to matching meteor 20101103_053624. Table 7 shows the consistency of the models with each of the meteors, both in the wide field fits and the narrow field brightness profiles. The thermal disruption model appears successful in the lowest height images for four meteors (20101016_075031, 20101020_094419, 20101020_100215 and 20101103_053624), but is marked as inconsistent. In each case, a release of small grains earlier in the ablation process produced a large peak which separated from the main peak and was clearly inconsistent with the observed luminosity at some point along the trail.
Success of fits to wide field (light curve and deceleration) and narrow field data for the thermal disruption and thermal erosion models.
6. Discussion
The meteors in this study show visible wakes which are generally less than 150 m long. In the wide field camera, this corresponds to less than two pixels, so in no case is the wake measurable with the wide field. The wakes predicted by the models would in most cases also be small in a wide field camera, but most can be clearly ruled out with the tracking system.
Smearing and blooming in the narrow field camera will actually make the observations easier to match, since we only consider a model to have failed when the predicted wake exceeds the observed wake. In general, the wake of the meteor may be longer than the observed wake, if some of the wake falls below the detection threshold; this does not pose a problem to the modelling, because the intensity from the model is scaled to match the peak observed intensity. If the predicted wake at any distance is brighter than the wake observed, then the model has overestimated the spread.
The thermal erosion model is clearly better at matching the light curve and observed deceleration of the meteors, due to its more tunable fragmentation timing. The thermal disruption model is specifically poorer at matching the light at the beginning of the light curve, and the deceleration toward the end. However, the strengths of the thermal erosion model in fitting wide field data (tied to very small released grains) are weaknesses when predicting the narrow field measurements. The small grain sizes combined with the relatively large remaining meteoroid mean significant relative deceleration and therefore very long wake, particularly toward the end of the trail, which does not match the observations. The thermal disruption model is worse at matching the wide field observations, but has in many cases smaller deceleration among the fragments, and therefore shorter wakes more consistent with the narrow field observations. Even the thermal disruption model, however, fails to predict the wake correctly in most of the observations. The small number of meteoroids in this study means that either model may work in other circumstances: for example, the thermal erosion model successfully predicted the very long wakes seen in Draconid meteors (Borovička et al. 2007).
We would expect models where only one grain size is used to have the smallest predicted wakes. In the thermal erosion model, this is not so, since the grains are released over a range of heights and therefore are found at different distances from the remaining mass. Similarly, in the thermal disruption model, the two events modelled with a single grain size showed significant wake; this was because the meteoroid fragmented in several steps, and grains released at different heights followed different trajectories.
Even in the two cases where the wake predicted by the thermal disruption model was consistent with the observed wake, the shapes of the wake were dissimilar. Meteor 20101106_065820 showed detached peaks in luminosity both in the model and in the observations, but the peaks did not always line up.
We might expect meteoroids with asteroidal orbits to be less likely to fragment and show wake than cometary meteors. In fact, of the three meteors with asteroidal orbits (not counting the North Taurid), two show very significant wake and fragmentation. The two North Taurids, on the other hand, have very weak wakes, and may be non-fragmenting. The other meteoroid with a Jupiter Family Comet orbit fragmented into many distinct pieces, although its wake was not very long, implying that the pieces were each a single body and not fragmenting strongly. All of the long period comets (including the Orionid), however, showed wake and sometimes what appear to be distinct fragments separating laterally. Even these, however, had the length of their wake generally overestimated by the models, implying that the fragmentation mechanism needs improvement.
7. Conclusions
This work highlights the lack of constraints on meteoroid ablation modelling, even with very precise light curves and deceleration information. In many cases, two different models were able to match the wide field observations with very different fragmentation processes and products, but neither one is an adequate explanation for what is really occurring during ablation, since both predict far more wake than is seen. The classic dustball model, where all grains are released before ablation begins, would produce worse fits for the same spread in grain sizes, since there would be more time for relative deceleration among the grains. The sample in the current study is not large enough to draw conclusions about the nature of fragmentation in different populations of meteoroids, though there are interesting indications that Jupiter-Family comets may be less prone to producing wake than other meteoroids.
This study shows meteors with clearly non-classical single body light curves, which nevertheless show very little of the wake expected for fragmenting objects. It is possible to model these objects with progressive fragmentation, where the object splits into two identical pieces, which then themselves split into identical halves, and so on; provided all the fragments are exactly the same size at all times there will be no discernible wake. This mechanism seems very unlikely for meteors showing no wake, but it may explain meteors with short wakes, if the fragments have similar but not identical masses. Another possibility is that these bodies do not fragment, and the light curve differs from the classical because of differential ablation of meteoroid components with different thermal properties.
Future studies will focus on modelling meteors with the narrow field images as a constraint: it is expected that this will reduce the number of meteors which can be fit with any given existing model. It’s likely that successful future models will need to incorporate different fragmentation mechanisms as well as compositional differences within grains to successfully match all the observations. Spectral work, to be done with the narrow field imager, should impose further constraints on differential ablation models, particularly since the light curves of different species may differ substantially (Borovička et al. 1999). Eventually, it may be possible to associate different mechanisms and models with different meteoroid populations, although meteoroids from the same parent may be heterogenous.
Acknowledgments
The camera infrastructure was funded by the Canadian Foundation for Innovation and the NASA Meteoroid Environment Office through co-operative agreement NNX11AB76A. JB was supported by grant no. P209/11/1382 from GA ČR.
References
- Borovička, J. 1990, BAICz 41, 391 [Google Scholar]
- Borovička, J., Popova, O. P., Nemtchinov, I. V., Spurný, P., & Ceplecha, Z. 1998, A&A, 334, 713 [NASA ADS] [Google Scholar]
- Borovička, J., Stork, R., & Bocek, J. 1999, M&PS, 34, 987 [Google Scholar]
- Borovička, J., Spurný, P., & Koten, P. 2007, A&A, 473, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brownlee, D., Joswiak, D., & Matrajt, G. 2012, M&PS, 47, 471 [Google Scholar]
- Campbell-Brown, M. D., & Koschny, D. 2004, A&A, 418, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campbell-Brown, M. D., Kero, J., Szasz, C., Pellinen-Wannberg, A., & Weryk, R. J. 2012, JGRA, 117, 9323 [NASA ADS] [CrossRef] [Google Scholar]
- Ceplecha, Z. 1987, BAICz, 38, 4, 222 [Google Scholar]
- Ceplecha, Z., Borovička, J., Elford, W. G., et al. 1998, Space Sci. Rev., 84, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Duda, R. O., & Hart, P. E. 1972, Comm. ACM, 15, 11 [CrossRef] [Google Scholar]
- Faloon, A. J., Thaler, J. D., & Hawkes, R. L. 2004, EM&P, 95, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, A. A., Hawkes, R. L., Murray, I. S., Campbell, M. D., & Leblanc, A. G. 2000, P&SS, 48, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Greenberg, J. M., & Li, A. 1999, SSR, 90, 149 [NASA ADS] [Google Scholar]
- Hawkes, R. L., & Jones, J. 1975, MNRAS, 173, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Hedin, A. E. 1991, JGR, 96, 1159 [Google Scholar]
- Jacchia, L. G. 1955, ApJ, 121, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, W. 1995, MNRAS, 275, 812 [NASA ADS] [Google Scholar]
- Kikwaya, J.-B., Campbell-Brown, M., & Weryk, R. J. 2011, A&A, 530, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murray, I. S., Hawkes, R. L., & Jenniskens, P. 1999, M&PS, 34, 949 [Google Scholar]
- Pecina, P., & Ceplecha, Z. 1983, Bull. astr. Inst. Czechosl., 34, 102 [Google Scholar]
- Picone, J. M., Hedin, A. E., Drob, D. P., & Aikin, A. C. 2002, J. Geophys. Res., 107, A12 [Google Scholar]
- Popova, O. P., & Nemtchinov, I. V. 1996, M&PSA, 31, 110 [NASA ADS] [Google Scholar]
- Rasband, W. S. 2012, Astrophysics Source Code Library, record ascl: 1206.013 [Google Scholar]
- Weryk, R. J., & Brown, P. G. 2012, P&SS, 62, 132 [Google Scholar]
- Weryk, R. J., Brown, P. G., Domokos, A., et al. 2008, EM&P, 102, 241 [Google Scholar]
- Weryk, R. J., Campbell-Brown, M. D., Wiegert, P. A., et al. 2013, Icarus, 225, 614 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Observations of meteors: the number of frames observed on each of the six cameras for each meteor.
Success of fits to wide field (light curve and deceleration) and narrow field data for the thermal disruption and thermal erosion models.
All Figures
 |
Fig. 1 Meteor 20101016_070052 observed with a) influx camera, b) wide field mirror camera, and c) narrow field mirror camera at the Tavistock site. The images have been inverted so that detail can be seen. The three frames are simultaneous. In the narrow field c), a trailed star is visible just in front of the meteor. |
| In the text | |
 |
Fig. 2 Narrow field images from each of the events, with scale bar. The meteors show a range of different characteristics, including different amounts of wake and fragmentation. |
| In the text | |
 |
Fig. 3 Model fits to light curves and positional data. The shaded area shows the heights where narrow field observations were made. Length difference refers to the difference between the predicted position of the meteor (given a constant speed) and the measured position. |
| In the text | |
 |
Fig. 4 Model fits to light curves and positional data. The shaded area shows the heights where narrow field observations were made. |
| In the text | |
 |
Fig. 5 Model fits to light curves and positional data. The shaded area shows the heights where narrow field observations were made. |
| In the text | |
 |
Fig. 6 Observed and predicted brightness profiles at the lowest observed height. The red line labelled JB is the thermal erosion model; the blue line labelled MCB is the thermal disruption model. Note that, in several cases, models consistent with the observations in this lowest height are not consistent at some earlier point in the trail. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


