EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 557 (September 2013) A&A, 557 (2013) A136 Full HTML
Free Access
Issue
A&A
Volume 557, September 2013
Article Number A136
Number of page(s) 8
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/201321992
Published online 24 September 2013

© ESO, 2013

1. Introduction

Transition and energy spectra data of the oxygen isoelectronic sequence are important in astrophysics and plasma physics applications. Accurate atomic data are essential for the interpretation of spectra from various astrophysical sources and in modeling of plasmas. The highly charged ions of iron are important to study because they are a constituent of astrophysical plasmas, especially in high temperature regions. Many researchers have studied O-like ions in the last 25 years. Baluja & Zeippen (1988) calculated excitation energies and transition probabilities for magnetic dipole (M1) and electric quadrupole (E2) transitions within the 2p4 ground-state configuration in the O I isoelectronic sequence for Z = 8–36. using the CIV3 code. The multiconfiguration Hartree-Fock calculations with relativistic corrections in the Breit-Pauli approximation (MCHF-BP) were performed by Tachiev & Froese Fischer (2002); Froese Fischer & Tachiev (2004) who computed energy and electric dipole (E1), E2, M1, and magnetic quadrupole (M2) transition data between all levels up to 2p33d for oxygen-like ions in the range Z = 8–20. Bhatia and Landi performed calculations for several oxygen-like ions such as Ne III (Bhatia et al. 2003) and Ca XIII (Landi & Bhatia 2005). Landi (2005) used the SUPERSTRUCTURE code to obtain energy levels, oscillator strengths, and radiative transition propabilities for all the oxygen-like ions with Z = 11–30. Deb & Hibbert (2007) presented accurate oscillator strengths, line strengths and radiative rates for 1073 E1 transitions among the 86 levels belonging to the 2s22p4,2s2p5,2p6, and 2s22p3(4So,  2Do,  2Po)3l configurations in Mg V using the CIV3 code.

Gaigalas et al. (1994) and Vilkas et al. (1994) used the second-order many-body perturbation theory (MBPT) with relativistic corrections in the Breit-Pauli approximation to compute energy spectra, electric dipole, quadrupole and magnetic dipole transitions in the oxygen isoelectronic sequence between the levels of the 1s22s22p4, 1s22s2p5 and 1s22p6 configurations for Z = 10–26. Froese Fischer et al. 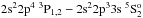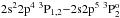(1998) the used multiconfiguration Dirac-Hartree-Fock (MCDHF) method to calculate transition rates for the and transitions in the oxygen-like ions for Z = 9–18. Vilkas et al. (1998, 1999) used multireference Møller-Plesset (MRMP) perturbation theory for the ground and low-lying excited states of oxygen-like iron and oxygen-like ions with nuclear charge up to Z = 60. No transition data were published. Safronova & Shlyaptseva (1999) used the 1/Z perturbation theory method with inclusion of relativistic and radiative corrections to calculate absolute energies and autoionization rates of the C-, N-, O- and F-like autoionizing doubly-excited states for Z = 18–26. Bogdanovich et al. used the configuration interaction method to calculate energy spectra for in Mg V, Si VII, and S IX ions (Bogdanovich et al. 1999); energy spectra and lifetimes for all states of first five configurations of Cl X (Bogdanovich et al. 2005); and energy spectra, oscillator strengths and the emission transition probabilities of oxygen-like chromium Cr XVII (Bogdanovich & Karpuškienė 2008).

During the last few years highly ionized ions of iron were of particular interest. Jonauskas et al. (2004) reported 656 energy levels and 214 840 E1, E2 and M1 transition probabilities in oxygen-like Fe XIX using multiconfiguration Dirac-Hartree-Fock (MCDHF). Landi & Gu (2006) produced a large amount of radiative and collisional data for ions of Fe XVII-XXII using the FAC code. Nahar (2011) presented an extensive set of oscillator strengths, line strengths, and radiative decay rates for allowed and forbidden transitions in Fe XIX using the relativistic Breit-Pauli R-matrix method.

The present work is motivated by the need to give a full set of consistent and highly accurate transition rates, including E1, E2, M1, M2 multipoles, for levels between the 2s22p4, 2s2p5 and 2p6 configurations for benchmarking. The paper is based on fully relativistic configuration interaction calculations of energies, transition rates, and lifetimes for all ions with Z = 9–36. The excellent description of the energy separations along the sequence makes it possible to crosscheck experimental energies for a number of ions. The calculations are also helpful in analyzing new data from EBITs, fusion plasmas, and astrophysical sources. The work complements previous work on the n = 2 and n = 3 transitions in the boron, carbon, nitrogen, fluorine and neon sequences (Rynkun et al. 2012a,b; Jönsson et al. 2010, 2011, 2012, 2013a).

2. Computational procedure

The multiconfiguration Dirac-Hartree-Fock method (Grant 2007) was used in the present work. Based on the Dirac-Coulomb Hamiltonian 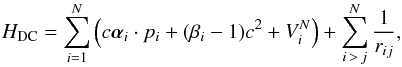(1)where VN is the monopole part of the electron-nucleus Coulomb interaction, α and β the 4 × 4 Dirac matrices, and c the speed of light in atomic units, the atomic state functions were obtained as linear combinations of symmetry adapted configuration state functions (CSFs) 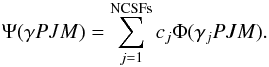(2)Here J and M are the angular momentum quantum numbers and P is parity. γj denotes other appropriate labeling of the CSF j, for example orbital occupancy and coupling scheme. Normally the label γ of the atomic state function is the same as the label of the dominating CSF. The CSFs are built from products of one-electron Dirac orbitals. Based on a weighted energy average of several states, the so called extended optimal level (EOL) scheme (Dyall et al. 1989), both the radial parts of the Dirac orbitals and the expansion coefficients were optimized to self-consistency in the relativistic self-consistent field procedure.

In subsequent relativistic configuration interaction (RCI) calculations the transverse photon interaction (Breit interaction) (3)was included in the Hamiltonian. The photon frequencies ωij, used for calculating the matrix elements of the transverse photon interaction, were taken as the difference of the diagonal Lagrange multipliers associated with the Dirac orbitals (McKenzie et al. 1980). In the RCI calculation the leading quantum electrodynamics corrections, self-interaction and vacuum polarization, were also included.

All calculations were performed with the GRASP2K code (Jönsson et al. 2007). For the calculations of spin-angular parts of matrix elements the second quantization method in coupled tensorial form and quasispin technique (Gaigalas et al. 2001, 1997) were adopted.

All calculations were done in jj-coupling. The level notations have been converted to LSJ coupling scheme using the newly developed JJ2LSJ program, part of the latest version of the GRASP2K code by Jönsson et al. (2013b).

3. Computation of transition parameters

The evaluation of radiative transition data (transition probabilities, oscillator strengths) between two states γ′P′J′M′ and γPJM built on different and independently optimized orbital sets is non-trivial. The transition data can be expressed in terms of the transition moment which is defined as 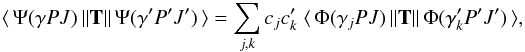(4)where T is the transition operator. For electric dipole and quadrupole (E1 and E2) transitions there are two forms of the transition operator, the length (Babushkin) and velocity (Coulomb) forms. For the multiconfiguration Dirac-Hartree-Fock solutions the agreement in the two values may be used as an indicator of accuracy (Froese Fischer 2009). The calculation of the transition moment breaks down to the task of summing up reduced matrix elements between different CSFs. Since the orbitals of the initial and final states are orthonormal but different, the two states γ′P′J′M′ and γPJM were transformed in such a way that the orbital sets became biorthonormal (Olsen et al. 1995). Standard methods were then used to evaluate the matrix elements for the transformed CSFs.

Table 1

Comparison of theoretical energy levels with values derived from observed wavelengths.

Table 2

Comparison of fully relativistic theoretical energy levels with values derived from observed wavelengths for Fe XIX.

Table 3

Comparison of fully relativistic theoretical energy levels with values derived from observed and semi-empirical (SE) wavelengths.

4. Generation of configuration expansions

It is often convenient to perform simultaneous calculations in the EOL scheme for states of the same parity occupying roughly the same region in space, as measured by the mean radius of the Dirac-Fock reference orbitals. In the present work simultaneous calculations were performed for the states belonging to the 2s22p4, 2s2p5, and 2p6, configurations. The configuration expansions were obtained using the active set method (Sturesson et al. 2007). Here CSFs of a specified parity and J symmetry are generated by excitations from a number of reference configurations to a set of relativistic orbitals. By applying restrictions on the allowed excitations, different electron correlation effects can be targeted. To monitor the convergence of the calculated energies and transition parameters, the active sets of orbitals were increased in a systematic way by adding layers of correlation orbitals. In the present work, valence and core-valence correlation effects were included.

All expansions were obtained by single and double (SD) excitations from 1s22s22p4 and 1s22p6 for even states and 1s22s2p5 for odd states to active sets with principal quantum numbers n = 3...8 and angular symmetries s,p,d,f,g,h from all shells, with the restriction that there be only a single excitation from the 1s shell. In this way the core-polarization effect of the outer 2s,2p on the core is taken into account. Orbitals were optimized simultaneously by layers (n) for all levels of the relevant configuration, namely 2s22p4, 2s2p5, or 2p6. The self-consistent field calculations for each layer of orbitals were followed by RCI calculations, including the Breit interaction. At the final stage the configuration expansions from the EOL calculations were augmented by expansions obtained from SD excitations to active sets with n = 8 and angular symmetries s,p,d,f,g,h to enlarged multireference sets. The multireference set was enlarged to contain all CSFs with with expansion coefficients greater than 0.0114 in the CSF calculation. Particularly important were some configurations with 3d orbitals. For the states of the 1s22s22p4 and 1s22p6 configurations, the enlarged multireference set was { 1s22s22p4,1s22p6,1s22s2p43d } whereas for 1s22s2p5 it was { 1s22s2p5,1s22p53d,1s22s22p33d }. Among the CSFs generated by SD-excitations from the multireference set only those interacting with the multireference states were kept. The leading QED effects – vacuum polarization and self-energy – were included in the final multireference RCI calculations.

The final expansion for the states of the 1s22s22p4 configuration contained 709 690 CSFs distributed over the J = 0,1,2 symmetry blocks. For the states of the 1s22s2p5 configuration there were 702 892 CSFs distributed over the J = 0,1,2 symmetry blocks. Finally, for the J = 0 state of 1s22p6 configuration there were 67 375 CSFs.

5. Results and evaluation of data

For lower degrees on ionization, the Breit-Pauli (BP) method has often been used in the past. In Table 1, results from three fully relativistic methods based on Dirac theory (RCI, MRMP, MBPT) are compared with Breit-Pauli methods (MCHF-BP, SS, and CIV3). From the differences, we see that in Ne III (Z = 10) some of the BP methods are among the most accurate but by Ca XIII (Z = 20) the fully relativistic methods that include the Breit and QED corrections have become the most accurate with the present RCI results having the lowest maximun difference with observed. For all levels there is good agreement between RCI and MRMP, except for the highest level. Unlike the present work, many early calculations (MCHF-BP, SS, CIV3, for example) treated the core as inactive. Table 1 shows the importance of the core-polarization correction for levels with a vacancy in the 2s shell. Present results are in much better agreement with observed levels.

Table 4

Comparison of lifetimes.

A very important ion is Fe XIX for which energies have been computed by a variety of relativistic methods, including the recently developed FAC code (Gu 2003). Differences with observed are reported in Table 2. Except for the energy of 2p61S, the MRMP energies are the most accurate but the RCI values are more regular in their difference with observed.

For ions in the region Z > 30 uncertainties in the “observed” energies become substantial. There are significant discrepancies for As XXVI, Se XXVII and Br XXVIII spectra between the NIST database values based on measurements reported by Kelly (1987) and those derived by Edlén (1983) from a variety of sources. Both are reported in Table 3 and for each method – (c) RCI, and (d) MRMP – the calculated energy level is given along with the differences from the observed values and Edlén values obtained from semiempirically fitted 1/Z expansions. For the 2s22p4 levels in Br XXVIII both theoretical results are in better agreement with the Edlén values.

On the whole, the RCI and MRMP calculations stand out as having the best agreement with observation. Their energy differences are about an order of magnitude smaller than those for other methods.

In Table 4 lifetimes from present calculations are compared with results from MCHF-BP calculations by Fischer and Tachiev and observations. As seen from the table, there is good agreement between theory and experiment for F II and Ne III but for the more highly ionized spectra, the agreement becomes even better. All the computed values are within the uncertainties of experimental measurement.

Table 5 gives calculated transition energies, weighted oscillator strengths gf, and transition rates A in the length gauge. For the electric multipole transitions, the ratio R between the transition rates in length and velocity gauges is given. A value close to R = 1 for an LS allowed electric multipole transition is a known indicator of accuracy (Froese Fischer 2009). For weak intercombination transitions, the transition amplitude depends sensitively on the mixing of two or more LS terms. Many-body perturbation studies, where calculations are restricted to positive energy states, have shown that there are important contributions to the rate in the velocity gauge from the negative energy continuum whereas rates in the length gauge are relatively unaffected. Variational methods do not explicitly limit the orbitals to have only positive energy components, so for weak intercombination transitions, the usability of R as an accuracy indicator is somewhat unclear. For the strong E1 transitions the ratio R is often close to unity. For the intercombination transitions there is a somewhat larger spread for R. For ions around Z = 24 (Cr XVII) there are internal cancellations in the calculation of the transition moment (Eq. (4)) for the 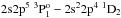transition making the transition rates comparatively low. The internal cancellations affect the two gauges differently, giving ratios R that differ from 1 by larger amounts. For a discussion about cancellation effects see Ynnerman & Froese Fischer (1995).

Table 5

Calculated transition energies (ΔE in cm-1), type of transition (T), weighted oscillator strength (gf), transition rate (A in s-1), and the accuracy (R) for E1, E2, M1, M2 transitions in F II.

Table 6

Comparison of transition rates in Mg V.

Table 6 displays E1, E2, M1 and M2 transition rates from different calculations and NIST critically evaluated data for Mg V. The NIST values are based on Tachiev & Froese Fischer (2002) calculations of line strengths and observed wavelengths and include an accuracy indicator which, for the highest accuracy rating (B+) corresponds to an estimated error of <7%. The accuracy of our transition rates is similar to the accuracy of the transition energies in Table 1 and, for this moderately ionized atom, there is good agreement between CIV3, MCHF-BP, and RCI.

Table 7 gives transition rates, including M1 and E2 transitions within the ground configuration, from different calculations and experiment in Fe XIX. Again, the NIST values are based on theoretical calculations for the line strength along with observed wavelengths and, as shown in the table, have a fairly low accuracy rating. The NIST values for E1 transitions in this table are based on Dirac-Hartree-Fock calculations by Cheng et al. (1979), whereas the E2 and M1 transitions are from a SUPERSTRUCTURE calculations (Loulergue et al. 1985). There is good agreement with the BPRM results of Nahar (2011) and the SS results of Landi (2005) who compute the transition rates by using observed wavelengths and only a computed line strength.

Table 7

Comparison of transition rates in Fe XIX.

The Online Table 8 is similar to Table 1 that reports the calculated and observed energy levels and their difference (in cm-1), the calculated and observed fine-structure splitting and the difference (in cm-1), as well as the lifetime (in s) of each level for all the spectra from F II – Kr XXIX. Similarly, Table 9 is the Online Version of Table 5 for all the E1, E2, M1, M2 transitions between the levels of the spectra from F II – Kr XXIX.

6. Conclusion

In this work, spectroscopic data for the levels of the 2s22p4, 2s2p5, and 2p6 configurations in F II to Kr XXIX are computed using a fully relativistic configuration-interaction method. Our computed energies agree very well with the experimental values, with differences between 300 and 600 cm-1 for the majority of the ions in the sequence. Some possible problems with experimental identification of lines in As XXVI, Se XXVII, and Br XXVIII have been pointed out. The energy levels for these three spectra, presented in this paper, agree much better with the Edlén (1983) values than with NIST databases (results for these ions are based on Kelly 1987). Our energy level calculations are considerably more accurate than other calculations (except for Vilkas and Ishikawa). There are excellent agreements with the most accurate MCHF-BP calculations at the low Z as well as with experimental lifetimes (Table 4). Basically, the calculations serve as benchmark calculations for transition probabilities for the 2s22p4, 2s2p5, and 2p6 configurations of the oxygen-like sequence without the need for observed transition energies.

Acknowledgments

P.J. and G.G. acknowledge support from the Visby program under the Swedish Institute. P.J. acknowledges financial support by the Swedish Research Foundation. G.G. acknowledges financial support by the European Communities under the FP7 contract of Association between EURATOM/LEI FU07-CT-2007-00063.

References

  1. Baluja, K. L., & Zeippen, C. J. 1988, J. Phys. B: At. Mol. Opt. Phys., 21, 1455 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bhatia, A. K., Thomas, R. J., & Landi, E. 2003, At. Data Nucl. Data Tables, 83, 113 [Google Scholar]
  3. Bogdanovich, P., & Karpuškienė, R. 2008, At. Data Nucl. Data Tables, 94, 623 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bogdanovich, P., Karpuškienė, R., Momkauskaitė, A., & Udris, A. 1999, Lith. Phys. J., 39, 9 [Google Scholar]
  5. Bogdanovich, P., Karpuškienė, R., & Martinson, I. 2005, Nucl. Instr. and Meth. in Phys. Res. B: Beam Interactions with Materials and Atoms, 205, 70 [Google Scholar]
  6. Calamai, A. G., Gwinner, G., Tordoir, X., Träbert, E., & Wolf, A. 2000, Phys. Rev. A, 61, 062508 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cheng, K. T., Kim, Y.-K., & Desclaux, J. P. 1979, At. Data Nucl. Data Tables, 24, 111 [NASA ADS] [CrossRef] [Google Scholar]
  8. Daw, A., Parkinson, W. H., Smith, P. L., &Calamai, A. G. 2000, ApJL, 533, 179 [NASA ADS] [CrossRef] [Google Scholar]
  9. Deb, N. C., & Hibbert, A. 2007, At. Data Nucl. Data Tables, 93, 585 [NASA ADS] [CrossRef] [Google Scholar]
  10. Dyall, K. G., Grant, I. P., Johnson, C. T., Parpia, F. A., & Plummer, E. P. 1989, Comput. Phys. Commun., 55, 425 [NASA ADS] [CrossRef] [Google Scholar]
  11. Edlén, B. 1983, Phys. Scr., 28, 51 [NASA ADS] [CrossRef] [Google Scholar]
  12. Fritzsche, S., & Grant, I. P., 1994, Phys. Lett. A, 186, 152 [NASA ADS] [CrossRef] [Google Scholar]
  13. Froese Fischer, C. 2009, Phys. Scr. T134, 014019 [Google Scholar]
  14. Froese Fischer, C., & Tachiev, G. I. 2004, At. Data and Nucl. Data Tables, 87, 1 [Google Scholar]
  15. Froese Fischer, C., & Tachiev, G. 2012, MCHF/MCDHF Collection, Version 2, Ref. No., Available online at http://physics.nist.gov/mchf, National Institute of Standards and Technology [Google Scholar]
  16. Froese Fischer, C., He, X., & Jönsson, P. 1998, Eur. Phys. J. D., 4, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Gaigalas, G., Kaniauskas, J., Kisielius, R., Merkelis, G., & Vilkas, M. J. 1994, Phys. Scr., 49, 135 [NASA ADS] [CrossRef] [Google Scholar]
  18. Gaigalas, G., Rudzikas, Z., & Froese Fischer, C. 1997, J. Phys. B: At. Mol. Opt. Phys., 30, 3747 [Google Scholar]
  19. Gaigalas, G., Fritzsche, S., & Grant, I. P. 2001, Comput. Phys. Commun., 139, 263 [NASA ADS] [CrossRef] [Google Scholar]
  20. Grant, I. P. 2007, Relativistic Quantum Theory of Atoms and Molecules (New York: Springer) [Google Scholar]
  21. Gu, M. F. 2003, ApJ, 582, 1241 [NASA ADS] [CrossRef] [Google Scholar]
  22. Jonauskas, V., Keenan, F. P., Foord, M. E., et al. 2004, A&A, 424, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Jönsson, P., & Bieroń, J. 2010, J. Phys. B, 43, 074023 [NASA ADS] [CrossRef] [Google Scholar]
  24. Jönsson, P., He, X., Froese Fischer, C., & Grant, I. P. 2007, Comput. Phys. Commun., 177, 597 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  25. Jönsson, P., Rynkun, P., & Gaigalas, G. 2011, At. Data Nucl. Data Tables, 97, 648 [Google Scholar]
  26. Jönsson, P., Bengtsson, P., Ekman, J., et al. 2012, At. Data Nucl. Data Tables, accepted, DOI: 10.1016/j.adt.2013.06.001 [Google Scholar]
  27. Jönsson, P., Alkauskas, A., & Gaigalas, G. 2013a, At. Data Nucl. Data Tables, 99, 431 [NASA ADS] [CrossRef] [Google Scholar]
  28. Jönsson, P., Gaigalas, G., Bieroń, J., Froese Fischer, C., & Grant, I. P. 2013b, Comput. Phys. Commun., 184, 2197 [NASA ADS] [CrossRef] [Google Scholar]
  29. Kelly, R. L. 1987, J. Phys. Chem. Ref. Data 16, Suppl. 1, 1 [Google Scholar]
  30. Landi, E. 2005, A&A, 434, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Landi, E., & Bhatia, A. K. 2005, A&A, 444, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Landi, E., & Gu, M. F. 2006, ApJ, 640, 1171 [NASA ADS] [CrossRef] [Google Scholar]
  33. Loulergue, M., Mason, H. E., Nussbaumer, H., & Storey, P. J. 1985, A&A, 150, 246 [NASA ADS] [Google Scholar]
  34. McKenzie, B. J., Grant, I. P., & Norrington, P. H. 1980, Comput. Phys. Commun., 21, 233 [NASA ADS] [CrossRef] [Google Scholar]
  35. Nahar, S. N. 2011, At. Data Nucl. Data Tables, 97, 403 [NASA ADS] [CrossRef] [Google Scholar]
  36. Olsen, J., Godefroid, M., Jönsson, P., Malmqvist, P. Å., & Froese Fischer, C. 1995, Phys. Rev. E, 52, 4499 [NASA ADS] [CrossRef] [Google Scholar]
  37. Kramida, A., Ralchenko, Yu., Reader, J., & NIST ASD Team 2012. NIST Atomic Spectra Database (ver. 5.0), [Online]. Available: http://physics.nist.gov/asd [2013, May 30]. National Institute of Standards and Technology, Gaithersburg, MD [Google Scholar]
  38. Rynkun, P., Jönsson, P., Gaigalas, G., & Froese Fischer, C. 2012a, At. Data Nucl. Data Tables, 98, 481 [Google Scholar]
  39. Rynkun, P., Jönsson, P., Gaigalas, G., & Froese Fischer, C. 2012b, At. Data Nucl. Data Tables, accepted, DOI: 10.1016/j.adt.2013.05.003 [Google Scholar]
  40. Safronova, U. I., & Shlyaptseva, A. S. 1999, Phys. Scr., 60, 36 [NASA ADS] [CrossRef] [Google Scholar]
  41. Sturesson, L., Jönsson, P., & Froese Fischer, C. 2007, Comput. Phys. Commun., 177, 539 [NASA ADS] [CrossRef] [Google Scholar]
  42. Tachiev, G. I., & Froese Fischer, C. 2002, A&A, 385, 716 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Träbert, E., Wolf, A., Pinnington, E. H., et al. 1998, Can. J. Phys., 76, 899 [NASA ADS] [CrossRef] [Google Scholar]
  44. Träbert, E., Wolf, A., Tordoir, X., et al. 2001, Can. J. Phys., 79, 145 [NASA ADS] [CrossRef] [Google Scholar]
  45. Träbert, E., Grieser, M., Hoffmann, J., et al. 2012, Phys. Rev. A, 85, 042508 [NASA ADS] [CrossRef] [Google Scholar]
  46. Vilkas, M. J., Merkelis, G., Kisielius, R., et al. 1994, Phys. Scr. 49, 592 [Google Scholar]
  47. Vilkas, M. J., Koc, K., & Ishikawa, Y. 1998, Chem. Phys. Lett., 296, 68 [NASA ADS] [CrossRef] [Google Scholar]
  48. Vilkas, M. J., Ishikawa, Y., & Koc, K. 1999, Phys. Rev. A, 60, 2808 [NASA ADS] [CrossRef] [Google Scholar]
  49. Yang, L., Church, D. A., Tu, S., & Jin, J. 1994, Phys. Rev. A, 50, 177 [NASA ADS] [CrossRef] [Google Scholar]
  50. Ynnerman, A., & Froese Fischer, C. 1995, Phys. Rev. A, 51, 2020 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Comparison of theoretical energy levels with values derived from observed wavelengths.

In the text
Table 2

Comparison of fully relativistic theoretical energy levels with values derived from observed wavelengths for Fe XIX.

In the text
Table 3

Comparison of fully relativistic theoretical energy levels with values derived from observed and semi-empirical (SE) wavelengths.

In the text
Table 4

Comparison of lifetimes.

In the text
Table 5

Calculated transition energies (ΔE in cm-1), type of transition (T), weighted oscillator strength (gf), transition rate (A in s-1), and the accuracy (R) for E1, E2, M1, M2 transitions in F II.

In the text
Table 6

Comparison of transition rates in Mg V.

In the text
Table 7

Comparison of transition rates in Fe XIX.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.