| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 51 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201321878 | |
| Published online | 12 August 2013 | |
Granulation properties of giants, dwarfs, and white dwarfs from the CIFIST 3D model atmosphere grid⋆
1 Zentrum für Astronomie der Universität Heidelberg, Landessternwarte, Königstuhl 12, 69117 Heidelberg, Germany
e-mail: ptremblay@lsw.uni-heidelberg.de; hludwig@lsw.uni-heidelberg.de; ecaffau@lsw.uni-heidelberg.de
2 Centre de Recherche Astrophysique de Lyon, UMR 5574: CNRS, Université de Lyon, École Normale Supérieure de Lyon, 46 allée d’Italie, 69364 Lyon Cedex 07, France
e-mail: Bernd.Freytag@ens-lyon.fr
3 Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
e-mail: msteffen@aip.de
4 GEPI, Observatoire de Paris, CNRS, Univ. Paris Diderot, Place Jules Janssen, 92190 Meudon, France
Received: 11 May 2013
Accepted: 5 July 2013
Three-dimensional model atmospheres for giants, dwarfs, and white dwarfs, computed with the CO5BOLD code and part of the CIFIST grid, have been used for spectroscopic and asteroseismic studies. Unlike existing plane-parallel 1D structures, these simulations predict the spatially and temporally resolved emergent intensity so that granulation can be analysed, which provides insights on how convective energy transfer operates in stars. The wide range of atmospheric parameters of the CIFIST 3D simulations (3600 < Teff (K) < 13 000 and 1 < log g < 9) allows the comparison of convective processes in significantly different environments. We show that the relative intensity contrast is correlated with both the Mach and Péclet numbers in the photosphere. The horizontal size of granules varies between 3 and 10 times the local pressure scale height, with a tight correlation between the factor and the Mach number of the flow. Given that convective giants, dwarfs, and white dwarfs cover the same range of Mach and Péclet numbers, we conclude that photospheric convection operates in a very similar way in those objects.
Key words: convection / stars: atmospheres
Table 1 and Appendix A are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
In late-type stars, giants, and cool white dwarfs, surface convection is responsible for the granulation pattern directly observed in high-resolution images of the Sun. Granulation is more difficult to observe directly in other stars, although it has been possible to constrain the lifetime and size of granules through asteroseismic studies of stochastically excited p-modes (Dupret et al. 2009; Ludwig et al. 2009a; Mathur et al. 2011; Samadi et al. 2013) and interferometry in the case of the red supergiant Betelgeuse (Chiavassa et al. 2009, 2010).
Early numerical hydrodynamical experiments (Gough et al. 1976; Massaguer & Zahn 1980) have provided predictions for the size and temperature contrast of granulation as a function of characteristic flow numbers. The radiation-hydrodynamics (RHD) 3D simulations, starting from the work of Nordlund (1982), have improved predictions for the solar granulation with more realistic stratifications. For many years, the observed values of intensity contrast between dark and bright granules in the Sun were significantly lower than those predicted from RHD simulations. However, it was shown recently that if the instrumental image degradation is taken into account properly, the simulations can reproduce the observed values very well (Wedemeyer-Böhm & Rouppe van der Voort 2009).
For 3D simulations of solar-like stars, computed with the CO5BOLD code (Freytag et al. 2012) and the Stein & Nordlund (1998) code, the relative intensity contrast and size of granules relative to the local pressure scale height (Hp) appear to be changing significantly with Teff (Trampedach et al. 2013). Furthermore, for hotter stars and supergiants, a bifurcation is observed from a regular pattern of bright cells and dark lanes towards a regime with small shallow cells and large granules with deep reaching downdrafts (Freytag et al. 2012). However, for objects with different gravities, granulation properties are in general fairly similar (Magic et al. 2013), albeit with a shift in Teff. Surface convection is still significant in white dwarfs at Teff up to 15 000 K for pure-H atmospheres (Tremblay et al. 2013), and up to 30 000 K for pure-He atmospheres (Bergeron et al. 2011).
Granulation properties can not be derived from existing plane-parallel 1D structures. Furthermore, the convective energy transfer, usually modelled with the mixing-length theory (Böhm-Vitense 1958, hereafter MLT), is parameterised in a different way in giants, stars, and white dwarfs (Fuhrmann et al. 1993; Bergeron et al. 1995; Ludwig & Kučinskas 2012). As a consequence, it is difficult to compare how convection works in stars with different surface gravities and temperatures.
In this work, we study how convective energy transfer behaves in the photosphere of stars by relying on 148 CO5BOLD 3D simulations for dwarfs, white dwarfs, and in a few cases, giants. In particular, we derive the relative intensity contrast of surface granulation, which is a measure of the deviation from a 1D plane-parallel approximation. This is an indication of the strength of 3D effects but in practice, the 3D effects on the mean structure and line formation are a complex function of local inhomogeneities (Nordlund et al. 2009; Tremblay et al. 2011b; Kučinskas et al. 2013) and do not scale well with the intensity contrast. Our 3D computations can also predict the characteristic size and lifetime for the granulation. These quantities are of interest for the understanding of the granulation background of asteroseismological observations. Compared to the study of Trampedach et al. (2013), we rely on a different code and include white dwarfs, sub-solar metallicity dwarfs, and giants.
We aim at defining how the granulation properties can be formulated as a function of the physical conditions in the photosphere. These relations are of interest, first of all, to set up new 3D simulations. Furthermore, such parameterisations can suggest how the observed properties of convection in the Sun are expected to be scaled to other objects. For instance, it is an open question whether small scale magnetic fields generated by a turbulent dynamo can exist in white dwarfs like it is observed in the Sun (Danilovic et al. 2010; Lites 2011). Finally, we hope that our analysis can provide insights on how to improve globally the current 1D models and the mixing-length theory.
We describe in Sect. 2 the 3D model atmospheres that we rely on for this study. We follow in Sect. 3 with a presentation of the characteristic granulation properties as derived from the grid of 3D simulations. We discuss these results in Sect. 4 and conclude in Sect. 5.
2. 3D model atmospheres
2.1. Giants and dwarfs
We rely on 88 simulations of giants and dwarfs computed with CO5BOLD and part of the CIFIST grid (Ludwig et al. 2009b; Caffau et al. 2011). These are non-gray RHD models with the surface gravity and entropy flux at the bottom of the atmosphere as input parameters. The implementation of the boundary conditions is described in detail in Freytag et al. (2012, see Sect. 3.2). In brief, the lateral boundaries are periodic, and the top boundary is open to material flows and radiation. The bottom layer is open to convective flows where a zero total mass flux is enforced. The Teff is not an input parameter, although we specify the entropy of the ascending material to obtain approximately the desired value, which is derived from the temporal and spatial average of the emergent stellar flux.
The models typically have a resolution of 140 × 140 × 150 (x × y × z) grid points. The vertical extent of the simulations, from the photosphere at Rosseland optical depth (τR) unity to the bottom boundary, is always several orders of magnitude (three or more) of pressure scale height, which ensures that convective eddies in the photosphere are not impacted by boundary conditions. The upper boundary extends beyond a mean τR of 10-6. The horizontal extent of the simulations was chosen so that at least of the order of ten granules are resolved at the surface.
We rely on band-averaged opacities to describe the band-integrated radiative transfer, based on the procedure laid out in Nordlund (1982), Ludwig et al. (1994) and Vögler et al. (2004). A total number of 5 bins was used for models of solar metallicity, while 6 bins were employed for models of sub-solar metallicity1. This setup should be more than sufficient for our study of wavelength-integrated (white light) intensity maps, which is much less sensitive to the binning procedure than detailed spectral synthesis.
We assume four different metallicities in the range − 3 < [Fe/H] < 0. The equation of state takes into account H and He ionization and H2 formation. The opacities are calculated with the Uppsala package (Gustafsson et al. 2008). Chemical abundances are from Grevesse & Sauval (1998), with the exception of CNO, which are updated following Asplund (2005). More details are provided in Ludwig et al. (2009b). In Table 1, the atmospheric parameters and composition of our different simulations are given.
 |
Fig. 1 Surface gravity and mean Teff for the 3D model atmospheres in the CIFIST grid. The top-left (circles), top-right (stars), bottom-left (squares) and bottom-right (triangles) panels represent different metallicities, with [Fe/H] = 0, − 1, − 2 and − 3, respectively. For simplicity, pure-hydrogen white dwarfs (open triangles) are represented along the [Fe/H] = − 3 stars (note the different scale for this panel). Teff values are colour-coded from red (cool) to blue (hot) and log g values (cgs units) are size-coded from small (high gravity) to large (low gravity) symbols. The x- and y-axis can be used as legends for the following figures. There is no link between white dwarfs and stars with the same sizes and colours. |
2.2. White dwarfs
We rely on 60 CO5BOLD simulations for pure-hydrogen atmosphere white dwarfs (spectral type DA) in the range 13 000 > Teff (K) > 6000 K. The 12 models at log g = 8.0 are described in detail in Tremblay et al. (2013). We have now extended the grid of models to log g = 7.0, 7.5, 8.5 and 9.0. The CO5BOLD setup for these additional models is identical to the log g = 8 case. In brief, the resolution is of 150 × 150 × 150 grid points, and the simulations extend well below and above the photosphere. We rely on an equation-of-state and opacity tables which have the same microphysics as the standard 1D models (Tremblay et al. 2011a). We opted for a 8 opacity bins setup for the radiative transfer scheme.
Compared to the dwarf and giant models described above, one important difference is that hotter white dwarfs have a convection zone that is thinner than the typical vertical dimension of the atmosphere. As a consequence, the 6, 4, 3, and 1 hottest models at log g = 7.0, 7.5, 8.0 and 8.5, respectively, were computed with a bottom layer that is closed to convective flows (zero vertical velocities). In that case, we imposed the radiative flux at the bottom based on the diffusion approximation. Other than the slightly different resolution, white dwarf models have been computed with a more recent version of CO5BOLD. The main difference is that we have now switched to a less dissipative 2nd-order reconstruction method to solve the hydrodynamical equations (Freytag et al. 2013), and no artificial viscosity was used. Furthermore, regarding the time integration scheme, the corner-transport upwind (CTU) method (Colella 1990) was adopted. However, we have verified that these different numerical parameters have almost no impact on the mean properties of white dwarfs (Tremblay et al. 2013), hence we believe that white dwarf models can be compared directly to dwarf and giant simulations.
2.3. Mean quantities
In Fig. 1, we present our set of 3D simulations in a HR-type diagram with log g vs. log Teff. The colour-(Teff) and size-coding (log g) introduced in this figure is used throughout this paper for dwarfs and giants (filled symbols) and white dwarfs (open triangles).
We derived a large number of mean thermodynamic and dynamic quantities from our sequence of 3D simulations that are representative of the photosphere. All quantities, unless otherwise noted, are spatial and temporal averages over the constant geometrical depth which corresponds to ⟨ τR ⟩ x,y = 1. This layer approximates the region of the photosphere where the intensity is formed, although 3D convection is a non-local phenomenon and surface granulation is also influenced by deeper layers. We initially restrict our analysis to one characteristic layer in order to compare granulation properties to local parameters, and Sect. 3.2 further describes the effect of deeper layers. The temporal average was performed over 250 or more snapshots in the last half of the simulations, where they are all relaxed. Furthermore, we determined the Teff values identified in Table 1 from the mean emergent flux of the same snapshots. Finally, the emergent intensity from these snapshots is the input to study the granulation properties in Sect. 3.
2.4. Independent variables
Our aim is to cover a large part of the HR diagram with our simulations, yet to find similarities between them. For describing the properties of granulation it is not clear whether Teff and log g are the most suitable control variables. Nevertheless, we note that the hydrostatic pressure scale height 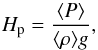 (1)where P is pressure and ρ the density, is inversely proportional to g and roughly proportional to Teff if we neglect molecular mass variations. To first order, we can therefore scale characteristic sizes as a function of the atmospheric parameters. Furthermore, the turnover timescale in the convective zone, or the advective timescale, is defined as tadv = Hp/vrms where vrms is the convective velocity
(1)where P is pressure and ρ the density, is inversely proportional to g and roughly proportional to Teff if we neglect molecular mass variations. To first order, we can therefore scale characteristic sizes as a function of the atmospheric parameters. Furthermore, the turnover timescale in the convective zone, or the advective timescale, is defined as tadv = Hp/vrms where vrms is the convective velocity ![\begin{equation} v^2_{\rm rms} = \langle v^2 \rangle - \frac{[\langle \rho v_{x} \rangle^2 + \langle \rho v_{y} \rangle^2 + \langle \rho v_{z} \rangle^2]}{\langle \rho \rangle^2}\cdot \end{equation}](/articles/aa/full_html/2013/09/aa21878-13/aa21878-13-eq34.png) (2)The density weighted mean velocity (mass flux) is removed from the rms value since it is sensitive to the setup of the numerical parameters and oscillations. Figure 2 presents the advective timescale with Hp and vrms derived from our 3D simulations and averaged over x, y, and t at ⟨ τR ⟩ x,y = 1. Clearly, the characteristic turnover time is anticorrelated with gravity, as are characteristic sizes.
(2)The density weighted mean velocity (mass flux) is removed from the rms value since it is sensitive to the setup of the numerical parameters and oscillations. Figure 2 presents the advective timescale with Hp and vrms derived from our 3D simulations and averaged over x, y, and t at ⟨ τR ⟩ x,y = 1. Clearly, the characteristic turnover time is anticorrelated with gravity, as are characteristic sizes.
The atmospheric densities are show in Fig. 3 as a function of Teff. It demonstrates that stars and white dwarfs share a common range of photospheric densities (− 8 < log ρ < − 4) despite the different surface gravities. The opacities typically increase with Teff and metallicity, hence the photosphere is pushed towards lower densities. On the other hand, higher gravities imply higher densities, although because of different opacities, the relation is not strict. However, it is seen that by increasing both Teff and log g, it is possible to keep the photospheric density constant.
 |
Fig. 2 Logarithm of the advective timescale (evaluated at ⟨ τR ⟩ = 1) as a function of the surface gravity. |
 |
Fig. 3 Logarithm of the density (evaluated at ⟨ τR ⟩ = 1) as a function of log Teff. |
 |
Fig. 4 Logarithm of the Mach number as a function of the logarithm of the density (both quantities evaluated at ⟨ τR ⟩ = 1). |
 |
Fig. 5 Logarithm of the Péclet number as a function of Mach number (both quantities evaluated at ⟨ τR ⟩ = 1). |
It is demonstrated in Fig. 4 that in the photosphere, the density correlates relatively well with the Mach number, the ratio of flow and sound speeds 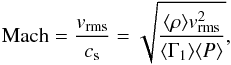 (3)where Γ1 is the first adiabatic exponent. We observe a small offset between white dwarfs, dwarfs and to a lesser degree giants for which we only have a few models. This is not entirely surprising since for a given density, the higher gravity objects have larger temperatures. The energy density is then higher, but the vertical velocity must also increase to obtain the desired convective flux, which is confirmed by the MLT equations. The hot white dwarfs are one exception, and they do not follow the trend since the convective to radiative flux ratio becomes increasingly small in these atmospheres. The CIFIST grid does not cover main-sequence A-stars where a similar downturn in the Mach number is observed from other CO5BOLD simulations (Kochukhov et al. 2007; Freytag et al. 2012).
(3)where Γ1 is the first adiabatic exponent. We observe a small offset between white dwarfs, dwarfs and to a lesser degree giants for which we only have a few models. This is not entirely surprising since for a given density, the higher gravity objects have larger temperatures. The energy density is then higher, but the vertical velocity must also increase to obtain the desired convective flux, which is confirmed by the MLT equations. The hot white dwarfs are one exception, and they do not follow the trend since the convective to radiative flux ratio becomes increasingly small in these atmospheres. The CIFIST grid does not cover main-sequence A-stars where a similar downturn in the Mach number is observed from other CO5BOLD simulations (Kochukhov et al. 2007; Freytag et al. 2012).
The Péclet number is the ratio of the radiative and advective timescales 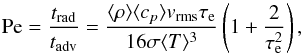 (4)where cp is the specific heat per gram, T the temperature, σ the Stefan-Boltzmann constant, and τe = ⟨ κR ⟩ ⟨ ρ ⟩ Hp the characteristic optical depth of a disturbance of a size Hp, with κR the Rosseland mean opacity per gram. This number indicates which will be the dominant energy transfer process for the formation and evolution of convective cells. This characteristic number is also proportional to the convective efficiency in the 1D MLT. The Péclet and Mach numbers have a tight relation in the photosphere according to Fig. 5, except for the hottest white dwarfs. This implies that Péclet number and density are also closely correlated. For log ρ ≲ − 6, the convection at τR ~ 1 becomes relatively inefficient and granules lose a significant part of their energy through radiation. The Péclet number is rapidly varying as a function of optical depth, and values in Fig. 5 should be taken as an order of magnitude estimate only.
(4)where cp is the specific heat per gram, T the temperature, σ the Stefan-Boltzmann constant, and τe = ⟨ κR ⟩ ⟨ ρ ⟩ Hp the characteristic optical depth of a disturbance of a size Hp, with κR the Rosseland mean opacity per gram. This number indicates which will be the dominant energy transfer process for the formation and evolution of convective cells. This characteristic number is also proportional to the convective efficiency in the 1D MLT. The Péclet and Mach numbers have a tight relation in the photosphere according to Fig. 5, except for the hottest white dwarfs. This implies that Péclet number and density are also closely correlated. For log ρ ≲ − 6, the convection at τR ~ 1 becomes relatively inefficient and granules lose a significant part of their energy through radiation. The Péclet number is rapidly varying as a function of optical depth, and values in Fig. 5 should be taken as an order of magnitude estimate only.
In the following, we rely on the logarithm of the Mach number as the reference variable to characterize most granulation properties. This quantity is not changing rapidly as a function of τR, hence the value at τR = 1 is a suitable control variable. Since Mach and Péclet numbers correlate well, and represent significantly different characteristics of the plasma, it is difficult to separate the effects of both characteristic numbers. We note that both numbers are derived from the simulated convective velocities, which is a quantity that can only be roughly approximated by 1D models. We will discuss further in Sect. 4.3 about how it is possible to overcome this issue.
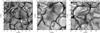 |
Fig. 6 Emergent bolometric intensity at the top of the horizontal xy plane for giant simulations at solar metallicity. The atmospheric parameters and the rms intensity contrast with respect to the mean intensity are given above the snapshots. The length of the upper bar in the top right is 10 times the pressure scale height at ⟨ τR ⟩ = 1. |
 |
Fig. 7 Emergent bolometric intensity for dwarf simulations at solar metallicity in the range 4000 < Teff (K) < 6750 with the atmospheric parameters given above the snapshots. |
 |
Fig. 8 Emergent bolometric intensity for dwarfs at different metallicities. In the first row, Teff = 4500 K, log g = 4.5, and [Fe/H] = − 1, − 2 and − 3 (from left to right). In the second row, Teff = 5900 K, log g = 4.5, and [Fe/H] varies again from − 1 to − 3. |
 |
Fig. 9 Emergent bolometric intensity for white dwarfs at Teff = 6000 (1st row), 9000 (2nd row), 11 000 (3rd row), and 12 500 K (4th row) and log g = 7.5, 8.0 and 8.5 (columns from left to right). |
3. Granulation properties
We derive in this section characteristic quantities computed from snapshots of the 3D simulations such as those presented in Fig. 6 (giants, solar metallicity), Fig. 7 (dwarfs, solar metallicity), Fig. 8 (dwarfs, different metallicities), and Fig. 9 (white dwarfs, pure-hydrogen). All snapshots are also available in Appendix A. It is immediately clear from the scales of the plots that gravity is the main factor in determining the size of convective cells, although granulation is otherwise visually very similar in most simulations across the HR diagram. The intensity contrast values, given above the snapshots, are however varying substantially with temperature. The following subsections aim at describing more quantitatively those observations.
The emergent intensity maps do depend on a certain range of the photosphere and proper (solar-type) granulation occurs when the transition from convectively unstable to stable is rather sharp. When the entropy minimum is rather wide, the layers where the overturning from up to down has to occur are not so well defined. In addition, the region where the visible light comes from is wider. This is likely the explanation why in cool white dwarfs (Fig. 9), where the entropy minimum is very wide and the Péclet number is large, granulation appears fuzzier than in dwarfs (Fig. 7).
In hotter white dwarfs, a different granulation pattern stands out with narrower cool downdrafts and hot cells with smoother edges. A similar effect is observed for red supergiants and main-sequence F- and A-stars (Freytag et al. 2012, see Fig. 15), both not included in this work.
In objects with a low intensity contrast, such as the white dwarfs at 6000 K in Fig. 9 but also main-sequence M-stars (Ludwig et al. 2006), vortical and knot structures are clearly seen in inter-granular lanes. Ludwig et al. (2006) suggest that the reduced level of horizontal shearing at low Mach number may be the explanation. Vortices are also observed and simulated in the Sun (Wedemeyer-Böhm et al. 2012), although they are less prominent in low resolution models.
3.1. Intensity contrast
The intensity contrast of surface granulation is a measure of the deviation from the plane-parallel approximation. The root-mean-square (rms) relative intensity contrast δIrms defined as 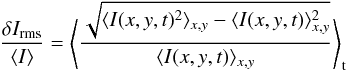 (5)is shown in Fig. 10 as a function of the Mach number in the photosphere. It is seen that the intensity contrast correlates well with Mach number over the full range of the HR diagram. This might not be entirely surprising since both the Mach number and the intensity contrast are a measure of the strength of convection. The low metallicity dwarfs appear to have a higher maximum intensity contrast than solar-like dwarfs and white dwarfs. This will be investigated further in Sect. 4. The white dwarf sequence has two branches at low Mach number, with cool white dwarfs under the quasi-adiabatic convection regime, and hot white dwarfs with small convective to radiative flux ratios. In both cases, the lower intensity contrast can be explained by a smaller amount of energy to be transported by convection. Given the rather different physical conditions (e.g. density and Péclet number) in those atmospheres, it is expected that the Mach number will not uniquely describe the intensity contrast.
(5)is shown in Fig. 10 as a function of the Mach number in the photosphere. It is seen that the intensity contrast correlates well with Mach number over the full range of the HR diagram. This might not be entirely surprising since both the Mach number and the intensity contrast are a measure of the strength of convection. The low metallicity dwarfs appear to have a higher maximum intensity contrast than solar-like dwarfs and white dwarfs. This will be investigated further in Sect. 4. The white dwarf sequence has two branches at low Mach number, with cool white dwarfs under the quasi-adiabatic convection regime, and hot white dwarfs with small convective to radiative flux ratios. In both cases, the lower intensity contrast can be explained by a smaller amount of energy to be transported by convection. Given the rather different physical conditions (e.g. density and Péclet number) in those atmospheres, it is expected that the Mach number will not uniquely describe the intensity contrast.
The behaviour observed in Fig. 10 is also predicted qualitatively by the mixing-length theory. The temperature fluctuation between a convective element and its surroundings is related to the convective velocity according to 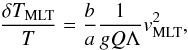 (6)where Q is the isobaric expansion coefficient, a and b are commonly used free parameters defining the convective flux and the velocity, respectively, and Λ is the mixing-length (Mihalas 1978; Tassoul et al. 1990; Ludwig et al. 1999). A relation can also be found for temperature fluctuations as a function of Péclet number (derived from the MLT convective efficiency). We have solved the MLT equations for the mean 3D structures and found that inside the convective zones, temperature fluctuations are indeed increasing with Mach number. However, it is difficult to compare directly the results to Fig. 10 since the τR = 1 region is sometimes convectively stable according to the MLT, and also because of the free parameters in Eq. (6). Nevertheless, MLT supports the view that the intensity contrast is a function of the Mach or the Péclet numbers.
(6)where Q is the isobaric expansion coefficient, a and b are commonly used free parameters defining the convective flux and the velocity, respectively, and Λ is the mixing-length (Mihalas 1978; Tassoul et al. 1990; Ludwig et al. 1999). A relation can also be found for temperature fluctuations as a function of Péclet number (derived from the MLT convective efficiency). We have solved the MLT equations for the mean 3D structures and found that inside the convective zones, temperature fluctuations are indeed increasing with Mach number. However, it is difficult to compare directly the results to Fig. 10 since the τR = 1 region is sometimes convectively stable according to the MLT, and also because of the free parameters in Eq. (6). Nevertheless, MLT supports the view that the intensity contrast is a function of the Mach or the Péclet numbers.
On the other hand, we can also study the relative temporal variation of the spatially averaged intensity defined as 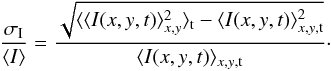 (7)For a fixed point on the stellar disk, i.e. without averaging, the temporal intensity variation is the same as the spatial variation δIrms from the principle of ergodicity. However, the temporal intensity variation decreases as more convective cells are included in the spatial average, hence it is a function of the horizontal extent of a simulation. Ludwig (2006) derived the following relation between the temporal and geometrical intensity variation
(7)For a fixed point on the stellar disk, i.e. without averaging, the temporal intensity variation is the same as the spatial variation δIrms from the principle of ergodicity. However, the temporal intensity variation decreases as more convective cells are included in the spatial average, hence it is a function of the horizontal extent of a simulation. Ludwig (2006) derived the following relation between the temporal and geometrical intensity variation 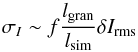 (8)where lgran is the characteristic size of granules and
(8)where lgran is the characteristic size of granules and 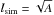 the linear size of the box. The factor f of order unity arises in part from the fact that the intensities are spatially correlated in granules and Ludwig (2006) approximates the value to 0.4 for solar granulation. We have computed σI and characteristic granulation sizes (see Sect. 3.2) for the CIFIST grid and find that f covers the full range 0.2 − 0.6. While it is out of the scope of this work, these results could be expanded to the full observable disk of stars to predict the photometric variability (or granulation power), especially in the case of giants with fewer and larger granules (Schwarzschild 1975).
the linear size of the box. The factor f of order unity arises in part from the fact that the intensities are spatially correlated in granules and Ludwig (2006) approximates the value to 0.4 for solar granulation. We have computed σI and characteristic granulation sizes (see Sect. 3.2) for the CIFIST grid and find that f covers the full range 0.2 − 0.6. While it is out of the scope of this work, these results could be expanded to the full observable disk of stars to predict the photometric variability (or granulation power), especially in the case of giants with fewer and larger granules (Schwarzschild 1975).
The temporal Teff variation σTeff is expected to scale approximately as one-fourth of the intensity variation. We note in Table 1 that for the CIFIST grid, σTeff < 0.6% which is indeed verified by Eq. (8) given a maximum observed value of δIrms ~ 25%, and the requirement that at least 3 × 3 granules are resolved in the simulations. This result is of practical interest for spectral synthesis applications. Typically, 3D spectra calculations rely on the order of 20 snapshots, although in many cases the snapshots are specifically chosen so that Teff does not deviate substantially from the average (Allende Prieto et al. 2013). Our results suggest that that even a random selection of about 20 snapshots would provide a very good representation (i.e. with an accuracy much better than 1%) of the mean atmospheric structure of any stellar simulation.
 |
Fig. 10 Rms relative intensity contrast as a function of the logarithm of the Mach number (evaluated at ⟨ τR ⟩ = 1). |
 |
Fig. 11 Mean power spectra as a function of the horizontal wavenumber (2π/λ) averaged over snapshots of the (bolometric) intensity of the Teff = 5000 K, log g = 4.5, [Fe/H] = 0 (left panel) and Teff = 12 500 K, log g = 8.0 (right panel) simulations. |
3.2. Characteristic size
We have performed a study of the characteristic power carrying lengths by computing a power spectrum as a function of wavenumber for all available emergent intensity maps. The mean power spectrum over all snapshots of one simulation is shown in Fig. 11 for two typical cases. All power spectra are available in Appendix A. We display power per logarithmic wavenumber interval for a more direct identification of the power carrying scales (Ludwig et al. 2002). The CIFIST grid was computed with the qualitative requirement that at least of the order of 3 × 3 cells are simulated. In other words, the power spectrum peak should be relatively well resolved for all simulations. We have derived the characteristic horizontal granulation size, i.e. the wavelength of the peak of the power spectra, with third-order polynomial fits (25 points around the maximum). The dwarf and white dwarf in Fig. 11 have rather similar power spectra. Over all simulations, the mean full-width at half-maximum (FWHM) is 2.1 in characteristic size unit, with a very small dependence on the atmospheric parameters.
It is well known that the shape of the granules can be influenced by either explicit or implicit (finite resolution) viscosity. Figure 12 illustrates that the power peak remains at the same wavenumber when horizontal resolution is increased by a factor of two. On the other hand, the shape of the high wavenumber tail is significantly different, with more fine structures in the high resolution case. For the purpose of this work, it demonstrates that the characteristic granulation size is rather insensitive to numerical parameters.
Early calculations of 2D model atmospheres have shown that granules typically have an horizontal size about 10 times the local pressure scale height, which is also a measure of the vertical extent of the granules (Freytag et al. 1997). In Fig. 13 (left panel), we present the ratio of the characteristic granulation size to the hydrostatic pressure scale height at ⟨ τR ⟩ = 1. We conclude that the characteristic size is far from a constant fraction of Hp. In the objects with the most vigorous convection, the ratio is typically around 10, although for objects with very low Mach numbers, the ratio reaches a plateau around a value of ~3–4. It is shown that dwarfs with solar metallicity have larger sizes and deviate slightly from the relation traced by sub-solar metallicity dwarfs and white dwarfs.
To understand the characteristic size variation, we consider a simple analytical model of convection (Steffen et al. 1989) with an horizontal arrangement of square cells of size L such that the mass flux is approximated by 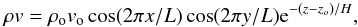 (9)where H is the vertical scale height of the momentum density and zo a reference layer. For such a pattern, the continuity equation implies that
(9)where H is the vertical scale height of the momentum density and zo a reference layer. For such a pattern, the continuity equation implies that 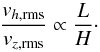 (10)where
(10)where 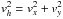 . We have verified that the momentum density and pressure scale heights are the same within a few percent, except for hot models with small convective fluxes. Hence, to first order, the variation of Char. size/Hp on Fig. 13 could simply be related to an increasing horizontal versus vertical velocity ratio (Steffen et al. 1989; Nordlund et al. 2009), which is presented in Fig. 14. We indeed observe that the horizontal velocities become proportionally larger for Mach numbers of order unity, although the slope of the Char. size/Hp relation as a function of Mach number is steeper than the vh/vz relation. We have found that the culprit for this discrepancy is that the Hp value at τR ~ 1, assuming hydrostatic equilibrium (Eq. (1)), does not represent particularly well the actual geometrical dimension of one (dynamical) pressure scale height in the 3D simulations. In the right panel of Fig. 13, we relied on the actual value of the pressure scale height below the photosphere that is found in the simulations
. We have verified that the momentum density and pressure scale heights are the same within a few percent, except for hot models with small convective fluxes. Hence, to first order, the variation of Char. size/Hp on Fig. 13 could simply be related to an increasing horizontal versus vertical velocity ratio (Steffen et al. 1989; Nordlund et al. 2009), which is presented in Fig. 14. We indeed observe that the horizontal velocities become proportionally larger for Mach numbers of order unity, although the slope of the Char. size/Hp relation as a function of Mach number is steeper than the vh/vz relation. We have found that the culprit for this discrepancy is that the Hp value at τR ~ 1, assuming hydrostatic equilibrium (Eq. (1)), does not represent particularly well the actual geometrical dimension of one (dynamical) pressure scale height in the 3D simulations. In the right panel of Fig. 13, we relied on the actual value of the pressure scale height below the photosphere that is found in the simulations ![\begin{equation} H_{\rm p, dynamical} = z(\langle\tau_\mathrm{R}\rangle = 1)-z(\ln\,[P/P_{\langle\tau_\mathrm{R}\rangle = 1}] = 1)~, \end{equation}](/articles/aa/full_html/2013/09/aa21878-13/aa21878-13-eq88.png) (11)as well as the mean Mach number over the same range. The dynamical pressure scale height can be significantly larger than the local hydrostatic estimate, to an extent that Char. size/Hp,dynamical is now varying by a factor of ~2 across the CIFIST grid, in very good agreement with our simple analytical model of mass conservation (Eq. (10)) and Fig. 14. A further study of the depths of the granules, in addition to their widths derived here, could reveal more information about which layers are relevant for the granulation formation.
(11)as well as the mean Mach number over the same range. The dynamical pressure scale height can be significantly larger than the local hydrostatic estimate, to an extent that Char. size/Hp,dynamical is now varying by a factor of ~2 across the CIFIST grid, in very good agreement with our simple analytical model of mass conservation (Eq. (10)) and Fig. 14. A further study of the depths of the granules, in addition to their widths derived here, could reveal more information about which layers are relevant for the granulation formation.
 |
Fig. 12 Mean power spectra as a function of the horizontal wavenumber for simulations at Teff = 5750 K, log g = 3.75, and [Fe/H] = − 3 with a resolution of 140 × 140 × 150 (solid line) and 220 × 220 × 150 (dotted line). |
3.3. Characteristic lifetime
We turn our attention in this section to the time evolution of granulation. The power spectra of the local temporal variation of intensity Ix,y(t) reach a nearly constant value at low frequencies, hence it is difficult to define a characteristic lifetime from the peak of the mean power spectra, averaged over all pixels, as we did for characteristic lengths. In the field of asteroseismology, the spectral power density P is often characterised by a generalised Harvey model (Harvey 1985; Ludwig et al. 2009a) 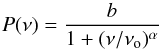 (12)where ν is the cyclic temporal frequency. All other variables are fitting parameters and in particular νo could be interpreted as the characteristic frequency of the granulation cycle. The Wiener-Khinchin theorem implies that we can derive the related autocorrelation function
(12)where ν is the cyclic temporal frequency. All other variables are fitting parameters and in particular νo could be interpreted as the characteristic frequency of the granulation cycle. The Wiener-Khinchin theorem implies that we can derive the related autocorrelation function 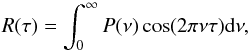 (13)where τ is the time lag. As an example, for an exponent α = 2 in Eq. (12), it is found that
(13)where τ is the time lag. As an example, for an exponent α = 2 in Eq. (12), it is found that 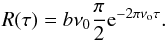 (14)It implies that the characteristic cycle timescale
(14)It implies that the characteristic cycle timescale 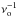 is 2π times larger than the e-folding decay time (te - fold) of the autocorrelation function. In Table 2, we provide the characteristic te - fold for three different power fitting functions. It shows that by varying the power spectrum fitting function, the related decay time can be significantly different. Since it is difficult to choose a single α parameter in Eq. (12) for all 3D simulations, we have decided to compute only the e-folding decay time of autocorrelation, averaged over all pixels. An estimate of the corresponding cycle timescale
is 2π times larger than the e-folding decay time (te - fold) of the autocorrelation function. In Table 2, we provide the characteristic te - fold for three different power fitting functions. It shows that by varying the power spectrum fitting function, the related decay time can be significantly different. Since it is difficult to choose a single α parameter in Eq. (12) for all 3D simulations, we have decided to compute only the e-folding decay time of autocorrelation, averaged over all pixels. An estimate of the corresponding cycle timescale 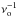 can be computed from Table 2.
can be computed from Table 2.
Relation between temporal frequency and decay time
For the CIFIST grid, we present in Fig. 15 the ratio of our derived te - fold decay time, and the semi-analytical advective timescale Hp/vrms, where vrms is also drawn from the 3D simulations. We find that the decay time correlates well with Mach number, and unsurprisingly, simulations with a large characteristic size to Hp ratio have longer lifetimes. The observed decay times would be roughly in agreement with the advective timescales by relying on characteristic sizes instead of Hp.
 |
Fig. 13 Left: ratio of the characteristic granular size to the pressure scale height as a function of the logarithm of the Mach number (both quantities evaluated at ⟨ τR ⟩ = 1). Right: same as left panel but with the actual pressure scale height below the photosphere that is found in the 3D simulations (see Eq. (11)). |
We observe that hot white dwarfs feature very short lifetimes, even given their relatively small granule sizes. According to the Péclet number values of Fig. 5, the characteristic radiative timescale is much smaller than the advective timescale in those atmospheres which could explain a faster evolution of granules. However, hot stars in the CIFIST grid with the same Péclet numbers still scale well with the advective timescale. The main difference between those objects is that the stars are fully convective below the photosphere while hot white dwarfs have a thin convective zone with the maximum convective to radiative flux ratio reaching a small value. The enhanced radiative energy transport below the photosphere in white dwarfs may have an effect on the evolution of granulation. It would be interesting to compare hot white dwarfs and A-stars with thin convective zones. The convection in main-sequence stars is also driven by helium ionization, hence these objects may behave differently than hot pure-hydrogen white dwarfs. Finally, our decay times could be compared to the granulation timescales derived from power spectra of Kepler or CoRoT observations (see, e.g., Mathur et al. 2011).
 |
Fig. 14 Ratio of the horizontal to vertical rms velocity as a function of the Mach number (both quantities evaluated at ⟨ τR ⟩ = 1). |
 |
Fig. 15 Ratio of the characteristic decay time to the advective timescale as a function of the logarithm of the Mach number (both quantities evaluated at ⟨ τR ⟩ = 1). |
4. Discussion
We have demonstrated that the characteristic granulation size, and to a lesser degree the relative intensity contrast and the characteristic lifetime, scale well with the Mach number in the intensity forming region. The Mach number is itself closely anti-correlated with the local density (except for hot white dwarfs), since a lower density implies higher vertical velocities to transport the same amount of energy by convection. To a lesser degree, the Mach number is also sensitive to the temperature of the photosphere, since a higher effective temperature implies a larger total energy to transport.
One significant surprise of our analysis is that for low Mach numbers, properties are very similar for cool white dwarfs with quasi-adiabatic photospheric convection and hot white dwarfs with low Péclet numbers and inefficient convection. In other words, the convective efficiency does not seem to be a dominant factor in the determination of the mean size and contrast of granules across the HR diagram.
4.1. Metallicity
The effects of metallicity on the granulation are subtle (see also Allende Prieto et al. 2013; Magic et al. 2013). For a fixed Teff and log g, the density in the photosphere is generally increasing for lower metallicities, hence the Mach number is lower, as are the characteristic granulation size and the intensity contrast (Houdek et al. 1999; Samadi et al. 2010). This can be observed qualitatively in Fig. 8 since the simulations at different metallicities have the same geometrical dimensions. However, this is only one aspect since for a given density or Mach number, the intensity contrast is generally higher for low metallicity stars (see Fig. 10). The source of this behaviour is likely the fact that for a given Mach number, the convective efficiency is slightly higher for sub-solar metallicities according to Fig. 5. Hence, the rising cells in low metallicity dwarfs loose less energy by radiation at τR ~ 1, and produce a slightly higher intensity contrast. The same effect would cause the hot white dwarfs with inefficient convection to have a slightly lower intensity contrast than cool white dwarfs with quasi-adiabatic convection, but the same Mach number.
 |
Fig. 16 Relative intensity distribution for white dwarfs at Teff = 6000 (left), 9000 (middle) and 12,500 K (right panel) and log g = 8.0. The Mach and Péclet numbers are identified on each panel. |
4.2. Convective efficiency
Our analysis has so far looked at the mean characteristics of granulation, disregarding the differences between upflows and downflows seen in the intensity snapshots of Figs. 6–9. In Fig. 16, we present the relative intensity distribution for three white dwarfs from the cool to hot end of the sequence. All intensity distributions are available in Appendix A. The rms relative intensity contrast previously discussed in this work is directly evaluated from the intensity distribution of individual snapshots. Figure 16 demonstrates that both upflows and downflows have a characteristic distribution which results in a double-peaked relative intensity distribution. The sign of the local intensity contrast does not necessarily imply a direction for the convective flow. For instance, some of the downflows may be very bright (Ludwig & Kučinskas 2012). Therefore, it is not easily possible from the intensity snapshots to characterise the rms contrast of upflows and downflows. Nevertheless, we can still look at the position of the peak of the respective distributions. Figure 16 shows that in some cases there is a significant asymmetry between upflows and downflows. For the 12 500 K white dwarf model, the downflows have an intensity peak further away from the mean intensity than the upflows, especially in comparison to the 9000 K case where upflows and downflows appear to have a similar distribution.
 |
Fig. 17 Fraction of the geometrical surface (A) where the intensity is higher than the average as a function of the logarithm of the Péclet number evaluated at ⟨ τR ⟩ = 1. The dashed line represents an even distribution of bright and dark cells. |
In Fig. 17 we derive the fraction of the geometrical surface where the intensity is higher than the average, as a function of Péclet number. It confirms the earlier observation made on intensity snapshots that for hot objects and especially white dwarfs, the fraction of the area occupied by bright granules can be considerably larger than for cooler objects. The minimum seen in Fig. 17 at about Pe = 1 suggests that variation of the Péclet number could be a significant factor for this asymmetry, although the Mach number certainly has a role as well given the second inflection in the white dwarf sequence at low Péclet numbers. In summary, Péclet number appears to have a noticeable effect on the shape of granules and the asymmetry between bright cells and dark lanes (roughly approximated as upflows and downflows), although it does not translate into a strong effect on the characteristic sizes.
4.3. Parameterisation of 3D convective properties
We have mentioned that the Mach number is a quantity that can not easily be predicted a priori of a 3D simulation. The MLT predicts velocities but they are rather depth dependent in the photosphere and the free parameters in the theory needs to be adjusted for this application, e.g. by comparing 1D and 3D velocities. We have therefore attempted to characterise granulation properties as a function of the atmospheric parameters, similarly to Trampedach et al. (2013). We find that the following parameterisations provide characteristic sizes and decay times with a standard deviation2 of ~30% which we believe is a reasonable error given that the characteristic values are estimates. ![\begin{equation} \frac{\rm Char.~size}{\rm [km]} = 13.5 g^{-1} [T_{\rm eff}-300\log g]^{1.75} 10^{0.05 \rm [Fe/H]}, \end{equation}](/articles/aa/full_html/2013/09/aa21878-13/aa21878-13-eq111.png) (15)
(15)![\begin{equation} \frac{\rm Decay~time}{\rm [s]} = 2.08 g^{-1} [T_{\rm eff}-300\log g]^{1.75} 10^{0.05 \rm [Fe/H]}, \end{equation}](/articles/aa/full_html/2013/09/aa21878-13/aa21878-13-eq112.png) (16)where Teff is in K units, g in cgs units, and white dwarfs are assumed to have [Fe/H] = − 4. Equations (15) and (16) are only valid within the range of the HR diagram studied in this work, i.e. for convective objects with Teff ≳ 600log g.
(16)where Teff is in K units, g in cgs units, and white dwarfs are assumed to have [Fe/H] = − 4. Equations (15) and (16) are only valid within the range of the HR diagram studied in this work, i.e. for convective objects with Teff ≳ 600log g.
Compared to the parameterisation given in Trampedach et al. (2013), we find sizes that are ~20% larger for solar-metallicity dwarfs. Furthermore, our rms intensity contrasts are on average ~10% lower. We have currently no explanation for this discrepancy. The comparison with observed granulation properties (Title et al. 1989; Rieutord et al. 2010; Mathur et al. 2011; Samadi et al. 2013) could help in further constraining the different predictions. However, the different codes are currently in fairly good agreement (Beeck et al. 2012) while the comparison with observations for stars other than the Sun shows larger deviations (Ludwig et al. 2009a; Mathur et al. 2011).
It is hoped that our findings that granulation is very similar across the HR diagram will help in improving the 1D models of convection. Given the completely different nature of 1D and 3D models, it is difficult to find any direct implications for the 1D MLT parameterisation. However, our results could be useful for more sophisticated models, such as the 2-column (up- and downflow) model of Stökl (2008). This treatment requires the geometry of both columns, and therefore would also require a more detailed study of the asymmetry between upflows and downdrafts.
5. Conclusions
The characteristic granulation properties were investigated for the 148 3D model atmospheres of dwarfs, giants, and white dwarfs in the CIFIST grid. We have derived the ratio of the characteristic horizontal size to the pressure scale height in the intensity forming region and showed that it is strongly correlated with the Mach number. The ratio increases from values of 3 (Mach = 0.1) to 10 (Mach ~ 1). This variation is caused by the increase of the horizontal to vertical velocity ratio as a function of Mach number and the resulting constraint from the mass conservation. A more quantitative explanation would require the computation of the characteristic depths of the granules and the dynamical pressure scale height over the same geometrical range.
The decay time and relative intensity contrast are also shown to be correlated with Mach number, but it appears that the convective efficiency, or Péclet number, which is rapidly changing as a function of depth, also has a considerable effect. The intensity contrast increases with the efficiency of convection for a constant Mach number. Finally, we provided fitting functions for the characteristic horizontal size and decay time of granulation across the HR diagram as a function of Teff, log g and [Fe/H] that can be useful for further hydrodynamical calculations and asteroseismic applications.
Our characteristic values certainly do not represent the full picture. A close examination of the intensity maps presented in this work shows that the shape of the individual convective cells, e.g. the brightness profile, the fuzziness of the edges and the apparition of vortices, is a function of the atmospheric parameters and does not necessarily scale well with the Mach number. These substructures may also be impacted by numerics and neglected magnetic fields. We observe an asymmetry between the size of the bright cells and dark narrow lanes which appears to be correlated with both the Mach and Péclet numbers in a complex way. Future works may study this aspect in more detail, for instance by combining intensity maps with a set of velocity maps at certain depths. The velocity maps may also provide characteristic depths for the granules reaching the photosphere, which would improve our understanding of surface granulation.
Online material
Grid of CIFIST 3D model atmospheres.
Appendix A: Intensity snapshots and related distributions from the CIFIST grid
 |
Fig. A.1 Left: emergent bolometric intensity at the top of the horizontal xy plane for the 148 simulations in the CIFIST grid. The figures are ordered with 1) increasing log g; 2) increasing Teff; and 3) decreasing [Fe/H]. The atmospheric parameters and the rms intensity contrast with respect to the mean intensity are given above the snapshots. The length of the upper bar in the top right is 10 times the pressure scale height at τR ~ 1. Center: mean power spectra as a function of the horizontal wavenumber (2π/λ) averaged over snapshots of the intensity map. Right: relative intensity distribution with the Mach and logarithm of Péclet numbers (both evaluated at ⟨ τR ⟩ = 1) identified on the panel. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
We exclude hot white dwarfs with a thin convective zone and short decay times in Fig. 15 since they are poorly represented by our parameterisation.
Acknowledgments
P.-E.T. is supported by the Alexander von Humboldt Foundation. 3D model calculations of white dwarfs have been performed on CALYS, a mini-cluster of 320 nodes built at Université de Montréal with the financial help of the Fondation Canadienne pour l’Innovation. This work was supported by Sonderforschungsbereich SFB 881 “The Milky Way System” (Subproject A4) of the German Research Foundation (DFG). B.F. acknowledges financial support from the Agence Nationale de la Recherche (ANR), and the “Programme Nationale de Physique Stellaire” (PNPS) of CNRS/INSU, France.
References
- Allen de Prieto, C., Koesterke, L., Ludwig, H.-G., Freytag, B., & Caffau, E. 2013, A&A, 550, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Beeck, B., Collet, R., Steffen, M., et al. 2012, A&A, 539, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergeron, P., Wesemael, F., Lamontagne, R., et al. 1995, ApJ, 449, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Bergeron, P., Wesemael, F., Dufour, P., et al. 2011, ApJ, 737, 28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., & Bonifacio, P. 2011, Sol. Phys., 268, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Chiavassa, A., Plez, B., Josselin, E., & Freytag, B. 2009, A&A, 506, 1351 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Chiavassa, A., Haubois, X., Young, J. S., et al. 2010, A&A, 515, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colella, P. 1990, J. Comput. Phys., 87, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Danilovic, S., Schüssler, M., & Solanki, S. K. 2010, A&A, 513, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dupret, M.-A., Belkacem, K., Samadi, R., et al. 2009, A&A, 506, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freytag, B. 2013, Mem. Soc. Astron. Italiana, in press [Google Scholar]
- Freytag, B., Holweger, H., Steffen, M., & Ludwig, H.-G. 1997, in Science wth the VLT Interferometer, ed. F. Paresce (New York: Springer), 316 [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2012, J. Comput. Phys., 231, 919 [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1993, A&A, 271, 451 [NASA ADS] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Gough, D. O., Moore, D. R., Spiegel, E. A., & Weiss, N. O. 1976, ApJ, 206, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harvey, J. 1985, Future Missions in Solar, Heliospheric & Space Plasma Physics, 235, 199 [Google Scholar]
- Houdek, G., Balmforth, N. J., Christensen-Dalsgaard, J., & Gough, D. O. 1999, A&A, 351, 582 [NASA ADS] [Google Scholar]
- Kochukhov, O., Freytag, B., Piskunov, N., & Steffen, M. 2007, IAU Symp., 239, 68 [Google Scholar]
- Kučinskas, A., Steffen, M., Ludwig, H.-G., et al. 2013, A&A, 549, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lites, B. W. 2011, ApJ, 737, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Ludwig, H.-G. 2006, A&A, 445, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ludwig, H.-G., & Kučinskas, A. 2012, A&A, 547, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ludwig, H.-G., Jordan, S., & Steffen, M. 1994, A&A, 284, 105 [NASA ADS] [Google Scholar]
- Ludwig, H.-G., Freytag, B., & Steffen, M. 1999, A&A, 346, 111 [NASA ADS] [Google Scholar]
- Ludwig, H.-G., Allard, F., & Hauschildt, P. H. 2002, A&A, 395, 99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ludwig, H.-G., Allard, F., & Hauschildt, P. H. 2006, A&A, 459, 599 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ludwig, H.-G., Samadi, R., Steffen, M., et al. 2009a, A&A, 506, 167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ludwig, H.-G., Caffau, E., Steffen, M., et al. 2009b, Mem. Soc. Astron. It., 80, 711 [NASA ADS] [Google Scholar]
- Magic, Z., Collet, R., Asplund, M., et al. 2013, A&A, in press, DOI: 10.1051/0004-6361/201321274 [Google Scholar]
- Massaguer, J. M., & Zahn, J.-P. 1980, A&A, 87, 315 [NASA ADS] [Google Scholar]
- Mathur, S., Hekker, S., Trampedach, R., et al. 2011, ApJ, 714, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D. 1978, Stellar Atmospheres, 2nd edn. (W. H. Freeman and Co.) [Google Scholar]
- Nordlund, Å. 1982, A&A, 107, 1 [Google Scholar]
- Nordlund, Å., Stein, R. F., & Asplund, M. 2009, Living Rev. Sol. Phys., 6, 2 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rieutord, M., Roudier, T., Rincon, F., et al. 2010, A&A, 512, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samadi, R., Ludwig, H.-G., Belkacem, K., et al. 2010, A&A, 509, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samadi, R., Belkacem, K., Ludwig, H.-G., et al. 2013, A&A, accepted [Google Scholar]
- Schwarzschild, M. 1975, ApJ, 195, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, M., Ludwig, H.-G., & Kruess, A. 1989, A&A, 213, 371 [NASA ADS] [Google Scholar]
- Stein, R. F., & Nordlund, A. 1998, ApJ, 499, 914 [Google Scholar]
- Stökl, A. 2008, A&A, 490, 1181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tassoul, M., Fontaine, G., & Winget, D. E. 1990, ApJS, 72, 335 [Google Scholar]
- Title, A. M., Tarbell, T. D., Topka, K. P., et al. 1989, ApJ, 336, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Trampedach, R., Asplund, M., Collet, R., Nordlund, Å., & Stein, R. F. 2013, ApJ, 769, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Tremblay, P.-E., Bergeron, P., & Gianninas, A. 2011a, ApJ, 730, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Tremblay, P.-E., Ludwig, H.-G., Steffen, M., Bergeron, P., & Freytag, B. 2011b, A&A, 531, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tremblay, P.-E., Ludwig, H.-G., Steffen, M., & Freytag, B. 2013, A&A, 552, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vögler, A., Bruls, J. H. M. J., & Schüssler, M. 2004, A&A, 421, 741 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer-Böhm, S., & Rouppe van der Voort, L. 2009, A&A, 503, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer-Böhm, S., Scullion, E., Steiner, O., et al. 2012, Nature, 486, 505 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Surface gravity and mean Teff for the 3D model atmospheres in the CIFIST grid. The top-left (circles), top-right (stars), bottom-left (squares) and bottom-right (triangles) panels represent different metallicities, with [Fe/H] = 0, − 1, − 2 and − 3, respectively. For simplicity, pure-hydrogen white dwarfs (open triangles) are represented along the [Fe/H] = − 3 stars (note the different scale for this panel). Teff values are colour-coded from red (cool) to blue (hot) and log g values (cgs units) are size-coded from small (high gravity) to large (low gravity) symbols. The x- and y-axis can be used as legends for the following figures. There is no link between white dwarfs and stars with the same sizes and colours. |
| In the text | |
 |
Fig. 2 Logarithm of the advective timescale (evaluated at ⟨ τR ⟩ = 1) as a function of the surface gravity. |
| In the text | |
 |
Fig. 3 Logarithm of the density (evaluated at ⟨ τR ⟩ = 1) as a function of log Teff. |
| In the text | |
 |
Fig. 4 Logarithm of the Mach number as a function of the logarithm of the density (both quantities evaluated at ⟨ τR ⟩ = 1). |
| In the text | |
 |
Fig. 5 Logarithm of the Péclet number as a function of Mach number (both quantities evaluated at ⟨ τR ⟩ = 1). |
| In the text | |
 |
Fig. 6 Emergent bolometric intensity at the top of the horizontal xy plane for giant simulations at solar metallicity. The atmospheric parameters and the rms intensity contrast with respect to the mean intensity are given above the snapshots. The length of the upper bar in the top right is 10 times the pressure scale height at ⟨ τR ⟩ = 1. |
| In the text | |
 |
Fig. 7 Emergent bolometric intensity for dwarf simulations at solar metallicity in the range 4000 < Teff (K) < 6750 with the atmospheric parameters given above the snapshots. |
| In the text | |
 |
Fig. 8 Emergent bolometric intensity for dwarfs at different metallicities. In the first row, Teff = 4500 K, log g = 4.5, and [Fe/H] = − 1, − 2 and − 3 (from left to right). In the second row, Teff = 5900 K, log g = 4.5, and [Fe/H] varies again from − 1 to − 3. |
| In the text | |
 |
Fig. 9 Emergent bolometric intensity for white dwarfs at Teff = 6000 (1st row), 9000 (2nd row), 11 000 (3rd row), and 12 500 K (4th row) and log g = 7.5, 8.0 and 8.5 (columns from left to right). |
| In the text | |
 |
Fig. 10 Rms relative intensity contrast as a function of the logarithm of the Mach number (evaluated at ⟨ τR ⟩ = 1). |
| In the text | |
 |
Fig. 11 Mean power spectra as a function of the horizontal wavenumber (2π/λ) averaged over snapshots of the (bolometric) intensity of the Teff = 5000 K, log g = 4.5, [Fe/H] = 0 (left panel) and Teff = 12 500 K, log g = 8.0 (right panel) simulations. |
| In the text | |
 |
Fig. 12 Mean power spectra as a function of the horizontal wavenumber for simulations at Teff = 5750 K, log g = 3.75, and [Fe/H] = − 3 with a resolution of 140 × 140 × 150 (solid line) and 220 × 220 × 150 (dotted line). |
| In the text | |
 |
Fig. 13 Left: ratio of the characteristic granular size to the pressure scale height as a function of the logarithm of the Mach number (both quantities evaluated at ⟨ τR ⟩ = 1). Right: same as left panel but with the actual pressure scale height below the photosphere that is found in the 3D simulations (see Eq. (11)). |
| In the text | |
 |
Fig. 14 Ratio of the horizontal to vertical rms velocity as a function of the Mach number (both quantities evaluated at ⟨ τR ⟩ = 1). |
| In the text | |
 |
Fig. 15 Ratio of the characteristic decay time to the advective timescale as a function of the logarithm of the Mach number (both quantities evaluated at ⟨ τR ⟩ = 1). |
| In the text | |
 |
Fig. 16 Relative intensity distribution for white dwarfs at Teff = 6000 (left), 9000 (middle) and 12,500 K (right panel) and log g = 8.0. The Mach and Péclet numbers are identified on each panel. |
| In the text | |
 |
Fig. 17 Fraction of the geometrical surface (A) where the intensity is higher than the average as a function of the logarithm of the Péclet number evaluated at ⟨ τR ⟩ = 1. The dashed line represents an even distribution of bright and dark cells. |
| In the text | |
 |
Fig. A.1 Left: emergent bolometric intensity at the top of the horizontal xy plane for the 148 simulations in the CIFIST grid. The figures are ordered with 1) increasing log g; 2) increasing Teff; and 3) decreasing [Fe/H]. The atmospheric parameters and the rms intensity contrast with respect to the mean intensity are given above the snapshots. The length of the upper bar in the top right is 10 times the pressure scale height at τR ~ 1. Center: mean power spectra as a function of the horizontal wavenumber (2π/λ) averaged over snapshots of the intensity map. Right: relative intensity distribution with the Mach and logarithm of Péclet numbers (both evaluated at ⟨ τR ⟩ = 1) identified on the panel. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


