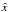| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A69 | |
| Number of page(s) | 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201321820 | |
| Published online | 02 September 2013 | |
YSO accretion shocks: magnetic, chromospheric or stochastic flow effects can suppress fluctuations of X-ray emission
1
CEA, IRAMIS,
Service Photons, Atomes et Molécules, 91191
Gif-sur-Yvette,
France
e-mail:
titos.matsakos@cea.fr
2
Laboratoire AIM, CEA/DSM – CNRS – Université Paris Diderot,
IRFU/Service d’Astrophysique, CEA Saclay, Orme des Merisiers, 91191
Gif-sur-Yvette,
France
3
LERMA, Observatoire de Paris, Université Pierre et Marie Curie and
CNRS, 5 Place J.
Janssen, 92195
Meudon,
France
4
Université Paris Diderot, Sorbonne Paris Cité, AIM, UMR 7158, CEA,
CNRS, 91191
Gif-sur-Yvette,
France
5
Laboratoire Lagrange, Université de Nice-Sophia Antipolis, CNRS,
Observatoire de la Côte d’Azur, 06304
Nice Cedex 4,
France
6
INAF – Osservatorio Astronomico di Palermo, Piazza del Parlamento
1, 90134
Palermo,
Italy
7
Dipartimento di Fisica e Chimica, Università degli Studi di
Palermo, Piazza del Parlamento
1, 90134
Palermo,
Italy
Received:
2
May
2013
Accepted:
15
July
2013
Context. Theoretical arguments and numerical simulations of radiative shocks produced by the impact of the accreting gas onto young stars predict quasi-periodic oscillations in the emitted radiation. However, observational data do not show evidence of such periodicity.
Aims. We investigate whether physically plausible perturbations in the accretion column or in the chromosphere could disrupt the shock structure influencing the observability of the oscillatory behavior.
Methods. We performed local 2D magneto-hydrodynamical simulations of an accretion shock impacting a chromosphere, taking optically thin radiation losses and thermal conduction into account. We investigated the effects of several perturbation types, such as clumps in the accretion stream or chromospheric fluctuations, and also explored a wide range of plasma-β values.
Results. In the case of a weak magnetic field, the post-shock region shows chaotic motion and mixing, smoothing out the perturbations and retaining a global periodic signature. On the other hand, a strong magnetic field confines the plasma in flux tubes, which leads to the formation of fibrils that oscillate independently. Realistic values for the amplitude, length, and time scales of the perturbation are capable of bringing the fibril oscillations out of phase, suppressing the periodicity of the emission.
Conclusions. The strength of a locally uniform magnetic field in YSO accretion shocks determines the structure of the post-shock region, namely, whether it will be somewhat homogeneous or if it will split up to form a collection of fibrils. In the second case, the size and shape of the fibrils is found to depend strongly on the plasma-β value but not on the perturbation type. Therefore, the actual value of the protostellar magnetic field is expected to play a critical role in the time dependence of the observable emission.
Key words: accretion, accretion disks / magnetohydrodynamics (MHD) / radiative transfer / shock waves / instabilities
© ESO, 2013
1. Introduction
The accretion process of young stellar objects (YSOs) is believed to take place by funneled streams that originate in the surrounding disk and flow along the field lines of the protostellar magnetosphere (Koenigl 1991; Hartmann et al. 1994; Romanova et al. 2003, 2004, 2008). The gas falls onto the surface of the central body with a supersonic velocity, close to the free-fall speed. Its impact on the chromosphere produces strong shocks of a few million Kelvin, a phenomenon that is observable in X-rays (Ulrich 1976; Gullbring 1994; Calvet & Gullbring 1998; Lamzin 1998, 1999; Bouvier et al. 2007b). Detailed observations of young stars have detected such emission (Kastner et al. 2002; Schmitt et al. 2005; Günther et al. 2006; Argiroffi et al. 2007; Robrade & Schmitt 2007; Brickhouse et al. 2010; Dupree et al. 2012), which has to be carefully distinguished from the coronal one. The presence of an accretion shock is probed by a denser (ne ≳ 1011 cm-3) and cooler (T ~ 2–5 MK) plasma, as compared to the more tenuous, at least by one order of magnitude, and hotter corona.
The time dependence of the accretion shock’s structure is determined by radiative processes, as well as by the topology and strength of the magnetic field (Sacco et al. 2008, 2010; Koldoba et al. 2008; Orlando et al. 2010). The typical field of protostars can be strong enough, on the order of kG (Johns-Krull 2007; Donati et al. 2007), such that it confines the infalling plasma inside magnetic flux tubes and prevents it from escaping sideways. Upon impact, a shock is transmitted into the chromosphere, and a reverse shock propagates along the stream. The simplest local configuration is to assume that the chromosphere is horizontal and threaded by a perpendicular uniform field, as depicted in Fig. 1. Material accumulates vertically and the thickness of the shocked region increases, building up a hot slab of a few million Kelvin. Considering the approximation of an optically thin stream, the hot slab radiates its energy away and collapses within the characteristic cooling time (~10–103 s). This process is expected to repeat quasi-periodically, giving rise to a pulsating emission. Such a cycle has been demonstrated and examined extensively in 1D numerical studies of YSO accretion shocks (Sacco et al. 2008; Koldoba et al. 2008; Sacco et al. 2010). In fact, it is a general feature of radiative shocks that the dependence of the cooling function on the temperature may trigger cooling instabilities. In turn, this may lead to the recurrent formation and collapse of the reverse shock, both in the hydrodynamical regime (e.g. Langer et al. 1981; Chevalier & Imamura 1982; Ramachandran & Smith 2005b; Sutherland et al. 2003; Mignone 2005) and in the presence of a transverse magnetic field (e.g. Toth & Draine 1993; Ramachandran & Smith 2005a).
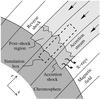 |
Fig. 1 A schematic low plasma-β configuration of an accretion shock. A strong magnetic field penetrates the chromosphere and confines the plasma in flux tubes. The accretion stream impacts on the surface and pushes the chromosphere down to the point where the ram pressure is equal to the stellar pressure. The computational box for the simulations presented in this paper is indicated with a dashed line. |
However, recent observational data of accreting YSOs do not show evidence for such an oscillatory structure (Drake et al. 2009; Günther et al. 2010). In particular, Drake et al. (2009) analyzed the time series of X-ray observations of TW Hya and excluded the presence of periodicity over the frequency range 0.0001–6.811 Hz, which they argue to be the most likely window (the upper limit of the relative amplitude, A, is 0.033 for the interval 0.0001–0.192 Hz and A = 0.056 for 0.192–6.811 Hz). Moreover, Günther et al. (2010) reach a similar conclusion having examined optical and UV data of TW Hya and AA Tau over the frequency ranges 0.02–3 Hz (A = 0.001) and 0.02–50 Hz (A = 0.005), respectively. The absence of periodicity can be attributed to several possible reasons. For instance, by taking radiation transfer effects into account, the cooling of the post-shock region may change and lead to a stable shock stalled inside the chromosphere (Chièze et al., in prep.). On the other hand, complex magnetic field topologies can invalidate the 1D approximation and thus its periodic behavior (Orlando et al. 2013). In a similar context, simulations performed in the high plasma-β regime (ratio of the thermal pressure over the magnetic one) indicate a rather smooth emission, thanks to the shocked material that escapes sideways from the accretion column and deflates the hot slab (Orlando et al. 2010). We also note that Sutherland et al. (2003) explored cooling instabilities of radiative shocks in the pure hydro-dynamical 2D case and found that the extra dimension together with small perturbations lead to inhomogeneous shocks. Their filamentary structure enhanced the cooling efficiency and generated turbulence that may introduce ambiguities in the derivation of velocity profiles.
On the other hand, several authors (e.g. Gullbring et al. 1996; Safier 1998; Bouvier et al. 2007a) have pointed out that accretion streams of young stars are clumped and inhomogeneous, while until now only homogeneous accretion flows have been modeled. A detailed multi-dimensional magneto-hydrodynamical (MHD) modeling of a density structured accretion flow impacting on the stellar surface is therefore required to investigate the complex structure and stability of the hot slab for an inhomogeneous stream.
The 1D accretion model that is often found in the literature is based on the assumption of
a locally strong and uniform field. By considering typical accretion stream velocities and
densities, namely vacc = 100–500 km s-1 and
ρacc = 10-13–10-11 g cm-3
(Sacco et al. 2010, and references therein), and a
local value of the magnetic field of B = 0.1–2 kG in the impact region,
the plasma-β value in the post-shock region1 is on the order 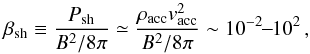 (1)where we have approximated
the thermal pressure of the shocked region, Psh, with the ram
pressure of the infalling gas. For the parameter space corresponding to
β ≲ 1, the plasma is constrained within vertical flux tubes in which case
the 1D approximation is justified.
(1)where we have approximated
the thermal pressure of the shocked region, Psh, with the ram
pressure of the infalling gas. For the parameter space corresponding to
β ≲ 1, the plasma is constrained within vertical flux tubes in which case
the 1D approximation is justified.
In this paper, we extend the above configuration and we perform 2D MHD simulations. During the evolution, we introduce either density perturbations in the accretion stream, as it is the case for a clumpy flow, or pressure variabilities in the chromosphere, similar to what is observed in the sun. We study the time dependence of the shock structure for several plasma-β values, looking for multi-dimensional mechanisms that could disrupt or even suppress the oscillation. We note that the presence of a strong magnetic field constrains significantly the plasma dynamics; for instance it can prevent the generation of large scale chaotic motion such as that observed in Sutherland et al. (2003).
The paper is structured as follows. Section 2 decribes the numerical setup and lists the simulation models. Section 3 derives simple analytical expressions to estimate the effects that perturbations can have on the temporal shock evolution. Section 4 presents our numerical results and discusses their relevance to real accretion shocks. Finally, Sect. 5 summarizes our work and reports our conclusions.
2. Theoretical framework
2.1. The MHD equations
The MHD perfect gas equations, including the appropriate terms suited for the study of
accretion shocks, are 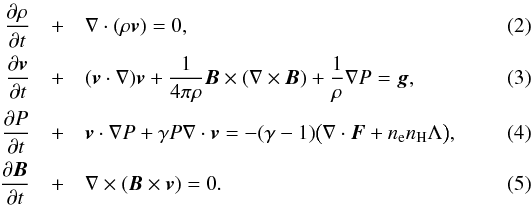 The
equations are written in cgs units for the variables, ρ,
P, and v, which denote the gas density,
pressure, and velocity, respectively. The magnetic field, B,
also satisfies the condition ∇·B = 0. The ratio of specific
heats is γ = 5/3 and g
represents gravity. The thermal conduction flux is given by
The
equations are written in cgs units for the variables, ρ,
P, and v, which denote the gas density,
pressure, and velocity, respectively. The magnetic field, B,
also satisfies the condition ∇·B = 0. The ratio of specific
heats is γ = 5/3 and g
represents gravity. The thermal conduction flux is given by
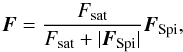 (6)where
(6)where
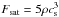 is the
saturated flux (Cowie & McKee 1977) and
cs the sound speed. The term
FSpi consists of two components, one along (∥)
and one across (⊥) the magnetic field lines (Spitzer
1962), given by
is the
saturated flux (Cowie & McKee 1977) and
cs the sound speed. The term
FSpi consists of two components, one along (∥)
and one across (⊥) the magnetic field lines (Spitzer
1962), given by 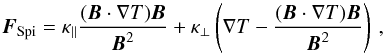 (7)where T
is the temperature, nH is the number density of hydrogen
atoms, and kB is the Boltzmann constant. The thermal
conduction coefficients are given by
κ∥ = −9.2 × 10-7 T5/3
and
(7)where T
is the temperature, nH is the number density of hydrogen
atoms, and kB is the Boltzmann constant. The thermal
conduction coefficients are given by
κ∥ = −9.2 × 10-7 T5/3
and 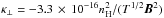 , respectively, both of which
are in units of erg s-1 K-1 cm-1. A mean atomic
weight of μ = 1.2 is considered, i.e.
ρ = μnHmH,
where mH is the hydrogen atomic mass. The electron number
density is denoted with ne and the gas is assumed to be always
fully ionized. The latter is a valid approximation for the post-shock region, the cooling
of which plays a key role in this study. The pre-shocked material is cold enough such that
the energy losses are negligible and the actual value of ne is
not important there.
, respectively, both of which
are in units of erg s-1 K-1 cm-1. A mean atomic
weight of μ = 1.2 is considered, i.e.
ρ = μnHmH,
where mH is the hydrogen atomic mass. The electron number
density is denoted with ne and the gas is assumed to be always
fully ionized. The latter is a valid approximation for the post-shock region, the cooling
of which plays a key role in this study. The pre-shocked material is cold enough such that
the energy losses are negligible and the actual value of ne is
not important there.
 |
Fig. 2 Adopted cooling function, Λ, as a function of the temperature. The negative slope in the temperature range T = 105–107 K is triggering cooling instabilities: the more the plasma cools the higher the energy losses are. |
The cooling function, Λ, is adopted from Orlando et al. (2010) and is shown in Fig. 2. It depends on the temperature and represents radiative losses of an optically thin plasma. The profile was derived with the PINTofALE spectral code (Kashyap & Drake 2000) using the APED V1.3 atomic line database (Smith et al. 2001) and considering metal abundances 0.5 times the solar ones (Telleschi et al. 2007). This abundance has been choosen because some observations tend to indicate that the accretion flow is depleted in metals (Stelzer & Schmitt 2004; Drake et al. 2005). Finally, in order to prevent the chromosphere from cooling, we define a temperature threshold, Tcut = 104 K, below which Λ is set to zero.
Finally, we make use of a flow tracer, Q, which is a passive scalar that obeys the advection equation: ∂Q/∂t + v·∇Q = 0. It does not interfere with the dynamics but simply follows the motion of the plasma and helps visualize its path.
 |
Fig. 3 Types of perturbation considered: a clumpy structure of the accretion stream (left; models Rnd#, IsSm#/IsLg#, ClSm#/ClLg#), an oblique impacting surface (middle; model Obl500), and an energy flux present in the chromosphere (right; models ChrFlx#). |
Numerical models.
2.2. Numerical setup
The simulations are carried out with PLUTO2, a numerical code for computational astrophysics (Mignone et al. 2007, 2012). We adopt the ROE solver for the integration and we apply second order accuracy on both space and time.
The configuration is simulated in 2D cartesian coordinates3, (x, z), neglecting surface curvature and stellar rotation, as shown in Fig. 1. We focus on the interior of the stream in order to remain as close as possible to the 1D problem. Therefore, we avoid influence from the effects at the interface between the corona and the funnel flow (e.g. Orlando et al. 2010). A chromosphere is initialized on the lower part of the computational box, underneath a hot corona (e.g. Sacco et al. 2008, 2010; Orlando et al. 2010). Gravity is assumed uniform, g = −(GM/R2)ẑ, with the mass and radius of the star equal to those of MP Mus, i.e. M = 1.2 M⊙ and R = 1.3 R⊙ (Argiroffi et al. 2007). For simplicity, both the chromosphere and the corona are assumed isothermal, with temperatures, Tchr = 104 K and Tcor = 106 K, respectively. The pressure and density profiles of each one have an exponential dependence such that the configuration is in equilibrium and pressure is continuous. We note that during the first steps of the simulations the corona is readily engulfed by the accretion stream and hence its presence is not important for this study. Finally, a uniform vertical magnetic field, B = B0ẑ, is initialized throughout the box and is evolved self-consistently during the simulation.
The accretion stream is not initially present in the domain but enters from the top. In particular, we prescribe the properties of the infalling plasma on the upper boundary, namely, velocity vacc = 500 km s-1, number density nacc = 1011 cm-3 and temperature Tacc = 103 K (e.g. Bary et al. 2008). These values, along with B, are kept fixed during the simulation, but see also Sect. 2.3 for more details on the applied perturbation. At the ghost cells of the bottom boundary, we specify zero velocities, we set the magnetic field equal to its initial uniform value, and we apply the isothermal equilibrium profiles for the density and pressure. Moreover, by fixing the physical quantities to a given value implies that MHD waves might be reflected. We have investigated the effect of such boundary conditions and found that they can be neglected. This can be seen from the reference simulation NoPert which reproduces the 1D oscillatory behavior reported in the literature (see Sect. 3.1). Lastly, at the left and right edges of the box we apply periodic boundary conditions.
The computational domain spans x = [0.0,0.5 × 10-3] R⊙ in the horizontal direction and z = [0.0,7.7 × 10-2] R⊙ in the vertical, and is resolved by a static grid of [128 × 2048] cells. We have not made use of Adaptive Mesh Refinement (AMR) since the nature of the problem is such that most parts of the computational domain require a high level of refinement. Besides, we also avoid the spurious perturbations that could be introduced by a dynamically evolving grid and would interfere with those applied physically in the system. Note that due to the significant elongation of the simulation box, all spatial distribution plots expand the horizontal direction by a factor of 2 and hence the figures look vertically compressed. The final time of the simulations is on the order of 5 or 10 ks, depending on the case under consideration, and corresponds approximately to 5–10 shock oscillations of the 1D case. Each simulation requires from a few to several thousands hours of computational time to complete, due to constraints imposed on the time step by the optically thin radiation cooling and thermal conduction. This prevented us from exploring the simulations for longer times.
2.3. Models and the applied perturbations
Table 1 lists the simulations that have been carried out, each one assuming a different type of perturbation which is visualized in Fig. 3. In general, we investigate five broad classes of models, a) one that introduces random density perturbations in the accretion stream; b) one that assumes isolated clumps in the infalling material; c) one that considers a fully clumped stream; d) one having an oblique surface of first impact; and e) one that includes variability in the chromosphere. For the density fluctuations of the infalling gas, we explore the minimum and maximum spatial scales that are defined by the resolution and size of the computational box, respectively.
In particular, the models Rnd# consider random density
perturbations of ~1% that take place at the cell level, or equivalently, at a scale of
~25 km. This is done by prescribing the density at the upper boundary in the following
way: 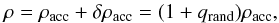 (8)where
qrand is a random number that follows a uniform distribution
in the range [−0.01, 0.01]. The value of
qrand is different for each ghost cell and it is randomized
repeatedly with a period of
Δtrand = Δz/vacc ≃ 0.05 s.
This interval corresponds to the time required for the stream to travel a distance
equivalent to the cell height, Δz.
(8)where
qrand is a random number that follows a uniform distribution
in the range [−0.01, 0.01]. The value of
qrand is different for each ghost cell and it is randomized
repeatedly with a period of
Δtrand = Δz/vacc ≃ 0.05 s.
This interval corresponds to the time required for the stream to travel a distance
equivalent to the cell height, Δz.
The models IsSm# and IsLg# consider
isolated clumps in the accretion stream, which are incorporated by adopting a Gaussian
profile with a constant effective width of σ0, a randomized
location x0, and a randomized time of appearance
t0. Specifically, the density at the upper boundary
condition is set as ![\begin{eqnarray} \rho &=& \rho_\mathrm{acc} + \delta\rho_\mathrm{acc} \nonumber \\ &=& \left[1 + q_\mathrm{cl} \exp{\left(-\frac{(x - x_0)^2 + v_\mathrm{acc}^2(t - t_0)^2} {\sigma_0^2}\right)}\right]\rho_\mathrm{acc}, \end{eqnarray}](/articles/aa/full_html/2013/09/aa21820-13/aa21820-13-eq109.png) (9)where
qcl = 10 is the peak density contrast and
t0 is the time that the clump enters the computational box.
The value of t0 is chosen in such a way that the clump is
initialized far away from the boundary. New values are given to
x0 and t0 every
Δtcl, a time interval large enough to ensure that the
boundary density is equal to ρacc before each new
randomization. Note that a small randomization applies also to
Δtcl in order to avoid an exactly periodic appearance of
clumps. For the case of large clumps, IsLg#, the parameters are
σ0 = 1000 km and
Δtcl = 2 min, whereas for the case of small clumps,
IsSm#, the parameters are
σ0 = 300 km and Δtcl = 30 s.
(9)where
qcl = 10 is the peak density contrast and
t0 is the time that the clump enters the computational box.
The value of t0 is chosen in such a way that the clump is
initialized far away from the boundary. New values are given to
x0 and t0 every
Δtcl, a time interval large enough to ensure that the
boundary density is equal to ρacc before each new
randomization. Note that a small randomization applies also to
Δtcl in order to avoid an exactly periodic appearance of
clumps. For the case of large clumps, IsLg#, the parameters are
σ0 = 1000 km and
Δtcl = 2 min, whereas for the case of small clumps,
IsSm#, the parameters are
σ0 = 300 km and Δtcl = 30 s.
The models ClSm# and ClLg# describe a fully clumped stream using the same gaussian distribution for the overdensities as for the isolated clumps, with the difference that the clumps appear so frequently that they may overlap. In particular, new values are given to x0 and t0 every Δtcl = σ0/vacc, which is equivalent to a vertical clump spacing comparable to their radius. Moreover, in order to simulate an accretion stream that is overall described by the value ρacc, we set the peak density of the gaussian distribution equal to that value. For numerical reasons, we apply a background uniform density which is 10 times lower than ρacc.
For the case of an oblique impacting surface, the assumption of periodic boundaries in
the horizontal direction is only valid in the low plasma-β regime, where
the magnetic field can effectively confine the plasma and prevent it from escaping
sideways. Therefore, we explore just one model for a large value of
B, Obl500. To achieve an oblique
impacting surface, we define the accreting gas variables only at the part of the top
boundary that satisfies the condition:
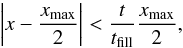 (10)where
xmax is the width of the computational box and
tfill = 15 min is the time that the stream needs to fill
up the whole domain. At each time step, the cross section of the stream increases giving a
conical shape to the impacting surface, with the value of
tfill effectively controlling its aperture.
(10)where
xmax is the width of the computational box and
tfill = 15 min is the time that the stream needs to fill
up the whole domain. At each time step, the cross section of the stream increases giving a
conical shape to the impacting surface, with the value of
tfill effectively controlling its aperture.
On the other hand, models ChrFlx# consider a homogeneous accretion
stream, and instead perturb the system from the lower edge of the computational box, i.e.
the chromosphere. In particular, we introduce an energy flux, of a similar type to what is
observed in the sun, by specifying a pressure variation on the bottom boundary that
depends on both time and space: 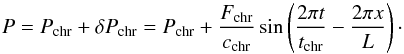 (11)In the above expression,
cchr is the chromospheric sound speed,
Fchr = 5 × 109 erg cm-2 s-1
is the energy flux assumed, tchr = 15 min is the periodicity
of the variation, and L = 3500 km its length scale (e.g. Bohn 1984; Judge
2006; Bello González et al. 2009; Beck et al. 2009, 2013). We have chosen a value for Fchr that is an
order of magnitude larger than the solar one because young stars are in general expected
to be more active than the sun. In addition, note that the assumed periodicity time scale
of the energy flux is a few times larger than that of the shock oscillation time, which
suggests that a value closer to the solar one, i.e. a few minutes, would perturb more
strongly the system. We also apply an appropriate variability to the density at the bottom
boundary such that the chromosphere remains isothermal and hence we avoid thermal
conduction effects that could diffuse the perturbation. We note that a purely temporal
fluctuation, equivalent to a 1D problem, is also relevant to the study of its effect on
the shock oscillations. However, such cases are explored in de Sá et al. (in prep.) and
hence we do not discuss them here.
(11)In the above expression,
cchr is the chromospheric sound speed,
Fchr = 5 × 109 erg cm-2 s-1
is the energy flux assumed, tchr = 15 min is the periodicity
of the variation, and L = 3500 km its length scale (e.g. Bohn 1984; Judge
2006; Bello González et al. 2009; Beck et al. 2009, 2013). We have chosen a value for Fchr that is an
order of magnitude larger than the solar one because young stars are in general expected
to be more active than the sun. In addition, note that the assumed periodicity time scale
of the energy flux is a few times larger than that of the shock oscillation time, which
suggests that a value closer to the solar one, i.e. a few minutes, would perturb more
strongly the system. We also apply an appropriate variability to the density at the bottom
boundary such that the chromosphere remains isothermal and hence we avoid thermal
conduction effects that could diffuse the perturbation. We note that a purely temporal
fluctuation, equivalent to a 1D problem, is also relevant to the study of its effect on
the shock oscillations. However, such cases are explored in de Sá et al. (in prep.) and
hence we do not discuss them here.
The simulations are performed in both a high and a low plasma-β regime, and in particular for magnetic fields ranging between 20 G and 500 G, or equivalently for post-shock β values from β ≲ 100 to β ≳ 0.01. This enables to isolate the hydrodynamical effects and expose the richness of the MHD formulation.
Finally, the model NoPert is a 2D representation of the 1D problem assuming a homogeneous accretion stream and a static chromosphere. It is the reference case in order to present the basic features of the shock evolution. We have chosen the value of 20G.
3. Analytical approach
3.1. Description of the equivalent 1D problem
The typical evolution of 1D accretion shocks, in the context of YSOs (Sacco et al. 2008, 2010; Koldoba et al. 2008), can be summarized by discussing model NoPert. Figure 4 shows the formation and collapse of the post-shock region. The impact of the accretion stream compresses the gas, heating it to temperatures of a few MK. The post-shock region steadily increases in height as the reverse shock travels upwards along the funnel. However, the optically thin radiation losses of the hot slab are significant, effectively cooling down the plasma. Within the characteristic cooling time, the temperature drops by almost 3 orders of magnitude and thus the pressure can no longer support the infalling gas. In turn, the post-shock region collapses, repositing material onto the chromosphere. Subsequently, a new hot slab starts to build up and the process is repeated. Since the X-ray emission depends on the density, temperature and volume of the hot plasma, the emitted radiation of the accretion shock will show a quasi-periodic temporal structure.
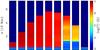 |
Fig. 4 Snapshots of the logarithmic temperature distribution during one oscillation of the reverse shock for the model NoPert. The dark blue color corresponds to the accretion stream, the light blue to the chromosphere and the red to the hot post-shock region which gradually cools down. The panels are separated by 108 s, showing the formation and recollapse of the post-shock region due to the cooling instabilities induced by the optically thin radiation cooling. |
 |
Fig. 5 The vertical structure of the emission-measure weighted temperature as a function of time. Cooling instabilities induce a quasi-periodic structure in the expected radiation with a period of roughly a thousand seconds. |
In fact, this can be seen in Fig. 5, which displays
the quantity: 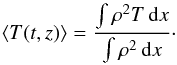 (12)This
emission-measure weighted temperature is calculated at each t and
z and provides an estimate of the time dependence of the expected
radiation (Orlando et al. 2010). Even though the
integration in the x direction is not important for this
x-symmetric simulation, it is particularly useful in the general 2D
cases. Evidently, the corresponding observable flux of model NoPert
is intermittent with an average periodicity of approximately a thousand
seconds. The small variation to the maximum height that the reverse shock reaches at each
oscillation, i.e. between 5 and 7 Mm, is attributed to the MHD waves that propagate in
the post-shock region and are reflected at the bottom boundary and the shock surfaces.
These perturbations, that are independent of x, create density peaks in
the hot slab which in turn affect the time at which the cooling instabilities are
triggered. For instance, the rightmost panels of Fig. 4 show that the vertical profile of the temperature during the collapse phase is
variable. Moreover, the cooling function adopted in our simulations is not smooth, as it
can be seen from Fig. 2, and hence its features in
the presence of waves may also contribute to producing nonidentical collapse phases.
Nevertheless, these are second order effects in the simulations and are neglected for the
rest of this study.
(12)This
emission-measure weighted temperature is calculated at each t and
z and provides an estimate of the time dependence of the expected
radiation (Orlando et al. 2010). Even though the
integration in the x direction is not important for this
x-symmetric simulation, it is particularly useful in the general 2D
cases. Evidently, the corresponding observable flux of model NoPert
is intermittent with an average periodicity of approximately a thousand
seconds. The small variation to the maximum height that the reverse shock reaches at each
oscillation, i.e. between 5 and 7 Mm, is attributed to the MHD waves that propagate in
the post-shock region and are reflected at the bottom boundary and the shock surfaces.
These perturbations, that are independent of x, create density peaks in
the hot slab which in turn affect the time at which the cooling instabilities are
triggered. For instance, the rightmost panels of Fig. 4 show that the vertical profile of the temperature during the collapse phase is
variable. Moreover, the cooling function adopted in our simulations is not smooth, as it
can be seen from Fig. 2, and hence its features in
the presence of waves may also contribute to producing nonidentical collapse phases.
Nevertheless, these are second order effects in the simulations and are neglected for the
rest of this study.
3.2. Discussion on the qualitative effects of perturbations
In this context, the question that arises is to what extent perturbations can disrupt this oscillatory stucture, and especially whether its periodic behavior is suppressed.
The key quantity that determines the evolution of the system is the characteristic cooling time, τcool. The 1D approximation assumes that a unique value of τcool describes the whole post-shock region, a fact that results in the quasi-periodic global behavior described above. However, if adjacent vertical flux tubes have either a small phase difference in their oscillations or a slightly different τcool value, then a significant horizontal gradient in the pressure of the post-shock region would develop due to the asychronous collapse.
In the case of a weak magnetic field, or equivalently in the high plasma-β regime, this will create large velocity components along the x direction that subsequently will lead to a chaotic plasma motion. The density inhomogeneities of the post-shock region will enhance the energy losses, shortening also the cooling time (Sutherland et al. 2003). On the other hand, the presence of a relatively strong vertical magnetic field will prevent horizontal interaction. For instance, an out-of-phase collapse of neighboring flux tubes will still retain their independent evolution4. Following Sacco et al. (2010) and Orlando et al. (2010), who have briefly described this mechanism, we refer to these magnetically confined vertical structures as fibrils. Hence, in the low plasma-β case, these fibrils can be approximated as isolated quasi-periodic emitters and the overall X-ray radiation is simply the sum of their individual contribution. Therefore, an out-of-phase oscillation would smooth out any global periodic signature in the observed flux, even though each fibril would follow the 1D quasi-periodic evolution described in Sect. 3.1.
3.3. Quantitative study of the fibril structure
In order to quantify the problem we first derive some simplified expressions for the fibril structure.
3.3.1. The cooling time scale of fibrils
A lower limit of the Mach number of the accreting gas is found by assuming a relatively
small infalling speed, vacc = 100 km s-1, for
a gas of a temperature, Tacc = 1000 K:
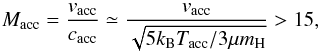 (13)where
cacc is the sound speed in the accretion stream and
kB the Boltzmann constant. Given this high value, the
shock can be generally assumed strong and hence its postshock temperature is
proportional to the velocity squared:
(13)where
cacc is the sound speed in the accretion stream and
kB the Boltzmann constant. Given this high value, the
shock can be generally assumed strong and hence its postshock temperature is
proportional to the velocity squared:
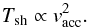 (14)Moreover, the
optically thin cooling time, τcool, can be estimated from
Eq. (4), since the plasma pressure
changes by ~Psh in that interval:
(14)Moreover, the
optically thin cooling time, τcool, can be estimated from
Eq. (4), since the plasma pressure
changes by ~Psh in that interval:
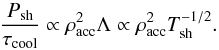 (15)Here we have used
the expression Λ ∝ T−1/2 as a rough
approximation in the temperature range 105–107 K, see Fig. 2. Combining the above relations and given the fact
that the kinetic energy of the accretion stream is converted to thermal pressure upon
impact,
(15)Here we have used
the expression Λ ∝ T−1/2 as a rough
approximation in the temperature range 105–107 K, see Fig. 2. Combining the above relations and given the fact
that the kinetic energy of the accretion stream is converted to thermal pressure upon
impact, 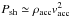 , the cooling time
is found to have the following dependence (e.g. Sacco et
al. 2010):
, the cooling time
is found to have the following dependence (e.g. Sacco et
al. 2010): 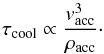 (16)
(16)
3.3.2. The length scales of the fibrils
Let h be the maximum height that the post-shock region attains and
d the width of the fibrils. The quantity h can be
estimated by multiplying the time that the reverse shock propagates,
τcool, with its velocity, which is proportional to
vacc (e.g. Sacco et al.
2010): 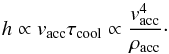 (17)The width of
the fibrils is relevant only in the low plasma-β regime, because
otherwise the magnetic flux tubes cannot constrain the plasma dynamics, and the
infalling gas is effectively mixed after the impact. In the former case, we can estimate
d from the horizontal component of Eq. (3) by assuming a small deformation of the flux tube and decomposing
the magnetic field as
(17)The width of
the fibrils is relevant only in the low plasma-β regime, because
otherwise the magnetic flux tubes cannot constrain the plasma dynamics, and the
infalling gas is effectively mixed after the impact. In the former case, we can estimate
d from the horizontal component of Eq. (3) by assuming a small deformation of the flux tube and decomposing
the magnetic field as 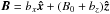 ,
with
bx,bz ≪ B0:
,
with
bx,bz ≪ B0:
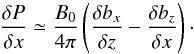 (18)The first term of the
right hand side represents the magnetic tension due to the curvature of the magnetic
fieldlines,
δbx/δz ~ bx/(h/2),
and the second term represents the gradient of the magnetic pressure. We neglect the
latter, since we do not expect a net difference in
bz between the inside and outside of
the fibril. Therefore,
(18)The first term of the
right hand side represents the magnetic tension due to the curvature of the magnetic
fieldlines,
δbx/δz ~ bx/(h/2),
and the second term represents the gradient of the magnetic pressure. We neglect the
latter, since we do not expect a net difference in
bz between the inside and outside of
the fibril. Therefore, 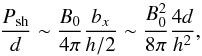 (19)where in the
last relation we used the property of the tangent, i.e.
bx/B0 ≃ (d/2)/(h/2).
Finally, we obtain:
(19)where in the
last relation we used the property of the tangent, i.e.
bx/B0 ≃ (d/2)/(h/2).
Finally, we obtain: 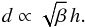 (20)This expression
relates the width of the fibril with its maximum height as well as the
plasma-β.
(20)This expression
relates the width of the fibril with its maximum height as well as the
plasma-β.
3.3.3. Hydrodynamical limit, no fibrils
In the high plasma-β regime, the time scale for the homogenization of the post-shock pressure is on the order of racc/csh ≃ 500 s. Here we have assumed a fraction of the solar radius for the accretion stream cross section, racc ~ 105 km, and a post-shock sound speed of csh ~ 200 km s-1. This time scale is comparable to τcool which suggests that any potential phase differences between adjacent vertical elements of the hot slab are likely to smooth out. As a result, there are no fibrils forming and the accretion shock is expected to maintain its periodic behavior in the high plasma-β regime.
3.4. The effects of perturbations
In the context of the simplified configuration of Fig. 1, the disruption of the global shock periodicity comes down to the search of a potential mechanism that can introduce a net and adequate phase difference in the oscillations of adjacent flux tubes, or equivalently a gradient in their τcool value. In general, perturbations are characterized by three quantities, a) amplitude; b) length scale and c) time scale. Since any small phase difference between fibrils will not increase further in the absence of perturbations, their amplitude cannot be arbitrarily small. However, a continuous perturbation may have cumulative results, and thus even small variabilities might be adequate, as long as they do not cancel each other’s effects in time. Moreover, their spatial extent should be larger than the fibril width, d, otherwise the contained post-shock region can be homogenized. Finally, the temporal scale of the perturbation should be comparable to the cooling time, τcool.
Below, we focus on the case of a strong magnetic field and we estimate the effects of general types of perturbations (Fig. 3) to the temporal evolution of the shock structure.
3.4.1. Density fluctuations in the accretion stream
A radial density profile across the accretion column will inevitably destroy the global
periodicity due to the different resulting cooling times of each vertical element
(Bonito et al., in prep.). However, here we do not account for such initial conditions,
but instead we study the perturbed uniform profile. By considering small variations to
the infalling gas density, since the velocity is not expected to fluctuate considerably,
Eq. (16) gives:
![\begin{equation} \tau_\mathrm{cool} \propto \frac{1}{\rho_\mathrm{acc} + \delta\rho_\mathrm{acc}} \simeq \frac{1}{\rho_\mathrm{acc}} \left[1 - \frac{\delta\rho_\mathrm{acc}}{\rho_\mathrm{acc}} + \left(\frac{\delta\rho_\mathrm{acc}}{\rho_\mathrm{acc}}\right)^2\right]\cdot \end{equation}](/articles/aa/full_html/2013/09/aa21820-13/aa21820-13-eq166.png) (21)If the density
perturbations are random, one has:
ρacc ± δρacc.
To first order, their effects cancel each other and τcool
remains unchanged. However, by taking second order terms into account, a net change does
appear in the cooling time. Nevertheless, the average value of
τcool is affected globally, i.e. at all
x, and hence the system will always be in phase. Consequently, we
should rather focus on lasting phase shifts that can be introduced between adjacent
fibrils, namely a local variation of δρacc.
Rewriting Eq. (16) we obtain:
(21)If the density
perturbations are random, one has:
ρacc ± δρacc.
To first order, their effects cancel each other and τcool
remains unchanged. However, by taking second order terms into account, a net change does
appear in the cooling time. Nevertheless, the average value of
τcool is affected globally, i.e. at all
x, and hence the system will always be in phase. Consequently, we
should rather focus on lasting phase shifts that can be introduced between adjacent
fibrils, namely a local variation of δρacc.
Rewriting Eq. (16) we obtain:
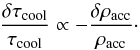 (22)Therefore, a clump with
a significant density constrast can considerably affect the local cooling time, within a
range comparable to its size. Note that the presence of several clumps, apart from
bringing the fibrils out of phase faster, could also reduce the required amplitude of
the perturbations due to their cumulative effect.
(22)Therefore, a clump with
a significant density constrast can considerably affect the local cooling time, within a
range comparable to its size. Note that the presence of several clumps, apart from
bringing the fibrils out of phase faster, could also reduce the required amplitude of
the perturbations due to their cumulative effect.
3.4.2. Perturbations in the chromosphere
A variation of δPchr and
δρchr may relocate locally and
temporarily the depth down to which the accretion shock can penetrate into the
chromosphere, as well as influence the post-shock cooling efficiency. Since pressure
fluctuations
(δPchr ~ 5 × 103 erg cm-3)
are larger than the ram pressure of the accretion shock
(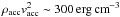 ),
the activity of the chromosphere is capable of influencing its evolution. In fact,
notice that even if we consider the solar energy flux, which is one order of magnitude
lower, the value of δPchr would still be on
the same order as
),
the activity of the chromosphere is capable of influencing its evolution. In fact,
notice that even if we consider the solar energy flux, which is one order of magnitude
lower, the value of δPchr would still be on
the same order as 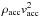 . Moreover, this
kind of variability is on the order of minutes with the typical lengths involved being a
few thousand km (e.g. Bohn 1984; Judge 2006; Bello
González et al. 2009; Beck et al. 2009,
2013). Therefore, it can act on the level of
fibrils, rather than on the whole shock structure, and also within the frequency window
of the expected oscillations. In other words, this type of perturbation has the
appropriate amplitude, spatial and temporal scales to potentially disrupt the
synchronization and hence affect the global quasi-periodic signature.
. Moreover, this
kind of variability is on the order of minutes with the typical lengths involved being a
few thousand km (e.g. Bohn 1984; Judge 2006; Bello
González et al. 2009; Beck et al. 2009,
2013). Therefore, it can act on the level of
fibrils, rather than on the whole shock structure, and also within the frequency window
of the expected oscillations. In other words, this type of perturbation has the
appropriate amplitude, spatial and temporal scales to potentially disrupt the
synchronization and hence affect the global quasi-periodic signature.
3.4.3. Shape of the impacting surface
Finally, even in the case of a homogeneous accretion stream and a static chromosphere, the starting time for each fibril oscillation is determined by the shape of the surface of first impact. For instance, if the center of the funneled gas cross-section hits the star earlier that its outer parts by an interval comparable to, or larger than, τcool then the formation and collapse of the fibrils will be out of phase.
4. Numerical study
The previous rough estimates indicate that introducing perturbations in the accretion shock system can potentially suppress the predicted periodic emission. In this section, we explore the actual effects of several types of realistic perturbations by performing numerical simulations and studying the time-dependent shock structure. We illustrate the involved processes in the dynamics, showing also the role of the magnetic field.
 |
Fig. 6 Density, temperature, plasma-β, and velocity distributions at t = 10 ks for the weak magnetic field model Rnd20. The colors blue/red are used for low/high values, and in particular ρ ∈ [10-13, 10-11] g cm-3, T ∈ [0, 4] MK, β ∈ [10-2, 102], vx ∈ [−5, 5] km s-1, vz ∈ [−500, 0] km s-1, and Q ∈ [0, 1]. The 1% density perturbations that are applied to this model are too weak to be visible. Due to the saturation of the density color, the exponential profile of the chromosphere cannot be seen. |
 |
Fig. 7 Density, temperature, plasma-β, velocities, and tracer distibutions at t = 10 ks for the strong magnetic field case Rnd500. The range of each plotted quantity is: ρ ∈ [10-13, 10-11] g cm-3, T ∈ [0, 2] MK, β ∈ [10-2, 102], vx ∈ [−5, 5] km s-1, vz ∈ [−500, 0] km s-1, and Q ∈ [0, 1]. |
 |
Fig. 8 Distributions of the temperature (on the left of each panel) and the plasma-β (on the right of each panel) for the models NoPert, Rnd20, Rnd50, Rnd100, Rnd250, and Rnd500 (left to right). The plotted ranges are: T ∈ [0, 5] MK and β ∈ [10-3, 103]. The snapshots do not correspond to the same time, but each one was chosen such that the fibril structure becomes more apparent. Note also that the aspect ratio is not the same as the rest of the figures: these plots are compressed vertically by a factor of 1.5. |
4.1. Random density perturbations in the stream
Figure 6 shows a snapshot of the spatial distribution of the physical quantities for the high plasma-β model Rnd20. Three regions can be identified from top to bottom: the tenuous and cold accretion stream, the denser post-shock region of a few million Kelvin, and the relatively colder isothermal chromosphere which is described by an exponential density profile. As expected, the post-shock region resembles closely the unperturbed case (NoPert) because the magnetic field is not strong enough to prevent pressure fluctuations from being smoothed out. This produces a chaotic motion of a few km s-1 as it can be seen in the panel of vx whose extrema correspond to ± 0.01vacc. The vertical velocity component of the shocked material has a similar signature but this is not apparent in the corresponding plot due to the different color range used (± vacc). Furthermore, the accreted material is reposited all over the surface of the chromosphere, as indicated by the tracer, Q.
Figure 7 displays the same physical variables as Fig. 6 but for the low plasma-β model Rnd500. Notice the fibril structure of the shocked material which is the result of the magnetic confinement of the plasma inside vertical flux tubes. The temporal evolution of each fibril is independent of its neighbours; some of them are forming, e.g. regions on the right part of each panel, whereas others are collapsing, e.g. regions on the left. This can be seen by looking at the vertical distribution of the temperature of a given fibril. A forming fibril has a rather uniform temperature along z. On the contrary, a collapsing fibril may have T varying by orders of magnitude along its height. The horizontal speed component is zero almost everywhere, showing that plasma mixing cannot take place easily in the low plasma-β regime. For the same reason, the tracer shows that the material accretes strictly vertically and any further mixing can take place only deeper in the chromosphere where the thermal pressure is stronger than the magnetic one. Finally, note that despite the small perturbation amplitude, a phase shift does develop among fibrils.
Figure 8 illustrates the dependence of the fibril size on the strength of the magnetic field. Although quantitative analysis is required to verify the approximate relation of Eq. (20), namely d ∝ 1/Bz, it seems to be valid to zeroth order (see Sect. 3.3.2). Note that the size of the fibrils does not depend on the perturbation length scale, which for these models is the cell width Δx, but only on the plasma-β value. This is also confirmed by all other simulations of Table 1. In addition, the fibrils seem to have a finer structure at the base close to the chromosphere and a thicker and rounded shape at their head.
Furthermore, by assuming an accretion stream radius of 5 × 104 km (Orlando et al. 2010), the computational box considered here represents approximately one hundredth of its diameter. This provides an estimate on the total number of fibrils that can form and also shows the overall complexity of the post-shock region even in the case of uniform magnetic fields. On the other hand, we have verified that our simulations capture correctly the width of the fibrils since it remains the same when increasing the resolution. Nevertheless, lower plasma-β values would demand smaller cell sizes due to the anticipated thinner fibrils. The above two points imply that simulating the entire stream together with the highly structured post-shock region is a rather computationally expensive task.
 |
Fig. 9 Emission-measure weighted temperature versus z and t for the models that consider 1% random density perturbations in the stream, i.e. Rnd20, Rnd50, Rnd100, Rnd250, and Rnd500 (top to bottom). |
In order to quantify the effects that the 1% random density fluctuations have on the periodicity of the system, we plot in Fig. 9 the emission-measure weighted temperature, ⟨T(z,t)⟩, for this class of models. Overall, and despite the formation of fibrils in the low plasma-β cases, a strong periodic signature can be observed in the cases Rnd20, Rnd50, Rnd250, and Rnd500. This is because the applied perturbation is small and it also has a zero net effect along x. In other words, fluctuations at each horizontal position cancel in time, making each flux tube, on average, identical to the rest. Recall that bringing the fibrils out of phase is not an unstable process and therefore their oscillations remain generally synchronized with only a small phase difference attributed to the small density fluctuations. Here, a stronger and less symmetric perturbation is required to produce an adequate phase shift among adjacent fibrils.
Nevertheless, model Rnd100 seems to lose its periodic signature in the long term. Its plasma-β at the post-shock region is β ~ 1 which suggests that the dynamics are neither dominated by purely hydro processes nor by the magnetic field alone, as it is the case for the other models. Instead, there is a complex interplay between the two that gives rise to 2D mechanisms which in turn disrupt the global periodic behavior even for such relatively small perturbations. Finally, by comparing Figs. 5 and 9 we observe that the maximum height attained by the perturbed cases is lower than that of the unperturbed, and also that their oscillation period is slightly shorter. For the high plasma-β cases this is due to the inhomogeneities produced in the hot slab, where the locally denser regions are susceptible to stronger energy losses. Effectively, this reduces the average τcool as it is also observed and discussed in Sutherland et al. (2003). On the other hand, even though the low plasma-β cases do reach a higher height than the weak B models, the small deformation of the flux tubes by the confined hot plasma invalidates the x-symmetry and, as a result, the fibrils do not attain the height of NoPert.
 |
Fig. 10 Density, temperature, horizontal velocity, and the fluid tracer for the isolated clump models IsSm20 (left panels) and IsLg500 (right panels). Blue/red color corresponds to low/high values, i.e. ρ ∈ [10-13, 10-11] g cm-3, T ∈ [0, 5] MK, vx ∈ [−50, 50] km s-1, and Q ∈ [0, 1]. The clumps, visible as elliptical spots in density distributions, are circular but appear elongated due to the compression of the vertical direction for visualization purposes. |
4.2. Isolated clumps or fully clumped stream
Figure 10 displays the physical quantities of two models that incorporate isolated clumps into the stream, IsSm20 and IsLg500. On the left, two small clumps are visible in the infalling gas and a third one that has just hit the reverse shock. The post-shock region is hotter where the clump interacts with the reverse shock. There, the basic physics is similar to that for the interaction of a supernova remnant shock with a cloud of the ISM, where the major factor is the density contrast of the clump with respect to the surrounding medium (e.g. Klein et al. 1994; see also Orlando et al. 2008, for a MHD study including the effects of anisotropic thermal conduction). The shock-clump interaction generates transmitted (into the clump) and reflected (into the post-shock material of the slab) shocks, whose temperature depends on the density contrast of the clump. The darkest portion of the shock front in the second panel of Fig. 10 is the shocked clump material and the red structure that surrounds it is the bow shock. The latter propagates into the shocked stream with a higher temperature than that of its environment. A strong velocity field appears locally, with the value of vx reaching almost half of the accretion speed, vacc. In fact, the hot slab shows overall much higher velocity values of chaotic motion than the model Rnd20; here the velocity is plotted in the range ± 0.1vacc with larger values saturating to dark blue or dark red, respectively. On the other hand, the strong magnetic field of model IsLg500 (on the right) does not allow pressure homogenization and hence there is no plasma mixing. The formation of fibrils is again evident in the system, but this time their oscillations are effectively brought out of phase. This is due to the large density contrast of the clumps which significantly modify the local value of τcool.
 |
Fig. 11 Density, temperature, horizontal velocity, and the fluid tracer for models ClLg20 (left panels) and ClSm500 (right panels), which assume a fully clumped accretion stream. The plotted value ranges are: ρ ∈ [10-14, 10-12] g cm-3, T ∈ [0, 5] MK, vx ∈ [−50, 50] km s-1, and Q ∈ [0, 1]. |
The general features observed in the isolated clump models are also seen in the cases of fully clumped streams. Figure 11 displays the spatial distribution of the physical quantities for ClLg20 and ClSm500. In these cases too, the dynamics of the post-shock region depends on the strength of the magnetic field and not on the type of perturbation. Even though the average density of the infalling gas, and hence the cooling time, is different than before, the temporal evolution is generally similar; the high plasma-β models show chaotic motion and mixing whereas the low plasma-β cases a fibril structure.
 |
Fig. 12 Emission-measure weighted temperature for the models that assume isolated clumps (left panels) and the a fully clumped stream (right panels). |
The periodic signature of all the models that consider clumps can be derived from Fig. 12. The presence of dense clumps increases the local cooling efficiency of the post-shock region and as a result the emission may vary strongly with z. The difference in the frequencies (when there is one) and the maximum height attained are attributed to the value of the average density of the accreting material. In particular, the high plasma-β models IsSm20, ClSm20, and ClLg20 maintain a quasi-periodic oscillatory character. On the other hand, the strong magnetic field models have their fibrils oscillating fully out of phase. As a result, the periodic behavior is heavily disrupted in most cases and suppressed in the model IsLg500. We note that the limited width and dimensionality of the box is contributing to these noisy profiles. If we had explored the whole accretion stream cross section or performed 3D simulations, the sum of individual out-of-phase fibril contributions would have provided a much smoother profile.
 |
Fig. 13 Spatial distribution of the temperature and of the horizontal velocity component for the models that consider an energy flux in the chromosphere. Plotted ranges: T ∈ [0, 5] MK, vx ∈ [−5, 5] km s-1, and Q ∈ [0, 1]. |
4.3. Perturbations in the chromosphere
Models ChrFlx# show the same magnetic-field-dependent features of the accretion shock structure that were discussed earlier, despite the intrinsically different perturbation type. The sinusoidal spatial profile of the chromospheric pressure fluctuations generates local vertical velocities in all three cases and also a horizontal motion when the magnetic field is weak enough. As it can be seen in Fig. 13, the upwards travelling sonic waves disrupt the lower edge of the post-shock region leading to a similar B-dependent morphology of the shocked material as the rest of the models in Table 1. The vx component is plotted in the range ± 0.01vacc but we note that the values of the chaotic motion can be by an order of magnitude larger close to the chromosphere. Furthermore, notice that ChrFlx100 displays a non-zero value of vx in the stream. This effect is created from MHD waves that travel along the accretion flow and force the material to follow the wavy structure of the magnetic field lines. Therefore, in the low plasma-β regime, any type of chromospheric fluctuations can also perturb the stream apart from the accretion shock. This effect is present in all models, even though weaker.
 |
Fig. 14 Emission-measure weighted temperature for the models that consider fluctuations in the chromosphere (top three) and for the case of an oblique surface of impact (bottom). |
The top three panels of Fig. 14 show the emission-measure weighted temperature versus time for the three models considering perturbations of chromospheric origin. Once again we confirm that the periodicity is present when the magnetic field is weak. In the same context, the independent fibril oscillations of the low plasma-β case hide any well-defined temporal patterns.
4.4. Oblique impacting surface
Finally, the bottom panel of Fig. 14 presents model Obl500. By definition, this case is prepared such that among flux tubes there is a phase shift on the starting time of the fibril oscillations. However, once the whole stream has entered the box, no further perturbations are introduced. The plot suggests that although the fibrils are initially out of phase, they gradually get synchronized. This implies that a coordinated oscilation of the fibrils is a stable state and that the weak interaction between the flux tubes favors the synchronization of the system.
5. Summary – conclusions
In the literature, theoretical studies and 1D numerical simulations predict an oscillatory behavior in the emission of accretion shocks. However, observational data appear not to confirm such an expectation. In this paper, we have explored whether the presence of perturbations could disrupt or even suppress this periodic signature. We have performed 2D MHD simulations of the interior of the accretion flow to investigate the effects of several realistic perturbations, such as a clumped stream or fluctuations in the chromosphere. We have explored a wide range of magnetic field values in order to understand its role in the dynamics. Our conclusions are summarized as follows:
-
The structure of the post-shock region is found to depend stronglyonly on the plasma-β value and only very weakly on the nature of the perturbation. In particular, a relatively strong magnetic field confines the plasma in flux tubes and leads to the formation of fibrils. Their size depends on the value of B and their evolution follows roughly a quasi-periodic oscillation that is almost independent of their neighbours. In the high plasma-β regime, the post-shock region shows chaotic motion and plasma mixing with the value of local velocity determined by the applied perturbation.
-
In the cases where the magnetic field is weak, the emission maintains a strong periodic signature. This is because the pressure fluctuations that appear in the post-shock region, due to the applied perturbations, are smoothed out and the entire hot slab forms and recollapses as a whole. However, both the oscillation frequency and the height reached by the reverse shock are lower than those of the unperturbed case due to the more efficient cooling, a byproduct of chaotic motion and the inhomogeneities it produces.
-
For strong magnetic fields, the global periodicy in the emission can be suppressed if the fibrils oscillate out of phase. This requires a perturbation that can effectively modify the cooling time and/or the trigger time among adjacent flux tubes. We point out that since observations of protostars suggest high magnetic field values, the low plasma-β models we have investigated in this paper are expected to be the most relevant for real YSOs.
-
In general, for a perturbation to have an effect on the system, it has to have a time scale comparable to the cooling time, a length scale comparable to the fibril width, and an adequate amplitude. All three criteria seem to be fulfilled by the typical perturbations expected to be present in the accretion shock system.
Freely available at http://plutocode.ph.unito.it
Acknowledgments
We would like to thank an anonymous referee for the helpful comments on the manuscript. The authors are grateful to A. Ciardi for his help and suggestions during the preparation of this study. We would also like to thank F. Thais for his support as well as A. Mignone, M. Flock, S. Matt, G. Herczeg, J. Bouvier, S. Cabrit, A. Maggio, A. Bonanos, T. Katsiyannis, R. Keppens, C. Xia, and R. Pinto for fruitful discussions. This work was supported by the ANR STARSHOCK project (ANR-08-BLAN-0263-07–2009/2013) and was granted access to the HPC resources of CINES under the allocation 2012-c2012046943 made by GENCI (Grand Equipement National de Calcul Intensif).
References
- Argiroffi, C., Maggio, A., & Peres, G. 2007, A&A, 465, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bary, J. S., Matt, S. P., Skrutskie, M. F., et al. 2008, ApJ, 687, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, C., Khomenko, E., Rezaei, R., & Collados, M. 2009, A&A, 507, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Rezaei, R., & Puschmann, K. G. 2013, A&A, 553, A73 [NASA ADS] [EDP Sciences] [Google Scholar]
- Bello González, N., Flores Soriano, M., Kneer, F., & Okunev, O. 2009, A&A, 508, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bohn, H. U. 1984, A&A, 136, 338 [NASA ADS] [Google Scholar]
- Bouvier, J., Alencar, S. H. P., Boutelier, T., et al. 2007a, A&A, 463, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvier, J., Alencar, S. H. P., Harries, T. J., Johns-Krull, C. M., & Romanova, M. M. 2007b, Protostars and Planets V, 479 [Google Scholar]
- Brickhouse, N. S., Cranmer, S. R., Dupree, A. K., Luna, G. J. M., & Wolk, S. 2010, ApJ, 710, 1835 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N., & Gullbring, E. 1998, ApJ, 509, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Imamura, J. N. 1982, ApJ, 261, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., & McKee, C. F. 1977, ApJ, 211, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Jardine, M. M., Gregory, S. G., et al. 2007, MNRAS, 380, 1297 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, J. J., Testa, P., & Hartmann, L. 2005, ApJ, 627, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, J. J., Ratzlaff, P. W., Laming, J. M., & Raymond, J. 2009, ApJ, 703, 1224 [NASA ADS] [CrossRef] [Google Scholar]
- Dupree, A. K., Brickhouse, N. S., Cranmer, S. R., et al. 2012, ApJ, 750, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Gullbring, E. 1994, A&A, 287, 131 [NASA ADS] [Google Scholar]
- Gullbring, E., Barwig, H., Chen, P. S., Gahm, G. F., & Bao, M. X. 1996, A&A, 307, 791 [NASA ADS] [Google Scholar]
- Günther, H. M., Liefke, C., Schmitt, J. H. M. M., Robrade, J., & Ness, J.-U. 2006, A&A, 459, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Günther, H. M., Lewandowska, N., Hundertmark, M. P. G., et al. 2010, A&A, 518, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L., Hewett, R., & Calvet, N. 1994, ApJ, 426, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Ibgui, L., Hubeny, I., Lanz, T., & Stehlé, C. 2013, A&A, 549, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johns-Krull, C. M. 2007, ApJ, 664, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Judge, P. 2006, in Solar MHD Theory and Observations: A High Spatial Resolution Perspective, eds. J. Leibacher, R. F. Stein, & H. Uitenbroek, ASP Conf. Ser., 354, 259 [Google Scholar]
- Kashyap, V., & Drake, J. J. 2000, Bull. Astron. Soc. India, 28, 475 [NASA ADS] [EDP Sciences] [Google Scholar]
- Kastner, J. H., Huenemoerder, D. P., Schulz, N. S., Canizares, C. R., & Weintraub, D. A. 2002, ApJ, 567, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, R. I., McKee, C. F., & Colella, P. 1994, ApJ, 420, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Koenigl, A. 1991, ApJ, 370, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Koldoba, A. V., Ustyugova, G. V., Romanova, M. M., & Lovelace, R. V. E. 2008, MNRAS, 388, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Lamzin, S. A. 1998, Astron. Rep., 42, 322 [NASA ADS] [Google Scholar]
- Lamzin, S. A. 1999, Astron. Lett., 25, 430 [NASA ADS] [Google Scholar]
- Langer, S. H., Chanmugam, G., & Shaviv, G. 1981, ApJ, 245, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A. 2005, ApJ, 626, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mignone, A., Zanni, C., Tzeferacos, P., et al. 2012, ApJS, 198, 7 [Google Scholar]
- Orlando, S., Bocchino, F., Reale, F., Peres, G., & Pagano, P. 2008, ApJ, 678, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Orlando, S., Sacco, G. G., Argiroffi, C., et al. 2010, A&A, 510, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Orlando, S., Bonito, R., Argiroffi, C., et al. 2013, A&A, submitted [Google Scholar]
- Ramachandran, B., & Smith, M. D. 2005a, MNRAS, 362, 1353 [NASA ADS] [CrossRef] [Google Scholar]
- Ramachandran, B., & Smith, M. D. 2005b, MNRAS, 357, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Reale, F., Orlando, S., Testa, P., et al. 2013, Science, 341, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Robrade, J., & Schmitt, J. H. M. M. 2007, A&A, 473, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., Wick, J. V., & Lovelace, R. V. E. 2003, ApJ, 595, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2004, ApJ, 610, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Romanova, M. M., Kulkarni, A. K., & Lovelace, R. V. E. 2008, ApJ, 673, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Sacco, G. G., Argiroffi, C., Orlando, S., et al. 2008, A&A, 491, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sacco, G. G., Orlando, S., Argiroffi, C., et al. 2010, A&A, 522, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Safier, P. N. 1998, ApJ, 494, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, J. H. M. M., Robrade, J., Ness, J.-U., Favata, F., & Stelzer, B. 2005, A&A, 432, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1962, Physics of Fully Ionized Gases (New York: Interscience) [Google Scholar]
- Stelzer, B., & Schmitt, J. H. M. M. 2004, A&A, 418, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sutherland, R. S., Bicknell, G. V., & Dopita, M. A. 2003, ApJ, 591, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Telleschi, A., Güdel, M., Briggs, K. R., Audard, M., & Scelsi, L. 2007, A&A, 468, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toth, G., & Draine, B. T. 1993, ApJ, 413, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Ulrich, R. K. 1976, ApJ, 210, 377 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 A schematic low plasma-β configuration of an accretion shock. A strong magnetic field penetrates the chromosphere and confines the plasma in flux tubes. The accretion stream impacts on the surface and pushes the chromosphere down to the point where the ram pressure is equal to the stellar pressure. The computational box for the simulations presented in this paper is indicated with a dashed line. |
| In the text | |
 |
Fig. 2 Adopted cooling function, Λ, as a function of the temperature. The negative slope in the temperature range T = 105–107 K is triggering cooling instabilities: the more the plasma cools the higher the energy losses are. |
| In the text | |
 |
Fig. 3 Types of perturbation considered: a clumpy structure of the accretion stream (left; models Rnd#, IsSm#/IsLg#, ClSm#/ClLg#), an oblique impacting surface (middle; model Obl500), and an energy flux present in the chromosphere (right; models ChrFlx#). |
| In the text | |
 |
Fig. 4 Snapshots of the logarithmic temperature distribution during one oscillation of the reverse shock for the model NoPert. The dark blue color corresponds to the accretion stream, the light blue to the chromosphere and the red to the hot post-shock region which gradually cools down. The panels are separated by 108 s, showing the formation and recollapse of the post-shock region due to the cooling instabilities induced by the optically thin radiation cooling. |
| In the text | |
 |
Fig. 5 The vertical structure of the emission-measure weighted temperature as a function of time. Cooling instabilities induce a quasi-periodic structure in the expected radiation with a period of roughly a thousand seconds. |
| In the text | |
 |
Fig. 6 Density, temperature, plasma-β, and velocity distributions at t = 10 ks for the weak magnetic field model Rnd20. The colors blue/red are used for low/high values, and in particular ρ ∈ [10-13, 10-11] g cm-3, T ∈ [0, 4] MK, β ∈ [10-2, 102], vx ∈ [−5, 5] km s-1, vz ∈ [−500, 0] km s-1, and Q ∈ [0, 1]. The 1% density perturbations that are applied to this model are too weak to be visible. Due to the saturation of the density color, the exponential profile of the chromosphere cannot be seen. |
| In the text | |
 |
Fig. 7 Density, temperature, plasma-β, velocities, and tracer distibutions at t = 10 ks for the strong magnetic field case Rnd500. The range of each plotted quantity is: ρ ∈ [10-13, 10-11] g cm-3, T ∈ [0, 2] MK, β ∈ [10-2, 102], vx ∈ [−5, 5] km s-1, vz ∈ [−500, 0] km s-1, and Q ∈ [0, 1]. |
| In the text | |
 |
Fig. 8 Distributions of the temperature (on the left of each panel) and the plasma-β (on the right of each panel) for the models NoPert, Rnd20, Rnd50, Rnd100, Rnd250, and Rnd500 (left to right). The plotted ranges are: T ∈ [0, 5] MK and β ∈ [10-3, 103]. The snapshots do not correspond to the same time, but each one was chosen such that the fibril structure becomes more apparent. Note also that the aspect ratio is not the same as the rest of the figures: these plots are compressed vertically by a factor of 1.5. |
| In the text | |
 |
Fig. 9 Emission-measure weighted temperature versus z and t for the models that consider 1% random density perturbations in the stream, i.e. Rnd20, Rnd50, Rnd100, Rnd250, and Rnd500 (top to bottom). |
| In the text | |
 |
Fig. 10 Density, temperature, horizontal velocity, and the fluid tracer for the isolated clump models IsSm20 (left panels) and IsLg500 (right panels). Blue/red color corresponds to low/high values, i.e. ρ ∈ [10-13, 10-11] g cm-3, T ∈ [0, 5] MK, vx ∈ [−50, 50] km s-1, and Q ∈ [0, 1]. The clumps, visible as elliptical spots in density distributions, are circular but appear elongated due to the compression of the vertical direction for visualization purposes. |
| In the text | |
 |
Fig. 11 Density, temperature, horizontal velocity, and the fluid tracer for models ClLg20 (left panels) and ClSm500 (right panels), which assume a fully clumped accretion stream. The plotted value ranges are: ρ ∈ [10-14, 10-12] g cm-3, T ∈ [0, 5] MK, vx ∈ [−50, 50] km s-1, and Q ∈ [0, 1]. |
| In the text | |
 |
Fig. 12 Emission-measure weighted temperature for the models that assume isolated clumps (left panels) and the a fully clumped stream (right panels). |
| In the text | |
 |
Fig. 13 Spatial distribution of the temperature and of the horizontal velocity component for the models that consider an energy flux in the chromosphere. Plotted ranges: T ∈ [0, 5] MK, vx ∈ [−5, 5] km s-1, and Q ∈ [0, 1]. |
| In the text | |
 |
Fig. 14 Emission-measure weighted temperature for the models that consider fluctuations in the chromosphere (top three) and for the case of an oblique surface of impact (bottom). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.