EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 557 (September 2013) A&A, 557 (2013) A27 Full HTML
Free Access
Issue
A&A
Volume 557, September 2013
Article Number A27
Number of page(s) 13
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201321792
Published online 20 August 2013

© ESO, 2013

1. Introduction

One of the challenges in stellar astrophysics is to determine the internal structure of stars. This can be done by studying their pulsation spectrum, a technique known as asteroseismology. The pulsations of some classes of stars, such as the Sun and solar-type stars, as well as the white dwarfs, can be interpreted by using the asymptotic theory of non-radial pulsations (Tassoul 1980; Unno et al. 1989). Their pulsation modes can then be precisely identified, leading to the asteroseismological determination of the stellar structure.

Mode identification is more difficult for δ Scuti stars because they are located at the intersection between the classical instability strip and the main sequence in the HR diagram, a region where the asymptotic theory of non-radial pulsations is invalid due to low-order modes (complicated by avoided crossing and mixed modes). Although there are examples of mode identification based on long-term ground-based observations (e.g. FG Vir – Breger et al. 2009; 44 Tau – Lenz et al. 2008), only a few modes have been identified by comparing the observed frequencies with modelling.

On the theoretical side, Balona & Dziembowski (1999) predicted the observation of a larger number of high-degree modes and new characteristics once the δ Scuti stellar light variations are measured at the millimagnitude (mmag) level. The space missions, MOST (Walker et al. 2003, Matthews et al. 2004), CoRoT (Baglin et al. 2006), and Kepler (Borucki et al. 2010, Koch et al. 2010) resulted accordingly in detecting of a large number of localized peaks in the Fourier power spectra of the stellar light curves but surprisingly in the detection of stars with limited frequency content, too, in both the low-amplitude and high-amplitude δ Scuti stars, as we now discuss.

Concerning the low-amplitude δ Scuti stars (LADS), HD 50844 (Poretti et al. 2009), HD 174936 (García Hernández et al. 2009), and HD 50870 (Mantegazza et al. 2012) showed an extremely rich frequency content of low-amplitude peaks in the range 0–30 d-1. A similar dense distribution was obtained in KIC 4840675 (Balona et al. 2012a). However, KIC 9700322 (Breger et al. 2011), one of the coolest δ Scuti stars with Teff = 6700 K, revealed a remarkably simple frequency content with only two radial modes, and a large number of combination frequencies and rotational modulations. Based on MOST data, Monnier et al. (2010) identified 57 distinct pulsation modes in α Oph above a stochastic granulation noise.

Among the high-amplitude δ Scuti (HADS) stars, nearly all the light variation of V2367 Cyg (Balona et al. 2012b) is attributed to three modes and their combination frequencies. However, several hundred other frequencies of very low amplitude are also detected in the star, the effective temperature of which is Teff = 7300 K. However, twelve independent terms beside the radial fundamental mode and its harmonics up to the tenth were identified in the light of CoRoT 101155310 (Poretti et al. 2011). Regarding the linear combinations of modes, only 61 frequencies were found down to 0.1 mmag. A much smaller number of low-amplitude modes were thus reported for this HADS star, although it has the same effective temperature as V2367 Cyg. As the examples show, the large number of low-amplitude modes were detected by various space missions, and in both of the largest subgroups of δ Scuti stars.

The question that therefore arises is the following. Are we really detecting the hundreds of excited modes predicted by theory, or is there a different cause that would explain the variety of observations? Although an investigation of the stellar energy balance proved that δ Scuti stars are energetically and mechanically stable even when hundreds of pulsational modes are present (Moya & Rodriguez-Lopez 2010), the richness can also be interpreted as non-radial pulsation superimposed on granulation noise (Kallinger & Matthews 2010).

It thus seems that we have reached a level of precision where the periodicities stemming from different physical processes can make the interpretation quite difficult. The appearance of the non-radial modes and granulation noise seem to wash out the physical separation of the LADS and HADS groups. It may be that only the selection mechanism of the excited modes is different in the two groups. However, we do not exactly know the nature of the selection mechanism. Any step towards understanding the selection mechanism of non-radial modes in δ Scuti stars would therefore be very valuable. A meaningful direction is to find some regularities, if there are any, among the increased number of observed frequencies based on a promising parameter such as the frequency spacings.

Some regularities in the spacings of δ Scuti stars were previously used from both the observational and the theoretical sides. Historically, radial fundamental and first and second overtones were reported (Wizinowich & Percy 1979; López de Coca et al. 1987; Poretti et al. 1992), and an additional radial fundamental to first overtone period ratio was found in 44 Tau. The latest modelling (Lenz et al. 2010) has confirmed the existence of the radial fundamental and first overtone among the observed frequencies, but the previously interpreted second overtone turned out to be an ℓ = 1, p3 mode. The additional radial sequence is identified as ℓ = 1, p1, and p2 modes. They are interpreted as trapped modes, the non-radial counterparts of radial modes (Lenz et al. 2008). The regular sequences can be used for a more accurate characterization of the general properties of A-F pulsating stars. García Hernández et al. (2009) interpreted the quasi periodicities in the frequencies as a signature of the large separation. In the following, we present frequency analyses for the δ Scuti star CoRoT 102749568 and an extended search for the regularities in the frequency spacings.

2. Observations and data processing

The CoRoT target 102749568 was discovered to be variable in the framework of a CoRoT PECS project. It is identified with the No. 211 in the field of HD 292192. We could detect a frequency of 8.70 d-1 (± 1 d-1 alias uncertainty) and amplitude of 0.02156 mag, but no other periodicity was found in the short discovery run.

CoRoT 102749568 (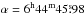, , 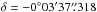at epoch: 2000) was observed during the first long run in the anti-centre direction (LRa01) from October 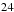, 2007 to March 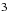, 2008 which means over 131 days. According to the Exo-Dat2, the CoRoT/Exoplanet input catalogue (Deleuil et al. 2009), its brightness and colour index were B = 15.006 and B−V = 0.598, and the spectral type and luminosity class are A5 IV (SED). Additional r and i values are given as 14.145 and 13.777 magnitudes. The Exo-Dat catalogue gives Teff = 7091 K for the temperature and E(B−V) = 0.45 for the colour excess. The JHK 2MASS values are 13.128, 12.912, and 12.802 mag. Contamination factor is rather low, less than 1 percent. The star is a δ Scuti type pulsator with a high probability (70%, Debosscher et al. 2009). Other possibilities are an sdBV type (11%) or an elliptical variable (9%), but colour indices and short period, respectively, ruled out these hypotheses. CoRoT observations were supported by ground-based multi-colour follow-up observations and spectroscopy.

2.1. Raw data

Corresponding to the generally used eight-minute time sampling on the exofields, 21 219 measurements were gathered and presented to us on N2 (science grade) level after reduction with the CoRoT pipeline (Samadi et al. 2006; Auvergne et al. 2009). We only used the valid zero-flag measurements (15 423, 72.7%). CoRoT 102749568 was observed in three CoRoT colours. Some additional obvious outliers were also omitted (15 252, 71.9%) from each colour. The CoRoT colour channels are described in detail by Paparó et al. (2011). In agreement with the CoRoT colour definition, the flux values are the highest (≈70 000 units) in red, about 15 000 units in green, and about 21 000 units in blue channels. The CoRoT colours were successfully applied to stars (CoRoT 101155310 – Poretti et al. 2011 and CoRoT 102781750 – Paparó et al. 2011) and to exoplanets (Borsa & Poretti 2013). In this paper we compare only the “CoRoT colour indices” to our multi-colour photometry. The white light fluxes that were summed up from the three colour channels yield the highest precision. A moving boxcar method (Chadid et al. 2010) was used to get rid of the slight trends and a few jumps in each colour. At the same step we converted the fluxes to magnitude. We also transformed the JD times to barycentric Julian dates in barycentric dynamical time (BJDTDB) using the applet of Eastman et al. (2010). The quality of the white light curve obtained by CoRoT is given in Fig. 1. We explain the least-squares solutions in Sect. 3.1.

thumbnail Fig. 1

Light curve of CoRoT target 102749568 (in white light) and fit with 3 (dashed line) and with 67 frequencies (continuous line).

2.2. Multi-colour photometry from the ground

We obtained multi-colour photometric data on CoRoT 102749568 at the Piszkéstető mountain station of Konkoly Observatory. Observations were performed on seven nights in winter of 2010–11 and on four nights in winter of 2011–12. The observations were made with a Princeton Instruments VersArray:1300B back-illuminated CCD camera attached to the 1-m RCC telescope and using standard BVRI filters. Table 1 contains the journal of observations. The ground-based observations confirmed that the target was not contaminated by any other star in the environment. We carried out the photometric reductions by using standard IRAF3 packages. After the aperture photometry of the field stars, we determined their instrumental colour indices and checked whether the light curves of the possible comparison stars were free of any instrumental effects or variability. Finally we selected two stars as comparisons (USNO-B1.0 0899-0101486 and USNO-B1.0 0899-0101543) and used their average light curve for the differential photometry. Their average instrumental b − v and v − i colour indices both differ from the variable stars’s with ≈0.06 mag.

Table 1

Journal of ground-based photometric observations on CoRoT 102749568 obtained in the B band.

We transformed the differential light curves to the standard Johnson-Cousins system using standard field observations. Finally we transformed the JD observational times to BJDTDB. Figure 2 presents the result of one night’s observations.

thumbnail Fig. 2

BVRI light curve obtained on the second observing night at Piszkéstető.

We determined the zero-point BVRI magnitudes of CoRoT 102749568 by calculating the comparisons’ BVRI values and obtained B = 15.018 ± 0.015, V = 14.392 ± 0.011, R = 13.919 ± 0.011, and I = 13.510 ± 0.019. These values are in good agreement with the ones given by the first version of Exo-Dat: B = 15.006 ± 0.059 and V = 14.408 ± 0.049.

3. Pulsational characteristics

3.1. Frequency analysis of the CoRoT data

A standard frequency analysis was independently done for each colour by the software packages MuFrAn (Kolláth 1990) and SigSpec (Reegen 2007). Investigations for amplitude, phase variability, significance, and errors were obtained with Period04 (Lenz & Breger 2005) and the photometry moduls of FAMIAS (Zima 2008). FAMIAS was also used to determine the phase differences and amplitude ratios from the CoRoT and ground-based multi-colour light curve for mode identification.

The different software packages resulted in the same solution concerning the frequencies with higher amplitude than 0.15 mmag. This limit represents the traditionally used S/N = 4.0 (Breger et al. 1993) significance limit. The SigSpec code down to the suggested value of the sig parameter (5.0) resulted in 81 peaks in r (σ = 0.018 mmag), 50 peaks in g, 52 peaks in b colours (0.03 mmag), and 94 frequencies in white light (0.017 mmag). Table 9 lists the 94 frequencies, their amplitude, phase and signal-to-noise ratio values, and the amplitudes and phases of the corresponding peaks in the CoRoT colours. The formal errors calculated by Period04 are given in parentheses.

thumbnail Fig. 3

Spectrum at different steps of the frequency search process: a) original spectrum, b)–f) show the spectrum after subtracting 3,11,16,41, and 67 peaks, respectively. The residual spectrum is presented until 55 d-1 and the significance level is also given over the range.

To achieve the highest probability of finding the regularities between the peaks, we present our frequency analyses on the white light results, where the low-amplitude, probably non-radial modes were more clearly obtained. The 0.0076 d-1 Rayleigh frequency of the whole data set guaranteed that the frequencies were properly resolved. The different steps of the period searching process is shown in Fig. 3. For better visibility, only the 0–25 d-1 range is displayed in the first five panels, since there are only orbital peaks above the noise level out of this range. Panel a gives the original spectrum dominated by a single high-amplitude peak at 9.70197 d-1 and two lower amplitude peaks at 9.93909 and 11.64346 d-1 values. Panels b, c, d, e, and f show the spectrum after subtracting 3, 11, 16, 41, and 67 frequencies, respectively. The residual spectrum in panel f is presented in the 0–55 d-1 region and the significance level is also given over the range. After excluding the possible linear combinations, 52 independent frequencies were found.

Table 2 gives the list of these 52 independent frequencies. The amplitudes and phases of the blue, green, and red colours are presented in addition to those in white light. The fits in Fig. 1 with 3 and 67 frequencies nicely show that most of the pulsational energy is concentrated in the first three modes. The remaining frequencies give only minor contribution to the light variation but we are able to detect them due to the high-precision measurements. The low-amplitude modes facilitate the detection of any kind of systematic spacing or other regularities among the frequencies.

The frequencies are not randomly distributed, as shown in Table 3. The mode density (8–10 modes/d-1) is significantly higher than the typical value for δ Scuti stars (5/d-1) given by Balona & Dziembowski (2011). These groups contain 32 modes, which means 63% of the independent modes.

Table 2

The 52 independent frequencies of CoRoT 102749568 to the traditional (S/N = 4.0) significance limit.

Possible linear combinations or g modes are shown in Table 4. The numbering of frequencies are the missing ones in Table 2 according to the decreasing amplitudes. The sum, differences, and harmonics are the typical linear combinations. Four frequencies show almost equidistant spacing in the 22–38 min range. Although it is near to the spacing of g modes in CoRoT 105733033, a δ Scuti/γ Doradus hybrid star (44.24 min, Chapellier et al. 2012) and near radial period ratios of two pairs of frequencies are also noticed, we are not convinced of the hybrid nature of CoRoT 102749568.

thumbnail Fig. 4

Frequency spacing of the 52 independent frequencies determined in the white light CoRoT data. The arrows denote the local maxima at the following frequency spacing values: 0.2034, 0.6619, 0.8470, 2.2077, and 2.7158 d-1.

We interpret the regularities of the linear combinations as reflecting the regularities of the p modes. Amplitude variability was checked on 2-3-5-10 day-long subsets. No systematic variation was found for the first 20 frequencies.

3.2. Regular spacing of modes

The search for regular spacings was suggested by pairs of frequencies having very similar ratio to the radial period ratio (0.77). Following the method used by Handler et al. (1997) and García Hernández et al. (2009), we investigated the periodicities in the 52 independent frequencies determined in the white light CoRoT data. The input data were the frequencies in the 5.6–22.7 d-1 region. The corresponding Nyquist period was 7.92394 d, which means that the spacing was properly resolved above a 0.13 d-1 value. The ordinate unit of the input data of this Fourier analysis is frequency, therefore the dimension of the Nyquist limit is time. The resulting FT is shown in Fig. 4. The highest amplitude peaks are at 0.2034, 0.6619, 0.8470, 2.2077, and 2.7158 d-1, suggesting very definite spacing amongst the frequencies. We call the attention to the broad double peak at the large value spacing. In general, the echelle diagram is used in the cases of strictly equidistant spacing (e.g. solar type oscillation). However, in the non-asymptotic regime, the echelle diagram is not the best tool for presenting the regularities4, at least for the whole set of frequencies. Nevertheless, the systematic spacing leads to regular patterns of the frequencies, for the highest amplitude ones.

Pattern recognition is a well-known technique that was successfully applied to white dwarf stars (Winget et al. 1991, 1994; Handler 1998). We present in Fig. 5 the frequency versus frequency difference diagram as a new tool for representing the patterns when the frequencies do not show strictly equidistant spacing. Along with the central peaks of the main groups (Table 3), dominant peaks of some less dense groups were also included (marked by boldface in Table 2). The structure of Fig. 5 is described in the caption. The diversity of the frequency differences clearly show the non-equidistancy that is most remarkable in the large separation region. Nevertheless, it gives very important details.

We can distinguish three sequences of modes connected to each other by the large separation. The different sequences cross each other, and are interweaved. The highest frequency peak at f13 = 17.595 d-1 is not included in any of these sequences. From a theoretical point of view, the expected large separations of δ Scuti stars in their last third of time in the MS range from 2.15 d-1 to higher values. Accepting the large frequency differences as the large separation between the consecutive radial orders, we distinguished three sequences containing three consecutive radial orders in each sequence. Three sequences mean that modes with three different ℓ values are excited. The labelling of the frequencies in the left part of Fig. 5 represents this conclusion. Since the frequency pairs in Sequence 1 (Table 5) have radial period ratios that are acceptable for the radial overtones, the zero point of the mode identification is fixed at the first label: l1,n1 = 0,0. This means that we identify the frequency at 7.54062 d-1 as the radial fundamental mode. The members of sequences, frequency differences between the members, period ratios, and the mode identification are summarized in Table 5.

Table 3

Grouping around 6 high-amplitude frequencies.

Table 4

Possible combination frequencies of CoRoT 102749568 or g-modes.

thumbnail Fig. 5

Patterns recognized among the highest amplitude modes are presented. The horizontal dashed lines give the frequencies marked by boldface in Table 2. The frequency differences corresponding to the dominant spacings in Fig. 4 are marked by vertical lines between the given frequencies at the actual values. Groups of spacing are divided by vertical dotted lines and labelled as low, intermediate, and large separations. Different sequences in the large separation are plotted by continuous, large dashed, and small dashed lines. The members of sequences are labelled by different ℓ values and consecutive radial orders (n) in the left part.

Following the general labelling we can state that the intermediate spacings appear between the frequencies with different ℓ values, either between the consecutive or the same radial orders. In the non-asymptotic regime we do not see the comb-like distribution of modes with odd and even ℓ values. However, we can find some regularities in the intermediate value spacing, too. In Table 6 the frequencies are listed in the order of increasing values. The identification based on the large separation is also given, together with the intermediate separation of the consecutive frequencies. The frequency difference is given in the line of the higher frequency value.

Larger and smaller intermediate separations regularly follow each other, although the values are not the same. The higher values (such as 1.124, 1.487, and 1.505 d-1) appear between the same radial orders of the ℓ = 1 and ℓ = 0 modes. The higher values are followed by lower values (0.817, 0.508, and 0.443 d-1) of the consecutive radial orders of ℓ = 2 and ℓ = 1 modes. The next set of lower values (0.606, 0.586, and 0.818 d-1) belong to the second consecutive radial orders of the ℓ = 0 and ℓ = 2 modes. Comparing the direct identification of nine frequencies based on the large separation (Table 5), we presented here the identification of 12 modes. The regular sequence of the larger and smaller intermediate separations allowed us to identify two modes in the large gap between 14.243 and 16.777 d-1 and the highest value frequency in Fig. 5 that was not included in any of the sequences. These identifications are marked by italics in Table 6. The large separations of these modes to the consecutive radial orders (2.5 or 2.84 d-1 for ℓ = 0 modes and 2.41 d-1 for the ℓ = 1 modes) falls within the large-separation range.

The observational explanation of the low-value spacing is not obvious. In Fig. 5 we present only those spacings that are around the central frequencies as doublets or triplets. A very pronounced example is a double peak at 10.82563 and 10.60715 d-1 with the same amplitudes. The triplet arrangement of the low-value spacings around the 9.70197 d-1 dominant mode that we identified as the radial first overtone questions the interpretation as a rotational splitting.

The most remarkable result of our frequency analyses is the identification of twelve modes using nothing else than the frequency values and our general knowledge of the pulsation.

Table 5

Three sequences are localized according to the largest spacings.

thumbnail Fig. 6

Phase differences and amplitude ratios obtained for the largest amplitude frequencies in different band passes, b and r CoRoT colours, and Johnson–Cousins BI.

3.3. Multi-colour mode identification

It is well-known that phase differences and amplitude ratios obtained in different bandpasses are correlated with the ℓ values (see e.g. Watson 1988). Although CoRoT colours are not calibrated, we tried to use the amplitude and phase differences of the modes between b and r colours for the mode identification. Figure 6a shows the first ten largest amplitude modes in the (φb − φr, Ab/Ar) plane. All of them, except f10, have negative phase differences, though f5 and f7 are close to zero. A positive value implies an l = 0 mode, but taking the error bars into account, we cannot state unambiguously that we see radial mode(s), even in the case of f10. Additionally, f10 is only a member of the group centred on the higher amplitude peak at 8.307 d-1.

The three largest amplitude modes dominating the CoRoT dataset can be found by our BVRI data as well. Table 7 summarizes their amplitude, phase, and S/N values. As the follow-up observations show, the 9.702 d-1 frequency remained the dominant one in the 2011/12 observing season. The amplitude of 11.643 d-1 frequency became larger than the second highest amplitude mode in CoRoT observation.

Table 6

Mode identification of 12 modes based only on the frequency spacing.

Table 7

Amplitude, phase, and S/N values of the CoRoT dataset’s three largest amplitude modes derived by the multi-colour, ground-based data.

All colours (Balona & Evers 1999; Garrido 2000) and the B−V colour index were used to place the three modes on the phase difference versus amplitude ratio plane. Unfortunately, the location of modes are different on the different planes, and the error bars are rather large, especially for the colour index. The phase difference of the dominant mode f1 gives a low negative value both in the B vs. V and in the B vs. R planes. In the B vs. V plane, f2 is close to it, but in the B vs. R plane, f3 is close to f1. The most definite arrangement of modes was obtained on the (φB − φI, AB/AI) plane (Fig. 6b). A positive phase difference of f1 is obtained, and even the error bar is in the positive region, and f2 and f3 are well-separated in the negative region. It is suggested that f1 is a radial mode (ℓ = 0), while f2 and f3 have different ℓ values.

4. Stellar parameters

4.1. Spectroscopy

A low-resolution spectrum R = 1300 of CoRoT 102749568 was acquired in January 2009 using the AAOmega multi-fibre spectrograph mounted at the 3.9-m telescope of the Australian Astronomical Observatory. We refer the reader to Sebastian et al. (2012) and Guenther et al. (2012) for details on the instrument set-up, observing strategy, and data reduction. By comparing the AAOmega spectrum with a grid of suitable templates, Guenther et al. (2012) classified CoRoT 102749568 as an F1 IV star. A visual inspection of the AAOmega spectrum revealed the presence of a moderate Hα emission (FWHM = 450 mÅ), whose nature will be discussed later.

Two high-resolution spectra of CoRoT 102749568 were obtained on two consecutive nights in January 2013 using the High Efficiency and Resolution Mercator Echelle Spectrograph (HERMES; Raskin et al. 2011) mounted at the 1.2-m Mercator telescope of Roque de los Muchachos Observatory (La Palma, Spain). We used the 2.5″ fibre, which provides a resolving power of R = 85   000 and a wavelength coverage of about 3800–9000 Å. The exposure time was set to 1800 and 3600 s on the first and second nights, respectively. The data were reduced using the automatic data-processing pipeline of the instrument, which includes bias subtraction, flat fielding, order tracing and extraction, wavelength calibration, and cosmic-ray removal. The two epoch spectra were corrected for barycentric motion and combined into a single co-added spectrum having a S/N ratio of about 10, 15, and 20 per pixel at 5000, 6000, and 8500 Å, respectively. The HERMES data revealed a rapidly rotating star with a projected rotational velocity of v sin i⋆ = 115 ± 20 km s-1. No radial velocity variation – at a level of ~4 km s-1 – was found between the two epoch spectra, which suggests that CoRoT 102749568 is most likely not a short-period binary system. The low S/N of the co-added spectrum, along with the relatively high v sin i⋆ did not allow us to perform a meaningful spectral analysis. Nevertheless, the high resolution of the HERMES data allowed us to investigate the nature of the Hα emission better. We found that the latter is relatively narrow (FWHM = 0.60 Å) and blue shifted by ~0.5 Å with respect to the core of the Hα absorption line, suggesting a non-stellar origin.

We used the calibration from Straizys & Kuriliene (1981) to convert the F1 IV spectral type of CoRoT 102749568 into effective temperature (Teff) and surface gravity (log g). Error bars were estimated taking the uncertainty in the spectral classification reported in Guenther et al. (2012) into account. We then refined the effective temperature and surface gravity by fitting the AAOmega spectrum with a grid of Kurucz stellar models (Kurucz 1979), constraining the Teff – log g parameter space around the previously derived values. Assuming a solar metallicity, we obtained Teff = 7000 ± 200 K and log g = 3.75 ± 0.25.

To estimate stellar mass, radius, luminosity, and age, we compared the location of the star on a log g vs. Teff H-R diagram with the Padova evolutionary tracks and isochrones from Girardi et al. (2000), as shown in Fig. 7. We obtained a stellar mass of M⋆ = 1.90 ± 0.35  M⊙ and a stellar radius of 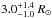, with a luminosity of 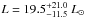and an age of 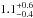Gyr.

thumbnail Fig. 7

Surface gravity vs. effective temperature diagram of CoRoT 102749568 (blue dot with error bars). The Girardi et al. (2000) evolutionary tracks for 1.4, 1.6, 1.9, 2.2, and 2.5 M⊙ are over-plotted with continuous lines. Both the zero-age main sequence line, and the isochrones for 1.1 and 1.8 Gyr are shown with dotted lines.

thumbnail Fig. 8

Dereddened SED of CoRoT 102749568. The best-matching NextGen synthetic spectrum is overplotted with a light blue line. The W3 (5.8 μm) and W4 (8 μm) WISE magnitudes were not used to estimate reddening and distance.

Table 8

Physical parameters of CoRoT 102749568 determined from spectroscopic and photometric observations and modelling.

The interstellar extinction (Av) and distance (d) to CoRoT 102749568 were derived following the method described in Gandolfi et al. (2008). We merged the Konkoly optical photometry with the infrared 2MASS and Wise data and built up the spectral energy distribution (SED) of the target star. The interstellar extinction was then derived by fitting simultaneously all the colours encompassed by the SED with synthetic magnitudes, as obtained from a NextGen model spectrum (Hauschildt et al. 1999) having the same photospheric parameters as the target star. We excluded the W3 (5.8 μm) and W4 (8 μm) WISE magnitudes as they are only upper limits. Assuming a black body emission at the star’s effective temperature and radius, we found Av = 0.8 ± 0.1 mag and 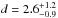Kpc. The dereddened SED of CoRoT 102749568 is shown in Fig. 8 along with the NextGen synthetic spectrum. The Wise data points at 5.8 μm and 8.0 μm show an apparent infrared excess with respect to the expected photospheric emission. We believe that this excess, along with the Hα emission detected both in the AAOmega and HERMES data, is caused by the strong background contamination arising from the nearby H II region Sh 2-284, on which CoRoT 102749568 is spatially projected.

Nevertheless, we checked the possibility that our target belongs to Sh 2-284, whose heliocentric distance is stated in the literature between 4 Kpc (Cusano et al. 2011) and 6 Kpc (Turbide & Moffat 1993). While the latter clearly rules out a cluster membership, the former is consistent within ~1σ with our determination of the heliocentric distance of CoRoT 102749568 (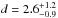 Kpc). However, the F-type stars listed by Cusano et al. (2011) are three to four magnitudes fainter than our target star. This suggests that CoRoT 102749568 is most likely a foreground object with respect to Sh 2-284.

4.2. Multi-colour photometry

Empirical relations are widely used to constrain some physical parameters. The period-luminosity relation for δ Scuti stars connects the pulsation to the stellar physical parameters. We can use it in two way. Knowing the period of the radial fundamental mode, we can get the physical parameters, however, if we know the physical parameters from other source (i.e. spectroscopy), then we can use the relation for finding the period of the radial fundamental mode and confirm the tentative mode identification suggested by multi-colour photometry. Knowing the physical parameters from spectroscopy, we followed the second way.

According to Figs. 6b and 6a the f1, f10, f4, f3, f5, and f7 frequencies could be radial modes. We inserted the period values in the period-luminosity relation of Poretti et al. (2008),

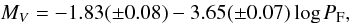and MV = 1.772, 1.539, 1.526, 2.061, 1.749, and 2.141 mag were obtained, respectively. Considering these values and the atmospheric parameters determined by spectroscopy, CoRoT 102749568 can be found both in the Teff–MV and Teff–log g plane near the red edge of the observed instability strip (see e.g. McNamara 2000, Uytterhoeven et al. 2011) and represents an evolved star from the zero-age main sequence. CoRoT 102749568 is obviously outside of the typical location of the HADS stars.

The luminosity, radius, and mass of CoRoT 102749568 were derived using a bolometric correction of BCV = 0.031 (Flower 1996; Torres 2010). We got R⋆ = 2.626, 2.923, 2.940, 2.298, 2.654, and 2.215 R⊙, M⋆ = 1.407, 1.744, 1.765, 1.078, 1.438, and 1.001 M⊙, and L⋆ = 14.849, 18.405, 18.626, 11.377, 15.175, and 10.566 L⊙ values.

Comparing these values to the luminosity, radius, and mass obtained from spectroscopy, we conclude that the f3 = 11.643 and f7 = 12.248 d-1 frequencies are definitely excluded as radial fundamental modes. The f10 = 8.375 d-1 and f4 = 8.307 d-1 frequencies give the closest values to the spectroscopic ones, but the dominant mode’s (f1 = 9.702 d-1) values are practically in the error bar, which means the dominant mode can be a radial mode. The closest values obtained from f10 and f4 suggest that the dominant mode maybe a radial first overtone, supporting the f26 = 7.5406 d-1 frequency as radial fundamental mode. The stellar parameters calculated from f26 as a radial mode are given in Table 8. The physical parameters agree with the spectroscopic value. Owing to the low amplitude of f26, the error bars of the amplitude ratio and phase differences are so large that f26 is not plotted in Fig. 6a. Based on the empirical period-luminosity relation and our spectroscopic investigation, we conclude that the dominant mode of CoRoT 102749568 is the radial first overtone and the 7.5406, 9.702, 12.248 d-1 sequence contains the radial fundamental and the second overtone modes. Table 8 summarizes the physical parameters determined from spectroscopy, photometry, and modelling of CoRoT 102749568.

5. Modelling

A detailed modelling of this star is beyond the scope of this work, but we have developed an analysis that compares different models, and some very interesting conclusions can be subtracted from a first study. We computed non-rotating equilibrium and adiabatic oscillation models. We used the evolutionary code CESAM (Morel 1997; Morel & Lebreton 2008) and the pulsation code GraCo (Moya et al. 2004; Moya & Garrido 2008) to calculate the equilibrium models and the adiabatic frequencies only with ℓ = [0, 3], respectively, for visibility reasons (Dziembowski 1977). Low-order modes must be enough to describe the highest amplitude modes. We constructed a grid of models covering the instability strip of the δ Scuti stars. We computed the range [1.25, 2.20] M⊙ in mass with a step of 0.01 and the range [− 0.52, 0.08] dex in [Fe/H] with a step of 0.2.

We then selected the only models fulfilling the spectroscopic Teff and log g displayed in Table 8 and additionally let the metallicity of the models move in the range [− 0.1,0.1] dex. This additional degree of freedom has a low impact on the determination of the physical characteristics of the models fulfilling observations. Our main goal was to check the spacing between 2–3 d-1 given in Fig. 4. According to García Hernández et al. (2013) this can be the signature of the large separation. Taking into account that the rotation velocity deduced in Sect. 4.1 has a frequency also in this region, we cannot decide that the two peaks between 2–3 d-1 are the consequence of the non-equidistant value of the large separation or one of them is a consequence of the rotation. The width of the peaks is an additional source of uncertainty. Therefore, we decided to be conservative and estimated that the large separations can be in the range [2.1, 2.75] d-1 for the modelling, but it could be half of or double this value.

After modelling we find that there are no models with the observed Teff, log g, and near solar metallicity with large separations in the ranges [1.05, 1.37] d-1 and [4.2, 5.5] d-1. Therefore, the peaks in Fig. 4 can be a direct measurement of the large separations. All models fulfilling the observed photometric uncertainty box, solar metallicity, and large separations in the range [2.1, 2.75] d-1 have physical parameters listed in Table 8. Here we can see that this new observable mainly constrains log g and related quantities.

Another possible source of information is the peak around 0.2 d-1 in Fig. 4. As the star evolves, its internal structure changes, and it affects the pulsational modes. Some effects appear such as the avoided crossing. This avoided crossing locally destroys any regular pattern at any given spherical degree ℓ. Therefore, as the average large separation is similar for every ℓ, the avoided crossing does not have a strong impact here, but other useful relations like the small separations are highly affected by this effect. Therefore, we do not expect an easy identification of the effect of avoided crossing and the identification of this spacing as a signature of the small separations is unlikely. Nevertheless, a comprehensive modelling must be done in order to finally discard this possibility or to claim that this is the first observational probe of the small seprations in a δ Scuti star.

This comprehensive modelling requires including of the effects of rotation. Assuming the physical parameters extracted with the FT method, the minimum possible value for the rotational velocity at equator would imply a deformation of the star that makes it necessary to use non-peturbative techniques to calculate the oscillations. Although the current non-pertubative methods predict no significant effects on large spacings, they predict a redistribution of the modes that is slightly different to pertubative predictions (Ligniéres et al. 2006; Reese et al. 2006). This combination of both methods (FT with non-rotating models, and non-perturbative oscillations based on 2D models) should be able to provide more insight into the mode identification for the present star.

6. Conclusions

The CoRoT δ Scuti star 102749568 shows only a limited number of peaks. The 52 independent modes are in the region of the radial and non-radial modes typical of δ Scuti stars. Both the observation and the non-rotating equilibrium and adiabatic oscillation models show the grouping of the frequencies and allow the determination of the large separation [2.1–2.75] d-1 in a δ Scuti star in the non-asymptotic regime.

The excited modes reveal an unexpected regular arrangement that allowed us to identify 12 modes based only on the observed frequencies. Five consecutive radial orders of the radial modes (from n = 0 to n = 4) are excited besides the four consecutive radial orders of ℓ = 1 and three consecutive radial orders of ℓ = 2 non-radial modes. The identification of some modes were extrapolated on the basis of the extreme regularity. Multi-colour photometry confirmed the identification of the highest amplitude modes. Physical parameters were derived from spectroscopy that allowed the inverse application of the period-luminosity relation. No disagreement was found with the observational identification.

The 9.70197 d-1 dominant mode is observationally identified as the radial first overtone (ℓ = 0, n = 1) mode but the preliminary model including low-value rotational effects gives g3 ℓ = 2 identification for it. The latter identification is consistent with the triplet structure found around the dominant mode. However, this identification must be taken with caution because it represents a minimization of the modelling, which requires refining rotation effects. It also modifies the other physical parameters considered (metallicity, convective parameters, etc.) to which the identification is likely quite sensitive. The radial fundamental (7.54062 d-1), the radial second overtone (12.24848 d-1) and the ℓ = 2, n = 1 (14.24347 d-1) modes have the same identification from the observation and from modelling.

The low periodicities found are too low to be connected with rotation; however, we cannot excluded that they are due to some rotational effects (like asymmetries). With our current tools (perturbative methods for the oscillation computation), those effects cannot be properly analysed (the rotational velocity of the star is in the limit of validity of pertubative methods) and non-peturbative techniques would be necessary. Interestingly, even for deformed stars, the effect of rotation is very small on large spacings, so the present modelling in combination on 2D equilibrium models and non-peturbative techniques for the oscillation is potentially a source of important information on the mode identification and on the internal rotation of the star.

The unexpected regularity of a δ Scuti star that is out of the asymptotic regime shows that the quasi-equidistancies can be found among the frequencies of space data. The potential of the mode identification based only on the frequency regularities is highly valuable. The space missions observed a lot of stars and the capacity of the ground-based spectroscopy was not enough for mode identification on high-resolution spectra. The tentative mode identification in each star observed in the non-asymptotic regime would make a step toward discovering the real nature of the mode-selection mechanism.

Online material

Table 9

The 94 frequencies of CoRoT 102749568 obtained in white light, above the sig parameter 5.0 calculated by SigSpec.

3

IRAF is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation.

Acknowledgments

M.P., Zs.B., J.M.B., and M.H. acknowledge the support of the ESA PECS project 4000103541/11/NL/KML. E.P. acknowledges financial support from the PRIN-INAF 2010 Asteroseismology: looking inside the stars with space- and ground-based observations. A.M. acknowledge the support of the projects Consolider-CSD2006-00070, ESP2007-65475-C02-02, and AYA2010-21161-C02-02, and the Madrid regional government grant PRICIT-S2009ESP-1496. A.M. acknowledge the support of the Comunidad de Madrid grant AstroMadrid (S2009/ESP-1496) and the projects AYA 2010-21161-C02-02,AYA2012-38897-C02-01, and PRICITS2009/ESP-1496. Á.S. acknowledges support from the Belgian Federal Science Policy (project MO/33/029). W.W. was supported by the Austrian Science Fonds, P22691-N16. J.C.S. acknowledges support from the Spanish Ministry through National Research grant AYA2012-39346-C02-01. D.G., E.G. are grateful to the user support group of AAT for all their help and assistance for preparing and carrying out the observations. They would like to particularly thank Rob Sharp, Fred Watson, and Quentin Parker. Based on observations obtained with the HERMES spectrograph, which is supported by the Fund for Scientific Research of Flanders (FWO), Belgium, the Research Council of K.U. Leuven, Belgium, the Fonds National Recherches Scientific (FNRS), Belgium, the Royal Observatory of Belgium, the Observatoire de Geneve, Switzerland, and the Thuringer Landessternwarte Tautenburg, Germany. This research has made use of the Exo-Dat database, operated at LAM-OAMP, Marseille, France, on behalf of the CoRoT/Exoplanet programme.

References

  1. Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Baglin, A., Auvergne, M., Barge, P., et al. 2006, in The CoRoT Mission, Pre-Launch Status, Stellar Seismology and Planet Finding, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, (Nordwijk, Netherlands: ESA Publications Division), ESA SP, 1036, 33 [Google Scholar]
  3. Balona, L. A., & Dziembowski, W. A. 1999, MNRAS, 309, 221 [NASA ADS] [CrossRef] [Google Scholar]
  4. Balona, L. A., & Dziembowski, W. A. 2011, MNRAS, 417, 591 [NASA ADS] [CrossRef] [Google Scholar]
  5. Balona, L. A., & Evers, E. A. 1999, MNRAS, 302, 349 [NASA ADS] [CrossRef] [Google Scholar]
  6. Balona, L. A., Breger, M., Catanzaro, M. S., et al. 2012a, MNRAS, 424, 1187 [NASA ADS] [CrossRef] [Google Scholar]
  7. Balona, L. A., Lenz, P., Antoci, V., et al. 2012b, MNRAS, 419, 3028 [NASA ADS] [CrossRef] [Google Scholar]
  8. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  9. Breger, M., Stich, J., Garrido, R., et al. 1993, A&A, 271, 482 [NASA ADS] [Google Scholar]
  10. Breger, M., Lenz, P., & Pamyatnykh, A. A. 2009, MNRAS, 396, 291 [NASA ADS] [CrossRef] [Google Scholar]
  11. Breger, M., Balona, L., Lenz, P., et al. 2011, MNRAS, 414, 1721 [NASA ADS] [CrossRef] [Google Scholar]
  12. Borsa, F., & Poretti, E. 2013, MNRAS, 428, 891 [NASA ADS] [CrossRef] [Google Scholar]
  13. Chadid, M., Benkő, J. M., Szabó, R., et al. 2010, A&A, 510, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Chapellier, E., Mathias, P., Weiss, W. W., et al. 2012, A&A, 540, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Cusano, F., Ripepi, V., Alcalá, J. M., et al. 2011, MNRAS, 410, 227 [NASA ADS] [CrossRef] [Google Scholar]
  16. Debosscher, J., Sarro, L. M., López, M., et al. 2009, A&A, 506, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Deleuil, M., Meunier, J. C., Moutou, C., et al. 2009, AJ, 138, 649 [NASA ADS] [CrossRef] [Google Scholar]
  18. Dziembowski, W. 1977, Acta. Astr., 27, 203 [Google Scholar]
  19. Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [NASA ADS] [CrossRef] [Google Scholar]
  20. Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
  21. Gandolfi, D., Alcalá, J. M., Leccia, S., et al. 2008, ApJ, 687, 1303 [NASA ADS] [CrossRef] [Google Scholar]
  22. García Hernández, A., Moya, A., Michel, E., et al. 2009, A&A, 506, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. García Hernández, A., Moya, A., Michel, E., et al. 2013 [arXiv:1307.2739] [Google Scholar]
  24. Garrido, R. 2000, in Delta Scuti and Related Stars, eds. M. Breger, & M. H. Montgomery, ASP Conf. Ser., 210, 67 [Google Scholar]
  25. Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Guenther, E. W., Gandolfi, D., Sebastian, D., et al. 2012, A&A, 543, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Handler, G. 1998, CoAst, 157, 106 [Google Scholar]
  28. Handler, G., Pikall, H., & O’Donoghue, D. 1997, MNRAS, 286, 303 [NASA ADS] [CrossRef] [Google Scholar]
  29. Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
  30. Kallinger, T., & Matthews, J. M. 2010, ApJ, 711, L35 [NASA ADS] [CrossRef] [Google Scholar]
  31. Koch, D. G., Borucki, W. J., Basri, G., et al. 2010, ApJ, 713, L79 [NASA ADS] [CrossRef] [Google Scholar]
  32. Kolláth, Z. 1990, Occ. Tech. Notes Konkoly Obs., Budapest, No. 1 [Google Scholar]
  33. Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
  34. Lenz, P., & Breger, M. 2005, CoAst., 146, 53 [Google Scholar]
  35. Lenz, P., Pamyatnykh, A. A., Breger, M., et al. 2008, A&A, 478, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Lenz, P., Pamyatnykh, A. A., Zdravkov, T., et al. 2010, A&A, 509, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Lignières, F., Rieutord, M., & Reese, D. 2006, A&A, 455, 607 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. López de Coca, P., Rolland, A., Garrido, R., et al. 1987, RMxAA, 15, 59 [Google Scholar]
  39. Maeder, A., & Meynet, G. 2004, A&A, 422, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Mantegazza, L., Poretti, E., Michel, E., et al. 2012, A&A, 542, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Matthews, J. M., Kuschnig, R., Guenther, D. B., et al. 2004, Nature, 430, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  42. McNamara, M. 2000, in Delta Scuti and Related Stars, eds. M. Breger, & M. H. Montgomery, ASP Conf. Ser., 210, 373 [Google Scholar]
  43. Monnier, J. D., Townsend, R. H. D., Che, X., et al. 2010, ApJ, 725, 1192 [NASA ADS] [CrossRef] [Google Scholar]
  44. Morel, P. 1997, Ap&SS, 124, 597 [Google Scholar]
  45. Morel, P., & Lebreton, Y. 2008, Ap&SS, 316, 61 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  46. Moya, A., & Garrido, R. 2008, Ap&SS, 316, 129 [NASA ADS] [CrossRef] [Google Scholar]
  47. Moya, A., & Rodriguez-Lopez, C. 2010, ApJ, 710, L7 [NASA ADS] [CrossRef] [Google Scholar]
  48. Moya, A., Garrido, R., & Dupret, M. A. 2004, A&A, 414, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Paparó, M., Chadid, M., Chapellier, E., et al. 2011, A&A, 531, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Poretti, E., Mantegazza, L., & Riboni, E. 1992, A&A, 256, 113 [NASA ADS] [Google Scholar]
  51. Poretti, E., Clementini, G., Held, E. V., et al. 2008, ApJ, 685, 947 [NASA ADS] [CrossRef] [Google Scholar]
  52. Poretti, E., Michel, E., Garrido, R., et al. 2009, A&A, 506, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Poretti, E., Rainer, M., Weiss, W. W., et al. 2011, A&A, 528, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Reegen, P. 2007, A&A, 467, 1353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Reese, D., Lignières, F., & Rieutord, M. 2006, A&A, 455, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Raskin, G., van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Samadi, R., Fialho, F., Costa, J. E. S., et al. 2006, in The CoRoT Mission Pre-Launch Status – Stellar Seismology and Planet Finding, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, ESA SP, 1306, 317 [Google Scholar]
  58. Sebastian, D., Guenther, E. W., Schaffenroth, V., et al. 2012, A&A, 541, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Straizys, V., & Kuriliene, G. 1981, Ap&SS, 80, 353 [NASA ADS] [CrossRef] [Google Scholar]
  60. Suárez, J. C. 2002, Ph.D. Thesis [Google Scholar]
  61. Suárez, J. C., & Goupil, M. J. 2008, Ap&SS, 316, 155 [NASA ADS] [CrossRef] [Google Scholar]
  62. Suárez, J. C., Goupil, M. J., & Morel, P. J. 2006, A&A, 449, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Suárez, J. C., Moya, A., Amado, P. J., et al. 2009, ApJ, 690, 1401 [NASA ADS] [CrossRef] [Google Scholar]
  64. Tassoul, M. 1980, ApJS, 43, 469 [NASA ADS] [CrossRef] [Google Scholar]
  65. Torres, G. 2010, AJ, 140, 1158 [NASA ADS] [CrossRef] [Google Scholar]
  66. Turbide, L., & Moffat, A. F. J. 1993, AJ, 105, 1831 [NASA ADS] [CrossRef] [Google Scholar]
  67. Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial oscillations of stars, 2nd edn. (Tokyo: University of Tokyo Press) [Google Scholar]
  68. Uytterhoeven, K., Moya, A., Grigahcene, A., et al. 2011, A&A, 534, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Walker, G. A. H., Matthews, J., Kuschnig, R., et al. 2003, PASP, 115, 1023 [NASA ADS] [CrossRef] [Google Scholar]
  70. Watson, R. D. 1988, Ap&SS, 140, 255 [NASA ADS] [CrossRef] [Google Scholar]
  71. Winget, D. E., Nather, R. E., Clemens, J. C., et al. 1991, ApJ, 378, 326 [NASA ADS] [CrossRef] [Google Scholar]
  72. Winget, D. E., Nather, R. E., Clemens, J. C., et al. 1994, ApJ, 430, 839 [NASA ADS] [CrossRef] [Google Scholar]
  73. Wizinowich, P., & Percy, J. R. 1979, PASP, 91, 53 [NASA ADS] [CrossRef] [Google Scholar]
  74. Zima, W. 2008, CoAst, 155, 17 [NASA ADS] [Google Scholar]

All Tables

Table 1

Journal of ground-based photometric observations on CoRoT 102749568 obtained in the B band.

In the text
Table 2

The 52 independent frequencies of CoRoT 102749568 to the traditional (S/N = 4.0) significance limit.

In the text
Table 3

Grouping around 6 high-amplitude frequencies.

In the text
Table 4

Possible combination frequencies of CoRoT 102749568 or g-modes.

In the text
Table 5

Three sequences are localized according to the largest spacings.

In the text
Table 6

Mode identification of 12 modes based only on the frequency spacing.

In the text
Table 7

Amplitude, phase, and S/N values of the CoRoT dataset’s three largest amplitude modes derived by the multi-colour, ground-based data.

In the text
Table 8

Physical parameters of CoRoT 102749568 determined from spectroscopic and photometric observations and modelling.

In the text
Table 9

The 94 frequencies of CoRoT 102749568 obtained in white light, above the sig parameter 5.0 calculated by SigSpec.

In the text

All Figures

thumbnail Fig. 1

Light curve of CoRoT target 102749568 (in white light) and fit with 3 (dashed line) and with 67 frequencies (continuous line).
In the text
thumbnail Fig. 2

BVRI light curve obtained on the second observing night at Piszkéstető.
In the text
thumbnail Fig. 3

Spectrum at different steps of the frequency search process: a) original spectrum, b)–f) show the spectrum after subtracting 3,11,16,41, and 67 peaks, respectively. The residual spectrum is presented until 55 d-1 and the significance level is also given over the range.
In the text
thumbnail Fig. 4

Frequency spacing of the 52 independent frequencies determined in the white light CoRoT data. The arrows denote the local maxima at the following frequency spacing values: 0.2034, 0.6619, 0.8470, 2.2077, and 2.7158 d-1.
In the text
thumbnail Fig. 5

Patterns recognized among the highest amplitude modes are presented. The horizontal dashed lines give the frequencies marked by boldface in Table 2. The frequency differences corresponding to the dominant spacings in Fig. 4 are marked by vertical lines between the given frequencies at the actual values. Groups of spacing are divided by vertical dotted lines and labelled as low, intermediate, and large separations. Different sequences in the large separation are plotted by continuous, large dashed, and small dashed lines. The members of sequences are labelled by different ℓ values and consecutive radial orders (n) in the left part.
In the text
thumbnail Fig. 6

Phase differences and amplitude ratios obtained for the largest amplitude frequencies in different band passes, b and r CoRoT colours, and Johnson–Cousins BI.
In the text
thumbnail Fig. 7

Surface gravity vs. effective temperature diagram of CoRoT 102749568 (blue dot with error bars). The Girardi et al. (2000) evolutionary tracks for 1.4, 1.6, 1.9, 2.2, and 2.5 M⊙ are over-plotted with continuous lines. Both the zero-age main sequence line, and the isochrones for 1.1 and 1.8 Gyr are shown with dotted lines.
In the text
thumbnail Fig. 8

Dereddened SED of CoRoT 102749568. The best-matching NextGen synthetic spectrum is overplotted with a light blue line. The W3 (5.8 μm) and W4 (8 μm) WISE magnitudes were not used to estimate reddening and distance.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.